Abstract
Since the past decade, rapid development in nanotechnology has produced several aspects for the scientists and technologists to look into. Nanofluid is one of the incredible outcomes of such advancement. Nanofluids (colloidal suspensions of metallic and nonmetallic nanoparticles in conventional base fluids) are best known for their remarkable change to enhanced heat transfer abilities. Earlier research work has already acutely focused on thermal conductivity of nanofluids. However, viscosity is another important property that needs the same attention due to its very crucial impact on heat transfer. Therefore, viscosity of nanofluids should be thoroughly investigated before use for practical heat transfer applications. In this contribution, a brief review on theoretical models is presented precisely. Furthermore, the effects of nanoparticles’ shape and size, temperature, volume concentration, pH, etc. are organized together and reviewed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
While most conventional heat transfer fluids have their limitations, development of a fluid to meet the ever-increasing demand of heat transfer fluids has become necessary. Choi et al. [1] of Argonne Laboratory proposed heat transfer fluids which are the colloidal suspension of nanoparticles (Al, Cu, Al2O3, CuO, SiC, CNT, etc.) in conventional fluids (water, ethylene glycol, engine oil, etc.), for superior heat transfer in various engineering applications. Small size and large surface to volume ratio of nanoparticles cause higher thermal conductivity, less clogging in flow channel and high heat transfer rate along with long-term stability of nanofluids, ensuring that they become the most desirable heating or cooling medium for today as well as for tomorrow.
Viscosity is an important flow property of fluids. Pumping power, pressure drop in laminar flow and convective heat transfer directly depend on the viscosity of fluids. Literally, analysis of viscosity is quite essential for determining the thermo-fluidic behavior of heat transfer fluids. Lots of research has been done in this field and it still needs more attention [2]. A number of papers have reported about the effects of particle shape, particle size, volume fraction and temperature on nanofluids’ viscosity. Wide variations exist in these studies. In addition, the effects of other factors such as surfactants, shear rate, particle aggregation, dispersion techniques, acidity or pH value have not been reported properly. The following part of this article presents an overview of the recent studies on viscosity of nanofluids.
Theoretical studies
There are some existing formulas to estimate the viscosity of nanofluids. Einstein [3] was the first to develop the nanofluid viscosity formula in 1906. His formula was based on the assumption of viscous fluid containing spherical particles at a very low volume fraction . The suggested formula is given below:
where is the viscosity of the nanofluid; \( \mu_{\text{f}} \) is the viscosity of the base fluid and \( \phi \) is the volume fraction of the particle in suspension. This formula shows a linear increase in viscosity with particle volume concentration. He considered non-interacting suspensions. This formula has some limitations, as it does not consider structure and particle–particle interaction within the solution and high particle concentrations.
In 1951, Mooney [4] proposed another model for higher concentrations of interacting spherical suspensions through the following expression:
where \( k \) is a constant, called self-crowding factor (1.35 < k < 1.91) and \( \xi \) is called the fitting parameter whose value is 2.5.
Krieger and Dougherty [5] in 1959 proposed a semi- empirical model for shear viscosity for randomly monodispersed hard spherical particles. The model is stated as:
where \( \phi_{\text{m}} \) is the maximum particle packing fraction, which varies from 0.495 to 0.54 and is approximately 0.605 at higher shear rates, and \( \eta \) is the intrinsic viscosity whose value is 2.5 for monodispersed suspensions of hard spheres.
In 1970, Nielsen [6] suggested the power law model to determine the viscosity of nanofluids of particle volume fraction more than 0.02 and the suggested mathematical expression is:
Two years after, i.e., in 1972, Batchelor [7] modified Einstein’s viscosity equation by introducing Brownian motion effect. The model was developed by considering isotropic suspension of rigid and spherical nanoparticles. His model is given as follows:
The above models are known as the classical models of nanofluids’ viscosity. By further development of mathematical modeling of viscosity, new models are developed by modifying these classical models.
In the year 1952, Brinkman [8] extended Einstein’s equation for use with moderate particle concentration. He considered the effect of addition of solute molecule to an existing continuous medium of particle concentrations less than 4 %. This correlation has more acceptance among the researchers. The empirical formula is as follows:
In 1967, Franken and Acrivos [9] developed a mathematical expression:
In 1972, Lundgren [10] proposed another equation as a Taylor series expansion of \( \phi \). This equation is referred to the reduction of Einstein’s formula:
In 1981, Graham [11] developed a generalized form of Franken–Acrivos model by introducing particle radius and inter-particle spacing that is well in accordance with Einstein’s formula for small \( \phi \). The model is expressed as follows:
where \( h \) is the inter-particle spacing and \( d_{\text{p}} \) is the radius of the particle.
In the same year, Kitano et al. [12] proposed a simple formula to predict the viscosity of a two-phase mixture:
In 1999, Bicerano et al. [13] suggested a correlation for viscosity of nanofluids. The correlation also shows the volumetric effect of viscosity:
Ward [14] offered an exponential model for up to 35 % of spherical particles as:
In 2003, Tseng and Chen [15] presented an exponential form of the effect of volume concentration upon viscosity of nickel/terpineol nanofluids:
In 2007, Avsec and Oblac [16] derived a viscosity model with the help of the proposed formula of Ward model [14] and Einstein model [1]. The expression is known as renewed Ward model:
Here, \( \phi_{\text{eff}} \) is the effective volume fraction, which can be found using the following relation derived from the model of Yu and Choi [17]:
where, h represents liquid thickness.
In 2007, Chen et al. [18] modified Krieger–Dougherty equation by considering the effects of variable packing fraction within the aggregate structure. The modified equation is presented as:
where \( a_{\text{a}} \) and \( a \) are the aggregates and primary particles, respectively, and D denotes the fractal index having a value of 1.8 for nanofluids. \( \phi_{\text{m}} \) is the maximum particle volume fraction whose value is determined experimentally.
Masoumi et al. [19] established a new theoretical model for determination of viscosity of nanofluids. Their model is based on Brownian motion of particles and is valid for alumina/water nanofluids:
where \( \rho_{\text{N}} \) is the density, \( d_{\text{N}} \) denotes the particle diameter, \( \delta \) indicates the distance between the nanoparticles and \( C \) and \( V_{\text{b}} \) are the two functions of temperature.
This model could be useful to calculate the effective viscosity in terms of particle diameter, particle volume fraction, particle density, etc.
Apart from volume fraction, temperature is very influential to viscosity of nanofluids. As a result, some correlations have been created to consider the effect of temperature on nanofluids’ viscosity.
Pak and Cho [20] developed a viscosity model based on particle volume fraction taking room temperature as reference. They reported that nanofluid viscosity was temperature dependent and viscosity decreased when temperature increased:
Kulkarni et al. [21] show temperature-dependent viscosity model for CuO–water nanofluids within a temperature range of 5–50 °C. This model shows the exponential decrease in viscosity when the temperature of the suspension is increased. The mathematical expression is given as follows:
where T is the temperature in Kelvin.
Nguyen et al. [22] also derived the following expression of temperature-dependent viscosity for particle volume fraction ranging from 1–4 %:
Namburu et al. [23] showed the relationship between viscosity and temperature in his following mathematical model valid for 1–10 % of Al2O3 nanofluids and a temperature range over \( - \) 35–50 °C:
where \( \mu_{\text{nf}} \) is the viscosity measured in centipoises (cP), A and B are two functions of particle volume fraction and T is the temperature in Kelvin.
Chandrasekhar et al. [24] proposed a mathematical expression for viscosity measurement. The expression includes contributions of electromagnetic, mechanical, as well as geometrical effects. The expression is:
where b and n are constants.
Abu-Nada [25] proposed a correlation for alumina/water nanofluids. He found viscosity as a function of temperature and particle volume fraction. He used experimental data of Nguyen et al. to develop the correlation. The correlation is:
This model was later compared with Brinkman model and it was found that Brinkman model is not fit for Nguyen et al.’s data.
Masud Hosseeini [26] developed a correlation valid only for Al2O3/water nanofluids. This empirical formula presents a dimensionless group model considering volume concentration, nanoparticle size, temperature and effect of the capping layer. They determined the parameters by the latest square regression technique. The formula is as follows:
where \( \phi_{\text{h}} \) is the hydrodynamic volume fraction of nanoparticles, d is the nanoparticle diameter, r is the thickness of the capping layer, T0 is a reference temperature, T is the measured temperature of the nanofluid and m is a factor that depends on the properties of the system (i.e., the solid nanoparticles, the base fluid and their interactions), while a, b and c are constants determined from experimental data. A summary of the viscosity models for nanofluids is given in Table 1.
In fact, no model is able to predict the exact value of viscosity of nanofluids. A broad range of variations occurs on comparing the experimental data with the theoretical values. As an example, Garg et al. [27] found four times increment in viscosity compared to Einstein viscosity law. Murshed et al. [28] also argued that no classical model could precisely predict the viscosity of nanofluids.
Experimental studies
Experimental investigation is very important for the analysis and validation of theoretical models proposed by researchers. Experimental investigation on viscosity of nanofluids reveals the rheological behavior that has equal importance in experimental as well as practical heat transfer applications. Several experiments on this particular topic show that particle shape and size, particle loading, temperature, surfactants and acidity (pH) have direct impacts on the viscosity of nanofluids. A brief review of such experimental investigations is given in the following portion of this article.
Effect of particle size and shape
The viscosity of the nanofluid suspension with the same nanoparticles varies with the particle size. Nguyen et al. [22] studied the particle size effect on the viscosity of alumina–water nanofluids. According to their observation, at 4 % particle volume concentration, 36 and 47 nm alumina/water nanofluids show almost the same viscosity and if the volume concentration is increased then fluids with bigger size nanoparticles shows higher viscosity than the smaller ones. In another literature, the same authors supported their previous experiment for higher particle fraction of 7 and 9 % [29]. According to He et al. [30], the viscosity of TiO2–distilled water nanofluids at different particle sizes (95 nm, 145 nm) increases with the increase in particle size. Figure 1 presents the increase in viscosity with the increase in particle size.
Increase in viscosity with increase in particle size [30]
However, some contradictions exist parallel to this trend. Namburu et al. [31] reported that viscosity reduced with increase in particle size for SiO2 nanoparticles. Chevalier et al. [32] also made the same statement while examining the viscosity of SiO2–ethanol nanosuspensions of three different particle sizes of 35, 94 and 190 nm. Other researchers such as Pastoriza-Gallego et al. [33], Lu and Fan [34] and Anoop et al. [35] found similar results for CuO–water and Al2O3–water nanofluids, respectively. Further, a very recent research by Agarwal et al. [36] on the synthesis and characterization of kerosene-based alumina nanofluids supported their works. In the analysis part, they explained that such trend in nanofluid behavior is because of the occurrence of higher interface resistance with fluid layer due to the presence of more surface area in case of smaller particles rather than bigger ones. Figure 2 presents the data where viscosity decreases with the increase in particle diameter.
Decrease in viscosity with increase in particle diameter [34]
The experimental analysis of Prasher et al. [37] was quite different. His result showed that nanofluid viscosity was not a function of nanoparticle diameter. They experimented with alumina nanoparticles of different diameters dispersed in propylene glycol and observed that viscosity merely changed with particle diameter. Their experimental findings are shown in Fig. 3.
Viscosity is not a function of particle diameter [37]
There are very few results available in the literature about the effect of particle shape on the viscosity of nanofluids [38, 39]. However, viscosity has strong dependence on the particle shape. Timofeeva et al. [39] reported that elongated particles increase the viscosity of nanofluids rather than spherical nanoparticles. Ferrouillat et al. [40] presented another interesting study on the influence of nanoparticle shape factor on convective heat transfer and performance of water-based SiO2 and ZnO nanofluids. They observed that a ZnO/water nanofluid with rod-shaped nanoparticles has slightly less viscosity as compared to that of polygonal particles. In case of SiO2/water nanosuspension, banana-shaped particles showed viscosity close to spherical nanoparticles. The results of their experiment are shown in the Fig. 4a, b.
a Viscosity of silica–water nanofluid; b viscosity of ZnO–water nanofluid [40]
Effect of volume concentration
A number of papers have been published on the effect of particle loading on the viscosity of nanofluids. Almost all the research showed that nanoparticle inclusion even at a low volume fraction in the host liquid increased the nanoparticle concentration and greatly increased the viscosity. Prasher et al. [37] reported on the viscosity change due to change in particle volume fraction. They observed that the viscosity of alumina–water nanofluids increased with an increase in nanoparticle volume fraction. Das et al. [41] and Putra et al. [42] reported on the Newtonian behavior of alumina–water nanofluids between 1 and 4 % particle volume concentration and showed that viscosity increased by increasing the volume concentration of nanoparticles. Duangthongsuk and Wongwises [43] noticed 4–15 % increase in viscosity of TiO2–water nanofluid with particle volume concentrations of 0.2–2.0 % within a temperature range of 15–53 °C. Chevalier et al. [32] noticed that the viscosity of SiO2–ethanol nanofluids increases with an increase in volume concentration. Schmidt et al. [44] did research on Al2O3 nanoparticles dispersed in decane and isoparaffinic polyalphaolefin (PAO) and finally reported about the same behavior of viscosity when they increased the particle volume fraction from 0.25 to 1 %. Ding et al. [45] also detected a rise in viscosity of nanofluids with the rise in CNT concentration. Chandrasekar et al. [24] studied the viscosity of alumina–water nanofluids of 0.33–5 % volume fraction and made a statement in favor of this trend. Furthermore, Naina et al. [46] examined the viscometric behavior of TiO2 nanoparticles dispersed in pure water over a volumetric concentration range of 0.5–2.5 % and temperature of 10–40 °C. For 2.5 vol % of TiO2–water nanofluids, a 50 % rise in viscosity was detected. Some researchers declared exceptional rise in viscosity with a rise in volume concentration. A detailed study can be found in references [29, 47, 48].
Thus with the addition of more particles, the effect of viscosity turns out to be detrimental to the heat transfer system. The enhancement of viscosity by increasing nanoparticle concentration is not valid for all cases.
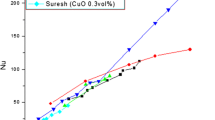
Hojjat et al. [49] observed the rheological behavior of various suspensions of Al2O3, TiO2 and CuO nanoparticles in aqueous solution of carboxymethyl cellulose at different temperatures. They found the viscosity of nanofluids and those of the base fluids to be the function of volume concentration and temperature. They noticed that the relative viscosity of Al2O3 and TiO2 nanofluids increases with increasing nanoparticle concentration, but the viscosity of CuO nanofluid was almost independent of nanoparticle concentration. Figure 5 describes the effect of volume fraction or volume concentration on viscosity of Al2O3 nanofluids.
Change in viscosity with rise in volume fraction [2]
Effect of particle size distribution
Goharshadi and Hadadian [50] described the effect of particle size distribution on the viscosity of nanofluids. According to these authors, nanofluids with a wide particle distribution have better packing ability than those of narrow particle distribution keeping constant volume fraction. This suggests that a wide distribution of nanoparticle provides more free space to move around and eventually makes the sample less viscous.
Effect of particle aggregation
Particle aggregation has no direct effect on the viscosity of nanofluids. However, due to micro-aggregation of nanoparticles, the effective volume fraction is quite higher than the actual volume fraction and leads to the rise in viscosity of nanofluids. To justify this, Chen et al. [51] introduced fractal geometry to predict the volume fraction increase. According to the fractal theory, the effective particle volume is given by:
where d and deff are diameters of the primary nanoparticles and aggregates, respectively, and D is the fractal index having typical values ranging from 1.6–2.5 for aggregates of spherical nanoparticles.
Now, it is possible to describe the measurements corresponding to water-based and glycerol-based nanofluids on modifying Krieger–Dougherty and Mooney model by replacing \( \phi \) with \( \phi_{\text{eff}} \). Duan et al. [52] conducted an investigation on the viscosity effect of 2-week-old Al2O3–water nanofluids and applied ultrasonication to measure the aggregation effect on viscosity. They indicated a rise of relative viscosity with nanoparticle aggregation and their measurement fits the modified Krieger–Dougherty model.
Effect of temperature
Evidently, temperature has an inherent relation with viscosity. The whole nanofluid research community recommends temperature as the most critical and influential parameter in this regard. The overall report indicates a very common downward trend in viscosity with an increase in temperature. As the temperature increases, the intermolecular attraction between the nanoparticles and their base fluids weakens [53]. Hence, the viscosity of nanofluids decreases with the increase in temperature. According to Andrade equation [54], the viscosity has the following relationship with temperature:
where \( \eta \) is the viscosity, T is the temperature and A and B are constants.
Vogel [55], Tamman and Filchers [56] modified Andrade equation by inserting a constant C. The modified equation is also known as the VTF equation, which is as follows:
The three parameters in this equation have clear physical meaning. A is the value of viscosity at infinite temperature and represents the energy associated with ‘cage’ confinement due to close packing of liquid molecules; C corresponds to the temperature at which viscosity becomes infinite.
This temperature is also called zero-mobility temperature, as the free volume or configurational entropy of the liquid vanishes. Goharshadi and Hadadian [57] intimated the report on the rheological properties of ZrO2–ethylene glycol nanofluid. They observed the same effect of temperature on viscosity. Additionally, the data fitted well with the VTF equation. Pastoriza-Gallego et al. [33] conducted an experiment on the viscosity of ethylene glycol-based alumina nanofluids and observed the same occurrence. Further, their data strongly follow the VTF equation.
Namburu et al. [31] reported that the rise in temperature diminishes the viscosity of nanofluids over a temperature range of –35 to 50 °C. There are other studies, which also present a similar effect of temperature on viscosity. Ferrouillat et al. [40] tested water-based SiO2 and ZnO for a temperature range of 20–80 °C. They found that viscosity decreased with an increase in temperature. Sundar et al. [58] investigated the viscosity of magnetic Fe3O4–water nanofluid within a temperature range of 20–60 °C. They found a decrease in viscosity as the temperature increased. Figure 6 presents the viscosity vs. temperature graph in which viscosity decreases with a rise in temperature.
Viscosity decreases with rise in temperature [2]
Unlike the above studies, Prasher et al. [37] and Chen et al. [18, 59] in their studies of Al2O3 and TiO2, respectively, in the temperature range of 20–60 °C, found no change in relative viscosity with increase in temperature.
Effect of pH
Wang Xian–Ju et al. [60] reported about an optimal value of pH at which the nanofluids show the least viscosity. They examined the effect of pH on dispersive stability. Sodium dodecyl benzenesulfonate (SDBS) was used as the surfactant. The pH value was controlled using hydrochloric acid (HCl) and sodium hydroxide (NaOH) in analytical grade. The least values of viscosity at weight fraction 0.1, 0.2 and 0.4 % were found to be 0.826, 0.846, and 0.865 mPa.s for alumina and 0.82, 0.838, 0.860 mPa.s for copper, respectively. Generally, the viscosity of alumina is higher than that of Cu at the same weight fraction and pH. Sediments on ion photographs (taken after 7 days) show alumina and Cu particles form agglomerates below pH 7 resulting in rapid sedimentation of particles and instability of suspensions. For alumina, pH of 7.5–8.9 and for copper pH > 7.6 show good dispersion, which stays for a long period due to higher charge on surface of nanoparticles.
Zhao Jia–Fei et al. [61] concluded that for nanoparticle diameter smaller than 20 nm, the viscosity depends on the pH of the silicon dioxide nanofluid. They observed fluctuation of viscosity between pH values from 5 to 7, especially for particle size less than 20 nm. Also for pH < 5, viscosity decreases and remains more or less constant. The authors believe the fractal dimension of aggregates and the electrical double layer of particles to be the main reasons behind this fluctuation. Figures 7 and 8 show the effect of pH on the viscosity of nanofluid suspensions.
Viscosity of nanofluids (particle diameter = 7 nm) and de-ionized water vs. pH value [61]
Effect of pH on the viscosity of nanofluids (at particle diameter = 12, 16, 20, 40 nm) [61]
Effect of the dispersion method
Different dispersion techniques can affect the viscosity of nanofluids [62]. Masuda et al. [63] measured the viscosity of TiO2 (27 nm)–water nanofluid at 4.3 % volumetric loading and noticed 60 % rise in viscosity. Wang et al. [64] observed the effective viscosity of Al2O3 (28 nm)–DIW-based nanofluids increased by 86 % for 5 % volume fraction. They used mechanical blending to disperse Al2O3 nanopowders in distilled water.
On the contrary, Pak and Cho [20] tested Al2O3 (13 nm)–water and TiO2 (27 nm)–water-based nanofluids, both at 10 % particle volume fraction, and found that viscosity increased several times than that of water. The large inconsistency could be due to the difference in dispersion technique and size. Pak and Cho also used adjusted pH values and applied electrostatic repulsion. The viscosity of nanofluids depends on the dispersion method and stabilization technique.
Effect of shear rate
Shear stress plays an important role to distinguish between Newtonian and non-Newtonian nanofluids. With an increase in shear rate particle–particle interactions become weaker and are even broken down and nanofluids show Newtonian behavior [50]. An investigation of Namburu et al. [65] showed that CuO nanoparticles in water and ethylene glycol behaved as Newtonian fluids. On the contrary, cobalt nanoparticles in the same base fluids exhibited non-Newtonian behavior. Abareshi et al. [66] noticed that Fe2O3–glycerol nanofluid showed shear thinning behavior.
Effect of surfactants
There is no much information about the effect of surfactants on nanofluids’ viscosity. In a recent experimental study, Hung et al. [67] found that addition of chitosan in MWCNTs/water nanofluids increased the viscosity of those nanofluids. Their results demonstrate that additive concentration of chitosan showed the proportional relationship for suspension performance. The chitosan concentration of 0.4 wt% provided good suspension performance for all concentration range of MWCNTs. The maximum enhancement in viscosity occurs conditions when the concentration of MWCNTs is 1.5 wt% and that of chitosan is 0.4 wt%. The viscosity increases 233 % compared with deionized water.
Li et al. [68] inspected the surfactant concentration on the viscosity of magnetic nanofluids and pointed out that the viscosity of nanofluids increased by raising the concentration of the surfactant.
Drzazga et al. [69] experimented with water-based copper oxide nanofluids with particle size 30–50 nm. They added nonionic surfactants (Rocacet O7 and Rokanol K7) to those nanosuspensions. When those nanosuspensions flowed through a 4 mm diameter pipe for Reynolds’s number between 8,000 and 50,000, drag reduction occurred due to which the friction factor of copper oxide nanofluids decreased. Their tested values were very near to theoretical values when compared with Blasius equation to verify pipe smoothness. They also observed that Rocacet O7 was suitable for lower Reynolds number, and drag reduction effect was better visible with Rokanol K7 for flows with higher Reynolds number.
Conclusion
This literature review shows that the viscosity of nanofluid depends on many parameters such as base fluids, particle volume fraction, particle size, particle shape, temperature, shear rate, pH value, surfactants, dispersion techniques, particle size distribution and particle aggregation. However, no theoretical formula is currently available to predict nanofluid viscosity with good accuracy. The experimental results showed that nanofluid viscosity did not show good agreement with theoretical models. This difference may be due to the effect of Brownian motion, assumptions made while deriving the models, mathematical modeling approach and dispersion techniques. The viscosity models discussed here are generally applied to measure the viscosity of nanofluids. However, the criterion for validating their results with experimental results and limitations still need more attention. There is no data for optimum size of nanoparticles that can give better stability and less aggregation. Further work is required to determine the new model for viscosity for nanofluids with different materials. The recent study shows that viscosity increases pumping power. Therefore, an alternative method is required replacing conventional coolants with nanofluids.
References
Choi, S.: Enhancing thermal conductivity of fluids with nanoparticles. In: Siginer, D.A., Wang, H.P. (eds.) Developments applications of non-newtonian flows, vol. FED-vol. 231/MD-vol. 66, pp. 99–105. ASME, New York (1995)
Mahbubul, I.M., Saidur, R., Amalina, M.A.: Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transf. 55(4), 874–885 (2012)
Einstein, A.: Eineneuebestimmung der moleküldimensionen. Annals. Phys. 324(2), 289–306 (1906)
Mooney, M.: The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 6(2), 162–170 (1951)
Krieger, I.M., Thomas, J.D.: A mechanism for non-Newtonian flow in suspensions of rigid spheres. Transactions Soc. Rheol. 3(1), 137–152 (1957)
Nielsen, L.E.: Generalized equation for the elastic moduli of composite materials. J. Appl. Phys. 41(11), 4626–4627 (1970)
Batchelor, G.K.: The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 83(01), 97–117 (1977)
Brinkman, H.C.: The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 20(4), 571 (1952)
Frankel, N.A., Acrivos, A.: On the viscosity of a concentrated suspension of solid spheres. Chem. Eng. Sci. 22(6), 847–853 (1967)
Lundgren, T.S.: Slow flow through stationary random beds and suspensions of spheres. J. Fluid Mech. 51(02), 273–299 (1972)
Graham, A.L.: On the viscosity of suspensions of solid spheres. Appl. Sci. Res. 37(3-4), 275–286 (1981)
Kitano, T., Kataoka, T., Shirota, T.: An empirical equation of the relative viscosity of polymer melts filled with various inorganic fillers. Rheologica. Acta. 20(2), 207–209 (1981)
Bicerano, J., Douglas, J.F., Brune, D.A.: Model for the viscosity of particle dispersions. J. Macromol. Sci. 39(4), 561–642 (1999)
Cheng, N.-S., Law, A.W.-K.: Exponential formula for computing effective viscosity. Powder Technol. 129(1), 156–160 (2003)
Tseng, W.J., Chen, C.-N.: Effect of polymeric dispersant on rheological behavior of nickel–terpineol suspensions. Mater. Sci. Eng. A. 347(1), 145–153 (2003)
Avsec, J., Oblak, M.: The calculation of thermal conductivity, viscosity and thermodynamic properties for nanofluids on the basis of statistical nanomechanics. Int. J. Heat Mass Transf. 50(21), 4331–4341 (2007)
Yu, W., Choi, S.U.S.: The role of interfacial layers in the enhanced thermal conductivity of nanofluids: a renovated Maxwell model. J. Nanopart. Res. 5(1-2), 167–171 (2003)
Chen, H., Ding, Y., Tan, C.: Rheological behaviour of nanofluids. New J. Phys. 9(10), 367 (2007)
Masoumi, N., Sohrabi, N., Behzadmehr, A.: A new model for calculating the effective viscosity of nanofluids. J. Phys. D.Appl. Phys. 42(5), 055501 (2009)
Pak, B.C., Cho, Y.I.: Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf Int. J. 11(2), 151–170 (1998)
Kulkarni, D.P., Das, D.K., Chukwu, G.A.: Temperature dependent rheological property of copper oxide nanoparticles suspension (nanofluid). J. Nanosci Nanotechnol. 6(4), 1150–1154 (2006)
Nguyen, C.T., et al.: Temperature and particle-size dependent viscosity data for water-based nanofluids–hysteresis phenomenon. Int. J. Heat Fluid Flow 28(6), 1492–1506 (2007)
Namburu, P.K., et al.: Numerical study of turbulent flow and heat transfer characteristics of nanofluids considering variable properties. Int. J. Therm. Sci. 48(2), 290–302 (2009)
Chandrasekar, M., Suresh, S., Chandra Bose, A.: Experimental investigations and theoretical determination of thermal conductivity and viscosity of Al2O3/water nanofluid. Exp. Therm. Fluid Sci. 34(2), 210–216 (2010)
Abu-Nada, E.: Effects of variable viscosity and thermal conductivity of Al2O3–water nanofluid on heat transfer enhancement in natural convection. Int. J. Heat Fluid Flow 30(4), 679–690 (2009)
Masoud Hosseini, S., Moghadassi, A.R., Henneke, D.E.: A new dimensionless group model for determining the viscosity of nanofluids. J. Therm. Anal. Calorim. 100(3), 873–877 (2010)
Garg, J., et al.: Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid. J. Appl. Phys. 103(7), 074301 (2008)
Murshed, S.M.S., Leong, K.C., Yang, C.: Thermophysical and electrokinetic properties of nanofluids–a critical review. Appl. Therm. Eng. 28(17), 2109–2125 (2008)
Nguyen, C.T., et al.: Viscosity data for Al2O3–water nanofluid—hysteresis: is heat transfer enhancement using nanofluids reliable? Int. J. Therm. Sci. 47(2), 103–111 (2008)
He, Y., et al.: Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transf. 50(11), 2272–2281 (2007)
Namburu, P.K., et al.: Experimental investigation of viscosity and specific heat of silicon dioxide nanofluids. Micro Nano Lett. IET 2(3), 67–71 (2007)
Chevalier, J., Tillement, O., Ayela, F.: Rheological properties of nanofluids flowing through microchannels. Appl. Phys. Lett. 91(23), 233103 (2007)
Pastoriza-Gallego, M.J., et al.: CuO in water nanofluid: influence of particle size and polydispersity on volumetric behaviour and viscosity. Fluid Phase Equilib. 300(1), 188–196 (2011)
Lu, W.-Q., Fan, Q.-M.: Study for the particle’s scale effect on some thermophysical properties of nanofluids by a simplified molecular dynamics method. Eng. Anal. Boundary Elem. 32(4), 282–289 (2008)
Anoop, K.B., Sundararajan, T., Das, S.K.: Effect of particle size on the convective heat transfer in nanofluid in the developing region. Int. J. Heat. Mass. Transf. 52(9), 2189–2195 (2009)
Agarwal, D.K., Aravind, V., Kumar, S.S.: Synthesis and characterization of kerosene–alumina nanofluids. Appl. Therm. Eng. 60(1), 275–284 (2013)
Prasher, R., et al.: Measurements of nanofluid viscosity and its implications for thermal applications. Appl. Phys. Lett. 89(13), 133108 (2006)
Timofeeva, E.V., et al.: Nanofluids for heat transfer: an engineering approach. Nanoscale Res. Lett. 6(1), 1–7 (2011)
Timofeeva, E.V., Routbort, J.L., Singh, D.: Particle shape effects on thermophysical properties of alumina nanofluids. J. Appl. Phys. 106(1), 014304 (2009)
Ferrouillat, S., et al.: Influence of nanoparticle shape factor on convective heat transfer and energetic performance of water-based SiO < sub > 2 </sub > and ZnO nanofluids. Appl. Therm. Eng. 51(1), 839–885 (2013)
Das, S.K., Putra, N., Wilfried, R.: Pool boiling characteristics of nano-fluids. Int. J. Heat Mass Transf. 46(5), 851–862 (2003)
Putra, N., Wilfried, R., Sarit, K.: DasNatural convection of nano-fluids. Heat Mass Transf. 39(8–9), 775–784 (2003)
Weerapun, D., Somchai, W.: Measurement of temperature-dependent thermal conductivity and viscosity of TiO2 water nanofluids. Exp. Therm. Fluid Sci. 33(4), 706–714 (2009)
Schmidt, A.J., et al.: Experimental investigation of nanofluid shear and longitudinal viscosities. Appl. Phys. Lett. 92(24), 244107 (2008)
Ding, Y., et al.: Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int. J. Heat. Mass. Transf. 49(1), 240–250 (2006)
Naina, H.K., et al.: Viscosity and specific volume of TiO2/water nanofluid. J. Nanofluids 1(2), 161–165 (2012)
Lee, S.W., et al.: Investigation of viscosity and thermal conductivity of SiC nanofluids for heat transfer applications. Int. J. Heat Mass Transfer 54(1), 433–438 (2011)
Tseng, W.J., Lin, K.C.: Rheology and colloidal structure of aqueous TiO2 nanoparticle suspensions. Mater. Sci. Eng A. 355(1), 186–192 (2003)
Hojjat, M., et al.: Rheological characteristics of non-Newtonian nanofluids: experimental investigation. Int. Commun. Heat Mass Transfer 38(2), 144–148 (2011)
Goharshadi, E.K., et al.: Nanofluids for heat transfer enhancement-a review. Phys. Chem. Res 1(1), 1–33 (2009)
Chen, H., et al.: Predicting thermal conductivity of liquid suspensions of nanoparticles (nanofluids) based on rheology. Particuology 7(2), 151–157 (2009)
Duan, F., Dingtian, K., Alexandru, C.: Viscosity affected by nanoparticle aggregation in Al2O3-water nanofluids. Nanoscale Res. Lett. 6(1), 1–5 (2011)
Thomas, S., Sobhan, C.B.P.: A review of experimental investigations on thermal phenomena in nanofluids. Nanoscale Res. Lett. 6(1), 1–21 (2011)
Andrade, E.N.da C.: LVIII.A theory of the viscosity of liquids.—Part II. London, Edinburgh, and Dublin Philos. Mag. J. Sci. 17(113), 698–732 (1934)
Meschede, D., Helmut, V.: Gerthsenphysik, 21st edn, p. 1288. Springer, Berlin (2002)
Fulcher, G.S.: Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 8(6), 339–355 (1925)
Goharshadi, E.K., Mahboobeh, H.: Effect of calcination temperature on structural, vibrational, optical, and rheological properties of zirconia nanoparticles. Ceram. Int. 38(3), 1771–1777 (2012)
Syam Sundar, L., Manoj, K.S., Antonio, S.: Investigation of thermal conductivity and viscosity of Fe3O4 nanofluid for heat transfer applications. Int. Commun. Heat Mass Transf 44, 7–14 (2013)
Chen, H., Yulong, D., Chunqing, T.: Rheological behaviour of nanofluids. New. J. Phys. 9(10), 367 (2007)
Xian-Ju, W., Li, X.-F.: Influence of pH on nanofluids’ viscosity and thermal conductivity. Chin. Phys. Lett. 26(5), 056601 (2009)
Jia-Fei, Z., et al.: Dependence of nanofluid viscosity on particle size and pH value. Chin. Phys. Lett. 26(6), 066202 (2009)
Kumar, P.C.M., Kumar, J., Suresh, S.: Review on nanofluid theoretical viscosity models. IJEIR 1(2), 128–134 (2012)
Masuda, H., et al.: Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. NetsuBussei 7(4), 227–233 (1993)
Wang, X., Xu, X., Choi, S.U.S.: Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat. Transf. 13(4), 474–480 (1999)
Namburu, P.K., et al.: Viscosity of copper oxide nanoparticles dispersed in ethylene glycol and water mixture. Exp. Therm. Fluid. Sci. 32(2), 397–402 (2007)
Abareshi, M., et al.: Fabrication, characterization, and measurement of viscosity of α-Fe2O3-glycerol nanofluids. J. Mol. Liq. 163(1), 27–32 (2011)
Hung, Y.-H., Wen-Chieh, C.: Chitosan for suspension performance and viscosity of MWCNTs. Int. J. Chem. Eng. 3(5), 347–353 (2012)
Li, Q., Yimin, X., Jian, W.: Measurement of the viscosity of dilute magnetic fluids. Int. J. Thermophys. 27(1), 103–113 (2006)
Drzazga, M., et al.: Influence of nonionic surfactant addition on drag reduction of water based nanofluid in a small diameter pipe. Chin. J. Chem. Eng. 21(1), 104–108 (2013)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Mishra, P.C., Mukherjee, S., Nayak, S.K. et al. A brief review on viscosity of nanofluids. Int Nano Lett 4, 109–120 (2014). https://doi.org/10.1007/s40089-014-0126-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40089-014-0126-3