Exponential finite difference methods for solving Newell–Whitehead–Segel equation

Abstract

This work presents two different finite difference methods to compute the numerical solutions for Newell–Whitehead–Segel partial differential equation, which are implicit exponential finite difference method and fully implicit exponential finite difference method. Implicit exponential methods lead to nonlinear systems. Newton method is used to solve the resulting systems. Stability and consistency are discussed. To illustrate the accuracy of the proposed numerical methods, some examples are delivered at the end.

1 Introduction

Nonlinear partial differential equations play an important role in modeling complicated phenomenon in physics, chemistry, biology, and mechanics. One of these equations is Newell–Whitehead–Segel (NWS) partial differential equation. It describes the appearance of the stripe pattern in two dimensions. On the other hand, this equation is applied as a mathematical model in different systems, such as Rayleigh–Benard convection, Faraday instability, and chemical reaction.

Newell–Whitehead equation has the form [15]:

$$\begin{aligned} U_t(x,t)-aU_{xx}(x,t)=bU(x,t)-cU^3(x,t); \end{aligned}$$

(1.1)

Segel modified the previous equation to the following form [22]:

$$\begin{aligned} U_t(x,t)=kU_{xx}(x,t)+aU(x,t)-bU^q(x,t), \end{aligned}$$

(1.2)

where a, b and k are real numbers with $k>0$ and q is a positive integer, U(x, t) may express a nonlinear distribution of temperature in an infinitely thin and long rod or as the flow velocity of a fluid in an infinitely long pipe with small diameter, and $aU-bU^q$ presents the effect of the source term.

Recently, researchers used different methods to find the analytical solutions of Problem (1.2). Aasaraii [1] used differential transform method to present the analytical solution, Pue-On [19] solved (1.2) by Laplace Adomian decomposition method. Jassim [11] applied Homotopy perturbation algorithm using Laplace transform to give analytical solution; however, Mahgoub and Sedeeg [13, 14] solved it by Elzaki Adomian decomposition method. Soori et al. [23] used the variational iteration method and Prakash et al. [18] utilized He’s variational iteration method to solve Problem (1.2).

For the numerical solution of Problem (1.2), Ruiz-Ramírez and Macías-Díaz [12] used non-standard symmetry-preserving method to compute bounded solution of a generalized NWS problem, Zahraa et al. [24] found numerical solutions by Cubic B-Spline methods, Patade and Bhalekar [17] used a new iterative method which was found by Jafari and Daftardar-Gejji [5] to give analytical solutions for NWS equation with initial condition, and Akinlabi and Edeki [2] used perturbation iteration transform method and gave approximate solutions for the initial value problems of NWS equation.

Different finite difference schemes have been developed for solving different differential equations, Bahadir [3] applied exponential finite difference method to KDV equation for small times, Ramos [21] used explicit finite difference methods for the equal width (EW) and regularized long-wave (RLW) equations, Inan and Bahadir [9] used Hopf–Cole transform to linearize Burgers’ equation, then they applied an explicit exponential finite difference method to find the numerical solution, also they presented an implicit exponential finite difference scheme for solving generalized Burgers–Huxley equation [10], Huang and Abduwali [7] used Crank-Nicolson method to modify the numerical scheme of generalized Burgers–Huxley equation, Celikten et al. [4] presented four different explicit exponential finite difference methods to solve modified Burgers’ equation, and Inan [8] applied Crank–Nicolson exponential finite difference scheme to generalized Fitzhugh–Nagumo equation.

The aim of this manuscript is to introduce two different finite difference schemes to compute the numerical solutions of Problem (1.2). The first one is implicit exponential finite difference scheme and the second one is fully implicit exponential finite difference scheme. Stability and consistency of both schemes are discussed. Moreover, the rate and order of convergence are discussed numerically. Some examples are presented to show the efficiency of these methods to solve the equation.

2 Numerical methods

In general, finite difference methods for solving partial differential equations depend on transforming a calculus problem into an algebra problem by discretizing the continuous domain into a discrete difference grid $(x_i,t_j)$, where $x_i=i\Delta x$; $0\le i \le N$, $t_j=j \Delta t ;j=0,1,2,\ldots ,\Delta x$ is the spatial mesh size and $\Delta t$ is the time step. Then, replacing the individual exact partial derivatives by algebraic finite difference approximations. In this work, we use the difference operators:

$$\begin{aligned} \left( \frac{\partial u}{\partial t} \right) _{i,j+1}\approx & {} \frac{u_i^{j+1}-u_i^j}{\Delta t}, \end{aligned}$$

(2.1)

$$\begin{aligned} \left( \frac{\partial ^2 u}{\partial x^2} \right) _{i,j+1}\approx & {} \frac{u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1}}{(\Delta x)^2}, \end{aligned}$$

(2.2)

where $u_i^j$ is the numerical approximation of the exact solution at point $(x_i,t_j)$.

The numerical solution of the proposed problem is obtained by solving the resulting system of algebraic equations [6].

2.1 Implicit exponential finite difference scheme (I-EFD)

The implicit exponential finite difference scheme of Eq. (1.2) is given by the form:

$$\begin{aligned} u_i^{j+1}=u_i^j \exp { \left( \frac{1}{u_i^j} \left[ r(u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1})+a\Delta t u_i^j -b \Delta t (u_i^j)^q \right] \right) }. \end{aligned}$$

(2.3)

2.2 Fully implicit exponential finite difference scheme (FI-EFD)

The fully implicit exponential finite difference scheme of Eq. (1.2) is given by the form:

$$\begin{aligned} u_i^{j+1}=u_i^j \exp { \left( \frac{1}{u_i^j} \left[ r(u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1})+a\Delta t u_i^{j+1} -b \Delta t (u_i^{j+1})^q \right] \right) }, \end{aligned}$$

(2.4)

where $u_i^j$ is the numerical exponential approximation of U(x, t) at the point $(x_i,t_j)$,$1\le i \le N-1$, $j=0,1,2,\ldots$, and $r=\frac{k\Delta t}{(\Delta x)^2}$.

An iterative method is applied to solve the nonlinear systems of algebraic equations (Eqs. (2.3) and (2.4)).

Suppose these nonlinear systems are given by the form:

$$\begin{aligned} G(u)=0, \end{aligned}$$

(2.5)

where $G=[g_1,g_2,\ldots ,g_{N-1}]^T$, $u=[u_1^{j+1},u_2^{j+1},\ldots ,u_{N-1}^{j+1}]^T$.

Newton method is used to solve the system (2.5) by the following way:

• 1. Set $u^{(0)}$, an initial estimate.

• 2. For $K=0,1,2,\ldots$ until convergence do:

  Solve: $u^{K+1}=u^K-J \left( u^{(K)} \right) ^{-1}G \left( u^{(K)} \right)$,

where $J(u^{(K)})$ is the Jacobian matrix.

The solution at every time level is considered an initial estimate to the solution at the next time level. At each time step, Newton iteration stops when $\left\Vert G(u^{(K)})\right\Vert _{\infty } \le 10^{-5}$; it usually needs two or three iterations.

Absolute, $L_\infty$ and $L_2$ norms will be used to measure the accuracy of both proposed methods which are defined, respectively, by:

$$\begin{aligned} \mathrm{error Abs}= & {} \left|u(x_i,t_j)-U(x_i,t_j)\right|, \end{aligned}$$

(2.6)

$$\begin{aligned} \mathrm{error} L_\infty= & {} \left\Vert u-U\right\Vert _{\infty }=\max \limits _{0\le i \le N} \left|u_i-U_i\right|, \end{aligned}$$

(2.7)

$$\begin{aligned} \mathrm{error} L_2= & {} \left\Vert u-U\right\Vert _{2}= \left( \Delta x \sum _{i=0}^{i=N} \left|u_i-U_i\right|^2 \right) ^{\frac{1}{2}}, \end{aligned}$$

(2.8)

where U is the exact solution of the proposed problem and u is the numerical exponential finite difference approximation.

3 Errors and consistency

3.1 Local truncation error (LTE)

Since the schemes are exponential, the investigation will be developed by expanding the exponential term of the schemes into a Taylor series, and using the first two terms of the expansion, then substituting the coefficients $u_i^{j+1}$,$u_{i+1}^{j+1}$, and $u_{i-1}^{j+1}$ by Taylor series expansions:

$$\begin{aligned}&u_i^{j+1}=u_i^j+\frac{\Delta t}{1!} \left( \frac{\partial u}{\partial t} \right) _{i,j}+\frac{(\Delta t)^2}{2!} \left( \frac{\partial ^2 u}{\partial t^2} \right) _{i,j}+\frac{(\Delta t)^3}{3!} \left( \frac{\partial ^3 u}{\partial t^3} \right) _{i,j}+\frac{(\Delta t)^4}{4!} \left( \frac{\partial ^4 u}{\partial t^4} \right) _{i,j}+\cdots , \end{aligned}$$

(3.1)

$$\begin{aligned} {}&u_{i+1}^{j+1}= u_i^j+\frac{\Delta x}{1!} \left( \frac{\partial u}{\partial x}\right) _{i,j}+\frac{\Delta t}{1!} \left( \frac{\partial u}{\partial t}\right) _{i,j}+ \frac{(\Delta x)^2}{2!}\left( \frac{\partial ^2 u}{\partial x^2}\right) _{i,j} +\frac{(\Delta t)^2}{2!}\left( \frac{\partial ^2 u}{\partial t^2}\right) _{i,j}\nonumber \\&+\Delta x \Delta t \left( \frac{\partial ^2 u}{\partial x \partial t}\right) _{i,j} +\frac{(\Delta x)^3}{3!} \left( \frac{\partial ^3 u}{\partial x^3}\right) _{i,j}+\frac{(\Delta t)^3}{3!} \left( \frac{\partial ^3 u}{\partial t^3}\right) _{i,j}+\frac{(\Delta x)^2}{2!} \Delta t \left( \frac{\partial ^3 u}{\partial x^2 \partial t}\right) _{i,j} \nonumber \\&+\Delta x \frac{(\Delta t)^2}{2!} \left( \frac{\partial ^3 u}{\partial x \partial t^2}\right) _{i,j}+\frac{(\Delta x)^4}{4!} \left( \frac{\partial ^4 u}{\partial x^4}\right) _{i,j}+\frac{(\Delta t)^4}{4!} \left( \frac{\partial ^4 u}{\partial t^4}\right) _{i,j} \nonumber \\&+\frac{(\Delta x)^2 (\Delta t)^2}{4} \left( \frac{\partial ^4 u}{\partial x^2 \partial t^2}\right) _{i,j} +\frac{(\Delta x)^3}{3!} \Delta t \left( \frac{\partial ^4 u}{\partial x^3 \partial t}\right) _{i,j}+\Delta x \frac{(\Delta t)^3 }{3!} \left( \frac{\partial ^4 u}{\partial x \partial t^3}\right) _{i,j}+\cdots , \end{aligned}$$

(3.2)

$$\begin{aligned}&u_{i-1}^{j+1}= u_i^j-\frac{\Delta x}{1!} \left( \frac{\partial u}{\partial x}\right) _{i,j}+\frac{\Delta t}{1!} \left( \frac{\partial u}{\partial t}\right) _{i,j}+\frac{(\Delta x)^2}{2!}\left( \frac{\partial ^2 u}{\partial x^2}\right) _{i,j}+\frac{(\Delta t)^2}{2!}\left( \frac{\partial ^2 u}{\partial t^2}\right) _{i,j}\nonumber \\&-\Delta x \Delta t \left( \frac{\partial ^2 u}{\partial x \partial t}\right) _{i,j} -\frac{(\Delta x)^3}{3!} \left( \frac{\partial ^3 u}{\partial x^3}\right) _{i,j}+\frac{(\Delta t)^3}{3!} \left( \frac{\partial ^3 u}{\partial t^3}\right) _{i,j}+\frac{(\Delta x)^2}{2!} \Delta t \left( \frac{\partial ^3 u}{\partial x^2 \partial t}\right) _{i,j}\nonumber \\&- \Delta x \frac{(\Delta t)^2}{2!} \left( \frac{\partial ^3 u}{\partial x \partial t^2}\right) _{i,j}+\frac{(\Delta x)^4}{4!} \left( \frac{\partial ^4 u}{\partial x^4}\right) _{i,j}+\frac{(\Delta t)^4}{4!} \left( \frac{\partial ^4 u}{\partial t^4}\right) _{i,j}+\frac{(\Delta x)^2 (\Delta t)^2}{4} \left( \frac{\partial ^4 u}{\partial x^2 \partial t^2}\right) _{i,j}\nonumber \\&-\frac{(\Delta x)^3}{3!} \Delta t \left( \frac{\partial ^4 u}{\partial x^3 \partial t}\right) _{i,j}-\Delta x \frac{(\Delta t)^3 }{3!} \left( \frac{\partial ^4 u}{\partial x \partial t^3}\right) _{i,j}+\cdots \end{aligned}$$

(3.3)

3.1.1 LTE of implicit exponential finite difference scheme (I-EFD)

The Eq. (2.3) can be written as:

$$\begin{aligned} u_{i}^{j+1} = u_i^j+r(u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1})+a\Delta tu_i^j-b\Delta t(u_i^j)^q. \end{aligned}$$

(3.4)

Substituting (3.1)–(3.3) into the resulting system (3.4), we get:

$$\begin{aligned} \left( \frac{\partial u}{\partial t} \right) _{i,j}+{\mathcal {O}}(\Delta t)=k\left( \frac{\partial ^2 u}{\partial x^2}\right) _{i,j} +{\mathcal {O}}(\Delta x)^2+au_i^j-b(u_i^j)^q. \end{aligned}$$

(3.5)

Therefore, LTE of (3.5) is:

$$\begin{aligned} LTE=\lim _{\Delta t,\Delta x\rightarrow 0} \left[ {\mathcal {O}}(\Delta t)+{\mathcal {O}}(\Delta x)^2 \right] =0. \end{aligned}$$

(3.6)

3.1.2 LTE of fully implicit exponential finite difference scheme (FI-EFD)

The Eq. (2.4) can be written as:

$$\begin{aligned} u_{i}^{j+1} = u_i^j+r(u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1})+a\Delta tu_i^{j+1}-b\Delta t(u_i^{j+1})^q. \end{aligned}$$

(3.7)

As the previous discussion in 3.1.1, we find:

$$\begin{aligned} \left( \frac{\partial u}{\partial t} \right) _{i,j}+{\mathcal {O}}(\Delta t)= & {} k\left( \frac{\partial ^2 u}{\partial x^2}\right) _{i,j} +{\mathcal {O}}(\Delta x)^2+a\left( u_i^j+{\mathcal {O}}(\Delta t)\right) -b\left( (u_i^j)^q+{\mathcal {O}}(\Delta t)\right) . \end{aligned}$$

(3.8)

$$\begin{aligned} LTE= & {} \lim _{\Delta t,\Delta x\rightarrow 0} \left[ {\mathcal {O}}(\Delta t)+ {\mathcal {O}}(\Delta x)^2 \right] =0. \end{aligned}$$

(3.9)

3.2 Consistency

Since the difference between the PDE and the finite difference scheme gives LTE, and according to (3.6) and (3.9), the proposed schemes are consistent with Eq. (1.2). And they are first order in time and second order in space.

4 Stability analysis

We consider Von-Neumann stability analysis to investigate stability of the linear form of NWS equation.

4.1 Stability of implicit exponential finite difference scheme (I-EFD)

We suppose $(u_i^j)^{q-1}=\alpha =constant$, so the linear form of (3.4) can be written as:

$$\begin{aligned} u_{i}^{j+1} = u_i^j+r(u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1})+a\Delta tu_i^j- \alpha b\Delta tu_i^j. \end{aligned}$$

(4.1)

By substituting the Fourier mode $u_i^j= \zeta ^j e^{I \beta i\Delta x}$; $I^2=-1$ into (4.1), we get:

$$\begin{aligned} \zeta ^{j+1}=g \zeta ^j ; g=\frac{1+a\Delta t -\alpha b \Delta t}{1+4r \sin ^2 \left( \frac{\beta \Delta x}{2}\right) }. \end{aligned}$$

Suppose that $\alpha =1$, so g has the form:

$$\begin{aligned} g=\frac{1+a\Delta t - b \Delta t}{1+4r \sin ^2 \left( \frac{\beta \Delta x}{2}\right) }. \end{aligned}$$

(4.2)

The stability condition is $\left|g\right| \le 1$.

When $a \le b$, the scheme is unconditionally stable.

When $a>b$, suppose that $a-b=c>0$:

$\implies -1-4r \sin ^2 \frac{\beta \Delta x}{2} \le 1+c \Delta t \le 1+4r \sin ^2 \frac{\beta \Delta x}{2} \implies c \Delta t \le 4r \sin ^2 \frac{\beta \Delta x}{2}$.

Therefore, the stability condition is:

$$\begin{aligned} a-b \le \frac{4r}{\Delta t}. \end{aligned}$$

4.2 Stability of fully implicit exponential finite difference scheme (FI-EFD)

We suppose $(u_i^{j+1})^{q-1}=\alpha =constant$, so the linear form of (3.7) can be written as:

$$\begin{aligned} u_{i}^{j+1} = u_i^j+r(u_{i-1}^{j+1}-2u_i^{j+1}+u_{i+1}^{j+1})+a\Delta tu_i^{j+1}- \alpha b\Delta tu_i^{j+1}. \end{aligned}$$

(4.3)

By substituting the Fourier mode $u_i^j= \zeta ^j e^{I \beta i \Delta x}$; $I^2=-1$ into (4.3), we get:

$$\begin{aligned} \zeta ^{j+1}=g \zeta ^j ; g=\frac{1}{1-a\Delta t +\alpha b \Delta t+4r \sin ^2 \left( \frac{\beta \Delta x}{2}\right) }. \end{aligned}$$

Suppose that $\alpha =1$, so g has the form:

$$\begin{aligned} g=\frac{1}{1-a\Delta t + b \Delta t+4r \sin ^2 \left( \frac{\beta \Delta x}{2}\right) }. \end{aligned}$$

(4.4)

The stability condition is $\left|g\right| \le 1$.

When $a \le b$, the scheme is unconditionally stable.

When $a>b$, the stability condition is $-1 \le \frac{1}{1-a\Delta t + b \Delta t+4r \sin ^2 \left( \frac{\beta \Delta x}{2}\right) } \le 1$.

If $1-a\Delta t + b \Delta t+4r \sin ^2 (\frac{\beta \Delta x}{2})>0$, then $a-b \le \min \{ \frac{2+4r}{\Delta t} , \frac{4r}{\Delta t} \}$, so the stability condition is:

$$\begin{aligned} a-b \le \frac{4r}{\Delta t}. \end{aligned}$$

If $1-a\Delta t + b \Delta t+4r \sin ^2 (\frac{\beta \Delta x}{2})<0$, then $a-b \ge max \{\frac{2+4r}{\Delta t} , \frac{4r}{\Delta t} \}$, so the stability condition is,

$$\begin{aligned}a-b \ge \frac{2+4r}{\Delta t}.\end{aligned}$$

5 Numerical results and stability discussion

In this section, we will discuss three different standard examples to test the both proposed methods.

Example 5.1

[16]

$u_t-u_{xx}-u+u^4=0 , (x,t)\in [0,1]\times [0,T]$.

The initial condition is:

$u(x,0)=\left( 1+e^\frac{3x}{\sqrt{10}}\right) ^{-\frac{2}{3}}$ with the boundary conditions:

$u(0,t)=\left( \frac{1}{2}+\frac{1}{2} \tanh (\frac{21t}{20})\right) ^{\frac{2}{3}}$,

$u(1,t)=\left( \frac{1}{2}+\frac{1}{2} \tanh (-\frac{3}{2\sqrt{10}}(1-\frac{7t}{\sqrt{10}}))\right) ^{\frac{2}{3}}$.

The exact solution is given as: $u(x,t)=\left( \frac{1}{2}+\frac{1}{2} \tanh (-\frac{3}{2\sqrt{10}}(x-\frac{7t}{\sqrt{10}}))\right) ^{\frac{2}{3}}$.

Stability of Example 5.1.

• Stability of I-EFD scheme

  In this problem, we have $a=1,b=1$; so, g in (4.2) is given as $g=\frac{1}{1+4r \sin ^2 (\frac{\beta \Delta x}{2})}$ which satisfies the condition $\left|g\right| \le 1$ and the scheme is unconditionally stable.

• Stability of FI-EFD scheme

  g in (4.4) is given as $g=\frac{1}{1+4r \sin ^2 (\frac{\beta \Delta x}{2})}$ and the scheme is also unconditionally stable.

Table 1 shows absolute errors of I-EFD, FI-EFD methods, and the methods of [24], where $T=1,\Delta x=0.0125$ and $\Delta t=10^{-4}$ (for finite difference methods). It also shows that the presented methods offer better results than the methods of [24]. Tables 2, 3 show $L_\infty$ and $L_2$ errors for $T=10, \Delta x=0.05$ and two different choices of $\Delta t$. These tables show that the errors of I-EFD and FI-EFD methods are almost equal, and they offer high accurate solutions.

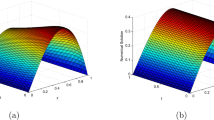
Figure 1 shows exact and numerical solutions computed by I-EFD method for $T=5, \Delta t=0.001$, and $\Delta x=0.05$. Figure 2 shows numerical solution computed by I-EFD method for $T=1, \Delta t=0.05$, and $\Delta x=0.1$.

Table 1 Absolute errors of Example 5.1 of I-EFD, FI-EFD (for $\Delta x=0.0125$, $\Delta t=10^{-4}$), and the methods of [24]

Table 2 $L_\infty$ and $L_2$ errors of Example 5.1 for $\Delta x=0.05$ and $\Delta t=10^{-3}$

Table 3 $L_\infty$ and $L_2$ errors of Example 5.1 for $\Delta x=0.05$ and $\Delta t=10^{-4}$

Fig. 1

I-EFD solution of Example 5.1 for $\Delta t=0.001$ and $\Delta x=0.05$

Fig. 2

I-EFD solution of Example 5.1 for $\Delta t=0.05$ and $\Delta x=0.1$

Example 5.2

[16]

$u_t-u_{xx}-3u+4u^3=0 , (x,t)\in [0,1]\times [0,T]$.

The initial condition is:

$u(x,0)=\sqrt{\frac{3}{4}}\frac{e^{\sqrt{6}x}}{e^{\sqrt{6}x}+e^{\frac{\sqrt{6}}{2}x}}$,

with the boundary conditions:

$u(0,t)=\sqrt{\frac{3}{4}}\frac{1}{1+e^{-\frac{9}{2}t}}$,

$u(1,t)=\sqrt{\frac{3}{4}}\frac{e^{\sqrt{6}}}{e^{\sqrt{6}}+e^{\frac{\sqrt{6}-9t}{2}}}$.

The exact solution is given as: $u(x,t)=\sqrt{\frac{3}{4}}\frac{e^{\sqrt{6}x}}{e^{\sqrt{6}x}+e^{(\frac{\sqrt{6}}{2}x-\frac{9}{2}t)}}$.

Stability of Example 5.2.

• Stability of I-EFD scheme

  In this problem, we have $a=3,b=4$, and so, g in (4.2) is given as $g=\frac{1-\Delta t}{1+4r \sin ^2 (\frac{\beta \Delta x}{2})}$ which satisfies the condition $\left|g\right| \le 1$ and the scheme is unconditionally stable.

• Stability of FI-EFD scheme

  g in (4.4) is given as $g=\frac{1}{1+\Delta t+4r \sin ^2 (\frac{\beta \Delta x}{2})}$ and the scheme is also unconditionally stable.

Table 4 shows absolute errors of I-EFD, FI-EFD methods, and the methods of [24], where $T=1, \Delta x=0.0125$ and $\Delta t=10^{-4}$ (for finite difference methods). It also shows that I-EFD and FI-EFD methods give more accurate results than the methods of [24]. Tables 5, 6 show $L_\infty$ and $L_2$ errors for $T=10, \Delta x=0.05$ and two different choices of $\Delta t$. These tables also show the high accuracy of the solutions.

Figure 3 shows exact and numerical solutions computed by I-EFD method for $T=5, \Delta t=0.001$, and $\Delta x=0.05$. Figure 4 shows numerical solution computed by I-EFD method for $T=1, \Delta t=0.05$, and $\Delta x=0.1$.

Table 4 Absolute errors of Example 5.2 of I-EFD, FI-EFD (for $\Delta x=0.0125$, $\Delta t=10^{-4}$), and the methods of [24]

Table 5 $L_\infty$ and $L_2$ errors of Example 5.2 for $\Delta x=0.05$ and $\Delta t=10^{-3}$

Table 6 $L_\infty$ and $L_2$ errors of Example 5.2 for $\Delta x=0.05$ and $\Delta t=10^{-4}$

Fig. 3

(I-EFD) solution of Example 5.2 for $\Delta t=0.001$ and $\Delta x=0.05$

Fig. 4

I-EFD solution of Example 5.2 for $\Delta t=0.05$ and $\Delta x=0.1$

Example 5.3

[16]

$u_t-u_{xx}-u+u^2=0 , (x,t)\in [0,1]\times [0,T]$.

The initial condition is:

$u(x,0)=\frac{1}{\left( 1+e^\frac{x}{\sqrt{6}}\right) ^2}$,

with the boundary conditions:

$u(0,t)=\frac{1}{\left( 1+e^\frac{-5t}{6}\right) ^2}$,

$u(1,t)=\frac{1}{\left( 1+e^{\frac{1}{\sqrt{6}}-\frac{5t}{6}}\right) ^2}$.

The exact solution is given as: $u(x,t)=\frac{1}{\left( 1+e^{\frac{x}{\sqrt{6}}-\frac{5t}{6}}\right) ^2}$.

Stability of Example 5.3.

In this problem, we have $a=1,b=1$, so as Example 5.1, both of the methods are unconditionally stable.

Table 7 shows absolute errors of I-EFD, FI-EFD methods, and the methods of [24], where $T=1, \Delta x=0.0125$ and $\Delta t=10^{-4}$ (for finite difference methods). It also shows that the results of the presented methods are better than the results of [24]. Tables 8, 9 show $L_\infty$ and $L_2$ errors for $T=10, \Delta x=0.05$ and two different choices of $\Delta t$. These tables clearly show that the numerical results of I-EFD and FI-EFD methods are in good agreement with the exact solution.

Figure 5 shows exact and numerical solutions computed by I-EFD method for $T=5, \Delta t=0.001$, and $\Delta x=0.05$. Figure 6 shows numerical solution computed by I-EFD method for $T=1, \Delta t=0.05$, and $\Delta x=0.1$.

Table 7 Absolute errors of Example 5.3 of I-EFD, FI-EFD (for $\Delta x=0.0125$, $\Delta t=10^{-4}$), and the methods of [24]

Table 8 $L_\infty$ and $L_2$ errors of Example 5.3 for $\Delta x=0.05$ and $\Delta t=10^{-3}$

Table 9 $L_\infty$ and $L_2$ errors of Example 5.3 for $\Delta x=0.05$ and $\Delta t=10^{-4}$

Fig. 5

I-EFD solution of Example 5.3 for $\Delta t=0.001$ and $\Delta x=0.05$

Fig. 6

I-EFD solution of Example 5.3 for $\Delta t=0.05$ and $\Delta x=0.1$

6 Rate and order of convergence

6.1 Rate of convergence

To compute the rate of convergence, we half the grid size h, and then use the formula:

$$\begin{aligned} \mathrm{rate}=\log _2\left( \frac{E^{h}}{E^\frac{h}{2}}\right) , \end{aligned}$$

(6.1)

where E is a norm given by:

$$\begin{aligned} E=\left[ \frac{\sum _{i=0}^{i=N} \left|U_i-u_i\right|^2}{\sum _{i=0}^{i=N} \left|U_i\right|^2}\right] ^{\frac{1}{2}}. \end{aligned}$$

(6.2)

6.2 Order of convergence

Definition 6.1

A sequence $\{ {x^{(k) } } \}$ [20] generated by a numerical method is said to converge to $\alpha$ with order $p\ge 1$ if:

$$\begin{aligned} \exists C>0 : \frac{ \left| x^{(k+1)} - \alpha \right|}{ \left| x^{(k)} - \alpha \right|^p} \le C ,\quad \forall k_0 \le k, \end{aligned}$$

where $k_0 \ge 0$ is a suitable integer.

To estimate p, we suppose $\left| x^{(k+1)} - \alpha \right| = \varepsilon _{k+1} , \left| x^{(k)} - \alpha \right| = \varepsilon _{k}$, and so, the previous inequality will be $\varepsilon _{k+1} \le C \varepsilon _{k} ^p$ .

Therefore:

$$\begin{aligned} p \approx \frac{ \log \left( \frac{\varepsilon _{k+1}}{\varepsilon _{k}} \right) }{\log \left( \frac{\varepsilon _{k}}{\varepsilon _{k-1}} \right) }. \end{aligned}$$

Table 10 shows rate and order of convergence of Example 5.1 using I-EFD and FI-EFD methods for $T=4$, $\Delta t=10^{-4}$, and $\Delta x$ changes as N changes. It also shows that I-EFD and FI-EFD are second-order accurate in space, and that the methods are consistent, because the error goes to zero as $\Delta x$ is getting smaller.

Table 11 shows rate and order of convergence of Example 5.1 using I-EFD and FI-EFD methods for $T=2$, $\Delta x=0.1$, and $\Delta t$ changes as N changes. It also shows that I-EFD and FI-EFD are first-order accurate in time, and that the methods are consistent, because the error goes to zero as $\Delta t$ is getting smaller.

Table 10 Rate and order of convergence for $T=4, \Delta t=10^{-4}$, and $\Delta x$ changes, Example 5.1

Table 11 Rate and order of convergence for $T=2, \Delta x=0.1$, and $\Delta t$ changes, Example 5.1

7 Conclusion

This manuscript introduced two different exponential finite difference methods, which are implicit exponential finite difference method and fully implicit exponential finite difference method for solving the NWS equation in (1.2). It is shown that both schemes are consistent. Furthermore, it is shown that the local truncation errors are first-order accurate in time and second-order accurate in space. Moreover, the numerical results confirmed the order of convergence in time and in space. The presented methods are computationally consistent, stable, convergent, and offer better accuracy than other methods.