Improving local path planning for UAV flight in challenging environments by refining cost function weights

Abstract

Unmanned Aerial Vehicles (UAV) constantly gain in versatility. However, more reliable path planning algorithms are required until full autonomous UAV operation is possible. This work investigates the algorithm 3DVFH* and analyses its dependency on its cost function weights in 2400 environments. The analysis shows that the 3DVFH* can find a suitable path in every environment. However, a particular type of environment requires a specific choice of cost function weights. For minimal failure, probability interdependencies between the weights of the cost function have to be considered. This dependency reduces the number of control parameters and simplifies the usage of the 3DVFH*. Weights for costs associated with vertical evasion (pitch cost) and vicinity to obstacles (obstacle cost) have the highest influence on the failure probability of the local path planner. Environments with mainly very tall buildings (like large American city centres) require a preference for horizontal avoidance manoeuvres (achieved with high pitch cost weights). In contrast, environments with medium-to-low buildings (like European city centres) benefit from vertical avoidance manoeuvres (achieved with low pitch cost weights). The cost of the vicinity to obstacles also plays an essential role and must be chosen adequately for the environment. Choosing these two weights ideal is sufficient to reduce the failure probability below 10%.

1 Introduction

Unmanned Aerial Vehicles’ (UAV) availability and use cases increase steadily [1]. Possible use cases include medical applications (first-aid drug delivery, delivery of defibrillators, tele-doctors), civil protection (search and rescue of large open areas, caves, and mines, disaster reaction, bushfire detection), military use (target identification, kamikaze drones, slaughter bots) and industry (inspection, maintenance, videography, and photography) [2, 3]. Whereas currently, most UAVs operate in Visual Line of Sight (VLoS) of their pilot, most use cases benefit or require operation beyond VLoS (BVLoS). Reliable and efficient obstacle avoidance algorithms add a layer of safety to piloted flight operations and enable fully autonomous or unpiloted UAV operations. Nonetheless, avoiding static and dynamic obstacles is still an unsolved challenge, especially for UAVs operating in confined, urban environments [4]. Small UAVs (sUAV) below 25 kg still have a huge unused potential because of their limited flight time, sensor range, and payload. Therefore, developing better obstacle avoidance algorithms accelerates the usability of sUAV and UAVs in various fields.

Path planning is commonly known as finding feasible paths between a given position and a goal point [5, 6]. A global path planner identifies a suitable path between a start point and a goal point based on given and complete information about the environment between the start and the goal. However, traditional global path planners cannot react to unknown or unforeseen obstacles. On the contrary, local path planners find suitable paths between the current position and the goal based on information gathered by a sensor system. Traditional local path planners do not have any additional information about the environment.

Some algorithms build or update a map while exploring the environment, known as Simultaneous Localization And Mapping (SLAM), and are still the focus of current research, e.g., [7]. In general, many different algorithms exist, including local and global path planning elements, sometimes extended by memory or (sliding) map strategy. Nonetheless, no algorithm is reliable and efficient enough to solve all path planning problems.

Many foraging animals prove that path planning based on local information gathered by their sensor systems (odometrical, visual, acoustic, olfactory information) works reliably, safely, and energy-efficient [8]. Therefore, we follow this approach and focus on local path planners. We investigate and optimise one of the most promising local path planning algorithms, the 3DVFH*, in the px4 avoidance implementation [9]. Like many other algorithms, this algorithm heavily relies on cost functions to identify the best path from several alternatives. Unfortunately, these cost functions rely on several weighting factors which need to be user-defined. We investigate the influence of the most relevant weighting factors on the failure probability of the 3DVFH* in multiple environments. We also propose the ideal weighting factors for every environment. We followed a three-step approach to identify the ideal parameter settings: first, we identified the most influencing weighting factors in a single parameter sweep of all factors. Second, we investigate the most influencing pairs of weighting factors for certain types of environments. Third, we optimise groups of environments in batches by choosing the best combination of the two most influencing parameters and redoing steps one and two with frozen parameters optimised in the previous optimisation steps. Finally, we investigate the interaction of the three parameters with the most considerable influence on the failure probability. To increase generalizability, we tested some characteristic dependencies with a second, heavier and dynamically different UAV.

The next section gives a detailed explanation of the methodology of this work. Section 3 shows and discusses the results, followed by a broad conclusion in Sect. 4.

2 Methodology

2.1 Boundary conditions

2.1.1 Algorithm

Most local path planners have multiple control parameters to adapt them to a particular situation. The algorithms often compare multiple alternative paths and choose the best path based on costs. Usually, these costs represent different aspects of local path planning, e.g., proximity to obstacles, path smoothness, deviation from a global path or the direct goal direction. By weighing these costs against each other, the relevance of the belonging aspect of path planning is defined mathematically.

Therefore, a local path planner with various costs also differentiates between various aspects of path planning. Consequently, a path planner with many different costs allows a more detailed investigation of the relevance of the aspects of path planning than an algorithm with few costs. Besides the pure number of cost terms, the capability to plan in 3D is highly relevant for investigating UAV flights.

Several local path planning algorithms exist. Most local path planners either rely on a sampling or an optimisation approach. Both share several commonalities. In general, sampling-based approaches explore several solutions in parallel and choose the first one fulfilling several criteria. Optimisation-based approaches systematically improve a candidate solution. Optimisation-based local path planners show better performance than sampling-based approaches. Some very capable algorithms are TopoTraj [10], FASTER [11] and the 3DVFH* [9]. TopoTraj uses a path-guided optimisation to identify topologically distinct paths. However, TopoTraj is designed to work out of the box with no interface to control its behaviour. The original authors are also unsure about its theoretical optimality and are still working on improvements [10]. FASTER always considers two paths in parallel. One safe path which lies completely in the known space. One opportunistic path, which lies in the known and unknown space. If a newly identified obstacle blocks the opportunistic path, FASTER switches to the safe path until a new opportunistic path is generated. This approach allows FASTER flight speeds. However, the interaction of the two trajectories increases the difficulty of investigating the effect of a specific change.

The literature review showed that the 3DVFH* and its implementation in the px4 avoidance fulfil the abovementioned requirements best. The 3DVFH* and its implementation are discussed in detail in [9]. The 3DVFH* uses a Vector Field Histogram (VFH [12]) to represent the environment. The VFH in the 3DVFH* represents the environment with a three-layered, 2D raster grid. Every cell of the raster grid represents a Volume in the real world. A binary layer contains the information on whether an obstacle occupies the Volume or is accessible. This information is based on a distance measurement of a sensor system. Another layer includes the distance between the sensor system and the detected obstacle—if an obstacle is present in this cell. The third layer contains information on the age of the distance measurement. The field of view moves with a moving robot. The 3DVFH* uses translational and rotational information to determine the distance to obstacles that were previously in the field of view but now lie outside the field of view.

The 3DVFH* uses the A* algorithm [13] to identify several candidate paths. The cost of every candidate path is estimated with a cost function.

$${c}_{{\text{total}}}={k}_{{\text{yaw}}}\cdot {c}_{{\text{yaw}}}+{k}_{{\text{pitch}}}\cdot {c}_{{\text{pitch}}}+{k}_{{\text{smooth}}}\cdot {c}_{{\text{smooth}}}+{k}_{{\text{obstacle}}}\cdot {c}_{{\text{obstacle}}}+{c}_{{\text{heuristics}}}$$

(1)

The weighting factors ${k}_{{\text{yaw}}}$, ${k}_{{\text{pitch}}}$, ${k}_{{\text{smooth}}}$ and ${k}_{{\text{obstacle}}}$ weight the importance of the different costs against each other. ${c}_{{\text{yaw}}}$, ${c}_{{\text{pitch}}}$, ${c}_{{\text{smooth}}}$, ${c}_{{\text{obstacle}}}$ and ${c}_{{\text{heuristic}}}$ represent the respective cost terms. A high yaw cost weight ${k}_{{\text{yaw}}}$ penalises horizontal evasion, whereas a high pitch cost weight ${k}_{{\text{pitch}}}$ penalises vertical evasion. A high ${k}_{{\text{smooth}}}$ leads to smoother paths and ${k}_{{\text{obstacle}}}$ ensures a safe distance from obstacles. ${c}_{{\text{heuristics}}}$ represent the heuristic cost of the candidate point. The idea of heuristic costs is derived from the algorithm A*, which estimates the total cost of the path from the current position to the goal position. Heuristic cost increases the algorithms’ goal driven behaviour.

2.1.2 Evaluating the 3DVFH*

Investigating the relevance of path planning aspects in various environments requires flight tests in multiple environments. Simulation of flights and environments allows extensive testing far beyond the testing capabilities of real-world flight testing. We use Gazebo Simulator [14] to simulate the environment and sensor data. Gazebo Simulator combines the Open Dynamics physics Engine (ODE) with OpenGL (Open Graphics Library). OpenGL is a programming interface to render 2D and 3D vector graphics. Gazebo Simulator allows the simulation of objects, a physics-based UAV and realistic sensor data (including sensor noise).

We define three categories of environment, each with several criteria describing each environment. Every category has multiple worlds representing this environment. Each category defines the primary type of obstacles. The first category, the simple obstacle environment, consists of flat rectangle obstacles in various dimensions on the ground and floating in the air (compare Fig. 1a). The second category, the natural obstacle environment, consists of tree-like structures on flat grounds, hills, or valleys (compare Fig. 1b). The third category, the urban obstacle environment, consists of cuboidal blocks in various dimensions aligned in rows similar to street buildings (compare Fig. 1c). Each category has several subcategories sharing the same criteria, e.g., all worlds with very tall buildings belong to the subcategory of large city centres, which is a subset of the urban environments. We use the subcategories to group the worlds more specifically and investigate the relevant aspects of path planning on a more detailed level. An overview of the subcategories is given in Table 5 in the Appendix.

Fig. 1

Example environments. Every ground tile is 1 m × 1 m a simple obstacle environment with 40 obstacles randomly placed. b nature-inspired environment with medium dense forest on a small hill. c City-inspired environment with up to 70-storey buildings and 4-lane main streets (left to right)

2.1.3 Evaluation criteria

Safety is the most critical criterion in the aviation industry. Therefore, this work focuses purely on safety. We define safety as a minimal failure probability $p$, according to:

$$p=\frac{{n}_{{\text{failed}}}}{{n}_{{\text{total}}}}$$

(2)

With ${n}_{{\text{failed}}}$ as the number of failed flights over the total number of flights ${n}_{{\text{total}}}$. A flight fails if the path planner fails to reach the goal in a reasonable amount of time. The reasons for this failure are irrelevant, e.g., if the UAV crashes or the path planner gets stuck in a no-progress loop. The simulation terminates prematurely if the UAV hovers at a fixed position for more than 5 s, circles multiple times in front of obstacles or flies up and down the same path multiple times. It also terminates if the UAV does not reach the goal in the distance $d$ to the starting point in a reasonable time ${T}_{{\text{max}}}$:

$$T_{\max } = 60{\text{s}} + d\, {\cdot}\, 2\,{\text{s}}\,{\text{m}}^{ - 1}$$

(3)

However, the maximum flight time ${T}_{{\text{max}}}$ is only a back up, in case none of the other conditions are fulfilled but the UAV is not able to reach the goal in a reasonable amount of time. Some exemplary flight paths are visualized in Fig. 2.

Fig. 2

Example flight paths. Grey boxes are obstacles. The green flight path is successful. The orange one is too long and reaches the flight time T_max. The red one meanders in front of some obstacles without progress towards the goal (Color figure online)

A standardised take-off manoeuvre (vertical climb to 5 m) is performed at the beginning of each flight. The path planner receives the goal position only after successful take-off. The UAV usually requires around ten to fifteen seconds from arming until moving towards the goal. During the final goal approach, the UAV occasionally circles around the goal, reducing flight speed or altitude. In extreme cases, this manoeuvre takes up to 45 s. Therefore, we assume 60 s for take-off and final goal approach in Eq. 3. Additionally, we assume an average flight speed of 4 m s⁻¹. The maximum flight speed is 5 m s⁻¹. Several test flights in various environments showed that the UAV usually flies at top speed. The average flight speed was always above 4 m s⁻¹. We define a path more than eight times longer than the distance between the start and the goal point as unacceptable. This definition leads to an acceptable time progress of 2 s m⁻¹.

2.1.4 Parameters

The px4 avoidance has several control parameters; all represent weighting factors relevant to path planning. Table 1 shows the control parameters discussed in this work.

Table 1 Investigated cost function weighting factors and their descriptions

We define proper weighting ranges based on a pre-study with randomly chosen worlds showing the general sensitivity of the weights, the information in [9], and the px4 avoidance default values. Table 2 shows the investigated range of the different weighting factors.

Table 2 Investigated interval for the different weighting factors plus the default value also tested

2.1.5 Simulated UAV

Our simulations used the 3DR Iris + UAV Quadcopter as a UAV model. The UAV was around 0.55 m in diameter (motor to motor) and weighs around 1.2 kg, including the battery. The UAV had three depth cameras looking front, left, and right. The sensor range of the depth cameras was 18 m.

2.2 Approach

Combining all possible weighting values leads to 213.840 different combinations. Simulating one setting in all environments takes around three days per computer. We had ten computers available, giving a total simulation time of 64.152 days or 175 years for all weighting value combinations. This simulation time was not acceptable. We also considered a Design of Experiments (DOE) approach. However, some of the weights or their interactions may be highly nonlinear. Additionally, a full-surface DOE would take quite a long time and is still limited to two-dimensional dependencies. Therefore, we chose a three-step approach to reduce the number of parameter combinations and the overall computation time while investigating multiple dependencies.

First, we performed a single parameter sweep in which we set all parameters to the default values except one that varied according to the parameter range and step size in Table 2. This process was repeated for all weights. The goal of this first step was the identification of the influence of the weighting factors. Weights that strongly influence the failure probability were considered relevant; weights that merely influence the failure probability were considered irrelevant. Steps two and three focused only on relevant weights. Additionally, this single parameter sweep identified the best weightings for the different environmental categories and subcategories.

Second, we investigated the interaction of the most influential weight pairs per subcategory and identified the best weighting values for those two weights. We investigated this interaction by simultaneously varying both weights around their optimum for the single parameter sweep of step one. For example, pitch and yaw weight influenced the failure probability in European-style cities with few skyscrapers but many medium-sized buildings and narrow streets the most. We then varied both weights simultaneously around their optimums of the single parameter sweep to identify their combined optimum. The found ideal weights were defined as the new default values. If the failure probability was more than 5%, step 1 was repeated for the considered subcategory. The two new default values were excluded from the parameter sweep, and only those that were not altered were varied again. If no weight of the second single parameter sweep reached a failure probability of zero, step two was repeated with a combined parameter sweep of the following two most influential weights. Again, the two weights with the lowest failure probability were fixed and set as new default values. If the failure probability was over 5%, step one was repeated once again, and so on.

Third, four weights stood out in the first and second steps and mainly contributed to the overall failure probability. These weights were investigated in more detail by varying these four in combination. We also investigated if these weights show any dependencies on each other.

3 Results and discussion

This section presents the three levels of investigation in three subsections. First, the single parameter sweep is discussed, focusing on investigating the most influential weights. Second, the consecutive double parameter sweep is presented, aiming to reach a minimal failure probability by optimising weights in groups of two, starting with the two most influential weights, followed by the subsequent two most influential weights, etc. Finally, the relevant weights are investigated further in a broad parameter sweep to identify the parameter’s dependencies and find a globally optimal solution. The discussion focuses on subcategories of environments that share the same criterion to identify weaknesses and strengths of the algorithm for specific environments.

3.1 Single parameter sweep

This section presents and discusses the influence of every single weight on the overall failure probability. The discussion includes the minimal achievable failure probability by varying one weight and the sensitivity of the weights, i.e., the difference between the highest and lowest failure probability. The discussion differentiates between different subcategories of environments.

We define a statistical significance level α of 0.05. The standard deviation of the baseline is 0.253%. This means that any sensitivity over 0.24% is statistically significant. However, this slight difference does not yield any practical relevance. Therefore, we define a practical relevance of 10% for the sensitivity. Additionally, we define a minimal failure probability below 10% as sufficient.

The following section discusses the sensitivity and the minimal failure probability of every weight in every environmental subcategory regarding their practical relevance. Overall, we define three regions. The first region contains subcategories with high sensitivity, i.e., high variability in failure probability between different weight values but a low minimal failure probability of the investigated weight. These subregions are sensitive to correct weight values, but the path planner can achieve low failure probabilities if set correctly. The second region contains subcategories with medium sensitivity and medium failure probabilities. The third region contains subcategories with high minimal failure probabilities and low sensitivity. The investigated weight hardly influences the failure probability in the subcategories in this region and has, therefore, only a weak influence on the failure probability of this type of environment.

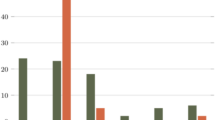
Smoothing speed xy and smoothing speed z weights hardly influence the failure probability of the 3DVFH*. Figures 3a and b show that the sensitivity of these weights is 10% or lower in all environmental subcategories, yielding no practical relevance to the overall failure probability. Subcategory 13 is the only category slightly above the 10% threshold. However, the sensitivity of subcategory 13 is significantly higher for other parameters (see Fig. 3g). Therefore, smoothing speed xy and smoothing speed z are not investigated further.

Fig. 3

Minimal failure probability and sensitivity of different subcategories for different cost function weights. a smoothing speed xy, b smoothing speed z, c velocity cost, d smoothing margin, e pitch cost, f yaw cost, g obstacle cost

Figure 3c shows that velocity cost weight has a much higher sensitivity than smoothing speed xy and smoothing speed z weights. Multiple subcategories have a sensitivity of around 50%, meaning that at least every second flight fails if the velocity cost weight is wrong. However, Fig. 3c also shows that the minimal failure probability in most subcategories is higher than 10% and, therefore, even in the best cases, is too high. Because of the high minimal failure probability, velocity cost weight will only be used if other parameters fail to optimise.

Figure 3d shows that the smoothing margin weight greatly influences the sensitivity of the 3DVFH*. It also allows for very low minimal failure probabilities below 10%. In fact, only two subcategories are in region 3, with low variability and a high minimal failure probability. Another six subcategories are above the acceptable minimal failure probability of 10%. In total, smoothing margin weight can reduce the minimal failure probability in half the subworlds to <10%. However, five of the eight subcategories with acceptable minimal failure probability have an unacceptable sensitivity above 10%. Therefore, smoothing margin weight is crucial for many subcategories and will be investigated further.

Figure 3e shows that pitch weight can significantly reduce the failure probability. Eleven out of 16 subcategories have a minimal failure probability below 10%, whereas only two subcategories have a failure probability above 50%. However, several subcategories are very sensitive to the correct choice of pitch weight. Two subcategories in Fig. 3d have a very high minimal failure probability.

Fortunately, these two subcategories have an acceptable minimal failure probability in Fig. 3e. The two subcategories in region 3 in Fig. 3e are in region 1 in Fig. 3d. Even though the minimal failure probably is not acceptable there, it is still much lower. Therefore, pitch weight is subject to further investigation.

Figure 3f shows that yaw weight has a high sensitivity. Substantially, more subcategories lie in region one than for the other parameters. Additionally, most subcategories in region 3 are around the maximally possible sensitivity concerning their relatively high minimal failure probability. Moreover, yaw weight has several subcategories with an acceptably low minimal failure probability. Therefore, yaw weight is subject to further investigation.

Figure 3g shows that obstacle cost weight has a similar sensitivity and minimal failure probability as pitch weight for most subcategories. Here, 11 of 16 subcategories have an acceptable minimal failure probability of 10% or less. However, 6 of these 11 subcategories also have a high sensitivity (region 1). Once again, the wrong choice of obstacle cost weight leads to a drastically increased failure probability. Two subcategories are in region 3; these two are the same subcategories as both subcategories in region 3 for smoothing margin degrees. The two subcategories in region 1 above the acceptable minimal failure probability for obstacle cost weight are also in region 3 and above the acceptable minimal failure probability in smoothing margin weight. This relationship suggests that obstacle cost and smoothing margin weights cannot solve a specific type of problem during the flight. Nonetheless, obstacle cost weight shows high sensitivity and acceptable minimal failure probabilities for most subcategories. Therefore, obstacle cost weight is subject to further investigation.

Figure 3 shows that smoothing margin and yaw weights have a medium sensitivity and medium potential to reduce the failure probability to an acceptable level. Figure 3 also indicates that pitch and obstacle cost weights have a high sensitivity and potential to reduce the failure probability in many subcategories to an adequate level. However, no weight alone can reduce the failure probability in all subcategories to an acceptable level.

Figure 4 clearly shows that the greatest reduction in minimal failure probability is achieved during the first step by choosing the optimal value for the most influential weight. Unfortunately, this weight and the optimal value differ between multiple subcategories. Therefore, the following section further analyses the different weights and values in those subcategories with high failure probabilities.

Fig. 4

Failure probability of various subcategories over the optimisation step. Every line represents another environment. Table 3 gives the weights used in the various optimisation steps. Step zero is the failure probability of the baseline with default values

Table 3 Overview of the weights with the lowest failure probability from a broad parameter sweep with a single parameter and the consecutive double parameter sweep

3.2 Consecutive double parameter sweep

The most relevant parameters for every subcategory are identified after identifying the minimal failure probability and sensitivity of all parameters. Next, the two cost function weights with the lowest minimal failure probability are varied around their single parameter sweep optimum—this is done separately for every subcategory.

Figure 4 shows the development of minimal failure probability over the optimisation course of the subcategories, which have an unacceptable failure probability after the first optimisation step. Taking the second most influential weight into account and choosing the optimal value for both values combined leads to another reduction in failure probability. If two weights are optimally selected for the particular subcategory, four more subcategories have a failure probability of 0%. However, after optimising one weight, these subcategories already have a failure probability below 10%. All other subcategories need further optimisation. Setting the optimal combination of the two most influential weights and varying all other weights in the predefined region leads to a minimal failure probability of <10% for the remaining subcategories. Combining the most influential weights of the remaining weights leads to 0% failure probability in all subcategories.

Figure 4 shows the potential of the 3DVFH* if the cost function weight is adequate for the environment. It also shows the various ideal values required for zero failure probability in the subcategories. The 3DVFH* reaches an acceptable failure probability of less than 10% in all subcategories after optimisation step 3. All subcategories, except number 15, have a failure probability below 5%, and most have a failure probability of 0%. Here, two questions arise. First, is it possible to find one combination of weights that works perfectly in all environments? This is impossible because the weights leading to the low failure probabilities in Fig. 3 differ significantly. Second, is it possible to define dependencies to find optimal weights easier? These dependencies might be either between weights, such that the algorithm’s overall number of control parameters is reduced. Alternatively, dependencies on the environment allow choosing the weights adapted to the environment. These dependencies will be discussed in Sect. 3.3.

Figure 4 also shows that the failure probability increases in some cases. We varied obstacle cost weight in increments of 2. However, the default value for obstacle cost is 8.5, while the closest value during our parameter study is 9. Therefore, in some cases, the failure probability increases slightly.

3.3 Dependencies

Table 3 shows the weights, which mainly contribute to reducing the failure probability below 10% or even to zero. Investigating Table 3 shows that out of the seven investigated weights, only five are required to reduce the failure probability significantly. Additionally, only a few pairs of weights lead to high reductions in failure probability. The second step, the double parameter sweep, shows that obstacle cost, pitch, and smoothing margin weighting interact in some way such that the failure probability can be reduced to zero. However, pitch and yaw weight in tall buildings’ subcategories seem more relevant.

The actual weights leading to the lowest failure probability differ. Therefore, the relationship of these weights is studied in a broader parameter study. Here, we have two goals. First, defining better default values leads to an overall reduced failure probability. Second, define dependencies between different weights so that the overall number of weights (and therefore control parameters of the algorithm) is reduced. A reduced number of weights is beneficial if the local path planner is used in environments that require different weights. We focus our discussion only on those subcategory environments which show a clear minimum and high sensitivity to the correct choice of parameters. Those subcategories which are less sensitive to the right choice of weight are neglected because optimal values in the more sensitive subcategories also lead to minimal failure probabilities in the less sensitive subcategories.

Subcategory 11 has a very high failure probability of 92% before optimisation. Choosing the correct weight for obstacle cost weight is crucial in this environment. However, the proper weight strongly depends on the weight for the smoothing margin, as seen in Fig. 5.

Fig. 5

Failure probability over smoothing margin and obstacle cost weight for subcategory 11. The red line indicates the default values. Colours indicate the failure probability (Color figure online)

Figure 5 shows that a minimal failure probability is achieved if

$${\text{Smooth}}=87^\circ -13.3 \frac{^\circ }{m}\cdot \mathrm{Obstacle\ Weight}$$

(4)

where ${\text{Smooth}}$ denotes the smoothing margin weight and ${\text{Obstacle\ Weight}}$ the obstacle cost weight in subcategory 11. However, Fig. 6 shows that a higher pitch weight is also necessary for a low failure probability in this subcategory. Generally speaking, a mediocre obstacle cost weight, mediocre to high pitch weight, and small smoothing margin weight lead to a minimal failure probability in environments like typical American city centres with very tall buildings (up to 75 stories) and wide streets. Here, horizontal avoidance maneuvers should be preferred.

Fig. 6

Failure probability over obstacle and pitch cost weight for subcategory 11. The red line indicates the default values (Color figure online)

Subcategory 15 shows very similar regions for optimal parameters. Subcategory 15 has the same type of buildings. However, the streets are much smaller than in subcategory 11. Subcategory 12 is less sensitive than subcategory 11: The valley seen in Fig. 5 is much wider for subcategory 12 and spans a minimum plateau for obstacle cost between 5 and 10, regardless of the smoothing margin weight. Subcategory 12 has small buildings and wide streets. All statements for subcategory 11 hold for these other subcategories, so these diagrams are not shown here.

All subcategories investigated so far benefit from higher pitch weight. Unfortunately, this does not work for subcategories with medium–tall but dense buildings, similar to many larger European cities. Figure 7 shows that, relatively independent of obstacle cost, a lower pitch weight is required for subcategory 14. If looking at subcategory 10, which has the same obstacles as subcategory 14, the picture is the same as in Fig. 7. This contradiction means there is no general optimum for pitch weight. However, specific common characteristics of the environment seem to demand certain cost weightings.

Fig. 7

Failure probability over obstacle weight and pitch cost weight for subcategory 14. The red line indicates the default values (Color figure online)

Considering yaw weight and its relation with pitch weight does not significantly improve the overall situation. Higher yaw weight reduces the failure probability in subcategories with medium–high buildings like subcategories 10 and 14 only slightly and only if pitch weight is poorly chosen (see Fig. 7). In general, environments require low pitch weight benefit from high yaw weight and vice versa. This relationship makes sense as both weights define the tendency to overfly obstacles or fly around them. Low pitch cost and high yaw weights lead to a high tendency to overfly, while high pitch and low yaw cost lead to a strong tendency to fly around. However, reasonably high yaw cost weight cannot diminish the negative effect of too high pitch cost for a certain situation.

3.4 Generalizability

Parts of the above discussed dependencies were also investigated with a second, different UAV. We used a generic flight model of a bigger UAV, inspired by the DJI Matrice 600 (15.5 kg MTOM, 18 m/s max flight velocity). The heavier UAV was also equipped with a heavier (and better) sensor system with a maximum range of 120 m. The tendencies and dependencies identified for the Iris discussed above could be confirmed for the heavier, faster UAV.

The dependency between smoothing margin degrees and obstacle cost for subcategory 11 is very similar (see Fig. 8 and compare to Fig. 5). As seen in Fig. 8 the valley in failure probability is shallower than the one for the lighter UAV, still the same characteristic relation between obstacle weight and smoothing margin is found.

Fig. 8

Failure probability over smoothing margin and obstacle cost weight for subcategory 11 with the heavier UAV. Colours indicate the failure probability (Color figure online)

The dependency between yaw and pitch weight in subcategory 10 was also found for the new, heavier UAV (see Fig. 9 and compare to Fig. 10). Here, the dependency on the pitch weight is weaker—the highest failure probability is lower—still the same tendency that a low failure probability is only achieved with a low pitch weight in subcategory 10 also applies for the heavy UAV.

Fig. 9

Failure probability over yaw and pitch cost weight for subcategory 10 with the heavier UAV

Fig. 10

Failure probability over yaw and pitch cost weight for subcategory 10. The red line indicates the default values (Color figure online)

The second UAV also displays the tendency that a low pitch weight is beneficial in subcategory 14 (see Fig. 11 and compare to Fig. 7).

Fig. 11

Failure probability over obstacle weight and pitch cost weight for subcategory 14 with the heavier UAV

In general, the flight paths of the heavier UAV are not substantially different from the paths of the light IRIS initially presented. The heavier UAV is faster but is also more agile. Therefore, both UAV also show similar behaviours in their failure probability when varying the different weights.

4 Conclusion

The 3DVFH* is a commonly used path planning algorithm that can fly safely and successfully through any environment. Our investigation showed that the algorithm found a path in all 2400 environments. However, the algorithm requires the correct choice of cost function weights to complete its flight missions successfully. We showed that yaw and pitch weight, obstacle cost weight, and smoothing margin weight are the most influential parameters of the 3DVFH*. However, the influence of each parameter and good values for each weight heavily depend on the environment. While we could reduce the failure probability in all environments to an acceptable level by optimising multiple weights for each environment specifically, we could not find a single optimum for all worlds. We showed that smoothing margin and obstacle cost weights requires a specific ratio to lead to minimal failure probability. However, we also showed that pitch weight, independent of all other weights, has different optima in different environments. Environments with tall American-style city centres benefit from high pitch weights, whereas European-style city centres with lower buildings benefit from low pitch weights. We also showed that yaw weight slightly influences pitch weight. However, the influence is insufficient to diminish a poorly chosen pitch weight effect.

This work recommends an obstacle cost weight of 3 and a pitch weight of 1 for environments with lower obstacles below roughly ten-story buildings. For environments with multiple significantly taller obstacles, like larger American city centres, a pitch cost weight of 15 and an obstacle cost weight of 5 lead to a considerably lower failure probability than the setting for more minor obstacles. All other weights should remain as the px4 Avoidance default values. This compromise leads to failure probabilities below 10% in all environments with the least possible parameter variations. However, flights performed with this general recommendation might fail in certain situations. A failure probability of zero requires a more specific choice of parameters depending on the environment. Table 4 gives an overview of the best settings for various environments. Partly, these settings contradict some of the general statements previously made. Other weights that comply with the general statements might be equally good and lead to a 0% failure probability in the given environments. However, the combinations of weights shown in Table 4 reached a failure probability of zero in the given environmental subcategories.

Table 4 Weight combinations of the 3DVFH* without any failed flights in the given environments

The differences in optimal weights indicate that an automated analysis, e.g., with a neural network for image analysis, might enable the full potential of the 3DVFH* by automatically choosing the ideal weights based on features of the current environment. Investigating the influence of the most influential weights of the 3DVFH* in algorithms with fewer parameters but generally better local path planning performance, e.g., FASTER [11], also yields a high potential for further reduction of failure probability.

Appendix

See Table 5 below.

Table 5 Overview of the different environmental subcategories