1 Introduction

Unmanned aerial vehicles (UAV) are ideal for a variety of applications. Due to limited autonomous obstacle avoidance capabilities, most commercial UAVs can only operate within their remote pilot’s Visual Line-of-Sight (VLoS). In contrast, most applications and business cases require fully autonomously operating UAV Beyond VLOS (BVLoS) in the long run [1,2,3]. Even though several obstacle avoidance algorithms exist, reliable and efficient evasion of static and moving obstacles is still challenging [4], especially for small UAVs below 5 kg with low computational power, sensor, and battery capacity. Hence, more robust and efficient obstacle avoidance algorithms are required [5]. Whereas obstacle detection [6] recently made much progress, the challenge remains to choose good avoidance manoeuvres after detecting an obstacle [4, 7].

Path planning is commonly known as finding feasible paths between a given position and a goal point [8, 9]. A global path planner identifies a suitable path between a start point and a goal point based on given information about the environment. However, traditional global path planners cannot react to unknown or unforeseen obstacles. Therefore, a traditional global path planner always needs an accurate and complete database and representation of the environment. On the contrary, local path planners find suitable paths between the current position and the goal based on information gathered by a sensor system. Traditional local path planners do not have any additional information about the environment, allowing them to operate in changing environments without additional effort. However, traditional local path planners have a higher risk of failing to find a feasible path from their current position to the goal point than global path planners. Local path planners are prone to trap themselves in situations where they cannot successfully plan to the goal because of their limited knowledge of the environment. Some other algorithms build or update a map whilst exploring the environment, known as Simultaneous Localization And Mapping (SLAM), e.g. [10]. However, SLAM algorithms struggle with the same problems as local path planners if they operate in unknown environments.

Additionally, SLAM algorithms need to identify previously seen feature points reliably. If the environment changes drastically, e.g. because of snow, since the initial mapping of a particular area, the SLAM algorithm needs to rebuild its map and cannot rely on the previously built map. Finally, SLAM algorithms are primarily designed to explore and not to find paths.

Many different algorithms exist that combine local and global path planning elements. They are sometimes extended by memory or (sliding) map strategies. All algorithms have advantages for specific applications. However, the current algorithms are limited to a specific range of operations with multiple requirements, constraints, and inefficiencies. In general, path planning has been researched extensively in the field of robotics. Many path planning algorithms were initially developed for moving ground robots (e.g. Dijkstra’s algorithm [11], the VFH* [12], this algorithm by Bautista et al. [13]). Often, these algorithms were extended for UAV operation. Therefore, many algorithms primarily plan in the 2D horizontal plane. Many algorithms prefer paths that keep a constant flight altitude. Sometimes the third dimension is only considered a backup if no other path is found. The preference for horizontal paths over vertical paths is also commonly seen in algorithms initially developed for 3D path planning.

Whilst flying over one obstacle and maintaining the new altitude evades all obstacles as tall as the initially evaded one, flying around one obstacle only avoids this obstacle. However, increasing the flight altitude consumes considerably more energy than flying around one obstacle. Especially during the final approach, an increase in flight altitude becomes increasingly inefficient the closer the UAV is to the goal point. Figure 1 exemplifies several alternative flight paths for a UAV. An example use-case in which take-off, short-distance flight, and landing in a city are required is a medical UAV that delivers a drug or instrument, e.g. a defibrillator, from its base station to its place of action. Whereas only a few feasible flight paths are shown, Fig. 1 illustrates the variety of possible paths.

Fig. 1
figure 1

Multiple alternative flight paths from start point A to endpoint B. Path 1 shows a vertical climb to cruise altitude, flight over the goal point, and vertical descent to the goal point. Paths 2 and 3 show a different climb to cruise altitude and decent to the goal. Path 4 shows a pure vertical evasion in case of an obstacle encounter. Path 5 shows a mixture of horizontal and vertical evasion. Path 6 shows pure horizontal evasion. Dotted lines indicate that the UAV flies behind the building, and shadows (path 6) indicate that the UAV flies in front of the building

Full size image

This work proposes a decision-maker as an extension for local path planning algorithms that rely on buildings’ height data to estimate the number and cost of required avoidance manoeuvres until the goal is reached. This information defines the ideal flight altitude and avoidance manoeuvre, i.e. horizontal or vertical avoidance.

This approach combines some of the advantages of a global path planner with the advantages of local path planning. Basing the altitude control algorithm on probabilities does not require an exact representation of the whole environment between start and goal, as all obstacle encounters are solved locally. However, the decision-maker also considers global path aspects when avoiding obstacles by including information from the probability models.

The remainder of this paper will first give an overview of the state of the art in Academia. Then, in the third chapter, a brief overview of the methodology will be given. Here, the focus lies on the data sources used to build a probability map of obstacle encounters over the flight altitude. This chapter 3 also discusses the information used to build the decision-maker. The end of chapter 3 presents our method to test the feasibility of this approach. Chapter 4 then gives the results of our feasibility tests, followed by a conclusion in chapter 5.

2 Literature review

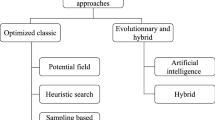
Two main categories of path planning exist: global path planning and local path planning. Global path planning aims at the identification of a suitable path from a start to a goal location in a mainly known environment. Therefore, global path planning usually depends on the information given by some kind of map. Local path planning aims at the identification of a suitable path from an agent’s current position towards a goal in a mostly unknown environment. Local path planners mainly rely on information the agent’s direct surroundings provided by a sensor system. Both, global and local path planning, are subjects of research for several decades with various algorithms and proposals. Some of the most important algorithms and concepts are briefly discussed here. A more thorough discussion of path planning algorithms is found in recent review papers, e.g. [8, 14, 15], or books, e.g. [16] or [17].

2.1 Global path planning

Whilst several hundred global path planning algorithms exist [15], many of them are based on the same algorithms or principles. The majority of algorithms rely on graphs or sampling, or a mixture of both.

Sampling-based global path planning is commonly used because of its simplicity. The basic procedure is (randomly) generating points, known as samples, in the environment. Multiple paths are formed by connecting these samples. Several algorithms use different methods to generate samples or connect them. The algorithm stops if a path is found between the start and the goal point.

Sampling-based global path planning can handle complex, high-dimensional environments. However, sampling-based algorithms require more computational effort than other approaches. Even though these algorithms produce near-optimal solutions, they do not produce optimal ones. They also struggle with certain situations leading to higher computation times or failure in finding suitable paths. The Rapidly Exploring Random Tree (RRT) algorithm [18] is a one of the most famous sampling-based algorithms and exists in many different variants.

Graph-based global path planners use graphs to represent the environment and possible paths. In general, nodes represent certain locations, and edges represent possible paths between these locations. The global path planning algorithm searches for the shortest path between two nodes. Edges can be associated with an additional cost or discount, which makes these edges more or less preferable. This procedure is called weighting. A graph containing differently weighted edges is called a weighted graph. Whilst searching the graph for solutions is quite efficient, building the graph requires some time. Dijkstra’s algorithm [11] or the newer A* algorithm [19] (and some of their many variants) are typical representatives of graph-based local path planners. The A* also relies on a heuristic, which may improve the efficiency of the path planner further. However, its performance depends on accuracy of the heuristic.

Recently, meta-heuristics are also commonly used for path planning. The path planning problem is formulated as an optimization problem, which is then solved by the meta-heuristic. Meta-heuristics use bio-inspired behaviour to efficiently identify good solutions. Most of them, are also resilient against local minima and converge to global minima. However, they are usually good in finding a good solution close to the minimum but are bad in actually identifying the minimum. Some algorithms commonly used are the Ant Colony Optimisation (ACO) [20] or the Genetic Algorithm (GA) [21].

2.2 Local path planning

Similar to global path planning many different local path planning algorithms exists, however, most of them rely on one of very few different principles: Sampling-based, force-based or optimization-based.

Sampling-based local path planners work the same as sampling-based global path planners, but with the information limited to the observable surrounding of the agent. Again, they are simple to implement and can be quick. However, they provide only near-optimal solutions and in general provide low-quality solutions [22].

Force-based relies on an artificial force field for path planning. Here, repulse and attractive forces are used to model different objects, i.e. obstacles are modelled with repulsive forces the goal is modelled with an attractive force. The path planner calculates the total force acting on the agent, which then naturally draws it towards the goal whilst avoiding obstacles. This approach is quite simple to implement. However, it is prone to fall in local optima trapping the agent in a dead end [23].

Most new local path planning algorithms rely on optimization to identify suitable paths. Either by adding an optimizer to one of the two previously discussed approaches or by following an alternative procedure. Here, various candidate paths, path sections or waypoints are defined and evaluated with the help of a cost function. Depending on method to define the candidates and the complexity of the cost function, the computational effort as well as the quality of the result differs [24].

3 Methodology

This work proposes a probabilistic model to define an ideal flight altitude and the best choice of avoidance manoeuvre if encountering an obstacle.

We analyse the height of buildings in all European capital cities and estimate the probability of encountering an obstacle at a given altitude. We also investigate the width and distance between obstacles. We define two strategies to evade obstacles—flying around or over obstacles. A particular cost is associated with every strategy, depending on the probability of encountering additional obstacles. The strategy with the lowest cost is applied by setting the control parameters of a local path planner to predefined settings.

We test the feasibility of our approach with the commonly used local path planner 3DVFH*, initially published in [25].

3.1 Database

A database with information about city buildings is required to develop the probabilistic model. The database needs to contain information about the:

  • Height of buildings

  • Area of buildings

  • Number of buildings at a given height

  • The distance between buildings (at a given height)

Currently, no database directly containing this information is available for various cities. However, multiple sources provide point clouds with height information of areas, including cities. One major contributor is the Copernicus Land Monitoring Service (CLMS) [26]. CLSM provides high-resolution information on land, land usage, and vegetation. One of their services is the urban atlas, which contains, amongst others, the “building height catalogue 2012” [27]. The building height catalogue 2012 contains a high-resolution raster layer map of all European capital cities. Additionally, various services also provide data for the USA. The data is either provided as a list of the tallest buildings (e.g. [28]), a complete list of buildings heights for specific cities (e.g. [29]), Digital Elevation Models (DEM, e.g. [30]), GeoInformationSystem (GIS) data of regions or cities (e.g. [31]) or LiDAR data (e.g. [32]). Despite the high availability of data, data structure, quality, resolution, and accuracy differ significantly for different regions and between sources. Because the Copernicus data set contains uniform data of all European capital cities with high resolution and high accuracy, this work focuses on this data set alone. However, including additional datasets in the proposed method is possible at any time and only requires minor adjustments of the proposed method.

The Copernicus data set contains a high-resolution geo-raster layer. The height information itself is presented as IRS-P5 stereo images [27, 33]. The database contains the inner and outer regions of the cities. However, some cities partly miss some information in the outer areas. Figure 2 shows the Berlin geo-raster layer taken from the Copernicus building height data set. The whole map of Berlin, i.e. the image in Fig. 2, has a 38 × 59 km size. Because the geo-raster layers represent such large portions of the cities, the data in these represent a large variety of urban environments.

Fig. 2
figure 2

Geo-raster map of Berlin from the Copernicus dataset [27]

Full size image

3.2 Height distribution of buildings

This subchapter analyses the height distribution of buildings of all European capitals based on the Copernicus building height catalogue 2012.

The Copernicus dataset discretises the environment and divides the world into cuboidal cells. Any cells centre point has the coordinates \({\varvec{x}} = {\left(x, y, z\right)}^{T}\), where \((x, y)\) represent the position on the ground plane, and z represents the height above the ground. The Copernicus database defines the highest obstacle at an altitude z for every position on the ground plane \((x, y)\). This definition allows for estimating the relative frequency of building height of the cities in the database. Figure 3 gives an overview.

Fig. 3
figure 3

Relative frequency of building height of buildings in 20 European capital cities

Full size image

of the building height of 20 cities in the Copernicus database. The figure shows that cities with higher buildings have a higher variation in building height than cities with mainly lower buildings. For example, Madrid (orange line) has the 25th percentile of building heights at 7 m, the median at 11 m, and the 75th percentile at 18 m. Reykjavik (light blue line) generally has smaller buildings. Reykjavik has the 25th percentile at 4 m, median at 5 m, and 75th percentile at 7 m. However, Fig. 3 also shows that the height distribution varies relatively narrowly. The mean building height of all cities varies between 6 m (Reykjavik) and 14 m (Madrid), which is also shown in Fig. 4 for the same 20 cities as depicted in Fig. 3.

Fig. 4
figure 4

Mean building height in 20 European capital cities based on the Copernicus database

Full size image

The relative frequency \(f\), also known as empirical probability, is defined as the number of times a specific event occurs over the total number of investigated scenarios, as depicted by the following equation:

$$f\left(z\right)=\frac{{n}_{z}}{N}$$
(1)

With respect to the height distribution of buildings in cities, \(z\) denotes the investigated height \(h\) above the ground, \({n}_{z}\) is the number of data points with \(z=h\) in the Copernicus database and \(N\) the total number of cells in the database.

We assume that an obstacle blocks all cells below its highest point, i.e. the point in the Copernicus database. Furthermore, the probability is the relative frequency over an infinite number of trials. Because the Copernicus base has 138 million data points, we can assume the probability \(p(h)\) that an obstacle is in a cell at altitude \(h\), i.e. the cell is blocked for further path planning:

$$p\left(h\right)\cong f(z\ge h)$$
(2)

Finally, the differences between the various European capital cities are relatively small. Therefore, we propose a single probability model representing the average probability of all cities in the Copernicus database at once. Figure 5 shows this average probability distribution, which the proposed decision-maker uses to predict obstacle encounter probabilities.

Fig. 5
figure 5

Average probability p(h) that a cell is blocked over the altitude derived from the Copernicus data set for all European capital cities

Full size image

The proposed algorithm shall consider the distance of gaps between buildings as well. Therefore, the Copernicus database needs to be analysed regarding this point.

We build a raster map based on the Copernicus database for every altitude \(h \in {\mathbb{N}}\) below the altitude of the highest building in this city. Every cell of every raster map is either free or blocked, depending on the altitude \(h\) of the raster map and the altitude of the entry in the geo-raster layer at the very same position. Figure 6 visualises an example of this map. Only looking at the closest occupied cells underestimates the distances, as neighbouring cells can be the same obstacle. Therefore, we cluster adjacent cells to one obstacle with the geodesic distance algorithm described in [34]. This gives the black bounding boxes in Fig. 6. Based on the bounding boxes, the size of the obstacles can be determined and gives the average altitude-dependent obstacle width \(\overline{{w }_{obst}} (h)\). UAV might fly in any direction. An UAV flying from left to right in Fig. 6 perceives another width \(w\) of the obstacle at the top right than a UAV flying from bottom to top. Therefore, we do not differentiate the orientation of obstacles and assume that every obstacle has two widths. The average width of all obstacles \(\overline{{w }_{obst}} (h)\) is then given by:

$$\overline{{w_{obst} }} \left( h \right){ } = \frac{\sum w\left( h \right)}{{2\,n\left( h \right)}}$$
(3)
Fig. 6
figure 6

Example of the raster map to identify the distance between obstacles gap and their width w

Full size image

where \(n\) denotes the number of obstacles at altitude \(h\).

As seen in Fig. 6, only considering the centre points will overestimate the distances between obstacles. However, the shortest distance between two obstacles is between the two cells, with the shortest distance between cell centres. Furthermore, the shortest distance between the two cells is always the shortest distance between two of their corners. Finally, the average of these distances gives the average gap between obstacles \(\overline{gap }(h)\).

3.3 Probability models

This work proposes the interaction of multiple probability models to predict the number of required obstacle avoidance manoeuvres between the current and goal positions. First, the probability of encountering one or numerous obstacles at a specified flight altitude \(h\) is determined based on the probability that a cell is blocked \(p(h)\) (see Eq. 2). Second, the probability of evading obstacles horizontally or vertically is estimated.

Generally, the probability \(P\) that a particular event \(X\) occurs exactly \(k\) times is denoted by:

$$P\left( {X = k} \right) = \left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)\,p^{k} \,\left( {1 - p} \right)^{{\left( {n - k} \right)}}$$
(4)

Here, \(n\) denotes the number of repetitions of the random experiment, \(p\) denotes the probability of event \(X\) per individual try \(n\). \(\left(\begin{array}{c}n\\ k\end{array}\right)\) is the binominal coefficient of the random experiment.

Applying the general mathematical formulation for obstacle avoidance gives \(X\) as the event of an obstacle encounter, \(n\) as the number of cells between the current and goal positions, and \(k\) as the number of obstacle encounters. Additionally, \(p\) depends on the flight altitude in our case. However, for any \(p(h)\) the dependency on the altitude \(h\) is omitted in the equations for the sake of readability; in any case, \(p=p(h)\).

If the UAV encounters an obstacle, two fundamentally different strategies are available. The UAV can either fly around the obstacle or fly over the obstacle. If the UAV overflies one obstacle, the UAV shall maintain the higher flight altitude until the final goal approach. Because the probability of encountering obstacles generally decreases with increasing flight altitude, the probability of encountering a second obstacle after vertically avoiding the first one is lower than for a horizontal avoidance manoeuvre. The proposed algorithm shall take those two different strategies into account. However, always overflying all obstacles is not efficient. Therefore, a cost is associated with any avoidance manoeuvres. The cheapest avoidance manoeuvre will be performed. The performed manoeuvre depends on the cost of the horizontal and vertical avoidance manoeuvres when the UAV encounters an obstacle. However, the cost of both avoidance manoeuvres depends on the cost of likely future avoidance manoeuvres.

This dependency, in turn, requires a new probability that gives the likelihood of a vertical or horizontal avoidance manoeuvre. This work tested the following strategy: If vertically evading \(k\) obstacles is the cheapest and the probability of meeting at least \(k+1\) obstacles until reaching the goal is higher than 50%, the algorithm assumes vertical evasion for the \(k+1\) obstacle. Otherwise, horizontal evasion is assumed for the \(k+1\) obstacle. The probability \(P\) to encounter more than \(k\) obstacles is given by:

$$P\left(X>k\right)=1-P\left(X\le k\right)$$
(5)
$$P(X > k) = 1 - \sum\nolimits_{i = 0}^{k} {\left( \frac{n}{i} \right)} \,p\left( h \right)^{i} \,\left( {1\, - p\left( h \right)} \right)^{n - i}$$
(6)

Similar to Eq. 4, \(X\) denotes the number of obstacle encounters, \(n\) the number of the number of cells between the current position and the goal \(d\). \(p(h)\) denotes the height dependent probability that a cell is blocked.

3.4 Decision maker and cost functions

The decision-maker uses cost functions to estimate the cost of the remaining path and defines which behaviour should be shown by the local path planner. The decision-maker estimates the cost of alternative series of horizontal and vertical avoidance manoeuvres based on the probability of encountering obstacles until the goal is reached iteratively. The cost function predicts the cost of vertical and horizontal evasion based on the probability that either manoeuvre leads to a severe reduction in cost.

We estimate the cost of pure horizontal evasion by multiplying the probability of meeting a certain number of obstacles times the cost to evade these obstacles. The cost of pure horizontal evasion \({c}_{h}\) is given by:

$$c_{h} = \mathop \sum \limits_{k = 1}^{d} P\left( {X = k} \right)\,k\,C_{OE,h}$$
(7)
$$c_{h} = \mathop \sum \limits_{k = 1}^{d} \frac{d!}{{k!\left( {d - k} \right)!}}\,p\left( h \right)\,\left( {1 - p\left( h \right)} \right)^{d - k} \,k\,C_{OE,h}$$
(8)

With \(d\) representing the remaining distance to the goal, \(p(h)\) being the probability that a cell is blocked in altitude \(h\).\({C}_{OE,h}\) denotes the cost to evade one obstacle horizontally and depends on the average smallest distance between two close buildings \(gap\). \({C}_{OE,h}\) is estimated by

$$c_{OE,h} = \left\{ {\begin{array}{*{20}c} {if{ }gap < safety{ }C_{OE,h} = \infty { }} \\ {if{ }gap \ge safety{ }C_{OE,h} = \frac{{\overline{{w_{obst} }} }}{{\overline{gap} }}} \\ \end{array} } \right.$$
(9)

Suppose the average distance between two different obstacles is less than a predefined safety margin to obstacles. In that case, the cost for horizontal evasion shall be very high because a long detour is most likely required to find a suitable gap. However, if the average gap between buildings is larger than the safety margin, horizontal evasion costs decrease with increasing gap size whilst it increases with increasing obstacle width. This relatively simple relationship shall penalise long detours if obstacles (will most likely) block large areas, whilst it rewards the likelihood of large gaps that increase the overall mission safety.

Estimating the cost of pure vertical evasion is not as straightforward as that of pure horizontal evasion. We assume that the flight altitude only decreases during the final goal approach. In turn, the algorithm shall keep its flight altitude after avoiding an obstacle vertically. This behaviour means that \(h\) is not constant, contrary to horizontal evasion manoeuvres. However, \(h\) is not increasing steadily but depends on the probability of encountering an obstacle and the probability that this obstacle is avoided vertically. The cost of pure vertical evasion cv is estimated by:

$${c}_{v}=\sum_{i=0}^{d}P\left(X>{k}_{i},{h}_{j}\right) {C}_{OE,V}$$
(10)
$$\left\{ {\begin{array}{*{20}l} {if} & {P\left( {X > k_{i} ,h_{j} } \right) \ge 0.5~} & {j~~ = j + 1} \\ {if} & {0.2 \le P\left( {X > k_{i} ,h_{j} } \right) < 0.5} & {j~~ = const} \\ {if} & {P\left( {X > k_{i} ,h_{j} } \right) < 0.2} & {c_{v} = \infty } \\ \end{array} } \right.$$
(11)

Again, \(P\) denotes the probability of encountering more than \({k}_{i}\) obstacles (see Eq. 5). \(d\) denotes the distance to the goal and \({h}_{j}\) the flight altitude. \(j\) represents an incremental increase in flight altitude. If the probability of encountering additional obstacles is high, the flight altitude is likely to increase, increasing \(j\) as well. If the probability to encounter additional obstacles is mediocre, the chosen flight altitude shall be kept constant. This means that the next avoidance manoeuvre will be vertical, most likely followed by horizontal ones. If the probability of encountering obstacles is very low, the next avoidance manoeuvre should also be a horizontal manoeuvre, therefore, \({c}_{v}\) is chosen high. \({C}_{OE,V}\) denotes the cost of vertical evasion of one cell. \({C}_{OE,v}\) is constant and a predefined cost factor.

Additionally, the cost to reach altitude \(h\), \({c}_{\Delta }\), is estimated by:

$${c}_{\Delta }={E}_{\Delta } \left(altitud{e}_{current}-h\right)$$
(12)

\({E}_{\Delta }\) denotes the cost for altitude increase, \(altitud{e}_{current}\) denotes the current altitude, and \(h\) denotes the final altitude.

Algorithm 1 shows the structure of the cost estimation tool. The algorithm estimates the cost to reach the goal for all altitudes \(h\) above the current altitude \(altitud{e}_{current}\) until the height of the highest building \({h}_{max}\). The probability of encountering an obstacle \(p\left(h\right)\) in line 3 is determined by Eq. 2. The cost of horizontal evasion at altitude \(h\) \({c}_{h}(h)\) and vertical evasion at altitude \(h\) \({c}_{v}(h)\) is estimated in lines 4 and 5 according to Eqs. 8 and 10, respectively.

Lines 8 to 10 in algorithm 1 identify the cheapest vertical and horizontal costs and the belonging altitudes \(bes{t}_{\dots }\). Finally, depending on the best strategy and altitude, cruise altitude \(altitud{e}_{cruise}\) and the control parameters of the used local path planner are set.

The decision-maker described in Algorithm 1 defines the ideal flight altitude based on the probability of obstacle encounters and sets the control parameters of the local path planner to enforce certain avoidance manoeuvres. However, the decision-maker never decreases its flight altitude until the final goal approach. The decision-maker is looking for the lowest height \(h\) at which the probability of encountering \(k\) or fewer obstacles \(p(X\le k,h)\) is smaller than a predefined threshold \(T\). A short empirical study showed that \(k=3\) and \(T=0.5\), yield satisfactory results. However, a deeper investigation is required to achieve optimal performance of the decision-maker.

Here, it shall be mentioned that the decision-maker is not supposed to plan the actual path. The decision-maker only defines the high-level strategy, the execution of the strategy is then performed by the local path planner. The high-level strategy is defined by setting certain control parameters, i.e. cost function weights, of the local path planner—more on that in the next chapter. The basic idea is the following: If the decision-maker identifies that a vertical avoidance manoeuvre is better than a horizontal avoidance manoeuvre, the weight of the cost of a vertical manoeuvre is reduced whilst the cost of a horizontal manoeuvre is increased. In this way, the decision-maker serves as some kind of experienced mentor giving recommendations to the local path planner. However, in the end, the local path planner remains as the “pilot” of the UAV and defines the best flight manoeuvre based on the input from the decision-maker and its surroundings.

Algorithm 1
figure a

Strategy definition

Full size image

3.5 Feasibility test

This work proposes a probability-based extension to an existing local path planner. Therefore, a local path planner is required to test its feasibility. Various versions of the Vector Field Histogram [12] are commonly used in local path planning for 2D and 3D local path planning. The 3DVFH* [25] is one of the most recent variations of the VFH and is implemented in the px4 avoidance flight controller. However, in this work, we rely on a self-developed implementation of the 3DVFH* presented in [35, 36]. At its core, the 3DVFH* evaluates several candidate paths and estimates their cost. The cost function combines yaw cost, i.e. a horizontal deviation from a straight path to the goal, pitch cost, i.e. a vertical deviation from a straight path to the goal, and different kinds of smoothing costs, i.e. the smoothness of the path and the variation in flight velocity. If any obstacle blocks a candidate’s path, the path is heavily penalised with obstacle costs. The heuristic cost estimate the cost of the remainder of the candidates path, simply based on the remaining Euclidean distance to the goal. Equation 13 gives a simplified version of the primary cost function and its main components, which are explained in more detail in [25, 35].

$${c}_{total}={k}_{yaw} {c}_{yaw}+{k}_{pitch} {c}_{pitch}+{k}_{smooth} {c}_{smooth}+{k}_{obstacle} {c}_{obstacle}+{c}_{heuristics}$$
(13)

The weighting factors \({k}_{yaw}\), \({k}_{pitch}\), \({k}_{smooth}\) and \({k}_{obstacle}\) weight the importance of the different costs against each other. \({c}_{yaw}\), \({c}_{pitch}\), \({c}_{smooth}\), \({c}_{obstacle}\) and \({c}_{heuristic}\) represent the respective cost terms. A high yaw cost weight \({k}_{yaw}\) penalises horizontal evasion, whereas a high pitch cost weight \({k}_{pitch}\) penalises vertical evasion. Depending on the desired flight strategy, the decision-maker chooses the weighting parameters of the local path planner, such that either manoeuvre is generally cheaper. However, the local path planner still performs the actual path planning.

We use a simulation to validate the feasibility of our proposed model with the 3DVFH*. We use MATLAB [37] and the UAV Toolbox to create the simulation environment. We also build forty worlds, which are similar in style from the average of the European capital cities (height distribution is not significantly different 2 sample t-test, p < 0,1). However, the created test environments/cities are completely different in detail. Figure 7 shows an example of a city-centre-like world. Other worlds with smaller obstacles and various spacings also exist. A quadrotor UAV equipped with a LIDAR system is used as a test vehicle.

Fig. 7
figure 7

Example of a city centre part of one of 4 test worlds

Full size image

We evaluate the 3DVFH* regarding its failure probability and its efficiency. A mission fails if the UAV does not reach the goal. The reason for this failure, e.g. a crash or infeasible path planning, is not further analysed. The overall failure probability \({p}_{fail}\) is determined by the number of failed flight \({n}_{f}\) and the total number of investigated flights \(N\), according to:

$${p}_{fail}=\frac{{n}_{f}}{N}$$
(14)

Additionally, we consider flight time and flight distance as efficiency criteria. The shorter the flight (both time and distance), the better. Finally, we also investigate an estimated energy consumption as an efficiency criterium. This estimation is based on discretising the whole flight mission into time steps. The total energy \({E}_{tot}\) consumed for a mission is the sum of all energies consumed during the individual time steps \({E}_{i}\).

$${E}_{tot}= \sum_{i}{E}_{i}$$
(15)

The energy per timestep \({E}_{i}\) is the sum of the change in kinetic energy \({E}_{kin}\), potential energy \({E}_{pot}\), and the energy required to generate a certain thrust \({E}_{thrust}\).

$${E}_{i}={\Delta E}_{kin,i}+{\Delta E}_{pot,i}+{E}_{thrust,i}$$
(16)

It is assumed that the velocity and attitude in each time step are constant. The energy required for attitude control is neglected. The energy required to accelerate the UAV during one timestep is estimated by the acceleration work, which is equal to the change in kinetic energy \(\Delta {E}_{kin}\), given by:

$${\Delta E}_{kin,i}=\frac{1}{2} m\Delta {v}_{i}^{2}$$
(17)
$$\Delta {v}_{i}=\sqrt{{\left({v}_{x,i+1}-{v}_{x,i}\right)}^{2}+{\left({v}_{y,i+1}-{v}_{y,i}\right)}^{2}+{\left({v}_{z,i+1}-{v}_{z,i}\right)}^{2}}$$
(18)

With \({\varvec{v}} = ({v}_{x}, {v}_{y}, {v}_{z})\) denoting the flight velocity. The energy required for altitude changes is given by the change in potential energy, according to:

$$\Delta {E}_{pot,i}= m g ({z}_{i+1}-{z}_{i})$$
(19)

Finally, the energy required to provide sufficient thrust is given by:

$${E}_{thrust, i}=\frac{{T}_{i}^\frac{3}{2}}{\sqrt{2 {S}_{ref} \rho }} \frac{\Delta t}{FOM}$$
(20)

\(\Delta t\) is the length of the time step, \({S}_{ref}\) is the reference area, i.e. the disc area, \(\rho\) denotes the air density, and \(FOM\) is the figure of merit of the rotors. \(FOM = 0.72\) is assumed for the simulation, since this is a typical value for comparable UAV propellers. The thrust of the UAV is denoted by T and estimated via:

$${T}_{i}\cong \sqrt{{\left(m g\right)}^{2}+D}$$
(21)

m denotes the weight of the UAV, g is the gravitational acceleration, and D is the drag force acting on the UAV. D is estimated from [36] with assuming low pitch angles.

4 Results and discussion

We tested the proposed algorithm in multiple environments and worlds; overall, 40 simulated test flights were performed. Figure 8 gives an overview of the performance of the baseline, the standard 3DVFH*, and our proposed method, the 3DVFH* extended with a probabilistic decision-maker, whilst Fig. 9 exemplarily shows a flight path in a typical test situation.

Fig. 8
figure 8

Comparison of the baseline and the proposed method in failure probability, the average flown distance over ground, average flight time, and average energy consumption. All values, except the failure probability, are for successful flights only

Full size image
Fig. 9
figure 9

Example flight path. a isometric view b side view c top view. Blue line indicates a section in which vertical avoidance is preferred and executed. The red line indicates a section which vertical avoidance generally is also preferred. However, the path planner identifies gaps between the buildings such that horizontal avoidance is still better than the best identified vertical avoidance path with the bias for vertical avoidance. The green line indicates the last section in which horizontal avoidance is preferred and also executed

Full size image

The most important difference between these two algorithms is in the failure probability. Whilst the baseline fails to reach the goal in 66% of all flights, our decision-maker enables the algorithm to reach the goal in all test scenarios. This strong reduction in failure probability shows that the introduction of global considerations is highly beneficial.

Figure 8 also shows that the decision-maker flies a longer distance to reach the goal of successful missions than the baseline. Looking at the position of the start and goal point in the 40 tested worlds gives the average direct distance between the start and the goal of 151 m. However, the proposed method finds paths where the baseline does not find paths. Looking only at these worlds in which the baseline is successful gives an average direct distance between the start and goal of only 143 m. If only those worlds are considered in which both algorithms succeed, the decision-maker finds slightly shorter paths than the baseline.

Figure 8 also clearly shows the weaknesses of our proposed algorithm-the mission time is longer, and the energy consumption is higher. The main reason is that the 3DVFH* struggles to decrease the flight altitude during the final goal approach as quickly as the decision-maker commands lower cruise altitudes. Figure 10 shows the flight path during one of the missions. In this mission, the area around the goal point does not contain any obstacles and is a free space. At 10 m distance to the goal, the decision-maker allows the UAV to reduce its flight altitude and approach the goal. However, Fig. 10 shows that the UAV is descending very slowly. The effective descent rate does not match the descent rate required by our Fig. 11 decision-maker to perform an efficient goal approach. Therefore, the descent of the final goal approach starts too late, and the UAV arrives too high over the goal point. From this point, the UAV performs a slow vertical descent. Because the UAV is not equipped with a camera looking downward, the 3DVFH* descends very slowly. Whereas this might be very useful in terms of safety, this long goal approach is the main reason for the longer flight time. The longer flight time, in turn, is the main reason for the higher energy consumption.

Fig. 10
figure 10

Typical flight path of the final goal approach of the 3DVFH* with the decision-maker

Full size image
Fig. 11
figure 11

Comparison of the flight path of the standard 3DVFH* (green) and the proposed combination of 3DVFH* and decision-maker. Grey boxes are obstacles. The flight path goes from left to right. The UAV keeps increasing its flight altitude because of the next obstacles

Full size image

If the final goal approach, i.e. the last 10 m, is neglected, the proposed method’s energy consumption is only around 10% higher than the baseline’s planned path. Again, the proposed method is able to find paths in longer worlds than the baseline. If looking only at those worlds in which both algorithms succeed, the energy consumption of our proposed method is slightly lower than the energy consumption of the baseline. However, the aim of the feasibility testing of this work is not the ideal integration of the decision-maker in the 3DVFH* but a general feasibility test. Optimising the final goal approach’s energy consumption and improving the decision maker’s integration in the 3DVFH* is subject to future work but does not significantly improve the general idea presented in this work.

Looking at the different flight missions in more detail shows that the decision-maker plans smarter than the standard 3DVFH*. Except for the final goal approach, the 3DVFH* acts as intended by the decision-maker. Figure 11 compares parts of the flight paths of the baseline and the proposed method. These obstacles are encountered at the beginning of a flight mission. The probability of encountering additional obstacles is high at this low flight altitude. Our approach shows two consecutive vertical avoidance manoeuvres as recommended by the decision-maker to reduce the probability of further obstacle encounters. The slope is defined by the 3DVFH* which takes the recommendation of the decision-maker into account and identifies the best path based on the cost of its cost function. The baseline already fails to find a path around the first (left) obstacle and tries to fly around it. Because of a series of taller obstacles with small gaps in the north/south direction, the baseline cannot fly past these obstacles. In the case of the standard 3DVFH*, the UAV meanders in front of the gap between two obstacles but cannot fly through the gap because the obstacles are too close. It also fails to find an alternative path and gets stuck in this situation.

5 Conclusion

When a UAV encounters an obstacle in an urban environment, at least two possible evasion strategies usually exist: fly around the obstacle or over the obstacle. Usually, local path planners find their way through an unknown environment by following predefined procedures and preferences. This work proposes a probability-based decision-maker to decide which of two avoidance strategies is used best by a local path planner during its flight mission. The decision-maker decides which strategy to use depending on the probability of encountering a specific number of obstacles until the final goal point is reached.

We analysed the height of buildings in European capital cities and estimated the probability that an obstacle is blocking the flight path of a UAV at a given flight altitude. Our proposed algorithm defines the ideal flight altitude and avoidance manoeuvre based on this probability. We implemented and combined the proposed method with the popular local path planning algorithm 3DVFH*. The test showed that our extended algorithm safely navigated through environments and reached the goal points that the standard version could not reach.

During our tests, the successful flights performed with the decision-maker were longer and required much more energy than without our decision-maker. The main problem is the limited descent rate of the path planned by the 3DVFH*, which leads to an unnecessary long goal approach. This problem could easily be solved by equipping the UAV with a down looking camera. In that case, flight time and energy consumption are only slightly higher than for the baseline–whilst maintaining the significantly lower failure probability.

In the future work, we will further investigate and optimise the goal approach to reduce flight time and energy consumption. The tuning parameters to identify the ideal flight altitude also require further optimization. Improving both aspects will reduce the energy consumption of the paths of the probabilistic decision-maker. However, possible improvements in integrating the proposed decision-maker in a specific algorithm do not lower the general potential of the approach presented in this work. The considerable reduction in failure probability shown here already demonstrates the proposed method’s capability and justifies further research.

Another point is that the path planner is naturally drawn towards certain altitudes which will congest this airspace if many UAVs are operating in the same area. This aspect can be taken into account by modifying the probability model.