Assessment of structural mechanical effects related to torsional deformations of propellers

Abstract

Lifting propellers are of increasing interest for Advanced Air Mobility. All propellers and rotors are initially twisted beams, showing significant extension–twist coupling and centrifugal twisting. Torsional deformations severely impact aerodynamic performance. This paper presents a novel approach to assess different reasons for torsional deformations. A reduced-order model runs large parameter sweeps with algebraic formulations and numerical solution procedures. Generic beams represent three different propeller types for General Aviation, Commercial Aviation, and Advanced Air Mobility. Simulations include solid and hollow cross-sections made of aluminum, steel, and carbon fiber-reinforced polymer. The investigation shows that centrifugal twisting moments depend on both the elastic and initial twist. The determination of the centrifugal twisting moment solely based on the initial twist suffers from errors exceeding 5% in some cases. The nonlinear parts of the torsional rigidity do not significantly impact the overall torsional rigidity for the investigated propeller types. The extension–twist coupling related to the initial and elastic twist in combination with tension forces significantly impacts the net cross-sectional torsional loads. While the increase in torsional stiffness due to initial twist contributes to the overall stiffness for General and Commercial Aviation propellers, its contribution to the lift propeller’s stiffness is limited. The paper closes with the presentation of approximations for each effect identified as significant. Numerical evaluations are necessary to determine each effect for inhomogeneous cross-sections made of anisotropic material.

1 Introduction

Novel aircraft configurations and propulsion architectures frequently rely on propellers due to their high propulsive efficiency. Propellers are long, slender, flexible beams subjected to aerodynamic and inertia loads. Particularly aircraft with VTOL capability require large diameters to reduce power demand in hover. Elastic deformations during operation impact the aerodynamic characteristics and thus the overall aircraft performance, most dominantly due to torsional rotations, i.e., a change in the angle of attack [1]. Besides General Aviation (GA) and Commercial Aviation (CA), Advanced Air Mobility (AAM) concepts popped up in recent years to a large extent. Depending on the aircraft and the intended flight mission, many of these concepts rely on propellers supporting enough thrust to lift the aircraft vertically. These propellers are referred to as lifting propellers in the following.

Multiple small-scale companies manufacture propellers for uncertified applications in light aircraft and new AAM concepts, including unmanned aerial vehicles. Some well-funded start-ups in this market try to design and manufacture their propellers without experience in this field. Unfortunately, especially lifting propellers for AAM offer some geometric and operational peculiarities. Those peculiarities require special attention regarding their aeroelastic coupling effects, which may differ from those of GA and CA propellers [2].

Determining the impact of elastic deformations on aerodynamic performance requires coupled simulations. Both high- and low-fidelity methods are available to investigate propeller loads and deformations. Gur and Rosen present propeller design and optimization strategies for conventional and unconventional propeller applications with reduced-order methods (ROM) [3, 4]. Within the last 2 decades, significant progress has also been made in the simulation and optimization of large propellers and propfans with high-fidelity methods [5,6,7]. Due to the computational cost of multiphysics simulations, reduced-order methods are still attractive for design and optimization purposes, since they provide fair accuracy at minimal cost [8, 9]. Especially smaller propeller manufacturers prefer to rely on ROM, experimental investigations, and engineering judgment instead of high-fidelity approaches. Numerous methods have been developed to determine the aerodynamic loads of propellers and rotors [10]. Most ROM rely on blade element theory, e.g., QPROP [11] or JBLADE [12]. Some reduced-order approaches also include the determination of deformations, commonly with the help of beam formulations [13, 14].

Unfortunately, only a little literature is available explaining the reasons for torsional deformations during the operation of propellers. Up to the 1960s, propellers powered most aircraft. Propeller manufacturers of that day, e.g., Hamilton Standard, had established design guidelines for aerodynamic and structural mechanical design [15]. Aeroelastic coupling effects were known and captured by analytical or semi-empirical approaches. With the rise of computational power, these guidelines have been transferred to computer programs [16]. In the 1980s, unducted fans (or advanced turboprops) were of specific interest due to increasing fuel prices [17]. Besides aerodynamics, some investigations were conducted regarding the structural simulation of the large propeller blades, e.g., by Friedmann and Kosmatka [18].

Structural mechanics and dynamics have been a significant research focus in the helicopter rotor industry for decades [19]. Multiple coupled aeroelastic design and simulation environments have been developed; some are commercially available [20]. Even though helicopter rotors differ from lifting propellers in various regards, both are rotating beams with similar material-related and geometric coupling effects. Thus, the modeling approaches of helicopter rotors regarding nonlinear beam formulations also apply to lift propellers.

Aerodynamic and centrifugal loads, geometric and material-related bending-torsion or extension–twist coupling, restraint warping, or initial twist can cause torsional deformations [21, 22]. Investigating these effects requires sophisticated ROM, high-fidelity simulations (2D shell or 3D solid elements), or experiments [23, 24]. Although Hodges or Kosmatka have explained their implementation in ROM [25, 26], available reduced-order approaches in common simulation environments may not capture all relevant phenomena. The cited methods of Hodges and Kosmatka can model and investigate all relevant phenomena, e.g., within finite-element formulation. Still, the final FE models do not assess the relevance of the specific effects they are capturing.

All propellers, rotors, or wind turbines are rotating beams with an initial twist due to the radial variation in circumferential velocity. The coupling of extension and torsion of initially twisted beams can be a major reason for torsional deformation besides aerodynamic and centrifugal torsional loads [27]. Established guidelines are available for GA and CA to capture these effects, e.g., by Amatt et al. [28]. It has not yet been investigated if these modeling approaches apply to the characteristics of lifting propellers and capture all relevant effects. This paper aims to assess the reasons for different propeller types' torsional deformations and validate the established guidelines' applicability to novel lift propellers. Tilting propellers or tilting rotors differ from lifting propellers regarding their flight mission and geometric characteristics, i.e., disk loading, inflow conditions, and activity factor. Therefore, both are outside the scope of this paper.

An analytical investigation is conducted to investigate the applicability of the existing design guidelines to lifting propellers. First, the authors explain the reasons for the extension–twist coupling of initially twisted beams and the centrifugal twisting moment. Second, the authors present a generic beam model based on a nonlinear analytical formulation published by previous authors. The model can rapidly illustrate the impact of different coefficients on torsional deformation. Third, the impact of the various coefficients is evaluated for different propeller types: GA, CA, and AAM (lifting) propellers. The investigation results shall enable engineers to judge whether the specific effect has to be considered within the design and simulation of lifting propellers. The relevant effects can directly be integrated into reduced-order methods.

Chapter 2 explains the extension–twist coupling and the centrifugal twisting moment, including the presentation of a theoretical model. Chapter 3 introduces a numerical model to simulate both effects. Five test cases validate the approach. The results of an extensive numerical assessment of reasons for torsional deformations are in chapter 4. The authors also present approximations for typical airfoil-shaped cross-sections. The results are concluded in chapter 5. The appendix includes further information and formula of the theoretical model.

2 Theoretical model

Propellers are long and slender structures. Depending on chord length and thickness, the cross-sections of propellers are most commonly solid or hollow with a single cell. Reinforcement of hollow layouts with a spar might become necessary for large chord lengths in CA but is not considered in the following. Solid cross-sections are still applied when dealing with low chord length and thin profiles (in an absolute manner) due to manufacturing benefits. The next chapter derives cross-sectional equilibrium equations valid for arbitrary cross-sections. A solid and a hollow rectangular cross-section are assumed to derive simple algebraic equations for a quantitative investigation.

2.1 Extension–twist coupling

We consider a straight beam with constant cross-sections and initial twist; see Fig. 1. x, y, and z represent the global, rotating coordinate system, x, $\eta$, and $\zeta$ the local, cross-sectional coordinate system, defined by the local major and minor principal axes.

Fig. 1

Rotating prismatical beam with initial twist

Each cross-section has a specific initial twist angle $\beta$ between its major principal axis and the global y-axis. The initial twist k before deformation is

$$k=\frac{d\beta }{dx}.$$

(1)

The extension–twist coupling of initially twisted beams is sometimes also called the trapeze effect [29]. The trapeze effect itself results in two separate effects. First, a tension load applied to initially twisted beams results in internal torsional loads tending to untwist the blade, even if no external torsional load acts on the structure. Second, the trapeze effect results in an additional torsional stiffness. Both effects are briefly explained in the two following subsections. Available approximations for GA and CA propellers are referenced within the corresponding paragraph.

2.1.1 Internal torsional moment due to the trapeze effect

Figure 2 illustrates a beam with a rectangular cross-section. The tension load T acts on the beam tip. The external torsional load is zero (${M}_{t}=0$). The initial twist angle $\beta$ decreases in radial direction, i.e., k is negative. We consider two adjacent radial stations separated by a distance Δr. We further assume constant normal stress at the cross-section

Fig. 2

Blade straightening and stiffening due to the trapeze effect

$${\sigma }_{x}=\frac{T}{A}=const.$$

(2)

The force dF acts between two infinitesimal small areas, dA₁ and dA₂, sharing the same cross-sectional coordinates $\eta$ and $\zeta$, see Fig. 2a and c). The x-component of the force is $d{F}_{x}={\sigma }_{x}$ dA₁. dA₁ and dA₂ have differing z-coordinates due to the initial twist. Accordingly, the force dF has a component dF_z. Multiplying the incremental force component dF_z at dA₁ with its y-coordinate results in an incremental torsional moment. Integrating over the cross-section yields a cross-sectional torsional moment, tending to straighten or untwist the blade under (tension) load. Amatt et al. derived an approximation for this internal torsional moment in [28] (Eq. 94), which neglects the impact of elastic deformations on actual twist under loads.

2.1.2 Increase in torsional rigidity due to the trapeze effect

We again consider the beam illustrated in Fig. 2, but with zero tension load and a nonzero external torsional moment ($T=0;{M}_{t}\ne 0$). Due to the external torsional load, the beam will twist (positive in the case of positive torsional load). It is readily apparent by the view onto the trailing edge (Fig. 2) that this twist compresses an incremental fiber connecting dA₁ and dA₂. The compression of the fiber results in an internal load. Due to the orientation of the fiber, the incremental force at dA₁ has a component in the z-direction. Since the force component has a lever arm in the y-direction, an incremental torsional load results. This internal torsional load counteracts parts of the external load and is proportional to the elastic twist. It is, therefore, commonly considered as an additional stiffness. Amatt et al. also derived an approximation for this effect in their design guidelines [28] (Eq. 125). However, they only consider the stiffening effect of the initial twist in combination with the elastic twist. Large elastic deformations without initial twist result in a similar nonlinear stiffening effect, which they do not account for. As shown in the results section, the neglection of this nonlinear stiffening is valid for most propeller types but does not generally hold for all rotating beams.

2.1.3 Nonlinear formulation of the extension–twist coupling of initially twisted beams

The approximations described by Amatt et al. [28] are simple and straightforward. Still, they neglect the coupling between tension load and elastic twist and the nonlinear coefficients of the extension–twist coupling. Therefore, the nonlinear analytical formulation by Rosen [22] is applied in the present investigation. Only a summary of the theory is presented here. A more comprehensive derivation is available in the original paper.

The deformation is assumed to be a superposition of Saint–Venant torsion and axial elongation ${u}_{1}$

$$u={u}_{1}+\theta \psi$$

(3a)

$$v=y\left({\text{cos}}\phi -1\right)-z{\text{sin}}\phi$$

(3b)

$$w=y{\text{sin}}\phi +z\left({\text{cos}}\phi -1\right),$$

(3c)

where $\psi$ is the Saint–Venant warping function, $\phi$ is the elastic twist angle of a cross-section, and $\theta$ is the elastic twist

$$\theta =\frac{d\phi }{dx}.$$

(4)

The bar is assumed to be free to warp at the ends. No small angle assumptions are made. Differentiation of Eqs. (3a–c) yield the nonlinear strain components. Restricting them to small strains and finite rotations, they are inserted into the potential of internal and external forces of the bar. The equilibrium equation becomes

$${M}_{t}=\frac{S}{A}T+\frac{{I}_{p}}{A}T\theta +G{J}_{s}\theta +E\left(K-\frac{{S}^{2}}{A}\right)\theta +E\frac{3}{2}\left(D-\frac{{I}_{p}S}{A}\right){\theta }^{2}+E\frac{1}{2}\left(F-\frac{{I}_{p}^{2}}{A}\right){\theta }^{3};$$

(5)

M_t is the sectional torsional moment, E is the Young’s modulus, and G is the shear modulus. The resulting geometric cross-sectional integrals are

$$D=\underset{A}{\overset{ }{\int }}{\left(\frac{\partial \psi }{\partial x}\right)\left({y}^{2}+{z}^{2}\right)}dA$$

(6)

$$F=\underset{A}{\overset{ }{\int }}{\left({y}^{2}+{z}^{2}\right)}^{2}dA$$

(7)

$${I}_{p}=\underset{A}{\overset{ }{\int }}{\left({y}^{2}+{z}^{2}\right)}dA$$

(8)

$${J}_{s}=\underset{A}{\overset{ }{\int }}\left[{\left(-z+\frac{\partial \psi }{\partial y}\right)}^{2}+{\left(y+\frac{\partial \psi }{\partial z}\right)}^{2}\right]dA$$

(9)

$$K=\underset{A}{\overset{ }{\int }}{\left(\frac{\partial \psi }{\partial x}\right)}^{2}dA$$

(10)

$$S=\underset{A}{\overset{ }{\int }}{\left(\frac{\partial \psi }{\partial x}\right)}dA.$$

(11)

Formula (5) is valid for arbitrary homogenous cross-sections. The first and second terms on the right side represent internal torsional moments due to the initial (1st) or elastic twist (2nd) combined with a tension load T. J_s is the Saint–Venant torsional stiffness. Terms 4–6 represent the linear (4th) and the nonlinear (5th and 6th) change of torsional rigidity due to elastic twist. Terms 4 and 5 are coupled with the initial twist. Cross-sections not offering two-fold symmetry further suffer from extension-bending and torsion-bending coupling, which is outside the scope of this paper.

To investigate the impact of the different coefficients stated in Eq. (5), a thin rectangular cross-section of width w and thickness t with t $\ll$ w is assumed. The warping function for hollow and solid cross-sections is approximately $\psi \approx -yz$. In this case, the initial twist contributes to the radial change of the warping function [30]

$$\frac{\partial \psi }{\partial x}=\frac{\partial \psi }{\partial \zeta }\frac{\partial \zeta }{\partial x} +\frac{\partial \psi }{\partial \eta }\frac{\partial \eta }{\partial x}=k\left(\eta \frac{\partial \psi }{\partial \zeta }+\zeta \frac{\partial \psi }{\partial \eta }\right)\approx k\left({\eta }^{2}-{\zeta }^{2}\right).$$

(12)

Inserting (12) in (6–11) simplifies Eq. (5) for solid cross-sections to

$${M}_{t}=\frac{T{w}^{2}k}{12}+\frac{T{w}^{2}\theta }{12}+\frac{Gw{t}^{3}\theta }{3}+\frac{E{w}^{5}t{k}^{2}\theta }{180}+\frac{E{w}^{5}tk{\theta }^{2}}{120}+\frac{E{w}^{5}t{\theta }^{3}}{360}.$$

(13)

Equation (13) is the governing equation for the cross-sectional elastic twist $\theta$. Integration over the beam length yields the global twist angles. The equation has also been derived by Danielson and Hodges [31]. They present a formulation for beams oriented arbitrarily in space, undergoing large deformation and small strains. Rosen [32] or Danielson and Hodges [31] have not explicitly derived the governing equation for hollow cross-sections. The authors, therefore, present the integrals (6–11) for hollow layouts in the appendix.

2.2 Centrifugal twisting moment

Centrifugal accelerations are the primary reason for tension loads in rotating propellers or rotors. External torsional loads may arise from aerodynamic loads due to a lever arm from the center of pressure to the shear center. The centrifugal twisting moment is an additional reason for torsional loads. Depending on the geometry, material, and operational conditions, the centrifugal twisting moment can be significantly greater than aerodynamic torsional loads. Due to the relevance of this load, a short derivation is presented.

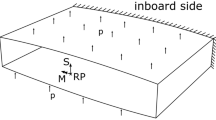
We consider a straight beam with rectangular, initially twisted cross-sections of length R with solid or hollow cross-sections; see Fig. 3. The beam rotates with angular velocity $\Omega$

Fig. 3

Incremental centrifugal twisting moment

$$\overrightarrow{\omega } =\left(\begin{array}{c}0\\ 0\\\Omega \end{array}\right).$$

(14)

The cross-sectional centrifugal load increment can be summarized as acting at the cross-sectional center of gravity. However, every infinitesimal mass point within a cross-section having a nonzero y-coordinate results in a centrifugal force component in the y-direction. We consider a point P(x, y, z $\ne$ 0). The infinitesimal centrifugal loads at point P are due to the centrifugal acceleration a

$$\begin{aligned} \overrightarrow {{dF_{{CF}} }} = \vec{a}dm = \, - \left( {\vec{\omega } \times \left( {\vec{\omega } \times \overrightarrow {{r_{P} }} } \right)} \right)dm. \\ & \rho \;\Omega ^{2} \left( {\begin{array}{*{20}c} x \\ y \\ 0 \\ \end{array} } \right)\;dA\;dx \\ \end{aligned}$$

(15)

In the case of twisted sections (initially or elastically twisted), i.e., for all propellers, rotors, and wind turbines, the centrifugal force dF_CF,y results in a torsional load due to the lever arm in z-direction

$$d{M}_{t,CF} =-d{F}_{CF,y}\cdot z=-\rho {\Omega }^{2}y z dA dx.$$

(16)

Integration over the cross-section yields the radial increment of the centrifugal twisting moment

$$\frac{{{\text{dM}}}_{{\text{t}},{\text{CF}}}}{{\text{dx}}}={{\text{M}}}_{{\text{t}},{\text{CF}}}^{\mathrm{^{\prime}}} =-\underset{A}{\overset{ }{\int }}\rho {\Omega }^{2}y z dA.$$

(17)

The local principal axes of the cross-section are $\eta$ and $\zeta$, see Fig. 4.

Fig. 4

Cross-sectional definitions

The actual pitch angle $\gamma$ during operation is the sum of the initial twist angle $\beta (x)$ and the elastic twist angle $\phi (x)$

$$\gamma =\beta +\phi$$

(18)

The transformation between global and local (cross-sectional) coordinate system is

$$y =\eta {\text{cos}}\gamma -\zeta {\text{sin}}\gamma$$

$$z =\zeta {\text{cos}}\gamma +\eta {\text{sin}}\gamma .$$

(19)

Inserting Eq. (19) into (17) and integrating over the cross-section yield the radial increment of the centrifugal twisting moments

$${M}_{t,CF}{\prime}\approx -\frac{\rho }{2}{\Omega }^{2}\left({{I}_{\zeta \zeta }-I}_{\eta \eta }\right){\text{sin}}2\gamma .$$

(20)

Equation (20) is valid for any homogenous cross-section with its tension center coinciding with the pitch axis of the rotating beam. If the section deforms in the y- and z-direction by $\Delta y$ and $\Delta z$, Eq. (20) becomes (derivation see Amatt et al. [28] Eq. 83)

$$M_{{t,CF}} ^\prime \approx - \frac{\rho }{2}\Omega ^{2} \left[ {\left( {I_{{\zeta \zeta }} - I_{{\eta \eta }} } \right){\text{sin}}2\gamma + \Delta y\Delta zA} \right].$$

(21)

3 Numerical model

The considerations above are based on cross-sectional equilibrium. The authors prepare a model and assumptions to calculate the cross-sectional tension load T, aerodynamic twisting moment M_t,Aero, the centrifugal twisting moment M_t,CF, and the global twist angle $\phi$.

3.1 Model derivation

We still focus on solid or hollow rectangular cross-sections with constant initial twist rate, chord length, and thickness. The tension load $T\left(r\right)$ is solely due to centrifugal forces

$$T\left(r\right)=\underset{V}{\overset{ }{\int }}\rho {a}_{x} dV=\underset{x=r}{\overset{R}{\int }}\rho {\mathrm{A\Omega }}^{2}x dx=\frac{1}{2}\rho A{\Omega }^{2}\left({R}^{2}-{r}^{2}\right).$$

(22)

The centrifugal twisting moment is determined by integrating Eq. (20) from the actual radial position r to the tip radius R

$${M}_{t,CF}\left(r\right)=\underset{x=r}{\overset{R}{\int }}{M}_{t,CF}{\prime} dx.$$

(23)

The initial twist angle is known a priori, but the elastic twist angle is not. Amatt et al. [28] neglect them in determining the centrifugal twisting moment for GA and CA propellers. Including the elastic twist requires an iterative solution, but the computational costs are vanishingly small. The authors, therefore, have chosen an iterative solution procedure.

Additional external torsional loads are due to aerodynamic forces. The offset between the cross-sectional pressure point and the shear center (origin) depends on both the airfoil and the structural layout. Typical values range from 0 to 20% chord length. Within this study, the distance is assumed to be 10% of the chord length, i.e., the beam width w. A hypothetical aerodynamic thrust per blade P is applied to the beam. The value of the thrust P will be discussed in Sect. 4.1. The thrust is assumed to be distributed in a triangular form, roughly approximating a realistic load distribution of a propeller

$$\frac{{\text{dP}}}{{\text{dx}}}=\frac{2{\text{P}}}{{\text{R}}}\frac{{\text{x}}}{{\text{R}}}=\frac{2{\text{P}}}{{{\text{R}}}^{2}}{\text{x}}.$$

(24)

The resulting aerodynamic torsional moment at a radial station x is

$${{\text{M}}}_{{\text{t}},{\text{Aero}}}\left({\text{x}}\right)=\underset{{\text{x}}={\text{r}}}{\overset{{\text{R}}}{\int }}\frac{2{\text{P}}}{{{\text{R}}}^{2}}{\text{x}}\frac{{\text{w}}}{10}\mathrm{ dx}={\text{P}}\frac{{\text{w}}}{10}\left(1-\frac{{{\text{r}}}^{2}}{{{\text{R}}}^{2}}\right).$$

(25)

The initial twist is too large for small angle assumptions to be valid. Still, the aerodynamic lift of each cross-section is approximately aligned with the minor principal axis. Hence, the assumption of the constant lever arm of 10% of the chord length is a valid approximation. Shear loads or bending moments are not considered in the model. The cross-sectional equilibrium of a solid rectangular cross-section becomes

$${M}_{t,Aero}+{M}_{t,CF}-\frac{T{w}^{2}k}{12}-\frac{T{w}^{2}\theta }{12}=+\frac{Gw{t}^{3}\theta }{3}+\frac{E{w}^{5}t{k}^{2}\theta }{180}+\frac{E{w}^{5}tk{\theta }^{2}}{120}+\frac{E{w}^{5}t{\theta }^{3}}{360}.$$

(26)

It is worth mentioning that k is negative for propellers, and the third term on the left side is a positive, i.e., a pitch-up torsional load. In the case of a positive elastic twist, the terms on the right side are all positive (stiffening) except the third one. For a handier visualization in the results section, Eq. (26) is abbreviated to

$${M}_{t,Aero}+{{\text{M}}}_{{\text{t}},{\text{CF}}}+{C}_{1}+{C}_{2}={C}_{3}+{C}_{4}+{C}_{5}+{C}_{6}.$$

(27)

The left side of Eq. (27) represents the external and the induced torsional loads, while the right side represents the twist-related internal torsional loads.

3.2 Validation of the numerical model

Rosen presents an experimental validation of Eq. (13) in his publication [32]. In the first step, the authors repeat the validation using three-dimensional finite elements instead of experiments and extend the validation to hollow cross-sections. In the next step, the derivation of centrifugal torsional and tension loads is validated by a simulation of a rotating beam with geometric properties similar to a propeller.

3.2.1 Validation test case 1 (Rosen’s test case 1 [32])

The first experiment investigates the torsional behavior of an initially twisted thin steel strip with a rectangular cross-section and the following data:

• Length: 600 mm

• Width: 10 mm

• Thickness: 0.5 mm

• Initial twist: 1283°/m

• Young’s modulus: 192,000 MPa

• Shear modulus: 74,500 MPa.

The geometry is loaded by a constant end tension load of 28.6 N and increasing torsional loads. Due to the length of the specimen, boundary conditions can be neglected.

Figure 5 plots the nondimensional torsional load versus the nondimensional twist rate, relative to the case of no torsional load and constant end tension load. The FEM results are in excellent agreement with the experimental results of Rosen but with less noise. The nonlinear theory is in good agreement with the validation data, showing errors below 3% compared to the FEM results. The dashed line represents the linear theory, neglecting the coefficients C₅ and C₆. Rosen concluded that these nonlinear terms are neglectable up to a nondimensional twist rate of $\theta w=0.05$, but this value depends on both material and geometric data. Both coefficients are, therefore, considered in all further simulations.

Fig. 5

Nondimensional end torsional load versus nondimensional twist rate of an initially twisted solid beam

3.2.2 Validation test case 2

Since Rosen derived Eq. (13) for solid rectangular cross-sections [32], the validation is repeated for a hollow rectangular cross-section with geometric properties similar to a propeller:

• Length: 1000 mm

• Width: 100 mm

• Cross-sectional thickness: 12 mm

• Skin thickness: 3 mm

• Initial twist: − 50°/m.

The material stiffness is the same as in the first experiment and will be kept constant for the complete validation section of this paper. The authors derive the equilibrium equation of the present model in the appendix. Figure 6 plots the torsional load versus the twist rate of a hollow cross-section. Errors range from − 8% to + 2%. The maximum torsional load equals 3000 Nm. The quadratic term (C₅) contributes less than 3% to the stiffness at maximum torsional load, and the cubic term (C₆) has a neglectable impact, resulting in an almost linear torsional stiffness. Further increasing the torsional load to investigate the nonlinear behavior results in skin buckling and is omitted, since such load magnitudes are outside the range of practical interest of typical propellers, as seen in the next chapter.

Fig. 6

Nondimensional end torsional load versus nondimensional twist rate of an initially twisted hollow beam

3.2.3 Validation test case 3 (Rosen’s test case 2 [32])

Rosen further investigated the twist rate at increasing end tension load within a second test case. The geometrical data of the second specimen are as follows:

• Length: 710 mm

• Width: 4.45 mm

• Thickness: 0.2 mm

• Initial twist: 1856°/m.

As stated by Rosen, applying high tension loads leads to compressive stresses at the edges of the strip while untwisting. Therefore, a constant end torsional load of Mt = 57.5Nmm was required to avoid buckling.

Figure 7 illustrates the nondimensional elastic twist rate at increasing tension loads. Errors between the nonlinear theory and FEM results are below 6%. Even though looking linear, the behavior is, in fact, nonlinear, but the effects C₂ and C₅ cancel each other approximately out, resulting in a linear-looking behavior. As in validation case 1, the FE results are in excellent agreement with the experimental data. The nonlinear theory is in good agreement with the validation results.

Fig. 7

Nondimensional end tension load versus nondimensional twist rate of an initially twisted solid beam

3.2.4 Validation test case 4

The validation is repeated for a hollow cross-section. The geometry of test case 2 is loaded by an end tension force. Figure 8 plots the dimensionless twist rate at increasing load. The tension stresses are equal to those of test case 3, but since the section is hollow, the absolute tension load decreases significantly. At the same time, the Saint–Venant torsional stiffness is reduced only to a small extent. Therefore, substantially lower twist rates occur. Further increasing the tension load is of no practical interest, since it would exceed the yield strength. The deviations seem to increase slightly compared to test case 3. The somewhat higher deviations are due to the relative thickness of the cross-section. All derivations of the present theory are processed with the assumption of small relative thicknesses. The cross-sectional integrals, as well as the warping function, lose accuracy with increasing thickness, therefore resulting in increasing deviations. Still, the model matches the FE results with errors below 10%.

Fig. 8

Nondimensional end tension load versus nondimensional twist rate of an initially twisted hollow beam

3.2.5 Validation test case 5

An initially twisted, solid rotating beam is considered to validate the calculation of the centrifugal torsion and tension load. The geometric data are

• Length: 1000 mm

• Width: 100 mm

• Thickness: 12 mm (solid)

• $\beta \left(r=0\right)=65^\circ$

• Initial twist: − 50°/m

• Density: 7850 kg/m.³.

The blade tip Mach number quantifies the rotational speed. The torsional deformation at the tip is measured. Figure 9 shows the comparison of FE-simulation results and the present theory. With errors of approximately 10%, a good agreement between both approaches confirms the model's applicability to phenomenological investigations.

Fig. 9

Torsional deformation of an initially twisted rotating steel beam at the beam tip

4 Results

4.1 Parameter space

This section investigates three generic beam types similar to specific propeller categories to assess the impact of the different effects. In this context, GA is represented by a typical four-seated single-engine aircraft, whereas CA is represented by a commercial transport aircraft with multiple engines. This classification is simplified and not exhaustive. A review of existing propeller designs yields typical geometric and operational properties to represent the three types, as summarized in Table 1.

Table 1 Comparison of blade characteristics

D is the propeller diameter. $\Delta \beta$ is the difference in the initial twist angles between the blade tip and root. k is the constant initial twist rate. w is the constant width of each beam and corresponds to typical chord lengths. t/w is the relative thickness. The thrust P is the force acting on each propeller blade in the triangular form described above.

Each propeller type is analyzed for different chord lengths and relative thicknesses. The relative thicknesses range from 2 to 18%. The thickness range's lower and upper boundaries are uncommon except for some applications. Still, they are included in the study to illustrate some trends. The blade tip Mach number is 0.7 = constant. Typical tip Mach numbers are below 0.7, so this value is considered conservative, since it leads to the highest centrifugal loads. The propellers are numerically analyzed at 11 radial stations, i.e., the beam is discretized into ten segments. A convergence study proved that further increasing the number of segments leads to neglectable variations of the results due to the constant cross-sectional layout.

The investigation includes three different materials. Table 2 lists the corresponding parameters. The aluminum alloy is the baseline material considered in most of the simulations. The properties of the steel alloy are the same as those from Rosen’s experimental tests [32]. A third isotropic material shall represent the stiffness and density of a carbon fiber-reinforced polymer (CFRP).

Table 2 Material properties

4.2 Results’ visualization

Several bar plots in the appendix illustrate the different impact of each effect defined in chapter 3.1. The results for a specific combination of propeller type, chord length, relative thickness, and radial station are separately visualized in the following manner. Each bar diagram consists of two columns representing the left and right sides of Eq. (27). The left column represents the left side of the equation, including the aerodynamic torsional moment M_t,Aero, centrifugal twisting moment M_t,CF, and the internal moments C₁ and C₂ due to initial and elastic twist. C₁ and M_t,Aero are positive in all cases (according to the assumptions). M_t,CF is negative as long as the local twist angle $\gamma$ is below 90° (very thin beams can reach this state without exceeding material allowables). C₂ is negative as long as $\theta$ is positive. Especially, in the root region, the sum of all external and induced moments can be negative, resulting in a positive value of C₂. The sum of all external and induced torsional loads is written above each diagram. The elastic torsional deformation at the blade tip (not at the actual section) is also displayed above the bars. It yields information on the impact of torsional deformation on aerodynamic performance. As a rule of thumb, torsional deformations below 0.1 deg have a low impact on overall performance.

The right column represents the internal reaction of each cross-section solely related to the elastic twist $\theta$ and their couplings with k (C₃–C₆). C₅ is negative in all cases. C₃, C₄, and C₆ are positive as long as the elastic twist is positive.

The sum of external and induced torsional loads equals the sum of C₃ to C₆ according to Eq. (27). Each column is normalized with the sum of their positive values Sum_pos, so the upper bar height is one. Due to the significantly varying sectional loads, this normalization was necessary for illustrative purposes. It should be noted that the two columns are normalized with different values of Sum_pos. Table 3 shows the values of each effect of Fig. 10 and the corresponding summations.

Table 3 Loads at an exemplary cross-section / Nm

Fig. 10

Explanation of results diagram

4.3 Discussion

Extensive parameter sweeps are conducted to investigate the parameter space. The corresponding plots illustrating the results of the assessment are in the appendix. Table 4 gives an overview of those figures.

Table 4 Overview of figures in the appendix

The first plot (Fig. 11) shows the load distribution versus the relative thickness for three chord lengths at 70% of the radius. The geometry is of solid aluminum and represents an AAM propeller. Regarding the external and induced torsional loads (left bar), all effects are found to have a significant contribution to the overall cross-sectional torsional loads. The aerodynamic torsional loads dominate for low chord lengths. The impact decreases with increasing thickness and chord length.

Except for narrow geometries, the extension–twist coupling C₁ exceeds the aerodynamic and centrifugal twisting moments. C₂ is important at low thicknesses, but its contribution reduces for high thicknesses. Still, the contribution is above 2% in most cases for t/w < 0.18 and above 5% for t/w < 0.10. The centrifugal torsional loads M_t,CF significantly contribute in all cases.

In most cases, the Saint–Venant torsional rigidity (C₃) dominates the overall torsional rigidity. C₄ plays a role in very wide or very thin cross-sections. The impact of C₅ and C₆ is noticeable only for high elastic twist rates $\theta$ and high width, since they are proportional to w⁵ times ${\theta }^{2}$ and ${\theta }^{3}$, respectively. High elastic twist rates solely occur for cross-sections with less than 4% relative thickness, but the elastic tip deformations in excess of 10° are of no practical interest regarding propeller applications. Even though the test cases with low thicknesses (t/w < 4%) reach high twist angles, the material allowables have not been exceeded in any case.

Figure 12 shows the load distribution vs. the dimensionless radial position of the geometries investigated in the previous plot for 12% relative thickness. The results show a relatively uniform distribution, i.e., the impact of each effect does not significantly depend on the radial position. Solely the centrifugal torsional loads increase toward the root region, since the angle of initial twist $\beta$ is highest at x = 0. Consequently, the elastic twist can be negative in the root region.

Figures 13 and 14 repeat the simulations of Fig. 11 with a hollow cross-section and a skin thickness of s = 1.5 mm and s = 3.0 mm, respectively. The relative cross-sectional thickness is limited to t/w ≥ 6%. Due to the hollow layout, the cross-sectional area is reduced, resulting in lower centrifugal loads, while the Saint–Venant torsional rigidity is less impacted. Accordingly, the impact of the aerodynamic torsional loads M_t,Aero increases compared to M_t,CF, C₁, and C₂. The Saint–Venant torsional rigidity dominates the overall rigidity. Even though the hollow layout reduces the sum of all torsional loads, the tip twist angles increase due to decreased torsional rigidity.

Figures. 15 and 16 show the impact of varying materials compared to the baseline in Fig. 11. The steel alloy has a specific stiffness comparable to aluminum. In contrast, the CFRP has similar absolute stiffness at a reduced density. Regarding the steel alloy, the increased density results in higher centrifugal and overall cross-sectional torsional loads. Accordingly, the aerodynamic torsional loads lose some importance but still have a significant impact, especially at low thicknesses. While the overall cross-sectional loads increase, the torsional deflections at the tip decrease. CFRP shows the opposite behavior: aerodynamic torsional loads are increasingly important due to decreased density. While the cross-sectional loads decrease, the torsional deformations increase only to a limited extent.

Figures. 17 and 18 show the torsional load distribution of a Commercial Aviation propeller and a General Aviation propeller, respectively. Both types have cross-sectional dimensions exceeding those of the AAM type. Accordingly, cross-sectional loads increase. Furthermore, the initial twist k is a multiple of the AAM type. Consequently, the k-related coefficients C₁, C₄, and C₅ are of increased significance. Especially, the C₁ term now dominates the torsional loads. Aerodynamic torsional loads have almost no impact for moderate thicknesses and chord lengths. The nonlinear coefficients C₅ and C₆ are still neglectable for relative thickness above 4%, even though C₅ is more pronounced compared to AAM propellers. M_t,CF has a significant impact on torsional loads in all cases due to high angles of initial twist $\beta$.

The impact of the elastic twist angle $\phi$ on the centrifugal twisting moment can be significant, especially for long and slender propellers as for AAM, since the initial twist angle is small and the elastic twist angles are high

$${M}_{t,CF}\sim {\text{sin}}\left(2\gamma \right)={\text{sin}}\left(2\beta +2\phi \right).$$

(28)

The impact of $\phi$ on M_t,CF reduces for CA and GA propellers as they have initial twist angles significantly greater than AAM and smaller elastic twist angles in most cases

$${\text{sin}}\left(2\beta \right){\text{cos}}\left(2\phi \right)+{\text{cos}}\left(2\beta \right){\text{sin}}\left(2\phi \right)\approx {\text{sin}}\left(2\beta \right)+{\text{cos}}\left(2\beta \right)2\phi \approx {\text{sin}}\left(2\beta \right).$$

(29)

The authors assume that Amatt et al. therefore neglected M_t,CF($\phi$), as they wrote their design guidelines for GA and CA propellers. If the magnitude of the elastic twist angle is known a priori or can be estimated, M_t,CF($\phi$) can be neglected. Since this is not the case in most design procedures, the authors advise determining the centrifugal torsional loads in the deformed state.

4.4 Approximations for airfoil-shaped cross-sections

The effects identified as important can be rapidly estimated with the help of approximations derived and published by Amatt et al. [28]. Their formulas are valid for solid and hollow cross-sections made of isotropic, homogenous material. The derivation of C₂ is straightforward and does not require an approximation

$${M}_{t,CF}\left(r\right)\approx \underset{x=r}{\overset{R}{\int }}-\frac{\rho }{2}{\Omega }^{2}\left[\left({{I}_{\zeta \zeta }-I}_{\eta \eta }\right){\text{sin}}2\gamma +\Delta y\Delta zA\right] dx$$

(30)

$${C}_{1}\approx \frac{1}{A}\left({I}_{\zeta \zeta }+{I}_{\eta \eta }\right)Tk$$

(31)

$${C}_{2}=\frac{1}{A}\left({I}_{\zeta \zeta }+{I}_{\eta \eta }\right)T\theta$$

(32)

$${C}_{5}\approx {C}_{6}\approx 0.$$

(33)

Amatt et al. [28] further present tabular data to estimate C₃ and C₄ for NACA 16 and 65 series profiles on page 35ff.

Using anisotropic materials (composites) or inhomogeneous materials (trim weight or foam inserts) requires numerically solving the cross-sectional integrals (6–11), (21), and (22).

5 Conclusion

The presented investigation yields the following conclusion:

• The centrifugal twisting moment M_t,CF plays a significant role in almost all cases. The correction of the initial twist angle $\beta$ by the elastic twist angle $\phi$ should be included in the analysis.

• The internal torsional load C₁ induced by the initial twist k significantly contributes to the net torsional load and cannot be neglected in any case.

• The internal torsional load C₂ induced by the elastic twist $\theta$ might not be neglectable for most common propellers. Further, they are more pronounced when low chord lengths and thicknesses are chosen, as for slender AAM propellers.

• The Saint–Venant torsional rigidity C₃ contributes significantly to the net stiffness in all cases.

• The linear torsional rigidity due to the initial twist C₄ contributes significantly for GA and CA propellers, but is neglectable for AAM.

• The nonlinear torsional rigidities C₅ and C₆ are of no practical interest for the investigated propeller types. They might play a role for very thin and wide propellers, e.g., for Prop-Fans.

• The approximations of Amatt et al. (neglection of C₂, C₅, and C₆) are well suited for preliminary design purposes in Commercial and General Aviation. C₂ is comparatively small except for very thin cross-sections. The authors still advise including C₂ in the simulation, since its contribution can exceed 5% for moderate thicknesses.

• The approach of Amatt et al. to determine the centrifugal twisting moment solely based on the initial twist should be corrected by the elastic twist iteratively, especially for AAM propellers. Regarding CA and GA propellers, the determination based on the initial twist is still a well-suited approximation with errors below 5%.

Table 5 summarizes the relevance of the investigated effects for the different propeller types. It also states if there are approximations available by Amatt et al. [28]. The table can be used as a guideline to include specific effects.

Table 5 Summary of the relevance of different effects

Appendix

1.1 Cross-Sectional integrals of hollow cross-sections

For rectangular hollow cross-sections, the inner and outer thicknesses and widths are

${w}_{o}=w$; ${w}_{i}=w-2s;$ ${t}_{o}=t$; ${t}_{i}=t-2s$ with s as the skin thickness.

With Eq. (12), the cross-sectional integrals defined by Rosen [32] are integrated in the local $\eta /\zeta$-coordinate system, assuming that the terms ${\zeta }^{2}/{\eta }^{2}$ and ${\zeta }^{4}/{\eta }^{4}$ are neglectable compared to unity

$$D=\underset{A}{\overset{ }{\iint }}\left(\frac{\partial\Psi }{\partial x}\right)\left({y}^{2}+{z}^{2}\right) dy dz=k\underset{A}{\overset{ }{\iint }}{\eta }^{4}\left(1-\frac{{\zeta }^{4}}{{\eta }^{4}}\right) d\eta d\zeta \approx k\frac{1}{80}\left({t}_{o}{w}_{o}^{5}-{t}_{i}{w}_{i}^{5}\right)=k F$$

$$F=\underset{A}{\overset{ }{\iint }}{\left({y}^{2}+{z}^{2}\right)}^{2} dy dz=\underset{A}{\overset{ }{\iint }}{\eta }^{4}{\left(1+\frac{{\zeta }^{2}}{{\eta }^{2}}\right)}^{2} d\eta d\zeta \approx \frac{1}{80}\left({t}_{o}{w}_{o}^{5}-{t}_{i}{w}_{i}^{5}\right)$$

$${I}_{p}=\underset{A}{\overset{ }{\iint }}\left({y}^{2}+{z}^{2}\right) dy dz=\underset{A}{\overset{ }{\iint }}{\eta }^{2}\left(1+\frac{{\zeta }^{2}}{{\eta }^{2}}\right) d\eta d\zeta \approx \frac{1}{12}\left({t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}\right)$$

$$K=\underset{A}{\overset{ }{\iint }}{\left(\frac{\partial\Psi }{\partial x}\right)}^{2} dy dz={k}^{2}\underset{A}{\overset{ }{\iint }}{\eta }^{4}{\left(1-\frac{{\zeta }^{2}}{{\eta }^{2}}\right)}^{2} d\eta d\zeta \approx {k}^{2}\frac{1}{80}\left({t}_{o}{w}_{o}^{5}-{t}_{i}{w}_{i}^{5}\right)={k}^{2} F$$

$$S=\underset{A}{\overset{ }{\iint }}{\left(\frac{\partial\Psi }{\partial x}\right)} dy dz=k\underset{A}{\overset{ }{\iint }}{\eta }^{2}\left(1-\frac{{\zeta }^{2}}{{\eta }^{2}}\right) d\eta d\zeta \approx k \frac{1}{12}\left({t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}\right)=k {I}_{p}$$

$${J}_{s}=\underset{A}{\overset{ }{\iint }}\left[{\left(-z+\frac{\partial\Psi }{\partial y}\right)}^{2}+{\left(y+\frac{\partial\Psi }{\partial z}\right)}^{2}\right] dy dz=\underset{A}{\overset{ }{\iint }}{\left(-\zeta +\frac{\partial\Psi }{\partial \eta }\right)}^{2}+{\left(\eta +\frac{\partial\Psi }{\partial \zeta }\right)}^{2} d\eta d\zeta \approx$$

$$\underset{A}{\overset{ }{\iint }}4{\zeta }^{2} d\eta d\zeta =\frac{1}{3}\left({w}_{o}{t}_{o}^{3}-{w}_{i}{t}_{i}^{3}\right).$$

The definition of the Saint–Venant torsional stiffness ${J}_{s}$ is valid for any arbitrary cross-section but requires the warping function to be known. Since $\psi =-yz$ is only an approximation, the results show errors of 8% at a relative thickness of $t/w=12\%$. Therefore, the following analytical expression is used to determine ${J}_{s}$ for all investigations presented in this paper [33]:

$${J}_{s}=\frac{{w}_{o}{t}_{o}^{3}}{16}\left[\frac{16}{3}-3.36\frac{{t}_{o}}{{w}_{o}}\left(1-\frac{{t}_{o}^{4}}{12{w}_{o}^{4}}\right)\right]-\frac{{w}_{i}{t}_{i}^{3}}{16}\left[\frac{16}{3}-3.36\frac{{t}_{i}}{{w}_{i}}\left(1-\frac{{t}_{i}^{4}}{12{w}_{i}^{4}}\right)\right].$$

The Bredt–Batho formula yields better results than the one above for thin-walled cross-sections but does not apply to medium- to thick-walled hollow cross-sections. Rosen [32] used the approximation ${J}_{s}=\frac{1}{3}w{t}^{3}$ for solid cross-sections with relative thicknesses of 5% and below, resulting in an error of less than 4%.

Inserting the cross-sectional integrals presented above in Eq. (5) yields

$${M}_{t,Ae}+{C}_{1}+{C}_{2}={C}_{3}+{C}_{4}+{C}_{5}+{C}_{6}$$

with

$${C}_{1}=-\frac{S}{A}T=-\frac{{I}_{p}}{A}kT=-\frac{1}{12} \frac{{t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}}{{t}_{o}{w}_{o}-{t}_{i}{w}_{i}}Tk$$

$${C}_{2}=-\frac{{I}_{p}}{A}T\theta =-\frac{1}{12} \frac{{t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}}{{t}_{o}{w}_{o}-{t}_{i}{w}_{i}}T\theta$$

$${C}_{3}=G{J}_{s}\theta =G\left(\frac{{w}_{o}{t}_{o}^{3}}{16}\left[\frac{16}{3}-3.36\frac{{t}_{o}}{{w}_{o}}\left(1-\frac{{t}_{o}^{4}}{12{w}_{o}^{4}}\right)\right]-\frac{{w}_{i}{t}_{i}^{3}}{16}\left[\frac{16}{3}-3.36\frac{{t}_{i}}{{w}_{i}}\left(1-\frac{{t}_{i}^{4}}{12{w}_{i}^{4}}\right)\right]\right)\theta$$

$${C}_{4}=E\left(K-\frac{{S}^{2}}{A}\right)\theta =E\left(F-\frac{{I}_{p}^{2}}{A}\right){k}^{2}\theta =E\left(\frac{1}{80}\left({t}_{o}{w}_{o}^{5}-{t}_{i}{w}_{i}^{5}\right)-\frac{1}{144} \frac{{\left({t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}\right)}^{2}}{{t}_{o}{w}_{o}-{t}_{i}{w}_{i}}\right){k}^{2}\theta$$

$${C}_{5}=E\frac{3}{2}\left(D-\frac{{I}_{p}S}{A}\right){\theta }^{2}=E\frac{3}{2}\left(F-\frac{{I}_{p}^{2}}{A}\right)k{\theta }^{2}=E\frac{3}{2}\left(\frac{1}{80}\left({t}_{o}{w}_{o}^{5}-{t}_{i}{w}_{i}^{5}\right)-\frac{1}{144} \frac{{\left({t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}\right)}^{2}}{{t}_{o}{w}_{o}-{t}_{i}{w}_{i}}\right){k\theta }^{2}$$

$${C}_{6}=E\frac{1}{2}\left(F-\frac{{I}_{p}^{2}}{A}\right){\theta }^{3}=E\frac{1}{2}\left(\frac{1}{80}\left({t}_{o}{w}_{o}^{5}-{t}_{i}{w}_{i}^{5}\right)-\frac{1}{144} \frac{{\left({t}_{o}{w}_{o}^{3}-{t}_{i}{w}_{i}^{3}\right)}^{2}}{{t}_{o}{w}_{o}-{t}_{i}{w}_{i}}\right){\theta }^{3}.$$

The coefficients can be directly inserted into Eq. (27). Assuming $s=t/2$, i.e., a solid cross-section, results in the same expression as Eq. (13) except the Saint–Venant torsional stiffness, which has been modified for both solid and hollow sections as described above.

1.2 Simulation results comparing the relevance of different effects

Advanced air mobility propeller

See Figs. 11, 12, 13, 14, 15 and 16.

Fig. 11

AAM Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses; baseline

Fig. 12

AAM Propeller–torsional loads and torsional rigidity vs. the radius for different chord lengths

Fig. 13

AAM Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses; hollow cross-section with 1.5 mm skin thickness

Fig. 14

AAM Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses; hollow cross-section with 3.0 mm skin thickness

Fig. 15

AAM Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses; steel propeller

Fig. 16

AAM Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses; carbon fiber composite propeller

Commercial aviation propeller

See Fig. 17.

Fig. 17

CA Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses

General aviation propeller

See Fig. 18.

Fig. 18

GA Propeller–torsional loads and torsional rigidity for different chord lengths and relative thicknesses