On the influence of elasticity on propeller performance: a parametric study

Abstract

The aerodynamic performance of propellers strongly depends on their geometry and, consequently, on aeroelastic deformations. Knowledge of the extent of the impact is crucial for overall aircraft performance. An integrated simulation environment for steady aeroelastic propeller simulations is presented. The simulation environment is applied to determine the impact of elastic deformations on the aerodynamic propeller performance. The aerodynamic module includes a blade element momentum approach to calculate aerodynamic loads. The structural module is based on finite beam elements, according to Timoshenko theory, including moderate deflections. Several fixed-pitch propellers with thin-walled cross sections made of both isotropic and non-isotropic materials are investigated. The essential parameters are varied: diameter, disc loading, sweep, material, rotational, and flight velocity. The relative change of thrust between rigid and elastic blades quantifies the impact of propeller elasticity. Swept propellers of large diameters or low disc loadings can decrease the thrust significantly. High flight velocities and low material stiffness amplify this tendency. Performance calculations without consideration of propeller elasticity can lead to decreased efficiency. To avoid cost- and time-intense redesigns, propeller elasticity should be considered for swept planforms and low disc loadings.

1 Introduction

The possibility of electrifying the powertrain of aircraft renewed the interest in propeller-based propulsion systems, e.g., for urban air mobility solutions (UAM) or unmanned aerial vehicles (UAV). Moreover, propellers are applied in General and Civil Aviation for light to heavy transport aircraft. The aerodynamic optimization of propellers has been under investigation since the early days of flight, e.g., by Betz [1], followed by other researchers. Larrabee described a practical method to design propellers according to the minimum induced loss condition [2]. Multiple propeller design or simulation tools were developed and published, e.g., XROTOR [3], QPROP [4], and JavaProp [5], to name only the most prominent. However, loads during operation can lead to significant deformations, impacting aerodynamic performance, as shown by Sodja et al. [6] or Yamamoto and August [7]. Elastic deformations can reduce (or increase) the thrust at a given rotational speed. Propeller manufacturers deliver a required thrust at specific design points, i.e., flight velocity and rotational speed. Consequently, a change in the aerodynamic performance will lead to a shift in the operating conditions or reduced overall efficiency.

To determine the aeroelastic performance of propellers, coupled aeroelastic simulation codes were developed by several researchers or industrial groups, e.g., Kosmatka and Friedmann [8], Gur and Rosen [9], or Billmann et al. at Hamilton Standard [10]. Gur and Rosen additionally demonstrated that implementing geometric and structural constraints regarding stress limits within a propeller optimization routine impacts the optimized propeller layout and operating conditions [11]. Modern approaches include structural or aeroelastic constraints in multidisciplinary optimization schemes [12].

Especially aircraft with VTOL capability require large propeller diameters to reduce power requirements in hover [13]. With increasing size, structural–mechanical effects and aeroelastic phenomena will play a decisive role within the design process, as already known from the development of helicopter rotors [14]. VTOL propellers expire significant transverse flow with no ability to adjust pitch angles within each rotation by a swashplate, impacting dynamic loads, vibrations, and performance. Modern propellers in civil and general aviation are swept in many cases to increase aerodynamic performance at high flight velocities or rotational speeds or to reduce acoustic emissions [15, 16]. As already known from fixed-wing aircraft, swept planforms result in geometric torsion bending coupling [17]. Although these phenomena are well known, adequate coupled simulations or optimizations require both time and expertise. Contra-rotating or ducted fans and propellers are recently investigated for new applications [18, 19] and may require further simulation effort.

Established propeller manufacturers in General Aviation see the opportunity to expand their product range and exploit new markets with propeller designs for UAM or UAV. However, due to the large variety of engines (both electric and combustion) and aircraft, the simulation of many specific propeller types would lead to an unattractive simulation effort for small- or medium-sized companies. Due to a lack of knowledge or ease of design, many of the available propeller models were not designed, optimized, or validated with high-fidelity coupled aeroelastic simulations but by basic aerodynamic calculations, empirical engineering judgment, and experimental tests. This paper shows that static ground tests cannot assess the aerodynamic impact of elasticity during take-off or cruise. Reliable experiments regarding cruise performance require flying testbeds or large wind tunnels. Furthermore, there are no general estimation procedures or guidelines to approximate the impact of propeller elasticity on the aerodynamic performance for different parameter settings.

This paper aims to point out and quantify general trends regarding the impact of propeller elasticity on aerodynamic performance and to identify parameter regions where the elasticity of propellers has a significant effect on aerodynamic performance. To assess the impact of propeller elasticity, the absolute and relative change of thrust will be calculated for different parameter variations. Knowledge of the relevance of diameter, disc loading, sweep, material stiffness, or operating conditions on the elastic deformations will enable propeller manufacturers to judge whether coupled aeroelastic or non-coupled aerodynamic simulations are advisable for preliminary design purposes. Consequently, the awareness of the aerodynamic impact of elasticity shall be increased for new propeller designs. With the help of this awareness, propeller manufacturers can avoid cost- and time-intensive experiments, redesigns, and insufficient performance characteristics.

Chapter 2 presents the general and numerical approach to investigate the impact of propeller elasticity on aerodynamic performance, including the structural and aerodynamic model description, their restrictions, and two validation test cases. Chapter 3 presents and discusses the results of parameter variations, which are concluded in chapter 4.

2 Methodology

2.1 General approach

Coupled aeroelastic simulations of different propeller designs will be processed under consideration of parameter variations to evaluate the aerodynamic impact of propeller elasticity. Aerodynamic performance by means of the thrust $T$ is calculated for different inputs. The relative change of thrust $\Delta T/T$ between a rigid propeller blade and an elastic one quantifies the impact of elasticity. Even though this paper only discusses the relative change of thrust, elastic deformations also impact the power consumption of the propeller in a similar manner, resulting in negligible changes of the propulsive efficiency.

Varied parameters are diameter, disc loading, sweep, material, flight velocity, and rotational speed. This study focuses on steady equilibrium states. For this purpose, one-dimensional finite beam elements are coupled with a blade element momentum theory within an in-house design environment called PropCODE (Propeller Comprehensive Optimization and Design Environment).

2.2 Numerical approach: PropCODE

Fig. 1 presents an overview of the numerical approach. The simulation environment generates a propeller design based on predefined boundary conditions and other inputs. Required inputs are diameter, aerodynamic airfoils, desired thrust at an optimum design point, sweep distribution, material, and skin thickness. The propeller design is determined according to Betz’s minimum induced loss condition at a predefined flight velocity and rotational speed [1]. The preprocessor of PropCODE also includes the determination of the two-dimensional aerodynamic coefficients of each airfoil. Additionally, the stiffness of each structural cross section is determined within a separate two-dimensional analysis. The following chapters provide further references and detailed explanations of each method.

In the first step, the aerodynamic module determines the aerodynamic loads. These loads are transferred to the structure module to calculate the mass loads and resulting deformations. The deformed geometry is used to iteratively compute the aerodynamic loads until the solution has converged, which requires only a few iterations in most cases. Generated thrust for both the rigid and the elastic calculation are prompted and assessed to evaluate the impact of elasticity. The results of the initial aerodynamic load determination of the undeformed geometry are referred to as rigid propeller performance.

Fig. 1

Program schematic

Restrictions This study is restricted to hollow, thin-walled cross sections. Propeller blades are fixed pitch and solely operated in steady flight. Variable pitch propellers are outside the scope of this study. Dynamic effects or aeroelastic stability are also not considered. Due to the beam element approach, general restrictions of this method apply, i.e., only long and slender blades can be adequately modeled.

Geometry designer Each geometry is individually determined according to the minimum induced loss condition for a specific design point, referring to the algorithm of Adkins and Liebeck [20]. All propellers in this study have a ClarkY airfoil. The geometry is internally described and manipulated with the help of the parametric geometry representation method published by Kulfan [21]. The parametric description allows the calculation of arbitrarily oriented cross sections. The material thickness of isotropic materials is determined according to static strength and buckling constraints. The limit stress regarding buckling is calculated with a modified semi-empirical formula originally published by Amatt [22].

Since carbon-fiber composites offer high strength, the required skin thickness regarding static strength would be very low, resulting in an inferior buckling behavior. Instead of increasing the skin thickness, the insertion of honeycomb structures, foam, or the application of integrally woven sandwich panels is more weight and cost-efficient. In this study, buckling stability is ensured by inserting integrally woven glass fiber sandwich preforms. Due to differing stiffnesses and masses, foam or honeycomb inserts may yield different results.

Different blade planforms exist, e.g., backward sweep, forward–backward sweep, or straight blades with partial tip sweep. For better comparability, the planforms of the quarter chord lines of all investigated propellers within this study have a 1-cosine shape:

$${y}_{p}=\left(1-\mathrm{cos}\left(\frac{{x}_{p}}{{x}_{p,tip}}\cdot \frac{\pi }{2}\right)\right)\cdot {y}_{p,tip}$$

(1)

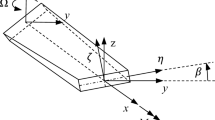
with (x_p, y_p, z_p) representing the propeller fixed, rotating coordinate system and the subscript tip indexing the coordinates of the blade tip, see Fig. 2. With R as the radius, the dimensionless blade tip shift TS quantifies the magnitude of sweep in the negative circumferential direction, i.e., a positive sweep is defined as backward.

Fig. 2

Blade planform of investigated propellers

$$TS=-\frac{{y}_{p,tip}}{R}.$$

(2)

Compared to the local sweep angle in degree, this dimensionless definition is more comparable to other blade planforms from a structural point of view since torsional moments depend on the lever arm.

Aerodynamic model The aerodynamic model is based on the blade element momentum theory. This approach requires pre-calculated airfoil data for broad Reynolds- and Mach-number regions. The airfoil data are calculated with XFOIL, published by Drela [23]. The nonlinear momentum approach also incorporates corrections for tip and root losses, sweep, and post-stall behavior. Further information on the model can be found in [24].

Structural model The structural model is based on Timoshenko beam theory and is adapted from [25]. The elastic axis of the geometry is represented by straight lines between the shear centers of each cross section, see Fig. 3. The determination of shear centers and the corresponding orthogonal cross sections is processed iteratively within the preprocessor before entering the coupled aeroelastic solver. The approach is based on Saint–Venant torsion. The cross-sectional stiffness determination is valid for thin-walled single-cell cross sections. The skin is modeled by classical laminate theory. Analytical formulations are used to determine the cross-sectional stiffness and the position of the shear center, tension center, and center of gravity [26].

Fig. 3

Propeller blade and coordinate systems

The applied beam elements have two nodes with six degrees of freedom each as shown in Fig. 4. The transversal and rotational deformations are interpolated within each element according to

$${\left\{u,v,w,{\theta }_{x},{\theta }_{y},{\theta }_{z}\right\}}^{T}={\varvec{N}}\boldsymbol{ }{\varvec{u}}$$

(3)

with ${\varvec{N}}$ containing the shape functions and ${\varvec{u}}$ describing the 12 nodal DoF of an element.

Fig. 4

Finite beam element

Cubic shape functions are applied for transverse deflections, and quadratic shape functions are included for nodal rotations around the y- and z-axis. The shape functions are adopted from [27]. Linear shape functions are added for longitudinal and torsional deformations. The isoparametric forms are listed in the appendix. The resulting linear stiffness and mass matrix agree with those developed by Przeminiecki [25]. The nonlinear static equilibrium equation in its discretized form is

$${\varvec{K}}\left({\varvec{u}}\right)\cdot {\varvec{u}}={\varvec{F}}\left({\varvec{u}}\right),$$

(4)

where K is the global stiffness matrix, u are the nodal deformations, and F represents the nodal loads.

Centrifugal loads stiffen rotating beams due to stress stiffening, sometimes called centrifugal stiffening. The geometrical stiffness matrix K^G captures this effect:

$${\varvec{K}}={{\varvec{K}}}^{{\varvec{L}}}+{{\varvec{K}}}^{{\varvec{G}}}\left({\varvec{u}}\right),$$

(5)

where K^L is the linear elastic stiffness matrix. K^G is a function of the elemental longitudinal loads, which are internally computed with the nodal deformations. A complete description of the matrices is presented in [25]. They are also listed in the appendix. Implementing the geometric bending stiffness matrix allows for considering the centrifugal stiffening of rotating beams. Nonetheless, propellers and rotors are initially twisted beams and experience further couplings between extension, bending, and twist, even for isotropic materials. Hodges and Dowell derived analytical expressions describing the coupling effects according to moderate deflections theory [28]. As presented in the validation section, neglecting this effect can lead to errors for large deformations. Composite materials impose further couplings and the ability to tailor the elastic behavior [29], but both are not considered in this study.

The nodal loads are differentiated into mass loads and aerodynamic loads:

$${\varvec{F}}={{\varvec{F}}}_{{\varvec{a}}{\varvec{e}}{\varvec{r}}{\varvec{o}}}\left({\varvec{u}}\right)+{{\varvec{F}}}_{{\varvec{m}}{\varvec{a}}{\varvec{s}}{\varvec{s}}}\left({\varvec{u}}\right).$$

(6)

The aerodynamic loads are determined with the previously described blade element momentum theory. Akima’s spline interpolation method [30] approximates both the elastic and the aerodynamic axis as well as section loads and deformations between the coordinates of each grid. Orthogonal projections connect both grids and enable load and deformation transfer, as described in [31]. In steady simulations, mass loads can be determined in matrix form as.

$${{\varvec{F}}}_{{\varvec{m}}{\varvec{a}}{\varvec{s}}{\varvec{s}}}={{\varvec{\omega}}}^{2}\boldsymbol{ }{\varvec{M}}\boldsymbol{ }\left({\varvec{r}}+{\varvec{u}}\right),$$

(7)

$\mathrm{where}\boldsymbol{ }{\varvec{\omega}}$ represents the matrix of rotational velocities, M the translational mass matrix, and r the nodal coordinates in the undeformed state. The impact of deformations on centrifugal loads is also referred to as spin softening. To account for spin softening, the translational nodal deformations have to be included in centrifugal loads determination [32]. Inserting equations (6) and (7) in (4) results in the linearized equilibrium state and can be written as

$${\varvec{K}}\left({\varvec{u}}\right)\cdot {\varvec{u}}={{\varvec{F}}}_{{\varvec{a}}{\varvec{e}}{\varvec{r}}{\varvec{o}}}\left({\varvec{u}}\right)+{{\varvec{\omega}}}^{2}\boldsymbol{ }{\varvec{M}}\boldsymbol{ }\left({\varvec{r}}+{\varvec{u}}\right).$$

(8)

Inserting equation (5) in (8) and rearranging yields the nonlinear static equilibrium equation, which has to be solved iteratively:

$$\left({{\varvec{K}}}^{{\varvec{L}}}+{{\varvec{K}}}^{{\varvec{G}}}\left({\varvec{u}}\right)-{{\varvec{\upomega}}}^{2}\boldsymbol{ }{\varvec{M}}\right)\cdot {\varvec{u}}={{\varvec{F}}}_{{\varvec{a}}{\varvec{e}}{\varvec{r}}{\varvec{o}}}\left({\varvec{u}}\right)+{{\varvec{\upomega}}}^{2}\boldsymbol{ }{\varvec{M}}\boldsymbol{ }{\varvec{r}}.$$

(9)

Validation The aerodynamic module was previously compared to other available methods, including approaches based on potential flow theory, commercial CFD tools applying RANS simulations, and experimental test data. The aerodynamic module agrees well with experimental and CFD data in most investigated cases, even though aeroelastic deformations were not considered [24].

Two comparisons are presented to validate the structural module described in this paper. First, a generic geometry is simulated with PropCODE and the commercial FEM software ANSYS Mechanical to illustrate the validity and limitations of the modeling approach. Second, steady aeroelastic simulation results are compared to experimental test data provided by the propeller manufacturer.

The rotating generic tube illustrated in Fig. 5 is loaded by a single force at the tip. The geometry is modeled with PropCODE (beam elements incorporating moderate deflection theory, referred to as 2nd order) and ANSYS. The simulations in ANSYS were performed with three different modeling approaches:

• 1. Linear beam elements (referred to as 1D linear)

• 2. Beam elements, incl. large deflections theory (referred to as 1D nonlinear)

• 3. Shell elements, incl. large deflections theory (referred to as 2D nonlinear)

Fig. 5

Spatial bending of a rotating elliptical tube

The elliptical cross section has a width of 50 mm and a height of 16 mm. The aluminum skin (E = 71,000 MPa, $\nu$=0.33) has a thickness of 1 mm. An arc describes the elastic axis in the x/y-plane. The arc has a radius of 3,000 mm and a length of 1,000 mm, measured from the origin to the tip in the global x-direction, resulting in a representative radius of R = 1,015 mm. The rotational speed for all load cases is 2,000RPM. The ratio of F_y/F_z is -10 = constant, i.e., F_y is pointing in the negative circumferential direction.

The tip deformations in the z-direction u_z,tip are normalized by the radius R and plotted versus the tip load F normalized by the centrifugal load F_mass at the bearing in Fig. 6. The linear approach is not suitable to represent the elastic behavior of rotating beams since the centrifugal stiffening effect is not considered in this theory. The other three methods yield nearly similar results up to a load of 7% ($\approx$ 500N) with deviations below 2%. With the load further increasing, the results diverge due to the limitations of the moderate deflection theory and cross-sectional deformations. The out-of-plane deformations of typical propeller designs during operation are unlikely to exceed 15% of the radius. Therefore, the moderate deflections theory is considered adequate to determine transversal deflections.

Fig. 6

Normalized directional tip deformation z-direction

Figure 7 illustrates the normalized tip deformation in the y-direction with increasing tip load. Centrifugal forces initially elongate the pipe into a more straight line, thus leading to positive deformations in the circumferential direction for zero external forces. This deformation reduces with increasing tip load due to the force component in the negative y-direction. Deformations in the y-direction impact the centrifugal loads. Since the linear approach does not consider this effect, it has errors even if no external loads are applied. The spin softening matrix incorporated in PropCODE represents this effect. It provides results similar to the nonlinear beam and shell elements with deviations below 2% (compared to beams) up to a tip load of 3% ($\approx$ 200N). Higher loads lead to a nonlinear bending deformation which is only captured by 3rd-order theory.

Fig. 7

Normalized directional tip deformation y-direction

Deformations in the y- and z-direction combined with the centrifugal or external loads lead to torsional loads and rotations. The rotation also changes the deformed structure’s stiffness and leads to nonlinear behavior. The large deformation theory captures these effects, but the linear or moderate deflection theories do not. This issue is also evident when considering elastic rotations in the next section.

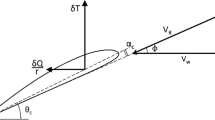
Elastic rotations, i.e., the change of angle of attack, is the most critical parameter for steady propeller simulations connecting the structural deformations and the aerodynamic performance. Figure 8 shows the elastic tip rotation of the tube versus the tip load. Nonlinear one- and two-dimensional FE approaches show excellent agreement. The linear FE approach deviates significantly due to the neglections mentioned above. The linear torsional deformations are solely based on the kinematic torsion bending coupling known from swept wings. PropCODE also shows deviations of up to 0.7° at all load cases. Even though the values are substantially closer to the nonlinear approaches than the linear approach, this deviation would lead to severe changes in aerodynamic loads.

Fig. 8

Change of the angle of attack at the blade tip

This discrepancy is due to the torsional loads induced by the combination of transversal loads and transversal deformations. Due to transversal deformations, forces in the y- or z-direction get a lever arm and lead to torsional loads. The applied geometric stiffness matrix couples longitudinal loads and bending stiffness but does not connect the transversal and torsional loads within the deformed state. This neglection is also recognizable by the assignment of the elemental geometric stiffness matrix in the appendix. The torsional deformations are represented relatively well, but this coupling effect should be implemented for further refinement concerning its high impact on aerodynamic loads.

All three modeling approaches of 2nd- and 3rd-order represent the elastic behavior relatively similar for small and moderate deflections. However, the limitations of PropCODE are present. The tip load of 15% (1,000N) exceeds the yield limit but is still presented here to illustrate the range of validity. With increasing loads, cross-sectional distortions impact the elastic behavior, i.e., the assumption underlying the Timoshenko beam theory of plane and undistorted cross sections is violated, even though the Saint–Venant warping function is included in ANSYS 1D. Nevertheless, the nonlinear one-dimensional approach can predict the structural behavior with neglectable errors. PropCODE suffers from errors regarding the torsional deflections but still represents the elastic behavior reasonably well for preliminary design purposes. Further improvements should include the coupling of transversal and torsional loads. The geometric extension twist coupling, also known as the trapeze effect, does not significantly contribute to the torsional stiffness of hollow cross sections, as shown by Popescu and Hodges [33], and was, therefore, considered to have no significant impact on the aerodynamic performance.

In the next step, simulation data are compared to experimental test data provided by the propeller manufacturer. One blade of the three-bladed propeller with a diameter of 1.6 m is shown in Fig. 9.

Fig. 9

Propeller geometry used for validation

The propeller is made of glass and carbon-fiber-reinforced epoxy. The cross-sectional position of the shear center, tension center, and center of gravity do not coincide. The solid root region is reinforced. Laboratory tests proved that no significant deformations occur at the bearing and the root region of up to 10% of the radius. Bending and torsional stiffnesses are, therefore, artificially increased in this region.

Previously published experimental test data are compared to aeroelastic and aerodynamic simulations, i.e., the propeller geometry is considered either elastic or rigid.

As indicated in Fig. 10, the rigid propeller performance overshoots the experimental test data. Including the elastic deformations reduces the calculated thrust due to aerodynamic torsional loads decreasing the pitch. The occurring deviations are a combination of manufacturing uncertainties, errors regarding the torsional deformation, and errors within the aerodynamic module. However, the simulation matches the test data relatively well. Further improvements to the structural model regarding bending torsion coupling might improve the fitting.

Fig. 10

Comparison of experimental and simulation data

Parameter space The varied design parameters are listed in Table 1 with the corresponding range of values. The investigated materials include high tenacity (HT) and high modulus (HM) carbon-fiber-reinforced polymer (CFRP), both with epoxy resin. The blade tip Mach number is ${M}_{tip}=\Omega R/a$ with $a$ as the speed of sound. The impact of varying rotational speeds on torque and, thus, blade retention, shaft, gearbox, and the engine is neglected. The propellers considered in the following section have two blades.

Table 1 Parameter space

3 Results

Figure 11 plots the relative change of thrust versus blade tip shift (sweep magnitude) for diameters D between one and four meters. Advance ratio J, disc loading DL, blade tip Mach number M_tip, flight velocity v_inf, and the material type are constant for all simulation points in this figure, but not the material thickness. The disc loading is adjusted within the geometry designer via the chord length and pitch distribution. The operating condition is comparable to take-off/climb.

Fig. 11

Relative change of thrust vs. blade tip shift and diameter; J = 0.33, M_tip = 0.55, v_inf = 20 $\frac{\mathrm{m}}{\mathrm{s}}$, DL = 450 $\frac{\mathrm{N}}{{\mathrm{m}}^{2}}$, material: Al 2025 T6

The impact of diameter variations on unswept blades is not very pronounced, but a combination of large diameters and high blade sweep results in severe geometric torsion bending coupling known from swept wings due to large absolute lever arms.

Figure 12 illustrates the relative change of thrust versus the blade tip shift for different materials. Propeller geometry and operating conditions are constant. Aluminum and carbon-fiber composites show similar results. The application of a steel alloy significantly reduces the impact of elasticity. The density, yield strength, and Young’s modulus of the applied steel alloy are about two to three times higher compared to Al 2025 T6. The skin thickness is not reducing to the same extent due to buckling constraints. The weight of the steel blade is about two times the weight of the aluminum blade. Since centrifugal forces significantly impact the stiffness of the propeller, which is also stiffer due to the increased Young’s modulus, the impact of elasticity severely reduces.

Fig. 12

Relative change of thrust vs. sweep and material; J = 0.33, M_tip = 0.55, v_inf = 20 $\frac{\mathrm{m}}{\mathrm{s}}$, DL = 450 $\frac{\mathrm{N}}{{\mathrm{m}}^{2}}$, D = 2.0 m

HM-CFRP offer high specific strength and stiffness. The absolute stiffness and strength are also higher compared to aluminum. Consequently, the determined skin thicknesses according to static strength are very low and result in bending stiffnesses comparable to those of the aluminum propellers. Buckling constraints additionally require the application of integrally woven sandwich panels or other inserts. These inserts result in additional weight, eliminating large portions of the theoretical weight savings. Finally, the results of quasi-isotropic HM-CFRP are comparable to those of Al 2025. Applying HT-fibers with reduced stiffness and higher strength further reduces the overall stiffness and results in an additional thrust decrease.

The authors want to emphasize that the different impacts of elasticity of the materials do not constitute an assessment of their suitability. Even though steel alloys are a feasible way of significantly reducing the aerodynamic impact of elasticity, they suffer from increased weight. Similarly, the impact of elasticity can be considerably reduced for aluminum alloys or composites by increasing the skin thickness, and thus weight and cost. Especially composite propellers offer high design flexibility to alter structural–mechanical properties. Propeller manufacturers or designers can trade off weight, cost, and performance if they know the corresponding effects.

The extent of the impact of elasticity also strongly depends on the propeller geometry. Figure 13 demonstrates the impact of different disc loadings. All considered propellers have a diameter of 2 m and are made of aluminum alloy. The operating point is the cruise flight with a freestream velocity of 40 m/s. The design disc loading the propeller shall deliver at its design point varies between 60N/m² and 380N/m². PropCODE realizes different disc loadings by varying the pitch and chord length distribution. The geometry corresponding to the disc loading of 220N/m² was previously investigated at a reduced flight speed of 20 m/s.

Fig. 13

Relative change of thrust vs. sweep and disc loading; J = 0.67, M_tip = 0.55, v_inf = 40 $\frac{\mathrm{m}}{\mathrm{s}}$, D = 2.0 m, material: Al 2025 T6

Low disc loadings severely impact aerodynamic performance. The contribution of the blade sweep to the overall relative thrust change is less pronounced at cruise than at climb compared to the impact of disc loading (the reason will be discussed at the end of this chapter). For constant diameters, chord length and pitch variations adjust the disc loading. Correspondingly, a higher disc loading results in an increased chord length and activity factor, i.e., reduced aspect ratio. Since the relative thickness is constant, propellers with lower aspect ratios are inherently stiffer, and the impact of elasticity on aerodynamic performance reduces significantly.

The results discussed so far indicate trends regarding the impact of geometry, sweep, and material on the relative change of thrust. Nevertheless, the results cannot be generalized quantitatively. Besides geometric parameters like airfoil or chord length distribution, the operating condition significantly influences the impact of propeller elasticity. Figure 14 plots the relative change of thrust versus the advance ratio at different operating points (0 m/s ≤ v_inf ≤ 40 m/s; 1,200RPM–1,800RPM). Geometry and material thickness are constant for all design points. The dotted line indicates the advance ratio of zero thrust at J = 0.9, indicating the limit of the operational range.

Fig. 14

Relative change of thrust vs. advance ratio; D = 2.0 m, TS = 10%, material: Al 2025 T6

A clear but noisy trend shows that increasing advance ratios decrease the thrust due to elastic deformations. As indicated by Sodja et al., the advance ratio is no longer a valid measure of similarity with changing operating conditions due to the nonlinearity of loads and stiffnesses [34]. Increasing flight speed reduces the local angle of attack at each blade section. This effect reduces the overall thrust, primarily at the inner parts of the blade, due to the lower circumferential velocity. While the overall thrust decreases with increasing flight speed, the thrust distribution shifts outwards to the weaker regions of the propeller. The absolute change of thrust $\Delta T$ due to deformations is less affected than the total thrust T. Accordingly, the relative change of thrust increases significantly in magnitude with increasing advance ratio. The experimental investigation of aeroelastic coupling within static ground tests is, therefore, rather unsuited to quantify the impact during cruise.

4 Conclusions

The design and simulation environment PropCODE is capable of performing coupled aeroelastic simulations of propellers within the preliminary design. Due to the incorporated methods, the code is limited to thin-walled hollow cross sections, long and slender beams, moderate deflections, and constant induced velocities within each annulus.

Steady aeroelastic propeller simulations illustrate the impact of propeller elasticity on aerodynamic performance. Large diameters, low disc loadings, and blade sweep result in deformations, decreasing aerodynamic performance significantly. High flight velocities can amplify, and a high blade stiffness or mass can reduce this effect. Stiffness and aerodynamic performance strongly depend on multiple parameters like the applied airfoils, sweep planform, and others, which were not investigated within this study. Therefore, the presented results only indicate general trends that quantitatively vary for different designs, materials, or operating conditions.

As a basic guide, aeroelastic simulations are advisable to determine aerodynamic performance for large-diameter propellers with swept planforms or low disc loadings. Unconventional designs or cross-sectional layouts deviating from those investigated here or soft materials like glass-fiber-reinforced polymers may show increased aeroelastic coupling. Applying other laminate layups or different types of reinforcement like foam or honeycomb may alter the results. To assess the impact of these effects, additional research in this field is required.

Appendix

1.1 Form functions

$$u\left(\xi \right)=\left(\begin{array}{c}u\\ v\\ w\\ {\theta }_{x}\\ {\theta }_{y}\\ {\theta }_{z}\end{array}\right)=\left[\begin{array}{cccccccccccc}{N}_{1}& 0& 0& 0& 0& 0& {N}_{2}& 0& 0& 0& 0& 0\\ 0& {N}_{3}& 0& 0& 0& {N}_{4}& 0& {N}_{5}& 0& 0& 0& {N}_{6}\\ 0& 0& {N}_{7}& 0& {N}_{8}& 0& 0& 0& {N}_{9}& 0& {N}_{10}& 0\\ 0& 0& 0& {N}_{11}& 0& 0& 0& 0& 0& {N}_{12}& 0& 0\\ 0& 0& {N}_{13}& 0& {N}_{14}& 0& 0& 0& {N}_{15}& 0& {N}_{16}& 0\\ 0& {N}_{17}& 0& 0& 0& {N}_{18}& 0& {N}_{19}& 0& 0& 0& {N}_{20}\end{array}\right]\cdot \left(\begin{array}{c}{u}_{1}\\ {u}_{2}\\ {u}_{3}\\ {u}_{4}\\ {u}_{5}\\ \begin{array}{c}{u}_{6}\\ {u}_{7}\\ {u}_{8}\\ {u}_{9}\\ {u}_{10}\\ {u}_{11}\\ {u}_{12}\end{array}\end{array}\right).$$

Longitudinal and torsional degrees of freedom

$$N_{1} \left( \xi \right) = N_{11} \left( \xi \right) = \frac{1 - \xi }{2},$$

$$N_{2} \left( \xi \right) = N_{12} \left( \xi \right) = \frac{1 + \xi }{2},$$

$\mathrm{where }\xi$ is the dimensionless coordinate in the longitudinal direction $(-1\le \xi \le +1)$

Bending degrees of freedom

$$N_{3} \left( \xi \right) = N_{7} \left( \xi \right) = \frac{1}{2}\left( {1 - \xi } \right) - \frac{1}{4}\psi \left( {\xi - \xi^{3} } \right),$$

$$N_{4} \left( \xi \right) = - N_{8} \left( \xi \right) = \frac{l}{8}\left\{ {1 - \xi^{2} - \psi \left( {\xi - \xi^{3} } \right)} \right\},$$

$$N_{5} \left( \xi \right) = N_{9} \left( \xi \right) = \frac{1}{2}\left( {1 + \xi } \right) + \frac{1}{4}\psi \left( {\xi - \xi^{3} } \right),$$

$$N_{6} \left( \xi \right) = - N_{10} \left( \xi \right) = - \frac{l}{8}\left\{ {1 - \xi^{2} + \psi \left( {\xi - \xi^{3} } \right)} \right\},$$

$$N_{13} \left( \xi \right) = - N_{17} \left( \xi \right) = \frac{3}{2l}\psi \left( {1 - \xi^{2} } \right),$$

$$N_{14} \left( \xi \right) = N_{18} \left( \xi \right) = \frac{1}{2}\left( {1 - \xi } \right) - \frac{3}{4}\psi \left( {1 - \xi^{2} } \right),$$

$$N_{15} \left( \xi \right) = - N_{19} \left( \xi \right) = - \frac{3}{2l}\psi \left( {1 - \xi^{2} } \right),$$

$$N_{16} \left( \xi \right) = N_{20} \left( \xi \right) = \frac{1}{2}\left( {1 + \xi } \right) - \frac{3}{4}\psi \left( {1 - \xi^{2} } \right),$$

${\psi }_{y}=\frac{1}{1+12\frac{E{I}_{zz}}{G{A}_{{s}_{y}}{L}^{2}}}, {{\psi }_{z}=\frac{1}{1+12\frac{E{I}_{yy}}{G{A}_{{s}_{z}}{L}^{2}}} }$ with ${GA}_{{s}_{y/z}}$ representing the cross-sectional shear stiffness in the y- and z-direction${\psi }_{y}$ applies to the second and sixth row while ${\psi }_{z}$ applies to the third and fifth row of the form function matrix

1.2 Stiffness matrices

The stiffness matrix ${\varvec{K}}$ consists of a linear, geometric, and spin softening matrix: ${\varvec{K}}={{\varvec{K}}}^{{\varvec{L}}}+{{\varvec{K}}}^{{\varvec{G}}}+{{\varvec{K}}}^{{\varvec{S}}}$

Linear stiffness matrix

$${{\varvec{K}}}^{{\varvec{L}}}=\left[\begin{array}{cccccccccccc}A& 0& 0& 0& 0& 0& -A& 0& 0& 0& 0& 0\\ & 12{\psi }_{y}D& 0& 0& 0& 6{\psi }_{y}DL& 0& -12{\psi }_{y}D& 0& 0& 0& 6{\psi }_{y}DL\\ & & 12{\psi }_{z}C& 0& -6{\psi }_{z}CL& 0& 0& 0& -12{\psi }_{z}C& 0& -6{\psi }_{z}CL& 0\\ & & & B& 0& 0& 0& 0& 0& -B& 0& 0\\ & & & & \left(1+3{\psi }_{z}\right)C{L}^{2}& 0& 0& 0& 6{\psi }_{z}^{ }CL& 0& \left(-1+3{\psi }_{z}^{ }\right)C{L}^{2}& 0\\ & & & & & \left(1+3{\psi }_{y}\right)D{L}^{2}& 0& -6{\psi }_{y} DL& 0& 0& 0& \left(-1+3{\psi }_{y}^{ }\right)D{L}^{2}\\ & & & & & & A& 0& 0& 0& 0& 0\\ & & & & & & & 12{\psi }_{z}D& 0& 0& 0& -6{\psi }_{z}DL\\ & & & & & & & & 12{\psi }_{y}C& 0& 6{\psi }_{z}CL& 0\\ & & & & & & & & & B& 0& 0\\ & sym.& & & & & & & & & \left(1+3{\psi }_{z}\right)C{L}^{2}& 0\\ & & & & & & & & & & & \left(1+3{\psi }_{y}\right)D{L}^{2}\end{array}\right]$$

$with\, A=\frac{EA}{L}, B=\frac{G{J}_{x}}{L}, C=\frac{E{I}_{yy}}{{L}^{3}}, D=\frac{E{I}_{zz}}{{L}^{3}}$

Geometrical stiffness matrix

$${{\varvec{K}}}^{{\varvec{G}}}=\frac{{F}_{x}^{(L)}}{60L}\left[\begin{array}{cccccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ & 60+12{\psi }_{y}& 0& 0& 0& 6{\psi }_{y}^{2}L& 0& -60-12{\psi }_{y}^{2}& 0& 0& 0& 6{\psi }_{y}^{2}L\\ & & 60+12{\psi }_{z}& 0& -6{\psi }_{z}^{2}L& 0& 0& 0& -60-12{\psi }_{z}^{2}& 0& -6{\psi }_{z}^{2}L& 0\\ & & & 0& 0& 0& 0& 0& 0& 0& 0& 0\\ & & & & \left(5+3{\psi }_{z}^{2}\right){L}^{2}& 0& 0& 0& 6{\psi }_{z}^{2}L& 0& \left(-5+3{\psi }_{z}^{2}\right){L}^{2}& 0\\ & & & & & \left(5+3{\psi }_{y}^{2}\right){L}^{2}& 0& -6{\psi }_{y}^{2}L& 0& 0& 0& \left(-5+3{\psi }_{y}^{2}\right){L}^{2}\\ & & & & & & 0& 0& 0& 0& 0& 0\\ & & & & & & & 60+12{\psi }_{y}& 0& 0& 0& -6{\psi }_{y}^{2}L\\ & & & & & & & & 60+12{\psi }_{z}& 0& 6{\psi }_{z}^{2}L& 0\\ & & & & & & & & & 0& 0& 0\\ & sym.& & & & & & & & & \left(5+3{\psi }_{z}^{2}\right){L}^{2}& 0\\ & & & & & & & & & & & \left(5+3{\psi }_{y}^{2}\right){L}^{2}\end{array}\right]$$

with ${F}_{x}^{(L)}$ as the normal load within the L^th element.

Spin softening matrix The spin softening matrix is defined as ${{\varvec{K}}}^{{\varvec{S}}}\left(\Omega \right)=-{\varvec{\omega}}\boldsymbol{ }{\varvec{M}}.$

The consistent mass matrix incorporates two submatrices associated with the translational and rotational mass. Only the translational mass matrix is applied to determine the centrifugal loads and the spin softening matrix.

$${\varvec{M}}=\rho AL\cdot \left[\begin{array}{cccccccccccc}\frac{1}{3}& 0& 0& 0& 0& 0& \frac{1}{6}& 0& 0& 0& 0& 0\\ & \frac{13}{35}& 0& 0& 0& \frac{11}{210}L& 0& \frac{9}{70}& 0& 0& 0& -\frac{13}{420}L\\ & & \frac{13}{35}& 0& -\frac{11}{210}L& 0& 0& 0& \frac{9}{70}& 0& \frac{13}{420}L& 0\\ & & & 0& 0& 0& 0& 0& 0& 0& 0& 0\\ & & & & \frac{{L}^{2}}{105}& 0& 0& 0& -\frac{13}{420}L& 0& -\frac{1}{140}{L}^{2}& 0\\ & & & & & \frac{{L}^{2}}{105}& 0& \frac{13}{420}L& 0& 0& 0& -\frac{1}{140}{L}^{2}\\ & & & & & & \frac{1}{3}& 0& 0& 0& 0& 0\\ & & & & & & & \frac{13}{35}& 0& 0& 0& -\frac{11}{210}L\\ & & & & & & & & \frac{13}{35}& 0& \frac{11}{210}L& 0\\ & & & & & & & & & 0& 0& 0\\ & sym.& & & & & & & & & \frac{{L}^{2}}{105}& 0\\ & & & & & & & & & & & \frac{{L}^{2}}{105}\end{array}\right]$$

where ${\varvec{\omega}}$ is the rotational matrix associated with the angular velocity $\Omega$ around the z-axis.

$${\varvec{\omega}}=\left[\begin{array}{cccccccccccc}{\Omega }^{2}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ & {\Omega }^{2}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ & & 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ & & & {\Omega }^{2}& 0& 0& 0& 0& 0& 0& 0& 0\\ & & & & {\Omega }^{2}& 0& 0& 0& 0& 0& 0& 0\\ & & & & & 0& 0& 0& 0& 0& 0& 0\\ & & & & & & {\Omega }^{2}& 0& 0& 0& 0& 0\\ & & & & & & & {\Omega }^{2}& 0& 0& 0& 0\\ & & & & & & & & 0& 0& 0& 0\\ & & & & & & & & & {\Omega }^{2}& 0& 0\\ & sym.& & & & & & & & & {\Omega }^{2}& 0\\ & & & & & & & & & & & 0\end{array}\right]$$