Tyre heat of multi-wheel bogie undercarriage at touchdown

Abstract

Almost all studies on tyre heat during aircraft touchdown are based on the assumption that the tyres touch the ground simultaneously, and the aircraft’s load is evenly distributed among each tyre. However, the unique design of multi-wheel bogie undercarriage on wide-body aircraft gives the tyres a specific touchdown sequence. The friction, heat, and thermal wear they face are entirely different. Therefore, this study establishes a model to simulate the dynamics of the multi-wheel bogie undercarriage and relies on Laplace’s equation to calculate the treads’ heat generation and temperature rise. The innovative three-dimensional tread temperature display method can further determine the tyre’s thermal wear. It is found that faster landing increases tyre heat by extending the friction time and distance for all tyres. Softer landing increases the independent rotation time of the early-touched tyres, thus significantly raising the tread temperature due to high frictional power density around the tread centreline areas.

1 Introduction

The aircraft tyres experience rapid and strong friction at touchdown. The friction energy raises the tread temperature, causing thermal wear. The lost rubber in the atmosphere damages the environment, and the thin tread also affects flight safety.

For a long time, many studies have discussed the heat on tyre tread based on software simulation or experiments. Alroqi utilized ANSYS to simulate the friction and heat of the 14 main tyres of the Boeing 747 during landing. He assumed simultaneous contact of these tyres with the ground and an even distribution of the aircraft’s load among them [1]. Zakrajsek and his team conducted experiments and utilized FEA software to investigate the touchdown friction of fighter tyres, focusing on a single tyre [2]. Konde also only used a single tyre to study its friction and heat on the runway [3]. However, no study has ever considered the multi-wheel bogie undercarriage commonly found on wide-body aircraft. In this configuration, the time when the tyres touch the ground varies, and the friction environment differs, necessitating a more accurate model for analysis.

Specifically speaking, for a narrow-body aircraft like Airbus A320, the main undercarriage has a total of four tyres, and the load allocated to each one is a quarter of the aircraft’s weight at the moment of touchdown. An assumption is made here that the nose gear does not contribute to weight distribution. This is because, upon aircraft touchdown, the main tyres typically make contact with the ground before the nose gear, and this time gap is usually greater than the time required for the main tyres to spin-up at touchdown. Bennett’s team employed LiDAR to capture tyre wear on the Bae-146 aircraft during multiple landings, revealing that the main tyres spin-up time was approximately 1.3 s. However, the nose gear touches down 2 to 4 s after the main tyres [4].

Such a setting is reasonable when simulating an ideal landing on narrow-body aircraft without crosswind and with all four tyres touching the ground simultaneously. However, when discussing the landing of the aircraft equipped with multi-wheel bogie undercarriage, a more realistic setting is required.

Fig.ure 1 shows the main undercarriage layout of the Airbus A-330. The bogie pitch trimmer lifts the front wheels in the longitudinal direction, and the rear wheels also descend around the bogie beam axis. The entire main undercarriage is tilted when viewed from the side. This unique design has the following purposes.

Fig. 1

A-330 main undercarriage schematics [5]

First of all, due to the compact design of the fuselage, it is difficult for the huge undercarriage structure to be retracted into the landing gear bay in the unfolded or ground state. Therefore, it is necessary to use a bogie pitch trimmer to convert the undercarriage to the folded state shown in Fig. 1. Second, the folded undercarriage can increase the vertical distance between the rear wheels and the belly fairing, making the aircraft higher. Such a design can increase the pitching angle during take-off and reduce the risk of tail strikes for long aircraft. Finally, the bogie pitch trimmer can act like a shock absorber to provide longitudinal pitch damping, especially on poorly paved ground. Otherwise, the front and rear tyres may oscillate around the bogie beam axis.

The front and rear position and touchdown sequence of the tyre of the main undercarriage of the A-330 are reversed. To prevent readers from misunderstanding and confusion, the front tyres of the main undercarriage are marked as the late-touched tyres, and the rear tyres are marked as the early-touched tyres. It should also be noted that the folding direction of the multi-wheel bogie undercarriage tyres is not fixed. The front tyres of the A-330 are lifted, but on the Boeing 767, they are the rear ones. In this study, we use the A-330 configuration shown in Fig. 1.

Our previous research successfully used the developed model to calculate the friction and heat of an individual tyre at touchdown, and the thermal analysis method involved was experimentally verified [6]. Building on this foundation, the objectives of this study will be:

• (1) model the multi-wheel bogie undercarriage to simulate the dynamics of different tyres at touchdown, including vertical displacement, angular acceleration, and friction power;

• (2) conduct a thermal analysis, use Laplace’s equation and a developed tread temperature display method to predict the tread temperature changes;

• (3) compare the tread temperature distributions and thermal wear states of different tyres of the main undercarriage at different landing speeds and vertical speeds.

Several assumptions simplify the modelling and avoid unnecessary calculations. First, wheel brakes are not applied, and the aircraft maintains a constant horizontal speed at the moment of touchdown. Second, the nose gear is ignored in the simulation. Third, no crosswind or bank angle is applied.

Fourth, unlike the stationary state, the aircraft does not transmit all its weight to the tyres at the early stages of touchdown because there is still lift. The lift is a dynamic physical quantity that depends on several factors such as the aircraft speed, wing area, airfoil, angle of attack, and flap configuration. We conducted landing tests on X-plane 11 using various aircraft, including the A-330, B737, and E175. The data reveals that within one second after the touchdown, the ratio of lift to the aircraft’s gravity varies significantly from 0.8 to 0.4, attributed to differences in landing controls and aircraft performance. Due to the instability of lift during touchdown, which is not within the scope of our study, we fixed the lift-to-gravity ratio at 0.5 to reduce uncertainty. In other words, only half of the aircraft’s gravity is transmitted to the tyres. In Appendix, we present sensitivity analysis to explore the impact of lift-to-gravity ratio on the results. We can observe that the ratio has no significant effect on the friction and thermal differences between tyres. However, it cannot be ignored that a higher ratio (resulting in a softer landing) will significantly increase thermal wear of each tyre. This is something that should be noted by airlines, among others.

2 Modelling

2.1 Multi-wheel bogie undercarriage modelling

An airbus patent application publication states that the bogie pitch trimmer should be able to adopt the position of the bogie beam that is at an angle of more than 30 degrees to the ground [7]. The A-330 flight crew operating manual clearly states the angle to be 33 degrees [5]. Another Airbus maintenance document shows that the wheel spacing in the longitudinal direction should be 1.981 m for all the A-330 series [8]. Therefore, a simple schematic is shown in Fig. 2.

Fig. 2

Schematic of A-330 multi-wheel bogie undercarriage

According to the schematic, $AC$ equals 1.981 m, $\angle C$ equals 33 degrees. If the aircraft is assumed to land at a constant vertical speed $vs$, the touchdown time gap between the early-touched and the late-touched tyres ${t}_{0}$ will be:

$${t}_{0}=\frac{{\text{BE}}}{{\text{vs}}}=\frac{\mathrm{tan\angle C}\cdot {\text{BC}}}{{\text{vs}}}=\frac{\mathrm{tan\angle C}\cdot {\text{AC}}}{2\cdot vs}$$

(1)

where $\mathrm{\angle C}=33^\circ$, $AC=1.981 m$.

When the early-touched tyres solely touch the ground, they face their own weight and the force from the bogie pitch trimmer. Therefore, the normal force of the early-touched tyres during the independent rotation period ${F}_{n0}$ will be:

$${F}_{n0}={m}_{1}\cdot g+\frac{{F}_{t}}{2}$$

(2)

where $g=9.81 m/{s}^{2}$, ${m}_{1}$ is the mass of any of the four tyres forming the main undercarriage, ${F}_{t}$ is the bogie pitch trimmer force acting to two early-touched tyres. The bogie pitch trimmer provides stiffness as a hydraulic device, but the exact parameters are difficult to obtain. To prevent misleading, the trimmer is assumed to provide a constant force.

In this stage, the vertical displacement of the early-touched tyres ${x}_{0}$ will be:

$${x}_{0}={F}_{n0}/{k}_{1}$$

(3)

where ${k}_{1}$ is the tyre stiffness.

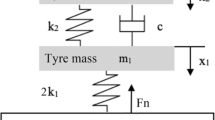
When the late-touched tyres join the friction, at which point the bogie pitch trimmer disengages, and the main undercarriage shock absorber starts to work. The entire system becomes a mass-spring-damper system with 2-DoF (Degree of Freedom). Figure 3 shows a simplified schematic of the undercarriage oleo structure [9]; $4\cdot {m}_{1}$, ${m}_{2}$ are the total mass of four tyres and aircraft load on these tyres; $4\cdot {k}_{1}$, ${k}_{2}$ are the stiffness of all the four tyres and shock absorber; c is the damping ratio of absorber; and x₁, x₂ are the displacements of tyres and absorber. We do not consider the damping characteristic of the tyre because it does not affect the system oscillation within the tyre spinning-up period. The ODEs (ordinary differential equations) of each mass are listed in Eqs. 4 and 5.

$${m}_{2}\ddot{{x}_{2}}+ C\left(\dot{{x}_{2}}-\dot{{x}_{1}}\right)+ {k}_{2}\left({x}_{2}-{x}_{1}\right)-{m}_{2}\cdot g=0$$

(4)

$$4m_{1} \ddot{x}_{1}^{{}} + C\left( {\dot{x}_{1} - \dot{x}_{2} } \right) + x_{1} \left( {4k_{1} + k_{2} } \right) - x_{2} k_{2} - 4m_{1} g = 0$$

(5)

Fig. 3

The layout of undercarriage 2-DoF system

These ODEs can be solved when an initial condition is given: $x_{1} = 0,\dot{x}_{1} = vs,x_{2} = 0,\dot{x}_{2} = vs$. Then, it is available to obtain the normal force of each tyre ${F}_{n1}$ based on Hooke’s law:

$${F}_{n1}=\frac{{{4k}_{1}x}_{1}}{4}={k}_{1}{x}_{1}$$

(6)

The tyre’s vertical displacement ${x}_{1}$ can also be used to work out the tyre centre height above the ground $R-{x}_{1}$. The semi-length of contact surface $AO$ can also be found:

$$AO=\sqrt{{R}^{2}-{\left(R-{x}_{1}\right)}^{2}}$$

(7)

It should be noted that Eq. 7 is also applicable when the early-touched tyres rotate alone, and the tyre displacement data should be substituted by Eq. 3.

The contact surface of aircraft tyre should be an ellipse, with a fixed ratio of its major axis to its minor axis $\varepsilon$. Therefore, the tyre contact surface’s width $W$ and area $A$ will be:

$$W=2\cdot \frac{AO}{\varepsilon }$$

(8)

$$A=\pi \cdot AO\cdot \frac{W}{2}$$

(9)

The displace angle of the contact surface $\Phi$ is expressed as follows, and all the relative parameters are marked in Fig. 4.

Fig. 4

The tyre deformation layout

$$\Phi ={{\text{sin}}}^{-1}(AO/R)$$

(10)

Equation 8 states a simplified method to calculate the tyre’s effective radius ${R}_{e}$ according to small angle approximation [10].

$${R}_{e}=\frac{AO}{\phi }=\frac{\sqrt{{R}^{2}-{\left(R-{x}_{1}\right)}^{2} }}{{{\text{sin}}}^{-1}\frac{\sqrt{{R}^{2}-{\left(R-{x}_{1}\right)}^{2} }}{R} }=\frac{R\sqrt{1-\frac{{\left(R-{x}_{1}\right)}^{2}}{{R}^{2}} }}{{{\text{sin}}}^{-1}\sqrt{1-\frac{{\left(R-{x}_{1}\right)}^{2}}{{R}^{2}}} }\approx R-\frac{{x}_{1}}{3}$$

(11)

The Burckhardt Formula gives the value of $\mu$ (coefficient of friction) depending on the tyre slip ratio $SR$, where ${C}_{1}=1.28, {C}_{2}=23.99, {C}_{3}=0.52$ for aircraft tyre on a dry asphalt runway [11]:

$$\mu = {C}_{1}\left(1-{e}^{-{C}_{2} SR}\right)-{C}_{3} SR$$

(12)

where $SR=1-\omega R/v$, $\omega$ is the tyre’s angular speed and $v$ is the aircraft’s speed.

The tyre friction ${F}_{x}$ will be the product of $\mu$ and tyre’s normal force, and the tyre angular acceleration $\alpha$ depends on the friction torque, considering the moment of inertia:

$${F}_{x}={F}_{n1}\cdot \mu$$

(13)

$$\alpha =\frac{{F}_{x}}{{m}_{1}\cdot {R}_{e}}$$

(14)

It is assumed here that the moment of inertia is calculated using the effective radius of the tyre, and the centre of gravity is considered centred at the centre-point, irrespective of the rim structure.

The tyre angular speed $\omega$ is the integration of angular acceleration over spinning time, while the tyre linear speed ${v}_{l}$ is the product of angular speed and the tyre’s effective radius.

$$\omega ={\int }_{0}^{t}\alpha dt$$

(15)

$${v}_{l}=\omega \cdot {R}_{e}$$

(16)

2.2 Heat generation modelling

First, it should find out the friction timing of each point of interest on the centreline around the entire tyre circumference to determine the experienced friction speed, force, and contact surface area.

Figure 5 takes a point of interest P on the circumference as an example, its displaced angle to the contact surface centre O is represented as β. $\beta =\pi$ represents a point of interest located at the top of the tyre, $\beta =0 or 2\pi$ represents a point located at the bottom of the tyre. The displaced angle reduces as the wheel spins anti-clockwise with an angular speed $\omega$. When P enters the contact surface, the time since touchdown will be its friction starting time ${t}_{s}$. When P leaves the contact surface, the time since the touchdown will be its friction ending time ${t}_{s}$. ${t}_{s}$ and ${t}_{e}$ of each point of interest follows this rule:

Fig. 5

The position of a point of interest P when entering the contact surface

$${\int }_{{t}_{s}}^{{t}_{e}}\omega dt=2\phi$$

(17)

The total friction time of each point of interest will be:

$$t={t}_{e}-{t}_{s}$$

(18)

For each point of interest, the experienced friction speed $\overline{{v }_{f}}$, friction force $\overline{{F }_{x}}$, and contact surface area $\overline{A }$ will be the average values in a specific time interval, defined by the ${t}_{s}$ and ${t}_{e}$.

$$\bar{v}_{f} = \frac{1}{{(t_{e} - t_{s} )/dt}}\sum\limits_{{i = n}}^{m} {v_{fi} }$$

(19a)

$$\bar{F}_{x} = \frac{1}{{(t_{e} - t_{s} )/dt}}\sum\limits_{{i = n}}^{m} {F_{xi} }$$

(19b)

$$\overline{A }=\frac{1}{{(t}_{e}-{t}_{s})/dt}\sum_{i=n}^{m}{A}_{i}$$

(19c)

where $dt=0.0001$, the time interval set in MATLAB. $m={t}_{e}/dt$ and $n={t}_{s}/dt$ for bounds of summation.

What needs to be noted here is that when calculating the average, we need to consider the upper and lower limits of the summation, which must be integers. However, in the database, the starting and ending times for friction are recorded as decimals. Therefore, it is necessary to divide by the time interval to obtain the time step. For instance, 0.0120 s is converted to the 120th time step for a time interval of 0.0001 s. This time interval is derived from time data with four decimal places. Through testing, it has been determined that this level of precision can ensure the stability of the calculation results.

The main idea of conducting the thermal analysis is to evenly divide the contact surface into many rectangular heat elements of equal size and calculate the heat of each element. Figure 6 shows an example element filled in red. This element on the tread will rub against the runway. It will also generate heat and transfer it to the point of interest at the original point $O$, where we will calculate the temperature change.

Fig. 6

The contact surface modelling for thermal analysis, tyre spins anti-clockwise

According to the layout shown in Fig. 6, the coordinate of the example heat element will be (${x}_{u}, {y}_{u}, 0$). As a result, the square of the distance between it and $O$ will be:

$${r}^{2} = {{\text{x}}}_{{\text{u}}}^{2}+ {{\text{y}}}_{{\text{u}}}^{2}$$

(19)

Equation 19 will be substituted into Laplace’s equation to calculate the temperature rise $\theta$. The original format of Laplace’s equation will be [12]:

$$\rho c\frac{\partial \theta }{\partial t} = k\left(\frac{{\partial }^{2}\theta }{\partial {x}^{2}}+\frac{{\partial }^{2}\theta }{\partial {y}^{2}}+\frac{{\partial }^{2}\theta }{\partial {z}^{2}}\right)+\dot{\phi } (x,y,z,t)$$

(20)

where $\dot{\phi }\left(x,y,z,t\right)=\rho c\cdot f(x,y,z,t)$, $\theta$ is the temperature rise, $x, y, z$ is the relative position of the point of interest and the heat element. The remaining physical quantities are annotated in Eq. 21.

A general solution of Laplace’s equation if considering continuous heat on the two-dimensional surface source will be [13]:

$$\theta =\frac{q}{\rho c {\left(4\pi a\right)}^\frac{3}{2}}{\int }_{0}^{t}{\int }_{-L/2}^{L/2}{\int }_{-W/2}^{W/2}\frac{{e}^{-\frac{{r}^{2}}{4a\left(t-\tau \right)}}}{{\left(t-\tau \right)}^\frac{3}{2}} dxdyd\tau$$

(21)

where $a=k/(\rho c)$, q is the friction power, $\rho$, c, k and $\alpha$ are the tread’s density, specific heat capacity, thermal diffusivity, and thermal conductivity, respectively. $t$ is the total friction duration of the point of interest, $\tau$ is the time step after the initiation of heat. It is assumed that thermal decomposition and thermal wear occurs when the tread temperature reaches the critical point of the material ${\theta }_{c}$.

This solution contains an integral part calculating the heat contribution of each element and integrates them over position and friction duration. The integration can only be solved numerically.

Equation 22 expresses the friction power per heat element $q$. The frictional heat does not spread equally to tyre and runway. The heat partition to the tyre tread will be about $90\%$ according to research [14].

$$q=0.9 {F}_{x}\cdot \overline{{v }_{f}}/ N$$

(22)

where $N=\frac{A}{{10}^{-9}}$

The number of heat elements N depends on the total contact surface area and a single heat element area, ${10}^{-9} {m}^{2}$ or $1 m{m}^{2}$ (the area of a rectangular with a side length of $1 mm$). This area is carefully determined through a series of tests. A larger area would result in inaccurate results, while a smaller area would have negligible impact on the outcome, accompanied by a considerable increase in computing time.

The proposed method so far can detect friction quantities of any point of interest on the tread centreline. However, the research scope is to cover the entire tread, particularly in the lateral (breadth) direction. Figure 7 illustrates the contact surface in the top view, where AO and BO are the semi-major and semi-minor axes. The elliptic equation of the contact surface will be:

Fig. 7

The top view of the tyre’s contact surface

$$\frac{{x}^{2}}{{BO}^{2}}+\frac{{y}^{2}}{{AO}^{2}}=1$$

(23)

A point of interest located on the centreline of the tread will need to follow $AC$ to cross the entire contact patch. However, if a point of interest located on either side of the centreline wants to cross the contact surface, i.e. from $A^{\prime}$ to $C^{\prime}$ through $O^{\prime}$, the ratio of the friction distances $A^{\prime}C^{\prime}$ to $AC$ will be:

$$\frac{{A}^{\prime}{C}^{\prime}}{AC}=\sqrt{1-\frac{{O}^{\prime}{O}^{2}}{{\left(\frac{AO}{\varepsilon }\right)}^{2}}}$$

(24)

Based on the same friction speed, Eq. 24 also gives the ratio of the friction times of two points of interest following $A^{\prime}C^{\prime}$ and $AC$. Consequently, the friction quantities can be calculated for any point of interest on the tread laterally spaced a gap $O^{\prime}O$ from the centreline. This proposed method has been used to study the effect of pre-rotation on tyre wear reduction and has been verified [15].

Table 1 lists the required physical variables for the modelling.

Table 1 The required variables in the modelling

3 Result and discussion

3.1 Landing at different aircraft speeds

The Eurocontrol Aircraft Performance Database indicates a typical landing speed of Airbus A-330–300 of $140 kt$ or $72 m/s$ [20]. The trimmer force of this type of aircraft needs to be at least $\mathrm{10,000} N$ to lift the tyres into the folded state. An ideal vertical speed should be around $100 fpm$ or $0.5 m/s$ [21].

The first test focuses on the influence of aircraft landing speed on the tread heat and wear on each main undercarriage tyre. Therefore, the vertical speed $vs$ remains constant. The landing speed $v$ is adjusted at 130, 140 and $150 kt$ or 67, 72 and $77 m/s$.

Figure 8 depicts the variation in tyre normal force at a landing speed of $67 m/s$. When only the early-touched tyres contact the ground, the normal force of each tyre measures only $\mathrm{6,246} N$. However, as the late-touched tyres also engage with friction, their normal force rapidly increases to $\mathrm{189,342} N$.

Fig. 8

Tyre normal force ($v$ = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

Figure 9 illustrates the change of tyre linear speed at the same landing condition. It can be seen that the early-touched tyres meet a low intensity of angular acceleration during the independent rotation period because, at this stage, they only face the normal force much less than the aircraft load and the resulting low friction torque.

Fig. 9

Tyre linear speed ($v$ = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

After 1.29 s, the late-touched tyres join the friction. At this time, the angular acceleration of the tyres rises significantly due to greater load, at which point the curves share the same gradient as all four tyres undergo the same load. The landing speed does not affect ${t}_{0}$ because the vertical movement of the undercarriage does not change.

Figure 10 shows the friction time of every point of interest on the centreline of the tyre circumference, which is unrolled to cover the entire rotation range. Generally speaking, after touchdown, the friction time will be reduced due to the increasing angular speed. The time will not drop to zero because it still takes time for the point of interest to cross the contact surface. The early-touched tyres spin more revs because of insufficient acceleration in the early stage.

Fig. 10

Friction time of every point of interest on the centreline of the tyre circumference ($v$ = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

Moreover, the friction time of the points of interest of the early-touched tyres experiences a noticeable peak (at around 150 rad in Fig. 10). Because the main undercarriage becomes a 2-DoF system at this point, the weight of the aircraft presses the tyres onto the runway, significantly increasing the contact surface area, and it takes longer for the point of interest to travel through the contact surface.

When the late-touched tyres have not yet made contact with the ground, the friction power of the early-touched tyres remains nearly unchanged (See left part of Fig. 11). This is attributed to the low angular acceleration and relatively low friction speed change. When the late-touched tyres join friction, the friction power of all tyres increases sharply due to the application of aircraft load. Notably, the friction power of the early-touched tyres is slightly less than that of the late-touched tyres. This difference arises because the early-touched tyres already possess a certain rotation speed, resulting in a smaller friction speed compared to the later-touched tyres.

Fig. 11

Friction power of contact surface ($v$ = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

The friction energy required to fully spin up each tyre is consistent at $1.03\times {10}^{6} J$ in this case. This uniformity arises from our simulation scenario, where tyres with identical mass and moment of inertia demand an equivalent amount of energy to reach a fixed speed.

Figure 12 illustrates the friction energy density at various points of interest along the centreline. This density is determined by the ratio of friction power to the contact surface area, representing the amount of heat absorbed per unit area of contact surface per unit time.

Fig. 12

Friction power density of every point of interest on the centreline of the tyre circumference (v = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

The density of the late-touched tyres tends to decrease due to the falling friction power and the increasing contact surface area. The change is more pronounced for the early-touched tyres. The low contact area of the early-touched tyres at the beginning of friction significantly raises the friction power density, even with low friction power. After the late-touched tyres join the friction, the contact area rises due to the aircraft load, resulting in a substantial drop in friction power density.

Figure 13 illustrates the final temperature of the tyres after ground contact. In this study, it is assumed that when the tyre speed matches the aircraft speed, the tyres enter the free-rolling stage with a zero slip ratio, and no friction or heat is generated.

Fig. 13

Tread centreline temperature (v = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

The peak points of both curves are situated at $0 rad$, marking the first point on the tread to touch the runway. Notably, the tread temperature of the early-touched tyres is significantly higher than that of the late-touched tyres. The maximum temperature for the early-touched tyres exceeds $800^\circ C$, in contrast to just $200^\circ C$ for the late-touched tyres.

Figure 14 shows the results at all three landing speeds. The increase in landing speed will drive the tread temperature, and the maximum value is almost proportional to the landing speed.

Fig. 14

Maximum tread temperature of all tyres at different landing speeds (${\text{vs}}$ = 0.5 m/s)

There needs to be more comparison to see the thermal wear state because the temperature change along the breadth of the tread is not considered. Therefore, Fig. 15 and Fig. 16 plot the temperature of the entire tread.

Fig. 15.

3D Tread temperature map of the early-touched tyre ($v$ = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

Fig. 16.

3D Tread temperature map of the late-touched tyre ($v$ = 67 m/s, ${\text{vs}}$ = 0.5 m/s)

These 3D maps show the giant difference in the temperature distribution of the early-touched and late-touched tyre treads. For the early-touched tyres, heat is concentrated in the area near the centreline of the tread due to the initial low contact area and extremely high friction power density. Hence, Fig. 15 shows a ridgeline along the tyre circumference. Piedmont areas with much lower temperature change can be seen below the ridgeline, painted in deep blue. These piedmont areas can only experience friction when all four tyres are on the ground. For the late-touched tyres, the tread temperature far from the first contact area is much lower, making the image a half-saddle shape. The overall temperature is significantly lower than that of the early-touched tyres.

Although the current method can only calculate the tread’s surface temperature, the temperature value can also represent the internal heat penetration. Previous study has also proved that the higher the surface temperature, the further the energy penetrates the interior of the rubber, the more the thermal wear [22].

If the temperature at a point of interest exceeds the critical point ${\theta }_{c}$, the difference is considered as the excess value. For instance, if a point of interest registers a temperature of $180^\circ C$, there is no thermal wear, and the excess value will be 0. However, if the temperature rises to $220^\circ C$, the excess value will become 20, considering a critical point of $200^\circ C$. The excess value of all points of interest across the entire tread can be summed, and the size of this numerical value can reflect the amount of thermal wear. Table 2 shows the results.

Table 2 Excess value of all tyres at different landing speeds (${\text{vs}}$=0.5 m/s)

A higher landing speed leads to more thermal wear. If the landing speed is increased from 67 to $77 m/s$, the total excess value of each early-touched tyres increase by $38\%$. In a horizontal comparison, the wear of the early-touched tyres is much greater than that of the late-touched ones because of a higher tread temperature.

3.2 Landing at different vertical speeds

The second test will see how the vertical speed affects the tread heat and thermal wear. In this case, the landing speed $v$ remains constant. The vertical speed $vs$ is adjusted at 60, 100 and $140 ft/m$ or 0.3, 0.5 and $0.7 m/s.$

Figure 17 shows the changes in tyre speeds at three vertical speeds. The increased vertical speed causes the late-touched tyres to contact the ground sooner, and the early-touched tyres have less independent rotation time. At a vertical speed of $0.3 m/s$, the early-touched tyres can accelerate to $28\%$ of the target speed in about 2 s. When the vertical speed is increased to $0.7 m/s$, the early-touched ones can only achieve $14\%$ in 1 s. The change of vertical speed leads to insignificant fluctuations in the normal force and friction force in the 2-DoF system. Therefore, it has little effect on the acceleration of the late-touched tyres.

Fig. 17

Tyre linear speed at different vertical speeds ($v$ = 72 m/s)

Figure 18 shows the friction power density of every point of interest at different vertical speeds. For the late-touched tyres, there is only one dashed line on the image since the data is not affected by vertical speed. On the other hand, the reduction in vertical speed significantly increases the early-touched tyres’ number of revolution in the independent rotation stage and the corresponding friction power density.

Fig. 18

Frictional power density of every point of interest on the centreline of the tyre circumference ($v$ = 72 m/s)

When the vertical speed becomes $0.7 m/s$, the early-touched tyres only spin $66 rad$ or $10.5 revs$ to be synchronized by the late-touched tyres, but when the vertical speed is reduced to $0.3 m/s$, it needs $365 rad$ or $58 revs$. The increase in independent spinning time and friction distance in the early stage can cause a large amount of heat to be concentrated in the centreline area of the tread.

Figure 19 lists the maximum temperature in different cases. Needless to say, softer landing leads to higher tread temperatures, and the late-touched tyres are not affected much.

Fig. 19

Maximum tread temperature of all tyres at different vertical speeds ($v$ = 72 m/s)

Figure 20 shows the tread temperature distribution at three vertical speeds in details. As the vertical speed increases, the ridgeline become shorter, and the overall colour of the ridgeline tends to be closer to blue representing low temperature. At the same time, it can be seen that the low-temperature piedmont areas increase because the tread in these positions has more time to absorb heat due to earlier contact with the ground.

Fig. 20.

3D Tread temperature map of the early-touched tyre ($v$ = 72 m/s, ${\text{vs}}$ = 0.3, 0.5 and 0.7 m/s)

It is worth mentioning a particular case shown in Fig. 21. When the vertical speed increases to $0.9 m/s$, the early-touched tyres that hit the ground first have only a limited time to rotate independently, which is not even enough for it to make a complete revolution. As a result, the temperature in the centreline region at the rear of the tread is greatly reduced. It can be observed in the Fig. 22 that the ridgeline transitions to the dark blue piedmont representing low-temperature change.

Fig. 21.

3D Tread temperature map of the early-touched tyre ($v$ = 67 m/s, ${\text{vs}}$ = 0.9 m/s)

Table 3 calculates the excess values in different cases. When the vertical speed is reduced from $0.7 m/s$ to $0.3 m/s$, the excess value of the early-touched tyres increase by 4.5 times, but that of the late-touched tyres only increases by about 50%. Vertical speed has a significant effect on the thermal wear of early-touched tyres and has a smaller effect on late-touched tyres.

Table 3 Excess value of all tyres at different vertical speeds (${\text{v}}$=72 m/s)

4 Conclusion and future work

Heavier wide-body aircraft are often equipped with multi-wheel bogie undercarriage, of which the bogie pitch trimmer is a common component designed to ensure that the tyres in the longitudinal direction do not land simultaneously. This study utilizes the developed model to analyse the performance of each tyre on the multi-wheel bogie undercarriage upon touchdown. The effects of aircraft landing speed and vertical speed on tyre friction and heat are emphatically demonstrated.

The results indicate that a higher landing speed increases tread heat by extending the friction time and distance for all tyres. A lower vertical speed enhances the independent rotation time of the early-touched tyres, thereby significantly elevating the tread temperature. During independent rotation, the early-touched tyres experience a normal force much lighter than the aircraft load, leading to a much lower tyre displacement and contact surface area. This results in a higher friction power density, even if the friction remains at a low level. All the energy concentrates in the centreline area of the tread, markedly escalating the temperature and thermal wear in these regions.

Such uneven thermal wear can particularly thin the tread at the centreline, making it more susceptible to reaching the legal limit and reducing the tyre service life. This study may contribute to aircraft maintenance, tyre wear prediction, and the design of multi-wheel bogie undercarriages.

One limitation of the study is the estimation of the trimmer damper force. In reality, a trimmer damper is similar to a shock absorber, providing stiffness. However, it is challenging to obtain relevant data to accurately simulate the trimmer damper using publicly information. Therefore, we assume that it exerts a fixed force and anticipate improving the simulation accuracy of the trimmer damper’s performance once authoritative data becomes available in the future.

Second, our model is applicable to scenarios where the tyres remain in contact with the ground after initial touchdown. In reality, many aircraft may experience bouncing during landing, causing the tyres to briefly leave and then re-establish contact with the ground. This necessitates further expansion of the model to account for such instances.

Future research directions also include analysing the friction and thermal performance of the tyres during aircraft braking (deceleration) and exploring potential differences between the front and rear tyres.

Appendix

See appendix Figs. 22 and 23.

Fig. 22

Maximum tread temperature of all tyres at different lift-to-gravity ratios ($v$ = 72 m/s, ${\text{vs}}$ = 0.5 m/s)

Fig. 23

Excess value of all tyres at different lift-to-gravity ratios ($v$ = 72 m/s, ${\text{vs}}$ = 0.5 m/s)

As previously mentioned, the aircraft wings generate lift to counteract a portion of the aircraft’s gravitational force at touchdown. In the appendix, we explore the influence of the lift-to-gravity ratio on research outcomes. The chosen ratio spans from 0.5 to 0.9, informed by comprehensive flight simulation results.

Figures A1 and A2 depict the maximum tyre temperature and the excess value representing wear at different ratios, respectively.

An evident observation is that, as the ratio increases, both temperature and wear rise. This is attributed to the heightened lift, resulting in a reduction of tyre load. Consequently, the tyre must undergo prolonged rubbing under low friction, leading to an increase in temperature. This finding aligns with the perspective outlined in Chapter 3.2.

It is also discovered that the ratio had no significant impact on the data variances between early-touched and late-touched tyres. Specifically, the temperature difference remained consistently stable at $674\pm 4^\circ C$, while the excess value difference fluctuated around 74,500. We also conducted tests at various landing and vertical speeds, yielding similar results.

We believe that the ratio has little impact on the objectives of this study, which focuses on the friction and heat differences between each tyre on the main undercarriage. However, this ratio has a significant impact on the absolute friction and heat of individual tyre. This finding may alert airlines, maintenance, and pilots to the fact that a too-soft landing (high lift-to-gravity ratio) can significantly increase tyre thermal wear level and reduce service life. In fact, a too-soft landing can also lead to other safety problems, such as runway overrun and excursion.

Since the lift-to-gravity ratio is unstable during the brief moment when the aircraft touches the ground and the tyres spin up, our study assumes that it is a constant value. However, in the future research, we could explore the use of a floating lift-to-gravity ratio to observe its impact on the tyres.