Temperature elevation of aircraft tyre surface at touchdown with pre-rotations

Abstract

The runway and landing gear speed difference causes non-negligible friction at touchdown, generating vital heat to raise the tyre tread temperature. The resulting material decomposition reduces tread thickness and significantly impacts flight safety and the environment. Airline operators also need to pay the cost of frequent tyre replacement. The pre-rotation strategy has been proposed to prevent high-speed friction at touchdown. Therefore, a mathematical algorithm is established on MATLAB to simulate the tyre friction and heat generation with various pre-rotation levels. The algorithm is validated by experiments, and a transient thermos-mechanical analysis on ANSYS is used as a reference. The presenting work is one of the few that uses theoretical modelling to simulate tyre heat generation. The formulas presented therein, including Laplace's equation, make the results reliable and traceable. It can be seen that the developed algorithm is capable of calculating the tyre temperature. The pre-rotation can efficiently reduce the friction strength at touchdown. However, when the pre-rotation speed is relatively low, a slight increase in maximum tyre temperature may occur, and the specific reasons for this will be in the discussion.

1 Introduction

When the aircraft conducts a landing, the much greater aircraft landing speed provides a favourable environment for the rapid but robust tyre friction at touchdown. The friction acting on the tyre contact surface exerts a great angular acceleration and allows the wheel to spin up in a very short period to match the aircraft’s speed. This process typically takes less than 0.1 s, according to the research by Alroqi [1] and Besselink [2].

The primary materials of tyre tread are natural rubber and nylon [3], with a critical point of about 200 °C [4, 5]. If the ambient temperature exceeds that critical point, nylon will no longer be able to maintain the strength of the rubber structure. On the other hand, several experiments were made. The maximum tyre temperature at touchdown is believed to reach 127 °C on an F-16 fighter in a USAF study [6]. Also, Alroqi studied Boeing 747 tyre temperature at touchdown, around 300 °C [1]. These studies show that the tread temperature varies significantly depending on the aircraft and landing scenarios.

Aircraft tyres will experience forced cooling after frictional heat, mainly caused by high-speed airflow convection. Research on this area is limited. Saibel and Tsai stated that the tyre temperature would not drop significantly [4]. It has been found that the average temperature decrease was around 13% in one minute, approximately only 0.2% in one second. Alroqi also said convection had little influence over temperature rises due to strong friction [1]. Therefore, the convection effect is neglected in the study.

There are several drawbacks of rubber decomposition. Bennet’s team scanned the aircraft emission at Manchester and Heathrow Airport. It has been found that the tyre smoke showed a level of magnitude greater than the engine smoke at the moment of touchdown [7]. British Airways also states that tyre erosion is considered one of the primary sources of PM₁₀ emissions like engine combustion [8]. Moreover, a thinner tyre tread can affect flight performance and cause a safety issue. A flight safety foundation report said a worn tyre could reduce landing gear friction and braking efficiency, especially when facing a wet runway or crosswinds. It might cause aircraft skidding, control loss or even runway excursion. This report also mentioned that low tyre friction could impact the landing gear spinning-up and delay the avionic signal transfer such as auto brake and spoiler manoeuvre [9]. NASA conducted similar research, and it was found that a worn tyre developed only about one-half the friction of a new tyre at a high landing speed [10]. As a result, regular tyre inspection and replacement are necessary, and the expenditure is an essential factor that many airlines cannot ignore.

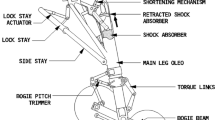
The landing gear pre-rotation is considered one of the ideal solutions to address the tyre wear problem. The equipment on the Cessna 550 is the only relevant application in the current aviation market, and Fig. 1 illustrates the system. Its primary purpose is to prevent flying debris damage on the fuselage caused by nose gear on the unpaved runway, and it can also reduce tyre friction wear [11]. The system uses both the engine bleeding air and the oncoming airflow to power the wheel by blowing the sidewall fins. However, no study has disclosed the effectiveness of this system for wear reducing.

Fig. 1

Some details about the pre-rotation system on Cessna 550. a The bleeding air system at the rear of fuselage [11]. b The exterior of the pre-rotation mechanism with airflow inlet [12]. c The control panel in cockpit [12]

Electric drive is an alternative way to spin the wheel. In the 1940s, the Lockheed company equipped the Constitution aircraft with an electric motor to pre-rotate the main landing gear before touchdown, called rotovane tyres [13]. A study has shown the advantages. The landing gear struts bored less stress due to lower friction. The pre-rotation did narrow the tyre speed gap, reducing material loss and extending tyre life. However, there was no specific data [14]. Therefore, effective modelling is required to discover tyre heat. The objects of this study are listed as follows.

• 1. Simulate the aircraft tyre friction and spinning-up according to a 2-DoF (Degree of Freedom) system.

• 2. Develop an algorithm to calculate tyre surface temperature based on Laplace’s heat equation. The temperature is an indicator to predict thermal wear and validate the efficiency of pre-rotation technology.

• 3. Use existing experiment results to verify the developed algorithm and conduct a transient thermos-mechanical analysis on ANSYS as a reference to assist the major results.

Several large airlines are conducting similar research. In 2020, Japan Airlines and Bridgestone announced the development of tyre wear prediction technology. The JAL said that an increased prediction accuracy would reduce tyre inventory and improve aircraft maintenance efficiency [15]. The USAF also conducts an evaluation programme of tyre life cycle cost. The wear prediction can help select a more appropriate tyre and save 14 million dollars over the lifetime of specific aircraft [16].

2 Modelling

A regional jet, Embraer ERJ-175, is selected as the modelling target. The Eurocontrol’s aircraft database and Embraer company provide the reference landing speed and the maximum landing weight (MLW) [17, 18]. Dunlop and Goodyear’s databases give the tyre specifications [19, 20]. Figure 2 illustrates the landing gear layouts, and Table 1 lists the landing performance and tyre parameters.

Fig. 2

The main landing gear layouts of an E-175 [21]. It has a tricycle configuration with two groups of landing gears, each contains two axle wheels. The nose gear is neglected in this study

Table 1 The aircraft landing performance and tyre specification

Several assumptions simplify the modelling and avoid unnecessary calculations.

• 1. First, wheel brakes are not applied after touching down, and the aircraft maintains a constant speed during wheel spinning-up.

• 2. Second, the main landing gears usually contact the runway first, followed by the nose wheel. This time gap is much longer than the wheel spinning-up time. Hence, the aircraft load will only be evenly distributed to the four main landing gears.

• 3. Last, not all aircraft load is transmitted to landing gear because the wing still generates enough lift at the early stages of touchdown. Few studies mention the specific proportion of lift shared by the wings, and it is a flexible value due to a very dynamic landing flare. Therefore, the proportion is assumed to be 50%, and further research is required.

• 4. Rubber is a hyperplastic material, and Mooney–Rivlin model is usually used to describe its nonlinear strain and tension relationship [22]. However, the primary source of tyre elasticity is internal inflation rather than a thin layer of rubber, and a linear relationship has been discovered in many tests [23,24,25]. Therefore, it can assume that a 2-DoF system is capable to describe the tyre vertical motion.

2.1 Landing gear modelling

The main landing gear system basically involves a wheel and a shock absorber (see Fig. 3). The shock absorber contains a spring and an air–oil hydraulic component, providing stiffness and damper functions that absorb impact energy and avoid bouncing at touchdown. The gear also serves as a spring because of the internal inflation. Therefore, the entire landing gear system can be treated as a mass-spring-damper system.

Fig. 3

Oleo strut simplified schematic [26]

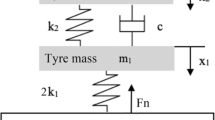
Accordingly, a simplified system layout is shown in Fig. 4 [27]; m₁, m₂ are the wheel mass and aircraft mass on wheel (under the second and third modelling assumptions, the tyre load ${m}_{2}$ is one-eighth of the aircraft’s landing weight to account for the number of tyres and the lift effects); k₁, k₂ are the stiffness of wheel and shock absorber; c is the damping ratio of absorber; and x₁, x₂ are the displacements of wheel and absorber. The damping characteristic of the tyre is ignored as it does not affect the system significantly, especially within the wheel spinning-up period. The ordinary differential equations (ODEs) of each mass are listed in Eqs. 1 and 2.

$$m_{2} \ddot{x}_{2} + c\left( {\dot{x}_{2} - \dot{x}_{1} } \right) + k_{2} \left( {x_{2} - x_{1} } \right) - m_{2} \cdot g = 0,g = 9.81 \;{\text{m/s}}^{2} ) ,$$

(1)

$$m_{1} \ddot{x}_{1} + c\left( {\dot{x}_{1} - \dot{x}_{2} } \right) + x_{1} \left( {k_{1} + k_{2} } \right) - x_{2} k_{2} - m_{1} \cdot g = 0.$$

(2)

Fig. 4

The layout of landing gear 2-DoF system with tyre load and tyre mass

These ODEs can be solved when an initial condition is given: x₁ = 0, ẋ₁ = vs, x₂ = 0, ẋ₂ = vs, where vs is the aircraft’s sink rate or vertical speed at touchdown. Please note that the tyre’s normal force F_n will not appear in the ODEs because this force is not directly exerted on the two masses (${m}_{1}$ and ${m}_{2}$), and Fig. 4 also shows ${F}_{n}$ applies on the runway surface only. However, it is available to obtain based on the tyre’s stiffness ${k}_{1}$ and displacement ${x}_{1}$, a simple application of Hooke’s law:

$${F}_{n}={{k}_{1}x}_{1}.$$

(3)

The tyre’s displacement ${x}_{1}$ can also be used to work out the wheel centre height above the contact surface R − x₁. Then, the semi-length of contact surface AO can be found with the Pythagorean theorem.

$$\mathrm{AO}=\sqrt{{R}^{2}-{\left(R-{x}_{1}\right)}^{2}.}$$

(4)

The tyre contact surface should be an ellipse because of an arc cross-section. Boeing conducts some research in this area, stating that the major axis of the ellipse will be 1.6 times the minor axis [28]. Therefore, the width and the area of the contact patch can be estimated.

$$W=2\cdot \frac{\mathrm{AO}}{1.6},$$

(5)

$$A=\pi \cdot \frac{\mathrm{AO}}{2}\cdot \frac{W}{2}.$$

(6)

The contact surface displaced angle Φ is expressed by Eq. 7. The effective tyre radius R_e will be less than the original radius because of the tyre compression (see Eqs. 8 and 9). All the relative parameters are marked in Fig. 5.

Fig. 5

The tyre deformation layout

$$\phi ={\mathrm{sin}}^{-1}\frac{\mathrm{AO}}{R},$$

(7)

$${R}_{\mathrm{e}}=\frac{AO}{\phi }=\frac{\sqrt{{R}^{2}-{\left(R-{x}_{1}\right)}^{2} }}{{\mathrm{sin}}^{-1}\frac{\sqrt{{R}^{2}-{\left(R-{x}_{1}\right)}^{2} }}{R} }=\frac{R\sqrt{1-\frac{{\left(R-{x}_{1}\right)}^{2}}{{R}^{2}} }}{{\mathrm{sin}}^{-1}\sqrt{1-\frac{{\left(R-{x}_{1}\right)}^{2}}{{R}^{2}}}}.$$

(8)

According to the small angle approximation [29, 30], the result of Eq. 8 can be simplified as a linear function:

$${R}_{\mathrm{e}}=R-\frac{{x}_{1}}{3}$$

(9)

2.2 Wheel friction modelling

The wheel slip ratio SR in Eq. 10 is a function of aircraft linear speed v and wheel linear speed v_l. The Burckhardt friction formula in Eq. 11 defines the friction coefficient $\mu$, where C₁ = 1.2801, C₂ = 23.99, C₃ = 0.51 and C₄ = 0.03 for an aircraft tyre on a dry asphalt runway [31]. The wheel friction force will be the product of friction coefficient and normal force ${F}_{x}={F}_{n}\cdot \mu$, and the wheel angular acceleration $\alpha$ depends on the friction torque (see Eq. 12).

$$\mathrm{SR}=\frac{v-{v}_{l}}{v},$$

(10)

$$\mu =\left[{C}_{1}\cdot \left(1-{\mathrm{e}}^{-{C}_{2}\cdot \mathrm{SR}}\right)-{C}_{3}\cdot \mathrm{SR}\right]\cdot {\mathrm{e}}^{-{C}_{4}\cdot \mathrm{SR}\cdot v},$$

(11)

$$\alpha =\frac{{F}_{x}}{{m}_{1}\cdot {R}_{\mathrm{e}}}.$$

(12)

If the wheel contacts the runway with a pre-rotation linear speed of v₀, its initial angular speed $\omega$ will be v₀/R. The wheel angular speed $\omega$ is the integration of angular acceleration over spinning time plus the initial angular speed, while the wheel linear speed ${v}_{\mathrm{l}}$ is the product of angular speed and the effective radius.

$$\omega ={\int }_{0}^{t}\alpha \mathrm{d}t + \frac{{v}_{0}}{{R}_{\mathrm{e}}},$$

(13)

$${v}_{\mathrm{l}}=\omega \cdot {R}_{\mathrm{e}}.$$

(14)

The following step detects the friction dynamic of each sampling point on the tyre circumference. Take a sampling point P in Fig. 6 as an example. The angle of point P to the contact surface centre O is represented as β. When Eq. 15 holds, P enters the contact surface and the value of t will be t_s, or the friction starting time. When Eq. 16 holds, P leaves the surface and the value of t will be t_e, or the friction ending time.

Fig. 6

Detect the sampling point friction timing

$${\int }_{0}^{t}\omega \mathrm{d}t>\beta -\phi ,$$

(15)

$${\int }_{0}^{t}\omega \mathrm{d}t>\beta +\phi .$$

(16)

For each sampling point, the experienced friction speed $\overline{{v }_{\mathrm{f}}}$, friction force $\overline{{F }_{x}}$ and contact surface area $\overline{A }$ will be the average values in a specific time interval, defined by the friction starting and ending time.

$$\overline{{v_{{\text{f}}} }} = \overline{{v_{{\text{f}}} \left( {t_{{\text{s}}} :t_{{\text{e}}} } \right)}} ,$$

(17)

where friction speed $v_{{\text{f}}} = v - v_{{\text{l}}}$

$$\overline{{F_{x} }} = \overline{{F_{x} \left( {t_{{\text{s}}} :t_{{\text{e}}} } \right)}}$$

(18)

$$\overline{A} = \overline{{A \left( {t_{s} :t_{e} } \right)}}$$

(19)

2.3 Heat transfer modelling

The contact surface is uniformly divided into many rectangular elements for the finite element analysis (FEA), as Fig. 7 shows. An example element U is presented by the dark grey parallelogram and the sampling point P is located at the contact surface centre point. According to this layout, the sampling point’s coordinate will be (0, 0, 0), and it will be (x_u, y_u, 0) for the heating element U. Afterwards, the square of distance r between an element U and a sampling point P is expressed in Eq. 18.

Fig. 7

The contact surface FEA layout with a single element U and a sampling point O

$${r}^{2}= {\left(0-{x}_{u}\right)}^{2}+ {\left(0-{y}_{u}\right)}^{2}+{\left(0-0\right)}^{2}={x}_{u}^{2}+{y}_{u}^{2}.$$

(20)

The distance data will be taken into the Laplace’s heat equation to work out the temperature rises, which has an initial format as follows [32].

$$\rho c\frac{\partial \theta }{\partial t} = k\left(\frac{{\partial }^{2}\theta }{\partial {x}^{2}}+\frac{{\partial }^{2}\theta }{\partial {y}^{2}}+\frac{{\partial }^{2}\theta }{\partial {z}^{2}}\right)+\dot{\phi } \left(x,y,z,t\right),$$

(21)

where $a=k/(\rho c)$ and $\dot{\phi }\left(x,y,z,t\right)=\rho c\cdot f(x,y,z,t)$

A general solution of Laplace’s equation if considering continuous heat on the two-dimensional surface source will be [33]:

$$q = \delta \cdot \overline{{F_{x} }} \cdot \overline{{v_{l} }} / N,$$

(22)

$$\theta = \frac{q}{{\rho c \left( {4\pi a} \right)^{\frac{3}{2}} }}\mathop \smallint \limits_{0}^{t} \mathop \smallint \limits_{ - L/2}^{L/2} \mathop \smallint \limits_{ - W/2}^{W/2} \frac{{{\text{e}}^{{ - r^{2} /4a\left( {t - \tau } \right)}} }}{{\left( {t - \tau } \right)^{\frac{3}{2}} }} {\text{d}}x{\text{d}}y{\text{d}}\tau ,$$

(23)

where q is the heat liberation rate per unit element, τ is the time after the heating starts, $\delta$ is the heat proportion, and is assumed to be 90% [1, 34].

The number of heated elements N depends on the total contact surface area in Eq. 19 and a single element area, which is 10^–6 m² (the area of a square with a side length of 1 mm). This value is carefully decided after a series of testing. Otherwise, a larger unit area will lead to an inaccurate result, and any lower unit area will not change the outcome significantly, followed by a much longer computing time. This solution of Eq. 23 contains an integral part, which calculates the heat contribution of each element and accumulates them in the form of integration over position and friction duration. The integration can be evaluated by numerical method.

In addition, the other parameters required for modelling are listed as follows.

• First, four initial wheel speeds v₀ are set for pre-rotation performance comparison: None (0%, 0 m/s), low-speed (25%, 15 m/s), medium-speed (50%, 30 m/s) and high-speed (75%, 45 m/s) pre-rotation, considering the referenced landing speed in Table 1.

• An ICAT (International Centre for Aerospace Training) paper expects an ideal sink rate of 60–180 fpm (feet per minute) at touchdown for commercial aircraft [35]. Therefore, the touchdown vertical speed or sink rate is set to 98 fpm or 0.5 m/s.

• For the thermal characteristics of natural rubber, the density ρ is 1200 kg/m³, the specific heat c is 2000 J/kg K, and the thermal conductivity k is 1900 W/m·K [1, 36].

• According to several NASA reports, the mainstream aircraft tyre stiffness is approximately 1.75 × 10⁶ N/m (Tyre VIII tyre for large jet) [23, 24]. The stiffness of the absorber is 4 × 10⁵ N/m, and the damping ratio is 6.25 × 10⁵ N s/m [25].

2.4 ANSYS modelling

In ANSYS's transient thermos-mechanical analysis, the wheel model is built using the tyre size in Table 1. Rim is ignored because heat is unlikely to reach the component. For meshing, the wheel circumference is evenly divided into 100 segments and the tread is divided into 11 segments. Therefore, there are 2288 nodes and 1351 elements. Figure 8 illustrates the results of tyre meshing. In addition, the runway is modelled as a long rigid block, which is 60 cm wide, 5 cm thick and 30 m long, with plenty of room for the wheel to spin.

Fig. 8

Meshing of the tyre

The connection type between the tyre and runway is "Frictional" in ANSYS Workbench. The tyre tread is the "contact body", and the runway is the "target body" (see Fig. 9). Furthermore, the interface treatment of the geometric modification should be set to "Adjust to touch" to ensure that all areas of the contact surface participate in the friction. Large deformation is also considered. Several commands are written by ADPL: keyopt,cid,1,1; rmodif,cid,15,1 and rmodif,cid,18,0.9. The first command ensures the "temperature" as a degree of freedom in the structure analysis. The second command defines that 100% of frictional energy converts to heat without loss. And the third command stipulates that 90% of the energy goes to the tyre.

Fig. 9

The connection type setting

In ANSYS Workbench, a joint restricts the moving direction of an object. As Fig. 10 shows, the purple-coloured joint is set on the inner circumference of the tyre like a rim. This joint allows the tyre to move along the Y-axis and rotate along the Z-axis. The runway block will also move along the X-axis to simulate aircraft speed. The wheel displacement and rotation data are imported from the MATLAB results to ensure the consistency of wheel rotation. The runway’s property is ignored here because it is set to rigid, and its temperature change is not the concern of this study. Figure 11 shows the modelling outline.

Fig. 10

The joint of landing gear

Fig. 11

The outline of FEA simulation in ANSYS

Finally, the flowchart in Fig. 12 shows how to use each modelling element to achieve the objectives step by step.

Fig. 12

The flowchart

3 Result

3.1 Initial verification

Rosu’s team conducted an experiment to detect the tyre tread temperature at sliding, the testbed is shown in Fig. 13 [35]. The test uses a tyre rubber sample cube with a contact surface of $0.02 {\mathrm{m}}^{2}\times 0.02{ \mathrm{m}}^{2}$. The applied load is 1000 N, the sliding speed is 4 m/s, and the sliding time is 0.5 s. The thermal cameras are unable to capture temperature data in this experiment because the contact surface is not exposed. Therefore, the team mounted a thermocouple inside the sample cube 6 mm from the contact surface to avoid frictional damage.

Fig. 13

The testbed of Rosu’s experiment. The tyre sample cube is installed on the carriage. The belt drives the carriage to 4 m/s and the hydraulic device on the carriage generates a load of 1,000 N. The track is made of asphalt

The given physical variables are imported into the developed algorithm for the FE analysis. The friction coefficient between rubber and track is 0.76 without any tyre spinning ($\mathrm{SR}=1$), according to the Burckhardt Formula in Eq. 11. Therefore, the total number of the heating element and the heat liberation rate per element can be calculated based on Eq. 22:

$$N = 0.02\;{\text{m}} \times 0.02\;{\text{m}} \div 10^{ - 6} {\text{m}}^{2} = 400,$$

(24)

$$q = 0.9 \times 1000\;{\text{N}} \times 0.76 \times 4\;{\text{ms}}^{ - 1} \div 400 = 6.84\, {\text{watt per element}}{.}$$

(25)

Because the sensor is not on the contact surface, the coordinate of the sampling point will be $(\mathrm{0,0},0.006)$. Consequently, the square of distance between each heating element and the sampling point will be:

$$r^{2} = \left( {0 - x_{u} } \right)^{2} + \left( {0 - y_{u} } \right)^{2} + \left( {0.006 - 0} \right)^{2} = x_{u}^{2} + y_{u}^{2} + 0.000036.$$

(26)

Substituting Eq. 26 into Laplace's equation (Eq. 23) gives a final temperature change of 29.52 °C (ambient temperature 20 °C). Compared with the result of 29.80 °C measured by Rosu's team, the error is only 0.94%. Although the experimental environment used for reference is different from the aircraft tyre friction scenario, the core idea of the developed algorithm is to use the Laplace equation to calculate the temperature change on the contact surface according to the friction, speed and time, applying to all sliding friction scenarios.

On the other hand, Alroqi tested a tyre sliding at a constant speed of 50 km/h (13.89 m/s) for 4 m. The tyre load is 250 kN, tyre radius is 0.7 m, the friction coefficient remains 0.76, the contact area is approximately 0.07 m², and the measured tread temperature reaches 186.4 °C [1]. The experiment environment is imported to the algorithm, the sliding time will be:

$$t = 4\;{\text{m}} \div 13.89\;{\text{ms}}^{ - 1} = 0.288\;{\text{s}}{.}$$

(27)

This time, the total number of heating element and the heat liberation rate per element will be:

$$N = 0.07\;{\text{m}}^{2} \div 10^{ - 6} \;{\text{m}}^{2} = 70,000,$$

(28)

$$q = 0.9 \times 250,000\;{\text{N}} \times 0.76 \times 13.89\;{\text{ms}}^{ - 1} \div 70,000 = 33.93 \;{\text{watt}}\;{\text{per}}\;{\text{element}}{.}$$

(29)

The calculated temperature change according to Eq. 23 is 175.13 °C, which has an error of 6.0% compared with Alroqi’s result. Many factors can lead to discrepancies between simulated and experimental data, such as the deformation of the sample during the friction, and there may be factors that have not been disclosed in the publication. Instead, the algorithm provides an ideal environment. But more importantly, the comparison validates the reliability of the model since it can rely on Laplace's equation to calculate the friction temperature and give reasonable values, and neither error exceeds the 90% confidence level. We aim to trim the algorithm to reach the 95% level in future.

3.2 Landing gear dynamic result

Figure 14 illustrates the vertical movement of the tyre and shock absorber by solving the ODEs (Eqs. 1 and 2). It clearly shows that both absorber and tyre exhibit a damped simple harmonic motion (DSHM). The influence of aircraft load causes a sink in displacement, while the spring intervention leads to an opposite effect. The entire system becomes stationary over time. In the equilibrium state, the tyre experiences a displacement of about 2 cm, while it is about 11 cm for the shock absorber.

Fig. 14

The displacement of shock absorber and tyre

Moreover, the tyre load is calculated using Eq. 3, and the result is plotted in Fig. 15. In equilibrium, the tyre normal force is 4100 kg or 40,221 N (g = 9.81 m/s²). Such a tyre load does not equal the ramp load because the aircraft wing still generates lift. Meanwhile, the FEA result by ANSYS is included in Fig. 15. The simulation time is only 0.15 s due to the limited computer performance, but the consistency of the two curves can be seen. In short, both profiles show that the wheel experiences the greatest normal force of approximately 85,000 N at 0.11 s, where the ANSYS gives an FEA result of 85,971 N and MATLAB gives a proposed value of 84,977 N.

Fig. 15

The plots of tyre load by ANSYS and MATLAB

The contact patch area is finally calculated using Eqs. 5 and 6, and it helps determine the density of heat transfer. The data is plotted in Fig. 16, and the FEA result is also plotted as a reference. The scatter data of FEA is consistent with the data drawn by MATLAB. The FEA result shows the contact surface area reaches the maximum of 0.039 m² at 0.11 s, while it is 0.038 m² by the MATLAB algorithm.

Fig. 16

The tyre patch area plot produced by ANSYS and MATLAB

3.3 Wheel friction result

The tyre friction data is shown in Fig. 17, and the FEA result is also included. The friction reaches its peak 0.1 s after the touchdown. At this point, the force value calculated by MATLAB is 63,824 N, while the FEA measured a value of 63,594 N.

Fig. 17

Tyre frictions by ANSYS and MATLAB

Figures 18 and 19 show the tyre speeds. We can see from Fig. 18 that the tyre angular speed does not maintain a constant value after matching the aircraft speed. Because the effective tyre radius continuously changes due to the suspension system, and the tyre angular speed is inversely proportional to the effective radius for a constant linear speed.

Fig. 18

The tyre angular speed at various pre-rotations

Fig. 19

The tyre linear speed at various pre-rotations

Figure 19 can be used to detect the wheel speed-up duration by finding when the linear speed reaches the target value of 60 m/s. A more detailed speed-up data is shown in Table 2. The data successfully proves the influence of pre-rotation on reducing the friction duration. For example, a 15 m/s pre-rotation reduces the duration by 13.8%, and a 45 m/s pre-rotation reduces the duration by 49.5%, about a half.

Table 2 The wheel spinning-up data

However, the other two types of data, sliding distance and spinning revolutions, do not seem to be related to the pre-rotation speed: when there is no pre-rotation, the tyre accelerates the longest, but it spins from stationary after touchdown. In the case of pre-rotation, although the tyre acceleration time is significantly shortened, it begins with an existing rotation speed. Therefore, the final sliding distances and revolutions could be similar.

3.4 Heat transfer result

Figure 20 shows the heat liberation rate during the tyre spinning-up. The difference in the strength of friction can be clearly seen. Without any pre-rotation, the rate reaches the peak of $1.71\times {10}^{6} \mathrm{W}$, while the value is reduced by nearly a third to $1.16\times {10}^{6} \mathrm{W}$ at a 15 m/s pre-rotation. When the pre-rotation speed comes to 30 m/s, the peak drops to only $6.63\times {10}^{5} \mathrm{W}$, less than half of the initial value.

Fig. 20

The heat liberation rate or the frictional power on the entire tyre patch, at different pre-rotation speeds

These curves rise first before falling. At the beginning of touchdown, despite a large relative speed between tyre and runway, the 2-DoF system does not transmit enough tyre load, leading to low frictional power at this time.

Table 3 states the total energy of the tyre at touchdown, indicating a significant reduction by pre-rotation. Specifically speaking, a low-speed case reduces the energy by 41.2%, a medium-speed case reduces it by 72%, and a high-speed pre-rotation can reduce the energy by a paramount proportion of 92%.

Table 3 The total frictional energy at different pre-rotations, which is the integration of heat liberation rate over spinning-up duration

Figure 21 shows the tread surface temperature, and Table 4 summarises the peak value. The temperature distribution is greatly affected by the pre-rotations. When aircraft lands with stationary wheels, the maximum temperature could reach 329 °C, and the temperature of almost a quarter of the circumference exceeds the critical point of 200 °C. When a low-speed pre-rotation is applied, the maximum temperature is reduced to 268 °C, but most of the circumferential temperature is higher than without. A high-speed pre-rotation generates a peak temperature of only 104 °C, and the thermal wear is prevented since the temperature of nowhere exceeds the critical point.

Fig. 21

The tread surface temperature at three pre-rotation speeds

Table 4 The maximum surface temperature

It has been found that the low-speed pre-rotation does not significantly reduce the tread temperature in general. After carefully investigating the data, a reasonable explanation is given: Although pre-rotation generally reduces frictional energy, the same point on the tyre circumference experience different friction under different pre-rotation speeds. Take the sampling point at 5 rad in Fig. 22 as an example: when there is no pre-rotation, the point starts friction at 0.109 s, and the tyre speed is already close to the aircraft speed, leading to low friction power. When the pre-rotation speed is increased to 30 m/s, that point starts friction earlier because of an initial speed, and the friction speed can still produce significant frictional power at this stage. Another sample is the point at 4 rad. It starts friction at 0.101 s without pre-rotation, and the heat liberation rate is about 500,000 W at that moment. However, the point experiences a greater rate of about 600,000 W when a 50% pre-rotation is applied.

Fig. 22

The friction starting time and the heat liberation rate of the specific sampling points

Additionally, the pre-rotations do not affect the vertical movement of the 2-DoF suspension system and the contact patch area. For a non-pre-rotating case, the tread that first touches the ground experiences a long friction duration because the wheel has to build up its speed from zero. Therefore, when the rear part of the tyre starts friction, the contact patch area increases significantly, and the frictional power density decreases accordingly. In contrast, the pre-rotated tyre spins quickly after touchdown, and there is not enough time for the contact patch area to grow. Hence, the frictional power density may still be at a very high level when the rear part of the tyre starts friction. Consequently, if the pre-rotation does not reduce the friction speed significantly, it is possible that the local temperature will increase instead.

3.5 FEA result by ANSYS

This section describes the results obtained by ANSYS. Its results should only be used as a reference rather than validation because the FEA and MATLAB algorithm are both simulations and cannot be used to verify each other. The following content shows the case without pre-rotation as an example.

Figure 23 shows the final temperature distribution of the non-pre-rotated tyre. FEA software can show the tyre temperature distribution more intuitively than the MATLAB algorithm. The reddest area is the part of the tyre that first touches the runway, where the temperature reaches 352 °C.

Fig. 23

The tyre tread temperature distribution without pre-rotation by ANSYS. The legend is shown on the top left. The viewpoint is at the bottom of the tyre, the aircraft moves to the right-hand side and the tyre spins clockwise

Figure 24 shows the temperature results from ANSYS and MATLAB. Two data show consistency in calculating the maximum temperature. However, clear difference exists in the interval from 1 to 3 rad, where the error climbs to 25%. In ANSYS, when the tyre load increases significantly in the late stage of friction, the tread edge may squeeze toward the centreline, causing it to bulge slightly from the ground, thereby reducing friction, as shown in Fig. 25, and the temperature generated by friction will be lower than the theoretical value.

Fig. 24

The comparison of tyre tread temperature results by FEA and MATLAB algorithm

Fig. 25

The friction distribution on the contact patch. The frictions on both sides are larger than that in the middle

4 Conclusion

A MATLAB algorithm is developed in this study to simulate the aircraft tyre tread temperature at touchdown with different levels of pre-rotations, the reliability and plausibility of the algorithm has been verified, and an FE analysis on ANSYS has be conducted to assist the research. This study discloses all the modelling steps and formulas and gives more reliable results. It has been successfully proved the role of pre-rotation on reducing the tyre heat, and a sufficient level of pre-rotation is able to prevent tyre’s thermal wear emission at touchdown. Some other features about pre-rotation are discussed as well.

For the same landing scenario, FEA software like ANSYS requires a lot of modelling, meshing steps, and tens of minutes of running time on a workstation. Instead, a carefully tuned MATLAB algorithm takes less than ten seconds to give similar results. Therefore, the developed algorithm can be used in high-intensity commercial scenes. For example, airlines need to predict tyre wear after each landing for each aircraft. Future work will optimize the algorithm and attempt to calculate the thermal wear volume.