Identifying challenges in maintenance planning for on-demand UAM fleets using agent-based simulations

Abstract

The novel aircraft architectures for Urban Air Mobility (UAM), combined with pure on-demand operations, mean a significant change in aircraft operation and maintenance compared to traditional airliners. Future flight missions and related variables such as the aircraft position or utilisation are unknown for on-demand operation. Consequently, existing methods to optimise aircraft assignment and maintenance planning cannot be transferred. This study examines the behaviour of an aircraft fleet in an on-demand UAM transport system regarding the interlinking between operation and maintenance. Initially, a potential maintenance schedule for UAM vehicles is deduced. A transport and maintenance simulation is introduced where aircraft are modelled as agents servicing a simple network. As aircraft reach their maintenance intervals, they transfer to one of the maintenance bases and compete for that resource. Since that competition can result in avoidable waiting times, the maintenance costs are extended by running costs for the bases and opportunity costs for missed revenue during these waiting periods. Opportunity costs are cost drivers. To reduce the waiting times, two operational approaches are examined: Extending the opening hours of the maintenance facilities and checking the aircraft earlier to reduce simultaneous maintenance demand. While an extension of operating hours reduces the overall maintenance costs, the adjustment of tasks is more effective to lower waiting times. Thus, an improved system needs to use a combined approach. That combination results in overall maintenance costs of approximately $ 58 per flight hour of which about seven percent account for the opportunity costs.

1 Introduction

Within this introduction, developments in the field of Urban Air Mobility (UAM) as well as a brief overview how the interlinking between operation and maintenance is researched and is followed by the structure of this study.

The concept of UAM is not a novelty of the past decade. Helicopter shuttles have existed since the 1950s in New York City¹ and by today, on-demand services are available in a few global cities to high-net-worth individuals.

Upcoming social changes and quickly advancing technologies indicate that UAM will leave its niche. The number of inhabitants of urban areas will increase by one billion within this decade, most of them in Asia [1]. Simultaneously, the disposable incomes in Asia will experience an upswing [2]. Growing cities face transportation challenges and the increasing income of several hundred million inhabitants will broaden their financial possibilities.

At the same time, fundamental obstacles for UAM have been overcome in recent years. The 5G standard for cellular networks provides the fundament for precise positioning of autonomous flying vehicles  [3]. Lithium-ion batteries have been constantly improved to specific energy and power rates that enable test flights for a range of Urban Air Mobility Vehicles (UAMVs) [4]. The integration of autonomous controls into personal vehicles is showcased in pilot cities and integrated into serial production². Customers self-evidently use app-based mobility providers transporting millions of passengers a day³.

These promising conditions are motivation for more than 100 companies to develop UAMVs. Risks, for instance manufacturers’ too optimistic promises or the effects of the COVID-19 pandemic on the attitude towards aviation and personal mobility, question the potential success of UAM.⁴

While the development of UAMVs is in full swing, the operational aspects of UAM are less regarded. To the best of our knowledge, besides one paper interviewing maintenance mechanics about challenges with electric UAMVs no research focusing on the maintenance and its operational implications for UAM has been conducted. Nonetheless, a tempting $ 5 billion revenue is the estimated market volume for UAM services, such as insurance, maintenance or certification for 2035 [5].

This study is a first step to picture and understand mechanisms between on-demand operation of UAM fleets and the requirements for the technical operational ecosystem. Therefore, a transport network simulation consisting of three major elements is developed in MATLAB. Vertiports are airports for UAMVs and are simplified as agglomeration of landing pads, from which the aircraft start and land on. The UAMVs are modelled as agents moving through the network servicing flight requests. The maintenance bases are equipped with a limited number of slots that can maintain one UAMV and have restricted opening hours. Initially, different settings of initial fleet ages are compared. The influence of operational parameters on the interlinking between maintenance and operation is investigated by changing the maintenance operation hours and checking aircraft prior to the end of their maintenance intervals. The most impactful parameters are combined to identify the best setup regarding maintenance costs and transport capacity within the scope of this simulation. With this work, a simple UAM operation and maintenance simulation is presented. The impact of operational decisions on the queuing for maintenance and the impact on the overall transport performance is demonstrated. Furthermore, readers will understand the importance of aircraft assignment for on-demand aviation regarding maintenance.

This publication is grouped into five sections as folows:

The following Sect. 2 provides the fundamentals of aircraft maintenance and covers literature simulating UAM transport networks as well as aircraft scheduling and assignment for on-demand operation. The identified research gap is presented subsequently.

The UAM maintenance simulation is introduced in Sect. 3. A generic UAM maintenance schedule is deduced as well as the composition of cost modelling is presented, before elementary parts of the simulation are shown.

The results are presented in Sect. 4. They consist of four parts, the initial simulation, evaluating the influence of different fleet ages at simulation begin and two studies to improve the interlinking between operation and maintenance and the best parameter combination.

Lastly, the conclusion and an outlook for future research options is drawn in Sect. 5.

2 Fundamentals and literature review

This section summarises relevant literature concerning first research for UAMV maintenance and aircraft maintenance in general, maintenance planning for on-demand aviation and UAM transport simulations. The existing research gap is concluded in the final step. Therefore, the structure is divided into four parts. Firstly, Sect. 2.1 provides a brief overview of available literature for maintenance of UAMV and at commercial airlines and its general scheduling. Second, Sect. 2.2 shows two different approaches to simulate UAM. The consecutive Sect. 2.3 combines both previous sections with literature about maintenance planning scheduling for different on-demand flight operations and outlines and why their optimisation approaches are limited in their applicability to our problem statement. Last and with the overview of the relevant literature, the research gap is identified in Sect. 2.4.

2.1 Aircraft maintenance and its planning

Within this subsection, the literature on maintenance considerations for UAMV is reviewed. Furthermore, a summary on maintenance interval development for civil airlines and their check scheduling procedures is provided.

2.1.1 Maintenance considerations for UAMV

Even with vibrant activity in the field of UAMV, maintenance for those vehicles is a widely untouched field. Thus, only three publications providing challenges or guidelines for maintenance of UAMV could be identified.

First, Holden et al. [6] provide some initial thoughts on how maintenance could look like for the case of Uber Elevate. Compared to a light helicopter, the authors estimate a maintenance cost reduction of approximately of about 50 % by increasing check intervals of electric motors to 10,000 FHs. Furthermore, they predict smaller checks in intervals of 100 FHs and a major one once a year.

Second, Rajendran and Srinivas present four major challenges for UAM [7]. One of the challenges is fleet maintenance and the authors highlight the necessity to reach a balanced utilisation of the resources required for maintenance checks. However, they do not include further information how they believe the actual maintenance tasks will look like.

The third work is by Naru and German, who organized a workshop with aircraft mechanics to identify challenges with electric UAMV [8]. Their observations were grouped into four main blocks: demanding a training standard for electric power-plant mechanics, the battery handling and exchange, the importance of modularity in design for easy maintenance access, impression of the UAMV concepts. Ideas on how maintenance and tasks for UAMV could be estimated are also not provided.

Jain et al. do not research maintenance for UAMV, but map challenges for electric aviation in general [9], that can be transferred to UAM applications. As Rajendran and Srinivas, the authors also identify a knowledge gap for the maintenance of electric aircraft. As key hurdles for electric aircraft, they identify a suitable battery capacity,the impact of different propulsion system configurations and regulatory uncertainties. Furthermore, they highlight the importance of integrating maintenance experts in early phases of aircraft design.

2.1.2 Aircraft maintenance intervals and scheduling

Maintenance is compulsory for every aircraft to maintain continuing airworthiness. The minimum scheduled maintenance and inspections requirements for a new aircraft type are determined by a maintenance review board consisting of experts from the manufacturer, authorities and operators [10, 11]. The resulting time between overhauls can be defined with three measures: Flight Hours (FHs), Flight Cycles (FCs) and calendar days [12]. The Remaining Useful Lifetime (RUL) describes the real or predicted time until a component or the whole aircraft must undergo a maintenance event and can be measured in the three introduced parameters. Calendar days are usually more relevant for low utilisation aircraft, as many task intervals are limited to a certain time or utilisation in FHs or FCs  [10]. These three measures apply to aircraft of the transport category and also to powered lift configurations, which include UAMVs [12].

The final maintenance programme is derived from the minimum maintenance requirements issued by the maintenance review board, the aircraft’s individual equipment installed and the requirements of the operator and technical operations provider [10, 13]. The scheduled maintenance tasks are combined to checks to minimize necessary downtimes by a appropriate grouping of maintenance activities, e.g., by avoiding duplicate access times. These grouped activities are typically expressed as ’letter checks’, starting from A-checks with high frequency but less invasive tasks up to less frequent D-checks with larger work scopes [14].

Furthermore, for traditional airliners, these checks are grouped into line and base maintenance. Line maintenance is integrated into the regular flight plan of the individual aircraft tail signs. Line maintenance is smaller in scope as well as shorter in duration assuring the nominal condition of the aircraft. The A-Checks are part of line maintenance and are conducted at the home base or at designated outstations, when aircraft have scheduled ground times, usually overnight [10].

Base or heavy maintenance has a more far-reaching extent, such as general overhaul of the aircraft, related repairs or updates of the aircraft, and is grouped depending on its scope in C- or D-Checks⁵. For airliners, the duration of these checks can reach multiple weeks and they are usually scheduled in times of lower demand, e.g. the winter [10].

Most airlines operate multiple aircraft. To comply with the maintenance requirements and ensure a high utilisation at the same time, the aircraft must be routed efficiently. Fleet Assignment Problems (FAPs) and routing of aircraft are part of scheduling problems and have been tackled by airlines and researchers in a large variety since the late 1980s [15,16,17].

On the basis of Sherali et al. [18], a simple explanation of FAPs is provided. Typically, FAPs are mixed-integer problems being based on the airline’s deterministic flight schedule to minimise the overall aircraft assignment costs as objective and so optimising the overall operational profit. They include at least three basic constraints. First, covering all missions in the flight plan once. Secondly, balancing out the number of arriving and departing aircraft for all airports. Last, the number of available aircraft must not be exceeded. Further constraints can be added, if required. The solution of the FAP can be integrated into further problems as the crew scheduling or the Aircraft Maintenance Routing Problem (AMRP) or they can be combined into one model [16, 19, 20]. While FAPs aim to optimise the object of operational profit, AMRPs ensure the aircraft are routed to maintain continuous airworthiness. AMRPs mostly include further boundary conditions, e.g. maintenance events that take place at the home base or at special outstations only. A solution to the AMRP exists, when the airlines’ flight plan can be split into a number of Euler tours for the individual aircraft. Euler tours are coherent routes that start and end at the same airport. A periodic fleet schedule is deduced from the set of Euler tours with the goal to enable sufficient ground times at the right stations to conduct regular maintenance events. [21]

The required time for C- and D-Checks is accounted for by decreasing the number of available aircraft in the FAP’s constraint for the check’s duration [18].

2.2 Simulating UAM transport networks

To research the interlinking between UAM operation and maintenance events, an operational environment for the flight movements must be developed. Such UAM transportation networks are modelled with two different approaches simulations. The first approach are specified transport modelling frameworks. They are developed to compare modal choices, traffic flows with humans modelled as agents iterating their plans until an equilibrium is achieved. The other approach is a stochastic simulation using a general programming language with UAMVs being usually the smallest unit. Both options are mostly tailored to a certain problem and have different features specified to the researchers’ needs. A short overview of both options is provided within this section.

MATSim is one option for a dedicated transport modelling framework as it is an open-source software that models individual persons with time-dependent travel plans and transport vehicles as agents. During the simulation, an iterative loop modifies the persons’ travel plans and scores the overall results until no significant improvements can be detected. For further information about MATSim see [22]. Rothfeld et al. [23] presented an UAM extension to MATSim’s ground-based network modelled as a second layer of airborne transportation. It enables travellers to switch between different modes of transportation to fulfil their travel plans. An initial analysis of the UAM extension is published by the same group of authors [24] for a hypothetical use case in Sioux Falls. A network of ten vertiports with one hundred vehicles is defined to analyse the effect of ground-based process time, vehicle speed, passenger capacity, fleet size, and network capacity on the passenger number and trip duration. More detailed research about operational parameters and methods for an automated vertiport placement can be found by Ploetner et al. [25] and Rothfeld et al. [26].

The second option of stochastic models is used by Kohlman and Patterson [27], who presented an object-oriented and stochastic transport network to size and compare different UAMV concepts. Their model is built from four parts accounting for the network and missions, the UAMVs, the vertiports and the demand. Within the network and mission models, the time steps and a rebalancing of vehicles is defined. UAMVs and vertiports are defined as a set of properties for the vehicle’s technical details, the number of landing pads at vertiports and their distribution, which form the network layout. They propose a simple and adaptable hexagonal shape suitable for a wide range of cities in the United States. Within that network, they analyse UAMV concepts regarding their fuel consumption, emissions, operating costs and the infrastructure investment costs for alternative fuel concepts.

A subsequent study by Kohlman et al. [28] considers an adjusted network layout for the San Francisco Bay Area (United States) using the adapted UAM simulation environment of [27]. Different types of UAMV designs are sized to serve within this network and compared regarding operational costs, emissions, average load factor and waiting time as passenger pooling is enabled.

Shiva Prakasha et al. [29] follow a similar approach developing an agent-based simulation environment for the design of UAMVs presenting Hamburg (Germany) as test case. Similarities in the simulation are found in the demand modelling and the uniform aircraft fleet compared to Kohlman and Patterson [27]. While Shiva Prakasha et al. model the vertiports without capacity limitation and disregard any detour from the beeline, their aircraft assignment uses a bidding model to assign one or two passengers to one UAMV making it more sophisticated.

The here presented studies focus on the impact of operational parameters on the UAM transport system performance [23, 25] or the aircraft sizing [27,28,29]. The impact and the related limitations of maintenance on the UAM transport performance has not been considered.

2.3 Fleet assignment problems and maintenance routing problems for on-demand operation

Unlike presented in the previous chapter, FAPs are not approached by airlines with transport simulations, but with mathematical optimisations as airline flight plans are known in advance and are deterministic. Besides classic operational concepts with a scheduled flight plan, on-demand flight services have been researched as well. The most prominent concept of them is the so called fractional ownership [30]. Owners are entitled to use a certain amount of flight hours of a certain aircraft fleet depending on their bought-in share, while the fractional ownership company covers aspects such as pilot training or aircraft maintenance for annual management fees [31]. Alike the UAM intends, fractional ownership companies follow a strategy to provide on-demand aviation. In the 2000s, also the idea of "per-seat and on-demand" aviation, a kind of shared flight hailing, with affordable small jets and their operational planning was researched (See: [32, 33]). Hence, research for scheduling problems with the focus on AMRP for fractional ownership companies as well as "per-seat and on-demand" aviation is presented in this section.

Keysan et al. [34] researched maintenance scheduling and planning for a fleet of light jets being operated on a "per-seat and on-demand" concept. The flight plan is generated the night before operation to determine the aircraft’s flight paths using a time-space network model being regularly updated. The maintenance checks must be scheduled within a certain tolerance around the maintenance intervals. Their scheduling uses a penalty function for the deviation from the optimal maintenance time, ensuring the aircraft are evenly distributed for the next maintenance checks. In their use case, an aircraft fleet is increased in different steps up to 288 jets, resulting in 86 % to 99 % maintenance capacity utilisation. The more evenly the integration of new aircraft into the fleet is, the higher is the utilisation.

Munari and Alvarez [35] used a standard mixed-integer programming model to research the optimal operation for fractional ownership aircraft fleets. They integrated maintenance constraints and researched upgrades in the aircraft type for requested missions to avoid (more expensive) repositioning flights. A total operating cost reduction of 1.7 % could be obtained on average by integrating upgrades. Similar to Keysan et al. [34], they scheduled the aircraft paths based on a fixed planning horizon, but with a length of 3 days.

Yang et al. [31] presented a decision support tool for the operation of fractional ownership companies. They investigated a simultaneous aircraft routing combined with maintenance events and crew restrictions for near optimal solutions with a 24 hour planning horizon. The maintenance events were considered as 2.5 hour long checks for randomly selected 20 % of the aircraft. The gap in the decision tool between optimal and near optimal solution was on average 3 %, but the calculation time was faster by two magnitudes. In a further study, Yang et al. [36] studied the dynamically changing environment for fractional ownership companies using three different types of heuristics to keep the changes to existing aircraft routing, generated in the last planning horizon, small. They researched strategies for reserve fleet, altering the ground times for the aircraft and repositioning of the aircraft. The largest operational costs savings of approximately 10 % were achieved using a reserve fleet in the size of 8 to 20 % of the regular fleet. The heuristics were tested in a generic simulation, emulating the behaviour of an operation for a fractional ownership company. The simulation generates random flight requests in a generic network with 100 airports for 36 hours to research the quantitative impact of the heuristics. Their generic approach is similar to the stochastic transport simulations, e.g. of [27] presented in the previous chapter.

The presented studies approach different scheduling problems, the earlier one by Keysan et al. [34] is an example of a pickup and delivery problem [32], the latter ones are rather traditional airline routing problems [18, 37]. Nonetheless, they share a certain foresight of future flight requests, that must be covered. The limited foresight is tackled with rolling horizon approaches by creating and regularly updating aircraft routings as further flight mission are added to the system [31]. In our use case of pure on-demand UAM however, there is no knowledge of firm future missions. At the same time, the presented work by Yang et al. [36] shows, that a simulation is an appropriate tool for testing heuristics and therefore a simulation is used our studies as well.

2.4 Research gap

As demonstrated in this section, maintenance considerations for UAMVs have hardly been addressed by past research. With the exception of the work by Naru and German [8], maintenance implications for UAM operations have not been covered thus far. To tackle this knowledge gap, we will focus in our study on the following two aspects:

First, a potential UAMV maintenance schedule for UAMV is derived in Sect. 3, as there is hardly any estimation how maintenance intervals for UAMVs could look like. The only source providing information does not include references, that back up their estimations [6].

Second, a transport and maintenance simulation is developed to understand the operation and maintenance interlinking for on-demand UAM operations. Civil aviation and its scheduling is different from on-demand UAM operation. Solving AMRPs as part of FAPs require definite flight plans to create paths for individual aircraft and for their operational optimisation. However, in our use case of pure on-demand UAM there is no information on future missions. Additionally, unlike the maintenance locations within airline networks, the UAM transport system will not necessarily have maintenance bases integrated into their network system, but at external sites [6, 38]. Consequently, the mathematical optimisations shown in Sect. 2.3 are not applicable to on-demand UAM. Besides understanding the interdependencies for a fleet of UAMV that requires maintenance, operational changes to improve the operation-maintenance interlinking are examined in Sect. 4.

3 UAM maintenance simulation

Within this section, the generic maintenance schedule for UAMVs is deduced and a presentation of the UAM maintenance as well as operational simulation, the costs and demand modelling is provided.

The constraints of an AMRP impose a different problem which is not transferable to on-demand operations. At the same time, a specific transport simulation with agents modelling individual passengers, provides an unnecessary high depth of detail and complexity. Consequently, a general transport simulation is the selected approach for this study. Prior to the simulation with a transportation modelling, a generic UAMV maintenance schedule is derived from existing Aircraft Maintenance Manuals (AMMs), an expert interview and a conclusion by analogy from automotive industry, which is presented in Sect. 3.1. The maintenance costs are expanded beyond the actual check costs to account for the different nature of on-demand mobility including opportunity costs for spilled mission requests and are shown in Sect. 3.2. The elements of the UAM maintenance model are explained subsequently in Sect. 3.3. An overview of the input and output parameters is given in Sect. 3.4 and 3.5. Last, the applied testing methods to the simulation are presented in Sect. 3.6.

3.1 Potential maintenance schedule for UAMV

No UAMV has been certified nor has a corresponding Certification Specification (CS) been issued. Hence, no UAMV maintenance manuals exist and an UAM maintenance schedule has to be derived. The European Union Aviation Safety Administration Special Condition VTOL-01 [39] provides hints to which standards UAMVs will probably be certified and consequently also defines the frame for its future maintenance requirements. Special Condition VTOL-01 features elements of both, aeroplanes and helicopters, inherent in the design of UAMVs and demands the same safety levels as for aircraft of the transport category CS-25. Nonetheless, they base the special condition mainly on CS-23 Amendment 5 for small airplanes and integrate elements of CS-27 for small rotorcraft. [39]

Consequently, the simple and generic maintenance intervals for UAMVs are condensed from two AMMs, one for a CS-23 and one for a CS-27 aircraft. Both reference aircraft are four-seater driven by piston engines [40, 41]. The maintenance intervals for UAMVs are displayed in Table 1 of Sect. 3.2.1. The FH-triggered checks are alternating, meaning every 100-FH since the last FH-triggered check, either one 100-FH or one 200-FH check is due. The FC-triggered checks are also alternating, so that every 1750 FC the aircraft either undergo the 1750-FC- or the 3500-FC-Check. All checks are conducted independent of each other, meaning shorter FH-based are not included in the more extensive FC-triggered checks.

An expert interview with an aircraft mechanic for transport category aircraft was conducted. He is also in charge of the maintenance for single-engine propeller-driven aircraft with four seats, such as Cessna 172R or Piper PA-28, in an aviation club for private pilots. He identified the potential number of Maintenance Man Hours (MMHs) for the 100 FH and 200 FH of those CS-23 aircraft checks based on his experience and the maintenance billings of the aviation club with 24 and 40 MMHs including preparation time. Those values are considered to be equal to MMHs for the 100 FH and 200 FH for UAMV.

They are also shown in Tab. 1. In absence of further information for the more extensive 1750-FC- and 3500-FC-Checks, the numbers of required MMHs are assumed by the authors with an increase by 50 % and 100 % compared to the 200 FH check and are shown in the same table as well.

The obtained MMHs from the expert interview, combined with the maintenance intervals, can be transferred to a MMH/FH ratio for the UAMVs. As the maintenance checks for the UAMVs are also FC driven, the numbers of FCs per FH must be assumed. A range between 1.5 and 3 flights per FH results in 0.38 to 0.44 MMHs/FH. That range is in line with the information provided by Robinson Helicopter Company, that states the MMHs/FH ratio of 0.4 for their light, four-seated, piston-engine-driven Robinson R44 [42]. The close proximity of both ratios indicates that our approach is suitable to identify maintenance intervals and MMHs.

3.2 Cost modelling

The goal of the cost modelling is to capture all costs related to maintenance of UAMVs. Maintenance costs for traditional airliners are often referred in literature to expenses for material and labour for the actual check costs $C_{C, i}$ [43, 44]. In this study a broader approach is chosen to cover all maintenance-related costs and therefore includes running costs $C_{R, j}$ for the infrastructure and equipment of maintenance sites and their operational expenses. Also, the opportunity costs $C_{Opp, l}$ are covered.

The composition of the overall maintenance costs $C_{Maint}$ is shown in Equation (1).

$$\begin{aligned} \begin{aligned} C_{Maint}=\!\sum _{i}^{n_{Checks}}C_{C, i}\!+\!\sum _{j}^{n_{Mech}}C_{R, j}\!+\!\sum _{l}^{n_{UAMV}}C_{Opp, l}\ \end{aligned} \end{aligned}$$

(1)

The basis for the financial figures of this cost modelling is the year 2020. Within this chapter, we aim for the first detailed maintenance costs estimation for UAMVs and their technical operation system. The subsequent estimations are subject to uncertainties because no UAMV is even certified yet. With our focus on matured system, it has to be noted that the integration phase of new technologies for UAMVs may result in higher initial maintenance costs.

3.2.1 Check costs C_{C, i} for maintenance events

The costs $C_{C}$ for maintenance checks are grouped into labour costs  $C_{Lab}$ and material costs $C_{Mat}$ [43, 44]. The rate for one MMH is set to $ 70, which is in line with the range for an aircraft mechanic of $ 53 to $ 81 (cf. [43, 44]) but noticeably lower than one MMH for a rotorcraft with $ 115 [45].

The labour costs are the product of the required MMHs with the rate for one MMH. Knowing the overall maintenance check costs, the material costs can be identified. Based on the maintenance billings, the previously introduced expert classifies the check costs for an 100-FH-Check for one of CS-23 aircraft within the range of $ 1,630 to $ 2,170. An average of $ 2,000 for one 100-FH-Check is assumed. The overall check costs minus the labour costs for the required 24 MMHs results in material costs of $ 320 for that check. The material costs for the 200-FH-Check are assumed by the authors to be doubled compared to a 100-FH-Check, resulting in check costs of $ 3,440.

According to the expert interview, smaller checks for CS-23 aircraft are mainly labour intensive, the more extensive checks usually require far more part replacements which increase their material costs. The expert did not provide information for the costs of more extensive checks. The 1750-FC-Check material costs are set to $ 6,400 by the authors, which is ten times the material expenses for a 200 FH check. Alike to an engine overhaul, the 3500-FC check is not meant to represents the costs for the overhaul of the UAMV’s battery and electric propulsion system. An overhaul for a piston engine of CS-23 aircraft is in the range of $ 18,000⁶ and $ 22,000⁷. These material costs are therefore assumed to be $ 20,000.

Fully electric UAMV power plants are expected to have far less unique rotating parts due to a reduction of complexity compared to other aircraft designs [6, 38, 46, 47]. Therefore, the material costs cannot be transferred directly, but must be scaled down. With the Pipistrell Velis, a first all-electric aircraft has been certified, however no maintenance costs are available for that aircraft [47]. As of 2022, full-electric aircraft have only been tested thus far and their commercial passenger service is yet to commence [48]. Consequently, a comparison beyond aviation is required, even though it may introduce additional uncertainties. Two studies investigated the operation cost for road vehicles and concluded lower maintenance costs of a battery electric vehicle compared to a vehicle with an internal combustion engine at 19 and 25 %, respectively [49, 50]. Based on their findings, the material costs basis of $ 20,000 is reduced by 20 % accounting for the overhaul of the propulsion system. The resulting material costs of $ 16,000 plus the labour expenses cause overall check costs of $ 21,600 for the 3500-FC-Check.

The overview of all maintenance intervals and the corresponding costs are shown in Table 1.

Table 1 Potential UAMV maintenance schedule and costs

3.2.2 Running costs C_R for maintenance sites

To maintain UAMVs, corresponding sites must be established and operated. Independent of their utilisation, running costs and their depreciation must be covered. As no UAMV maintenance facilities exist today, their potential costs are deduced by analogy from costs of existing aircraft maintenance shops. The investment for a new engine shop in Poland with more than 1,000 employees is estimated with a minimum of $ 180 Mio.⁸ resulting in an expense of about $ 180,000 per workplace. However, facilities for engine overhauls are costlier than ones for other aspects of aircraft maintenance according to an expert from Lufthansa Technik’s business development. Therefore, UAMV maintenance facilities are assumed to be less costly resulting in an estimated investment of $ 100,000 per workplace for this simulation.

All investments for the UAMV maintenance bases are assumed to be depreciated over 15 years. That time span is a trade-off between six to eleven years for tools⁹ and 25 years for shipyards in Germany, which are considered comparable regarding their depreciation to aircraft hangars.¹⁰ Consequently, the annually depreciation $C_{Invest}$ for the investment in a maintenance base is $ 6,667 per workplace assuming the above-mentioned investment costs.

In times with slack $t_{Slack}$, when mechanics wait for one UAMV to be checked, running costs such as their wages or payment for the administrative overhead, still accumulate. As the personal planning can lower these slack costs $C_{Slack}$, they are assumed to be half the wrap rate for one MMHs with $ 35/h.

The running costs $C_{R, j}$ are shown in Eq. 2).

$$\begin{aligned} \begin{aligned} C_{R, j} = C_{Invest, j} +t_{Slack, j} \cdot C_{Slack}\ \end{aligned} \end{aligned}$$

(2)

3.2.3 Opportunity costs C_Opp

Opportunity costs $C_{Opp}$ compensate for missed revenue for a stakeholder, when one choice is made over another. The simulation in this study is maintenance-centric and does not include any revenue earned during paid flight missions. At the same time, UAMVs cannot generate revenue when waiting for a maintenance check and for the duration of the maintenance events themselves. However, maintenance events are essential to maintain airworthiness and keep the aircraft in a condition to generate revenue. Hence, there is no option to avoid them and only additional ground times beyond the essential maintenance check times are considered for opportunity costs in this study. Therefore, only ground times that exceed the minimum maintenance downtimes are considered for the calculation of opportunity costs $C_{Opp}$, independent whether the aircraft must wait when the base is occupied or closed.

The opportunity costs are calculated similar to the average revenue during $t_{Opp}$. For airlines, revenue is the product of yield with Revenue Passenger Kilometers (RPKs) [51]. Equation (3) is a modification of that approach tailored to UAM. The ticket price is the transport fare $C_{Fare}$ per distance d and shown as first factor of the equation. The RPKs are shown in the second factor of Equation (3). They are the product of available seats $n_{Seats}$ with the average Passenger Load Factor $PLF_{av}$ and the average distance $d_{av}$ covered by a vehicle during operations without maintenance per time t multiplied with the actual opportunity time $t_{Opp}$.

$$\begin{aligned} \begin{aligned} C_{Opp,l} = \frac{C_{Fare}}{d} \cdot \frac{n_{Seats} \cdot PLF_{av} \cdot d_{av}}{t} \cdot t_{Opp,l} \ \end{aligned} \end{aligned}$$

(3)

All variables, besides $d_{av}$, are constant and known prior to a simulation’s start. Depending on the input change, the overall transport capacity might change and so the average flight distance $d_{av}$ could change as well. For simplification, the $d_{av}$ is calculated and averaged for one test run of the simulation without any maintenance event and is kept constant. Hence, the hourly opportunity costs equal the average hourly revenue per aircraft, when no maintenance is considered. The hourly opportunity costs are kept constant for all simulations at $ 153.2/h.

3.3 Transport and maintenance simulation

The four main elements and the mechanisms of the UAM transport and maintenance simulation are presented in this section. Kohlman and Patterson’s publication [27] serves as inspiration for transport modelling and network. For further and more detailed information regarding the transport simulation, we encourage to read their publication.

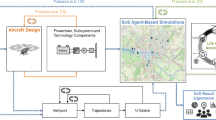
The length of our UAM transport and maintenance simulation for one run is set to 365 days. The length of one time step is 10 s resulting in 8,640 steps per day (cf. [27]) and accumulates to about 3.2 Mio. time steps for the length of 365 days. A simplified structure of this simulation routine is shown in Fig. 1.

Fig. 1

Simplified structure of simulation

Within the demand and dispatch model, a flight request for one vertiport per time-step might be generated. If a flight request is generated with the help of the aircraft assignment and operational decisions element, a UAMV is chosen for the mission, if available. Also, it is controlled whether a landing pad at the starting vertiport of the mission is available. For the flight mission, the aircraft parameter such as the number of FHs or FCs are updated. These pieces of information are fed back into the assignment and operational decisions part as they might cause that one UAMV is no longer available for flight missions when a maintenance check is due. Moreover, the vertiports and maintenance bases are updated and the information is integrated into the aircraft assignment and operational decisions elements. Those four elements are explained further in the following subsections.

3.3.1 Demand and dispatch model

Both, the flight demand from one vertiport and its dispatch location are stochastically determined. For each of the 3.2 Mio. time steps and seven vertiports, a uniformly distributed random number between 0 and 1 is compared to the vertiport’s demand probability function. If that random number is lower or equal to the function’s value at that time step, a flight is requested for that vertiport. The demand probability functions differ for the central and outer vertiports and are displayed in Fig. 2. For example, at the center cub at 8 am the probability is 0.14, indicating that the random number must be 0.14 or less in order to trigger a flight request at that vertiport. The destination is also determined with a uniformly distributed random number and depends on the vertiports’ demand weightings, which are shown in Tab. 3. Round flights from and to the same vertiport are not possible, the destination is always a different vertiport. In this simulation, all outer vertiports have the same constant probability of becoming the destination while the central vertiport has double the probability of one outer vertiport.

Fig. 2

Demand distributions based on [27]

Repositioning flights can be triggered, when a flight request cannot be serviced due to a missing available UAMV. Unsuccessful requests are not serviced at a later point in time. If a missing vehicle is the reason and a uniformly distributed random number surpasses the rebalance parameter shown in Tab. 3, a repositioning flight is triggered. The UAMV is ferried from the vertiport with the most available vehicles. A large set of random numbers is stored and used in the same order for every simulation of this study. So, repeatability is ensured and changing random numbers are prevented from masking or exaggerating modifications of the parameters.

3.3.2 Aircraft assignment and operational decisions

Whenever a flight mission is requested, one UAMV must be assigned. Only the UAMVs that are instantly available at the departing hub are considered to service the flight. Nonetheless, when two or more UAMVs are available, a choice must be made. An equal wear of the fleet is favourable concerning the long-term fleet planning and uniform maintenance requirements [52, 53].

Assigning one of multiple available aircraft to a flight mission may take many parameters into account and become highly complex. Aware of the complexity of FAPs for traditional airlines, a very simple method to assign UAMVs is integrated. Complying with the demand for an even usage, the aircraft with the least FHs since the begin of the simulation is assigned to a flight mission. It is crucial to assign the aircraft according to FHs since simulation start and not, for example, the overall FHs of the UAMVs. That selection ensures an equal usage of the aircraft fleet. Otherwise, the initial difference in FH at the beginning of the simulation would be equalled, resulting in uneven usage.

The battery is charged after every flight to avoid any restrictions for future flight missions, the battery level triggering charging is set to 99 %.

3.3.3 Vertiport and maintenance base model

A simple and adaptable network model is chosen for the purpose of this study. Vertiports are uniformly arranged in a hexagonal pattern; one central vertiport is surrounded by six outer ones being an adaptable approach suitable for many cities with a ring highway [27, 54]. The network layout is shown in Fig. 3 including all point-to-point connections. Unlike Fig. 3 indicates, flights are modelled as straight and not curved line between two vertiports. Each vertiport is defined by a number of landing pads, the position in the network and a weighting for its flight activities. The landing pads can only be occupied by one UAMV per time, that is either starting or landing. Further separation of the vehicles or air traffic management is not included into our simulation. While the number of landing pads are limited for vertiports, the number of parking slots for ready vehicles is assumed to be unlimited.

Fig. 3

Network layout based on [27]

Maintenance bases are similar in structure to vertiports. Modifications are their unlimited number of landing pads and the limitation of hangar bays in which UAMVs can be checked simultaneously. Each maintenance bay has a number of allocated mechanics who are assumed to work on one UAMV simultaneously. The duration of the maintenance checks is the fraction of the required MMH divided by the number of simultaneously working mechanics. Moreover, the bases can be either opened or closed according to their opening hours shown in Tab. 3. During closure, the maintenance work is paused and resumed, when the base opens again.

Future vertiports are believed to be at traffic hubs, airports, business districts or highway cloverleafs [54,55,56]. Of those sites, only an airport might provide enough space for UAMV maintenance. All others are not feasible to include large facilities and hence maintenance bases are believed to be at off-grid places [6, 38].

The two maintenance bases for this simulation are located centrally between the vertiports 1, 2, 3 and 4 respectively 1, 5, 6 and 7 and are also marked in Fig. 3. UAMVs reaching the end of an interval limit after a flight, proceed to the closer maintenance base. Vehicles at the central vertiport are distributed equally to either base.

3.3.4 UAMV model

UAMVs are the smallest unit in the simulation and are defined by a set of properties, such as their tail-sign or cruise velocity. They are modelled as agents servicing the demand within the network. Different mission segments are modelled with a timer-controlled state machine. The timer determines, how long a vehicle remains in a state before transitioning to the consecutive one. States can be either of fixed or of variable length. Variable state lengths depend on the cruise distance or whether a landing pad is available. Tab. 2 provides an overview of the state definitions for all types of flight missions. It also includes the consecutive states, their length and the required energy rate during that state. Similar states are also defined for repositioning flights and maintenance-related segments. The length of the maintenance checks depends on which check of Tab. 1 is due.

The battery is modelled as black box and its energy level is tracked unit-less between 1.0 for full and 0.0 for empty. After each mission, the battery is fully recharged. The recharging time depends on the mission and how deep the battery has been discharged. The recharging rate is set to 1C so that the charging time is linear-distributed between zero to one hour, depending on the level of discharge. The energy depletion rate for various states is referred to the cruise consumption rate $P_{Cruise}$ of 1/5112 indicating that the battery capacity would last 5112 s in cruise [28]. If multiple UAMVs are in hold for one vertiport, they are prioritised according to their remaining battery level. The vehicle with the lowest battery level is transferred to landing first.

Table 2 UAMV operational states based on [27]

All UAMV timers are incremented each time step. When a timer reaches the segment length, the UAMV is transferred to the next state. If the cruise segment has finished and all landing pads are occupied, the vehicle is not transferred to Landing but to Hold. UAMVs in hold have priority over all other vehicles and proceed to landing as soon as a landing pad becomes available.

The state unloading is followed by a Battery Charge after each flight mission. Also, there are no battery level restrictions regarding future missions to keep the level of unnecessary complexity low.

Cruise segments are modelled and indicated as straight lines between two vertiports.

Restrictions in airspace and air traffic control instructions cause detours from the beeline and for compensation, a routing factor of 1.42 is applied to missions [28]. For repositioning flights and transfers to or back from maintenance checks, the UAMV states 0 to 8 also apply. Preparation times for actual checks is included in the maintenance checks themselves.

In our simulation, we consider a mature UAM transport system with a fleet of 160 aircraft. Those aircraft are integrated into the fleet stepwise in five tranches of 32 UAMVs each. At the start of the simulation, the tranches have an average age of 500, 750, 1000, 1250 and 1500 FCs respectively with a standard deviation of 50 FCs among each tranch. With the average trip length, the corresponding FHs for each aircraft at the start of the simulation are calculated.

3.4 Input parameters

An overview of the simulation’s input parameters is provided in Tab. 3.

Table 3 Input parameters

In orientation of this section, the parameters are grouped into different categories. The assigned values are used for the initial simulation in Sect. 4.2. Numbers before the semicolon apply to outer vertiports, numbers behind apply to the central port.

3.5 Model performance monitoring

The nature of on-demand UAM transport differs from classic airline operation and accordingly its metrics have to be adjusted. An overview of performance metrics for this study is presented in Tab. 4. The two most significant metrics, maintenance costs and the network availability, are shortly explained. Maintenance costs are crucial for the operator, whereas for passengers the availability of the transport system is paramount. The network availability is the ratio of fulfilled transport requests divided by all requested flights. If it undercuts a certain level, passengers might consider the service to be unreliable and the operator might be challenged with decreasing passenger numbers and revenue.

Table 4 Performance metrics

3.6 Testing and verification

The simulation was created from scratch and was tested during each development step by different means:

• Tracking every aircraft’s path and movement.

• Counting the unserviced requested flights in two different ways and cross-checking the results.

• Comparing the overall number of ready UAMVs to the demand probability function.

• Tracking the energy level in the batteries to picture the vehicles’ change of operational states and compared them to results of Kohlman and Patterson’s publications [28].

• Running a test simulation with one vehicle and comparing the results with the expectations.

4 Simulation results

Subsequent to the introduction of the UAM simulation in the previous chapter, the results of the simulations are presented in this section. Three simulations are shown in detail and examine the impact of changes in one starting condition and two selected operational parameters on the interlinking between maintenance and operation. Initially, a maintenance-free scenario and the baseline help to understand the transport and maintenance simulation and provide references to compare later modifications to. The maintenance-free scenario, used for the scaling of the maintenance bases, is shown in Sect. 4.1, while the baseline is presented first in Sect. 4.2.

First, the distribution of the initial usage of the aircraft fleet is examined in  4.3.1. Second, the options to extend the opening hours of the maintenance base and trade vehicles’ RUL for earlier checks and changing the UAMV assignment are shown in Sects. 4.3.2 and 4.3.3. The simulation with the best parameter combination, shown in Sect. 4.3.4, leads to the lowest maintenance costs and combines the most sensitive parameters of previous sections.

4.1 Set-up for the initial simulation

Initially, a simulation with 160 UAMVs and over a period of 365 days is run without any maintenance events to size the right maintenance capacity and to serve as a reference for later comparisons.

Also, the upper bound of the network availability is determined with a daily average of 76.8 %. Later simulations in the following chapters with maintenance events will be compared to that theoretical maximum. There are two reasons, why in the maintenance-free case not all flight request can be fulfilled. The first reason is that no UAMV is available at the vertiport at the moment of the fight request, the second one is that no landing pad is available. The UAMVs have logged an average of 5.17 FHs per day and service a daily average of 11.27 flight missions leading to 2.18 FCs/FH. With the maintenance schedule in Tab. 1 the average MMHs/FH can be calculated to 0.41 MMHs/FH for one UAMV. Hence, a fleet of 160 UAMVs with an average of 5.17 FHs a day will require a total of approximately 337 MMHs a day. For the baseline simulation, a total daily maintenance capacity of 360 MMHs is provided by two maintenance bases being approximately 107 % of the averagely required daily MMHs. Both maintenance bases are alike and are equipped with two hangar bays for two simultaneous checks. In each bay ten mechanics are assumed to work in parallel providing 10 MMHs per simulation hour. The bases’ opening hours are from 8am to 5pm representing a daytime operation.

4.2 Baseline

The initial simulation is based on the input parameters of Tab. 3 and serves as reference for subsequent comparisons. During the 365 simulated days, an average of 1826 daily flights are conducted. The daily network availability varies between 71 % and 81 % with an average daily network availability of 75.4 %. The comparable network availability with 98.2 % is the ratio of the network availability for that baseline divided by the network availability of the maintenance -free simulation of Sect. 4.1. The UAMV wear is evenly distributed over all vehicles in this simulation. After one year of simulation, on average 1890 FHs are logged with a standard deviation of just 0.19 FHs. Including repositioning flights and transfers to and back from maintenance, aircraft are used on average 5.2 FHs a day. The daily number of revenue flights fluctuate between 1615 and 1880, while the number of repositioning flights fluctuates between 18 and 49. On days with a lower number of revenue flights (due to the aircraft being maintained or waiting for it) more repositioning flights are required.

In Fig. 4, the daily MMHs of both bases and the daily fleet waiting hours are shown for the simulation time of one year. The average utilisation of the maintenance bases is at 85.9 % and it varies daily between 14.9 % and 100 %. Even if the overall capacity is designed to be sufficient for the average daily demand, at 149 days of the simulation period, the capacity of 360 MMHs is fully tapped.

Fig. 4

Daily Fleet waiting and base working hours

On every day of the year, vehicles must wait. The highest waiting hours are accumulated on days with a complete maintenance base utilisation. Waiting hours also occur on days, where the utilisation is below 100 %. First, that can be caused by slack time in the beginning of the day followed by the later arrival of too many UAMVs that cannot be serviced at the same time. Second, vehicles arrive at the bases after closing or before opening time and hence need to wait for their maintenance checks. The waiting hours for the aircraft fleet are on average 193 h per day and range between a minimum of 11 and a maximum of 768 h a day. A ‘frequency’ of approximately 20 days in the pattern of waiting hours can be observed. With an daily average utilisation of approximately 5.2 FH a day, those peaks in the waiting hours are in the same frequency as the occurrence of the 100, respectively, the 200 FH checks.

For a closer inspection, the daily MMHs are subdivided into the check types and are shown in Fig. 5 for the days 170 to 290. The pattern of the smaller A and B checks seems to be equally distributed. That behaviour can be explained with the standard deviation of 50 for the initial FC distribution at simulation start. However, for the larger D checks a pattern can be observed in the figure (Note: C checks are not visible in that excerpt of Fig. 5).

Fig. 5

Daily fleet waiting and base working hours

In times, when there are no C or D checks, the waiting times are smaller as there is overall less demand for the maintenance resource. The D checks can be grouped into five blocks. However, these blocks in Fig. 4 are mainly due to the fluctuations of the smaller checks.

The development of the absolute maintenance costs and the accumulated fleet FHs over the course of the simulation are shown in Fig. 6.

Fig. 6

Abs. maintenance costs and accumulated fleet FH

The accumulated fleet FHs are shown as solid grey line. The graph increases almost linearly, but flattens very slightly on days with high waiting hours, for example on the days 48 to 52 (Hardly visible in that plot). The maintenance costs in absolute numbers are displayed as the black dashed line. The absolute costs exhibit a similar, but more pronounced behaviour than the waiting hours. Each maintenance event triggers discrete costs, which arise at the check, and cause the gradual incline. In periods of low maintenance activities or when mostly less expensive A and B checks are due, the slope is flatter. That is the case between day 130 and 180. In times of a high base utilisation, long waiting hours or when costlier checks are conducted, the slope is steeper. The steeper incline is observed between day 180 and 280.

Both graphs of the previous figure combined, form the maintenance costs per FH and are displayed in Fig. 7. The maximum daily increase in absolute costs is comparable for an early and a late day in the simulation, while the overall fleet FHs are constantly increasing over time. As a consequence, the impact of costs for a single check on the maintenance costs/FH is more significant at simulation begin.

Fig. 7

Abs. maintenance costs and accumulated fleet FH

The first peak in the graph is caused by the costs of checks until day 12, before the shop utilisation slightly drops (See Fig. 4), divided by the still comparable low overall fleet FHs. The second peak in the graph has the same reason, this time caused by the reduction in maintenance activities at around day 32. The more overall costs and FHs are accumulated, the smaller the percentual impact of the increasing check costs becomes and as consequence, the smaller is the variation in the graph. The decline of the graph between approximately day 120 and 180 is caused by a lower maintenance base utilisation and low fleet waiting hours in that period. The following rise and peaks in the graph is the reason of the starting D checks at around day 180, which are ongoing until approximately day 280. After one year of network transportation and technical operation the maintenance costs reach $ 93/FH.

For a more detailed view of the maintenance costs and their composition after 365 days is displayed in Fig. 8. Only $ 44 account for the actual check (Labour and material costs), which is 47 % of the total costs. While another 3 % account for running the maintenance bases and the slack time of the mechanics. The remaining part of approximately $ 46 accounts for the opportunity costs accounting for approximately one half of the complete maintenance costs and are primarily caused by long waiting times for the checks.

Fig. 8

Abs. Maintenance costs and accumulated fleet FH

Even if the network availability shows that approximately only one of 50 flights is not serviced due to maintenance restrictions, the high number of opportunity costs underlines that the interlocking between operation and maintenance is far from good in this baseline scenario. Within the next sections, the influences of changing starting conditions and adaptions in operation are presented.

4.3 Parameter studies

Within the scope of this section, different types of parameter studies are presented. The first parameter study is a modification of the simulation’s boundary conditions. The initial usage of the UAMVs at simulation start is compared in five different scenarios in 4.3.1. The second type focuses on operational options to improve the operation and maintenance interlocking. For that purpose, the maintenance capacity is extended by increasing the opening hours in Sect. 4.3.2. Furthermore, we examine how reassigned, earlier maintenance checks can reduce the fleet waiting hours and hence lower the maintenance costs in 4.3.3. Lastly, the increased maintenance capacity and the earlier maintenance checks are combined to find the overall best option regarding low maintenance costs and a high network availability in 4.3.4.

4.3.1 Initial UAMV age at simulation Start

In the last section, the influence of the initial UAMV FHs and FCs is noticeable in the frequency of maintenance checks (See Fig. 4). To further research the impact of the UAMV age at simulation begin, the baseline and four further scenarios are investigated within this subsection. The scenarios are indicated with the numbers 1, 2, 4 and 5. The baseline of Sec. 4.2 is numbered with 3 in this section.

• 1. All UAMVs are of almost the same age. They logged an average of 500 FCs with a standard deviation of 50 FCs at simulation begin.

• 2. The UAMVs are delivered in two batches. One half of the aircraft logged an average of 500 FCs with a standard deviation of 50 FCs. The other half has an average of 1500 FCs with a standard deviation of 150 FCs.

• 3. The baseline of Sec. 4.2.

• 4. The UAMVs are delivered in ten batches. The first batch has an average 500 FCs with a standard deviation of 50 FCs. While the standard deviation is kept unchanged, the average FCs are increased in nine steps of 250 FCs each to up 2750 FCs for the last batch.

• 5. Linear distribution. The logged FCs are distributed in 160 equal steps for all 160 aircraft between 0 and 3500.

A visualisation of the FCs distributions for the five different scenarios is shown in Fig. 9.

Fig. 9

Distribution of the flight cycles at simulation start

In Tab. 5 the most important Key Performance Indicators (KPIs) for the five scenarios are compared. On a macroscopic level, a major trend can be observed: The more equally the initial FCs of the UAMV are distributed, the lower the waiting times and the maintenance costs are and as a consequence, the network availability is higher. For the scenario 1, approximately every eighth request cannot be serviced due to the maintenance related waiting times. For scenario 5, only one in 83 flight requests remains unserviced.

Table 5 KPI of changed initial FC distribution

The maintenance costs are split up into the different cost components in following figure 10. The most significant difference is in the opportunity costs, which decrease for scenarios 1 to 5. The opportunity costs are the consequences of the differences in the vehicles waiting hours, which are also reduced from scenario 1 to 5. As the base utilisation is increasing from scenario 1 to 5, the the slack time of the mechanics is reduced and hence the running costs decline as well.

Fig. 10

Cost break down for different initial FCs distributions

The slight variations in the costs for maintenance material and labour are the consequences of the different overall number of checks and a different check distribution during the simulation period. Those changes are caused by the different starting conditions of the five scenarios. For instance, in scenario 3 (Baseline) the overall number of checks is higher with 3,106 compared to scenario 2 with 3,077. However, in scenario 2, there are six more C checks with signifcantly higher material costs and hence the material costs are slightly higher than in scenario 3.

The big differences in the average waiting time and the network availability can be illustrated with a comparison of the daily MMHs and fleet waiting time. Both KPIs are exemplarily shown for both extremes, the scenarios 1 and 5, in Fig. 11. The behaviour of the non-shown scenarios 2 to 4 is a transition between both shown subfigures. The MMHs are plotted in light grey, while the waiting hours are shown in black.

Fig. 11

Comparison of waiting hours and MMHs

On the left-hand side of Fig. 11, in subfigure (a), the fleet waiting hours appear periodically, as can be seen in the large amount of waiting hours between approximately day 275 and 340. The periodic appearance of the maintenance checks is the consequence of the vehicles being in roughly the same age at simulation begin and the equal usage of the vehicles during operation. A small time period in which the end of the maintenance intervals of all UAMVs are reached are the consequence. Hence too many UAMVs require maintenance at the same time. As the capacity of the bases is limited, they become bottlenecks and vehicles must wait to be maintained. Especially the time intensive checks cause thousands of waiting hours, which also decrease the network availability on maintenance-intense days. Between day 290 and 310 only 27 % of the flight requests could be serviced.

In Fig. 11 (b) the waiting time fluctuates and does not follow a certain pattern. At the same time, the utilisation of the bases is comparable constant and hence the maximum daily waiting hours are smaller by approximately one magnitude.

The different starting scenarios result in different levels of operation and maintenance interlocking. Especially in scenario 1, a different aircraft assignment or maintenance planning is fundamental for a reliable operation. The further the aircraft are spread in their life, the better the maintenance interacts with flight operation.

4.3.2 Maintenance capacity

From the maintenance provider’s point of view, there is the option to influence the transport capacity and consequently also the overall maintenance costs by adapting the maintenance capacity. That adaption can be implemented by increasing the number of mechanics working simultaneously or by extending the opening hours of the maintenance bases. In the baseline simulation approximately 70,000 overall fleet waiting hours pile up. 63 % of them are accumulated in times when the maintenance bases are closed, the remaining 37 % are caused when UAMVs must wait while the base is opened and all maintenance bays are already occupied. As the number of waiting hours is larger when the bases are closed, the maintenance capacity is increased by adapting the opening hours of the shops. With the increasing capacity, two opposing trends set in. On the one hand-side, a higher maintenance capacity reduces the waiting time and hence the costs related to that are lowered. On the other hand-side, the extended opening hours reduce the utilisation of the shops as the initial maintenance size provides already 107 % of the theoretically required capacity.

The maintenance capacity is increased in eight steps of 1 h to closing times from 17:00 to 24:00. In Tab. 6 the most important KPIs are compared.

Table 6 KPI of extended maintenance capacity

The overall maintenance costs are reduced for longer opening hours of the maintenance bases. However, the steps in cost reduction decrease for later closing times of the maintenance shops and reach a minimum at a closing time of 23:00. Afterwards the costs rise again. While the costs for labour and material of the checks remain similar, the change in maintenance costs comes primarily from opportunity and running costs. The network utilisation improves continuously with longer shop opening hours.

Fig. 12 provides a detailed cost break down. The costs for the actual maintenance checks, the material and labour costs, are almost constant as the number of both check types, the FH-based and the FC-based ones, only varies a little. The low variation is due to the slightly different number of maintenance checks as displayed in the two right columns of Tab. 6.

The running and opportunity costs show the expected opposing behaviour. The opportunity costs are reduced for longer operation hours of the maintenance bases as the waiting hours decrease. However, with a further increase in the opening hours, that effects starts to be limited. The running costs behave in the opposed manner, as longer opening hours mean less utilisation and hence more slack time of the mechanics starts to increase the costs. The closing time of 23:00 combines the lowest overall costs and the highest network availability. If the maintenance facilities are opened longer, the overall maintenance costs increase again.

Fig. 12

Cost break down for different maintenance capacities

In Fig. 13 a comparison of the daily MMHs and the fleet waiting time of the baseline scenario with the scenario with a closing hour of 23:00 is displayed between day 30 and day 130. For the baseline, the maximum shop capacity is fully utilised on 150 of 365 days, while the maximum capacity of 640 MMHs a day is never required, when maintenance is run until 23:00.

Fig. 13

Comparison of waiting hours and MMHs

The fluctuation in the utilisation is also higher for longer opening hours. At the same time, the utilisation of the maintenance shops is just at 52 %. That low utilisation indicates, that there is room for improvement with a more sophisticated scheduling and maintenance planning approach. Rescheduled maintenance checks to an earlier time point with the intension to reduce waiting times is one options. That approach is presented in the next chapter.

4.3.3 Trading remaining useful lifetime for earlier checks

Within this section, the option of performing maintenance checks prior to the end of the UAMV RUL is examined. The factor F_RUL describes how much of an interval can be exchanged for an earlier maintenance check. For example, F_RUL = 10 % indicates that either the 100-FH- or 200-FH-Check can be conducted after 90 FHs since the last FH-driven check. Alike, the FC-based checks can be conducted after 1575 FCs instead of 1750 FCs since the last FC-driven maintenance event. To do so, UAMVs are transferred to a maintenance base if the three following conditions are met:

• The vehicle is in state Ready at one of the vertiports 1, 3 or 6, which are the closer ones to the bases.

• More than 1-F_RUL of the regular FHs or FCs are logged.

• More maintenance bays are available than vehicles heading towards them.

If more UAMVs fulfil these conditions at the same time, the vehicle with the highest FHs since the last check will be assigned to the earlier maintenance check. Checking the UAMVs earlier means RUL is spoiled. Additional checks do not only results in additional material and labor costs, but also add (unnecessary) ground time to the UAMVs. Hence, the time for the additional checks must also be considered as opportunity time and causes additional opportunity costs $C_{Opp, RUL}$ which are included for all F_RUL > 0.

F_RUL is varied in seven steps between 2.5 % and 20 %. In the baseline simulation (F_RUL = 0 %) no earlier checks are possible. In Tab. 7 the KPI are for the different simulations are displayed.

Table 7 KPI for RUL trading

Three trends are observed in the table: Allowing earlier maintenance checks in general reduces the maintenance costs and lowers the waiting times. As a consequence, the comparable network availability is increased as well. The overall number of conducted maintenance checks increases and so does the base utilisation for an increasing F_RUL. For the maintenance costs, the waiting times and the network availability, a minimum is found between a F_RUL = 2.5 % and F_RUL = 7.5 %.

A detailed breakdown of the maintenance costs is displayed in Fig. 14. The overall lowest maintenance costs are found for conducting checks up to 5 % prior of the intended checks. Afterwards the maintenance costs increase again.

Fig. 14

Cost break down for RUL trading

There are two reasons for that: The number of checks increases and hence the labour and material costs as well as $C_{Opp, RUL}$ are higher. The second reason is the increase in waiting hours. Assigning UAMVs for earlier checks, as long as the capacity is available, has the side effect, that the maintenance bay will be occupied. The occupation length depends on the actual check and varies between 2.4 and 8 h. If one aircraft arrives at the maintenance facilities because the regular FH or FC threshold is reached, it must wait. The earlier vehicles are allowed to be maintained, the higher is the shop utilisation. Hence the chance, that UAMVs with regular assigned maintenance checks cannot be maintained directly after arrival also increases. As a consequence, the waiting time increases as well.

In the last section a general trend was noticeable: When the waiting hours are reduced, the network availability increases. This observation is only partly valid in this parameter study. Not only the waiting UAMVs cause the ’non-availability’ of the aircraft, but also when they are maintained unnecessarily often, which causes additional ground-time. Hence, more and earlier checks do not only increase the maintenance cost, but also reduce the availability of the UAMV fleet. That interconnection explains why for F_RUL = 7.5 % the average daily waiting time is lowest, but the network availability is slightly lower compared to F_RUL = 5 %.

Fig. 15 is an excerpt of the daily fleet waiting and working hours of both maintenance bases for the days 45–155.

Fig. 15

Comparison of waiting hours and MMHs

The baseline has higher maximum and average daily waiting times, while the working hours are more balanced for F_RUL = 5 %. The full maintenance capacity of 360 h is more seldom utilised for F_RUL = 5 % and the daily minimum working hours are higher compared to the baseline.

When reassigning maintenance checks before they become mandatory, the best option regarding maintenance costs and and also network availability is for an F_RUL = 5 %.

4.3.4 Best parameter simulation

In the previous sections, the influences of individual adaptions in operation are examined. To find the best possible combination within the scope of this simulation, the two parameters for changing the operating hours of the maintenance base and performing earlier checks are analysed in combination.

The ranges of the varied parameters is shown in Tab. 8.

Table 8 Varied parameters for best combination

In total 30 different combinations are simulated, of which the best 27 regarding low maintenance costs and a high average comparable network availability are displayed in Fig. 16. The same level of F_RUL is indicated with the same symbols in the plot. The size of the symbols indicates the closing time of the maintenance bases. The later the maintenance closes, the larger the symbols are plotted. Low maintenance costs and a high network availability are both desired goals. A Pareto-frontier is shown as dashed line and connects the best options. Those Pareto-optimal solutions are marked with the letters (a), (b) and (c) in Fig. 16.

Fig. 16

Comparison of costs and availability (with bigger symbols for longer opening hours)

The further left and the higher the markers are located in the figure, the more favourable the results are. The six results for an F_RUL = 2.5 % show the overall best solutions followed by results for F_RUL = 5 % and F_RUL = 7.5 %.

All three Pareto-optimal solutions are obtained for a maintenance base closing hour of 21:00, however the impact of the closing time is not as significant as the impact of F_RUL. Indicated with (a) in Fig. 16 is the simulation with F_RUL = 2.5 %, (b) represents a F_RUL = 5 %. (c) is the result of F_RUL = 7.5 %.

A comparison among them unveils the following trends: First, the comparable network availability varies only slightly. For all Pareto-optimal solutions, the range is between 99.65 and 99.69 % which is a difference of approximately 0.4 ‰. For that range in network availability, about one in 285 to 323 flights cannot be serviced due to maintenance restrictions. Second, the impact on the maintenance costs is more significant. Between (a) and (c) the costs vary between approximately 58 and $ 61/FH being a percentual difference of 3.7 %. Third, longer operation hours of the maintenance bases reduce the overall costs until 21:00, for closing hours of 22:00 the overall costs rise again. As the percentual reduction in maintenance costs is significantly higher than the percentual loss for comparable network availability in the Pareto-optimal solution (a), that scenario is considered as the best case.

Fig. 17 shows the fleet waiting time and the working hours of the Pareto-optimal solution (a) for the course of the simulation. The average daily fleet waiting time is only 23 hours. At the same time, full maintenance capacity of 560 MMHs a day is never fully required and the average maintenance utilisation is at 61 %.

Fig. 17

Waiting and working hours

The cost breakdown of the Pareto-optimal solution (a) is shown in Fig. 18. In the initial simulation of Sect. 4.2, opportunity costs account for about half of the overall costs. For this parameter set, they account for only 7 % of the overall costs. However, the share of running and slack costs is increased as the opening hours are extended from approximately 3 % of the baseline to 16 %. Approximately three quarters of maintenance costs of $ 58/FH now reflect material and labor costs for the actual checks, quantifying the improved interlinking between operation and maintenance events.

Fig. 18

Maintenance costs breakdown

The utilisation of the maintenance bases is still comparable low, which causes the higher share of running costs in the maintenance costs on the other hand side. It can be concluded, that even the best case is far from overall theoretical possible optimum. To approach the optimum with no waiting time of the vehicles and maintenance utilisation of 100 % or very close to it, a more sophisticated maintenance scheduling is necessary. A first idea to achieve that goal is presented in further research possibilities in the next section.

5 Conclusion and outlook

This study is the first work to research a potential maintenance schedule for UAMVs and the interlinking between maintenance and on-demand operation for UAM. It is meant as a basis for further explorations in the field of UAM maintenance and its scheduling.

A simulation is presented as feasible approach to picture the interaction between vehicle operation and maintenance events. Initially, a potential maintenance schedule for UAMVs is derived based on literature and an expert interview. It is integrated into an agent-based simulation consisting of three major elements: The vertiports, the UAMVs and the maintenance bases. The simulation demonstrates the interlinking between operation and maintenance for a number of performance parameters; most important are the serviced flight requests and maintenance costs. The wider maintenance cost modelling approach showed that opportunity costs for not serviced flight missions have a decisive impact on the maintenance costs for on-demand UAM and must not be disregarded. The quantitative influences of one boundary condition and two operational parameters are analysed in three parameter studies. Extending the opening hours and reassigning the maintenance checks to an earlier date are feasible options to improve the interlocking between maintenance and operation. A concluding optimum search identified a heuristic so that 99.7 % of the flight requests compared to a maintenance free scenario, could be fulfilled. In that best parameter simulation, the heuristic combines extended base opening hours with earlier maintenance checks and results in maintenance costs of approximately $ 58/FH.

After deducing a potential UAMV maintenance schedule and the examination of operational boundary conditions and decisions, we want to summarize the main observations (O) of this paper. Under the assumptions made for the UAMV maintenance and transport simulation, these are as follows:

$O_{1}$:

A transport simulation is a feasible approach to picture the interaction between on-demand operation and maintenance events and to research boundary conditions as well as operational changes.

$O_{2}$:

The initial distribution of the fleet age has a strong impact on the queuing for maintenance events. It hence influences the maintenance costs and network availability. Fleets with a strong spread in the initial aircraft age at simulation start, face less waiting time for maintenance, while fleets with a similar aircraft age cause long waiting hours.

$O_{3}$:

Increasing the maintenance capacity by extending the opening hours reduces the waiting times and increases the slack time. For those opposing trends a minimum can be identified.

$O_{4}$:

The option for earlier checks proofed to be efficient to reduce the waiting time and hence the maintenance costs. For earlier maintenance checks, there is also an optimum as too earlier checks increase the number of unnecessary checks, ground time and block the maintenance facilities.

$O_{5}$:

A combination of extended shop working hours and earlier maintenance checks provides a comparable network availability of 99.7 % and maintenance costs of $ 58/FH.

At the same time, we noticed limitations (L) of our settings and results and want to include them in the following list. For all limitations, we propose potential improvements to resolve them.

$L_{1}$:

The assignment of UAMVs to flight mission is preliminary based on a single parameter (numbers of FHs). In Sect. 4.3.3, a first step towards a UAMV ’flow control’ for maintenance checks is presented as three conditions are required for an earlier check. A more elaborated approach would be the implementation of a conflict detection for maintenance checks. If more slots are required than are available at the same time, the conflicting aircraft could be assigned differently to avoid waiting times.

$L_{2}$:

The opportunity costs are assumed as constant in the simulation. However, opportunity costs are actually demand-dependent. For example, if a UAMV waits for a maintenance check at 2 a.m. and there is a limited demand, which can be serviced with a small number of remaining aircraft, there are actually no opportunity costs. The opposite is in times of highest demand, where more flight request cannot be serviced. The opportunity costs can be turned into a time-dependent variable by coupling them with the actual demand distribution curve of Fig. 2, which would make this simulation more realistic.

$L_{3}$:

The smaller FH-based and the larger FC-based checks are conducted independently of each other. A simple solution is to include the smaller FH-based checks into the larger FC-based checks.

$L_{4}$:

Maintenance checks cause discrete increases of the costs in the simulation period. At the same time, the maintenance costs per FH converge towards a certain value and hence, a certain simulation duration is necessary. One option to reduce calculation time could be a scaled down model with a shorter runtime that is able to provide comparable solutions and conclusions.

$L_{5}$:

The number of parking slots at vertiports and maintenance bases is unlimited. With the implementation of a limited the number of parking slots at the vertiports as well as at the maintenance bases could make the transport simulation more realistic.

$L_{6}$:

In this study, some boundary conditions have not been changed. For example, only one type of UAMV and maintenance schedule is researched. The transport network was not altered and the demand curve has not been changed. Diverse UAMV types with different performance parameters and maintenance schedules are believed to be another field for further investigation. Also, changes in the network layout, the demand model are worth to be researched. The same applies for a ramp-up of operation or a fleet replacement process with a later generation of aircraft requiring a different amount of maintenance.

$L_{7}$:

Within this research only scheduled maintenance events are examined. Including unscheduled events after an unusual finding during a scheduled maintenance check or after an incident during operation with variable lead times would be another element of uncertainty to the maintenance scheduling. It could be used to quantify the quality of operation and maintenance interlinking.

$L_{8}$:

In the simulations, the battery was charged with 1 C. Changing the recharging rate for batteries could show an interesting correlation between the charging speed and maintenance. Especially if a battery degradation model, that includes the effects of charging speed on the loss of battery capacity and power, is implemented.