Skip to main content
SpringerLink
Log in

The Aircraft Maintenance Routing Problem

  • Chapter
  • First Online:
Optimization and Logistics Challenges in the Enterprise

Part of the book series: Springer Optimization and Its Applications ((SOIA,volume 30))

Summary

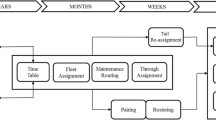
The airline network is one of the world’s most sophisticated, yet very complex, networks. Airline planning and scheduling operations have posed many great logistics challenges to operations researchers. Optimizing flight schedules, maximizing aircraft utilization, and minimizing aircraft maintenance costs can drastically improve the airlines’ resource management, competitive position and profitability. However, optimizing today’s airline complex networks is not an easy task. There are four major optimization problems in the airline industry including flight scheduling problem, fleet assignment problem, crew pairing problem, and aircraft maintenance routing problem. These problems have been widely studied over the past few decades. Yet, they remain unsolved due to the size and complexity. In this chapter, we provide a review of advances in optimization applied to these logistics problems in the airline industry as well as give a thorough discussion on the aircraft maintenance routing problem. Several mathematical formulations and solution methods for the aircraft maintenance routing problem will also be presented. Later, we conclude the current research and discuss possible future research of this problem.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

Refereneces

  1. C. Barnhart, N. Boland, L. Clarke, E. Johnson, G. Nemhauser, and R. Shenoi. Flight string models for aircraft fleeting and routing. Transportation Science, 32(3):208–220, 1998.

    Article  MATH  Google Scholar 

  2. C. Barnhart, E. Johnson, G. Nemhauser, and P. Vance. Crew scheduling. In R.W. Hall, editor, Handbook of Transportation Science, pages 493–521. Kluwer Scientific Publishers, 1999.

    Google Scholar 

  3. N. Boland, L. Clarke, and G. Nemhauser. The asymmetric traveling salesman problem with replenishment arcs. European Journal of Operational Research, 123:408–427, 2000.

    Article  MATH  MathSciNet  Google Scholar 

  4. G. Chartrand and O. Oellermann. Applied and Algorithmic Graph Theory. McGraw-Hill, 1993.

    Google Scholar 

  5. L. Clarke, C. A. Hane, E. Johnson, and G. Nemhauser. Maintenance and crew considerations in the fleet assignment. Transportation Science, 30(3):249–260, 1996.

    Article  MATH  Google Scholar 

  6. L. Clarke, E. Johnson, G. Nemhauser, and Z. Zhu. The aircraft rotation problem. Annals of Operations Research, 69:33–46, 1997.

    Article  MATH  Google Scholar 

  7. A. Cohn and C. Barnhart. Improving crew scheduling by incorporating key maintenance routing decisions. Operations Research, 51(3):387–396, 2003.

    MATH  MathSciNet  Google Scholar 

  8. J. Cordeau, G. Stojkoviac, F. Soumis, and J. Desrosiers. Benders decomposition for simultaneous aircraft routing and crew scheduling. Transportation Science, 35(4):375–388, 2001.

    Article  MATH  Google Scholar 

  9. M. Elf and V. Kaibel. Rotation planning for the continental service of a European airline. In W. Jager and H. Krebs, editors, Mathematics - Key Technologies for the Future: Joint Projects between Universities and Industry, pages 675–689. Springer, 2003.

    Google Scholar 

  10. A. Erdmann, A. Nolte, A. Noltemeier, and R. Schrader. Modeling and solving an airline schedule generation problem. Annals of Operations Research, 107:117–142, 2001.

    Article  MATH  MathSciNet  Google Scholar 

  11. FAA. Federal Aviation Regulations. URL: http://www.faa.gov/avr/afs, 2002.

  12. M. Gamache and F. Soumis. A method for optimally solving the rostering problem. In G. Yu, editor, Operations Research in the Airline Industry, pages 124–157. Kluwer Academic Publishers, 1998.

    Google Scholar 

  13. R. Gopalan and K. Talluri. The aircraft maintenance routing problem. Operations Research, 46(2):260–271, 1998.

    Article  MATH  Google Scholar 

  14. C. Hane, C. Barnhart, E. Johnson, R. Marsten, G. Nemhauser, and G. Sigismondi. The fleet assignment problem: Solving a large-scale integer program. Mathematical Programming, 70:211–232, 1995.

    MathSciNet  Google Scholar 

  15. D. Klabjan, E. Johnson, G. Nemhauser, E. Gelman, and S. Ramaswamy. Airline crew scheduling with time windows and plane count constraints. Transportation Science, 36(3):337–348, 2002.

    Article  MATH  Google Scholar 

  16. Z. Liang and W. Chaovalitwongse. Novel network based model for aircraft maintenance routing problem. Technical report, Rutgers University, Industrial & Systems Engineering Department, 2007.

    Google Scholar 

  17. V. Mak and N. Boland. Heuristic approaches to the asymmetric travelling salesman problem with replenishment arcs. International Transactions in Operational Research, 7:431–447, 2000.

    Article  MathSciNet  Google Scholar 

  18. A. Mercier, J. Cordeau, and F. Soumis. A computational study of Benders decomposition for integrated aircraft routing and crew scheduling problem. Computer & Operations Research, 32:1451–1476, 2005.

    Article  MathSciNet  Google Scholar 

  19. A. Mercier and F. Soumis. An integrated aircraft routing, crew scheduling and flight retiming model. Computer & Operations Research, 34:2251–2265, 2007.

    Article  MATH  Google Scholar 

  20. R. L. Phillips, D.W. Boyd, and T.A. Grossman. An algorithm for calculating consistent itinerary flows. Transportation Science, 25:225–239, 1991.

    Article  MATH  Google Scholar 

  21. D. Ryan and B. Foster. An integer programming approach to scheduling. In A. Wren, editor, Computer Scheduling of Public Transport: Urban Passenger Vehicle and Crew Scheduling, pages 269–280. North-Holland, 1981.

    Google Scholar 

  22. A. Sarac, R. Batta, and C. Rump. A branch-and-price approach for operational aircraft maintenance routing. European Journal of Operational Research, 175:1850–1869, 2006.

    Article  MATH  Google Scholar 

  23. H. Sherali, E. Bish, and X. Zhu. Airline fleet assignment concepts, models and algorithms. European Journal of Operational Research, 172:1–30, 2006.

    Article  MATH  Google Scholar 

  24. C. Sriram and A. Haghani. An optimization model for aircraft maintenance scheduling and re-assignment. Transportation Research Part A, 37:29–48, 2003.

    Google Scholar 

  25. K. Talluri. The four-day aircraft maintenance routing problem. Transportation Science, 32(1):43–53, 1998.

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial and Systems Engineering, Rutgers University, Piscataway, NJ 08854

    Zhe Liang & Wanpracha Art Chaovalitwongse

Authors
  1. Zhe Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wanpracha Art Chaovalitwongse
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhe Liang .

Editor information

Editors and Affiliations

  1. Department of Industrial and Systems, Rutgers State University of New Jersey, Frelinghuysen Rd. 96, Piscataway, 08854, U.S.A.

    Wanpracha Chaovalitwongse

  2. Corporate Strategic Research, ExxonMobil Research and Engineering, Route 22 East 1545, Annandale, 08801, U.S.A.

    Kevin C. Furman

  3. Dept. Industrial & Systems, University of Florida, Weil Hall 303, Gainesville, 32611-6595, U.S.A.

    Panos M. Pardalos

Rights and permissions

Reprints and permissions

Copyright information

© 2009 Springer-Verlag US

About this chapter

Cite this chapter

Liang, Z., Chaovalitwongse, W.A. (2009). The Aircraft Maintenance Routing Problem. In: Chaovalitwongse, W., Furman, K., Pardalos, P. (eds) Optimization and Logistics Challenges in the Enterprise. Springer Optimization and Its Applications, vol 30. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-88617-6_12

Download citation

Publish with us

Policies and ethics

Search

Navigation