Introduction

As a special type of oil and gas reservoir, volcanic rocks have attracted more and more attention. At present, Only a limited number of volcanic oil and gas reservoirs have been uncovered and deemed viable for development, and the research appears to be insufficiently thorough (Chen et al. 2022), in particular, the mechanical properties of deep volcanic rocks were less studied, it is very important to study the brittleness characteristics of deep volcanic rocks for efficient and high-yield development of volcanic rock reservoir energy. Volcanic gas reservoirs possess abundant resources and present extensive opportunities for exploration and development. Developing volcanic gas reservoirs is challenging due to the intricate reservoir characteristics and significant heterogeneity they possess. Volcanic rocks, being a distinctive category of oil and gas reservoirs, have garnered increasing interest and focus in recent times. At present, there is limited investigation into the mechanical properties of volcanic rocks (Chen et al. 2022). The resource potential of volcanic gas reservoirs is substantial, and has a broad prospect of exploration and development. Because the gas reservoir is a dual medium, there are multiple fractures extending at the same time in the construction of volcanic rock reservoir, which is easy to lead to the failure of fracturing construction. It is also a difficult problem that is northng explored and studied all over the world. From a certain point of view, the higher the brittleness index is, the easier the reservoir is to be reformed and the higher the recovery efficiency is. However, the volcanic rock reservoir contains relatively developed natural fractures, which will greatly affect the brittleness of the reservoir rock (Heap et al. 2021), and then directly or indirectly affect the fracture-making ability of the reservoir rock during hydraulic fracturing. Accurate evaluation of rock brittleness is of great significance in petroleum exploration and development (Wang et al. 2022).

While many researchers have studied the brittleness characteristics of rocks, Zhao (2020) used fracture energy theory to study the brittleness characteristics of reservoir rocks, and the research results showed that the main parameters affecting the brittleness of tight oil reservoirs in Dagang oilfield were Young's modulus, expansion Angle and peak strain. By using mineral composition method and acoustic logging method, the variation range of brittleness index of shale reservoir was studied, and the high brittleness region of shale reservoir was determined (Ariketi et al. 2017). Baouche (Baouche et al. 2022) studied the brittleness characteristics of carbonate from the physical and mechanical aspects of rocks, and based on this, studied its frackability. Mustafa (Mustafa et al. 2022) used data-driven machine learning methods to predict the mineral formation of shale, which helps to evaluate brittle and ductile regions in shale reservoirs. By studying the geology and rock mineral composition of shale reservoirs in Pakistan, Sohail (2022) found that the shale reservoirs in Pakistan were similar to those in North America and have good development prospects. Liu et al. (2022) studied the influence of typical cemented fractures in volcanic rock reservoirs on the propagation of hydraulic fractures. Based on the indoor hydraulic fracturing test and numerical simulation, cross-validation was carried out to verify the reliability of the numerical method and provide technical means for selecting favorable fracturing areas. Jia et al. (2013) conducted large-scale true triaxial volcanic rock hydraulic fracturing test in the laboratory, analyzed the fracturing capacity of volcanic rock by scanning the three-dimensional geometric shapes of hydraulic fracturing fractures before and after the test using industrial CT technology, and proposed key technical issues to improve the fracturing capacity of volcanic rock. Chen et al. (2022) analyzed conventional volcanic rock hydraulic fracturing, acid erosion hydraulic fracturing and proppant carrying acid erosion hydraulic fracturing through laboratory experiments, clarified the influence of acid erosion and proppant embedment on volcanic rock hydraulic fracturing, and studied the influence of different proppant sizes and acid types on fracture conductivity. Yang (2020) conducted a series of fracturing experiments on volcanic rock samples containing natural fractures and an injection method of multiple flow pulses was proposed to increase the fracture complexity. Xia (2022) reviewed the relationship between rock brittleness and mechanical properties such as stress drop coefficient after the peak of stress–strain curve as Well as influencing factors of brittleness failure. In addition, the existing methods for estimating rock brittleness index are summarized and their applicability is briefly discussed. Wang et al. (2022) proposed a new brittleness index evaluation method based on the consideration of rock damage, and calculated rock damage based on energy. By analyzing the changes of rock brittleness when confining pressure and temperature rise, the newly proposed brittleness index of rock was verified. Shi et al. (2021) proposed a brittleness evaluation method for fragile rocks, which used acoustic emission technology to study the relationship between acoustic emission (AE) energy released during the fracture process of rock samples and brittleness. According to the energy accumulation and dissipation in pre-peak and post-peak stages, a brittleness evaluation method based on cumulative sound energy was proposed. Heap et al. (2021) analyzed the influences of stress–strain curves and the evolution of volcanic porosity and acoustic emission activities on the brittleness and ductility of volcanic rocks in triaxial experiments. It was pointed out that brittleness is usually characterized by shear fracture formation and increased porosity and permeability, ductile deformation can be distributed (crumbed pore collapse) or local (compaction zone), characterized by decreased porosity and permeability. By analyzing the available data, it was concluded that the tuff deforms due to localized catalytic cracking, and the volcanic rocks form compaction zones (collapsed pore planes connected by microcracks). The brittle failure envelope and compaction yield limit of volcanic rocks were compared.

Based on the above understanding, most of the research focused on the law of hydraulic fracturing fracture propagation in volcanic rock reservoir, and there is a lack of research on the rock properties of volcanic rock, especially the impact on the mechanical properties of deep volcanic rock. In addition, due to the special properties of volcanic rocks, evaluating the brittleness characteristics of volcanic rocks by the method of evaluating the brittleness characteristics of other rocks has certain limitations. For example, Zhou (2018) paper does not pay enough attention to the release of post-peak energy. Therefore, it is necessary to fully understand the brittleness characteristics of deep volcanic rock reservoir through advanced experimental means and mechanical methods to minimize the damage to the reservoir and meet the process requirements. This paper conducted triaxial tests under different confining pressures on volcanic rocks at two different depths (3000 m–3500 m), and used different brittleness evaluation methods to study the brittleness characteristics of deep volcanic reservoir rocks. According to the triaxial test, the stress–strain characteristics of volcanic rocks are defined, and an improved brittleness evaluation method suitable for volcanic rocks is proposed according to the special mechanical properties of volcanic rocks. Understanding the brittleness characteristics of deep volcanoes can provide reference for the exploration and development of deep volcanic rocks.

Gological background and microscopic characteristics

Geological background

Songliao Basin, influenced by the Mongol-Okhotsk Ocean tectonic domain and the paleo-Pacific tectonic domain, has undergone three tectonic evolution stages: fault depression period, depression period and inversion period (Wu et al. 2010; Feng et al. 2021). The research object of this study is deep volcanic rocks in Xujiaweizi fault depression, Songbei, which have large resources, short development time, low utilization ratio of reserves and high development potential. Figure 1 shows the exploration results of deep strata in northern Songliao Basin.

Fig. 1
figure 1

Map of deep exploration results in northern Songliao basin

Full size image

Mineral components

Mineral composition analysis is one of the basic methods to determine rock properties, which is of great significance to the study of geological sedimentary characteristics and reservoir evaluation. The Bruker AXS D8-Focus X-ray diffractometer (Fig. 2) in Germany was used to analyze the rock and mineral components. The experimental test and analysis system was conducted by irradiating X-rays on the samples placed in the center of the spectrometer (Angle finder), and X-ray diffraction was generated on the samples. The X-ray diffraction pattern can be obtained by measuring and recording the intensity of the X-ray while changing the incident Angle and diffraction Angle of the sample (Table 1, Fig. 3).

Fig. 2
figure 2

Bruker AXS D8-Focus X-ray diffractometer

Full size image
Table 1 Rock and mineral analysis results of No.1 Well
Full size table
Fig. 3
figure 3

Analysis results of mineral components in core of Well No.1 by X-ray diffraction

Full size image

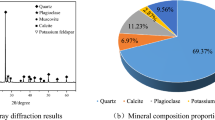
XRD mineral analysis showed that the main components of the core minerals in Well No.1 were albite and quartz, of which albite accounts for about 63.28% of the total mineral composition, followed by quartz, accounting for about 1/5 of the total mineral composition, followed by microcline, accounting for 13.66%, and chlorite, accounting for less than 2% (Table 2, Fig. 4).

Table 2 Rock and mineral analysis results of No.2 Well
Full size table
Fig. 4
figure 4

Analysis results of mineral components in core of Well No.2 by X-ray

Full size image

XRD mineral analysis showed that the main components of the core minerals in Well No.2 were albite and quartz, of which albite accounts for about 50% of the total mineral composition, followed by quartz, accounting for about 1/4 of the mineral composition, and then microcline, accounting for about 1/2 of the quartz, calcite and chlorite account for a relatively small proportion, no more than 10% (Fig. 5).

Fig. 5
figure 5

Bar chart of mineral composition

Full size image

As can be seen from the XRD test results, the brittle mineral content in Well No.2 was significantly higher than that in Well No.1, indicating that the rocks in Well No.2 have better brittle properties.

Microstructure

The essence of the change of macroscopic mechanical characteristics of rock is the macroscopic reflection of the change of microscopic structure of rock. The overall analysis of microscopic structure characteristics can also analyze the difference of mineral particle size, the spatial distribution of each mineral arrangement and the structural characteristics of internal pores and micro-cracks.

The collected rock cores (IN the same batch as the mechanical test cores) were analyzed using ZEISS SUPRA55 field emission scanning electron microscope (SEM) of Shanghai Institute for Advanced Studies, Chinese Academy of Sciences. The experimental testing and analysis system adopted the patented GEMINI tube design and annular In-Lens SE detector. It is characterized by stable beam flow and high resolution, and can conduct high-resolution imaging and elemental composition analysis of both conductive and non-conductive samples (Fig. 6).

Fig. 6
figure 6

ZEISS SUPRA55 field emission scanning electron microscope

Full size image

As can be seen from the sem microstructure diagram, the confining pressure of volcanic rocks increased with the increase in the depth of the strata. Under the action of higher confining pressure, volcanic rocks were relatively compact and the distribution of particles is relatively uniform (Figs. 7, 8).

Fig. 7
figure 7

SEM photos of Well No.1

Full size image
Fig. 8
figure 8

SEM photos of Well No.2

Full size image

Theoretical basis

Brittleness of rock can be defined as the property of rock failure due to small deformation under the action of force. However, there is no unified definition for rock brittleness research at present, because the formation process of rocks is complicated, for example, evaluating brittleness characteristics by mineral analysis will ignore the influence of the internal skeleton structure of rocks. In this paper, several representative methods of rock brittleness evaluation were used to evaluate the rock brittleness of deep volcanic rock reservoir under different confining pressures (Fig. 9).

Fig. 9
figure 9

Brittleness evaluation method for stress–strain curve characteristics

Full size image

Brittleness evaluation method based on stress–strain curve characteristics (Hucka et al. 1974)

The method (Coates et al. 1966) defines brittleness as the ratio of elastic strain to total strain value.

$$ {\text{BI}}_{1} = \frac{{\text{Reversible strain}}}{{\text{Total strain}}} = \frac{{{\text{DE}}}}{{{\text{OE}}}} $$
(1)

Brittleness evaluation method based on energy dissipation

Tarasov (Tarasov et al. 2013) considered the energy accumulated after the peak of the stress–strain curve as one of the factors to be considered in the evaluation of rock brittleness.

Figure 10 showed the energy balance at three deformation stages: peak stress (point B), post-peak intermediate stage, and total failure (point C). The area of the red triangle here corresponds to the elastic energy stored in the sample during the above three deformation stages. The gray area represents the post-peak rupture energy. The test results showed that the elastic energy accumulated in the sample material under peak stress can be converted into the fracture energy after peak stress.

Fig. 10
figure 10

Brittleness evaluation method of energy dissipation (Tarasov et al. 2013)

Full size image

The brittleness index represents the degree of inherent instability of a material upon failure. Therefore, the diagram in Fig. 10 can be used to determine brittleness based on energy parameters. In order to simplify the estimation of the elastic energy dWe extracted from the material sample during the post-peak failure process between point B and point C.

$$ {\text{d}}W_{e} = \frac{{\sigma_{B}^{2} - \sigma_{C}^{2} }}{2E} $$
(2)

In the curve, the fracture energy dWr after the peak is composed of the extracted elastic energy dWe plus the additional energy corresponding to the gray area ABCD.

$$ {\text{d}}W_{a} = \frac{{\sigma_{B}^{2} - \sigma_{C}^{2} }}{2M} $$
(3)

The post-peak rupture energy dWr is described by the following equation:

$$ {\text{d}}W_{r} = {\text{d}}W_{e} - {\text{d}}W_{a} = \frac{{(\sigma_{B}^{2} - \sigma_{C}^{2} )(M - E)}}{{2{\text{EM}}}} $$
(4)

And the calculation formula can be obtained:

$$ {\text{BI}}_{2} = \frac{{{\text{d}}W_{r} }}{{{\text{d}}W_{e} }} = \frac{M - E}{M} $$
(5)

Methods for brittleness evaluation of mineral composition

Brittleness is essentially a property of rock materials. The important property that separates different rock materials is their mineral composition. Mineral composition and their relative content affect the physical and mechanical properties of rock materials, among which, the content of brittle minerals plays an important role in the brittleness of rock materials (Jarvie et al. 2007; Rickman et al. 2008; Jin et al. 2015)

$$ {\text{BI}}_{3} = \frac{{W_{Q} + W_{C} }}{{W_{{{\text{total}}}} }} $$
(6)
$$ {\text{BI}}_{31} = \frac{{W_{Q} }}{{W_{Q + c + cl} }} $$
(7)
$$ {\text{BI}}_{32} = \frac{{W_{{{\text{QFM}} + C}} }}{{W_{{{\text{total}}}} }} $$
(8)

where Wx = proportion of mineral component x; Q = Quartz; C = Carbonate; CL = Clay; QFM = Quartz + Feldspar + Mica.

Data and methods

Sample preparation

From the cylindrical sample with a diameter of 25 mm in the drilling area of the cylindrical core, the standard cylindrical core for rock mechanics experiment was obtained by cutting and grinding the end face (Fig. 11), (Fig. 12)

Fig. 11
figure 11

Deep downhole cylindrical core (unprocessed)

Full size image
Fig. 12
figure 12

Standard cylindrical core after processing

Full size image

Test instrument and test method

The equipment used in this Test is MTS815 Flex Test GT program controlled servo rock mechanics test system, which is equipped with servo controlled automatic three-axis compression and measurement system. See Fig. 13.

Fig. 13
figure 13

American MTS815 Flex Test GT rock mechanics test system

Full size image

Performance indicators: vertical maximum force: 4600 kN, vertical piston stroke: 100 mm, maximum confining pressure: 140 MPa, strain rate adaption range 10–2 to 10–71/s, fatigue frequency: 0.001–0.5 Hz, the overall stiffness of the test frame: 11.0 × 109 N/m, the test system loading is stable, the measurement and control accuracy is high, all the test process and data are controlled and collected by computer, avoid manual reading error and error.

As the buried depth range of underground core is 3000–4000 m and belongs to deep rock, the depth range where the core is located was set to be covered by four confining pressures of 20, 40, 60 and 80 MPa.

Triaxial test data

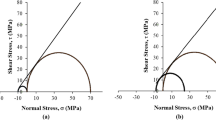
To evaluate the brittleness of rocks, triaxial test data under different confining pressures were needed. Axial extensometers and circumferential extensometers were set on the sample to monitor the radial deformation of the sample, and then the instrument computer system calculates the axial strain and radial strain according to the sample size, as shown in Fig. 14. The compressive strength, elastic modulus and Poisson's ratio of standard volcanic rock samples were calculated by triaxial test data (Table 3, Figs. 15, 16).

Fig. 14
figure 14

Sample installation process diagram

Full size image
Table 3 Rock mechanics parameters under triaxial compression in Well No.1
Full size table
Fig. 15
figure 15

Stress–strain curve (Well No.1)

Full size image
Fig. 16
figure 16

Volcanic rock sample after test photo (Well No.1)

Full size image

In Well No.1, the dispersion of rock mechanics parameters under uniaxial compression was small. The mean uniaxial compressive strength was 154 MPa, the mean elastic modulus was 23 MPa, and the mean Poisson's ratio was 0.085. The sample was destroyed by vertical splitting.

Under triaxial compression, the maximum deviatoric stress increased with the increase in confining pressure, and the elastic modulus changes little under the confining pressure of 20, 40 and 60 MPa, while the elastic modulus changed greatly under the confining pressure of 80 MPa, and the Poisson's ratio changed little.

The maximum deviatoric stress under the triaxial condition was higher than that under the uniaxial condition, and the elastic modulus under the confining pressure of 20, 40 and 60 MPa had little difference with that under the uniaxial condition. Triaxial specimens showed oblique shear failure under triaxial conditions, and with the increase in confining pressure, the fracture characteristics of shear plane became more obvious (Table 4, Figs. 17, 18).

Table 4 Rock mechanics parameters under triaxial compression in Well No.2
Full size table
Fig. 17
figure 17

Stress–strain curve (Well No.2)

Full size image
Fig. 18
figure 18

Volcanic rock sample after test photo (Well No.2)

Full size image

In Well No.2, the rock mechanics parameters of uniaxial compression were relatively discrete. The mean uniaxial compressive strength was 154 MPa, the mean elastic modulus was 15.05 MPa, and the mean Poisson's ratio was 0.06. The sample was destroyed by vertical splitting.

Under triaxial compression, the maximum deviatoric stress increased with the increase in confining pressure, but the elastic modulus and Poisson's ratio changed little.

The maximum deviatoric stress, elastic modulus and Poisson's ratio under the triaxial condition were higher than those under the uniaxial condition. The triaxial specimens showed oblique shear failure under triaxial conditions (Figs. 19, 20, 21, 22).

Fig. 19
figure 19

Stress–strain curve characteristics

Full size image
Fig. 20
figure 20

Brittleness evaluation of Well No.1

Full size image
Fig. 21
figure 21

Brittleness evaluation of Well No.2

Full size image
Fig. 22
figure 22

Stress–strain curve Energy dissipation diagram

Full size image

Test results and analysis

Brittleness evaluation method based on stress–strain curve characteristics

Formula (9) is the brittleness evaluation method based on stress–strain curve characteristics (Tables 5, 6).

$$ {\text{BI}}_{1} = \frac{{\text{Reversible strain}}}{{\text{Total strain}}} = \frac{{{\text{DE}}}}{{{\text{OE}}}} $$
(9)
Table 5 Summary of brittleness evaluation of Well No.1
Full size table
Table 6 Summary of brittleness evaluation of Well No.2
Full size table

Brittleness evaluation method based on energy dissipation

Formula (10) is the brittleness evaluation method based on energy dissipation (Tables 7, 8, Figs. 23, 24).

$$ BI_{2} = \frac{{dW_{r} }}{{dW_{e} }} = \frac{M - E}{M} $$
(10)
Table 7 Summary of brittleness evaluation of Well No.1
Full size table
Table 8 Summary of brittleness evaluation of Well No.2
Full size table
Fig. 23
figure 23

Brittleness evaluation of Well No.1

Full size image
Fig. 24
figure 24

Brittleness evaluation of Well No.2

Full size image

Brittleness evaluation method of mineral composition

Formula (11) is the brittleness evaluation method based on energy dissipation (Tables 9, 10)

$$ {\text{BI}}_{3} = \frac{{(W_{Q} + W_{C} )}}{{W_{{{\text{total}}}} }} $$
(11)
Table 9 Summary of brittleness evaluation of Well No.1
Full size table
Table 10 Summary of brittleness evaluation of Well No.2
Full size table

Summary of brittleness evaluation

As is seen from Figure (a), when we used the brittleness evaluation method based on stress–strain curve characteristics, the volcanic brittleness of Well No.1 (depth 3500 m) changed slightly with the increase in confining pressure, but when we used the brittleness evaluation method based on energy dissipation, the volcanic brittleness of Well No.1 (depth 3500 m) presented a state of large fluctuations with the increase in confining pressure, It presented a trend of decreasing—increasing—decreasing—increasing, and reached the lowest value when the confining pressure was 20 MPa (Fig. 25).

Fig. 25
figure 25

Summary of brittleness evaluation

Full size image

It is seen from Figure (b) that the volcanic brittleness of Well No.2 (3000 m depth) decreased with the increase in confining pressure and reached the lowest value when the confining pressure was the highest. As is seen from Figure (c), the volcanic rock brittleness index of the two Wells changed smoothly with confining pressure, and there was no large drop.

As is seen from Figure (d), with the increase in volcanic depth, the brittleness index decreased, not only because the shallow volcanic rock had a high content of brittle minerals, but also because with the increase in depth, the confining pressure of volcanic rock would also increase. Combined with the microscopic structure diagram, under the action of higher confining pressure, volcanic rock was relatively dense and had a large cohesive force between particles. Therefore, deep volcanic rocks were not prone to brittle failure, which was why the volcanic rock brittleness index of Well No.1 changed relatively gently with confining pressure.

Discussions

Improved angular brittleness evaluation method based on internal friction

Hucka (1974) introduced a brittleness evaluation method based on the internal friction Angle of rocks, as shown in formula (12):

$$ BI = {\text{Sin}} \phi = \frac{{\frac{\partial R}{{\partial \sigma_{n} }}}}{{1 + \left( {\frac{\partial R}{{\partial \sigma_{n} }}} \right)^{2} }} $$
(12)

R–Resistance to deformation

σn–Normal stress

ϕ–Angle of internal friction

Zhou (2018) believed that the internal friction Angle of the two rocks is the same, but the brittleness index of the two rocks may be different. Therefore, based on Hucka, a brittleness evaluation method combined with the pre-peak and post-peak characteristics of stress–strain curve was proposed, as shown in formula (13)–(16):

$$ BI = k_{1} \times k_{2} \times \sin \phi $$
(13)
$$ k_{1} = e^{\frac{E}{10M}} $$
(14)
$$ k_{2} = \frac{{\sigma_{p} - \sigma_{r} }}{{\sigma_{p} }} $$
(15)
$$ M = \frac{{\sigma_{r} - \sigma_{p} }}{{\varepsilon_{r} - \varepsilon_{p} }} $$
(16)

σP—Compressive strength

σr—Residual strength

In the study of Tarasov (2013), E/M represents the ratio of elastic energy released to elastic energy recovered, and (M-E)/M represents the ratio between the fracture energy and the recovered elastic energy after the peak. In this paper, it can be seen from the triaxial test of volcanic rocks that the stress–strain curve after the peak showed a sudden decline, indicating that a large amount of energy was released after the failure of volcanic rocks, this difference can be seen in the stress–strain curve comparison diagram shown in Fig. 26., especially under the action of high stress, the energy release of volcanic rocks is more rapid than that of reference objects. Therefore, it was suitable to use the fracture energy to evaluate the brittleness index. Thus, “E/M” in Zhou (2018) paper was replaced by “(M-E)/M”. The following was an improved angular brittleness evaluation method based on internal friction, as shown in formula (17)–(20):

$$ BI_{4} = k_{1} \times k_{2} \times \sin \phi $$
(17)
$$ k_{1} = e^{{\frac{M - E}{{10M}}}} $$
(18)
$$ k_{2} = \frac{{\sigma_{p} - \sigma_{r} }}{{\sigma_{p} }} $$
(19)
$$ M = \frac{{\sigma_{r} - \sigma_{p} }}{{\varepsilon_{r} - \varepsilon_{p} }} $$
(20)
Fig. 26
figure 26

Stress–strain curve comparison diagram

Full size image

Application of improved angular brittleness evaluation method

Introduction to the method of calculating cohesion and internal friction angle

According to the data obtained from the triaxial compression test, the cohesion and internal friction Angle of the rock can be calculated by using the Moercoulomb failure criterion. As shown in formula (21):

$$ \sigma_{1} = A\sigma_{3} + B $$
(21)

where \(A = \frac{1 + \sin \phi }{{1 - \sin \phi }}\), \(B = \frac{2C\cos \phi }{{1 - \sin \phi }}\).where \(\phi = \arcsin \left( {\frac{A - 1}{{A + 1}}} \right)\) \(C = \frac{B}{2\sqrt A }\).

Application of BI4

The C and ϕ under different confining pressures were obtained by the above method, as follows (Tables 11, 12, 13, Figs. 27, 28, 29):

Table 11 Calculation results of c and φ
Full size table
Table 12 BI4 of Well No.1
Full size table
Table 13 BI4 of Well No.2
Full size table
Fig. 27
figure 27

Fitting curve of σ3–σ1

Full size image
Fig. 28
figure 28

σ1-σ3 at different confining pressures in Well No.1

Full size image
Fig. 29
figure 29

σ1-σ3 at different confining pressures in Well No.2

Full size image

It is seen from Fig. 30. that the improved brittleness evaluation method based on internal friction Angle had almost the same rule as the brittleness evaluation method based on stress–strain curve characteristics (BI1) and the brittleness evaluation method based on energy dissipation (BI2), indicating the feasibility of the improved brittleness evaluation method. Firstly, in Well No.1, the brittleness index fluctuated with the increase in confining pressure, and it always changed with the increase in confining pressure during the period of 20–40 MPa. Secondly, in Well No.2, the brittleness evaluation method based on stress–strain curve characteristics (BI1) and the brittleness evaluation method based on energy dissipation (BI2) had the same change trend, and the brittleness index decreased with the increase in confining pressure. Finally, from the perspective of the depth of the two Wells, the overall brittleness index of Well No.2 was obviously higher than that of Well No.1, indicating that the brittleness index decreases with the increase in rock depth, which was consistent with the results obtained by the brittleness evaluation method of mineral composition (BI3), again proving the feasibility of the improved brittleness evaluation method based on internal friction Angle.

Fig. 30
figure 30

Results of improved brittleness evaluation method

Full size image

Conclusions

This paper conducted triaxial compression tests and XRD tests under different confining pressures of volcanic rocks at depths of 3000 m and 3500 m, and used the brittleness evaluation method based on stress–strain curve characteristics (BI1), the brittleness evaluation method based on energy dissipation (BI2) and the brittleness evaluation method based on mineral composition (BI3) to evaluate the brittleness characteristics of the underground cores of the two Wells. An improved angular brittleness evaluation method based on internal friction was proposed, and the following conclusions were obtained:

  1. 1.

    Using the brittleness evaluation method based on stress–strain curve characteristics (BI1), the volcanic rock brittleness of Well No. 1 (depth 3500 m) decreased with the increase in confining pressure, and the volcanic rock brittleness of Well No. 2 (depth 3000 m) showed a decreasing trend with the increase in confining pressure, and reached the lowest value when the confining pressure was the highest.

  2. 2.

    When using the brittleness evaluation method based on energy dissipation (BI2), the brittleness of volcanic rocks in Well No. 1 (depth 3500 m) presented a state of fluctuation with the increase in confining pressure, but it can be seen that the overall trend was still decreasing with the increase in confining pressure. The brittleness of volcanic rocks in Well No. 2 (3000 m depth) showed a decreasing trend with the increase in confining pressure.

  3. 3.

    The brittleness evaluation method based on mineral composition (BI3) showed that with the increase in volcanic rock depth, its brittleness index decreased, not only because of the high content of brittle minerals in deep volcanic rocks, but also because the confining pressure of volcanic rocks increases with the increase in depth. Under the action of higher confining pressure, volcanic rocks were relatively dense and have greater cohesion between particles. Therefore, deep volcanic rocks are not prone to brittle failure.

  4. 4.

    Using the improved brittleness evaluation method based on internal friction Angle, the experimental results were almost consistent with the brittleness evaluation method based on stress–strain curve characteristics (BI1) and the brittleness evaluation method based on energy dissipation (BI2), which indicated the feasibility of the improved brittleness evaluation method.