Introduction

Groundwater, a naturally occurring vital resource is overexploited nowadays in many parts of the world to meet the growing human demand for drinking, agriculture, urban, and industrial purposes (Deepa and Venkateswaran 2018; Mahammad and Islam 2021). Groundwater is a purer form of water as it is always clear, colourless, and odorless and maintains a relatively constant temperature compared to surface water (Fatoba et al. 2017). Therefore, two/third of the world’s population uses groundwater alone to meet their necessary demands (Adimalla and Taroor 2020). The groundwater extraction in India is maximum than any other countries of the world utilizing for irrigation (89%), domestic (9%), and industrial (2%) purposes (Margat and van der Gun 2013; Ahada and Suthar 2018). Unfortunately, in India, the deterioration of groundwater quality is increasing rapidly due to overexploitation of groundwater without a balanced recharge, uncontrolled uses of agrochemicals and fertilizers that percolate into the aquifer system (Wagh et al. 2017). Besides, industrial wastewater, municipal solid waste, and domestic wastewater also add water pollutants. Moreover, geology, chemical weathering of rocks, quality of recharge water, and water-rock interaction of an area have a greater influence on the hydrochemical characteristics of the groundwater (Trabelsi et al. 2012). Consequently, the contaminated groundwater affects human health, the balance of the aquatic ecosystem, economic development, and social prosperity as well (Milovanovic 2007; Zahedi et al. 2017). Therefore, the periodic monitoring of hydrochemical characteristics of groundwater and hydraulic parameters of aquifer holding the groundwater is required for the proper planning and management of groundwater (Fatoba et al. 2017).

Numerous studies have been carried out throughout the world using the groundwater quality parameters to assess the suitability of groundwater for irrigation, drinking, and domestic purposes (Salifu et al. 2017; Kumari et al. 2019; Barik and Pattanayak 2019; Srivastava 2019; Singh et al. 2020; Kurdi and Eslamkish 2017; Duraisamy et al. 2019; Egbueri et al. 2020; Khan and Jhariya 2017; Tiwari et al. 2017; Abdullah et al. 2019). Srivastava and Parimal (2020) have studied the hydrochemistry of groundwater and used the various weathering indices to assess the suitability of water for irrigation purposes. Anbazhagan and Nair (2004) have used the geographical information system (GIS) to represent the spatial variation of various geochemical elements in Panvel Basin, Maharashtra, India. Several multivariate statistical techniques such as cluster analysis (CA), factor analysis (FA), and principal component analysis (PCA) have been employed by many researchers to identify the significant parameters of groundwater quality (Abdelaziz et al. 2020). Zheng et al. (2016) applied CA, discriminate analysis (DA), PCA, and FA to evaluate the surface water quality and categorized the physicochemical parameters of water quality in the Second Songhua River basin in China. Bhuiyan et al. (2016) used multivariate statistics along with a geostatistical technique for the analysis and interpretation of complex datasets of groundwater of the southeastern coastal region of Bangladesh. They also indicated the pollution sources that are responsible for variation in physicochemical parameters and metal contents in groundwater systems.

To assess the surface water and groundwater quality, several approaches have been studied during the last few decades. The water quality index (WQI) tool can be used to assess water quality by transforming a huge number of parameters into a single index (Tyagi et al. 2013; Minh et al 2019; Abdelaziz et al. 2020). The WQI method was first introduced by Horton (1965) by using ten parameters of water quality. Furthermore, the new WQI developed by Brown et al. (1970) is similar to Horton (1965) which was based on weights to individual parameters (Tyagi et al. 2013). However, numerous modifications of water quality indices viz. Weight Arithmetic Water Quality Index (WAWQI), National Sanitation Foundation Water Quality Index (NSFWQI), Canadian Council of Ministers of the Environment Water Quality Index (CCMEWQI), Oregon Water Quality Index (OWQI), etc. have been formulated by several organizations (Tyagi et al. 2013). The Damodar Fan Delta is one of the agriculture-dominated areas in West Bengal especially for rice cultivation and it has a serious constraint regarding groundwater quality and quality. Several studies related to groundwater quality especially in arsenic contamination have been carried out covering the present study area (Acharyya and Shah 2007; Pal and Mukherjee 2009, 2010). Moreover, there has been an increase in the number of semi-critical community development (C.D.) blocks in the Damodar Fan Delta (DFD). In 2004, only two semi-critical C.D. blocks (Memari II and Pandua) were situated in the DFD, whereas in 2013, 13 semi-critical C.D. blocks (Kalna II, Memari II, Raina I, Chanditala I, Chanditala II, Dhaniakhali, Jangipara, Khanakul I, Pandua, Polba-Dadpur, Pursurah, Singur, and Tarakeswar) was located in the DFD (CGWB 2006, 2017). Therefore, the stages of groundwater development and its consequences on agricultural practices have been stressed by various scholars (Das et al. 2021; Majumder and Sivaramakrishnan 2014). However, the suitability of groundwater for drinking purposes in the context of the present study area has not been attempted so far. Therefore, the main objectives of the present study are as follows.

  1. 1.

    To analyse the groundwater quality parameters of the Damodar fan delta.

  2. 2.

    To assess the water quality index for drinking purposes using the fuzzy-AHP MCDM technique.

Study area

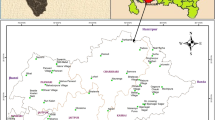
Damodar fan delta (DFD) consists of two alluvial fans -Memari fan trending toward the east and Tarakeswar fan trending toward the south (Acharyya and Shah 2007; Mallick and Niyogi1972; Niyogi 1975). It extends from 22° 31′ 09″ N to 23° 20′ 00″ N latitude and 87° 49′ 00″ E to 88° 29′ 33″ E longitude comprising an area of ~ 3206 km2 (Fig. 1). It lies in the interfluves of Hooghly River located in the east and the Damodar River located in the west and surrounded by Kusumgram fan in the north. The DFD is a younger deltaic plain characterized by the Holocene deposit (Acharyya and Shah 2007). The Damodar River, popularly known as the ‘Sorrow of Bengal,’ is an important western tributary of the Ganga River (Rudra 2010).

Fig. 1
figure 1

Location of the study area

Full size image

Geologically, the study area is a part of the Bengal basin which is a structural depression surrounded by the Chotanagpur plateau to the west, Rajmahal trap to the north, and Chattagram-Tripura hills to the east (Rudra 2010). The Damodar Fan Delta is located in the stable shelf zone of the Bengal basin (Sengupta 1972). The study area is located in the alluvial plain of West Bengal. The elevation of the study area ranges from 7 m (near Amta) to 37 m (near Barddhaman town). The slope of the study area is almost gentle. The general slope trends toward the east and the southeast. In the study area, the climate is characterized by tropical humid to sub-humid type. The maximum temperature is 31.80 °C, which is recorded in May whereas the minimum temperature is 19.85 °C recorded in December (Bhattacharyya 2011). On average, annual rainfall amounts to 1600 mm with its concentration in the monsoon period (Bhattacharyya 2011). The study area reveals the four types of soil texture—very fine, fine, fine loamy, and coarse loamy (NBSS & LUP 1992). Agriculture is the mainstay of the economy with rice as the main crop of the study area. Purba Barddhaman district located in the study area is known as the ‘rice bowl’ of West Bengal for huge production (Dutta 2012).

Data sets

The groundwater quality data for the present study of April 2019 were collected from the Central Ground Water Board (CGWB), the Government of India. The 12 groundwater physical–chemical parameters such as TDS, F−, Cl−, Fe−, NO3−, pH, SO42−, Ca2+, Mg2+, Na+, K+ and HCO3− of 29 wells have been analyzed using a robust methodology. The depth of groundwater level of wells varies from 1 to 18.25 m. The sample wells are of 3 types, such as dug well (DW), tube well (TW), and piezometric well (PW). The error of ion balance has been computed for the water parameters of 29 sample wells. The ion balance error of all the sample wells in the present study falls within ±10 % indicating a good accuracy of analysis. Moreover, to assess the land use and land cover of the study area, a supervised classification has been made using linear imaging self-scanning (LISS IV) images of the National Remote Sensing Council (NRSC) with 5 m resolution, dated December 2014. Apart from that, the borehole data 6 locations were collected from the department of public health engineering (PHE), the Government of West Bengal to portray the sub-surface lithological compositions.

Methodology

The fuzzy analytic hierarchy process (FAHP) was developed to weight criteria in decision-making by using the output of the experts’ opinions. The weighted value was assigned by pair-wise comparison for each of the 12 groundwater quality parameters. The experts compared the parameters by pair-wise variables comparison using fuzzy triangular number scales. The FAHP process of weighting was assigned in four steps and GWQI was then calculated. The inverse distance weighting (IDW) interpolation has been used to display the results of the GWQI (Fig. 2).

Fig. 2
figure 2

Methodological flowchart

Full size image

The fuzzy-AHP pair-wise comparison approach

Generally, GWQI is developed using the four steps including the selection of parameters, obtaining the sub-index value, assigning weights of the water quality parameters, and aggregating the sub-indices to produce the final water quality score (Abbasi and Abbasi 2012). Basically, techniques of assigning weights of the water quality parameters are classified into two broad categories—(a) statistical-based objective methods and (b) participatory-based subjective methods (OECD 2008). In the first category, the weights are assigned based on the statistical analysis of the data of water quality parameters whereas, in the second category, the weights are determined using the judgment of experts, policymakers, and practitioners from different agencies of a certain area (Sutadian et al. 2017). Several studies used CA and PCA to find out the identical parameters and to define the weights for the development of GWQI (Boateng et al. 2016; Badeenezhad et al. 2020). However, PCA can only reduce the dimensionality of large data sets based on the variation of variables (Minh et al 2019). The entropy method has been applied to determine the weights of water parameters (Gorgij et al. 2017). The analytic hierarchy process (AHP) multi-criteria decision-making (MCDM) technique has also been used by many researchers to generate the weights of water quality parameters in the GWQI (Chakraborty and Kumar 2016; Sutadian et al. 2017; Sarkar and Majumder 2021). However, AHP does not rely solely on human decisions (Haider et al. 2017). Therefore, FAHP has been applied by the researchers as it is more accurate to give interval judgment than fixed value judgments. It also reduces uncertainty in assigned relative weight (Minh et al. 2019). The fuzzy set was first developed by Zadeh (1965) and combined with Saaty’s priority theory to reduce human ambiguity (Bellman and Zadeh 1970).

In the present study, the FAHP technique has been used to achieve relative weights of groundwater quality parameters for the development of GWQI. In the present study, geometric mean method proposed by Buckley (1985) has been used. The process of FAHP was divided into four steps—(a) hierarchy construction development, (b) pair-wise comparisons represented by fuzzy numbers, (c) the fuzzy triangular number calculation, and (d) fuzzy weights.

  • Step I: Hierarchy Construction Development

The first level was the overall objective to determine the quantification of the potential of groundwater resources; the second level was the comparison of water quality parameters (Fig. 3) (Minh et al. 2019). The fuzzy triangular number was used as a scale which was transferred from linguistic terms corresponding to Saaty’s scale (1980) in Table 1 through pair-wise comparison matrices. The higher weighting of a parameter shows the high importance of that parameter. Finally, the groundwater quality was assessed based on classes of groundwater quality index (GWQI).

  • Step II: The pair-wise comparisons represented by fuzzy numbers

Fig. 3
figure 3

The hierarchy structure for the performance evaluation process of groundwater quality assessment

Full size image
Table 1 Linguistic terms and the corresponding triangle fuzzy scale
Full size table

Decision-making was based on the opinions of five experts in the present study. The fuzzy triangular number scales were used to compare between two parameters and find out the more important parameter. The parameters were compared by transferring them from linguistic terms to fuzzy numbers. The pair-wise contribution matrix is expressed in Eq. 1.

$$\tilde{A }=\left[\begin{array}{ccc}\tilde{1 }& \begin{array}{cc}{\tilde{a }}_{12}& \cdots \end{array}& {\tilde{a }}_{1n}\\ \begin{array}{c}{\tilde{a }}_{21}\\ \vdots \end{array}& \begin{array}{c}\begin{array}{cc}\tilde{1 }& \end{array}\\ \begin{array}{cc}\vdots & \ddots \end{array}\end{array}& \begin{array}{c}{\tilde{a }}_{2n}\\ \vdots \end{array}\\ {\tilde{a }}_{n1}& \begin{array}{cc}{\tilde{a }}_{n2}& \cdots \end{array}& \tilde{1 }\end{array}\right]=\left[\begin{array}{ccc}\tilde{1 }& \begin{array}{cc}{\tilde{a }}_{12}& \cdots \end{array}& {\tilde{a }}_{1n}\\ \begin{array}{c}1/{\tilde{a }}_{21}\\ \vdots \end{array}& \begin{array}{c}\begin{array}{cc}\tilde{1 }& \end{array}\\ \begin{array}{cc}\vdots & \ddots \end{array}\end{array}& \begin{array}{c}{\tilde{a }}_{2n}\\ \vdots \end{array}\\ 1/{\tilde{a }}_{n1}& \begin{array}{cc}1/{\tilde{a }}_{n2}& \cdots \end{array}& \tilde{1 }\end{array}\right]$$
(1)

where \({\tilde{a }}_{ij}\) measure denotes a pair of criteria i and j, let \(\tilde{1 }\) be (1, 1, 1), when i equal j (i.e., \(i=j\)); if \(\stackrel{\sim }{1,}\) \(\stackrel{\sim }{2,}\) \(\tilde{3 }, \tilde{4 },\) \(\tilde{5 },\) \(\stackrel{\sim }{6,}\) \(\tilde{7 }\), \(\tilde{8 }\), \(\tilde{9 }\) measure that criterion i is relatively important to criterion j and then \({\tilde{1 }}^{-1},\) \({\tilde{2 }}^{-1},\) \({\tilde{2 }}^{-1},\) \({\tilde{3 }}^{-1}\), \({\tilde{4 }}^{-1},\) \({\tilde{5 }}^{-1},\) \({\tilde{6 }}^{-1}\), \({\tilde{7 }}^{-1},\) \({\tilde{8 }}^{-1},\) \({\tilde{9 }}^{-1}\) measure that criterion j is relatively important to criterion i.

  • Step III: Determine the Fuzzy Triangular Number

The geometric mean method proposed by Buckley (1985) was used to determine the criterion’s fuzzy geometric mean (Eq. 2).

$$ \tilde{r}_{i} = (\tilde{a}_{i1} \otimes \tilde{a}_{i2} \otimes \cdots \otimes \tilde{a}_{in} )^{1/n} $$
(2)

where \({\tilde{a }}_{in}\) is fuzzy comparison value of criterion i to criterion n; therefore, \({\tilde{r }}_{i}\) is the geometric mean of fuzzy comparison value of criterion i to each criterion.

  • Step IV: Fuzzy weighting

The final fuzzy weights were calculated following Eq. 3.

$$ \tilde{w}_{i} = \tilde{r}_{i} \otimes (\tilde{r}_{i} \otimes \cdots \otimes \tilde{r}_{n} )^{ - 1} $$
(3)

where \({\tilde{w }}_{i}\)= \({lw}_{i}, {mw}_{i}, {uw}_{i}\), where \({lw}_{i},{mw}_{i},\) \({uw}_{i}\) stand for the lower, middle, and upper values of the fuzzy weight of the criterion i, respectively.

Water quality index

The water quality index provides a reliable picture about groundwater and surface water quality mostly for domestic uses and it is easily understandable to decision-makers about the quality and possible uses of any waterbody (Hamlat and Guidoum 2018). The GWQI includes three steps—(a) defining relative weights, (b) quality rating scale, and (c) sub-index of the parameters.

Step I: Relative weight \((Wi)\) of the parameters has been calculated using the weighted arithmetic GWQI method (Eq. 4)

$$ W_{i} = \frac{{w_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} }} $$
(4)

where \(Wi\) is the relative weight, \(wi\) is the weight of each parameter, and n is the number of parameters.

Step II: Quality rating scale (\(Qi\)) is calculated by dividing the concentration value for each of the quality parameters in each water sample to the standard concentration values for drinking water which were specified by the Bureau of Indian Standard (BIS) (2012, 2015) and World Health Organization (WHO 2011) (Eq. 5).

$$ Qi~ = ~\left( {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {S_{i} }}} \right. \kern-\nulldelimiterspace} {S_{i} }}} \right) \times 100 $$
(5)

where \(Qi\) is the quality rating, \({C}_{i}\) is the concentration of each parameter in the water sample, and \({S}_{i}\) is drinking water standard for each parameter.

Step III: The sub-index value is calculated for each chemical parameter (Eq. 6)

$${Sl}_{i} = {W}_{i} \times {Q}_{i}$$
(6)

where\( {Sl}_{i}\) is the sub-index of i parameter, \({Q}_{i}\) is the quality rating scale based on the concentration of i parameter, and \({W}_{i}\) is the relative weight.

Step IV: Water quality index (WQI) is calculated following the above calculations (Eq. 7). The sum of sub-indices of each of the water samples defines the WQI value. As the WQI has been used in the context of assessing groundwater quality, the index has been denoted as GWQI for the present work.

$$WQI = \sum{Sl}_{i}$$
(7)

Results

Spatial variation of groundwater parameters

The pH value of the groundwater denotes whether the water is acidic or alkaline. The low value of pH indicates acidic water whereas the high value represents alkaline water (Boateng et al. 2016). According to the BIS (2012), the acceptable limit of pH is 6.5–8.5 for drinking purposes. Typically it has no direct influence on human health but it can influence the solubility of many salts and determine the level of contaminants in water resources (Khosravi et al. 2017). The pH value of the groundwater in the study area ranges from 7.42 to 9.73 with an average value of 8.08 (Fig. 4). The spatial distribution of the pH value depicts that ~ 10% of the wells contain more than the acceptable limit of pH concentration in the study area (Fig. 5a).

Fig. 4
figure 4

Box plot showing the nature of the major ionic chemistry

Full size image
Fig. 5
figure 5

Spatial distribution of groundwater quality parameters a pH, b TDS, c Iron, and d Fluoride

Full size image

The TDS is an essential parameter to determine the suitability of water for drinking and irrigation purposes (Wagh et al. 2019; Sarkar and Islam 2019). The bulk of total dissolved solids include bicarbonates, sulfates, and chloride of calcium, magnesium, sodium, potassium, silica, potassium chloride, nitrate, and boron (Pradhan and Pirasteh 2011). The TDS value is found to fluctuate from 104 to 1281 mg/L and the average value was 538.72 mg/L (Table 4). Only ~ 4% of the sample wells contain acceptable limits of turbidity in the present study area. Based on the TDS concentration, Carroll (1962) classified water into four types such as freshwater (0–1000 ppm), brackish water (1000–10,000 ppm), saline water (10,000–100,000 ppm), and brine water (> 100,000 ppm). Besides, 29 sample sites fall in the freshwater category whereas two sample sites fall in the brackish water category in the study area. The spatial variation of TDS shows that the maximum concentration of the TDS is located in the eastern part of the study area (Fig. 5b).

Iron (Fe−) in groundwater can be derived from geological, industrial, domestic discharge, or mining industries (Karakuş 2019). The iron concentration in the groundwater ranges from 0 to 6.97 mg/L and the average value is 0.68 mg/L (Table 1). From the analysis, it is found that ~ 7% of sample wells of the study area occupy the acceptable limit of iron concentration provided by BIS (2012). The spatial variation map depicts that maximum iron concentration is found in the western part of the study area (Fig. 5c).

Fluoride (F−) occurs as natural elements in groundwater in the Indian sub-continents (Ahada and Suthar 2018). Mukherjee and Singh (2018) reported that the higher concentration of F− in groundwater is attributed to geogenic sources mainly from country rocks containing fluorine-bearing minerals (apatite, fluorite, biotite, muscovite, and hornblende). The F− concentration in the study area differs from 0 to 1.22 mg/L with an average value of 0.29 (Fig. 5d).

According to WHO (2011), the acceptable limit of sodium (Na+) in drinking water is 200 mg/L. In the present study, Na+ concentration value ranges from 9 to 290 mg/L with a mean value of 85.24 mg/L. About 7% of groundwater sample contains > 200 mg/L (Fig. 6a). The high concentration of Na+ occurs in groundwater due to the weathering of silicate minerals from rocks and the solubility of salt present in the soil as a result of evaporation, human activities, and agricultural activities (Kumar et al. 2015). Furthermore, according to the WHO (2011) standard, the acceptable limit of potassium (K+) is 12 mg/L. In this study, K+ content varies between 1 and 210 mg/L with a mean value of 23.62 mg/L. According to the results, ~ 41% of groundwater samples show potassium content > 10 mg/L (Fig. 6b).

Fig. 6
figure 6

Spatial distribution of major cations a sodium, b potassium, c calcium, and d magnesium

Full size image

In the study, calcium (Ca2+) content varies from 6 to 130 mg/L with a mean value of 36.69 mg/L (Fig. 6c). As compared to the analytical results with BIS (2012), ~ 14% of groundwater samples are located above the threshold limit. The main sources of Ca2+ in drinking water come from geological units, agricultural wastes, and industrial wastes (Kumaravel et al. 2014). Moreover, magnesium (Mg2+) is another important contributor to water hardness and its contribution remarkably influences the chemistry of groundwater (Ahada and Suthar 2018). In the study, Mg2+ concentration ranges from 4 mg/L to 50 mg/L with a mean value of 24.07 mg/L (Fig. 6d). According to BIS standard (2012), ~ 27.59% sample exceeds the acceptable limit of magnesium concentration.

A high concentration of sulfate (SO42−) in drinking water may cause a laxative effect on the human body system (Kumar et al. 2015). According to BIS (2012) standard, the acceptable limit of SO42− is 200 mg/L. In the present study, the SO42− concentration value varies from 0 to 103 mg/L with a mean value of 15.07 mg/L. From the results, it is found that all samples had an SO42− value fall within the acceptable limit (Fig. 7a). Furthermore, chloride (Cl−) ion is often naturally available in chlorine form in groundwater and it has very low mobility in water (Khosravi et al. 2017). The presence of chloride in groundwater is due to weathering, leakage of soil sediments, minerals, as well as urban and industrial wastewaters into water resources (Kumar et al. 2015). Moreover, Cl− contents in the present study vary between 14 and 493 mg/L with a mean value of 127.34 mg/L. According to BIS standard (2012), the acceptable limit of Cl− in drinking water is 250 mg/L. The results of the study reveal that ~ 10% of groundwater samples exceed the threshold value of Cl− concentration (Fig. 7b). In the study area, the amount of nitrate (NO3−) content in the groundwater ranges from 0 to 23 mg/L, with a mean value of 4.48 mg/L. According to BIS (2012), the acceptable limit of NO3− concentration in drinking water is 45 mg/L. The results of the study reveal that all the samples had the nitrate value falling within the acceptable limit (Fig. 7c).

Fig. 7
figure 7

Spatial distribution of major anions a sulfate, bchloride, c nitrate, and d bicarbonate

Full size image

The presence of bicarbonate (HCO3−) in natural water is influenced by the level of soluble carbon dioxide, temperature, pH, cations, and some soluble salts (Khosravi et al. 2017). The concentration of HCO3− in groundwater is usually higher than that of surface water (Kumar et al. 2015). According to BIS (2015), the acceptable limit of HCO3− concentration in drinking water is 244 mg/L. The concentration of HCO3− in the study area ranges from 61 to 616 mg/L with a mean value of 274.17 mg/L. The result shows that ~ 51% of the sample exceeds the acceptable limit of HCO3− concentration that depicts the poor quality of drinking water (Fig. 7d, Tables 2, 3, 4).

Table 2 Matrix table
Full size table
Table 3 Groundwater quality standard and relative weights
Full size table
Table 4 Descriptive statistics of the groundwater quality parameters
Full size table

Groundwater suitability for drinking purpose using GWQI

The GWQI summarizes a significant number of parameters of groundwater quality in a general method into a single number, and it is a helpful technique to assess and manage the groundwater resources. The value of GWQI for groundwater quality ranges from 35.52 to 273.02 with an average value of 81.87. However, the GWQI has been classified as excellent water (< 50), good water (50–100), poor water (100–200), very poor water (200–300), and unsuitable for drinking (> 300) (Wagh et al. 2017; Hamlat and Guidoum 2018; Minh et al. 2019). The GWQI in the study has been classified into four classes (Fig. 8).

Fig. 8
figure 8

Spatial distribution of GWQI

Full size image

If the GWQI is less than 50, the water has excellent quality. Moreover, the index ranging from 50–100 indicates good quality of water, the index in the range of 100 to 200 indicates poor water quality and > 200 represents very poor quality for drinking purposes in the present study area. The result shows that 13.79% of the total sample wells (4 wells) are the excellent quality while the 3.45% (1 well) sample is of very poor quality. The results also show that 68.97% of the samples (20 wells) are registered as very good quality and 13.79% (4 wells) samples as poor water quality for drinking purposes in the present study area. The spatial distribution of the GWQI reveals that very poor quality water well (W22) is located in the eastern part of the study area. The location of the poor water wells (W1, W4, W20, and W25) is concentrated in the northwestern part of the Barddhaman town, the southern part of the study area in the Haripal C.D. block and the Pandua C.D. block. The excellent water quality wells (W5, W10, W19, and W28) are located in the western and central parts of the study area. Besides, good water quality wells are located in other parts of the study area.

Discussion

The weightage analysis of the 12 groundwater quality parameters based on FAHP depicts that TDS, F−, Fe−, and Cl− are considered as the major elements which affect GWQI with weights of 0.27, 0.19, 0.14, and 0.1, respectively. The LULC distribution of the study area has a significant effect on the GWQI. In the northwestern part, well 1 and well 3 fall in the poor water quality zone which is covered by the built-up area near the Barddhaman town (Fig. 9a). In the southern part of the study area, one well (W20) falls in poor water quality zone due to the high concentration of TDS and HCO3− and Fe−, which reveals the high salinity of the groundwater. This may be due to the mixing of saline water (sourced from the Bay of Bengal in the south through the Hooghly River) with the groundwater (Sarkar et al. 2021) (Fig. 9a).

Fig. 9
figure 9

a Land use and land cover, b lithological composition of the selected boreholes of the study area

Full size image

Furthermore, sub-surface lithological compositions play an important role in water quality. The subsurface lithologs have been encountered in the 6 boreholes of the study area (Fig. 9b). The lithological layers consist of clay, sand in various textures from very fine coarse with different colours including white, grey, black, yellow, and brown along with kankar, gravels, and pebbles. Grey clay consists of a high concentration of organic matter representing the flood sediments whereas brown sand reveals the greater concentration of illite, siderite, as well as iron-oxyhydroxidecoated grains in the Damodar River floodplain (Pal and Mukherjee 2010). In well 22, the GWQI is very poor due to the high concentration of iron. In the borehole (BH5) located at the sample well site W22, the blackish clay has been found from the depth of 6.1–27.45 m overlain by fine grey sand from the depth of 3.05–6.1 m and topsoil up to 3.05 m depth. The groundwater in well 19 is excellent due to the low concentration of Fe. The borehole (BH1) consists of fine brown sand from the depth of 15–64 m overlain by coarse brown sand from the depth of 9–15 m, black clay from the depth of 3–9 m, and topsoil up to the depth of 3 m from the surface. Therefore, it reveals that blackish clay is associated with the iron concentration in groundwater.

Besides, the influence of geological compositions of rocks, climatic conditions, and anthropogenic controls on groundwater quality is important to assess the hydrochemical behavior of groundwater in an area. In the present study, the Piper plot and Gibbs plot have been applied to ascertain the types of weathering, the influence of rock, precipitation and evaporation, etc. that influence groundwater composition.

Piper plot proposed by Piper (1944) has been used to determine the geochemical classification and hydrochemical evolution of groundwater in the study area (Fig. 10a). The difference in milliequivalent percentage between alkaline earth (Ca2+ + Mg2+) and alkali metals have been plotted on the X-axis and the milliequivalent percentage difference between weak acidic (HCO3−) anions and strong acidic anions (Cl− + SO42−) have been plotted on the Y-axis. The resultant diagram portrays 8 classes. It shows that ~ 45% of the sample wells fall in the magnesium bicarbonate type while ~ 14% of sample wells fall into the sodium chloride type. Besides, only one-sample well (W4) has been found in the Calcium chloride type. Apart from that ~ 35% of sample wells fall into mixed type. The results of the Piper diagram represent that majority of the sample wells (~ 66%) are categorized as alkaline earth while the remaining wells fall into the alkalies. Moreover, it also represents that 20 sample wells (~ 69%) fall into the weak acids category while the remaining wells fall into the strong acids. The results indicate the dominance of alkaline earth and weak acids of all the samples due to the interaction between the alkaline earth and alkali metals that originate from soil or rock interactions with strong acidic anions and weak acidic anions in groundwater.

Fig. 10
figure 10

Piper diagram and Gibbs plot to assess the major process controlling groundwater chemistry a Hydrochemical classification of the groundwater samples using Piper diagram, b Gibbs plot for cations and c Gibbs plot for anions

Full size image

The Gibbs plot is widely used to determine the relationship between water composition and lithological characteristics of the aquifer (Kumar et al. 2015). It represents the source of chemical constituents into three distinct fields such as precipitation, rock, and evaporation dominant (Gibbs 1970). The ratios of anions and cations, i.e., Na+/(Na+ + Ca2+) (Fig. 10b) and Cl−/(Cl− + HCO3−) (Fig. 10c) of sample wells are plotted against the relative value of TDS. The Gibbs plot of the present study indicates that the majority of the sample (~ 52%) falls in the evaporation dominant field. It is observed that many of the sample wells are located near agricultural area and evaporation increases salinity by increasing of Cl− and Na+ in relation to the increase in TDS. In addition, anthropogenic inputs such as agricultural fertilizers, and irrigation also influence the evaporation by the increase in Na+ and Cl−, and thus, TDS is increased (Wagh et al. 2019). In the present study area, rice is the most dominant crop which is grown in autumn (Aus), winter (Aman), and summer (Boro). Rice is followed by jute, potato, wheat, oilseeds, etc. The Boro crop requires more irrigation water from government canals, wells, and minor irrigation schemes as it is grown in the summer period. Nitrogen, phosphate, and potash fertilizers are dominantly used in the agricultural field (District Statistical Officer 2021). Therefore, the agricultural activity in the study area has a greater influence on groundwater quality. The Gibbs plot also shows ~ 48% of the samples are located in the rock dominant field of the diagram. The dominance of the rock-water interaction field reveals the interaction between rock chemistry and the chemistry of the percolated waters underground (Kumar et al. 2015).

Conclusion

In the study area, groundwater is an important source of water for drinking, domestic and irrigation purposes. Therefore, the present study used 12 physiochemical parameters of 29 sample wells to analyze and evaluate the quality of groundwater for drinking purposes. Besides, spatial variation of water quality parameters and water quality index were analyzed in the GIS environment. The FAHP technique was used to calculate the weights of the parameters for the GWQI. The results show that the bicarbonate content of 51% of sample wells exceeds the acceptable limit of drinking water, which is maximum in the study area. Furthermore, higher concentrations of TDS, pH, fluoride, chloride, calcium, magnesium, and sodium are found in few locations of the study area. The results also depict that iron and potassium concentration is maximum located in the eastern part of the study area, which is, respectively, 21 and 23.23 times higher than the maximum acceptable limit. The results demonstrate that nitrate and sulfate contents of all sample wells fall within the acceptable limits. The result shows that 13.79% of the sample are excellent while 3.45% of the samples are very poor. The results also show 68.97% of the samples are of very good quality and 13.79% of the samples of poor water quality for drinking purposes. From the results, it is observed that very poor quality water is located in the eastern part, and the poor water well is located in the northwestern part of the study area. Besides, excellent water quality wells are located in the western and central part and good water quality wells are located rest of the study area.

The FAHP-based GWQI has successfully been applied to assess the groundwater quality for drinking purposes in the DFD. It is pertinent to mention here that water-stressed conditions due to the exploitation of the groundwater at an accelerating rate for irrigation and pollution of groundwater due to anthropogenic inputs such as fertilizer poses threat to the supply of safe drinking water at an adequate quantity. This study has demonstrated that the spatial variability in the groundwater quality in the DFD with its major driving forces. Therefore, this study would help policymakers and stakeholders to find strategies for planning and management of groundwater quality at the local level.