Abstract
In many hydraulic structures, side weirs have a critical role. Accurately predicting the discharge coefficient is one of the most important stages in the side weir design process. In the present paper, a new high efficient side weir is investigated. To simulate the discharge coefficient of these side weirs, three novel soft computing methods are used. The process includes modeling the discharge coefficient with the hybrid Adaptive Neuro-Fuzzy Interface System (ANFIS) and three optimization algorithms, namely Differential Evaluation (ANFIS-DE), Genetic Algorithm (ANFIS-GA) and Particle Swarm Optimization (ANFIS-PSO). In addition, sensitivity analysis is done to find the most efficient input variables for modeling the discharge coefficient of these types of side weirs. According to the results, the ANFIS method has higher performance when using simpler input variables. In addition, the ANFIS-DE with RMSE of 0.077 has higher performance than the ANFIS-GA and ANFIS-PSO methods with RMSE of 0.079 and 0.096, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Side weirs are among the principal parts in several hydraulic structures, such as irrigation and drainage, flood control and sewer network structures. De Marchi (1934) introduced the first mathematical relation of side weirs. The author assumed that the specific energy of the downstream and upstream of a side weir is equal. Equation (1) is introduced by the author to calculate the discharge changes by moving along the side weir.
where dQ/dx is the discharge change by moving along the side weir, Cd is the discharge coefficient, y is the flow depth and w is the channel width.
The simplest side weirs have a rectangular shape. Many studies have been conducted to specify the characteristics of rectangular side weirs. However, besides the advantages of rectangular side weirs like easy construction, such side weirs have low efficiency (Bilhan et al. 2011). In case of overflow, there are two choices: first, the length of the rectangular side weir can be increased, and second, side wire efficiency can be increased. Increasing the side weir length leads to increasing the tributary channel—a choice that seems costly. The economical alternative is to increase the side weir efficiency. Modifying side weir shape could increase side weir efficiency between 1.5 and 4.5 times (Kumar and Pathak 1987; Cosar and Agaccioglu 2004; Ghodsian 2004; Emiroglu et al. 2010b; Aydin and Emiroglu 2013; Mirnaseri and Emadi 2013).
The ANFIS method, as a hybrid soft computing method of the Artificial Neural Network (ANN) and fuzzy logic knowledge, is widely used in various modeling (Khajeh et al. 2009; Talei et al. 2010; Petkovic et al. 2013a, b) and prediction (Dastorani et al. 2010; El-Shafie et al. 2011; Wahida Banu et al. 2011; Wu and Chau 2013) engineering problems.
In numerous studies, the ANFIS method has been successfully used to simulate the characteristics of side weirs. Dursun et al. (2012) applied ANFIS to predict the characteristics of semi-elliptical side weirs. Kisi et al. (2013) simulated the discharge coefficient of rectangular side weirs using ANFIS and concluded that ANFIS performs much better than linear and non-linear regression methods. Emiroglu and Kisi (2013) utilized ANFIS to simulate the discharge coefficient of trapezoidal side weirs and compared the results with the ANN method. The authors concluded that the ANFIS model could predict the trapezoidal side weir discharge coefficient with higher accuracy. Seyedian et al. (2014) used ANFIS to investigate the effect of changing the side weir length, flow depth and side weir height on the discharge coefficient.
The ability to predict the modified side weir discharge coefficient is significant in their design process. Soft computing methods are broadly used for the evaluation of modified side weir characteristics (Bilhan et al. 2010; Kisi et al. 2012; Onen 2014a, b).
Discharge coefficient of the modified side weir that is investigated in the present study is simulated in various studies. Zaji and Bonakdari (2014) compared the performance of Multi-Layer Perceptron Neural Network (MLPNN), Radial Basis Neural Network (RBNN), and linear and non-linear PSO based equations in modeling the modified side weir discharge coefficient. The authors concluded that the RBNN model has higher performance compare with the other regression methods in simulating the considered side weir discharge coefficient. Zaji et al. (2015) simulated the present side weir discharge coefficient using the PSO based RBNN method. The authors concluded that the PSO algorithm successfully improved the RBNN performance. Bonakdari et al. (2015) used ANFIS as sensitivity analyzer to find the most appropriated input variables in simulating the discharge coefficient of the present side weir. Zaji et al. (2016b) applied two types of Support Vector Machine (SVM) to simulate the considered modified side weir. In the first type, the radial basis kernel function is used and in the second type, the polynomial kernel function is employed. In addition, the sensitivity analysis on the input variables was done by examining six different input combinations. The results showed that both types of SVM method perform better when higher number of input variables are used and the radial basis kernel function performs better compare with the polynomial kernel function. Zaji et al. (2016a) compared the firefly based SVM with the simple SVM in simulating the present side weir discharge coefficient. The authors concluded that firefly optimization algorithm has a high role in accurate simulation of the side weir discharge coefficient. Shamshirband et al. (2016) uses the simple ANFIS in predicting the discharge coefficient of the present side weir. The authors concluded that ANFIS has a high capability in simulating the discharge coefficient of side weirs. Zaji and Bonakdari (2017) tried to find the optimum SVM method in simulating the considered side weir’s discharge coefficient. To do that, eight different SVM models with linear, polynomial, Gaussian, exponential, Laplacian, sigmoid, rational quadratic, and multiquadratic kernel functions and concluded that the polynomial kernel function performs better compare with the other kernels. Zaji et al. (2017) aim was to develop simple and practical equations to estimate the discharge coefficient of the considered side weir. The PSO algorithm is utilized to optimize the coefficients of the considered equations. The results showed that the side weir’ discharge coefficient could be modeled using simple and practical equations, accurately.
The aim of this study is to model the discharge coefficient of a modified triangular side weir using three novel hybrid ANFIS methods, i.e., ANFIS-DE, ANFIS-GA and ANFIS-PSO. The models are investigated with eight different input combinations to find the most appropriated input variables. Training and validation of the ANFIS models were done using the experimental study of Borghei and Parvaneh (2011). The results of the most appropriate ANFIS model are compared with the previous findings of Borghei and Parvaneh (2011) and Emiroglu et al. (2010a).
Materials and methods
In the first part of this section, the experimental study by Borghei and Parvaneh (2011) is introduced. Then the optimization algorithms used namely DE, GA and PSO and ANFIS are presented. Finally, the statistics errors applied to find the performance of each model are presented.
Experimental study
The training and validation of the modified side weir was done using the experimental study by Borghei and Parvaneh (2011). The discharge coefficient of the proposed side weir is nearly twice higher than that of a simple rectangular side weir. A schematic overview of the modified side weir is shown in Fig. 1. The laboratory flume is made of glass walls with 11 m length and 0.4 m width. The experiments were done with various side weir parameters including length (L), height (w), weir included angle (θ), upstream flow depth (y1) and upstream Froude number (Fr1). Table 1 represents the parameter intervals considered. The experiments were carried out with ± 1 mm and ± 0.0001 m3/s accuracy in the head and discharge measurments.
Schematic overview of the improved triangular side weir (Borghei and Parvaneh 2011)
Input variables
To evaluate the most appropriate input variables, eight different input combinations are studied in this research. The variables of each input combination are shown in Table 2. To use the hybrid ANFIS methods in practical situations as well as to compare the accuracy of the proposed models with previous studies, the input variables should be non-dimensional. Therefore, all of the input variables used are non-dimensionalized.
According to Table 2, the input combinations from In#1 to In#8 have 5, 4, 3, 3, 3, 3, 2, and 1 variables. Therefore, by moving from the first input combination to the last, the number of input variables decreases, but their complexity increases. The goal of investigating input combinations is to identify the performance of the ANFIS-DE, ANFIS-GA and ANFIS-PSO methods with more, but simpler input variables (such as In#1) compared with the less, but more complex input variables (such as In#8).
Differential evolution
Differential evolution, introduced by Storn and Price (1997), is a population-based optimization algorithm. The main difference between DE and other evolutionary algorithms is the utilization of the direction and difference between individuals. In the DE algorithm, initially, the mutation process is performed on the individuals, after which the crossover process is done. In the mutation process, the following steps are taken: (i) Select a parent individual, such as x i (t); (ii) Randomly select two other individuals from the current population, (x j (t) and x k (t)); (iii) Calculate the trial vector according to Eq. (2).
where β is the scale coefficient. Next, using the trial vector determined from the mutation process, crossover is done and a new child is created as follows:
where J represents the crossover points. There are many ways to determine the J parameter as presented in more detail by Storn and Price (1997). Following crossover evaluation, the fitness function is used to calculate the cost of the crossover child \(f(x^{\prime}_{i} (t))\) and to compare it with the cost of the parent \(f(x_{i} (t))\). If the child cost is lower than the parent cost, \(x^{\prime}_{i} (t)\) is transferred to the next generation; otherwise, the parent (\(x_{i} (t)\)) is transferred to the next generation directly. The DE algorithm is represented in Fig. 2.
Genetic algorithm
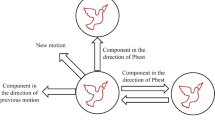
The genetic algorithm (Holland 1975) is one of the most common optimization algorithms employed in various engineering problems. A schematic overview of the GA is shown in Fig. 3. The GA begins the optimization process with a random initial population. The goodness of each individual is then evaluated using the fitness function. The goodness of the individuals is represented as the cost of each individual. In a minimization problem, the individual that has a lower cost is sorted as a better one. After evaluating the cost of the initial population, the individuals are sorted according to their cost. The best individuals are separated according to elite percentage and put into an elite population. The elite population is directly transferred to the next generation. The other individuals of the next generation are obtained by crossover and mutation processes. These processes serve to differentiate the next generation from the current one. The crossover process uses two individuals of the current generation as the parents and evaluates the two new children and transfers them to the next generation. The crossover process is described in more detail by Olariu and Zomaya (2005). The mutation process is meant to maintain diversity between current and subsequent generations (Glover and Kochenberger 2003).
Particle swarm optimization
Particle swarm optimization (Kennedy and Eberhart 1995) is a common optimization algorithm used in various problems. A schematic overview of the PSO is shown in Fig. 4. PSO starts with some random particles. Using the fitness function, the cost of particles is evaluated according to their positions.
Each particle has three parameters: the current position, its best individual position and the best position among all particles. Using these parameters, the velocity of each particle is obtained as follows:
where xPbest is the best individual position of each particle, xGbest is the best position of all particles, w is the inertia coefficient, c1 is the personal learning coefficient, c2 is the global learning coefficient, and r1 and r2 are random coefficients with uniform distribution. Determining the constants of c1, c2, w is presented in more detail by Poli et al. (2007). Next, the new position of each particle is calculated as:
Adaptive neuro-fuzzy interface system
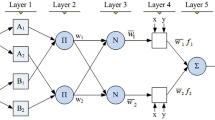
In the current paper, three bell-shaped membership functions are used for each input. The maximum and minimum of the membership functions are 1 and 0, respectively. An ANFIS schematic overview with four inputs is illustrated in Fig. 5.
The first-order Sugeno model with fuzzy IF-THEN rules of Takagi and Sugeno along with two inputs is used for modeling.
The first layer supplies the input variables to the next layer and formed from the input variables’ membership functions (MFs).
where \(\mu (i)_{i}\) are MFs.
In this study, bell-shaped MFs (2) with maximum equal to 1 and minimum equal to 0 are chosen.
A bell-shaped function depends on three parameters a, b and c. Parameter b is a positive constant and c is located at the middle of the curve (Fig. 6).
For each MF, the membership layer (second layer) is checked for the weights. It receives the input values from the 1st layer and acts as MFs to represent the fuzzy sets of the respective input variables. The second layer send the products out by multiplying the incoming signals. The second layer nodes are non-adaptive.
Each node output represents the firing strength of a rule or weight.
The third layer is called the rule layer.
The nodes of the third layer (rule layer) done the pre-condition matching of the fuzzy rules. Therefore, by computation the activation level of rules, with the number of layers being equal to the number of fuzzy rules. The third layer nodes are used to calculation the weights which are normalized. The third layer is also non-adaptive and every node calculates the ratio of a rule’s firing strength to the sum of all rules’ firing strengths as:
The outputs of this layer are called normalized firing strengths, or normalized weights.
The fourth layer is the defuzzification layer and it provides the output values resulting from the inference of rules. Every node in the fourth layer is an adaptive node with the node function:
where \(\{ p_{i} ,q_{i} ,r_{i} ,s_{i} ,t\}\) is the parameter set and in this layer it is denoted as consequent parameters.
The last layer, namely the output layer, sums up all the inputs coming from the fourth layer and transforms the fuzzy classification results into a crisp (binary). The single node in the fifth layer is not adaptive and it calculates the overall output as the summation of all incoming signals:
In this paper, ANFIS works with three different evolutionary algorithms, DE, GA and PSO to adjust the parameters of the membership functions. The use of optimization techniques has the benefit of being less computationally expensive for a given network topology size. The membership functions investigated in this study are triangular-shaped.
Performance evaluation
To determine the performance of the investigated methods and also to compare the models with each other, the statistical parameters used are Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), coefficient of determination (R2) and average absolute deviation (δ%). δ% calculates the non-dimensional error of the model in percent, but RMSE and MAE calculate the model error on the same scale as the output parameters. Therefore, it can be concluded that to evaluate a models’ performance, it is necessary to consider these statistics together. RMSE, MAE, R2 and δ% are defined as follows:
where t i is the observed values of Cd obtained from the laboratory results, o i is the numerical method’s output of Cd, and N is the number of samples.
Results
Investigation of input combinations
In the present study, the performance of three hybrid methods, namely ANFIS-DE, ANFIS-GA and ANFIS-PSO is investigated with regards to discharge coefficient prediction. The hybrid methods were considered with eight different input combinations according to Table 2. Table 3 demonstrates the performance of the ANFIS-DE models with the different input combinations. From this table, it can be concluded that the first and second input combinations with RMSE of 0.077 and 0.078, respectively, in the test dataset perform much better than the other input combinations. In addition, it is clear that by moving from the first input combination to the eighth, the modeling error significantly increases. Therefore, it is concluded that ANFIS-DE preforms much better with more, but simpler input variables rather than less, more complex input variables.
The scatterplot of the ANFIS-DE method for various input combinations is shown in Fig. 7. In this figure, the trendline and trendline equation are shown. The trendline equation is defined as:
where C1 and C2 are the equation constants. A value of C1 closer to 1 and a value of C2 closer to 0 represent a more accurate model. This figure indicates that for all input combinations, ANFIS-DE is trapped in overestimation for Cd < 0.8 and trapped in underestimation for Cd > 0.8. In addition, the ANFIS-DE method exhibits close performance when using the first and second input combinations.
ANFIS-GA was modeled with the investigated input combinations. Table 4 represents the performance of the ANFIS-GA method with various input combinations. From this table, it is obvious that ANFIS-GA has significantly higher performance when using the first input combination. One of the most important parameters in the performance evaluation of a model is training dataset performance. When training dataset accuracy is much higher than testing dataset accuracy, it can be concluded that the model is trapped in over-fitting. Therefore, the comparison between the best ANFIS-GA and ANFIS-DE models signifies that despite the models’ close performance in the testing dataset, the training dataset performance of the ANFIS-GA with RMSE of 0.040 is most likely trapped in over-fitting, and the ANFIS-DE result with RMSE of 0.057 in the training dataset is more reliable. Table 4 shows that similar to the ANFIS-DE method, ANFIS-GA has higher performance when five simple input variables (In#1) are used for modeling rather than fewer but more complex input variables (such as In#7 and In#8).
The scatterplots of the ANFIS-GA models with various input combinations are shown in Fig. 8. This figure shows that the ANFIS-GA method absolutely has an overestimation tendency. Therefore, for the majority of input combinations, the ANFIS-GA predictions are found above the exact line. The results indicate that ANFIS-GE cannot predict the discharge coefficient when using the six-input combination.
To compare the results of the three investigated hybrid ANFIS models, the ANFIS-PSO method was modeled with eight input combinations and the performance evaluation results are represented in Table 5. Much like the ANFIS-DE and ANFI-GA, from this table it is obvious that the first input combination performs much better than the other input combinations. A comparison of the ANFIS-PSO with RMSE of 0.096 with the ANFIS-GA and ANFIS-DE with RMSE of 0.079 and 0.077 in the testing dataset, respectively, indicates that the PSO did not perform as well as the GA and DE in the hybrid ANFIS methods for discharge coefficient prediction. In addition, by comparing the training and testing dataset performance, it appears that the ANFIS-PSO is totally trapped in over-fitting and the results of this method cannot be used in practical situations.
The scatterplots of the ANFIS-PSO method are shown in Fig. 9. Like the ANFIS-GA method, PSO has a tendency to overestimate the discharge coefficient. However, the same as the other hybrid ANFIS methods, the ANFIS-PSO method performs much better when using the first input combination. Thus, it can be concluded that ignoring the modeling method, the discharge coefficient has high reliability to the w/b, y1/b, L/b, sin(θ/2), and Fr1. So, because of the non-dimensionality of these input combinations, it can be successfully used as the input variables of the modified side weir discharge coefficient.
An overview of the three considered hybrid ANFIS models with various input combinations is shown in Fig. 10. The performance of each model in the training and testing datasets is represented by RMSE statistic error. According to this figure, the close performance of ANFIS-DE in the testing and training datasets represents that this method is not trapped in over-fitting. However, the ANFIS-GA and ANFIS-PSO methods are often trapped in over-fitting. Hence, it can be concluded that the DE algorithm can be successfully used in the ANFIS hybrid method. In addition, according to the testing and training trendlines in Fig. 10, it can be absolutely concluded that the models have higher performance with the 5–3 variable input combinations (In#1–In#6), but by decreasing the input variable number to less than 3, the performance of the models decreases significantly.
Residual comparison between the hybrid ANFIS models
The residual scatterplots of the best ANFIS-DE, ANFIS-GA and ANFIS-PSO are presented and compared in this section. In Fig. 11, the residual of the three hybrid ANFIS methods with the first input combination is shown for the training and testing stages, separately. The horizontal axis of this figure is the number of samples and the vertical axis is the residual of the considered models. The comparison between the models is done using the concept of standard deviation (SD), which is defined as follows:
where Res i is the residual of the ith sample, \(\overline{\text{Res}}\) is the average of all samples’ residuals and N is the number of samples. 95% of all residual samples fall in the 2 × SD to − 2 × SD range. From Fig. 11, it can be seen that the ANFIS-GA method with 2 × SD of 0.134 has the lowest residual in the test dataset. However, the high difference between the ANFIS-GA training and testing residuals signifies that the ANFIS-GA is trapped in over-fitting. The ANFIS-DE with residuals of 0.115 and 0.152 in the training and testing processes, respectively, shows an accurate and non-over-fitting model that could be used in practical situations. Figure 7 represents that the ANFIS-PSO is the weakest among the considered methods, and with a low residual of 0.060 in the training process and high residual of 0.188 in the testing process, it falls extremely in over-fitting.
Comparison of the best hybrid ANFIS models with previous studies
In this section, the results of ANFIS-DE, the best hybrid ANFIS method with the first input combination are compared with prior studies of Borghei and Parvaneh (2011) (Eq. 16) and Emiroglu et al. (2010a) (Eq. 17). The comparison of the proposed models is shown in Fig. 12. This figure indicates that the ANFIS-DE method with R2 of 0.8488 performs significantly better than Eqs. (16) and (17) with R2 of 0.7208 and 0.0898, respectively. In addition, it is evident that Eq. (17) can absolutely not be employed for discharge coefficient prediction. The low performance of Eq. (17) signifies that each modified side weir needs a separate study and the equation of a simple triangular side weir cannot be used for the modified triangular side weir.
Conclusion
In this study, three different hybrid ANFIS methods, namely ANFIS-DE, ANFIS-GA and ANFIS-PSO were used to evaluate the discharge coefficient of a modified triangular side weir. To evaluate the most appropriate hybrid ANFIS model, eight different input combinations were tested on the models. The first input combination consists of five simple input variables. By moving from the first input combination to the last, the number of variables decreases and their complexity increases. The results show that all of the considered methods performed significantly better when using the first input combination. Subsequently, the results of the three hybrid ANFIS models with the first input combination were compared with each other using standard deviation. According to the results, the difference between the training and testing errors in the ANFIS-GA and ANFIS-PSO models is very high and these models’ results are not reliable to use in practical situations. Finally, the results of the ANFIS-DE method with the first input combination of w/b, y1/b, L/b, sin(θ/2), and Fr1 was compared with previous works by Borghei and Parvaneh (2011) and Emiroglu et al. (2010a). The results indicate that ANFIS-DE performs much better compared with the previous equations. Therefore, it could be conceded that separate studies are required for each modified side weir and the results for the triangular side weir cannot be used as a modified triangular side weir discharge coefficient equation.
References
Aydin MC, Emiroglu ME (2013) Determination of capacity of labyrinth side weir by CFD. Flow Meas Instr 29:1–8. https://doi.org/10.1016/j.flowmeasinst.2012.09.008
Bilhan O, Emiroglu ME, Kisi O (2010) Application of two different neural network techniques to lateral outflow over rectangular side weirs located on a straight channel. Adv Eng Softw 41:831–837. https://doi.org/10.1016/j.advengsoft.2010.03.001
Bilhan O, Emiroglu ME, Kisi O (2011) Use of artificial neural networks for prediction of discharge coefficient of triangular labyrinth side weir in curved channels. Adv Eng Softw 42:208–214. https://doi.org/10.1016/j.advengsoft.2011.02.006
Bonakdari H, Zaji AH, Shamshirband S, Hashim R, Petkovic D (2015) Sensitivity analysis of the discharge coefficient of a modified triangular side weir by adaptive neuro-fuzzy methodology. Measurement 73:74–81. https://doi.org/10.1016/j.measurement.2015.05.021
Borghei SM, Parvaneh A (2011) Discharge characteristics of a modified oblique side weir in subcritical flow. Flow Meas Instr 22:370–376. https://doi.org/10.1016/j.flowmeasinst.2011.04.009
Cosar A, Agaccioglu H (2004) Discharge coefficient of a triangular side-weir located on a curved channel. J Irrig Drain Eng 130:410–423. https://doi.org/10.1061/(ASCE)0733-9437(2004)
Dastorani MT, Afkhami H, Sharifidarani H, Dastorani M (2010) Application of ANN and ANFIS models on dryland precipitation prediction (case study: Yazd in central Iran). J Appl Sci 10:2387–2394. https://doi.org/10.3923/jas.2010.2387.2394
De Marchi G (1934) Saggio di teoria del funzionamento degli stramazzi laterali. L’Energia elettrica 11:849–860
Dursun OF, Kaya N, Firat M (2012) Estimating discharge coefficient of semi-elliptical side weir using ANFIS. J Hydrol 426–427:55–62. https://doi.org/10.1016/j.jhydrol.2012.01.010
El-Shafie A, Jaafer O, Seyed A (2011) Adaptive neuro-fuzzy inference system based model for rainfall forecasting in Klang River, Malaysia. Int J Phys Sci 6:2875–2888
Emiroglu ME, Kisi O (2013) Prediction of discharge coefficient for trapezoidal labyrinth side weir using a neuro-fuzzy approach. Water Resour Manag 27:1473–1488. https://doi.org/10.1007/s11269-012-0249-0
Emiroglu ME, Kaya N, Agaccioglu H (2010a) Discharge capacity of labyrinth side weir located on a straight channel. J Irrig Drain Eng 136:37–46. https://doi.org/10.1061/(ASCE)IR.1943-4774.0000112
Emiroglu ME, Kisi O, Bilhan O (2010b) Predicting discharge capacity of triangular labyrinth side weir located on a straight channel by using an adaptive neuro-fuzzy technique. Adv Eng Softw 41:154–160. https://doi.org/10.1016/j.advengsoft.2009.09.006
Ghodsian M (2004) Flow over triangular side weir. Sci Iran 11:114–120
Glover F, Kochenberger GA (2003) Handbook of metaheuristics. Springer, Berlin
Holland JH (1975) Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. U Michigan Press, Ann Arbor
Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of IEEE international conference on neural networks, vol 2. Perth, Australia, pp 1942–1948
Khajeh A, Modarress H, Rezaee B (2009) Application of adaptive neuro-fuzzy inference system for solubility prediction of carbon dioxide in polymers. Expert Syst Appl 36:5728–5732. https://doi.org/10.1016/j.eswa.2008.06.051
Kisi O, Emin Emiroglu M, Bilhan O, Guven A (2012) Prediction of lateral outflow over triangular labyrinth side weirs under subcritical conditions using soft computing approaches. Expert Sys Appl 39:3454–3460. https://doi.org/10.1016/j.eswa.2011.09.035
Kisi O, Bilhan O, Emiroglu ME (2013) Anfis to estimate discharge capacity of rectangular side weir. Proc Inst Civ Eng Water Manag 166:479–487. https://doi.org/10.1680/wama.11.00095
Kumar CP, Pathak SK (1987) Triangular side weirs. J Irrig Drain Eng 113:98–105. https://doi.org/10.1061/(ASCE)0733-9437(1987)113:1(98)
Mirnaseri M, Emadi A (2013) Hydraulic performance of combined flow rectangular labyrinth weir-gate. Middle East J Sci Res 18:1335–1342. https://doi.org/10.5829/idosi.mejsr.2013.18.9.12374
Olariu S, Zomaya AY (2005) Handbook of bioinspired algorithms and applications. CRC Press, Boca Roton
Onen F (2014a) GEP prediction of scour around a side weir in curved channel. J Environ Eng Landsc Manag 22:161–170. https://doi.org/10.3846/16486897.2013.865632
Onen F (2014b) Prediction of scour at a side-weir with GEP, ANN and regression models. Arab J Sci Eng 39:6031–6041. https://doi.org/10.1007/s13369-014-1244-y
Petkovic D, Cojbasic Z, Lukic S (2013a) Adaptive neuro fuzzy selection of heart rate variability parameters affected by autonomic nervous system. Expert Syst Appl 40:4490–4495. https://doi.org/10.1016/j.eswa.2013.01.055
Petkovic D, Pavlovic ND, Cojbasic Z, Pavlovic NT (2013b) Adaptive neuro fuzzy estimation of underactuated robotic gripper contact forces. Expert Syst Appl 40:281–286. https://doi.org/10.1016/j.eswa.2012.07.076
Poli R, Kennedy J, Blackwell T (2007) Particle swarm optimization. Swarm Intell 1:33–57
Seyedian SM, Ghazizadeh MJ, Tareghian R (2014) Determining side-weir discharge coefficient using anfis. Proc Inst Civ Eng Water Manag 167:230–237. https://doi.org/10.1680/wama.12.00102
Shamshirband S, Bonakdari H, Zaji AH, Petkovic D, Motamedi S (2016) Improved side weir discharge coefficient modeling by adaptive neuro-fuzzy methodolog. KSCE 20:1–7
Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11:341–359
Talei A, Chua LHC, Quek C (2010) A novel application of a neuro-fuzzy computational technique in event-based rainfall-runoff modeling. Expert Sys Appl 37:7456–7468. https://doi.org/10.1016/j.eswa.2010.04.015
Wahida Banu RSD, Shakila Banu A, Manoj D (2011) Identification and control of nonlinear systems using soft computing techniques. Int J Model Optim 1:24–28. https://doi.org/10.7763/ijmo.2011.v1.5
Wu CL, Chau KW (2013) Prediction of rainfall time series using modular soft computing methods. Eng Appl Artif Intell 26:997–1007. https://doi.org/10.1016/j.engappai.2012.05.023
Zaji AH, Bonakdari H (2014) Performance evaluation of two different neural network and particle swarm optimization methods for prediction of discharge capacity of modified triangular side weirs. Flow Meas Instr 40:149–156. https://doi.org/10.1016/j.flowmeasinst.2014.10.002
Zaji AH, Bonakdari H (2017) Optimum support vector regression for discharge coefficient of modified side weirs prediction. INAE Lett 2:25–33
Zaji AH, Bonakdari H, Shamshirband S, Qasem SN (2015) Potential of particle swarm optimization based radial basis function network to predict the discharge coefficient of a modified triangular side weir. Flow Meas Instr 45:404–407. https://doi.org/10.1016/j.flowmeasinst.2015.06.007
Zaji AH, Bonakdari H, Khodashenas SR, Shamshirband S (2016a) Firefly optimization algorithm effect on support vector regression prediction improvement of a modified labyrinth side weir’s discharge coefficient. Appl Math Comput 274:14–19. https://doi.org/10.1016/j.amc.2015.10.070
Zaji AH, Bonakdari H, Shamshirband S (2016b) Support vector regression for modified oblique side weirs discharge coefficient prediction. Flow Meas Instr 51:1–7
Zaji AH, Bonakdari H, Shamshirband S (2017) standard equations for predicting the discharge coefficient of a modified high-performance side weir. Sci Iran. https://doi.org/10.24200/SCI.2017.4198
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bonakdari, H., Zaji, A.H. New type side weir discharge coefficient simulation using three novel hybrid adaptive neuro-fuzzy inference systems. Appl Water Sci 8, 10 (2018). https://doi.org/10.1007/s13201-018-0669-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-018-0669-y