Introduction

Side weirs are widely used in hydraulic structures such as irrigation and drainage systems, deviation and flood control structures, channel overflow structures, etc. Accurate prediction of the discharge coefficient is one of the most important phases of the side weir designing process. Attempts to find a mathematical method for side weirs discharge coefficient prediction were initiated by De Marchi (1934). The author assumed that the specific energy of the flow remains constant before and after the side weir, so the author calculated the per unit length of the flow discharge over the side weirs according to the following equation:

$$- \frac{dQ}{dx} = \frac{2}{3}Cd\sqrt {2g} \left( {y - w} \right)^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}} ,$$
(1)

where \(dQ/dx\) is the variation of the upstream discharge relative to its longitudinal position, Cd is the discharge coefficient, g is the gravity acceleration, y is the flow depth, and w is the side weir height. Various studies have been done to find the discharge coefficient of rectangular side weirs (Ackers 1957; Ghodsian 2003; Muslu 2001; Muslu et al. 2003; Nadesamoorthy and Thomson 1972; Ranga Raju et al. 1979; Singh et al. 1994; Swamee et al. 1994; Yu-Tech 1972; Yuksel 2004).

Increasing the discharge capacity of side weirs needs to increase the length of them. Increasing the side weirs’ length leads to increasing the width of the tributary channels. However, there are two problems in widening the tributary channels. First, in most of cases it is not an economical alternative. Second, in some practical situations such as the projects that are done in mountainous regions, there is environmental limitation against widening the channels. Many studies shown that changing the shape of the side weirs could increase the efficiency of them significantly (Cosar and Agaccioglu 2004; Emiroglu et al. 2010b; Ghodsian 2004; Kumar and Pathak 1987; Ramamurthy et al. 1986). So that, reshaping the side weirs is considered as one of the simplest ways to increase the performance of them.

The discharge coefficient of labyrinth side weirs was studied by Emiroglu et al. (2010a). The authors concluded that these types of side weirs are 1.5 to 4.5 times more efficient compare with the simple rectangular side weirs and developed the following equation to calculate the discharge coefficient of labyrinth side weirs located on straight channels.

$$Cd = \left[ {18.6 - 23.535\,\left( {\frac{L}{b}} \right)^{0.012} + 6.769\,\left( {\frac{L}{l}} \right)^{0.112} - 0.502\,\left( {\frac{w}{{Y_{1} }}} \right)^{4.024} + 0.094\sin \theta - 0.393Fr_{1}^{2.155} } \right]^{ - 1.431} ,$$
(2)

where b (m) is the channel width, L (m) the weir length, w (m) the height of crest, Y 1 (m) the upstream flow depth, θ (deg) the labyrinth side weir included angle and Fr 1 the upstream Froude number.

Borghei and Parvaneh (2011) proposed a new shape of a labyrinth side weir that was over 2.33 times more efficient than that of a rectangular side weir. For predicting its discharge coefficient, the authors proposed the Eq. (3) by using non-dimensional parameters, as follows:

$$Cd = \left[ { - 0.18\left( {\frac{{Fr_{1} }}{{\sin \theta^{\prime}}}} \right)^{0.71} - 0.15\left( {Fr_{1} } \right)^{0.44} + \left( {\frac{w}{{Y_{1} }}} \right)^{0.7} } \right] \times \left[ { - 2.37 + 2.58\left( {\frac{{w\sin \theta^{\prime}}}{{Y_{1} }}} \right)^{ - 0.36} } \right],$$
(3)

where θ′ is the modified oblique side-weir included angle.

Recently, the artificial intelligence methods are widely employed in different hydraulic engineering fields because of the flexibility of them in simulating the complex problems such as open channel velocity simulation (Gholami et al. 2015; Sun et al. 2014), local scour modelling (Najafzadeh et al. 2016, 2017), water quality modelling (Heddam 2016), sediment transportation (Lagos-Avid and Bonilla 2017; Safari et al. 2016), etc.

SVR is one of the most popular fields of artificial intelligence methods that is used in various different fields of water resource engineering such as modeling the discharge coefficient as one of the most important processes in designing the side weirs (Bonakdari et al. 2015; Hossein Zaji et al. 2015; Shamshirband et al. 2016; Zaji and Bonakdari 2014; Zaji et al. 2015), scour depth prediction (Goel 2011; Hong et al. 2012; Neerukatti et al. 2013; Pal et al. 2011; Sharafi et al. 2016), rainfall-runoff modelling (Lin et al. 2013; Nikam and Gupta 2014; Seo et al. 2014; Wang et al. 2013), sediment transportation (Jain 2012; Kakaei Lafdani et al. 2013; Kisi 2012), Lake water level prediction (Cimen and Kisi 2009; Khan and Coulibaly 2006), and evapotranspiration estimation (Chen 2012; Kisi 2013).

The purpose of this study is to investigate the performance of the SVR method in predicting the discharge coefficient of modified labyrinth side weirs and to compare it with the performance of two different nonlinear regression models obtained from previously published studies. The SVR scenarios were developed and compared with eight different kernels and six different non-dimensional input combinations. Finding the appropriate kernel functions should be done for each problem that solved with the SVR, something never done before for discharge coefficient prediction problems.

Materials and Methods

In the first part of this section, the experimental dataset that was used for verifying the numerical model is introduced, in the second part, the constructing of the SVR model is described and explained.

Experimental Dataset

The experimental dataset of Borghei and Parvaneh (2011) was used in this study. The main channel was of 11 and 0.4 m in length and width, respectively (Fig. 1). As shown in Fig. 1, in the modified labyrinth side weir, the conventional triangular side weir with included angle of θ is divided into two right triangles with an included angle of θ′ = θ/2. Two hundred tests were performed in different geometrical situations to calculate the discharge coefficient (Cd) of the modified labyrinth side weir. The experimental range of the weir length (L), side weir height (w), modified oblique side weir included angle (θ′), upstream Froude number (Fr 1 ) and total discharge (Q 1 ) are shown in Table 1. The accuracy of the discharge and water head measurements was ±0.0001 (m3/s) and ±1 (mm), respectively.

Fig. 1
figure 1

Schematic plan and cross section of modified labyrinth side weir of Borghei and Parvaneh (2011)

Full size image
Table 1 Range of tested variables (Borghei and Parvaneh 2011)
Full size table

Support Vector Regression (SVR)

Support vector machine (SVM) that uses in two branches of classification and regression was introduced by Vapnik (2000). In the regression branch of SVM, named SVR, the main goal is to find a functional dependency between inputs, \(X = \left\{ {\vec{x}_{1} ,\;\vec{x}_{2} ,\; \ldots ,\;\vec{x}_{n} } \right\}\) that \(\vec{x}_{i} \in R^{m}\) and the targets \(T = \{ t_{1} ,\;t_{2} ,\; \ldots ,t_{n} \}\) that \(t_{i} \in R\). In this study, the inputs are taken from the non-dimensional parameters of the geometrical and hydraulic conditions of the side weir and the target is the values of the discharge coefficient (Cd). The accuracy of the SVR model is directly related to a good choice of the positive constants of two parameters namely C and ε. The ε constant is used in the loss function (L ε ) that is used in order to penalize the model in the case of big errors occur (Eq. 4).

$$L_{\varepsilon } (t_{i} ,y_{i} ) = \left\{ {\begin{array}{*{20}c} {0\,\,\quad \left| {t_{i} - y_{i} } \right| \le \varepsilon } \\ {\zeta \,_{i} \quad \left| {t_{i} - y_{i} } \right| > \varepsilon } \\ \end{array} } \right..$$
(4)

According to this equation, the loss function is equal to 0, if the difference between the targets (t i ) and the outputs (y i ) is smaller than ε. Otherwise it is equal to a non-negative slack variable (\(\zeta_{i}^{ + }\),\(\zeta_{i}^{ - }\)). C is a positive constant that is used as trade-off parameter utilized in the regularized risk function (Cimen 2008; Smola 1996) as follow:

$$R_{reg} \left[ {y_{i} } \right] = C\sum\limits_{i = 1}^{n} {(\zeta_{i}^{ - } + \zeta_{i}^{ + } )} + \frac{1}{2}w^{T} w\quad such\;that\;\left\{ {\begin{array}{*{20}c} { - t_{i} + y_{i} + \varepsilon + \zeta_{i}^{ + } \ge 0} \\ {t_{i} - y_{i} + \varepsilon + \zeta_{i}^{ - } \ge 0} \\ {\zeta_{i}^{ - } \;and\;\zeta_{i}^{ + } \ge 0} \\ \end{array} } \right.,$$
(5)

where w is the weight vector. There are many kernel functions possible to be used in the SVR model such as Linear, Polynomial, Gaussian, etc. Despite the fact that the Gaussian kernel function is the one most applied in the SVR method (Caputo et al. 2002), there is no definite rule which kernel function should be chosen for a specified problem. In this study, eight different kernel functions were tried to find the most appropriate one for predicting the discharge coefficient of the modified labyrinth side weir (Table 2). In addition, from Table 2 one can discern that other kernel functions, except for linear kernel function, have one constant that must be determined. So that, the constants of C, ε and kernel functions’ constants were determined by trial and error method. To do this, some loops were added to the main program of the SVR, which changed the values of these constants and analyzed the accuracy of the model in each situation in finding the more appropriate conditions. About one hundred runs were completed for each kernel function and eight hundred runs carried out in total.

Table 2 Used kernel function equations
Full size table

Model Performance Evaluation

To assess the performance of the SVR model, root mean square error (RMSE), mean absolute error (MAE), average absolute deviation (%δ) and coefficient of determination (R 2) were used of. The benefit of using the RMSE, MAE and  %δ together was that two of them (RMSE and MAE), had the same unit and scale as the variables of the model and one of them (%δ) is non-dimension and just perfect for comparing the error with the real value of the variables of the model (Pulido-Calvo and Portela 2007). R 2 shows the degree of how well the experimental results were simulated by the SVR model. RMSE, MAE,  %δ and R 2 are shown in the Eqs. (6–9).

$$RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {Cd_{i(EXP)} - Cd_{i(SVR)} } \right)}^{2} ,}$$
(6)
$$MAE = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {Cd_{i(SVR)} - Cd_{i(EXP)} } \right|} ,$$
(7)
$${\text{R}}^{2} = \left[ {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {Cd_{i(EXP)} - \overline{{Cd_{(EXP)} }} } \right)\,\left( {Cd_{i(SVR)} - \overline{{Cd_{(SVR)} }} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {Cd_{i(EXP)} - \overline{{Cd_{(EXP)} }} } \right)^{2} } \sum\nolimits_{i = 1}^{n} {\left( {Cd_{i(SVR)} - \overline{{Cd_{(SVR)} }} } \right)^{2} } } }}} \right]^{2} ,$$
(8)
$$\% \delta = \frac{{\sum\nolimits_{i = 1}^{N} {\left| {Cd_{i(SVR)} - Cd_{i(EXP)} } \right|} }}{{\sum\nolimits_{i = 1}^{N} {Cd_{i(SVR)} } }} \times 100.$$
(9)

Results

Determine the Best Kernel Function

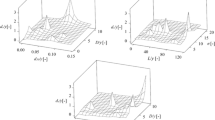
The SVR method was employed in various conditions to evaluate the discharge coefficient of the modified labyrinth side weir. Sixty percent of the whole dataset was selected randomly for the training process and the rest forty percent of the dataset was used for testing the models. The SVR models were compared by using eight different kernel functions to find the best kernel for estimating the discharge coefficient of the labyrinth side weirs problem. These models were modified by using the non-dimension input parameters of \(w/L,Fr_{1} /\sin \theta^{\prime},w/Y_{1}\) and \(w\sin \theta^{\prime}/Y_{1}\). Table 3 shows the results of the performance statistics of the different SVRs. From this table, it is clear that the Polynomial kernel function, with RMSE of 0.051 and 0.047 in train and test processes, respectively, performs much better than the other ones. One can see that also the Gaussian, Rational quadratic, Exponential and Laplacian kernel functions perform very close to the Polynomial kernel function and display good accuracy. This Table 3 also shows that the Exponential and Laplacian kernel functions perform very similarly to each other and a change in the sigma change sensitivity does not change the performance of the models. By comparing the Gaussian and Exponential kernel functions, it can be discerned that reduce the \(\left\| {x - x^{\prime}} \right\|\) change sensitivity led to reducing the accuracy of the SVR model.

Table 3 The RMSE, MAE, and %δ statistics of SVR models in various kernel functions
Full size table

Figure 2 shows the comparison of the SVR models with various kernel functions for the testing data. In this figure, the linear fit-line of \(y = C_{1} x + C_{2}\) is shown by a filled line and the exact line by a dashed line. It shows that the closer C 1 and C 2 get to one and zero, respectively, the results are spread more uniformly at two sides of the exact line, and the model is not trapped in over- or under-estimation. Over- and under-estimation occurred, when the numerical model predicted the Cd coefficient as more or less than the observed reality, respectively. As one can see from this figure, the Polynomial kernel function leads to an SVR model with C 1 and C 2 of 0.992 and 0.006, respectively with almost no over- and under-estimation. Following the Polynomial kernel function, the Gaussian kernel function has the best uniformity of prediction. One can see from this figure that all the SVR models have a tendency to over-estimation at a Cd value lower and under-estimation at a one higher than 0.7.

Fig. 2
figure 2

The scatter plots of SVR models with various kernel functions in test data

Full size image

By looking at the SVR model with the linear kernel function, despite the fact that this model estimates the Cd with low accuracy, it is worth noting that it has a high R 2 value (because of the proximity of its output data to the mean of the output data).

Determination of the best input combination

To determine the best input combination for predicting the discharge coefficient of a modified labyrinth side weir, six different input combinations were examined. All the SVRs were modeled by using a polynomial kernel function, selected as the best kernel function according to evaluations done above. Each input combination contained some non-dimensional parameters, obtained by combining the crest height (w), weir length (L), upstream flow depth (Y 1 ), upstream Froude number (Fr 1 ) and the included angle \((\theta^{\prime})\) of the modified oblique side weir. Table 4 shows the performance statistics of the different SVR models with various input combinations. According to this table, the first input combination (used for kernel selection) with RMSE of 0.051 and 0.047 in the train and test processes, respectively, shows the best performance in comparison with the other input combinations, although the second combination is also very close to the best one. The numbers 3–6 of the input combinations were constructed with fewer input parameters to find out if the SVR model performed better in such conditions; the results show that with decrease the number of input parameters, the errors increase, and the SVR method performs much better in cases with more input parameters. By comparing the first and second input combinations, it can be concluded that w/L is more effective than Fr 1 . Besides, comparing the results of the fifth and sixth input combinations, one can conclude that Y 1 is more effective than L in predicting the discharge coefficient of the modified labyrinth side weir.

Table 4 The RMSE, MAE, and %δ statistics of SVR models in various input combinations
Full size table

In Fig. 3, the scatterplots of various SVR models were compared in different input combinations. According to this figure, the SVR model with first input combination performs better than the other models and is not trapped in over- or under-estimation. As seen from this figure, the performance of the SVR model with the second input combination looks almost like the one with the first input combination. However, the second input combination over-estimate values for lower Cd and under-estimate for higher Cd. The figures of SVR models with input combination of 3–6 shows that with reducing the input parameters, the over-estimation and under-estimation have increased.

Fig. 3
figure 3

The scatterplots of SVR models with various input combinations in test data

Full size image

The results of the investigation of the characteristics of the SVR models show that the optimum SVR model with the polynomial kernel function, using \(w/L,Fr_{1} /{ \sin }\theta^{\prime},w/Y_{1}\) and \(w{ \sin }\theta^{\prime}/Y_{1}\) as input parameters, leads the most accurate model in predicting the discharge coefficient of a modified labyrinth side weir. In this part of the paper the results of Borghei and Parvaneh (2011) and Emiroglu et al. (2010a) were compared with the SVR model. As mentioned before, in order to develop the SVR model, sixty percent of the whole dataset is considered as the training dataset and the rest forty percent is considered as the testing dataset. However, in this part, the results of the SVR’s training and testing datasets are aggregated together to have the ability of comparing the entire dataset with the previous equations. Table 5 shows the comparisons of the performance statistics of the SVR, Borghei and Parvaneh (2011) and Emiroglu et al. (2010a) for the whole datasets. From this table, one can see that the SVR model by RMSE of 0.050 performs much better than the other models. The Borghei and Parvaneh (2011) equation has reasonable accuracy by RMSE of 0.121, but the accuracy of the Emiroglu et al. (2010a) equation in modeling the discharge coefficient of a modified labyrinth side weir is very low.

Table 5 The RMSE, MAE, and %δ statistics of SVR model with two other models
Full size table

In Fig. 4 the residuals of the SVR, Borghei and Parvaneh (2011) and Emiroglu et al. (2010a) are shown by a filled line, filled squares and un-filled squares, respectively. According to this figure, the SVR residuals for the majority of the data are between −0.1 and 0.1, while those of Borghei and Parvaneh (2011) are between −0.3 and 0.3 and of the Emiroglu et al. (2010a) between −1 and 0.7. The low performance of Emiroglu et al. (2010a) in modeling the discharge coefficient of a modified labyrinth side weirs shows that a separate study must be performed for each type of side weir, so the equation of triangular side weirs could not be used for modified labyrinth side weirs.

Fig. 4
figure 4

The residuals of SVR and two other models for the whole dataset

Full size image

Conclusion

Ability to predict the discharge capacity of side weirs accurately is one of the most important elements in designing economical and safe side weir structures. In this study, the SVR method was used in designing a model to estimate the discharge coefficient of modified labyrinth side weirs. To find the optimum SVR model, eight different kernel functions were examined to find the best one. The results show that, despite the Gaussian kernel function being advocated in various papers (Azamathulla and Wu 2011; Cimen and Kisi 2009; Kisi and Cimen 2012), the polynomial kernel function performs best in predicting the discharge coefficient of modified labyrinth side weirs in comparison with the other kernel functions investigated. To find the best combination, six different input combinations were examined. Comparing the results showed that the \(w/L,Fr_{1} /{ \sin }\theta^{\prime},w/Y_{1}\) and \(w{ \sin }\theta^{\prime}/Y_{1}\) input combination has the highest accuracy. The results of comparing the optimum SVR model with the two published equations of Borghei and Parvaneh (2011) and Emiroglu et al. (2010a) show that the SVR model performance was superior to the empirical relations in predicting the discharge coefficient of modified labyrinth side weirs.