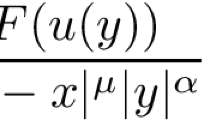Abstract
In this article, we investigate the existence of positive solutions to the following class of quasilinear Schrödinger equations involving Stein-Weiss type convolution
where \(N\ge 2, 0<\mu <N,\, \beta \ge 0,\) and \(2\beta +\mu < N.\) The potential \(V:{\mathbb {R}}^N\rightarrow {\mathbb {R}}\) is a continuous function satisfying \(0<V_0\le V(x)\) for all \(x\in {\mathbb {R}}^N\) and some suitable assumptions. The nonlinearity \(f:{\mathbb {R}}^N\times \mathbb {R}\rightarrow {\mathbb {R}}\) is a continuous function with critical exponential growth in the sense of the Trudinger-Moser inequality and \(F(x,s)=\int _{0}^s f(x,t)dt\) is the primitive of f.

Similar content being viewed by others
Data Availability
Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.
References
Hasse, R.W.: A general method for the solution of nonlinear soliton and kink Schrödinger equation. Z. Phys., B 37, 83–87 (1980)
Bass, F., Nasanov, N.N.: Nonlinear electromagnetic-spin waves. Phys. Rep. 189, 165–223 (1990)
Kurihara, S.: Large-amplitude quasi-solitons in superfluids films. J. Phys. Soc. Japan 50, 3262–3267 (1981)
Ritchie, B.: Relativistic self-focusing and channel formation in laser-plasma interactions. Phys. Rev. E 50, 687–689 (1994)
Liu, J.Q., Wang, Y.Q., Wang, Z.Q.: Solutions for quasilinear Schrödinger equations via the Nehari method. Comm. Partial Differ. Eqs. 29, 879–901 (2004)
Liu, J.Q., Wang, Z.Q.: Soliton solutions for quasilinear Schrödinger equations. I. Proc. Amer. Math. Soc. 131, 441–448 (2003)
Ruiz, D., Siciliano, G.: Existence of ground states for a modified nonlinear Schrödinger equation. Nonlinearity 23, 1221–1233 (2010)
Liu, Q., Liu, X.Q., Wang, Z.Q.: Multiple sign-changing solutions for quasilinear elliptic equations via perturbation method. Comm. Partial Differ. Eqs. 39, 2216–2239 (2014)
Liu, X.Q., Liu, J.Q., Wang, Z.Q.: Quasilinear elliptic equations with critical growth via perturbation method. J. Differ. Eqs. 254, 102–124 (2013)
Colin, M., Jeanjean, L.: Solutions for a quasilinear Schrödinger equation: a dual approach. Nonlinear Anal. 56, 213–226 (2004)
do Ó, J.M., Miyagaki, O.H., Soares, S.H.M.: Soliton solutions for quasilinear Schrödinger equations: the critical exponential case. Nonlinear Anal. 67, 3357–3372 (2007)
do Ó, J.M., Miyagaki, O.H., Soares, S.H.M.: Soliton solutions for quasilinear Schrödinger equations with critical growth. J. Differ. Eqs. 248, 722-744 (2010)
Jeanjean, L., Luo, T.J., Wang, Z.Q.: Multiple normalized solutions for quasi-linear Schrödinger equations. J. Differ. Eqs. 259, 3894–3928 (2015)
Stein, E.M., Weiss, G.: Fractional integrals on \(n\)-dimensional Euclidean space. J. Math. Mech. 7, 503–514 (1958)
Lieb, E.H., Loss, M.: Analysis, Graduate Studies in Mathematics. AMS, Providence, Rhode island (2001)
Pekar, S.: Untersuchung über die Elektronentheorie der Kristalle. Akademie Verlag, Berlin (1954)
Dalfovo, F., Giorgini, S., Pitaevskii, L.P., Stringari, S.: Theory of Bose-Einstein condensation in trapped gases. Rev. Modern Phys. 71, 463 (1999)
Penrose, R.: Quantum computation, entanglement and state reduction. R. Soc. Lond. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 356, 1927–1939 (1998)
Lieb, E.H.: Existence and uniqueness of the minimizing solution of Choquard nonlinear equation. Studies Appl. Math., 57, 93-105 (1976/77)
Lions, P.L.: The concentration compactness principle in the calculus of variations part-I. Rev. Mat. Iberoamericana 1, 185–201 (1985)
Moroz, V., Van Schaftingen, J.: Groundstates of nonlinear Choquard equations: Hardy-Littlewood-Sobolev critical exponent. Commun. Contemp. Math. 17, 1550005 (2015)
Moroz, V., Van Schaftingen, J.: Existence of groundstates for a class of nonlinear Choquard equations. Trans. Amer. Math. Soc. 367, 6557–6579 (2015)
Moroz, V., Van Schaftingen, J.: Groundstates of nonlinear Choquard equations: existence, qualitative properties, decay asymptotics. J. Funct. Anal. 265, 153–184 (2013)
Moroz, V., Van Schaftingen, J.: A guide to the Choquard equation. J. Fixed Point Theory Appl. 19, 773–813 (2017)
Moser, J.: A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20, 1077–1092 (1971)
Cao, D.: Nontrivial solution of semilinear elliptic equations with critical exponent in \({\mathbb{R} }^2\). Comm. Partial Differ. Eqs. 17, 407–435 (1992)
do Ó, J.M.: \(N\)-Laplacian equations in \(\mathbb{R}^N\) with critical growth. Abstract Appl. Anal. 2, 301–315 (1997)
Adimurthi, A.: Existence of positive solutions of the semilinear Dirichlet problem with critical growth for the n-Laplacian. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 17, 393–413 (1990)
de Figueiredo, D.G., Miyagaki, O.H., Ruf, B.: Elliptic equations in \({\mathbb{R} }^2\) with nonlinearities in the critical growth range. Calc. Var. Partial Diff. Eqs. 3(2), 139–153 (1995)
Deng, Y., Peng, S., Wang, J.: Nodal Solutions for a Quasilinear Elliptic Equation Involving the p-Laplacian and Critical Exponents. Adv. Nonlinear Stud. 18, 17–40 (2018)
Moameni, A.: Existence of soliton solutions for a quasilinear Schrödinger equation involving critical exponent in \({\mathbb{R} }^N\). J. Differ. Eqs. 229, 570–587 (2006)
Wang, Y., Yang, J., Zhang, Y.: Quasilinear elliptic equations involving the \(N\)-Laplacian with critical exponential growth in \({\mathbb{R} }^N\). Nonlinear Anal. 79, 6157–6169 (2009)
de Souza, M., Severo, U.B., Vieira, G.F.: On a nonhomogeneous and singular quasilinear equation involving critical growth in \({\mathbb{R} }^2\). Comput. Math. Appl. 74, 513–531 (2017)
de Souza, M., Severo, U.B., Vieira, G.F.: Solutions for a class of singular quasilinear equations involving critical growth in \(\mathbb{R}^2\). Math. Nachr. 1–21 (2022)
Alves, C.O., Cassani, D., Tarsi, C., Yang, M.: Existence and concentration of ground state solutions for a critical nonlocal Schrödinger equation in \({\mathbb{R} }^2\). J. Differ. Eqs. 261, 1933–1972 (2016)
Arora, R., Giacomoni, J., Mukherjee, T., Sreenadh, K.: \(n\)-Kirchhoff-Choquard equations with exponential nonlinearity. Nonlinear Anal. 186, 113–144 (2019)
Biswas, R., Goyal, S., Sreenadh, K.: Quasilinear Choquard equations involving N-Laplacian and critical exponential nonlinearity. Math. Methods Appl. Sci. 45, 9483–9503 (2022)
Arora, R., Giacomoni, J., Mukherjee, T., Sreenadh, K.: Polyharmonic Kirchhoff problems involving exponential non-linearity of Choquard type with singular weights. Nonlinear Anal. 196, 111779 (2020)
Du, L., Gao, F., Yang, M.: On elliptic equations with Stein-Weiss type convolution parts, (2022), arxiv:1810.11759
Biswas, R., Goyal, S., Sreenadh, K.: Multiplicity results for \( p \)-Kirchhoff modified Schrödinger equations with Stein-Weiss type critical nonlinearity in \({\mathbb{R} }^ N\). Differ. Integral Eqs. 36, 247–288 (2023)
Melgaard, M., Yang, M., Zhou, X.: Regularity, symmetry and asymptotic behaviour of solutions for some Stein-Weiss-type integral systems. Pacific J. Math. 317, 153–186 (2022)
Su, Y.: Fractional p-Laplacian Problem with Critical Stein-Weiss Type Term. J. Geom. Anal. 33, 160 (2023)
Yang, M., Rădulescu, V.D., Zhou, X.: Critical Stein-Weiss elliptic systems: symmetry, regularity and asymptotic properties of solutions. Calc. Var. Partial Differ. Eqs. 61, 109 (2022)
Adimurthi, Yang, Y.: An Interpolation of Hardy Inequality and Trudinger-Moser Inequality in \(\mathbb{R}^N\) and Its Applications, Int. Math. Res. Not., 2010, 2394–2426 (2009)
do Ó, J.M.: Semilinear Dirichlet problems for the \(N\)-Laplacian in \(\mathbb{R}^N\) with nonlinearities in critical growth range. Diff. Integral Equ. 5, 967-979 (1996)
Adimurthi, Sandeep, K.: A singular Moser-Trudinger embedding and its applications, Nonlinear Differ. Equ. Appl. NODEA 13, 585–603 (2007)
Severo, U.B.: Existence of weak solutions for quasilinear elliptic equations involving the \(p\)-Laplacian. Electron. J. Differ. Eqs. 56, 1–16 (2008)
Brezis, H.: Functional analysis, Sobolev spaces and partial differential equations. Universitext Springer, New York (2011)
Guedda, M., Veron, L.: Quasilinear elliptic equations involving critical Sobolev exponents. Nonlinear Anal. 13, 879–902 (1989)
Acknowledgements
The second author would like to thank the Science and Engineering Research Board, Department of Science and Technology, Government of India for the financial support under the grant SPG/2022/002068.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Here, we prove the generalized Pohozaev identity for the following quasilinear equation:

where \(1<p\le N,\) \(0<\mu <N, \beta \ge 0,\) and \(2\beta +\mu \le N.\) The nonlinearity \(f:{\mathbb {R}}^N\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a continuous function and \(F(x,s)=\int _{0}^s f(x,t)dt\) is the primitive of f. Similar results for the semilinear Choquard equations with Laplacian operator, readers are referred to [23, 39].
Proposition 6.1
Let \(w\in W^{1,p}({\mathbb {R}}^N)\cap L_{loc}^\infty ({\mathbb {R}}^N) \) be a weak solution to problem (\(Q_{*}\)). Then
Proof
Using the idea of [49], let \(w_{\epsilon }\) be the classical solution in \(C^{3}_{loc}({\mathbb {R}}^N{\setminus } \{0\})\) of
Then \(w_{\epsilon }\) is bounded in \(C^{1,\theta }({\mathbb {R}}^N{\setminus } \{0\})\) independently of \(\epsilon \in (0,1]\) and converges to w in \(C^{1,{\tilde{\theta }}}({\mathbb {R}}^N{\setminus } \{0\})\) for any \(\theta < {{\tilde{\theta }}}\) as \(\epsilon \rightarrow 0\). For \(0<{\textrm{r}}<{\textrm{R}}\), define \(\phi _{r,R}\in C_{c}^{\infty }({\mathbb {R}}^N)\) with \(0\le \phi _{r,R}\le 1\), \(\phi _{r,R}(x)=0\) in \(|x|<\frac{r}{2}\) and \(\phi _{r,R}(x)=1\) on \(r<|x|< R\) with \(|\nabla \phi _{r,R}(x)|<\frac{c}{R}\). By testing the equation against the function \(\psi _{r, R}(x)= \phi _{r,R} (x \cdot \nabla w_\epsilon (x))\) and integrate over \({\mathbb {R}}^N\), we have
Now we compute for every \(R>r>0\),
Letting \(\epsilon \rightarrow 0\), \(r \rightarrow 0\) and \(R\rightarrow \infty \), we obtain
thanks to Lebesgue’s dominated convergence Theorem. Next, we have
Similarly, taking \(\epsilon \rightarrow 0\) in the left hand side of the last relation,
and using this,
Finally, we get
Taking \(r \rightarrow 0\) and \(R\rightarrow \infty \), by Lebesgue’s dominated convergence theorem,
Hence, combining the above estimates and taking \(\epsilon \rightarrow 0\), we obtain
This completes the proof of the proposition. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Biswas, R., Goyal, S. & Sreenadh, K. Quasilinear Schrödinger Equations With Stein-Weiss Type Convolution and Critical Exponential Nonlinearity in \({\mathbb {R}}^N\). J Geom Anal 34, 54 (2024). https://doi.org/10.1007/s12220-023-01505-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-023-01505-5
Keywords
- Quasilinear Schrödinger equation
- N-Laplacian
- Stein-Weiss type convolution
- Trudinger-Moser inequality
- Critical exponent