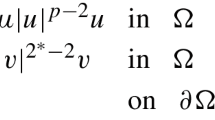Skip to main content

Advertisement

SpringerLink
Log in

Critical Stein–Weiss elliptic systems: symmetry, regularity and asymptotic properties of solutions

  • Published:
Calculus of Variations and Partial Differential Equations Aims and scope Submit manuscript

Abstract

In this paper, we study the following weighted nonlocal system with critical exponents related to the Stein–Weiss inequality

$$\begin{aligned} \left\{ \begin{aligned} -\Delta&u=\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{v^{p}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) u^{q}, \\ -\Delta&v =\frac{1}{|x|^{\alpha }}\left( \int _{{\mathbb {R}}^N}\frac{u^{q}(y)}{|x-y|^{\mu }|y|^{\alpha }}dy\right) v^{p}, \end{aligned} \right. \end{aligned}$$

By using moving plane arguments in integral form, we obtain symmetry, regularity and asymptotic properties, as well as sufficient conditions for the nonexistence of solutions to the nonlocal Stein–Weiss system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Beckner, W.: Pitt’s inequality with sharp convolution estimates. Proc. Am. Math. Soc. 136, 1871–1885 (2008)

    Article  MathSciNet  Google Scholar 

  2. Beckner, W.: Weighted inequalities and Stein–Weiss potentials. Forum Math. 20, 587–606 (2008)

    Article  MathSciNet  Google Scholar 

  3. Caffarelli, L., Gidas, B., Spruck, J.: Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth. Commun. Pure Appl. Math. 42, 271–297 (1989)

    Article  MathSciNet  Google Scholar 

  4. Caffarelli, L., Kohn, R., Nirenberg, L.: First order interpolation inequalities with weights. Compos. Math. 53, 259–275 (1984)

    MathSciNet  MATH  Google Scholar 

  5. Chen, L., Liu, Z., Lu, G.: Symmetry and regularity of solutions to the weighted Hardy–Sobolev type system. Adv. Nonlinear Stud. 16, 1–13 (2016)

    Article  MathSciNet  Google Scholar 

  6. Chen, W., Li, C.: Classification of solutions of some nonlinear elliptic equations. Duke Math. J. 63, 615–622 (1991)

    Article  MathSciNet  Google Scholar 

  7. Chen, W., Li, C., Ou, B.: Classification of solutions for a system of integral equations. Commun. Partial Differ. Equ. 30, 59–65 (2005)

    Article  MathSciNet  Google Scholar 

  8. Chen, W., Li, C., Ou, B.: Classification of solutions for an integral equation. Commun. Pure Appl. Math. 59, 330–343 (2006)

    Article  MathSciNet  Google Scholar 

  9. Chen, W., Li, C.: Methods on Nonlinear Elliptic Equations. AIMS Book Series on Differential Equations and Dynamical Systems, vol. 4 (2010)

  10. Chen, W., Jin, C., Li, C., Lim, J.: Weighted Hardy–Littlewood–Sobolev inequalities and systems of integral equations. Discrete Contin. Dyn. Syst. S, 164–172 (2005)

    MathSciNet  MATH  Google Scholar 

  11. Chen, W., Li, C.: The best constant in a weighted Hardy–Littlewood–Sobolev inequality. Proc. Am. Math. Soc. 136, 955–962 (2008)

    Article  MathSciNet  Google Scholar 

  12. Dou, J., Zhu, M.: Reversed Hardy–Littewood–Sobolev inequality. Int. Math. Res. Not. 19, 9696–9726 (2015)

    Article  MathSciNet  Google Scholar 

  13. Du, L., Gao, F., Yang, M. On elliptic equations with Stein–Weiss type convolution parts. Math. Z. (2022). https://doi.org/10.1007/s00209-022-02973-1

  14. Du, L., Yang, M.: Uniqueness and nondegeneracy of solutions for a critical nonlocal equation. Discrete Contin. Dyn. Syst. 39, 5847–5866 (2019)

    Article  MathSciNet  Google Scholar 

  15. Gidas, B., Ni, W., Nirenberg, L.: Symmetry of positive solutions of nonlinear elliptic equations in \({\mathbb{R}}^{N}\), mathematical analysis and applications. Adv. Math. Suppl. Stud., 7a, Academic Press, New York. part A, pp. 369–402 (1981)

  16. Gidas, B., Spruck, J.: Global and local behavior of positive solutions of nonlinear elliptic equations. Commun. Pure Appl. Math. 34, 525–598 (1981)

    Article  MathSciNet  Google Scholar 

  17. Jin, C., Li, C.: Quantitative analysis of some system of integral equations. Calc. Var. Partial Differ. Equ. 26, 447–457 (2006)

    Article  MathSciNet  Google Scholar 

  18. Lei, Y.: Qualitative analysis for the static Hartree-type equations. SIAM J. Math. Anal. 45, 388–406 (2013)

    Article  MathSciNet  Google Scholar 

  19. Lei, Y.: Liouville theorems and classification results for a nonlocal Schrödinger equation. Discrete Contin. Dyn. Syst. 38, 5351–5377 (2018)

    Article  MathSciNet  Google Scholar 

  20. Lei, Y., Li, C., Ma, C.: Asymptotic radial symmetry and growth estimates of positive solutions to weighted Hardy–Littlewood–Sobolev system of integral equations. Calc. Var. Partial Diffe. Equ. 16, 1–13 (2016)

    Google Scholar 

  21. Li, C.: Local asymptotic symmetry of singular solutions to nonlinear elliptic equations. Invent. Math. 123, 221–231 (1996)

    Article  MathSciNet  Google Scholar 

  22. Li, C., Ma, L.: Uniqueness of positive bound states to Schrödinger systems with critical exponents. SIAM J. Math. Anal. 40, 1049–1057 (2008)

    Article  MathSciNet  Google Scholar 

  23. Li, X., Yang, M., Zhou, X.: Qualitative properties and classification of solutions for elliptic equations with Stein–Weiss type convolution part. Sci. China Math. https://doi.org/10.1007/s11425-021-1918-1

  24. Li, Y.: Remark on some conformally invariant integral equations: the method of moving spheres. J. Eur. Math. Soc. 6, 153–180 (2004)

    Article  MathSciNet  Google Scholar 

  25. Liu, S.: Regularity, symmetry, and uniqueness of some integral type quasilinear equations. Nonlinear Anal. 71, 1796–1806 (2009)

    Article  MathSciNet  Google Scholar 

  26. Liu, X., Lei, Y.: Existence of positive solutions for integral systems of the weighted Hardy–Littlewood–Sobolev type. Discrete Contin. Dyn. Syst. 40, 467–489 (2020)

    Article  MathSciNet  Google Scholar 

  27. Lieb, E., Loss, M.: Analysis, Graduate Studies in Mathematics. American Mathematical Society, Providence (2001)

    Google Scholar 

  28. Lieb, E.: Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities. Ann. Math. 118, 349–374 (1983)

    Article  MathSciNet  Google Scholar 

  29. Miao, C., Xu, G., Zhao, L.: Global well-posedness, scattering and blow-up for the energy-critical, focusing Hartree equation in the radial case. Colloq. Math. 114, 213–236 (2009)

    Article  MathSciNet  Google Scholar 

  30. Stein, E.: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series, vol. 43. Princeton University Press, Princeton (1993)

  31. Stein, E., Weiss, G.: Fractional integrals on \(n\)-dimensional Euclidean space. J. Math. Mech. 7, 503–514 (1958)

    MathSciNet  MATH  Google Scholar 

  32. Strauss, W.: Existence of solitary waves in higher dimensions. Commun. Math. Phys. 55, 149–162 (1977)

    Article  MathSciNet  Google Scholar 

  33. Wei, J., Xu, X.: Classification of solutions of higher order conformally invariant equations. Math. Ann. 313, 207–228 (1999)

    Article  MathSciNet  Google Scholar 

  34. Yu, X.: Liouville type theorems for integral equations and integral systems. Calc. Var. Partial Differ. Equ. 46, 75–95 (2013)

    Article  MathSciNet  Google Scholar 

  35. Ding Y., Gao F., Yang M., Semiclassical states for Choquard type equations with critical growth: critical frequency case. Nonlinearity 33, 6695–6728 (2020)

Download references

Acknowledgements

Minbo Yang was partially supported by NSFC (11971436, 12011530199) and ZJNSF (LZ22A010001, LD19A010001). The research of Vicențiu D. Rădulescu was supported by a grant of the Romanian Ministry of Research, Innovation and Digitization, CNCS/CCCDI-UEFISCDI, project number PCE 137/2021, within PNCDI III.

Author information

Authors and Affiliations

  1. Department of Mathematics, Zhejiang Normal University, Jinhua, 321004, Zhejiang, People’s Republic of China

    Minbo Yang & Xianmei Zhou

  2. Faculty of Applied Mathematics, AGH University of Science and Technology, 30-059, Kraków, Poland

    Vicențiu D. Rădulescu

  3. Department of Mathematics, University of Craiova, 200585, Craiova, Romania

    Vicențiu D. Rădulescu

  4. China-Romania Research Center in Applied Mathematics, Craiova, Romania

    Vicențiu D. Rădulescu

Authors
  1. Minbo Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vicențiu D. Rădulescu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xianmei Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vicențiu D. Rădulescu.

Additional information

Communicated by P. H. Rabinowitz.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, M., Rădulescu, V.D. & Zhou, X. Critical Stein–Weiss elliptic systems: symmetry, regularity and asymptotic properties of solutions. Calc. Var. 61, 109 (2022). https://doi.org/10.1007/s00526-022-02221-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00526-022-02221-8

Mathematics Subject Classification

Search

Navigation