Experts’ intuitive mathematical discourses about integration in complex analysis

Abstract

Although complex analysis is part of the study programs of many mathematics undergraduates, little research has been done on how individuals interpret basic concepts from complex analysis. To address this gap, this paper investigates how experts individually think about complex path integrals. For this purpose, the commognitive framework is used to conceptualize experts’ interpretations of mathematical concepts discursively, namely in terms of so-called intuitive mathematical discourses. A total of nine interpretations of complex path integrals, so-called discursive images, as well as eight sets of rules governing their construction, so-called discursive frames, are derived from expert interviews. These interpretations range from a rejection of intrinsic meaning to connections with real and vector analysis, mean values, and individual formulations of theorems. The paper also raises questions for the inclusion of the results into teaching and addresses further research.

1 Introduction

Supporting individuals’ understanding of the Riemann integral has been the subject of extensive research in mathematics education, resulting in the identification of viable interpretations such as the directed area under its graph, the accumulation of a quantity represented by the function, the mean value of the function up to a scaling factor, or the reconstruction of a rate of change (see e.g., Biza et al., 2022; Ely & Jones, 2023; Greefrath et al., 2016). Similarly, individuals can make sense of real path integrals of vector fields physically in terms of work and flux (e.g., Braden, 1987; Dray & Manogue, 2023; Jones, 2020; Ponce Campuzano et al., 2019).

While such interpretations of integrals in real analysis are viable and support student learning, the case of integration in complex analysis – more precisely: the complex path integral (CPI) $\int_\gamma f(z) \,\mathrm{d}z$ of a function $f$ along a piecewise continuously differentiable path $\gamma$ – appears to be more problematic. For instance, some authors of complex analysis textbooks even claim that “[a] simple geometrical interpretation as in the case of real integrals is impossible” (Knopp, 1945–1947/1996, p. 39) or that “students are mystified on first exposure to this concept, and working examples by the formula $\int_a^b f\left(\gamma\left(t\right)\right) \gamma'(t) \,\mathrm{d}t$ can be a baffling experience” (Gluchoff, 1991, pp. 641–642; notation adapted). Moreover, recent research reports indicate that both students and experts have difficulties in interpreting CPIs (Hancock, 2018; Oehrtman et al., 2019; Soto & Oehrtman, 2022), even though students and experts are known to make use of personal interpretations of the mathematical concepts they work with (e.g., Burton, 1999, 2004; Sfard, 1994; Tall & Vinner, 1981; among others). Therefore, it is worth investigating whether there are interpretations of CPIs that could potentially help make sense of them. Moreover, since integrals reappear throughout mathematics (e.g., in calculus, real and vector analysis, and measure theory), one may ask whether and how interpretations for real integrals relate to their counterparts in complex analysis.

Mathematical experts, both as university teachers and as authors of mathematical texts, are an important source of information here. Therefore, this paper addresses this research gap by asking how experts individually think about complex path integrals. It contributes to mathematics education at university level research in two ways: First, it complements previous strands of research, which have adopted an acquisitionist point of view on individuals’ ways to think about mathematical concepts (Sfard, 2006, pp. 153–158; Sfard, 2008, pp. 76–80), with a participationist perspective as proposed in the commognitive framework (Sfard, 2008).¹ For this to be done, I introduce the notion of intuitive mathematical discourse. Second, this notion allows for the unraveling of nine expert interpretations of complex path integrals, referred to as discursive images, and nuanced insights into eight characteristic ways, referred to as discursive frames, which experts follow to develop their interpretations.

2 Review of mathematical literature and educational research on complex path integrals

Complex analysis is a relatively new field in undergraduate mathematics education research, which is in stark contrast to its relevance in many mathematics curricula. While educational research on complex analysis has focused primarily, but intensively, on the teaching and learning of complex numbers and differentiation (cf. Hanke, 2022; Soto-Johnson et al., 2016; and Troup et al., 2023, for surveys), reports on complex integration are scarce. In particular, insights into experts’ interpretations of complex path integrals are still singular, and the interpretations from the literature do not appear to be as widespread as in the case of real integrals. Both are reviewed now.

2.1 A reminder from the mathematical literature

The mapping $x+iy \mapsto \begin{pmatrix} x \\ y \end{pmatrix}$ induces a Banach space isomorphism ${\mathbb{C}}\cong {\mathbb{R}}^{2}$. Throughout, unless otherwise stated, let $\emptyset \ne\Omega \subseteq \mathbb{C}$ denote a domain (i.e., $\Omega$ is open and connected), $f=u+iv \colon \Omega \to \mathbb{C}$ a continuous function, and $\gamma \colon [a,b] \to \Omega$ a piecewise continuously differentiable path in $\Omega$ (i.e., $\gamma$ is continuous and there is a subdivision $a={t}_{0}<\dots <{t}_{n}=b$ such that $\gamma_{|[{t}_{k-1}, {t}_{k}]}$ is continuously differentiable for $k=1, \dots, n$).² Then, the complex path integral $\int_\gamma f(z) \,\mathrm{d}z$ exists and may be defined in multiple ways such as (see Hanke, 2022)

• the complex number

$$\int_a^b f\left(\gamma(t)\right) \gamma'(t) \,\mathrm{d}t;$$

(1)

• the limit of complex Riemann sums of the form

  $$\sum_{k=1}^m f(\gamma(\xi_k)) \left(\gamma(t_k)-\gamma(t_{k-1})\right),$$

  (2)

  where $a={t}_{0}<\dots <{t}_{m}=b$, $\xi_k \in [{t}_{k-1}, {t}_{k}]$, $k=1, \dots, m$, and $\underset{k=1,\ldots,m}{\max}(t_k - t_{k-1}) \to 0$ as $m\to \infty$, hence mimicking the definition of Riemann integrals;

• the decomposition into real and imaginary parts

  $$\int_\gamma\begin{pmatrix}u\\-v\end{pmatrix}\mathrm d\mathbf T+i\int_\gamma\begin{pmatrix}v\\u\end{pmatrix}\mathrm d\mathbf T\colon=\int_\gamma u\,\mathrm dx-v\,\mathrm dy+i\int_\gamma v\,\mathrm dx+u\,\mathrm dy,$$

  (3)

given by real path integrals of the second kind of the vector fields $\begin{pmatrix} u \\ -v \end{pmatrix}$ and $\begin{pmatrix} v \\ u \end{pmatrix}$ along $\gamma$ as a path in ${\mathbb{C}}\cong {\mathbb{R}}^{2}$; or

• the product of a certain average

  $$\underset{z}{\text{av}}\left[f(z)T(z)\right]$$

  (4)

and the length of $\gamma$, where $z$ ranges along the path and $T$ is the unit tangential field attached to $\gamma$ (Gluchoff, 1991; cf. Hanke, 2024).

Since these definitions borrow notions for real integrals, it is plausible that individuals may attempt to transfer interpretations for real integrals to the complex case. As was illustrated with the quote by Knopp (1945–1947/1996), complex analysis textbooks however rarely provide such interpretations explicitly, but there are some that might help the reader make sense of $\int_\gamma f(z) \,\mathrm{d}z$ (cf. Forst & Hoffmann, 2012; Needham, 1997; Ponce Campuzano, n.d.; Wegert, 2012)³:

• Deriving the parametrization $z=\gamma(t)$ and plugging $\mathrm{d}z = \gamma'(t) \,\mathrm{d}t$ into $\int_\gamma f(z) \,\mathrm{d}z$, Eq. (1) is obtained as the result of a formal computation.

• Since complex numbers may be identified as vectors and their product as a rotation-dilation, the sum in Eq. (2) may be interpreted as the concatenation of vectors resulting from the multiplication of function values with displacement vectors of points on the path (Needham, 1997).

• The decomposition in Eq. (3) means that the real part of the CPI is the work done by a particle in the force field ${\textbf{w}}_f\colon=\begin{pmatrix}u\\-v\end{pmatrix}$ (the vector field corresponding to the conjugate $\overline{f}$, not $\begin{pmatrix} u \\ v \end{pmatrix}$) along $\gamma$ and the imaginary part is the flux of a particle moving in the field $\textbf{w}_f$ across $\gamma$ (e.g., Braden, 1987; Needham, 1997).

• The definition in terms of the average in Eq. (4) mimics the interpretation of integrals as averages for Riemann integrals (e.g., Greefrath et al., 2016). However, the average is formed for the product $f \cdot T$, not $f$.

Finally, I recall the most important theorems about integrals of holomorphic (i.e., complex differentiable) functions for later reference:

• Cauchy’s integral theorem: If $\Omega$ is simply connected, $\gamma$ is closed, and $f$ is holomorphic, then $\int_\gamma f(z) \,\mathrm{d}z = 0$.

• Cauchy’s integral formula: If $f$ is holomorphic and ${z}_{0}\in\Omega$, then

  $$f(a) = \frac{1}{2 \pi i} \int_{\partial B(z_0,r)} \frac{f(z)}{z-a} \,\mathrm{d}z$$

  (5)

for all $r>0$ such that the closure of the open ball $B({z}_{0},r)$ of radius $r$ around ${z}_{0}$ is contained in $\Omega$ and $a\in B({z}_{0},r)$. If ${z}_{0}=a$, this formula simplifies to $f(a) = \frac{1}{2\pi} \int_0^{2\pi} f\left(a+re^{it}\right) \mathrm{d}t$; in other words, $f(a)$ is the average of $f$ on the circle of radius $r$ around $a$. Note that neither the integral $\int_{\partial B(a,r)} f(z) \,\mathrm{d}z$ nor the average in Eq. (4) is involved here.

• Residue theorem: If $\Omega$ is simply connected, $A\subseteq\Omega$ is finite, $f\colon \Omega \setminus A \to \mathbb{C}$ is holomorphic, and $\gamma$ is a closed path in $\Omega \setminus A$, then $\int_\gamma f(z) \,\mathrm{d}z = 2\pi i \sum_{a\in A} \mathrm{Res}_a (f) \mathrm{Ind}_a (\gamma)$, where $\mathrm{Res}_a (f)$ denotes the residue of $f$ at $a$ and $\mathrm{Ind}_a (\gamma)$ denotes the winding number of $\gamma$ around $a$.

• The identity theorem states that if $f$ and $g$ are holomorphic functions on $\Omega$ such that $\left\{ z\in\Omega : f(z)=g(z) \right\}$ has an accumulation point in $\Omega$, then $f=g$. Thus, “local” information about the function values of a holomorphic function uniquely determines them “globally”. In the following, this property is called “rigidity”.

2.2 Educational research on complex integration

Beginning with Danenhower (2000), researchers in complex analysis education have coined the dictum “thinking real, doing complex” to mean that individuals may think of concepts in complex analysis as if they were real, even though they know that the quantities are in fact complex. Hancock (2018, p. 392) summarized three varieties of this phenomenon as follows: “(1) purposefully avoiding inappropriate applications of it; (2) extending real intuition to the complex setting erroneously; and (3) extending real intuition to the complex setting in productive ways”. That is, interpretations for notions from real analysis may be in part transferred productively to complex analysis but they may also be potentially misleading.

At the expert level, Oehrtman et al.’s (2019) interviews showed that even experts may erroneously transfer interpretations for Riemann or real path integrals to CPIs. For example, some of the experts assumed that CPIs represent work or flux of the integrand as is the case for real path integrals of the second kind, and most experts found it hard to interpret CPIs geometrically. One expert, however, had created a personal story: He imagined that a ship was sailing along $\gamma$, the captain wanted to plot its route on a map, and $f$ represented a measure of the ship’s position. The expert then argued that the addends in Eq. (2) were distortions of small segments of the ship’s route by a factor given by $f$. Hence, the sum in Eq. (2) and consequently $\int_\gamma f(z) \,\mathrm{d}z$ “gives you the exact description of your imputed curve” (Oehrtman et al., 2019, p. 413). This study suggests that interpretations for CPIs may be highly individual and that, even though they may be erroneous from a mathematical point of view, they may be valuable to experts.

At the student level, Hancock’s (2018) interview study revealed that students also struggle interpreting CPIs, but that they may also be careful to transfer their interpretations for real integrals to complex analysis to avoid overgeneralizations. Adding to this observation, Soto and Oehrtman (2022) interviewed pairs of students in a complex analysis course and asked them to explain what the integral of a complex function might be before the students had been introduced to this notion in class. The authors observed that the students identified the idea of accumulation to interpret integrals in general, but could not say what is accumulated in this case.

As research is still scarce, further exploratory studies like the present one may reveal a wider range of individual interpretations for CPIs and the mechanisms for their construction (e.g., by finding out how precisely interpretations for real integrals may be transferred).

3 Theoretical framework

3.1 Interpretations of mathematical concepts in previous research

Many studies have adopted a cognitive perspective to explain individual interpretations of mathematical concepts in one way or another, for example in terms of “mental images” (German: “Vorstellungen”), “concept images”, “conceptions”, or “intuition” (see e.g., Burton, 1999, 2004; Fischbein, 1987; vom Hofe & Blum, 2016, Simon, 2017; Tall & Vinner, 1981; Tirosh & Tsamir, 2020). Based on such approaches, educators assume that people do not only work with mathematical concepts in terms of their definitions, but they use personal interpretations as well. Research following these approaches has led to significant insights into how individuals think about and work with mathematical concepts.

Since these approaches require an interpretive act of relating empirical observations to the aforementioned cognitive constructs, a complementary approach is to adopt a discursive perspective and focus on what is put forward in communication (cf. Sfard, 2006). To paraphrase Wittgenstein, “that I imagine [interpret] this or that is not a matter of what goes on in me but of the story I tell” (Hacker, 1990, p. 397; emph. orig.). The commognitive framework (Lavie et al., 2019; Sfard, 2008) allows for such a focus by conceptualizing thinking as a form of participation in discourses: Based on the tenet of “thinking as communicating” (Sfard, 2008), individual ways of thinking about mathematical concepts can also be considered in terms of discourse. This also allows for nuanced insights into how individuals construct their personal interpretations of mathematical concepts.

3.2 The commognitive framework

The commognitive framework (Sfard, 2008) conceptualizes mathematics as a form of discourse and thinking as communicating. In line with the previous observations, “[c]ognitive processes may thus be defined as individualized forms of interpersonal communication, whereas communication itself is described as a collectively performed rule-driven activity” (Sfard, 2008, p. 91). Consequently, “thinking mathematically means participating in a historically developed discourse known as mathematical” (Sfard, 2020, p. 96; emph. orig.). In this context, interpreting mathematical concepts is both a collective and individual endeavor resulting in stories about mathematical concepts that participants in a mathematical discourse, the discursants (Sfard, 2008, p. 297), tell to make the concepts accessible to themselves or others.⁴

According to Sfard (2023, p. 3; emph. orig.), a “discourse of X refers to a type of communication that is used in telling stories about X”. For instance, “complex analysis” is a discourse about complex path integrals and related mathematical objects. However, it must be kept in mind that there is not a single complex analysis discourse, but that complex analysis discourses develop locally, for example in research communities or classrooms.

Discourses are set apart by the use of keywords, visual mediators, endorsed narratives, and routines (Sfard, 2008). Keywords constitute what the discourse is about and how objects of the discourse can be described. Visual mediators are visible means discursants may use such as symbols, letters, or pictures. Narratives are considered endorsed when they are accepted by a community of discursants after processes of substantiation. More precisely, substantiation is the “discursive process of making sure that a given narrative can be endorsed” (Sfard, 2008, p. 302; see also pp. 231–234) and a narrative is endorsed if it “is regarded as reflecting the state of affairs in the world and labeled as true” (Sfard, 2008, p. 298; emph. orig.). Narratives can be object-level rules or metarules: “[o]bject-level rules are narratives about regularities in the behavior of objects of the discourse, whereas metarules define patterns in the activity of the discursants trying to produce and substantiate object-level narratives” (Sfard, 2008, p. 201; emph. orig.). Finally, routines are sets of metarules in a discourse (e.g., locally established ways of defining, calculating, or substantiating). They may be described as reactions to task situations, that is, “any setting[s] in which a person considers herself bound to act” based on “past situations which she interprets as sufficiently similar to the present one” (Lavie et al., 2019, pp. 159–160).

It must be stressed that object-level rules and metarules depend on the discourses in which they are situated. That is, they may be endorsed in one discourse but not in another. In this study, I engage experts in a specific type of discourse, in which they interpret CPIs in a personal way and in which they may deviate from the rigorous endorsed rules of scholarly complex analysis discourses (cf. Viirman, 2021). This specific type of discourse will now be defined.

3.3 Intuitive mathematical discourse

I define an intuitive mathematical discourse (IMD) about X as

“a type of communication that is shaped by [discursants’] descriptions of their intuitive understanding of X. This discourse is about X and other mathematical objects the [discursants] relate to X. It contains keywords revolving around X but also keywords like ‘mental image’, ‘intuitive’, ‘vivid’, ‘non-rigorous’, ‘visual’ etc. An intuitive mathematical discourse is shaped in interaction, that is, it depends on the situations that give rise to [discursants’] discursive actions in response to one of the various task situations, in which they are asked to describe their intuitive understanding of X or a proposition about X” (Hanke, 2022, pp. 54–55).⁵

These discourses arise when discursants engage in task situations that require them to explain a mathematical concept in an individual way, to describe what they consider to be their interpretations (or other related keywords they prefer in this context), or to make the concept accessible to themselves or others beyond a rigorous definition. As such, IMDs are a form of personal discourses – at first glance an “oxymoron” (Sfard, 2008, p. 127) – comprising personal patterns of discussing mathematics in relation to individuals’ intuitive understanding.

To further characterize IMDs about X, it is instructive to discuss what the keywords, visual mediators, narratives, and metarules (as routines are sets of metarules) are. Keywords, visual mediators, and narratives may be identical to those in mathematical discourses about X, but they may also come from other discourses the discursants find appropriate. As defined above, keywords, narratives, and visual mediators in IMDs may also include those around “mental image”, “conception”, “intuitive”, etc., which a discursant has met in similar task situations (e.g., in the context of Riemann integrals even though she or he discusses CPIs).

The commognitive version of an interpretation of a mathematical concept is now called a discursive image: A discursive image about X is a narrative “constructed in response to any task situation to express one’s own intuitive understanding about X or to make X accessible for others” (Hanke, 2022, p. 56). Discursive images can be on object- or meta-level and they may or may not be accompanied with the use of visual mediators. In this respect, the authority of what counts as an interpretation remains with the discursants.

Routines in IMDs may contain metarules from mathematical discourses. Discursants engaging in IMDs may deviate from scholarly mathematical metarules though and construct discursive images based on their personal ways of engaging with the mathematical concept at hand. Therefore, the metarules governing the construction of discursive images and intuitive substantiations (i.e., substantiations a discursant considers plausible, vivid, not rigorous, or not requiring further elaboration; see above) are especially important. Loosely based on Heyd-Metzuyanim et al.’s (2018) idea of frame in commognitive research, I define discursive frames in intuitive mathematical discourses as

“sets of metarules […] which express ‘individual’s expectations originating in repetitive interactions’ (Heyd-Metzuyanim et al., 2018, p. 26) and guide discursants in intuitive mathematical discourses in constructing discursive images and intuitive substantiations. Discursive frames may not be made explicit by the participants themselves and have to be made explicit by the commognitive researcher” (Hanke, 2022, p. 61).

In this sense, discursive frames are certain routines in IMDs. It should be emphasized though that discursive frames are not necessarily identical to routines in scholarly mathematical discourses. Rather, they are sets of metarules individuals specifically follow to deal with task situations that require them to explain their personal intuitive understanding, to react to quests for interpretation (according to their personal judgment), to provide means for making abstract mathematical concepts accessible, etc. Discursants may thus construct narratives about the objects or discursants of an IMD, in particular discursive images, when following the rules of a discursive frame. In that respect, a discursive frame is said to govern the construction of a discursive image.

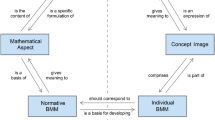
Figure 1 illustrates the notions just defined: It summarizes the components of intuitive mathematical discourses and emphasizes that discursive frames govern the construction of discursive images.

Fig. 1

Schematic depiction of an intuitive mathematical discourse (Fig. 4.1 from Hanke, 2022, p. 57)

IMDs may be enacted in various situations, not only in specifically designed interviews as in this study. For example, students may ask their teachers for discursive images because they may feel unable to grasp one on their own (see again the quote from Gluchoff (1991)), or colleagues may ask each other how they intuitively explain a notion in class. These discourses may also arise as researchers’ personal discourses when they hypothesize or convince themselves why something is true without rigorous proofs (cf. Burton, 2004; Sfard, 1994).

Now, having defined intuitive mathematical discourses, including discursive images and discursive frames, the research question for this study is as follows:

What are experts’ discursive images about complex path integrals in their intuitive mathematical discourses and what discursive frames govern their construction?

4 Method

4.1 Data collection

Semi-structured expert interviews (Pfadenhauer, 2009) with three mathematicians (Uwe, Dirk, and Sebastian, all pseudonyms) from German universities were conducted. Each expert specializes in a mathematical field related to analysis, complex analysis, or measure theory, and has taught real and complex analysis before. Their teaching experience ranged between 10 and 20 years. They were informed that my research was aimed at their personal interpretations of notions from complex analysis, but not that I would also ask specifically about integration. At the beginning of the interviews, the experts were encouraged to speak freely and to articulate their intuitive understanding in any way they deemed appropriate. The interview situation was characterized by mutual trust and at no time did the experts hesitate to share their individual thoughts (e.g., Dirk and Sebastian even expressed uncertainties as to whether their interpretations were accurate but shared them nevertheless).

The interviews covered the role of visualization and experts’ other interpretations in the sense above in mathematics in general and in complex analysis in particular. The main mathematical notions discussed were holomorphic functions, CPIs, and integral theorems. Related to CPIs, (1) I recalled the area interpretation for Riemann integrals and asked whether something similar is possible for the number $\int_\gamma f(z) \,\mathrm{d}z$; that is, I asked for a geometric meaning as an initial prompt on CPIs. However, I must emphasize that the experts were encouraged to mention whatever they considered relevant instead of a geometric meaning. Further, I asked (2) how the experts would intuitively substantiate Cauchy’s integral theorem, (3) Cauchy’s integral formula, and (4) why holomorphic functions on simply connected domains have anti-derivatives, while merely continuous functions do not, in contrast to the case of real functions on intervals in $\mathbb{R}$ where continuity is sufficient. The full interview guideline (in German with English translations) can be found in Hanke (2022, app. D).

The interviews lasted around 90 to 120 min and were videotaped and transcribed. The experts received printouts for questions (1) and (3) as well as blank sheets of paper to write on. Hand-written records were collected.

4.2 Analysis of intuitive mathematical discourses

The analysis of the transcripts was done sequentially, respecting commognitive methodology according to Sfard (2013). For instance, this means that keywords and narratives were taken literally (“verbal fidelity”), and all conclusions were supported by data segments and their plausibility was evaluated with other data segments (“empirical accountability”).

More precisely, discursive images about CPIs were identified as those narratives the experts produced in response to the task situations in the interviews, in which they were asked to describe CPIs in a way they considered intuitive for themselves or potentially for others, and in which they described their interpretations according to their own judgment (see “Section 3.3”). Indeed, all experts explicitly used keywords such as “mental image” (German: Vorstellung”) etc. in relation to CPIs. These narratives ranged from paraphrases of mathematical theorems to highly individual narratives, which would not be endorsable in scholarly discourses. Some of the discursive images found in this study were joint constructions by the expert and the interviewer-researcher, which is also highlighted in the results section.

Occasionally, the experts explicitly mentioned metarules that governed the construction of their discursive images when they talked about themselves or described what they were doing. Often, however, I had to hypothesize potential metarules and look for other data segments (e.g., dealing with the same interview question) in which experts’ discursive actions could be described with these metarules, too. Hence, metarules, which often remain tacit and contingent (Sfard, 2008, pp. 203–208), were derived here abductively as “analytical statement[s] with which the observed performance is consistent” (Kontorovich, 2021, p. 5). For example, when an expert used elements from vector analysis, I examined how exactly he established a connection to CPIs. For instance, Uwe realized the integrand $f \cdot \gamma'$ (short for $f\left(\gamma(t)\right) \gamma'(t)$) in Eq. (1) in terms of the scalar product $\Big\langle \begin{pmatrix} f \\ if \end{pmatrix}, \gamma' \Big\rangle$, which operates on $\mathbb{C}^2 \times \mathbb{C}^2$. To do so, he used the representation of a complex number as a vector in $\mathbb{R}^{2}$ or as a real matrix of the form $\begin{pmatrix} a & -b \\ b & a \end{pmatrix}$ at some but not all places: In the term $\Big\langle \begin{pmatrix} f \\ if \end{pmatrix}, \gamma' \Big\rangle$, he used the complex function ${\gamma}'$ as an element of $\mathbb{R}^{2}$ (and thus of $\mathbb{C}^{2}$) and $\begin{pmatrix} f \\ if \end{pmatrix}$ as a vector in $\mathbb{C}^{2}$, in which the complex function $f$ is not realized further as an element of $\mathbb{R}^{2}$. Uwe’s discursive action here may thus be described with the metarule that allows him to switch freely between the representation of complex numbers as elements of $\mathbb{C}$ or $\mathbb{R}^{2}$ or as matrices in order to establish a connection between elements from vector and complex analysis. For instance, this metarule belongs to the “vector analysis”-frame (see “Section 5.3”).

By grouping together thematically coherent metarules, discursive frames were formed. They can be seen as ideal-type descriptions of the experts’ discursive actions in the interviews. This way, discursive frames “provide insights that go beyond the specific cases at hand” (“generalizability”; Sfard, 2013, p. 161). In line with this commognitive criterion, I present the discursive frames in this generalized way in the results section.

The results were further validated in discussion sessions with another expert in complex analysis and with an expert in commognitive research.⁶

5 Results

The main results are eight discursive frames (F1)–(F8) governing the production of nine discursive images (D1)–(D9) in experts’ intuitive mathematical discourses about complex path integrals as found in the three expert interviews. The discursive frames are called

• (F1) “restriction of generality”-,

• (F2) “theorematic”-,

• (F3) “vector analysis”-,

• (F4) “tool”-,

• (F5) “no meaning”-,

• (F6) “area”-,

• (F7) “mean value”-, and

• (F8) “holomorphicity ex machina”-frame

and will be discussed in detail in the subsequent sections.

An overview of the discursive frames and a complete list of the discursive images is presented in Fig. 2: The discursive frames are shown in grey and the discursive images in color. The discursive images from the interview with Uwe are shown in orange, those from the interview with Dirk in blue, and those from the interview with Sebastian in green.⁷ Note that sometimes related discursive images were grouped under the same number (e.g., (D4.1), (D4.2), and (D4.3) for (D4)).

Fig. 2

Overview of the eight discursive frames and nine discursive images found in the expert interviews (Fig. 12.1 from Hanke, 2022, p. 232, slightly adapted) (Discursive images are cited verbatim from the interviews (translated from German) or slightly condensed from original sequences of utterances)

I begin with three general remarks about the results. (1) None of the discursive images found in this study occurred across experts. (2) The overlap of the grey boxes in Fig. 2 shows that a combination of the frames (F1) and (F2) was used to construct (D1) and (D6) and a combination of (F1) and (F8) for (D9). (3) The asterisks in the figure show that the frames (F1), (F2), and (F3) appeared in multiple interviews and the others in only one. This indicates that the first three frames are more universal and the others more personal. In this regard, Table 1 shows the distribution of discursive frames in each expert interview.

Table 1 Appearance of discursive frames in each expert’s IMD about CPIs (Table 12.1 from Hanke, 2022, p. 231)

Unfortunately, the limited space does not allow me to illustrate the analyses in full depth. Therefore, I summarize constitutive elements of each frame and illustrate (F3), (F6), (F7), and (F8) with longer excerpts from the transcripts.⁸

5.1 (F1) The “restriction of generality”-frame

Discursants following this discursive frame use one general metarule, namely restricting the generality of mathematical objects, to produce a discursive image about CPIs. This means that a discursive image was formed, in which $f$ was restricted to holomorphic functions or functions with anti-derivatives or $\gamma$ to closed paths instead of continuous functions and general paths. As such, followers of this frame added additional constraints the interviewer did not make when asking for interpretations of $\int_\gamma f(z) \,\mathrm{d}z$.

Overlapping with (F2) and (F8) and using the aforementioned metarule, the experts produced three (groups of) discursive images about CPIs ((D1), (D6), and (D9)). For instance, Dirk searched for a long time for a geometric interpretation of $\int_\gamma f(z) \,\mathrm{d}z$ for arbitrary $f$ and $\gamma$, but could not produce an explicit narrative relating the integral to a geometric quantity (see (F6)). He then stated the narrative (D6) “$\int_\gamma f(z) \,\mathrm{d}z = F(\gamma(b))-F(\gamma(a))$”, hence implicitly restricting $f$ to functions with anti-derivatives and recalling the formula from the fundamental theorem of calculus for complex functions, which signals the use of (F2).

5.2 (F2) The “theorematic”-frame

This discursive frame governs the use of a theorem to construct a discursive image about the CPI. Corresponding metarules center around recalling a theorem and substantiating it with a personal narrative. Since theorems usually add constraints on the mathematical objects, (F2) was combined with (F1) to produce the discursive images (D1) and (D6) (see above). Note that (D1) and (D6) are considered discursive images here because they were produced in response to the task situation to interpret CPIs.

Considering the product of $f(z)$ and $\mathrm{d}z$ (see (F3)), Uwe explained that “one best doesn’t imagine anything at all” for this product. Then, before the interviewer could even finish another question, he continued to derive (D1):

Uwe: So, I mean, I am of course, of course, only interested in this for holomorphic functions, because this is, this is simply a tool in complex analysis [Int.: Mmh.], path integrals. […] And, uhm, therefore this is only interesting for holomorphic functions and, well, there one knows the residue theorem and it tells one exactly which mental image one should have of it, namely: If the path is only passing around isolated singularities of f, I simply have to look at f in the singularities and calculate the residues there, then I also know what this, what this integral means, what comes out of the integral. In the end, this is what the path integral means. The sum of residues, the weighted one.

Here, Uwe restricted the generality to holomorphic functions (potentially with a set of isolated singularities; the closed-ness of $\gamma$ is also implicitly contained in the application of the residue theorem), valued this as the only situation he was “interested in”, and uttered a personal version of the residue theorem. In particular, he evaluated this “mental image”, which I condensed into (D1), as one that “one should have” and as the “meaning” of the CPI.

5.3 (F3) The “vector analysis”-frame

This discursive frame consists of metarules that center around establishing analogies between objects and narratives from complex and vector analysis. These include recalling propositions from a mathematical discourse regarded as related and specifying what the analogy is about, for example by saming (i.e., seeing different objects as similar) and baptizing (i.e., calling them by a name) (Sfard, 2008, pp. 169–170) objects seen as the same.

After Uwe rejected a geometric meaning for CPIs (see (F5)) and before uttering his version of the residue theorem (see (F2)), he established a close connection between integrals from vector and complex analysis:

Uwe: There are path integrals of first, second, and third kind, I like to say. [Int.: Mmh.] Of first kind is a scalar, uhm, path integral, which, whoa, no idea, is especially important for calculating arc length […]. Then, there is the path integral of second kind, which is incredibly important in physics for some kind of work along some kind of paths, where one has a scalar product, and then there is the complex path integral, and for this, one does not have any imagination at all at first. [Int.: Mmh.] There is complex multiplication, so to speak. […] and there one best doesn’t imagine anything at all [giggles].

Uwe made explicit that he sees different integrals as the same (namely as instances of the notion of “path integral”) and baptized the CPI as of the “third kind”. The discursive image (D2) could therefore be derived from this excerpt.

Another striking example for this frame is also found in the interview with Uwe: Using the metarule to identify complex numbers with vectors in ${\mathbb{R}}^{2}$ or certain matrices as explained in “Section 4.2”, he changed the product $f \cdot \gamma'$ (see Eq. (1)) into a scalar product, which appears in the definition of real path integrals of the second kind: He represented $f$ as a matrix and $\gamma'$ as a vector and produced the equation

$$\begin{pmatrix} f_1 & -f_2 \\ f_2 & f_1 \end{pmatrix} \begin{pmatrix} \gamma_1' \\ \gamma_2' \end{pmatrix} = \Big\langle \begin{pmatrix} f \\ if \end{pmatrix}, \gamma' \Big\rangle$$

($f_1 = \mathrm{Re}(f)$, $f_2 =\mathrm{Im}(f)$). Integrating both sides, one obtains the discursive image (D3) “$\int_\gamma f(z) \,\mathrm{d}z = \int_a^b \begin{pmatrix} f \\ if \end{pmatrix} \mathrm{d}\mathbf{T}$”, which is thus a joint construction from Uwe and the researcher (Hanke, 2020, 2022, pp. 257–260; note that the right-hand side in (D3) is another way to write the right-hand side in Eq. (3)).

5.4 (F4) The “tool”-frame

Narratives constructed according to this frame value complex path integrals as tools in complex analysis. This frame appeared in the interview with Uwe only. It contains metarules, according to which the discursant may use CPIs for purposes such as proving theorems or computing real integrals, thus sees CPIs as tools (see (D4.1–3)). In fact, this evaluation as a tool points to mathematical routines for proving theorems such as the power series expansion for holomorphic functions or computing Riemann integrals with the help of complex analysis (cf. Lang, 1999). One very brief example shall suffice to illustrate this frame (see (D4.2)):

Uwe: […] It just turns out that this is a powerful tool in complex analysis with which you can prove many things […].

Dirk, on the other hand, questioned “how satisfying” it is to value CPIs as tools and thus did not support this point of view.

5.5 (F5) The “no meaning”-frame

One overarching metarule governs this discursive frame, namely rejecting a meaning of $\int_\gamma f(z) \,\mathrm{d}z$. It appeared in the interview with Uwe only. According to this frame, the discursant rejects any meaning and may additionally indicate in which sense there was none (e.g., no geometric meaning as for Riemann integrals or no physical meaning as for real path integrals of the second kind).

Having recalled the area interpretation for integrals, the interviewer asked Uwe “Uhm, now, what meaning […] does this complex number [$\int_\gamma f(z) \,\mathrm{d}z$] have, which you get through such an integration process in the complex setting? […].” Uwe responded “None” multiply and that the complex path integral had no “geometric meaning at all” (D5.1) or no “special meaning in themselves” (D5.2). In this way, Uwe temporarily ended the discussion about a meaning of $\int_\gamma f(z) \,\mathrm{d}z$ until the interviewer reiterated the question “Nothing at all?” and Uwe went on to discuss path integrals of several kinds as illustrated above (see (F3)). Note that although he initially rejected any meaning of CPIs, Uwe actually produced the most discursive images about them (see Fig. 2).

While Sebastian and Dirk also rejected a potential transfer of the area and work/flux interpretations for real integrals, they never questioned that $\int_\gamma f(z) \,\mathrm{d}z$ had any meaning at all.

5.6 (F6) The “area”-frame

This discursive frame, which appeared in the interview with Dirk, consists of metarules related to finding a geometric quantity to realize a mathematical object. It thus includes metarules for producing visual mediators realizing areas or other geometric objects (e.g., vector fields). For example, in real analysis, metarules such as drawing the graph of a function and shading the area enclosed by the graph and the $x$-axis are widely applied in the context of integration.

While Uwe and Sebastian stated that there was no interpretation of $\int_\gamma f(z) \,\mathrm{d}z$ related to areas, Dirk attempted to find an interpretation based on areas or other geometric quantities:

Dirk: […] but in principle one would like to, uhm, resort to such a picture, right [points to Fig. 3a.]. [incompr., likely: And now] it’s not an interval in R, but a path. Let’s say this here is C, right [begins to draw Fig. 3b.], and, uhm, this is not necessarily helpful, such a picture, since the values are complex. [continues talking and drawing Fig. 3b.] […] This is the trace of the path, right [adds the letter $\gamma$ to Fig. 3b.], and that, that the function has certain values and that one somehow computes this area [points to the shaded area in Fig. 3b.]. Uhm, this may be a crutch, but, uh, well, one has to consider [adds the ${\mathbb{C}}$ to the axis pointing upwards in Fig. 3b.] that the values here are complex, right. So, one cannot draw it like that. […]

Fig. 3

Visual mediators realizing areas for Riemann and real path integrals of the first kind (from Fig. 14.3 and 14.4 in Hanke, 2022, pp. 278–279)

Dirk tried to adapt metarules for representing real integrals as areas and to produce a visual mediator that represented $\int_\gamma f(z) \,\mathrm{d}z$ (see also Hanke, 2020, 2022). He noted that the visual mediators in Fig. 3 were insufficient especially since the axis pointing upwards should actually represent $\mathbb{C}$. He insisted

Dirk: […] Nevertheless it has to be possible, uh, to develop a picture for that.

but in the end, he did not succeed in finding a discursive image or visual mediator for the CPI meeting his judgment for an appropriate picture.

5.7 (F7) The “mean value”-frame

This discursive frame appeared in the interview with Sebastian only. It contains metarules for connecting mean values and integrals. Characteristic is the use of “mean value” as an overarching concept to interpret integrals in general and CPIs in particular.⁹

After being reminded of the area interpretation for real path integrals of the first kind by the interviewer, Sebastian argued as follows:

Seb.: I find this bad […] [laughs].

Int.: Yes, but this interpretation is standard, […] so canonical that one does not even need to mention it, I’d say.

Seb.: Yes, yes, exactly. But I find that one/ I would always tell my [students]: Actually, one should think about mean values, in particular when one has Lebesgue integration in mind. [Int.: Mmh.] [emphatic: And measures.] [Int.: Yes.] It is about measuring. And, uhm, this geometric intuition can destroy this higher-dimensional situation. […] And therefore, I find it much better if one imagines: Integration is mean value formation. [Int.: Mmh.] And by coincidence it turns out to be the area in the one-dimensional setting.

Int.: And which/ Mean value of what?

Seb.: Yes, of what’s, uh, in the integrand, so to speak. […] Yes, uh, for me this is simply the mean value of the complex numbers, which I grab along this path [traces a circular curve with his finger on the table]. […] And, uhm, in my view, this has nothing to do with area […] This is actually the rotation [traces again a circular curve] that one measures on the plane.

Here, Sebastian argued that he conceives integration as a process of measuring and forming a mean value. This supports the corresponding metarule of saming different integral concepts and applying the general interpretation of integrals as mean values or as an act of measuring. The corresponding discursive images Sebastian endorsed are that integration is mean value formation and measuring in general (D7.1–2). It is remarkable that Sebastian mentioned the above interpretations here in response to the quest for an interpretation for the CPI. This underlines that the interpretations of integrals as mean values and measuring are important for him. He also adapted them to conclude that the CPI is a mean value of the complex numbers from the integrand along the path (D8.1). However, it must also be emphasized that the CPI does not actually measure the average of the function along the path (see Eq. (4), Gluchoff (1991), and Hanke (2024)).

Afterwards, Sebastian explained that complex numbers can be interpreted as an “amplitwist” (i.e., a dilation-rotation; Needham, 1997) and continued to specify the previous general interpretation for integrals as averages to CPIs. Furthermore, he produced the visual mediator in Fig. 4, which shows a closed path $\gamma$ and $f$ as a mapping from the trace of $\gamma$ into another plane:

Int.: […] Naively asked: Where is this complex number [points to $\int_\gamma f(z) \,\mathrm{d}z$], so can one see it in the sketch or is it just/

Seb.: Well […] Okay, for me the imagination is just so that I think of a small neighborhood at each point [points to (ii) in Fig. 4] and from that I see how the effect of f is in some abstract [plane] lying somewhere else [points to (iii) in Fig. 4] […]. So, the number f of z, yes, the number f of z has/ uh, really is a linear amplitwist for me [turns his hands]. And this effect is averaged along this path, and this is what the integral means to me.

[…]

Int.: Mmh. So, when I try to para/ paraphrase what this mean value means, is it for you like that at each point of the path the mapping somehow turns and stretches and when I do this along the whole path and compute the integral, the number that it computes to is the average rate of turning and the average rate of stretching at the same time? [gestures for the turning and stretching]

Seb.: [nods] Somehow in this direction exactly. So, this is at least my/ this is at least the image I have in mind. […] I don’t claim that this is completely consistent, but this is my mental image.

Fig. 4

Singularity in the interior of a path and $f$ as an amplitwist (modified Fig. 15.5 from Hanke, 2022, p. 311)

Here, Sebastian expressed clearly that the meaning of the CPI for him is the average of the effect that $f$ induces as an amplitwist on the points on the path, which is confirmed by a paraphrase of the interviewer (see (D8.2–3)). Note that Sebastian explicitly described these interpretations as an “image [he has] in mind” and his “mental image”. Henceforth, this interview passage and others, in which Sebastian used these interpretations to substantiate Cauchy’s integral theorem, justify that Sebastian endorsed the discursive images (D7.1–2) and (D8.1–3) (see Hanke, 2022, 2024, for more about the mean value interpretation).

5.8 (F8) The “holomorphicity ex machina”-frame

This frame’s name is inspired by the “deus ex machina”, an event or power that solves a seemingly unsolvable problem. It was reconstructed from the interview with Sebastian. I recalled in “A reminder from the mathematical literature” in what sense holomorphic functions can be conceived as “rigid”. In this context, Sebastian argued that “there are no local or global properties” of holomorphic functions and that they imply each other. As an applicant of this frame, Sebastian used the interpretation of holomorphicity as a property of complex functions that is strong enough to force integral theorems to be true. Hence, the main underlying metarule in this frame is holomorphicity is forcing integral theorems on us.¹⁰

The following excerpt stems from the discussion of Cauchy’s integral formula:

Seb.: [...] there are no local or global properties, it’s all always the same, I can gather enough information, uh, on this path here, about this point, so to speak [refers to (ii) and the path in Fig. 4]. And, uhm, I am doing this while I am, uh, including a pole there [refers to the denominator in Eq. (5)]. Well, uhm, this is probably no good, uh, not a particularly fine intuitive explanation, but this is the imagination for me at least, […] with the help of these properties, that, uh, local properties are global properties, I, at least, uh, can expect that something like this [Cauchy’s integral formula] is possible. […]

Then, the interviewer paraphrased whether Sebastian argued that it was “not unbelievable that such a formula holds” and he agreed:

Seb.: Exactly, that is where I start, so to speak. Uh, I would also say, uh, to students first of all, uh: Well, could you imagine that something like this could be true? And, uhm, answer: Yes, because, uh, holomorphic functions have the property that one can also measure global properties with the help of path integrals.

In this excerpt, Sebastian used the rigidity property of holomorphic functions to substantiate that he could “expect that something like this [Cauchy’s integral formula] is possible” and “that one can also measure global properties with the help of path integrals” (see (D9.2)). In particular, he called this application of the rigidity of holomorphic functions an “intuitive explanation” and “imagination” (even if not a “good” or “fine” one). Moreover, he used this rule to argue for Cauchy’s integral theorem as well:

Seb.: [...] And therefore, also on closed paths [points to Fig. 4] it is not surprising that one somehow gets zero, for example, if, if it [the integrand] is holomorphic. […] of course, it may be that I have a singularity here or something like that [adds the blob shape at (i)], or that there is a pole, or whatever. And then it is of course hard to imagine that from the points, which are out here [points to (ii)], you can see this here [points to (i)]. Well, and/ But this comes again from the mysterious connection (idiosyncratic German: mysterische Zusammenhang) that a complex-analytic function is locally determined completely. This means it is possible to know from a local inspection [points again to (ii)] what is happening here inside [points to (i)].

Following this discursive frame, Sebastian thus did not only argue that Cauchy’s integral theorem was “not surprising” but also that “local properties” of a function on the trace of $\gamma$ determine a singularity enclosed by the path. In the context of integration, this justifies the discursive image “the CPI can detect whether a holomorphic function has a singularity in the interior of a closed path” (D9.1), even though the integration is carried out along the path, not inside, as a joint construction by Sebastian and the researcher. Henceforth, the discursive images (D9.1–2) were endorsed in this interview.

6 Conclusion and discussion

In this study, a discursive perspective based on the newly developed notion of intuitive mathematical discourse (IMD) was developed to account for experts’ interpretations of complex path integrals (CPIs). Interpretations of mathematical concepts were conceptualized as discursive images (i.e., narratives in IMDs) and sets of rules governing their construction as discursive frames. This lens proved to be useful because CPIs are difficult to visualize, so other means must be used to interpret them, and the literature only partially presents interpretations as simple as those for real integrals.

The research question was answered with eight discursive frames in experts’ IMDs about CPIs, which enabled the production of nine discursive images. These discursive frames thus function as governing principles for the construction of expert interpretations for CPIs. The results thus contribute to research on expert mathematical thinking at university level, particularly in complex analysis, and add fine-grained insights into the dictum “thinking real, doing complex”. It was shown that experts in complex analysis do not only interpret CPIs with elements from real and vector analysis though. Several other ways were revealed in this study, too: These include utilitarian aspects (in the “tool”- and “no meaning”-frame), are based on general mathematical metarules (in the “restriction of generality”- and “theorematic”-frame), could have partly been anticipated from previous research and interpretations for real integrals (in the “vector analysis”- and “area”-frame), while others are more personal and subtle and ground in a thorough familiarity with advanced mathematical ideas (in the “mean value”- and “holomorphicity ex machina”-frame). In addition, experts may deviate from scholarly metarules to construct discursive images. However, no expert in this study discussed the idea of accumulation (cf. Soto & Oehrtman, 2022). Regarding the area interpretations for integrals in real analysis, it was observed that two experts in this study, Uwe and Sebastian, found this interpretation unsatisfactory for CPIs, while Dirk tried to transfer it to them, however not successfully. Regarding the mean value interpretation, Sebastian was the only one who adapted it to construct discursive images abouts CPIs (cf. Hanke, 2024).

This study is limited by the small sample size. Nevertheless, together with the findings by Oehrtman et al. (2019) and the review of mathematical literature (cf. Hanke, 2022), it can be concluded that individual sense-making of integrals in complex analysis is not as consistent and widespread as teaching materials and educational research on their real cousins might suggest: Experts follow rather personal ways, which in turn may not be endorsable from a scholarly perspective, while the interpersonal use of some discursive frames also suggests commonalities. Another limitation is that the data were collected in a laboratory setting, and it would be relevant to know whether expert IMDs about CPIs in other contexts (e.g., in teaching or discussions with colleagues) share the discursive frames found here.

Further research may address how experts evaluate the documented interpretations of CPIs on a larger scale, and whether and how some of them may be transformed into instructional materials to support novices (cf. Winsløw et al., 2021). However, as experts’ IMDs about CPIs are based on their in-depth knowledge of real, vector, and complex analysis, their implementation in teaching may be challenging. One research gap in this regard is how experts incorporate their interpretations of CPIs into their teaching (cf. Pinto, 2019). In addition, more research is needed to address the student perspective (cf. Hancock, 2018; Soto & Oehrtman, 2022) and to examine whether there are overarching characteristics of experts’ or students’ intuitive mathematical discourses about other mathematical concepts.