Abstract
We articulate a student perspective on task design in mathematics education, foregrounding a dynamic relationship between intentions of task designers, teachers, and students. First, we characterize a student perspective on task design. Second, we provide theoretical perspectives that we use as tools to account for different facets of task design from a student perspective. Third, we elaborate on “tensions of intentions” between designers, teachers, and students when considering the use of tasks to promote students’ mathematical learning. Fourth, we address mathematical tasks and the student: characterizing task context from a student perspective, contrasting reflective and emergent task design, and discussing theoretical and methodological approaches that take into account the student perspective. We conclude with implications for research and practice.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Mathematical task design continues to be an important area of research in mathematics education (Margolinas et al., 2013; Clarke, et al., 2014; Watson & Ohtani, 2015; Jones and Pepin, 2016). The mathematical tasks with which students engage can shape students’ mathematical learning opportunities and their experiences with mathematics as a whole (Watson & Mason, 2007). Yet, students’ opportunities to learn mathematics can vary depending on the kinds of tasks with which they engage (Henningsen & Stein, 1997; Shimizu, Kaur, Huang, & Clarke 2010). In this Special Issue, we aim to extend thinking around mathematical task design by focusing on a complex, layered relationship between task designers, teachers, and students.
Researchers have had increasing interest in investigating a student perspective on task design, resulting in a student theme at the International Commission on Mathematical Instruction (ICMI) study on mathematical task design (Ainley & Margolinas, 2015) and a Research Forum on mathematical tasks and the student, at a meeting of the International group for the Psychology of Mathematics Education (PME) (Clarke et al., 2014). In the PME Research Forum, Clarke et al. (2014, p. 119) brought together a collection of research studies to “equip researchers to better situate the student within research on instructional task design”. Looking ahead, Ainley and Margolinas (2015) called for research using “alternative methods to understand student perspectives more fully, particularly in the context of innovative task design” (p. 137). Together, the collection of papers in this Special Issue represents a response to this call. Many contributors to this Special Issue attended the student theme group at the ICMI study on mathematical task design. In this Special Issue, contributors have further developed research presented at the ICMI study, extending in their thinking and practice, enriched by the work of each other. Some contributors have an explicitly methodological aim and, for others, the focus is more on innovative task design, analyzed or approached with a student perspective.
We articulate a student perspective on task design in mathematics education, foregrounding a dynamic relationship between intentions of task designers, teachers, and students. We organize this survey paper into four main sections. First, we characterize a student perspective on task design. Second, we provide theoretical perspectives that we use as tools to account for different facets of task design from a student perspective. Third, we elaborate on “tensions of intentions” between designers, teachers, and students when considering the use of tasks to promote students’ mathematical learning. Fourth, we address mathematical tasks and the student: characterizing task context from a student perspective, contrasting reflective and emergent task design, and discussing theoretical and methodological approaches that take into account the student perspective. We conclude with implications for research and practice.
2 A student perspective on task design
By mathematical task, we mean more than a written mathematical problem (e.g., Clarke & Mesiti, 2013; Sierpinska, 2004). From our perspective, a mathematical task includes a designer’s intended purpose for the task, a teacher’s intentions in implementing a task, students’ activity in undertaking a task, and artifacts (problem statement, tools and constructed objects, including student written materials) employed in and generated by the actions of teachers and students during the process of task completion:
Differences between social, cultural and curricular settings, together with differences between participating classroom communities, shape the performative realization of a mathematical task. This challenges reductionist attempts to characterize instructional tasks independent of these considerations. (Clarke & Mesiti, 2013, p. 175).
In this view, mathematical tasks are a form of social practice, undertaken by teacher and students as a collective. We use designers to refer to those designing the tasks, including researchers, teachers, and curriculum developers. We use teachers to refer to those enacting the tasks, including researchers, university instructors, and elementary and secondary school teachers. We use students broadly, to include elementary students, secondary students, and adult learners. By including adult learners, we allow for the possibility of teachers and laypersons as students. Similar to a lesson plan, a task may include a designer’s anticipation of a variety of quite specific student responses. Yet, a task, like a lesson plan, may be very different in execution from the forms of anticipated practice that constituted a designer’s or teacher’s intentions. Teacher and student intentions, actions, and interpretations all contribute to the form ultimately taken by the task as a collective social performance.
When addressing a student perspective in task design, researchers have used images of “gap filling” (Ainley & Margolinas, 2015) or paradox (Brousseau, 1984). From this view, there is either a gap to be filled between designers’ and teachers’ intentions for tasks and students’ perspectives of tasks, or a paradox, that the more explicit a teacher becomes about the desired student behaviors from engaging in a task, the less likely these behaviors will emanate from the kinds of awareness the teacher intends. In this survey paper, we argue for a different approach, to more equitably position students’ perspectives with designers’ and teachers’ intentions. We follow the recommendation of Clarke et al. (2014, p. 119): “research into the design and use of mathematical tasks in instructional settings must accommodate student intentions, actions and interpretations to at least the same extent as those of the teacher”. We use the phrase “a student perspective on mathematical task design” to mean task design that acknowledges and makes room for a tension of intention between a designer’s intentions in developing a mathematical task, a teacher’s intentions in implementing mathematical tasks, and students’ perspectives when experiencing those mathematical tasks. We include both designers’ intentions and teachers’ intentions, because we recognize that task designers may be different from teachers implementing tasks with students.
We do not want to be taken to be assuming that intentions are easy, or even possible, to know. As humans, we are not aware of the motivations for our own actions, let alone the actions of others. However, we do assume that tasks are designed with some anticipation of what might occur through the doing of the task, or a range of possible scenarios, and it is this anticipatory thinking that we mean by a task designer’s ‘intention’. Similarly, we are not making an assumption that we can know how a student experiences a task, but we can observe their responses and we can consider the extent to which these responses match or otherwise the anticipatory work done in planning.
Implicit in the concerns being addressed here is a duality of tension. First, it is reasonable to assume that the instructional use a teacher makes of a task will not necessarily align precisely with a task designer’s intentions. In fact, one can argue that teachers have a professional obligation to adjust “pre-fabricated” tasks to better match the local curriculum and the needs and capabilities of their students. Second, it is also reasonable to assume that whatever the instructional intentions of the teacher, the various responses of individual students to the stimulus provided by the task will not be perfectly aligned with the teacher’s intentions or with each other. This variation in the manner in which the individuals in a class engage with (and interpret) a task will reflect the natural variation in educational background and mathematical capability of the various students, but it will also reflect the extent to which the task prescribes the form of student response, or affords some agency on the part of the student, in shaping that response.
The classroom enactment of a mathematical task can be thought of as a nexus of such tensions between intentions of designers, teachers and students. Each is positioned differently in relation to the task as performed in any setting and any attempt to understand (and optimize) the instructional use of mathematical tasks must consider how the prioritization of the intentions of the three categories of “task stakeholder” might adequately accord with the educational goals of the situation. These goals might include the use of a task to introduce new mathematical content, to consolidate a taught procedure, to provide an opportunity for students to apply a procedure in a new situation, to assess student understanding of a concept or procedure, or even to create conditions for student deployment or development of more generic problem solving or collaborative skills. Our reflection on a productive use of a task must be seen in the context of the purpose for which that task is being used.
3 Theoretical perspective
In the mathematics classroom, the teacher, the students, and the tasks provide key structural elements through which the classroom’s social activity is constituted. Task development, selection, and sequencing by teachers represents the initiation of an instructional process that includes task performance (collaboratively by teacher and student) and the interpretation of the consequences of this enactment (again, by teacher and student). For some time, learning theorists have viewed cognitive activity as not simply occurring in a social context, but as being constituted in and by social interaction (e.g., Hutchins, 1995). From such a perspective, the activity that arises as a consequence of a student’s completion of a task is itself a constituent element of the learning process and the artifacts (both conceptual and physical) employed in the completion of the task serve simultaneous purposes as scaffolds for cognition, repositories of distributed cognition, cognitive products, as well as having metacognitive and affective dimensions. During the process of task completion, the effectiveness of the task in promoting learning will also be contingent on student intention (with respect to the task) and teacher interpretation (with respect to the students’ activity).
Current attempts to model the complexity of the mathematics classroom have generated interest in theories capable of accommodating consideration of artifactsFootnote 1 as well as individuals. Theories such as Activity Theory (Engeström, 1987) and Distributed Cognition (Hutchins, 1995) foreground the mediational role of artifacts in facilitating learning, and locate tasks among those mediating artifacts, which also extend to mathematics textbooks, digital technologies [and] language (Rezat & Strässer, 2012).
Rezat and Strässer (2012) identify students’ mathematics-related activity as an example of the Vygotskian conception of an instrumental act, where a student’s interaction with mathematics is mediated by artifacts such as mathematical tasks. Most importantly, recognizing the function of mathematical tasks as tools for the facilitation of student learning leads us to the further recognition that (à la Vygotsky) the use of a tool (i.e., a task) fundamentally affects the nature of the facilitated activity (i.e., student learning). Rezat and Strässer (2012) have re-conceptualized the familiar didactical triangle (teacher–student–mathematics) as a socio-didactical tetrahedron, where the vertices are teacher, student, mathematics and mediating artifacts (Fig. 1). This reconception of didactical relationships recognizes that connections represented by the sides of the original didactical triangle require mediation. The vehicles of this mediation are artifacts, which include everything from textbooks and digital tools to tasks and language. Use of the socio-didactical tetrahedron provides us with an important tool by which to give recognition to the mediational role of tasks in the teaching and learning of mathematics.
The socio-didactical tetrahedron (Rezat & Strässer, 2012)
One virtue of the socio-didactical tetrahedron is that it facilitates the separate consideration of triangles forming each face of the tetrahedron, as well as the vertices of each of those triangles. To describe each face, we paraphrase Rezat and Strässer (2012, p. 645): the triangle teacher-task-student represents the teacher’s role as an orchestrator of students’ task-mediated mathematical activity; the triangle student-task-mathematics represents a student’s task-mediated activity of learning mathematics; the triangle teacher-task-mathematics represents a teacher’s task-mediated activity of doing and teaching mathematics; the original didactical triangle (student–teacher–mathematics) constitutes the base of the model. The tetrahedral structure offers an important representation of the complex relationships involved in the social practice of enacting a mathematical task.
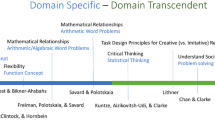
When considering any one face, one can do so from a perspective of a vertex not included on that face. For example, we can consider the teacher-task-student face from the perspective of the mathematics vertex. One way to distinguish between contributions in this Special Issue is by the kind of mathematics students have opportunities to investigate. The contributors promote students’ development of forms of sophisticated mathematical reasoning, which are more than procedural expertise. Some contributors fostered students’ domain-specific reasoning (Best & Bikner-Ahsbahs, 2017; Frieman, Polotskaia, & Savard, 2017; Johnson, McClintock, & Hornbein, 2017; Savard & Poloskaia, 2017; Strømskag, 2017), while other contributors fostered students’ domain-transcendent reasoning (Chan & Clarke, 2017; Graven & Coles, 2017; Kuntze, Aizikovitsh-Udi, & Clarke, 2017; Lithner, 2017; Lozano, 2017). By domain specific reasoning, we mean reasoning related to mathematical content (e.g., number, algebra, geometry). By domain transcendent reasoning, we mean reasoning that transcends conventional mathematical content (e.g., generic actions, like the framing and refuting of a hypothesis). The use of perspective, from a vertex to nonadjacent triangular face, provides a way to purposefully attend to the interconnectedness of all four vertices (student, teacher, mathematics, and tasks.)
4 Tensions of intentions: designers, teachers, and students
The socio-didactical tetrahedron in Fig. 1 helps us to better articulate and elaborate possible tensions when considering the use of tasks for learning mathematics. We take each edge of the tetrahedron to indicate a relationship. It is in the relationship between these relationships that tensions can arise, for example:
-
the teacher/designer’s intentions for a task (teacher-task) may not map well onto students’ experiences of mathematics when engaging in that task (student–mathematics).
-
the mathematics, potentially embedded, in a task (mathematics-task) may not map well onto mathematics that students actually use (student–mathematics).
-
the teacher’s perceptions and awareness of mathematics (teacher–mathematics) may not align with those of the students’ (student–mathematics) in the doing of a task, leading to difficulties in communication.
-
the teacher’s relationship with a student (teacher–student) may constrain the possible relationships a student can have with the mathematics being offered (student–mathematics), for example, in the extent to which the subject is experienced as a negotiation of “right/wrong”.
The teacher, the student, and tasks are key structural elements constituting the social activity of a mathematics classroom and the socio-didactical tetrahedron makes clear the role of mathematics as the key mediating referent for the elements on the student–teacher-task face.
Task designers may hold a tacit assumption that completing mathematical tasks chosen or designed by the teacher will result in students learning the intended mathematics. Yet, there is no direct relationship between task completion and mathematics learning (e.g., Margolinas, 2004). The metaphors of “gaps” or “paradox” (Ainley & Margolinas, 2015; Brousseau, 1984) mentioned in Sect. 2, above, can only operate on the assumption that the doing of particular actions (by students, in completing a task) should lead to specific elements of learning. If we give up this illusion and embrace the inevitable uniqueness of each student’s experience of a task, then different kinds of question arise. Rather than thinking about how to “minimize” gaps, a focus can shift to different ways of designing tasks in the first place.
By taking into account students’ voice and agency, researchers have offered task design constructs and principles that suggest ways in which task design and implementation may focus on students’ task experiences (e.g., Ainley, Pratt, & Hansen, 2006; Bikner-Ahsbahs & Janßen, 2013; Clarke & Mesiti, 2013; Coles & Brown, 2013). Ainley, Pratt, and Hansen (2006) introduced the constructs of task purpose and utility, defining a task’s purpose and utility from the perspective of the student rather than the task designer. Clarke and Mesiti (2013) showed how teachers could enact tasks that build on students’ real-time responses. Coles and Brown (2013) offered design principles through which teachers could begin tasks by providing students opportunities to make distinctions and then work with those distinctions to develop mathematical thinking and fluency. Bikner-Ahsbahs and Janßen (2013) used an open-ended task to spark mathematical discussion. Defining a task’s purpose from a student perspective serves as one way for designers to position students’ intentions for a task to at least the same extent as teachers’ intentions. When teachers implement tasks in ways that acknowledge the viability of students’ interpretations of a task, it opens up opportunities for students to have rich mathematical experiences.
In a special issue of the Journal of Mathematics Teacher Education, Jones and Pepin (2016) raised an initial question in relation to the role of task design in the process of teaching and learning. Drawing on Brown’s (2009) conceptualization of “pedagogical design capacity” to describe a teacher’s “capacity to utilize existing curricular resources effectively to design instruction” (p. 106), Jones and Pepin argued that it is fundamental that teachers and designers be partners in task design. Because Jones and Pepin focused on the teacher’s role in task design, we would not expect the student to be present in their framing of issues. We do wonder, however, what implications arise from viewing teachers’ roles in task design in terms of capacities. In particular, a notion of capacity suggests there are some teachers who have it and some who are in deficit, reminding us of the conceptualization alluded to by the use of gaps between task intentions and student activities. The use of capacity perhaps serves to background the partnering relationships within which these posited capacities play out, and it is just these relationships that we see as helpfully highlighted by the socio-didactical tetrahedron.
Jones and Pepin (2016) identified four areas to which researchers should attend when engaging in task design: objects to design; tools to use (and conditions under which to use those tools); care in the use of digital tools; and involvement of teachers in task design. We argue for a fifth area: student experience of the task. In a task milieu, students bring their own perspectives, and they have viable ways of constructing meaning for tasks, even if those ways are different from the teacher’s intent in the didactical contract (Brousseau, 1997). Depending on the purpose, tasks need to be sufficiently open to provide a pretext for the articulation of student understandings and sufficiently directive to elicit the kinds of responses required for a specific instructional purpose. Insofar as the didactical contract is a negotiated co-construction of obligations and responsibilities between the teacher and the students, every task both invokes and contests the terms of this contract. Differences in the students’ and teacher’s milieu mean that tasks can be ambiguous from the perspective of the student, even if a teacher thinks that she has clearly defined the task.
5 Mathematical tasks and the student
Researchers have shown that the setting (e.g., a school setting versus an everyday setting) can impact students’ performance on tasks that from an expert’s perspective entail the same mathematical ideas (e.g., Nunes, Schliemann, and Carraher, 1993; Saxe, 1988). Individuals do not come to school settings free from their out of school lived experience (Martin, 2007). In classrooms, students learn (often tacitly) what doing school mathematics is like, and it is impossible to disentangle the implementation of a task from students’ conceived ways of working on tasks (Coles & Brown, 2013). The entanglement of teachers’/designers’ intentions and students’ perspectives highlights how complex a task becomes when researchers take into account the students’ interpretation of a task (Ainley & Margolinas, 2015).
Ainley and Margolinas (2015) proposed two ways in which designers can use a student perspective to inform task design: reflective and emergent task design. Reflective task design occurs separately from a setting in which a teacher enacts a task with students. In reflective task design, designers develop tasks to take into account student perspectives. In contrast, emergent task design occurs during the implementation of a task. In emergent task design, teachers develop in-the-moment tasks to account for student perspectives. We make purposeful use of the phrases take into account and account for. By take into account, we mean task design that anticipates diverse student perspectives, typically occurring separately from task enactment. By account for, we mean task design that responds to diverse student perspectives, typically occurring in the moment. Reflective task design takes into account student perspectives, and emergent task design accounts for student perspectives. In the next four subsections, we build on the notions of reflective and emergent task design, providing a characterization of task context that takes into account the student perspective, and we discuss theoretical and methodological approaches that take into account the student perspective.
5.1 Students’ understanding of the meaning and purpose of the mathematical activity they undertake: task context
Designers may incorporate “real world” contexts when designing mathematical tasks. Some tasks that involve seemingly real situations are word problems. Yet, implementing tasks including such contexts may not provide all students the same kinds of opportunities to learn mathematics (e.g., Ainley & Margolinas, 2015; Boaler, 1993b; Clarke & Helme, 1998; Gerofsky, 1999). Gerofsky (1996, 1999) illustrated how mathematical word problems function as literary genre, such that “word problems imitate and recall other word problems, not our lived lives” (1999, p. 37). Furthermore, students can have different interpretations of work entailed by tasks involving seemingly real situations, and those interpretations may account for differences in students’ performance on tasks (Boaler, 1993a; Clarke & Helme, 1998). To address students’ differences in opportunities to learn mathematics and in their interpretation of work entailed by a task, it is useful to characterize task context such that context takes into account the student perspective.
It is insufficient to define task context as a situation given in a problem statement (e.g., Boaler 1993b; Clarke & Helme, 1998). Boaler (1993b) argued that students’ interaction with the context of a mathematical task is an individual, dynamic process that can take myriad forms. Problematizing ways in which students might “construe” task contexts, Clarke and Helme (1998) distinguished students’ interpretations of task contexts from situations described in a statement of a task. Students’ interaction with tasks is a dynamic process, task context should extend beyond just a situation described by a task, and also take into account individuals’ interaction with mathematical tasks.
Researchers have characterized task context in ways that take into account interpretations of those individuals working on tasks (e.g., Clarke & Helme, 1998; Johnson, 2014; van Oers, 1998). Van Oers (1998) asserted “what counts as context depends on how a situation is interpreted in terms of activity to be carried out” (p. 481). Johnson (2014) argued that task context included students’ conceptions: “context involves an individual’s conception of a problem that could be solved” (p. 340). Arguing that classroom tasks provide an avenue through which teachers and students co-construct social situations for learning, Clarke and Helme (1998) defined context as “an individual construction in response to these socially-enacted situations” (p. 133). To take a student perspective on task content means that it is impossible to separate a task context from meanings that students make from the task.
Meanings students make from tasks go beyond familiarity with a context (e.g., a sporting event). Meanings entail students’ experiences in and out of school, their existing conceptions of the purpose of mathematics tasks in classroom settings, students’ conceptions of what problem a task is intending for them to solve, their affective response to the task, any metacognitive skills they might choose to employ and the influence of the meaning making of other students. From this perspective, students dynamically construct contexts as they engage in goal-oriented activity when solving a task. By goal, we mean goals from the perspective of individual students (see Simon, Tzur, Heinz, & Kinzel, 2004). To restate our central premise: students working on the same task may have different goals, and those goals may not be the same as the goals of their teacher or of the task designer.
5.2 Using a student perspective to inform task design: reflective task design
In reflective task design, designers can incorporate task questions that invite a variety of student perspectives. Drawing on an enactivist perspective, Coles and Brown (2013) designed a task with a starting question: “what is the same and what is different?” to invite a range of perspectives about two static images of rectangles. In a similar vein, Johnson (2013) used the question “what is changing and what is staying the same?” to invite a range of interpretations about a dynamic animation of a growing rectangle. By posing such questions, teachers can explore the mathematical perspectives that students bring to a task situation and build on those perspectives to provide opportunities for students to learn.
Task designers can use reflective task design to develop principles to guide task design to take into account the student perspective. To address a tension between students’ intentions to use algorithms and teachers’ intentions to provide students with open-ended problem solving opportunities, Savard et al. (2013) developed a design principle to promote “holistic reasoning about mathematical structures” (Ainley & Margolinas, 2015, p. 129). The design principle of Savard et al. (2013) suggests how designers can take into account an anticipated student intention: a rush to use algorithms, rather than to engage in problem solving.
Teachers can use reflective task design to adapt existing tasks for their own purposes. Clarke and Mesiti (2013) described how a teacher used a seemingly closed task, solve a system of linear equations, to provide students opportunities to draw out key features of a pair of simultaneous equations. Despite the promises of reflective task design, teachers may still experience challenges when enacting tasks. Strømskag (2013) demonstrated how a teacher’s intention for students to glean general properties from a single example was not transparent to students. Furthermore, when responding to a perceived tension, teachers may enact mathematical tasks in less productive ways. Lithner et al. (2013) found that teachers might respond to students’ potential frustrations, by letting “the teaching act collapse”, (Ainley & Margolinas, 2015, p. 127) and taking responsibility from the students by removing ambiguity from the task. When enacting tasks, teachers navigate students’ intentions, and this navigation may be tacit or explicit on the part of teachers.
Designers have used a student perspective on reflective task design to promote students’ domain-specific mathematical reasoning. To promote elementary students’ additive and multiplicative reasoning, Savard and Poloskaia (2017) developed Mathematically Incoherent Situations (MIS) tasks. Best and Bikner-Ahsbahs (2017) designed tasks intended to foster secondary students’ flexible rather than fragmented interpretation of function. Strømskag (2017) designed a task to promote university students’ reasoning about a theorem in elementary number theory. Through task design principles, underlying the development of tasks, researchers can make explicit how they take into account the student perspective. Savard and Polotskaia (2017) included a specific design principle based on their anticipations that students might look for particular numbers given in a task, not general features.
Other designers have used a student perspective on reflective task design to promote students’ domain transcendent mathematical reasoning. Synthesizing across research programs, Lithner (2017) provided design principles for tasks promoting algorithmic reasoning (AR) and creative mathematical reasoning (CMR). The challenges associated with the CMR task design principles involved the designers taking into account students’ responses to CMR tasks, which are more open ended than AR tasks. Using a modelling approach to investigate statistical thinking, Kuntze et al. (2017) found that hybrid tasks were effective in fostering adult learners’ critical and statistical thinking. Furthermore, Kuntze et al. (2017) demonstrated how reflective task design can encompass both domain specific and domain transcendent mathematical reasoning.
Designers engaging in reflective task design may leverage digital learning environments to promote students’ domain-specific mathematical reasoning. Frieman et al. (2017) examined how primary elementary students working with a digital learning environment might develop symbolic algebraic reasoning. Johnson et al. (2017) used a Ferris wheel dynamic computer environment to provide secondary students opportunities to engage in covariational reasoning. In developing each of the digital learning environments, researchers engaged in reflective task design to take into account students’ reasoning.
5.3 Using a student perspective to inform task design: emergent task design
In emergent task design, teachers make in-the-moment design decisions, accounting for students’ responses to tasks. From a student perspective on task context, any task can have potential ambiguity. By ambiguity, we do not mean a lack of clarity. Rather, we mean a possibility for directions beyond what may have been a task designers’ original intent. Emergent tasks (Best & Bikner-Ahsbahs, 2017; Bikner-Ahsbahs & Janßen, 2013), which promote students’ diverse learning processes and ways of working, are one way in which teachers may embrace potential ambiguity in any task. Bikner-Ahsbahs & Janßen (2013) used emergent tasks to refer to situations such that “the teacher conceives the mathematical potential of a learning opportunity and translates it into a task” (p. 154). Best and Bikner-Ahsbahs (2017) describe the central role of the student in emergent tasks: “emergent tasks adapt the content to the students; they take up ideas a student produces or the regularities the student has found and transform them into tasks” (p. 7).
Emergent task design has proven useful for promoting students’ algebraic and functional reasoning. After presenting an analysis of a student’s thinking, Best and Bikner-Ahsbahs (2017) provided multiple examples of emergent tasks that a teacher might enact in response to the student. Johnson et al. (2017) described how Johnson, serving as an interviewer in a one-on-one clinical interview setting, responded to a students’ conception of a task situation with an emergent task. Best and Bikner-Ahsbahs (2017) and Johnson et al. (2017) illustrate the crucial role of a teacher in enacting emergent tasks. Student responses cannot always be predicted and opportunities for learning require teachers to respond contingently.
Enacting emergent tasks is a challenging endeavor for teachers, because enactment requires teachers “to understand a mathematical problem students have encountered within the interest-dense situation and to translate it into a task for the class” (Ainley & Margolinas, 2015, p. 133). Engaging in reflective task design focused on the student perspective may promote teacher’s enactment of emergent tasks during instruction. Chan and Clarke (2017) investigated secondary students’ interactions when working on tasks designed to promote students’ collaborative problem solving. Theorizing learning as participation in practice, Chan and Clarke (2017) found that teachers’ attention to students’ mathematical, sociomathematical, and social negotiations serve as a useful entry point for instructional interventions. Furthermore, analyzing instruction involving the use of emergent tasks can prove valuable for teachers. Using a task involving area and perimeter, Coles and Brown (2013) explored how through use of principles of task design, teachers began to develop the ability to implement emergent tasks. When implementing emergent tasks, teachers make in-the-moment decisions to adapt tasks, or even develop new tasks, to account for students’ perspectives.
5.4 Using a student perspective to inform theoretical and methodological approaches for task design
When using a student perspective to inform theoretical and methodological approaches for task design, designers position the perspective of a student alongside the perspective of designers. In task design, researchers may develop epistemic student(s), which Steffe (2010), building from Piaget’s theory, describes as researchers’ models of possible conceptions that students may have when beginning work on a task. Simon’s (1995) theoretical construct of a hypothetical learning trajectory (HLT), places the teacher’s perspective of a student’s perspective at its center. In articulating the HLT, Simon (1995) described the back and forth process between a teacher’s task design decisions and a teacher’s perspective of student’s thinking: “a reflexive relationship between the teacher’s design of activities and consideration of the thinking that students might engage in as they participate in those activities” (p. 133). When using HLTs to guide reflective task design, designers acknowledge the inevitability of emergent task design. Simon (1995) alluded to emergent task design when describing a teacher’s enactment of a lesson guided by a HLT: “the learning environment evolves as a result of interaction among the teacher and students as they engage in the mathematical content” (p. 133). Researchers may develop epistemic students from different theoretical frames. Drawing on the Theory of Didactical Situations, Strømskag (2017) posited a methodology for instructional design, placing the generic and epistemic student at the center. When developing an epistemological model, Strømskag (2017) includes epistemic students’ “opportunities to learn the targeted mathematical knowledge” (this issue). By developing epistemic students, designers can incorporate at student perspective to inform theoretical approaches for task design.
Using enactivist theory, Graven and Coles (2017) examined how teachers’ specifications for tasks afforded and constrained students’ learning opportunities. Graven and Coles investigated teachers’ interpretations of both a designer’s task design and then their early elementary students’ responses to the same mathematical tasks, embedded in number stories. Graven and Coles suggest that the major strands of task design (e.g., design research DBRC, 2003; the Theory of Didactical Engineering, Artigue and Perrin-Glorian 1991; Realistic Mathematics Education; Van den Heuvel-Panhuizen, 2003) have all developed iterative processes that share an aim of reducing gaps between task designer intention, teacher implementation and student learning. However, for Graven and Coles, differences of intention were not conceptualized as problematic “gaps” but rather as sources for learning. They provide evidence that it is precisely those contexts where there was space for multiple interpretations, divergent intentions and a negotiation of meaning, which were productive, in terms of learning. What is required, however, is an attitude of resisting the desire for the unambiguous and an acceptance of working with uncertainty (e.g., see Coles & Scott, 2015).
Lozano (2017) introduced a methodological approach addressing mathematical tasks, mathematics classroom cultures, and mathematics learning. Lozano put forward a methodological tool comprising seven dyads, against which student behavior, and through that, the wider classroom culture and context, can be analyzed. These dyads are: active/passive; attentive/inattentive; working individually/working with others; freedom/constraint; explaining/having correct answers; knowing how and knowing why/remembering. Through the use of this analytical tool, Lozano demonstrated how it is possible to approach the relationships between tasks, classroom cultures and students’ learning of mathematics. Like reflective task design that takes into account the student perspective, Lozano’s innovative methodology represents reflective research design that places the student experience at the center of concerns. The focus on relationships within this methodology fits well both with the enactivist stance within which this research is placed (e.g., see Bateson, 1972) and also more recent, materialist, methodological thinking (e.g., see de Freitas & Sinclair, 2014).
Researchers can experience logistical challenges when collecting data for studies investigating students’ interactions with mathematical tasks in larger group settings, such as whole classrooms. For example, a single microphone or video camera is insufficient to record numerous student–student interactions in a classroom. Technological advances can assist in the documentation of student–student and student–teacher interactions, while students attempt different types of mathematical tasks. The laboratory classroom described by Chan and Clarke (2017) offers the possibility of simultaneous recording of every action (including all spoken utterances) undertaken by twelve pairs of students all attempting the same task, at the same time, under the same conditions. Access to data sets such as those reported by Chan and Clarke (2017) can open up opportunities for researchers to network different theoretical lenses to investigate students’ experiences with mathematical tasks.
6 Conclusion
In the negotiation of perspectives (across designer, teachers and students) there is the possibility of expanding particular viewpoints and a coming to know of alternative ways of seeing. To illustrate, we appeal to the notion of agile practice, from business literature: a capacity to adapt our planned activity to the demands of circumstance and situation (Madeyski, 2009). The agility of action can be promoted among teachers, who must respond to the anticipated unpredictable phenomena of student response, and students, for whom contemporary curricula prioritize a flexibility of thought, able to accommodate novel problem situations. The development of agile practice is one perspective on the well-established problem solving agenda, dating from the 80s, and motivated by publications such as Toffler (1970). The consequent goal of a student equipped with maximally adaptive problem solving skills posed (and continues to pose) significant challenges for task designers and for teachers.
Analogous to agile practice, the idea of horizontal expertise as a curricular goal (Engeström, 1987) poses challenges for the design and use of mathematical tasks. When designers and teachers set horizontal expertise as a goal, they problematize a conception of classroom goals from not only their perspectives, but also the perspectives of students. We contrast a goal of horizontal expertise with a goal of vertical expertise, in which designers and teachers may seek to move students through predictable acquisition of hierarchically sequenced skills and concepts. A focus on horizontal expertise opens up possibilities for different kinds of goals that can transcend conventional mathematical content, including goals focusing on student agency and interaction.
In a seemingly paradoxical manner, our focus on the student perspective has returned our attention to the critical role of the teacher in the mathematics classroom. When viewing the project of task design as minimizing a gap between design intention and actual learning, there is the possibility of minimizing the influence and importance of the teacher—as though tasks might work directly on students’ cognitive capacities. Through foregrounding the perspective of the student, we have found the studies above point to the vital and subtle work of the teacher, able to anticipate, accommodate, hear, respond to, and build upon student ideas. Rather than viewing the different perspectives that designers, teachers and students bring to the doing of a task as constituting problematic gaps, we suggest rather that these multiple perspectives constitute a space of possibilities (Davis, 2004). When handled with sensitivity, such spaces can enrich all participants, again, drawing attention back to the crucial role of the teacher.
Notes
‘Artifact’ derives from the Latin “arte factum” meaning something made through the use of skill.
References
Ainley, J., & Margolinas, C. (2015). Accounting for student perspectives in task design. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education (pp. 115–142). Switzerland: Springer International Publishing.
Ainley, J., Pratt, D., & Hansen, A. (2006). Connecting engagement and focus in pedagogic task design. British Educational Research Journal, 32(1), 23–38.
Artigue, M., & Perrin-Glorian, M.-J. (1991). Didactic engineering, research and development tool: Some theoretical problems linked to this duality. For the Learning of Mathematics, 11(1), 3–17.
Bateson, G. (1972). Steps to an ecology of mind. Chicago: University of Chicago Press. (2000).
Best, M., & Bikner-Ahsbahs, A. (2017). The function concept at the transition to upper secondary school level: Tasks for a situation of change. ZDM Mathematics Education. doi:10.1007/s11858-017-0880-6.
Bikner-Ahsbahs, A., & Janßen, T. (2013). Emergent tasks—spontaneous design supporting in-depth learning. In A. Watson, M. Ohtani, J. Ainley, J. Bolite Frant, M. Doorman, C. Kieran, A. Leung, C. Margolinas, P. Sullivan, D. Thompson, & Y. Yang (Eds.). Proceedings of ICMI Study 22: Task Design in Mathematics Education, (pp. 153–162). Oxford: International Commission on Mathematics Instruction.
Boaler, J. (1993a). Encouraging the transfer of ‘school’ mathematics to the ‘real world’ through the integration of process and content, context and culture. Educational Studies in Mathematics, 25(4), 341–373. doi: 10.1007/bf01273906.
Boaler, J. (1993b). The role of contexts in the mathematics classroom: Do they make mathematics more “real”? For the Learning of Mathematics, 13(2), 12–17.
Brousseau, G. (1984). The crucial role of the didactical contract in the analysis and construction of situations in teaching and learning mathematics. Theory of Mathematics Education, 54, 110–119.
Brousseau, G. (1997). Theory of didactical situations in mathematics. In N. Balacheff, M. Cooper, R. Sutherland & V. Warfield. Dordrecht, NL: Kluwer.
Brousseau, G., Sutherland, R., & Warfield, V. (1997). Theory of Didactical situations in mathematics 1970–1990. Translation from French: M. Cooper, N. Balacheff. Dordrecht: Kluwer.
Brown, M. (2009). The teacher–tool relationship: Theorizing the design and use of curriculum materials. In J. T. Remillard, B. Herbel-Eisenman & G. Lloyd (Eds.), Mathematics teachers at work: Connecting curriculum materials and classroom instruction (pp. 17–36). New York: Routledge.
Chan, M. C. E., & Clarke, D. (2017). Structured affordances in the use of open-ended tasks to facilitate collaborative problem solving. ZDM Mathematics Education. doi:10.1007/s11858-017-0876-2. (this issue).
Clarke, D., Strømskag, H., Johnson, H. L., Bikner-Ahsbahs, A., & Gardner, K. (2014). Mathematical tasks and the student. In P. Liljedahl, C. Nicol, S. Oesterle, & D. Allan (Eds.) Proceedings of the 38th Conference of the International Group for Psychology of Mathematics Education and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education. (Vol. 1, pp. 117–143), Vancouver, Canada: PME.
Clarke, D. J., & Helme, S. (1998). Context as construction. In O. Bjorkqvist (Ed.), Mathematics teaching from a constructivist point of view (pp. 129–147). Vasa: Faculty of Education, Abo Akademi University.
Clarke, D. J., & Mesiti, C. (2013). Writing the student into the task: Agency and Voice. In A. Watson, M. Ohtani, J. Ainley, J. Bolite Frant, M. Doorman, C. Kieran, A. Leung, C. Margolinas, P. Sullivan, D. Thompson, & Y. Yang (Eds.). Proceedings of ICMI Study 22: Task Design in Mathematics Education, (pp. 175–184). Oxford: International Commission on Mathematics Instruction.
Coles, A., & Brown, L. (2013). Making distinctions in task design and student activity. In A. Watson, M. Ohtani, J. Ainley, J. Bolite Frant, M. Doorman, C. Kieran, A. Leung, C. Margolinas, P. Sullivan, D. Thompson, & Y. Yang (Eds.). Proceedings of ICMI Study 22: Task Design in Mathematics Education, (pp. 183–192). Oxford: International Commission on Mathematics Instruction.
Coles, A., & Scott, H. (2015). Planning for the unexpected in the mathematics classroom: teacher and student change. Research in Mathematics Education, 17(2), 121–138.
Davis, B. (2004). Inventions of teaching: a genealogy. New York: Lawrence Erlbaum Associates.
DBRC. (2003). Design-based research: an emerging paradigm for educational inquiry. Educational Researcher, 32(1), 5–8.
de Freitas, E., & Sinclair, N. (2014). Mathematics and the body: Material entanglements in the mathematics classroom. New York: Cambridge University Press.
Engeström, Y. (1987). Learning by expanding. An activity-theoretical approach to developmental research. Helsinki: Orienta-Konsul-tit Oy.
Freiman, V., Polotskaia, E., & Savard, A. (2017). Using a computer-based learning task to promote work on mathematical relationships in the context of word problems in early grades. ZDM Mathematics Education. doi:10.1007/s11858-017-0883-3. (this issue)
Gerofsky, S. (1996). A linguistic and narrative view of word problems in mathematics education. For the Learning of Mathematics, 16(2), 36–45.
Gerofsky, S. (1999). Genre analysis as a way of understanding pedagogy in mathematics education. For the Learning of Mathematics, 19(3), 36–46.
Graven, M., & Coles, A. (2017). Resisting the desire for the unambiguous: productive gaps in researcher, teacher and student interpretations of a number story task. ZDM Mathematics Education. doi:10.1007/s11858-017-0863-7. (this issue)
Henningsen, M., & Stein, M. K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 8, 524–549.
Hutchins, E. (1995). Cognition in the wild. Cambridge, MA: MIT Press.
Johnson, H. L. (2013). Designing covariation tasks to support students reasoning about quantities involved in rate of change. In A. Watson, M. Ohtani, J. Ainley, J. Bolite Frant, M. Doorman, C. Kieran, A. Leung, C. Margolinas, P. Sullivan, D. Thompson, & Y. Yang (Ed.). Proceedings of ICMI Study 22: Task Design in Mathematics Education, (pp. 213–220). Oxford: International Commission on Mathematics Instruction.
Johnson, H. L. (2014). A role of context in constructivist model building: What problem is the learner solving? Constructivist Foundations, 9(3), 339–341.
Johnson, H. L., McClintock, E., & Hornbein, P. (2017). Ferris wheels and filling bottles: a case of a student’s transfer of covariational reasoning across tasks with different backgrounds and features. ZDM Mathematics Education. doi:10.1007/s11858-017-0866-4. (this issue)
Jones, K., & Pepin, B. (2016). Research on mathematics teachers as partners in task design. Journal of Mathematics Teacher Education, 19(2), 105–121.
Kuntze, S., Aizikovitsh-Udi, E., & Clarke, D. (2017). Hybrid task design: Connecting learning opportunities related to critical thinking and statistical thinking. ZDM Mathematics Education. doi:10.1007/s11858-017-0874-4. (this issue)
Lithner, J. (2017). Principles for designing mathematical tasks that enhance imitative and creative reasoning. ZDM Mathematics Education. doi:10.1007/s11858-017-0867-3. (this issue)
Lithner, J., Jonsson, B., Granberg, C., Liljekvist, Y., Norqvist, M., & Olsson, J. (2013). Designing tasks that enhance mathematics learning through creative reasoning. In A. Watson, M. Ohtani, J. Ainley, J. Bolite Frant, M. Doorman, C. Kieran, A. Leung, C. Margolinas, P. Sullivan, D. Thompson, & Y. Yang (Ed.). Proceedings of ICMI Study 22: Task Design in Mathematics Education, (pp. 221–230). Oxford: International Commission on Mathematics Instruction.
Lozano, M. D. (2017). Investigating task design, classroom culture, and mathematics learning: An enactivist approach. ZDM Mathematics Education (this issue).
Madeyski, L. (2009). Test-driven development: An empirical evaluation of agile practice. Berlin: Springer.
Margolinas, C. (2004). Points de vue de l’élève et du professeur: Essai de développement de la théorie des situations didactiques. Université de Provence. http://tel.archives-ouvertes.fr/tel-00429580/fr/. Accessed 29 May 2017.
Margolinas, C. (2013). Task design in mathematics education. Proceedings of ICMI Study 22. ICMI Study 22. hal.archives-ouvertes.fr. Retrieved from https://hal.archives-ouvertes.fr/hal-00834054/. Accessed 29 May 2017.
Martin, D. B. (2007). Mathematics learning and participation in the African American context: The co-construction of identity in two intersecting realms of experience. In N. Nasir & P. Cobb (Eds.), Improving access to mathematics (pp. 146–158). New York: Teachers College Press.
Martin, D. B. (2007). Mathematics learning and participation in the african american context: The co-construction of identity in two intersecting realms of experience. In N. Nasir & P. Cobb (Eds.), Improving access to mathematics: Diversity and equity in the classroom (pp. 146–158). New York: Teachers College Press.
Nunes, T., Schliemann, A., & Carraher, D. (1993). Street mathematics and school mathematics. Cambridge: Cambridge University Press.
Rezat, S., & Sträßer, R. (2012). From the didactical triangle to the socio-didactical tetrahedron: artifacts as fundamental constituents of the didactical situation. ZDM—The International Journal on Mathematics Education, 44(5), 641–651.
Savard, A., & Polotskaia, E. (2017). Who’s wrong? Tasks fostering understanding of mathematical relationships in word problems in elementary students. ZDM Mathematics Education. doi:10.1007/s11858-017-0865-5. (this issue).
Savard, A., Polotskaia, E., Frieman, V., & Gervais, C. (2013). Designing covariation tasks to support students reasoning about quantities involved in rate of change. In C. Margolinas (Ed.), Task design in Mathematics Education. Proceedings of ICMI Study 22 (pp. 269–276). Oxford, United Kingdom.
Saxe, B. G. (1988). Candy selling and math learning. Educational Researcher, 17(6), 14–21.
Shimizu, Y., Kaur, B., Huang, R., & Clarke, D. J. (Eds.). (2010). Mathematical tasks in classrooms around the world. Rotterdam: Sense Publishers.
Sierpinska, A. (2004). Research in mathematics education through a keyhole: Task problematization. For the Learning of Mathematics, 24(2), 7–15.
Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26, 114–145.
Simon, M. A., Tzur, R., Heinz, K., & Kinzel, M. (2004). Explicating a mechanism for conceptual learning: Elaborating the construct of reflective abstraction. Journal for Research in Mathematics Education, 35, 305–329.
Steffe, L. P. (2010). Perspectives on collaborative research in mathematics education with interdisciplinary connections. New perspectives and directions for collaborative research in mathematics education: Papers from a planning conference for WISDOMe. WISDOMe Monograph (Vol. 1, pp. 11–28). College of Education, University of Wyoming.
Strømskag, H. (2013). Shortcomings in the milieu for algebraic generalisation arising from task design and vagueness in mathematical discourse. In C. Margolinas (Ed.), Task design in Mathematics Education. Proceedings of ICMI Study 22 (Vol. 1, pp. 231–239). Oxford, United Kingdom.
Strømskag, H. (2017). A methodology for instructional design in mathematics—with the generic and epistemic student at the centre. ZDM Mathematics Education. doi:10.1007/s11858-017-0882-4 (this issue).
Toffler, A. (1970). Future shock. New York: Random House.
Van den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics, 54(1), 9–35.
van Oers, B. (1998). From context to contextualizing. Learning and Instruction, 8(6), 473–488.
Watson, A., & Mason, J. (2007). Taken-as-shared: A review of common assumptions about mathematical tasks in teacher education. Journal of Mathematics Teachers Education, 10(4), 205–215.
Watson, A., & Ohtani, M. (2015). Themes and issues in mathematics education concerning task design. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education: An ICMI study (pp. 3–15). Berlin: Springer.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Johnson, H.L., Coles, A. & Clarke, D. Mathematical tasks and the student: navigating “tensions of intentions” between designers, teachers, and students. ZDM Mathematics Education 49, 813–822 (2017). https://doi.org/10.1007/s11858-017-0894-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-017-0894-0