Abstract
We present an objective, singularity-free, path independent, numerically robust and efficient geometrically non-linear Reissner-Mindlin shell finite element formulation. The formulation is especially suitable for higher order ansatz spaces. The formulation utilizes geometric finite elements presented by Sander [74] and Grohs [34] for the interpolation on non-linear manifolds. The proposed method is objective and free from artificial singularities and spurious path dependence. Due to the fact that the director field lives on the unit sphere, a special linearization procedure is required to obtain the stiffness matrix. Here, we use the simple constructions of Absil et al. [2, 3], which yields an easy way to obtain the correct tangent operator of the potential energy. Additionally, we compare three different interpolation schemes for the shell director that can be found in the literature, where one of them is applied for the first time for the Reissner-Mindlin shell model. Furthermore, we compare the exponential map to the radial return normalization as procedure to update the nodal directors and conclude the superiority of the latter, in terms of fewer load steps. We also investigate the construction of a consistent tangent base update scheme. Path independence, efficiency and objectivity of the formulation are verified via a set of numerical examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This work presents a geometrically exact Reissner-Mindlin shell formulation with consistent interpolation of the director field. It is singularity free, path independent and objective as well as numerically efficient and robust. The origins of geometrically non-linear shell formulations can be traced back to [24]. For a historical review of non-linear shell theory in general we refer to [80] or [94] and for the historical context of Reissner’s developments we refer to [64]. A concise summary of geometrically exact shell formulation using stress resultants we refer to [101].
Classical shell theories can be grouped into Kirchhoff–Love and Reissner–Mindlin type models. The former rely on a kinematic description that is based on the midsurface position only, whereas the latter incorporate independent rotations of the director field, thus taking into account transverse shear deformation. Here, the director field is usually associated with the material fibers in normal direction in the undeformed configuration.
The treatment of this non-linear director field is discussed with respect to two major aspects in this paper: first, correct linearization of potential energy and second, feasible interpolation of the director in order to meet the requirements of being singularity-free, path independent and objective. Special attention is devoted to interpolation schemes with higher continuity, for instance using non-uniform rational B-splines (NURBS) as ansatz functions.
Such an inextensional single director shell model leads to a finite element formulation with five degrees of freedom per node. Three of them are the midsurface positions and the remaining two are increments associated with rotational change of the director, e.g., incremental rotations or director increments. Historically, these non-standard degrees of freedom gave rise to several uncertainties concerning a correct or optimal finite element formulation with respect to accuracy and efficiency. Mainly, two questions are crucial:
-
Which is the correct linearization process required to develop a well-defined and consistent iterative solution scheme?
-
Which interpolation scheme yields accurate results and does not violate fundamental properties, such as objectivity?
2 Historical Remarks
Correct linearization to obtain the stiffness matrix and, in particular, symmetry of the stiffness matrix are often discussed issues. In [82], Simo derived a tangent operator in the context of beams that may be unsymmetric away from equilibrium for a potential taking values from \({\mathcal {S}}{\mathcal {O}}(3)\). This is a result of using the second variation as a tool to construct the tangent operator.
Later, Simo [83] concluded that the Hessian (more precisely, the Riemannian Hessian) can be obtained by symmetrizing the unsymmetric second variation. We stress that this procedure is only useful for manifolds that can be classified as compact Lie Groups, which does not apply for the two-dimensional unit sphere. A short note on the history of unsymmetric tangent operators can be found in ([66], Ch. 1.7). Some of the questions concerning linearization were discussed in [53]. There, the authors concluded that a tangent operator can be unsymmetric, if it is constructed from the second variation. But they also pointed out that this construction does not lead to a well-defined operator.Footnote 1 The authors concluded that, therefore, the Hessian is the correct quantity to use as tangent operator since it is a well-defined tensorial quantity. For this Hessian, several works concluded that it needs to be symmetric for a torsion-free connectionFootnote 2, [2, 53, 56, 67, 70, 83, 91].
Furthermore, symmetry of the Riemannian Hessian does also hold during iteration. Nevertheless, symmetry of the tangent operator is still controversially discussed, see e.g. [92]. Therefore, to avoid uncertainties, we present the variation and linearization in detail and try to avoid vagueness. The resulting process of variation and linearization strongly depends on the results from [2]. We also refer to [20] for the interested reader. Using these results, the problem of optimization on non-linear manifolds can be solved elegantly using only Euclidean quantities and projection onto the manifold to simplify the construction of the gradient and the Hessian.
Historically, director rotations in Reissner-Mindlin type shell formulations were first formulated in terms of angle pairs that live in linear spaces in \({\mathbb {R}}^2\). This linearity naturally leads to a symmetric stiffness matrix. The shortcomings of this description is that it contains singularities, which may lead to convergence problems and limit the magnitude of the rotation, see e.g. [18, 23, 45, 63]. It is worth noting that the hairy ball theorem, see ([21], Sect. 2), excludes a singularity-free parametrization over a single domain in \(\mathbb {R}^2\) of the unit sphere \({{\mathcal {S}}}^2\). Therefore, the singularity requires a switch of parametrization in its vicinity. Additionally, these formulations require an involved evaluation of trigonometric functions for the residual and the stiffness matrix, see [63]. A similar history can be observed for Kirchhoff-Love rods, starting from [5], where Euler angles are used to rotate the cross section frame. Earlier, [7] proposed to include the Taylor expansion of the rotations only up to the quadratic term, which leads to a formulation allowing moderate rotations but non-objective results. An alternative solution of the problem is to avoid parametrization of the unit sphere in the first place.
To overcome the singularities of a parametrization, direct interpolation of the director was used in [43]. Here, the update of the nodal directors was done in terms of director increments that are expressed in the midsurface tangent vectors. This formulation leads to an objective and path independent approach. This approach and some of the aforementioned interpolation approaches are compared in [49]. An alternative approach was proposed by Simo and co-workers for Timoshenko beams [82] and for Reissner-Mindlin shells [84]. There, the authors exploited the manifold structure of \({{\mathcal {S}}}{{\mathcal {O}}}(3)\) and \({{\mathcal {S}}}^2\). The Riemannian manifold \({{\mathcal {S}}}{{\mathcal {O}}}(3)\) is the compact three-dimensional Lie Group called special orthogonal group and the Riemannian manifold \({{\mathcal {S}}}^2\) is the two dimensional unit sphere. These can be defined as \({{\mathcal {S}}}{{\mathcal {O}}}(3) = \{ {\textbf {X}}\in {{\,\textrm{Mat}\,}}_3(\mathbb {R})~|~ {\textbf {X}}^T {\textbf {X}}= {\textbf {I}}~\wedge ~ \det {\textbf {X}}=1 \}\) and \({{\mathcal {S}}}^2 = \{ {{\textbf {x}}}\in {{\,\textrm{Vec}\,}}_3(\mathbb {R})~|~ {{\textbf {x}}}^T {{\textbf {x}}}= 1 \}\). Additionally, \({{\,\textrm{Mat}\,}}_n(\mathbb {R})\) and \({{\,\textrm{Vec}\,}}_n(\mathbb {R})\) define all \(n \times n\) matrices and all n-sized vectors, respectively. The interest in \({{\mathcal {S}}}^2\) stems from the fact that the kinematic description of the Reissner-Mindlin model does not contain a stretch of transverse fibers (thickness change in direction of the director).Footnote 3 The approach from Simo and co-workers for the numerical treatment of the Reissner-Mindlin shell model leads to a singularity free formulation in terms of rotational parameters.
Nevertheless, this formulation is path dependent and non-objective due to the interpolation of rotation increments. Moreover, keeping track of fields of history variables at every quadrature point is necessary. [26] pointed out these shortcomings and presented a cure for the case of a non-linear Timoshenko beam formulation. In this formulation, the nodal quantities living in \({{\mathcal {S}}}{{\mathcal {O}}}(3)\) are interpolated, in contrast to the erroneous interpolation of quantities in the tangent space \(T{{\mathcal {S}}}{{\mathcal {O}}}(3)\). This approach yields an objective and path independent formulation. The proposed formula is well-known in computer graphics and is called SLERP (Spherical Linear intERPolation), see [70]. In ([26], Ch. 5b), this concept is extended to higher order polynomials, but it is still restricted to one-dimensional spaces. Therefore, it is only useful for beams. For a summary of different interpolation schemes for beams and their drawbacks we refer to [68].
For the two-dimensional representation in the context of shells, generalization of SLERP does not lead to a satisfying concept. For example, the formulation proposed in [6] generalizes SLERP and leads to an objective and path independent approach but it suffers from a spurious dependency of the computational results on node numbering, see ([6], Eq. 40). Furthermore, since the nodal director components are arguments inside trigonometric functions, evaluation and linearization are expensive. Additionally, the trigonometric function \(\arccos (x)\) (and its derivatives) exhibit poor numerical behavior near \(x=1\). As a result, a perturbation has to be applied for the special case of plane reference states and in general it is not possible for the nodal directors to be parallel.
Recently proposed isogeometric formulations limit the transverse shear to be geometrically linear, thus circumventing the treatment of large rotations [61, 16], where the latter approach inherits this property directly from the formulation of [14, 15]. In [61, 51] the ansatz space needs to be \(C^1\)-continuous between elements due to the presence of second derivatives in the weak form. This necessity is inherited from the Kirchhoff-Love model, as the shear deformation is hierarchically added to the Kirchhoff-Love formulation. Within patches, this continuity constraint can be trivially fulfilled using splines as shape functions. However, \(C^1\)-continuous patch coupling, as in [47], requires special attention and may compromise the elegance of the approach. Nevertheless, the formulations [61] and [51] are path independent and objective.
An isogeometric approach that includes the director rotation in a non-linear fashion has been proposed by [29]. It is based on the non-linear formulation of [86] and thus suffers from similar shortcomings, such as path dependence and non-objectivity inherited from the history fields at every integration point, see ([29], Table A.2.).
Finally, the formulation of [78] has to be mentioned, which inherits objectivity and path independence from the continuous model at the cost of solving a small non-linear minimization problem at every integration point to obtain the interpolated value. This formulation is constructed for Cosserat shell models with drilling rotations, which necessitates interpolation in \({{\mathcal {S}}}{{\mathcal {O}}}(3)\). The resulting finite elements are called geodesic finite elements.
Table 1 summarizes various shell formulations and their properties concerning objectivity, path independence, history variables and singularities.
In view of the aim to construct a formulation that enjoys all desired properties, the following can be concluded: Due to the difficulties arising from an interpolation of incremental rotations (non-objective, path dependent) and the interpolation of angles (singularities), interpolating the director field appears to be the most attractive option. An important issue in this context is the constraint that the director needs to have unit length, which is not naturally satisfied by standard interpolations. In the following we discuss three different approaches to interpolate the director field.
Nodal Finite Elements (NFE)
If the directors have unit length at the nodes only, as it is done in [15, 16, 43, 63], the constraint is violated in the domain. We will refer to this approach by the name Nodal Finite Elements.
In the following, we discuss two recent approaches to satisfy the unit length condition also in the domain. They are deduced from general constructions found in mathematical literature.
Geodesic Finite Elements (GFE)
The first approach is based on the works of Sander [73, 75] and Grohs [34] to generalize the concept of interpolation from vector spaces to manifolds. If such an interpolation is used, the resulting finite elements are called geodesic finite elements (GFE). These finite elements automatically inherit objectivity and path independence of the continuous formulation. This is due to the fact that the interpolation scheme is constructed from a weighted (geodesic) distance measure on the corresponding manifold. Since distances are invariant to rotations by definition, objectivity follows directly. Furthermore, due to the intrinsic nature, the interpolation always stays on the manifold and therefore this approach preserves unit length of the director in the domain. The major drawback is the implicit definition of the interpolation, which involves a non-linear minimization problemFootnote 4 at each integration point. This interpolation scheme is applied on the Reissner-Mindlin shell for the first time in this work.
Projection-Based Finite Elements (PBFE)
The second approach is projection-based interpolation, based on the works of Sprecher [90] and subsequent papers, e.g. Grohs et al. [36], which present a framework for finite elements that interpolate on manifolds by a closest point projection from an embedding space onto the manifold. The finite elements are constructed as in the nodal approach and then projected onto the corresponding manifold.
Luckily, the closest point projection of a vector in \(\mathbb {R}^3\) onto \({{\mathcal {S}}}^2\) has a closed form, namely the trivial normalization of the vector. This interpolation of projecting the vector back onto \({{\mathcal {S}}}^2\) was also used in [85], but only for the reference director field. A more involved version of this approach can be found in [30]. We refer to the resulting finite elements by the name Projection-Based Finite Elements (PBFE) in this paper.
Projection-based finite elements can be regarded as a special case of geodesic finite elements, where the distance measure for the interpolation is the one of the embedding space. For example, for the interpolation on \({{\mathcal {S}}}^2\) the distance measure is the Euclidean distance from \(\mathbb {R}^3\). Due to the construction of the interpolation as a distance measure, objectivity and path independence are inherited from geodesic finite elements.
Additionally, geodesic finite elements and projection-based finite elements are summarized as the group of geometric finite elements. Both interpolations (geodesic and projection-based) yield a path independent and objective discrete problem. The corresponding proofs can be found in ([36], Ch. 1.3) and ([74], Ch. 2.4, Lemma 2.5–2.6).
3 Scope of this Work
We use the projection-based finite element concept and the linearization results from [2, 3] to construct a sound shell formulation. The underlying shell theory is identical to the one put forward by Simo and Fox [84]. In summary, the presented shell finite element formulation enjoys the following desirable features:
-
It inherits the objectivity of the continuous model.
-
The magnitude of total rotations is not limited.
-
The unit length constraint of the interpolated director is satisfied in the domain.
-
As no history fields at the integration points are introduced, interpolation of the director is path independent.
-
The formulation goes without trigonometric functions. This simplifies linearization and results in a compact and fast implementation.
-
No singularities occur, as parametrization of the unit sphere is avoided.
-
The stiffness matrix is symmetric without neglecting any terms and without applying symmetrization procedures.
-
The resulting element vectors and matrices are invariant to node numbering.
Any of the above features can be found in shell formulations in the literature. However, to the authors’ best knowledge, there is no shell finite element formulation that enjoys all of them.
Beyond presentation of a novel shell finite element formulation, the following aspects are covered in the paper:
-
It is shown that the unit length of the director in the domain is crucial for using higher order interpolation schemes to circumvent a degeneration of the convergence order.
-
We show the superiority of the radial return normalization (projection-based retraction) for the nodal director instead of using the exponential map.
-
The non-linear space \({{\mathcal {S}}}^2\), in which the director is defined, needs special attention. Therefore, the consistent linearization process is presented in detail. A symmetric tangent operator is consistently derived rather than symmetrizing an initially unsymmetric result.
-
We show that the consistent linearization process yields an additional contribution to the stiffness matrix and provide a physical interpretation of this term.
-
We compare three update schemes for the nodal director tangent base, where two can be found in the literature and one is newly introduced.
-
We show the advantageous features of projection-based finite elements for the Reissner-Mindlin model.
The paper is organized as follows: In Sect. 4 we present the Reissner-Mindlin shell model up to the total potential energy in the total Lagrangian setting. After this, we deduce the construction of the correct gradient (residual, internal forces) and the correct Hessian (stiffness matrix) for an arbitrary energy living on \(M=\mathbb {R}^3 \times {{\mathcal {S}}}^2\) in Sect. 5. We apply these results onto the Reissner-Mindlin shell problem where only the Euclidean partial derivatives, i.e., the variation and linearization are needed to construct the correct Riemannian gradient and Riemannian Hessian following the results from [2, 3]. We obtain these Euclidean quantities in Sect. 5.3.
After the introduction of the correct operators, we establish our consistent interpolation in Sect. 6. In particular, we use projection-based finite elements (PBFE) for our shell discretization living in the space \(M=\mathbb {R}^3 \times {{\mathcal {S}}}^2\). Here, the midsurface displacement lives in \(\mathbb {R}^3\) and the unit director lives on \({{\mathcal {S}}}^2\). With this at hand, we explore several numerical examples to compare the presented approach with geodesic finite elements and nodal finite elements and conclude the superior behavior of the projection-based finite elements, especially in the context of higher order ansatz functions. This is done in Sect. 10. Furthermore, we investigate in our numerical examples the usage of the mixed interpolation point (MIP) technique to improve the convergence behavior, as introduced in [52]. Additionally, we compare the geometric meaning of the three interpolations (NFE, PBFE, GFE) in 10.2.
The notation used in the present work is a mixture of the one used in the classical papers of Simo and co-workers and the one of [36] and [2, 74]. Moreover, some quantities are newly introduced, see Table 2.
4 Non-linear Shell Theory Including Transverse Shear Deformation
4.1 Geometry and Kinematics
First, we define the geometric description of a shell structure as
Therefore, \({{\mathcal {M}}}\) represents the set of functions mapping from \({\varOmega }\) onto \(M = \mathbb {R}^3 \times {{\mathcal {S}}}^2\). The set \({\varOmega }\subset \mathbb {R}^2\) is the two-dimensional parameter space with the points
where \({\tilde{\textbf {{\textbf {E}}}}}_{{\alpha }}\) denote Cartesian base vectors. Furthermore, we introduce the map \({\varvec{\varphi }}: {\varOmega }\rightarrow \mathbb {R}^3\), defining the position vector of the midsurface of the shell, and the so-called director \({{\textbf {t}}}: {\varOmega }\rightarrow {{\mathcal {S}}}^2\), a field of unit vectors which are initially normal to the midsurface. The independent representation of \({\varvec{\varphi }}\) and \({{\textbf {t}}}\) allows the kinematic description of transverse shear deformation and thus realizes a Reissner-Mindlin type model. Using these quantities we can define the stress-free shell body as reference configuration
here \(h^-\) and \(h^+\) denote top and bottom surface coordinates of the shell and \(h=(h^+-h^-)\) is the shell thickness. Similarly, a configuration at time t is given by
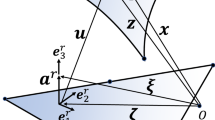
For the total Lagrangian setting the kinematics are summarized in Fig. 1. With this, the reference and current position of a point of the shell body are given as
where we introduced the maps \(\hat{\varvec{{\Phi }}}: {{\mathcal {A}}}\rightarrow {{\mathcal {B}}}_t\) and \(\hat{\varvec{{\Phi }}}_0: {{\mathcal {A}}}\rightarrow {{\mathcal {B}}}_0\). \({{\mathcal {A}}}={\varOmega }\times [h^-,h^+]\) represents the three-dimensional parameter space, which can be also seen in Fig. 1. The deformation is then defined as a mapping \(\chi _t: {{\mathcal {B}}}_0 \rightarrow {{\mathcal {B}}}_t\) with
Kinematics and mappings of the Reissner-Mindlin shell model. We denote \({{\mathcal {B}}}_0 \) and \( {{\mathcal {B}}}_t \) as the Lagrangian and Eulerian manifold. \({{\mathcal {B}}}^C \) denotes the corresponding midsurfaces. Furthermore, we denote the two-dimensional and three-dimensional parameter space by \({\varOmega }, {{\mathcal {A}}}\). Here, \(\hat{\varvec{{\Phi }}},\hat{\varvec{{\Phi }}}_0 \) and \({\varvec{\chi }}\) denote the non-linear point maps between the spaces. The standard Cartesian bases associated with \({{\mathcal {B}}}_0,{{\mathcal {B}}}_t \) and \({\varOmega }\) are \(\{{\textbf {E}}_i \}_{i=1,3}, \{{\textbf {e}}_i \}_{i=1,3} \) and \(\{{\tilde{\textbf {{\textbf {E}}}}}_i \}_{i=1,3}\) respectively. \(\{{\textbf {A}}_1,{\textbf {A}}_2,{{\textbf {t}}}_0 \}\) and \(\{{\textbf {a}}_1,{\textbf {a}}_2,{{\textbf {t}}}\}\) are curvilinear co-variant bases at \({\textbf {X}}\) and \({{\textbf {x}}}\), similar to the definitions from [55]
For the base vectors \({{\textbf {g}}}_i \) and \({\textbf {G}}_i \) of both configurations it follows from Eq. (4.5)
where the base vectors of the reference and current midsurfaces \({\textbf {a}}_{\alpha }={\varvec{\varphi }}_{,{\alpha }}\) and \({\textbf {A}}_{\alpha }={\varvec{\varphi }}_{0,{\alpha }}\) are introduced. These relations are summarized in Fig. 1.
In view of the later introduction of the so-called effective stress resultants in Eq. (4.13), we define kinematic tensors based on the reference midsurface basis \( \{{\textbf {A}}_{\alpha },{{\textbf {t}}}_0\} \). The tensor of effective strains
is composed of the components of the Green-Lagrange strain tensor,
referring to the midsurface metric \({\textbf {A}}^i \otimes {\textbf {A}}^j \). Here, the usual Reissner-Mindlin kinematic assumptions \({{\textbf {t}}}_{,{\alpha }}\cdot {{\textbf {t}}}=0 \) and \({{\textbf {t}}}\cdot {{\textbf {t}}}={{\textbf {t}}}_0\cdot {{\textbf {t}}}_0 = 1 \) apply. The quadratic part \(\rho _{{\alpha }{\beta }}\) of \(E_{{\alpha }{\beta }}\) in \(\xi ^3\) is usually neglected. For the implications of this, see ([22], Chapter 9.1.3, Equation 9.34) or ([22], Chapter 3.7, Annahme A4). The effective membrane strain \({\varvec{\varepsilon }}\), curvature \({\varvec{\kappa }}\) and transverse shear strain \({\varvec{\gamma }}\)Footnote 5, implied by Eq. (4.9), read
4.2 Continuous Potential Energy of the Reissner-Mindlin Model
In the case of the Reissner-Mindlin shell model, the total potential energy functional depends on the function of the midsurface position \({\varvec{\varphi }}\in {{\mathcal {X}}}(\mathbb {R}^3)\) and the function of the director field \({{\textbf {t}}}\in {{\mathcal {X}}}({{\mathcal {S}}}^2)\), as in Eq. (4.5). Therefore, the functional \( {{\hat{{\varPi }}}}\) takes values from the non-linear manifold \({{\mathcal {M}}}\), which results in some non-trivial considerations concerning mainly the interpolation and linearization of these values. The total potential energy \({{\hat{{\varPi }}}}: {{\mathcal {M}}}\rightarrow \mathbb {R}\) reads
where \({{\mathcal {B}}}_0^C\) denotes the shell midsurface and \({{\mathcal {B}}}_0\) is the three-dimensional shell body. Here, \(\hat{\varvec{{\Phi }}} \in {{\mathcal {M}}}={{\mathcal {X}}}(M)\) is an element of the continuous configuration space. Furthermore, \({\bar{\psi }}\) denotes a generic strain energy volume density functional and \({{\hat{\psi }}}\) denotes a generic strain energy midsurface density functional.
We introduce the constitutive relations from the pre-integrated potential \({{\hat{\psi }}}\) resulting from a standard Coleman-Noll procedure as
The corresponding tensor quantities
are called second Piola Kirchhoff effective symmetric stress resultants. They do not represent the physical membrane forces, moments and shear forces, but they are energetically conjugate to the the effective strains defined in Eq. (4.10). For an explanation why the energy can be written in terms of the effective symmetric stress resultants, see [84, 19]. In Appendix 1, we show how to obtain the physical Cauchy stress resultants from these quantities. Again, since this energy expression contains values from \(\hat{\varvec{{\Phi }}}\in {{\mathcal {M}}}\), i.e. from \({{\mathcal {S}}}^2\), we have to take special care of its variation and linearization, which is carried out in Chapter 5. Before this, we make consideration about non-linear infinite-dimensional function spaces.
4.3 Dealing with Non-linear Infinite-Dimensional Function Spaces
Variation and linearization of a functional depending on quantities living in continuous vector spaces is a well understood topic in the context of solving PDEs in such spaces. In the case of quantities living in non-linear spaces, the situation becomes more difficult. For instance, in the continuous (infinite-dimensional) case, the important Sobolev space \(W^{1,2}({\varOmega },M)\) does not always possess the structure of a Banach manifold ([35], Ch. 3.2). Linearization and smoothness in these spaces is non-trivial, because the geometric structure can be unknown.
In Fig. 2, this situation corresponds to going down from the continuous potential \({{{\hat{{\varPi }}}}} \) on the left to the continuous weak form \({{{\hat{G}}}}\). The continuous weak form also needs to be linearized and therefore a connection on \({{\mathcal {M}}}\) has to be introduced to arrive at the linearized continuous weak form. This may or may not result in a consistent formulation if one moves from there to the right by discretization.
In order to manage this delicate situation, we restart from the continuous potential at the top left corner of Fig. 2. From there move to the discrete potential by direct discretization, following the red dash-dotted path to the right. Subsequently, there are several paths to develop an iterative solution scheme for a functional potential. Nevertheless, we introduce the Sobolev spaces where the continuous quantities live in. We first introduce the corresponding spaces as \( W^{k,p}({\varOmega },\mathbb {R}^3) \times W^{l,q}({\varOmega },{{\mathcal {S}}}^2) = {\mathbb {W}}_{k,p}^{l,q}({\varOmega },\mathbb {R}^3 \times {{\mathcal {S}}}^2)\) where \({\varvec{\varphi }}\in W^{k,p}({\varOmega },\mathbb {R}^3) \) and \({{\textbf {t}}}\in W^{l,q}({\varOmega },{{\mathcal {S}}}^2) \).
Numerical evidence suggests that only weak first order derivatives \((k=l=1)\) are needed, but we are not aware of any proofs. Lacking a more rigorous choice, we use the space \({\mathbb {W}}_{k,p}^{l,q}({\varOmega },\mathbb {R}^3 \times {{\mathcal {S}}}^2)={\mathbb {W}}_{k,p}^{l,q}({\varOmega },M)\) with \(M= \mathbb {R}^3 \times {{\mathcal {S}}}^2\) as surrogate. For more details we refer to [59]. Our model coincides with the one in Ch. 7.6. Moreover, Corollary 8.1 of [59] states that for a pure bending case at least one minimizer exists for \({\varvec{\varphi }}\in H^2({\varOmega },\mathbb {R}^3) = W^{2,2}({\varOmega },\mathbb {R}^3)\) and \({{\textbf {t}}}\in H^1({\varOmega },{{\mathcal {S}}}^2) = W^{1,2}({\varOmega },{{\mathcal {S}}}^2)\). Unfortunately, this is not useful for our case, since the minimizer corresponds to a deformation of Kirchhoff-Love type. For a theoretical treatment of these discrete and continuous non-linear function spaces of Sect. 4.3, we refer to [35, 40, 41, 42].
5 Discretization, Variation and Linearization
5.1 Dealing with Non-linear Discrete Configuration Spaces
We start in the top left corner of Fig. 2 at the continuous problem represented by the potential \({{\hat{\varPi }}}(\hat{\varvec{{\Phi }}}) \). Next, we discretize the continuous quantities in the potential to end up with the discrete finite element functions in the space \(V_h^{M}({\varOmega }) \subset {\mathbb {W}}_{k,p}^{l,q}({\varOmega },M)\). At this point we can formulate the first-order optimality condition in terms of the discrete test function space \( T_{\varvec{{\Phi }}^{\textrm {h}}}V_{\textrm {h}}^M({\varOmega }) \) by moving down from the discrete potential to the discrete weak form.
Alternatively, and more easily, we may first move to the algebraic settingFootnote 6 with the following procedure: We extract the nodal quantities from the finite element functions via the operator \({{\mathcal {E}}}\) and end up in the algebraic space \(M^n\), where n denotes the number of nodes. Here, the nodal evaluation operator \({{\mathcal {E}}}\) is defined as in [77] after Theorem 2.3. In the next step (now in the top right corner), using the construction of Absil et al. [3], the discrete variation and linearization can be obtained purely in the Euclidean embedding space and a projection afterwards. In this space, we can simply use partial derivatives instead of covariant derivatives. Moreover, we can treat the cumbersome Riemannian linearization (from weak form and discrete weak form, respectively, downwards via covariant derivatives) as a problem in Euclidean space. Thus, we can simply use the Gâteaux derivative in the Euclidean continuous vector space, which is easy to compute. The result is projected onto the tangent space of the manifold to obtain the correct Riemannian gradient and Riemannian Hessian, respectively, the residual and stiffness matrix of the Reissner-Mindlin formulation. With these algebraic quantities at hand, we can solve the non-linear minimization problem iteratively, ending up at the bottom right of Fig. 2.
The derivations sketched above, are described in more detail in the following, starting in Sect. 5.2 with the generic construction of the algebraic Riemannian gradient and Riemannian Hessian and eventually arriving at the element vectors and matrices in Sect. 7. Sect. 8 introduces the so-called retractions, defined in [2], which project nodal updates from the corresponding tangent space back onto the manifold. They are needed to generalize the standard addition to incrementally update the nodal displacements.
5.2 Computing the Gradient and the Hessian for the Algebraic Setting
5.2.1 The Intrinsic Approach
This section explains why the intrinsic algebraic linearization is cumbersome and why we use the extrinsic constructions of [2, 3], see Sects. 5.2.2 and 5.2.3. Starting point is the algebraic minimization problem of the functional \({\varPi }\)
which corresponds to the top right corner of Fig. 2. In the following we assume a Newton-Raphson-type solution process. For such an approach we need a residual quantity that typically arises from a weak form due to some virtual work principle, or, as in this case, simply as derivatives of \({\varPi }\). Furthermore, the Newton method requires the linearization of the residual at a specific point, which yields the Hessian operator. For the intrinsic approach we have to introduce a parametrization of the space M. For the midsurface vector space \(\mathbb {R}^3 \) this parametrization and the derivatives can be trivially constructed. Therefore, we focus on a single director \({{\textbf {t}}}\) living in \({{\mathcal {S}}}^2\). To point out the crucial aspects, we switch to index notation \({{\textbf {t}}}= t^{i} {\textbf {e}}_i\), where \({\textbf {e}}_i\) is the i-th Euclidean unit vector of \(\mathbb {R}^3 \) and \(i\in \{1,2, 3 \}\). A feasible parametrization of \({{\textbf {t}}}({\varvec{\alpha }})\in {{\mathcal {S}}}^2 \) is
Similar to [63] with \({\alpha }_1 \in [0, 2\pi [\) and \({\alpha }_2 \in [0, \pi ]\). The two-dimensional parameter space \(\mathbb {R}^2\) is then parametrized as \({\varvec{\alpha }}= {\alpha }^{\beta }{\hat{{\textbf {{\textbf {e}}}}}}_{\beta }\) where \({\hat{{\textbf {{\textbf {e}}}}}}_{\beta }\) is the \({\beta }\)-th Euclidean unit vector of \(\mathbb {R}^2\) with \({\beta }\in \{1,2\} \). Therefore, for the director the minimization reads
with the chain rule the first derivative of the potential \( {\varPi }({{\textbf {t}}}({\varvec{\alpha }}))\) is obtained as
where \(\frac{{\partial }t^i}{{\partial }{\alpha }^{\beta }} \) can be identified as the components of the two base vectors \({{\textbf {g}}}_{\beta }({\varvec{\alpha }})\) of the tangent space at \({{\textbf {t}}}\), such that
Due to the inevitable singularity in the parametrization Eq. (5.2) according to the hairy ball theorem, \({{\textbf {g}}}_{\beta }({\varvec{\alpha }})\) are doomed to vanish at some point \({\varvec{\alpha }}\), which leads to divergence of the solution procedure.
The second derivatives are straightforwardly obtained as
which can be recast to
The Christoffel symbol \(\varGamma _{{\beta }{\gamma }}^{\kappa }\) is defined as \(\frac{{\partial }^2{{\textbf {t}}}}{{\partial }{\alpha }^{\beta }{\alpha }^{\gamma }}=\frac{{\partial }{{\textbf {g}}}_{\beta }}{{\partial }{\alpha }^{\gamma }} = \varGamma _{{\beta }{\gamma }}^{\kappa }{{\textbf {g}}}_{\kappa }\). To find the stationary point \({\varvec{\alpha }}^*\), for which \({{\,\textrm{grad}\,}}{\varPi }({{\textbf {t}}}({\varvec{\alpha }})) =0\), a Newton-Raphson scheme can be used, where the first order Taylor expansion of the weak form is set to zero,
Eq. (5.8) is then solved for \(\Updelta {\varvec{\alpha }}_K \) and with this the configuration is simply updated as
To summarize, we repeat the singularities of the gradient and Hessian in Eqs. (5.5) and (5.7). Furthermore, the resulting quantities tend to be expensive to evaluate, due to the involved dependence on trigonometric functions inherited from the parametrization of Eq. (5.2). Both drawbacks can be circumvented using the extrinsic approach from [2, 3], which we will use and discuss in the following. As historical note, we mention [60, 65], who use a similar concept, which was also exploited by [6] to obtain the derivatives of their formulation. In contrast to the forecasted advantages, we point out that the trivial update formula of Eq. (5.9) will become more involved in the extrinsic approach and this will lead to the so-called retractions, described in Sect. 8. Furthermore, we mention that \({{\textbf {g}}}_{\alpha }\) is similar to the later introduced 3\(\times \)2 matrix \(\varvec{{\Lambda }}\).
5.2.2 The Extrinsic Approach: Projection of the Euclidean Gradient
The construction of the gradient and Hessian from [2] can only be applied in an algebraic setting. Therefore, we start from the discretized functional \({\varPi }^h: V_h^{{{\mathcal {M}}}}({\varOmega }) \rightarrow \mathbb {R}\). With the operator \({{\mathcal {E}}}: V_{\textrm {h}}^{{{\mathcal {M}}}} \rightarrow M^n\) it can be cast into a discrete function \({\varPi }: M^n \rightarrow \mathbb {R}\), which depends on n nodal values of the manifold M. The relation of \(V_{\textrm {h}}^{{{\mathcal {M}}}}\) and \(M^n\) for non-linear manifolds is more delicate than the case where \({{\mathcal {M}}}\) is a vector space. Especially the inverse \({{\mathcal {E}}}^{-1}\) is not unique in every case, as stated in ([74], Theorem 3.2). However this non-uniqueness is not an issue for Reissner-Mindlin energies, since the director does not vary by \(180^{\circ }\) from node to node. Nevertheless, with this at hand, we move in Fig. 2 from the top left to the top right corner. In the following we first describe the projection of gradients and Hessians.
We first introduce the standard concept of projecting a gradient, defined in an embedding space, onto a submanifold in such a way that it yields the correct gradient on the submanifold. This idea goes back at least to Rosen [71, 72]. The later projection of the Hessian has not such a long tradition, at least the authors could not find anything older than [65]. Here, M can be an arbitrary manifold and is not restricted to \({\mathbb {R}}^{3}\times {{{\mathcal {S}}}}^{2}\).
Any (co-)vector of a Euclidean embedding space can be decomposed into a tangential part and a normal part of a Riemannian submanifold \(M \subset {\mathbb {R}}^n\), see Fig. 3 and ([2], Chapter 3.6.1). For an arbitrary vector \({\varvec{\eta }}\in T_{{\textbf {x}}}\mathbb {R}^n\cong \mathbb {R}^n\) with its leg at \({{\textbf {x}}}\in \mathbb {R}^n\) this can be written as
here \(P_{{\textbf {x}}}\) denotes the projection onto \(T_{{\textbf {x}}}M\) and \(P_{{\textbf {x}}}^\perp \) is the projection onto \({(T_{{\textbf {x}}}M)}^\perp \).
We consider a function \({\bar{{\varPi }}}: \mathbb {R}^n \rightarrow \mathbb {R}\) defined on \(\mathbb {R}^n\) and a function \({\varPi }: M \rightarrow \mathbb {R}\), which is the same as \({\bar{{\varPi }}}\) with the restriction to take only values from M. The gradient of \({\varPi }\), which is a co-tangent vector, can then be expressed as the gradient of \({\bar{{\varPi }}}\), projected onto the submanifold M,
see also Fig. 3.
5.2.3 The Extrinsic Approach: Construction of the Riemannian Hessian
From the aforementioned projection to construct the Riemannian gradient, we can derive a similar reasoning to obtain the Riemannian Hessian. For two vectors \({\varvec{\eta }},{\varvec{\xi }}\in T_{{\textbf {x}}}M\) we get
here we made use of the relation \(\nabla _{\varvec{\eta }}=P_{{\textbf {x}}}{\textrm {D}}_{\varvec{\eta }}\), which stems from ([2], Ch. 5.3.3, Eq. 5.15). Additionally, \(\nabla _{\varvec{\eta }}\) denotes the covariant derivative, whereas \({\textrm {D}}_\eta \) describes a standard Euclidean directional derivative. Since \(P_{{\textbf {x}}}\) is a projection matrix, we additionally have the idempotency property \(P_{{\textbf {x}}}P_{{\textbf {x}}}=P_{{\textbf {x}}}\).
Thus, the Riemannian Hessian can be expressed by using four quantities, namely (i) the projection \(P_{{\textbf {x}}}\) from the embedding space onto the tangent space of the submanifold, (ii) the directional derivative of \(P_{{\textbf {x}}}\) in \(({\textrm {D}}_{\varvec{\eta }}P_{{\textbf {x}}})\), (iii) the gradient \({{\,\textrm{grad}\,}}{\bar{{\varPi }}}\) and (iv) the Hessian \({{\,\textrm{Hess}\,}}{\bar{{\varPi }}}\) of the Euclidean extension of the functional. This construction is obtained from [3]. With this we can calculate the Riemannian Hessian without any Christoffel symbols and using an extrinsic view without any singularities, since no parametrization, such as angles, are introduced.
In particular, for the case of the unit sphere \({{\textbf {x}}}\in {{\mathcal {S}}}^n\) the projection is
where \({\textbf {I}}\) is the identity matrix. For the partial derivative \({\textrm {D}}_{\varvec{\eta }}P_{{\textbf {x}}}\) we obtain
With this result we compute the product \(P_{{\textbf {x}}}({\textrm {D}}_{\varvec{\eta }}P_{{\textbf {x}}}) \) in Eq. (5.12) as follows
where the identities \({\varvec{\eta }}=P_{{\textbf {x}}}{\varvec{\eta }}\) and \(P_{{\textbf {x}}}{{\textbf {x}}}= {\varvec{0}}\) of the projection have been exploited. Naturally, we have for \(M={{\mathcal {S}}}^2\)
By comparing coefficients, we obtain
as Riemannian Hessian. Using \({\varvec{\eta }}=P_{{\textbf {x}}}{\varvec{\eta }}\), we can rewrite Eq. (5.16) in the form
which underlines the symmetry of the Riemannian Hessian.
5.2.4 Gradient and Hessian Final Form
We go back to the algebraic Reissner-Mindlin potential \({\varPi }(\varvec{{\Phi }})\), which takes values from \(M^n = (\mathbb {R}^3 \times {{\mathcal {S}}}^2)^n\). The aim is to move from the top right corner to the bottom right corner in Fig. 2. We restrict the subsequent derivations to the contributions of two nodes I and J, which can then be assembled to the full gradient and Hessian. Furthermore, if we use uppercase letters as indices no sum convention is applied. We express this explicitly by using the usual notation \(\sum _{I=1}^N\). First, the results from Eqs. (5.17) and (5.18) can be generalized for the midsurface \({\varvec{\varphi }}_I\). The tangent space of \(\mathbb {R}^3\) can be identified with itself \(T_{\varvec{\varphi }}\mathbb {R}^3\cong \mathbb {R}^3\) and we have as projection the identity \(P_{{\varvec{\varphi }}_I}={\textbf {I}}\). With this result at hand we find the projector \(P_{\varvec{{\Phi }}_I}: \mathbb {R}^6 \rightarrow T_{\varvec{{\Phi }}_I} M=T_{{\varvec{\varphi }}_I}\mathbb {R}^3 \times T_{{{\textbf {t}}}_I}{{\mathcal {S}}}^2 \cong \mathbb {R}^3 \times T_{{{\textbf {t}}}_I}{{\mathcal {S}}}^2 \) as
We can now fully define the contribution of node I to the Riemannian gradient \({{\,\textrm{grad}\,}}_I {\varPi }(\varvec{{\Phi }})\), similar to Eq. (5.11), as
To obtain the Hessian we need to specify the quantity \(P_{\varvec{{\Phi }}_I} ({\textrm {D}}_{\Updelta \varvec{{\Phi }}_I} P_{\varvec{{\Phi }}_J} ) \) as
where \(\delta _{IJ}\) is the Kronecker delta, taking care of the fact that \({\textrm {D}}_{\Updelta \varvec{{\Phi }}_I} P_{\varvec{{\Phi }}_J} ={\varvec{0}}\) for \(I\ne J\).
Using the results from Sect. 5.2.3, the contribution of nodes I and J to the Hessian reads
With the definitions from Eqs. (5.19) and (5.21) this can be expanded to
The Hessian inherits the dimensions \(6\times 6\) from the embedding space \(M_{{\textrm {E}}}=\mathbb {R}^3 \times \mathbb {R}^3\). With reference to the five-dimensional configuration space \(M=\mathbb {R}^3 \times {{\mathcal {S}}}^2\), however, it has to be reduced to \(5\times 5\). Moreover, the six-dimensional Hessian has a non-trivial kernel, since \(P_{{{\textbf {t}}}_I}\) projects a normal at \({{\textbf {t}}}_I\) onto the zero vector, \(P_{{{\textbf {t}}}_I} {{\textbf {t}}}_I={\varvec{0}}\). In particular, we have for a vector \({{\textbf {q}}}_I={[0\; 0\; 0\; {\alpha }{{\textbf {t}}}_I^T]}^T, {\alpha }\in \mathbb {R}\) as result
Therefore, Hessian-vector products are only non-zero in the tangent space of \(T_{{{\textbf {t}}}_I} {{\mathcal {S}}}^2\). Using this information, we apply a base change of the Hessian to get a final stiffness matrix with dimensions \(5 \times 5\), see ([78], Eq. 23) or similarly [84].
At this point, we postulate a generic tangent space of the director \({{\textbf {t}}}_I\) which we introduce as
see Fig. 4. Several options to explicitly obtain this nodal tangent space are presented in Section C.3. A generalization of this tangent space base that includes the midsurface can be written as
since the tangent space of \(\mathbb {R}^3\) is \(\mathbb {R}^3\) itself.
In Appendix 3, we present three different tangent base update schemes. The first two are based on parallel transport of the tangent base vectors from the old state to the new one. We will call these IncPT for incremental parallel transport and IncVT for incremental vector transport, see Algs. 4 and 3. The first one (IncPT) is similar to the approaches by, e.g. [29, 86]. The second one (IncVT) is newly introduced in this work. Both methods differ only slightly, but IncVT is computationally faster since it avoids evaulation of trigonometric functions and uses less multiplications. The third one is based on stereographic projection (SP), see Algo. 5. This tangent base construction is proposed in ([74], Eq. 31) for the general unit sphere \({{\mathcal {S}}}^{n-1} \).
In contrast to the first two schemes the stereographic projection does not need information of the old state. Instead the only information needed is the current nodal director to construct the new basis.
Since, by definition, the columns of \(\varvec{{\Lambda }}_I\) are elements of \(T_{{{\textbf {t}}}_I}{{\mathcal {S}}}^2\), we have \(P_{{{\textbf {t}}}_I} \varvec{{\Lambda }}_I=\varvec{{\Lambda }}_I\). Moreover, we always assume \({{\textbf {t}}}^{\alpha }_I\) to be unit vectors and \({{\textbf {t}}}_I^1 \cdot {{\textbf {t}}}_I^2 =0\). This yields \(\varvec{{\Lambda }}_I^T \varvec{{\Lambda }}_I= {\textbf {I}}_{2\times 2}\), which simplifies the formulation. Therefore, by rewriting Eq. (5.23), we can finally define the Riemannian stiffness matrix
With this tangent space representation we can also rewrite the three-dimensional director update \(\Updelta {{\textbf {t}}}_I \in T_{{{\textbf {t}}}_I}{{\mathcal {S}}}^2 \) as
with two degrees of freedom \(T_I^{\alpha }\) for the director update in the tangent plane \(T_{{{\textbf {t}}}_I}{{\mathcal {S}}}^2\). This construction is identical to the notation used by Simo et al. [86]. Additionally, since \({\textbf {K}}^{JI}_{5\times 5}\) is expressed in the tangent space of the nodal director, we also need to express the residual in the base given by Eq. (5.25). The corresponding version of Eq. (5.20) reads
At this point, we want to discuss why it is problematic to directly insert this base \(\varvec{{\Lambda }}_I\) into the energy like \({\varPi }({{\textbf {t}}}_I+ \varvec{{\Lambda }}_I {\textbf {T}}_I)\) and differentiate everything to obtain a formulation with five degrees of freedom. For the geometrically linear case this is a valid procedure, since the tangent space does not change during deformation. For the geometrically non-linear case this does not hold, since \(\varvec{{\Lambda }}_I\) is a function of \({{\textbf {t}}}_I\), which, in turn, changes during deformation. This results in a complicated linearization procedure (e.g. linearizing Algorithm 5). Furthermore, this ends up in the situation where the derivatives are not continuous, since the parametrization of the tangent space, due to the hairy ball theorem, contains singularities. The linearization of an incremental approach, see Algorithms 4 and 3 in the appendix, is complicated and not well-defined, because of the non-additive relation between the degrees of freedom and the tangent space of the director.
Finally, we have expressions for the Riemannian gradient and Riemannian Hessian that can be purely constructed from the Euclidean gradient and the Euclidean Hessian of the function \({\bar{{\varPi }}}\). With these, we can trivially compute by standard Euclidean partial derivatives the missing quantities and finally truly move down in Fig. 2 from the top right to the bottom right. Here, we apply the iterative Riemannian Newton-Raphson scheme to solve our non-linear optimization problem \(\min {\varPi }(\varvec{{\Phi }})\) or finding the root of the residual \({\textbf {R}}\). The resulting iterative scheme is summarized in Algo. 1, which differs from ([2], Alg. 5) by using the tangent space representation, similar to [78, 86].

5.3 Euclidean Variation and Linearization of the Continuous Reissner-Mindlin Energy
The last missing ingredient are the partial derivatives of the algebraic potential energy, see Eqs. (5.26) and (5.28). These can be simply obtained using e.g. automatic differentiation. Nevertheless, we choose another route in the following. Due to the fact that all quantities live in the six-dimensional Euclidean embedding space \(M_{\textrm {E}}=\mathbb {R}^3 \times \mathbb {R}^3\), the usual rules apply. We can therefore take a step back and derive everything in the continuous space \({\mathbb {W}}_{k,p}^{l,q}({\varOmega },M_E)\). Here, the stiffness matrix and the residual Eqs. (5.26) and (5.28) can be computed by using standard Gâteaux directional derivatives. Using this approach we obtain a template for the differential operators, the residual and the stiffness matrix. This template is independent of a particular interpolation scheme. Accordingly, in subsequent derivations we can start from the continuous Euclidean setting in the space \({\mathbb {W}}_{k,p}^{l,q}({\varOmega },M_E)\), which contains \(\hat{\bar{\varvec{{\Phi }}}}\). We start by applying the axiom of minimum of potential energy in this setting and obtain the first variation of \(\hat{{\bar{{\varPi }}}}(\hat{\bar{\varvec{{\Phi }}}})\) as
In the notation used for the energy \(\hat{{\bar{{\varPi }}}}(\hat{\bar{\varvec{{\Phi }}}})\), the hat indicates a continuous quantity and the bar denotes a function which lives in the embedding space. For simplicity and better readability, however, we refrain from introducing expressions like \(\hat{{\bar{{\textbf {a}}}}}_i\) for the base vectors and just stick to \({\textbf {a}}_i\). Instead, we restrict this notation to the total potential energy \(\hat{{\bar{{\varPi }}}}\), its density \(\hat{{\bar{\psi }}}\), the weak form \(\hat{{{\bar{G}}}}\) and the state variables \(\hat{\bar{\varvec{{\Phi }}}}\). The variation \(\updelta \hat{\bar{\varvec{{\Phi }}}}\) lives in \({\mathbb {W}}_{k,p}^{l,q}({\varOmega },\hat{\bar{\varvec{{\Phi }}}}^{-1}TM_{\textrm {E}})\), but we can identify this space with \({{\mathcal {M}}}_{\textrm {E}}={{\mathcal {X}}}(\mathbb {R}^6)\), since \(TM_{\textrm {E}}\) is a linear space. This simplifies the space in which the variation takes place to \({\mathbb {W}}_{k,p}^{l,q}({\varOmega },M_{\textrm {E}})\).
From Eq. (5.29) we can directly introduce the variations of the kinematic quantities.
5.3.1 Variations of Kinematic Quantities
The variation of the kinematics, Eq. (4.10), reads
These quantities can be rearranged according to Voigt notation, since the effective stress resultants are symmetric.
Introducing the quantities
the continuous strain-displacement differential operator of the Euclidean problem is obtained as
where the first superscript denotes the corresponding strain: “m” for membrane, “b” for bending and “s” for shear. The second superscript denotes the variables for which the variation takes place: “m” for midsurface displacement and “d” for the director. The vector of strain variations is thus \(\updelta {\textbf {E}}_{\textrm {V}}= {{\mathcal {B}}}\updelta \hat{\bar{\varvec{{\Phi }}}}\). In line with this notation, we introduce the following notation for the effective stress resultants
We can now write the Euclidean weak form by inserting \({{\mathcal {B}}}\) and \({\tilde{\textbf {{\textbf {S}}}}} \) into Eq. (5.29) as
or, in a more compact notation,
5.3.2 Linearization of the Continuous Euclidean Weak Form
Linearization of a weak form living in a vector space is a standard exercise in finite element analysis. With the Gâteaux derivative we obtain the following expression for the Euclidean linearization of the weak form
The two individual contributions resulting from application of the product rule of differentiation represent the classical separation of the tangent stiffness into a geometric and a material part. In the following derivations we take care of these contributions separately.
5.3.3 Material Part
The material part can be straightforwardly computed as
The material tangent moduli can be written in a local Cartesian coordinate system as
5.3.4 Geometric Part
By computing the Gâteaux derivative, the geometric part is obtained as
which, in turn, can be rewritten as
to implicitly define \({{\textbf {k}}}^{\textrm {g}}\). Furthermore, we used the definitions
We finally obtain
We stress that discretizing this quantity would yield the Euclidean algebraic stiffness matrix of an extensible director formulation living in \(\mathbb {R}^3\). This would result in a 6-parameter formulation but without any stiffness associated with the thickness stretch, due to the missing corresponding strain in Eq. (4.9). The reduction to a 5-parameter model is done as follows: We discretize Eqs. (5.45) and (5.38) and extract the Euclidean algebraic Hessian and the Euclidean algebraic residual from Eqs. (5.45) and (5.38). These are plugged into Eqs. (5.26) and (5.28) to obtain the Riemannian algebraic stiffness matrix and Riemannian algebraic residual.
So far, these derivations are general and no specific director interpolation was introduced. Therefore, we next specify interpolations of the director.
6 Director Interpolation
6.1 Motivation
We want to establish a Euclidean algebraic version of the internal forces of Eq. (5.38) and the tangent stiffness of Eq. (5.45). For this we first need to establish a consistent interpolation of the inextensible director. Consistency of the interpolation means satisfaction of the following properties. These are objectivity, path independence, invariance to node numbering, no singularities and unit length in the domain. At the end of this chapter we arrive at the algebraic element vectors and matrices in Sect. 7, which can be implemented directly. Furthermore, we show a possible C++-implementation of these quantities in Appendix 7. But before we derive the algebraic element vectors and matrices, we discuss properties of interpolation schemes for the director field found in literature.
6.2 Classical Interpolation Schemes
In the literature there are innumerable ways of interpolating the director in the non-linear Reissner-Mindlin model. Each of them have their unique advantages and drawbacks. In order to clarify some underlying issues and their origins, we take a small detour. It is tempting to simply define an angle pair \({\alpha },\beta \) to obtain a parametrization of quantities living on the unit sphere. Inevitably, this comes along with singularities according to the “hairy ball theorem”, see [37, 57, 62, 63, 97]. It is apparently straightforward to identify these angles as degrees of freedom and to apply standard interpolation such that \({\alpha }=\sum _{I=1}^n N^I {\alpha }_I,{\beta }=\sum _{I=1}^n N^I {\beta }_I\), see ([97], Eq. 54) and ([37], Eq 5.1). The director can then be constructed as \({{\textbf {t}}}={\textbf {R}}({\alpha },{\beta }){{\textbf {t}}}_0\). Unfortunately, using an additive update, such that \({\alpha }_I^{k+1}= {\alpha }_I^k + \Updelta \alpha _I\), leads to a non-objective formulation, since rigid body rotations do not cancel in the strain measures. Similar drawbacks can be found in [38, 79], where an incremental rotation vector \(\Updelta {\varvec{\theta }}\) is interpolated. The incremental quantities live in a linear space, where standard interpolation schemes apply. Because this contradicts the intrinsically non-linear nature of the problem, this construction leads to a non-objective formulation. This is also due to the results of [26].
The problem can be avoided by constructing nodal directors as \({{\textbf {t}}}_I={\textbf {R}}_I{{\textbf {t}}}_0^I\), and directly interpolating them, \({{\textbf {t}}}=\sum _{I=1}^n N^I {\textbf {R}}_I{{\textbf {t}}}_0 \), instead of the (rotational) degrees of freedom. The rotation matrix \({\textbf {R}}\) is updated multiplicatively as \({\textbf {R}}_I^{k+1} = \Updelta {\textbf {R}}(\Updelta {\alpha }_I,\Updelta {\beta }_I){\textbf {R}}_I^{k}\). This formulation uses incremental degrees of freedom \(\Updelta {\alpha }_I,\Updelta {\beta }_I\), see [30]. The relation between the director at the interpolation point and the nodal degrees of freedom is then
Equation (6.1) illustrates the complicated dependency of the interpolation scheme on the degrees of freedom.
The formulation is objective and the singularity that comes along with the parametrization of the unit sphere is practically irrelevant, since the iterative changes of the angles \(\Updelta {\alpha }_I,\Updelta {\beta }_I\) are typically small.
However, the procedure leads to a non-compact formulation and involves numerically expensive evaluations of trigonometric functions. Moreover, the interpolation does not conserve the director length. For low order finite elements and fine meshes this is not a big issue, but for higher order elements, which are typically larger, the effect is not only stronger but it results in a degeneration of the convergence order. This dramatic consequence, which is barely mentioned in the literature, is studied in detail in Sect. 10.2. The director \({{\textbf {t}}}\) can be normalized to remove this problem. However, as a consequence the expressions get even more involved. As an alternative to preserve the director length within the domain, several formulations introduce the director \({{\textbf {t}}}_{GP}\) as a history field at each Gauss point, see [17, 29, 86]. In these formulations, only the increment \(\Updelta {{\textbf {t}}}\) is interpolated from the nodes \(\Updelta {{\textbf {t}}}_{GP} =\sum _{I=1}^n N^I(\xi ^1,\xi ^2) \Updelta {{\textbf {t}}}_I\). This is then used to update the directors at each Gauss point as follows
or
where \(\Updelta {\varvec{\theta }}_I = \Updelta {{\textbf {t}}}_I \times {{\textbf {t}}}_I\) and \({\textbf {e}}_3={[0,0,1]}^T\). The resulting scheme is non-objective and path dependent in nature, which was also proven by [26]. Additionally, the interpolated increment \(\Updelta {{\textbf {t}}}_{GP}\) is not automatically in the tangent space of \({{\textbf {t}}}_{GP}\), which can also lead to undesired consequences. The drawbacks of some of these formulations are also discussed in [73].
The entire procedure seems to be error prone in terms of singularities, non-objectivity and path dependence. Moreover, the evaluation and linearization can be expensive due the involved interpolation schemes.
An apparently attractive option to circumvent these drawbacks is to avoid parametrization of the unit sphere and the introduction of rotation matrices in the first place. This can be trivially done, if relations of submanifolds and their embedding are exploited, as proposed in [2] on an abstract level, not related to finite elements. It is shown in the following, how this can be applied to the Reissner-Mindlin model.
6.3 Interpolation, Variation and Linearization of the Midsurface Position Field
At first, we present the quantities of the midsurface interpolation. These can be trivially obtained by the standard interpolation procedure
here \(N^I(\xi ^1,\xi ^2)= N^I\) is the basis function of node I. Obviously, here the linearization of the variation \(\Updelta \updelta {\varvec{\varphi }}^{\textrm {h}}\) of the field \({\varvec{\varphi }}^{\textrm {h}}\) vanishes, since the variation does not depend on the nodal values \({\varvec{\varphi }}_I\). This is different for the director field \({{\textbf {t}}}\), which will be treated next.
6.4 Interpolation, Variation and Linearization of the Director Field
In contrast to interpolation of the midsurface position, for the director field we use a non-linear interpolation scheme to ensure unit length. Here, we apply the projection-based approach used in [36, 90]. A similar approach can also be identified in a somewhat involved format in [30].
First, we construct the reference nodal directors \({{\textbf {t}}}_{0,I}\) according to the algorithm proposed in [28]. The reference director field and its spatial derivatives read
The algorithm in [28] returns the nodal reference directors \({{\textbf {t}}}_{0,I}\) in such a way that the interpolated directors of Eq. (6.5) at the integrations points are as normal as possible to the reference midsurface. Furthermore, the unit length constraint is also only fulfilled approximately. In general, however, the interpolated reference directors at each integration point are neither unit vectors nor are they normal to the midsurface. Still, in this algorithm the error is minimized in a least square sense. To cure at least the non-unit length of the interpolated reference director, we normalize it and obtain for the reference director field and its spatial derivatives
where the derivative of the closest point projection w.r.t. to its argument reads
Thus, the only remaining potential error for the reference interpolation of the director is its angle deviation from the surface normal. Note that the nodal directors do in general not have unit length, this is only true for the interpolated director. The treatment of this effect in the nodal update algorithm can be seen in Algo. 2.
Second, we introduce the projection-based interpolation for the current director field as
In the following, for a more compact notation we omit the superscript \({\textrm {h}}\), denoting discretized quantities. Moreover, the following operators are introduced:
With these operators the variation and linearization of the director quantities can be derived as
and the linearization of the variation reads
The partial derivatives of the projector onto the unit sphere \(\varvec{{{\mathcal {P}}}}\) are summarized in Appendix 4. Furthermore, the first derivative \(\varvec{{{\mathcal {P}}}}'\) does not coincide with the nodal projection \(P_{{{\textbf {t}}}_I}\) and only the numerator is a projection matrix, since \({(\varvec{{{\mathcal {P}}}}')}^n= \frac{1}{||{{\textbf {w}}}||^n}\varvec{{{\mathcal {P}}}}'\) instead of \({(\varvec{{{\mathcal {P}}}}')}^n= \varvec{{{\mathcal {P}}}}'\). Additionally, the quantities of Eq. (6.11) always occur in a scalar product with \({\textbf {a}}_{\alpha }\). They can be rewritten as
7 Element Vectors and Matrices
In the following, we present the quantities required to obtain the algebraic optimization problem. First, we present the Euclidean quantities and afterwards we apply the base change using \(\varvec{{\Lambda }}_{\varvec{{\Phi }}_I}\) and the projections to obtain the Riemannian quantities.
7.1 Internal Forces and Material Part of the Stiffness Matrix
Using the aforementioned definitions for the interpolation, the Euclidean algebraic strain-displacement operator — resulting from the continuous one from Eq. (5.35) — for a generic node I can be given as
With this and the fundamental lemma of variational calculus we can derive the Euclidean algebraic internal forces as
and the material part of the Euclidean stiffness matrix as
7.2 Geometric Part of the Stiffness Matrix
With the linearization of the variation of the strains and the definitions in Eq. (5.44) we obtain the following discrete quantities.
7.2.1 Contribution from Membrane Strains
For the membrane strains we have
using the abbreviation
The membrane contribution to the geometric stiffness matrix is thus
7.2.2 Contribution from Curvature
For the linearization of the variation of the curvature we get
Using the short cuts
the bending contribution to the geometric stiffness matrix reads
7.2.3 Contribution from Transverse Shear
Similarly, we obtain for transverse shear
This can be rearranged using the following short cuts
The corresponding contribution to the geometric stiffness matrix is
Finally, the Euclidean geometric stiffness contribution for a pair of nodes I and J is
This results in the total Euclidean algebraic stiffness matrix
as needed for the left part in Eq. (5.26). The last missing part for the stiffness matrix is the product in the last part in Eq. (5.26), i.e. \({{\textbf {t}}}_J^T \frac{{\partial }{\bar{{\varPi }}}}{{\partial }{{\textbf {t}}}_J}\).
Introducing the external potential \({\varPi }^{\text {ext}}\), as defined in Appendix 6, and inserting Eq. (7.2) the Euclidean residual \({\textbf {R}}_I^\text {euk}\) is obtained as
From the results of Appendix 6 we know that the external moment load vector lies in the tangent space of \({{\textbf {t}}}_J\) (for conservative loading) and this results in
since \({{\textbf {t}}}_J^T{\textbf {F}}_\text {ext}^{{{\textbf {t}}}_J}=0\). The stiffness matrix thus further simplifies, because it is now independent of the external loads.
If we introduce the following tangent base matrix, which consists of the tangent base of \(\mathbb {R}^3\), which is the identity, and the tangent base of \({{\mathcal {S}}}^2\) at node I, which is \(\varvec{{\Lambda }}_I\), we have
Recalling Eq. (5.26) and plugging in Eqs. (7.3), (7.13) and (7.15) to (7.17) we can derive the reduced Riemannian stiffness matrix
With the reduced discrete Riemannian strain-displacement operator of node I
we obtain the stiffness matrix
The part \({{\textbf {t}}}_J^T {\textbf {F}}_{\text {int}}^{\text {euk},{{\textbf {t}}}_J} {\textbf {I}}_{2\times 2} \delta _{IJ}\) is missing in similar formulations in the literature, with the exception of [86], where it can be found as last part in Eq. (B.5) and in Chapter C.2.4 (v) Geometric-diagonal. Furthermore, we stress that this contribution does not vanish at equilibrium, since only the tangential part of the residual vanishes at equilibrium. Therefore, an eigenvalue analysis to study stability problems does not yield the correct results, if this quantity is neglected. Additionally, it also does not vanish with mesh refinement. We study the influence of this quantity on the number of iterations in Sect. 10.
This additional quantity can be represented more explicitly by expanding the involved products as
with
The interested reader is refered to Appendix 8 for a geometric and physical interpretation of \({\textbf {K}}^{{\textrm {g}}2,\text {riem}}\).
Furthermore, with Eqs. (7.17) and (7.15) the final Riemannian gradient or residual in the tangent space representation reads
where \(\varvec{{\Lambda }}_{\varvec{{\Phi }}_J}^T P_{\varvec{{\Phi }}_J}=\varvec{{\Lambda }}_{\varvec{{\Phi }}_J}^T\) has been used.
Now, with Eqs. (7.23) and (7.20) we have all ingredients to apply Algo. 1, except the definition of retractions.
8 Retractions
Incremental solution procedures of non-linear problems require the update of the unknown variables. In displacement based methods in mechanics, these variables are the positions of the nodes, which are updated by the displacement increments. This is trivially accomplished by addition of the variables
Since all occurring variables live in \(\mathbb {R}^n\), this addition is well-defined.
In the following, the generic variable \({{\textbf {x}}}\) denotes an arbitrary quantity living in the manifold M. In our specific application, ths quantity is the director \( {{\textbf {t}}}\). In the general case of M being a non-linear manifold, the update of these variables is non-trivial, since the variable \({{\textbf {x}}}\) lives in the manifold M, but the update \(\Updelta {{\textbf {x}}}\) lives in the tangent space \(T_{{\textbf {x}}}M\) at \({{\textbf {x}}}\).
Therefore, a naive addition \({{\textbf {x}}}+\Updelta {{\textbf {x}}}\) results in a quantity which is not an element of M anymore. Hence, we need a retraction, which is an operator \(R_{{\textbf {x}}}(\Updelta {{\textbf {x}}}): T_{{\textbf {x}}}M \rightarrow M\), that maps the tangent vector \(\Updelta {{\textbf {x}}}\) back onto the manifold. This is illustrated in Figs. 5 and 6, for the general case and the case of the unit sphere, respectively.
The most prominent example of such an operator is the Riemannian exponential map, which maps the tangent vectors on locally uniquely defined geodesic curves \({\varvec{\gamma }}\) of the manifold. Since in most cases the computation of the exponential map is expensive or even not possible in closed form, an alternative attenuated concept of retractions can be defined, see ([2], Chapter 4.1) or more recently [1]. Additionally, this notion of retractions goes back to [4]. Luckily, for the unit sphere a closed form of the exponential map is available. For a shell formulation with an inextensible director in the nona-linear manifold \({{\mathcal {S}}}^2\) we end up with two different feasible possible retractions. The first retraction is the exponential map \(R_{{\textbf {x}}}^{em}\) of the unit sphere, which projects the quantity from the tangent space onto a geodesic curve. It can be written as
The second possible retraction, namely the projection-based retraction \(R_{{\textbf {x}}}^{pb}\), see [2] or [90], is defined as closest point projection onto the manifold, that is
The projection-based retraction and the Riemannian exponential map coincide up to second order in a Taylor expansion. As shown in ([2], Chapter 4, p. 76) or ([90], Chapter 1.5.1), the Taylor expansions read
Consequently, for small increments \(||\Updelta {{\textbf {x}}}||\) both retractions (or update schemes) yield similar updated quantities. Nevertheless, in the neighborhood of the solution even a first order retraction will still lead to quadratic convergence of 1. For a proof we refer to ([20], Theorem 6.5). The projection-based retraction was also used in [43] and was named radial return normalization in [18]. In Sect. 10.2.2 we will show the superiority of this procedure. In order to avoid confusion with the projection-based interpolation of the director, we use the term radial return normalization in the following, in spite of the fact that projection-based retration appears to be the denomination mostly used today, especially in the mathematical literature [90]. This renaming does only make sense for the case of the unit sphere, since for other manifolds the projection-based retraction is of course not a radial return.
9 Improving the Convergence Properties
We additionally use the mixed interpolation point (MIP) technique from [52] to further improve the convergence of the equilibrium iteration. This technique can be traced back to [48] and [49], where it is recommended to use for the first few iterations the stresses of the last converged step to compute the geometric stiffness matrix. In the MIP method at every integration point a Hellinger-Reissner functional is introduced, with the stresses at the integration points as free variables. These are eliminated via static condensation at integration point level. The corresponding stress values are only used for computation of the geometric stiffness matrices \({\textbf {K}}^{{\textrm {g}},\text {riem}}\) and in \({\textbf {K}}^{{\textrm {g}}2,\text {riem}}\) as
but the stresses for the internal forces are computed in the usual way as
where \({\textbf {E}}^V={[{\varvec{\varepsilon }}^V~{\varvec{\kappa }}^V~{\varvec{\gamma }}^V]}^T\). The subscript k denotes values from the previous iteration. For linear material laws the procedure to obtain the alternatives stresses for the geometric stiffness can also be interpreted as a linearized Taylor expansion from the previous iteration to the current one. This reads
Thus, the current stresses for the geometric tangent are extrapolated from the stresses and the strain-displacement operator of the previous step. This leads to significantly fewer iterations and allows much larger load steps. The corresponding improvements are numerically studied in Sect. 10.
For the converged state, where \(\Updelta \varvec{{\Phi }}={\varvec{0}}\), the stresses from the purely displacement based formulation are recovered and therefore at equilibrium the stiffness matrix corresponds to the one obtained with a primal formulation in terms of displacements. Therefore, the MIP technique does not pollute the final result, but it only influences convergence behavior. The reason for this can be found in [52]. The benefit of this method can be interpreted as a circumvention of an iteration locking phenomenon due to the highly different membrane and bending stiffnesses, which can be cured using the MIP technique.
10 Numerical Examples and Discussion
10.1 Overview
In the following we want to emphasize various properties of the presented formulation using numerical examples. Completely geometrically non-linear kinematic equations are used in all simulations. First, we compare the chosen projection-based director interpolation (PBFE) to the nodal (NFE) and geodesic (GFE) approach in Sect. 10.2. Furthermore, we study the influence of the MIP scheme as mentioned in Sect. 9 on the number of iterations required for convergence. The influences of the chosen tangent base update scheme and nodal director update scheme are also shown. After this, we study the problem of a doubly curved shell subject to a deformation and a subsequent rigid body rotation to show the objectivity and path independence of the formulation. We also investigate the consequences of neglecting the additional contribution \({\textbf {K}}^{{\textrm {g}}2,\text {riem}}_{5n \times 5n}\), equation ((7.21)), to the geometric stiffness matrix. We proceed with the study of a path following example with branch switching of an L-shaped shell. Finally, a simulation of wrinkling patterns and qualitative comparison to an experimental result demonstrates the applicability of the shell element formulation to more complex problems.
For all simulations, Non-Uniform Rational B-Spline (NURBS) are used as ansatz and test spaces, as proposed in [44]. We denote these spaces in the following as e.g. “P2C1” denoting quadratic NURBS with \(C^1\)-continuity between elements. The cases of P1C0 and P2C0 reproduces the standard Q1 and Q2 finite elements, respectively. Unless stated otherwise, we use the radial return normalization as nodal director update and the incremental vector transport (IncVT) as tangent base update as shown in Algo. 4. As default we use the projection-based finite elements (PBFE). Within the incremental-iterative solution procedure, load control with equidistant load increments is used. Additionally, we use a St.-Venant-Kirchhoff material law. In local Cartesian coordinates, the corresponding material tangent reads
with
where the vanishing normal stress condition is already enforced. Here, E is Young’s modulus, \(\nu \) Poisson’s ratio and h the shell thickness. A shear correction factor is not applied. No specific measures are taken to avoid membrane locking and transverse shear locking in this context. The focus is on the aforementioned aspects of consistency, efficiency, objectivity and path-independence.
Furthermore, to use a Cartesian material law we construct a Cartesian reference frame \(\theta ^i{\tilde{\textbf {{\textbf {A}}}}}_i\) from \(\xi ^i{\textbf {A}}_i\) identical to ([29], Eq. 9–13). The only change is the definition of the shape function derivatives \(N_{,{\alpha }}=\frac{{\partial }N}{{\partial }\xi ^{\alpha }}\), which are now carried out as \(N_{,{\alpha }}=\frac{{\partial }N}{{\partial }\theta ^{\alpha }}\) which is done by constructing the Jacobian \(\frac{{\partial }\xi ^{\alpha }}{{\partial }\theta ^{\beta }}\) between both coordinate frames. Explicitly, this yields \(N_{,{\alpha }}=\frac{{\partial }N}{{\partial }\theta ^{\alpha }}= \frac{{\partial }N}{{\partial }\xi ^{\alpha }}\frac{{\partial }\xi ^{\alpha }}{{\partial }\theta ^{\beta }}\). This is only done once before the start of the simulation and the derivative values are stored at the integration points. Additionally, this simplifies the strain measures due to \({\tilde{\textbf {{\textbf {A}}}}}_{\alpha }\cdot {\tilde{\textbf {{\textbf {A}}}}}_{\beta }={\delta }_{{\alpha }{\beta }} \).
10.2 Comparison of Nodal, Projection-Based and Geodesic Interpolation
10.2.1 Theoretical Comparison
In this section, we discuss the difference of three director interpolation schemes, which are all path independent and objective. In the projection-based approach (PBFE) from Eq. (6.8) the interpolation is
The first alternative is the nodal approach (NFE), in which the director is interpolated without normalization
This scheme corresponds to the interpolation approaches used in [15, 16, 43, 63, 87], where the inextensibility condition is only fulfilled at the nodes. The aforementioned schemes from literature differ by the definition of the degrees of freedom and the stiffness matrix. Therefore, it may not be possible to directly compare the NFE approach described herein to the mentioned references. The NFE residual and stiffness matrix can be constructed from the PBFE approach by skipping normalization of the director and by replacing \(\varvec{{{\mathcal {P}}}}'={\textbf {I}}, \varvec{{{\mathcal {Q}}}}_{{\alpha }}=\varvec{{{\mathcal {X}}}}_{{\alpha }{\beta }}=\varvec{{{\mathcal {S}}}}_{{\alpha }}={\varvec{0}}\) in all quantities. Compared to PBFE this results in a simpler formulation.
The third alternative are the geodesic finite elements (GFE), which use the interpolation scheme
taken from ([74], Eq. 29). Solving of the local minimization problem Eq. (10.5) at each integration point is documented in Appendix 5.
We obtain the values \(\frac{{\partial }{{\textbf {t}}}_{\text {GFE}}}{{\partial }{{\textbf {t}}}_I}\) and \(\frac{{\partial }^2{{\textbf {t}}}_{\text {GFE}}}{{\partial }{{\textbf {t}}}_I\partial {{\textbf {t}}}_J}\) for the Euclidean gradient and Euclidean Hessian, respectively, using the forward mode of the automatic differentiation tool Autodiff [50]. Here, we first solve the director interpolation minimization problem using the double number format. After this, we use the converged director as initial iterate for the calculation of the derivatives using the dual2nd number format to obtain the derivatives. Using the converged director as predictor, calculation of this derivative mostly takes only one or two iterations in dual2nd format to converge to machine precision. For higher order interpolations, e.g. P4C3 the algorithm sometimes needed up to four iterations to converge. The idea, to first converge the values and then differentiate them, can be found in ([32], Ch. 4). Furthermore, in [32] and [13] the convergence to the correct derivatives for Newton methods is proven.
The differences between the three interpolation schemes are first explained on a theoretical basis. Similar to the GFE definition, the nodal and the projection-based approach can be reformulated as closed form solutions of minimization problems. The three approaches can thus be represented as
These abstract definitions can be interpreted geometrically as shown in Fig. 7, see also [76] for a discussion of interpolation on manifolds. One can see, that the nodal approach violates the unit length condition in the domain. For GFE and PBFE this constraint is exactly satisfied, since the minization takes place on the manifold. Since GFE and PBFE satisfy this constraint exactly, both of them suffer from the following problem: Consider two directors that point in exactly opposite directions. The geodesic that connects them is not unique and the interpolation is ambigious. This problem only arises for very coarse meshes and even then we consider this event rare. Therefore, we argue that this is an interesting issue but a theoretical one. For the interested reader, we refer to Chapter 4 of [73]. Furthermore, GFE also uses the distance measure of the manifold and therefore it is fully intrinsic since it does not depend on a particular embedding. Also the hybrid nature of the projection-based approach becomes obvious, as it relies on the distance measure of the embedding space but the minimization is solved for values on the manifold. In particular, loosely speaking, PBFE inherits the simplicity of NFE and the accuracy of GFE.
Graphical comparison of interpolation between two nodal directors \({{\textbf {t}}}_1,{{\textbf {t}}}_2\), using the schemes of Eq. (10.6). The blue line indicates the used distance measure and the red dashed line indicates the space in which the minimization problem is formulated, i.e. where the interpolated director lives in
In contrast to nodal interpolation, projection-based interpolation and geodesic interpolation are not exactly integrated by Gauss quadrature even for the simple case of \( N^I(\xi ^1,\xi ^2)\) being Lagrange polynomials. This is the case, since the interpolation formula of PBFE involves irrational fractions of the ansatz functions whereas for GFE the dependence of \(\xi ^1,\xi ^2 \) on the director \({{\textbf {t}}}\) cannot even be expressed in closed form.
Still, we use Gauss integration in the numerical examples that fits the order of the used NURBS function spaces and numerical studies revealed that increasing the number of quadrature points leaves the results practically unchanged.
In [36] numerical evidence is given that for the case of the unit sphere geodesic finite elements are superior to the projection-based formulation in terms of \({\textrm {h}}\)-convergence. However, in ([36], Ch. 5.1) they also mention that the projection-based approach is 10 times as fast and therefore an overall superiority of PBFE can be deduced in terms of computational efficiency. As already mentioned, this is due to the implicit definition of the geodesic interpolation, which leads to a small minimization problem at each integration point, see [75], whereas for projection-based finite elements an explicit formula is available. The implicit definition of GFE does also lead to the need of using automatic differentiation for the derivatives which explains the major speed difference. Furthermore, we stress that the obtained convergence rates for \({\textrm {h}}\)-refinement are not backed up by theory, since no error estimates for this type of energy are available. Furthermore, since refraining from interpolating the directors directly can lead to non-objective results, difficulties in conserving the total angular momentum arise in dynamic simulations. Therefore, Simo et al. refrained in [87] from the involved interpolations of [86], which used history fields at the integration points, and simply sticked to NFE to be able to conserve total angular momentum. A similar reasoning for rods can be found in [69]. We hypothesize that this also holds for PBFE and GFE. In the following example we finally compare performance of the different interpolations applied to the Reissner-Mindlin shell.
10.2.2 Pure Bending of a Straight Beam
In order to compare the interpolation schemes NFE, PBFE and GFE, we consider the example of pure bending of a straight beam. The straight beam is clamped at one end and a moment load is applied at the opposite free end, see Fig. 8. The moment that is needed to coil the beam to a full circle is obtained as follows: Since the deformed configuration is a full circle, the geometry of the final deformed configuration is known. This can be used to obtain the analytic (Green-Lagrangian) strain function through the cross section. In combination with the material law from Eq. (10.1) we can derive the stresses, which we integrate through the cross section to obtain the stress resultants, using Eq. (A.8). The normal force and the transverse shear force must be identically zero. From these constraints, the correct moment load can be derived as
with \(I=bh^3/12\). This moment load can then be translated to a moment line load at the corresponding edge, see Fig. 8. Furthermore, we point out that this is in line with the value \(M^{\text {lin}}=2\pi EI/L\) found in the literature [22, 63, 86]. This solution assumes a linear stress-strain relation using Biot strains. It is also valid for very thin beams. Additionally, if we do not neglect the quadratic part \(\rho _{{\alpha }{\beta }}\) in the strains in Eq. (4.9) the factor of the difference term in M changes from 2/3 to 1.
Comparison of Interpolations All results for this example are obtained using the IncVT-update for the tangent space of the director, which is explained in Appendix 3 in Algorithm 4. As director update we use the radial return normalization. This combination allows to apply the moment to turn the straight beam into a full circle in a single load step. The iteration of the load step is considered as converged if the Euclidean norm of the displacement correction drops below \(1 \times 10^{-12}\).
The different interpolations are tested for several polynomial orders and an increasing element count for a thickness of \(h=1\hbox {cm}\). The results are summarized in Fig. 9. The diagrams on the left show the absolute error of the tip rotation plotted versus the number of elements in length direction. More precisely, for one of the directors at the tip \({{\textbf {t}}}^{\text {tip}}\) the quantity \(|\pi -{{\,\textrm{atan2}\,}}( -t^{\text {tip}}_3,t^{\text {tip}}_1 )| \) is computed. The diagrams on the right show the runtime needed for evaluation of all element matrices, accumulated over all iterations.
All interpolation schemes require the same number of iterations to satisfy the convergence criterion. Additionally, we use up to 3600 elements, if the absolute tip rotation error is above \(1 \times 10^{-7}\). In order to obtain errors smaller than \(1\times 10^{-8}\) by introducing more elements, we witnessed numerical issues due to the conditioning of the stiffness matrix. This results in a diminishing convergence order and the error can not be further reduced. These results are not reported in the figures.
Figure 9a and b show that for the case of linear Q1 elements the convergence behavior is practically identical for all three interpolation schemes. This indicates that omitting director normalization, as it is proposed by many authors, is in fact acceptable for linear elements. The runtimes shown in Fig. 9b reveal that the GFE approach is significantly more expensive than both PBFE and NFE. The latter two exhibit almost identical performance, with a marginal advantage for the NFE approach.
For second order elements with \(C^1 \)-continuity (P2C1) the results are quite different, see Fig. 9c and d. For the NFE approach the underlying Newton-Raphson process does not converge for all discretizations, even if the process is subdivided into 100 increments. For sufficiently fine meshes convergence is achieved, but the resulting curve indicates only quadratic \({\textrm {h}}\)-convergence while both the GFE and PBFE approach achieve convergence within a single load step and the curves indicate cubic \({\textrm {h}}\)-convergence. Both schemes yield similar results but PBFE is again superior in terms of runtime, as seen in Fig. 9d. The inferior behavior of the NFE approach can be advocated to the fact that for higher order elements the geometric effect of not normalizing the director is more pronounced.
Further elevation of the polynomial order to \(p=4\) and \(C^3\)-continuity increases these effects, see Fig. 9e and f. Here, for the NFE approach, the Newton-Raphson process does not converge for an element count below 20. Furthermore, the convergence order remains quadratic for NFE, in contrast to PBFE and GFE, for which the curves indicate a quintic convergence order. Moreover, the PBFE and GFE approach start to differ and the GFE approach is slightly superior in terms of absolute error in the tip rotation in the range of almost an order of magnitude, for fine meshes. Comparing runtimes, however, the PBFE approach clearly outperforms GFE, although it can be forecasted that GFE will eventually surpass NFE also in terms of runtime for very small errors due to the degeneration of convergence order of the latter.
In summary, these results strongly indicate a superiority of PBFE to GFE in terms of overall efficiency. However, it does of course not prove it. The investigations here only deal with the one-dimensional interpolation quality since the deformation is uni-axial. In [36] there is a comparsion for \({{\mathcal {S}}}^2\) harmonic maps up to a polynomial order of three but there the differences of \({\textrm {h}}\)-convergence are small. Additonally, we refer the interested reader to [76], where “Abbildung 4” provides a nice visualization of the PBFE and GFE interpolation schemes. Furthermore, the difference between PBFE and GFE in terms of computational speed is reported in the literature as a 10-fold difference [36]. These results are obtained with ADOL-C [33], which uses a mixed forward and backward mode. In contrast to this, we witnessed for our experiments a 100-fold speed difference using the forward mode of [50], which indicates that this is not the best choice to differentiate the geodesic director interpolation algorithm. Nevertheless, the overall picture remains unchanged concerning the speed of the different interpolations. Furthermore, since automatic differentiation is not always an option and we expect the differences in accuracy of PBFE and GFE to only play a role for high interpolation orders, we still recommend PBFE.
Figure 10a and b show results for a \(p=2,C^0\) ansatz basis in order to study the case of not exploiting the highest possible continuity of \(C^{p-1}\). The same effects as in Fig. 9 occur, except the problem of non-convergence of the NFE approach for coarse meshes. In particular, it must be stressed that also here the convergence order of the nodal approach is not optimal.
The specific behavior of the NFE approach for higher order interpolation can be explained by regarding plots of the normalized tip rotation versus the number of degrees of freedom, Fig. 11. Apparently, NFE overestimates the deformation and reacts too softly. This behavior results from the fact that for higher polynomial orders the dimension of individual elements are larger for a given total number of degrees of freedom. Therefore, the differences of the nodal directors also increase and consequently the deviation from unit length of the interpolated director increases. In particular, this results in directors being too short and an artificial thinning of shell. This, in turn, reduces bending stiffness, which leads to the mentioned artificial softening. In contrast to this, PBFE and GFE strictly converge from the “stiff” side even for the case of P4C3, since it always exactly preserves the unit length of the interpolated director.
Comparison of Director Update and Tangent Base Update The example of pure bending of a straight beam is now used to study the influence of using the MIP method for the geometric stiffness and to compare three different update procedures for the tangent base of the director with regard to the required number of iterations. A fine discretization of 50 \(5^\textrm {th}\) order elements is used in order to minimize the effect of locking. Only one single load step is taken for coiling the beam to a full circle. The two incremental approaches incremental vector transport (IncVT) Algo. 4, incremental parallel transport (IncPT) Algo. 3 and stereographic projection (SP) Algo. 5 are taken into account in combination with a pure displacement scheme (disp) and the MIP scheme for calculation of the geometric stiffness. All results are obtained using projection-based interpolation (PBFE) as well as radial return normalization \(R_{{\textbf {x}}}^{\text {pb}}\).
The results are shown in Table 3 for various values of the beam thickness. For a thick beam (\(h=2.0\,\hbox {cm}\)) applying the MIP method reduces the number of required iterations from 29 to 16 for all versions of the tangent base update. The results remain independent of the update procedure down to a thickness of \(h=0.01\,\hbox {cm}\), but the absolute number of iterations increases significantly for the standard geometric stiffness, while along with MIP the required number of iterations is constantly equal to 16.
Overall, no significant and systematic difference between the incremental approaches (IncVT, IncPT) and the stereographic one (SP) can be observed. For \(h=0.01\,\hbox {cm}\) and larger the results are exactly identical. For extremely thin structures, some differences are observed, however, with no distinct trend in favor of one of the three versions. During the numerical studies it has been found that different results are obtained when using direct solvers. This indicates that arithmetic effects, probably related to the conditioning of the system of equations, are significant. Therefore, drawing conclusions concerning the effects of the tangent base algorithm is prohibitive for the extremely thin cases.
The convergence behavior of the Newton-Raphson scheme observed for this example is superior to that of formulations found in literature. In [28] 5 load steps are needed for convergence and in [93] 125 load steps are needed with 715 accumulated iterations.
Pure bending of a straight beam; deformed geometry after the first iteration; left: exponential map \(R^{em}_{{\textbf {t}}}(\Updelta {{\textbf {t}}})= \exp _{{\textbf {t}}}(\Updelta {{\textbf {t}}})\), right: radial return normalization \(R^{\text {pb}}_{{\textbf {t}}}(\Updelta {{\textbf {t}}})= {{\mathcal {P}}}_{{\textbf {t}}}(\Updelta {{\textbf {t}}})\). The plot of the surface, the control polygons and control points are obtained using [89]
When using the exponential map \(R_{{\textbf {x}}}^{\text {em}}\) no convergence can be achieved in only one load step for this example. The dramatic failure of the exponential map procedure for this specific setting can be explained by examining the deformed geometry after the first iteration, which corresponds to the linear solution. The diagrams in Fig. 12 show the deformed center line along with the nodal directors for the exponential map (left) and the radial return normalization (right). Obviously, the directors are far from being normal to the midsurface for the former case, even including self-penetration of the material, while for the latter the rotated directors and the deformed center line match quite well. The reason is that the radial return normalization approach naturally limits the rotations within one iteration to \(< 90^{\circ }\). In fact, the underlying problem is almost linear in the rotations but highly non-linear in the midsurface displacements. The exponential map yields the correct solution of the rotations in one iteration but the mid-surface displacements lag behind and, in combination, yield an unphysical state with self-penetration. This explains the divergence using the exponential map.
In summary, for the director update the normalization procedure appears to be superior to the exponential map due to the following reasons:
-
The radial return update is cheaper due to the easy normalization, circumventing trigonometric functions.
-
The Taylor expansions of both procedures coincide up to second order, which yields similar results for small updates, see Eq. (8.4)
-
For large increments the normalization seems to be more robust due to the natural limitation of the rotation increments within one iteration, which can be incoherent with the mid-surface displacements.
Table 4 shows the iteration history for this example with a thickness of \(h=1\,\hbox {cm}\), confirming quadratic convergence of the Riemannian Newton-Raphson scheme for both the displacement-based and the MIP approach.
10.3 Deformation and Subsequent Rigid Body Rotation of a Doubly Curved Freeform Surface
Inspired by numerical examples from [45] and [46] we consider a curved shell structure undergoing a rigid body rotation, while a constant force is acting on the shell. The purpose of this study is to evaluate the objectivity of the presented formulation. Again, we restrict these investigation to the projection-based interpolation (PBFE). A doubly curved free form surface is used to obtain a challenging setup, since several formulations exist for which objectivity is obtained for the special case of plane reference configurations. Geometry and material data are taken from [28].
The system and boundary conditions are presented in Fig. 13. The bottom edge is simply supported and all other edges are free. In [28] the problem data are given without units. At the top edge a line load \(p_Y=10\) per unit length in global Y-direction is prescribed. Material data are given as Young’s modulus \(E=1.2\cdot 10^6\) Poisson’s ratio \(\nu =0.3\) and the shell thickness is \(h=0.1\). We study the objectivity on the coarsest mesh, because this is the most challenging case, using three cubic B-Spline elements per direction. This configuration, including the directors at the control points, is shown in Fig. 14.
Coarsest free form surface representation with control polygons, control points and directors at the control points. The plot of the surface, the control polygons and control points are obtained using [36]
The results obtained with the present formulation are compared with the full and reduced integrated four-node shell elements S4 and S4R of the finite element software ABAQUS [88]. The two different meshed used are shown in Fig. 15.
First, we apply the load \(p_Y\). The resulting Y-displacements of point A for different methods and discretizations are summarized in Table 5. Obviously, the displacements are severely underestimated with the present formulation and a coarse discretization with cubic elements. This can be explained by the effect of locking, mainly membrane locking, which has to be expected in this purely displacement-based approach. This, however, does not compromise the discussion of objectivity.
After this, the free form surface is subjected to a rigid body rotation around the Y-axis, see Fig. 16 by applying inhomogeneous Dirichlet boundary conditions at the bottom edge. The rotation is applied in increments of \(22.5^{\circ }\) and a total of 100000 load steps are applied, resulting in 6250 full turns. For the simulations using the present approach, the corresponding equilibrium iteration is considered as converged if the Euclidean norm of the displacement correction drops below \(1\times 10^{-12}\). For the simulation with ABAQUS we changed the ABAQUS control routine values \(R_n^{\alpha }, C_n^{\alpha }\) from default (0.005, 0.01) to (\(1 \times 10^{-12}\),\(1\times 10^{-12}\)), which usually leads to a termination of the iterations when the maximum entry in the displacements corrections drops at least below \(1 \times 10^{-8}\). Nevertheless, no major difference in the results was obtained using the ABAQUS default values.
Deviation of y-displacement of point A in Fig. 13 during rotation
Figure 17 shows the absolute changes of the Y-displacement of point A (which is supposed to remain constant during rotation), plotted versus the number of turns. For the proposed formulation the relative error is bounded by \(1 \times 10^{-12}\), which underlines the objectivity of the formulation. This property is backed up by theory, see ([36], Ch. 1.3). Since the deformation does not depend on the number of turns it also confirms path independence of the formulation. In contrast to this, the results obtained with the S4 and S4R element of ABAQUS indicate non-objectivity. The absolute errors are several orders of magnitudes larger and—more importantly—these errors do not diminish with mesh refinement. For the S4R element the non-objective error even increases. Nevertheless, after every full turn the original displacement is obtained, which indicates path independence.
Influence of the second geometric stiffness contribution This numerical example studies the influence of the non-standard contribution to the geometric stiffness matrix \({\textbf {K}}^{{\textrm {g}}2,\text {riem}}_{5n \times 5n}\) (Eq. (7.21)) on the iteration history. Its effect can be interpreted as preventing an artificial geometric stiffness with respect to the nodal director change, see Appendix 8. As one can see in Eq. (7.21), only moments and transverse shear forces contribute to this geometric stiffness. Furthermore, it only contributes to diagonal terms to the stiffness matrix. Departing from these algebraic facts, we reuse the example of Sect. 10.3 to show the influence in a simulation. To increase the moment stress resultants we increase the load \(p_Y\) to 30. This load is applied for different mesh sizes in three equidistant load steps. After the load has been applied, a prescribed rotation is imposed with a magnitude of \(11.25^{\circ }\) within each load step. These load steps are considered converged, if the Euclidean norm of the displacement correction drops below \(1 \times 10^{-11}\).
The resulting iteration counts are summarized in Table 6. Also the effect of whether or not the MIP method is used is documented. It is apparent that this stiffness quantity saves between one to three iterations. This is true for both load cases, \(p_Y\) and support rotation.
10.4 Out-of-Plane Buckling of an L-Shaped Plate
This example is designed to demonstrate the capability of the proposed formulation to follow complex load-displacement characteristics. For this we use the L-shaped plate example, which can be found in [9, 78, 81, 86, 97]. The L-shaped plate and the corresponding boundary conditions are shown in Fig. 18. The material parameters are set to \(E=71240\,\hbox {N}/\hbox {m}\hbox {m}^{2}\) and \(\nu = 0.31\). The thickness is \(h=0.6\,\hbox {mm}\). The left end is fully clamped and the upper edge A-B is subject to a line load \(q_X= {\lambda }\frac{1}{30}~\hbox {N}/\hbox {mm}\). In this definition of the load, we follow [78], although in most publications a point load at point A or B or at the center of the edge is applied, which gives rise to a singularity. We use a discretization with bi-quadratic \(C^0\)-continuous ansatz functions. Figure 18 shows a mesh with 63 elements; in addition a uniformly refined mesh with 2800 elements is used.
An arclength method is used for path following. Accompanying eigenvalue analyses are used to check for critical points. As soon as a negative eigenvalue is observed, the corresponding critical load factor \({\lambda }_{\text {crit}}\) and eigenvector \({\varvec{\phi }}\) are identified via extended systems [98, 99]. For the given problem, these belong to a bifurcation point, with the eigenvector indicating the buckling mode. Our results — also including the cases of point loads at A and B — are compared to results from the literature in Table 7. Here, for better comparability, a finite element mesh with 99 elements (\(15 \times 3\) elements for each of the longer rectangular patches) is used.
For branch switching, the eigenvector is then used as predictor in the next load step in order to follow the secondary equilibrium path and to study the post-buckling behavior. For the extended systems the directional derivative \(\frac{\textrm {d} }{\textrm {d} \epsilon } {\textbf {K}}(\varvec{{\Phi }}+\epsilon {\varvec{\phi }})|_{\epsilon =0}\) of the stiffness matrix is needed, where \({\varvec{\phi }}\in T_{\varvec{{\Phi }}} M^n\). For this we use the liftedFootnote 7 function to evaluate the derivative in the tangent space. To obtain this derivative within machine precision, we use a complex step derivative [54].
Figure 19 shows the convergence of the load-displacement curves of points A and B and their corresponding out-of-plane Z-displacement. Here, the convergence of the critical load can be seen and furthermore the convergence of the post buckling path. The deformed structure, including the nodal directors, is shown in Fig. 20 for a load value of \(\lambda =2.35\). Figure 21 shows the convergence of the critical load factor for all three discussed load cases. The refinement factor k refers to the multiplicity of elements per edge compared to the coarsest mesh shown in Fig. 18.
10.5 Shearing of a Rectangular Sheet
In this last example we demonstrate the performance of the formulation for a more challenging setup. Similar to Example 6.4 in [78] we simulate an experiment of Wong and Pellegrino [95]. The experiment consists of a rectangular sheet with dimensions \(380\,\hbox {mm} \times 128\,\hbox {mm}\) and a thickness of \(0.025\,\hbox {mm}\). This results in an extremely large slenderness of \(15\,200\) if the thickness is compared to the longer sides of the rectangular sheet. The material properties mentioned in [95] are \(E=3500\,\hbox {N}/\hbox {m}\hbox {m}^{2}\) as Young’s modulus and \(\nu =0.31\) as Poisson’s ratio. The two short vertical edges are free and the two long horizontal edges are fully clamped. These boundary conditions and the mesh are shown in Fig. 22. In the experiment the upper edge is moved horizontally by \({\delta }_h=3\,\hbox {mm}\) and during the process a different number of wrinkles occur and vanish due to mode jumping. Wong and Pellegrino mention a small vertical prestress before the experiment is started but no numbers are given. We use an initial vertical displacement of \({\delta }_v=0.05\,\hbox {mm}\), which was also used in the simulations in [96].
Due to the slender geometry, it is extremely demanding—if at all possible—to compute the problem using an arc-length method. Wong and Pellegrino therefore resort to a stabilization technique available in the commercial code ABAQUS [88] as “pseudo dynamic solution procedure”. As an alternative, we solve this challenging problem similar to Sander et al. [78] using a Riemannian trust-region method, see [2] for details. This method guarantees global convergence [2]. This property allows to solve the problem by applying the displacement in one single load step.
In short, a standard Newton-Raphson scheme Algo. 1 can be interpreted as a method to find the stationary points of the second order model \(m_{\varvec{{\Phi }}_k}\) of the real energy \({\varPi }\) in a neighborhood of \(\varvec{{\Phi }}_{k}\). To construct the next update \(\Updelta \varvec{{\Phi }}\) in the solution process the incremental Newton-Raphson problem can be formulated as
With this, the nodal values are updated and the new model around \(\varvec{{\Phi }}_{k+1}\) is constructed. Since this method returns a stationary point in every iteration, an increase in energy can occur between iterations. Depending on this property the Newton-Raphson iteration can diverge. The trust-region method instead trusts this model \(m_{\varvec{{\Phi }}_k}(\Updelta \varvec{{\Phi }})\) in Eq. (10.8) of the true energy \({\varPi }\) only in a region around the center \(\varvec{{\Phi }}_k\) and restricts the length of the next iterate such that \(||\Updelta \varvec{{\Phi }}||_{\textbf {M}}< \Updelta _{{\textrm {T}}{\textrm {R}}}\). Additionally, the update value \(\Updelta \varvec{{\Phi }}\) is constrained to yield a decreasing energy value. This yields the constrained minimization problem
where \(||{{\textbf {x}}}||_{\textbf {M}}= \sqrt{{{\textbf {x}}}^T {\textbf {M}}{{\textbf {x}}}}\) denotes the norm with respect to a generic preconditioner \({\textbf {M}}\). Several ways to solve this trust-region subproblem of Eq. (10.9) exist in the literature, see [25]. We choose the preconditioned Steihaug-Toint truncated conjugate gradient method using an incomplete Cholesky decomposition (Eigen::IncompleteCholesky) of the Eigen library [39] as preconditioner \({\textbf {M}}\). This method does not always yield the correct minimum of the model, if the minimum lies at the boundary, but only returns a sufficient energy decrease. Furthermore, depending on the trust in the current model \(m_{\varvec{{\Phi }}_k}\) that the algorithm has, the trust-region radius \(\Updelta _{{\textrm {T}}{\textrm {R}}}\) is adjusted in every iteration.
We use a mesh of \(240\times 80\) elements with quadratic \(C^0\)-continuous shape functions as in [78], along with the projection-based interpolation from Eq. (10.6)\(_2\). The mesh is shown in Fig. 22. This results in \(19\,200\) elements and \(387\,205\) degrees of freedom. Additionally, in contrast to the involved including of imperfections in [96], we start the solution of every trust-region subproblem in Eq. (10.9) from a random vector \(\Updelta \varvec{{\Phi }} \) that is scaled such that it lies inside the initial trust-region. This is done for the first load step, which applies a prestress via a prescribed vertical displacement \({\delta }_v=0.05\,\hbox {mm}\). This load step is accepted if the displacement norm drops below \(1 \times 10^{-8}\). This remaining distortion in \(Z-\)direction is enough to break the initial symmetry and to trigger buckling.
Due to the globally convergent nature of the trust region algorithm, we may apply the entire horizontal displacement of the upper edge of \(\delta _h=0.5\,\hbox {mm}\) or \(\delta _h=3\,\hbox {mm}\), respectively, in one single load step. Obviously, the deformation history of the developing wrinkles is captured better, if more intermediate equilibrium points are used. But for this example we observed that the final state does not differ much, qualitively, if we use one hundred increments instead of a single load step. The iteration is accepted as converged, if the norm of the displacement correction drops below \(1 \times 10^{-6}\) in this second load step. The left hand side in Fig. 23 corresponds to a horizontal displacement of \(\delta _h=0.5\,\hbox {mm}\). In the diagram on the bottom left the wavenumber (15 “valleys”) of the simulation coincides with the on observed in the experiment. Furthermore, the amplitudes of the wrinkles are captured quite satisfactorily. For the larger displacement \(\delta _h=3\,\hbox {mm}\) (pictures on the right in Fig. 23) the number of valleys in the experiment is 19 as opposed to 20 in our simulation. The amplitude of the wrinkles is less well captured, especially for the wrinkles at the right and left boundary. However, the results still coincide qualitatively; in particular, the different inclination of the wrinkles and their hierarchical geometry at the the top and bottom edge are clearly visible in the contour plot.
Comparison of the shearing experiment of [95] and results of our simulation; \(240 \times 80\) elements with quadratic \(C^0\)-continuous shape functions; left: \(\delta _h=0.5\,\hbox {mm}\), right: \(\delta _h=3\hbox {mm}\)
11 Conclusion
Various aspects of a consistent geometrically non-linear Reissner-Mindlin shell formulation and its finite element discretization are discussed. We paid special attention to interpolation of the director, the inextensibility condition and consistent linearization.
Objectivity, path independence and efficiency of the formulation are discussed and confirmed by numerical examples. As one of the most important results, we conclude that a combination of the projection-based interpolation and a radial return normalization is the most recommended choice.
Projection-based interpolation is particularly useful for higher order ansatz functions, for instance in the context of isogeometric analysis. We conclude that, at least for uni-axial bending, fulfilling the inextensibility condition for the director only at the nodes and neglecting it in the domain, as it is frequently done, is acceptable for (bi-)linear shape functions. For higher order shape functions it deteriorates the rate of convergence.
For the update of the tangent bases of the nodal directors, incremental vector transport (IncVT) has been proposed as a numerically more efficient alternative to incremental parallel transport. Both schemes are free from singularities. In many cases, however, stereographic projection is the recommended scheme, because it requires the least numerical effort. For the case of external moment loads, however, depending on the implementation, stereographic projection may be unfeasible because of the singularity. In such cases, IncVT may be the better choice.
Additionally, we presented the steps how to generate from a continuous minimization problem formulated on a manifold an algebraic problem. Here, we pointed out the role of an additional part of the stiffness matrix which improves convergence behavior and allows even larger load steps.
We expect that the entirety of issues discussed in this work can improve standard large rotation shell formulations found in the literature, even if they use only (bi-)linear ansatz functions and fulfill the inextensibility condition for the director at the nodes only.
Additionally, if all these recommondations are applied, one ends up with a formulation completly free from trigonometric functions, despite its capability to track large rotation deformations. This is not only benefical from a numerical point of view. We also highlight the more compact theory and a formulation which is—in our view—easier to understand. To facilitate further benchmarking of the proposed element, the C++ routines for the strain-displacement operator and the geometric stiffness matrix are published in Appendix 7. Additionally, we provide an implementation of the element using projection-based interpolation in MATLAB [58]. It contains the example from Sect. 10.2.2 and the example of Sect. 10.3 without the support rotation. The element and its stress-based counterpart are also currently implemented in the publicly available multi-disciplinary finite element code KRATOS [27] in the IgaApplication.
Change history
20 April 2022
A Correction to this paper has been published: https://doi.org/10.1007/s11831-022-09725-8
24 November 2022
A Correction to this paper has been published: https://doi.org/10.1007/s11831-022-09832-6
Notes
In this context, well-defined means that the tensorial character of the quantity is retained, i.e. the eigenvalues of the operator should be independent of the parametrization.
The most prominent torsion-free connection is the Levi-Civita connection. Furthermore, a torsion-free connection induces the symmetry of the Christoffel symbols of the connection. A geometrical interpretation of this is: The parallel transport of a tangent space from point A to B does not twist the corresponding tangent space along the (geodesic) curve connecting A and B.
This is implied by the Reissner-Mindlin assumption of vanishing normal stresses. Due to these vanishing normal stresses there is no energy contribution of the thickness stretch and therefore it can be calculated purely by an appropiate postprocess.
Here, we choose \({\textbf {A}}^{\alpha }\) instead of \( {\textbf {A}}^{\alpha }\otimes {\textbf {A}}^3\) as base for \({\varvec{\gamma }}\) in order to obtain a vector representation.
The equivalence of both approaches is proven for a functional \({{\mathcal {J}}}:H^1({\varOmega },M)\rightarrow \mathbb {R}\) in [77, Ch. 4, Theorem 4.1].
Lifting a function denotes the process of converting a function \(f: M \rightarrow \mathbb {R}\) to a function living on the current tangent space \({{\hat{f}}}: T_{{\textbf {x}}}M \rightarrow \mathbb {R}\), see e.g. [2]. This lifting is done by composing the function evaluation with a suitable rectraction \({{\hat{f}}}(\Updelta {{\textbf {x}}}) = f(R_{{\textbf {x}}}(\Updelta {{\textbf {x}}})) \), where \({{\textbf {x}}}\in M \) and \(\Updelta {{\textbf {x}}}\in T_{{\textbf {x}}}M \).
References
Absil PA, Malick J (2012) Projection-like retractions on matrix manifolds. SIAM J Optim 22(1):135–158. https://doi.org/10.1137/100802529
Absil PA, Mahony R, Sepulchre R (2008) Optimization algorithms on matrix manifolds. Princeton University Press, Princeton. https://doi.org/10.1515/9781400830244
Absil PA, Mahony R, Trumpf J (2013) An extrinsic look at the riemannian hessian. In: Nielsen F, Barbaresco F (eds) Geometric science of information. Springer, Berlin, Heidelberg, pp 361–368. https://doi.org/10.1007/978-3-642-40020-9_39
Adler RL, Dedieu JP, Margulies JY, Martens M, Shub M (2002) Newton’s method on Riemannian manifolds and a geometric model for the human spine. IMA J Numer Anal 22(3):359–390. https://doi.org/10.1093/imanum/22.3.359
Antman SS (1974) Kirchhoff’s problem for nonlinearly elastic rods. Q Appl Math 32(3):221–240
Areias P, Rabczuk T, Dias-da-Costa D (2013) Assumed-metric spherically interpolated quadrilateral shell element. Finite Elem Anal Des 66:53–67. https://doi.org/10.1016/j.finel.2012.11.006
Argyris J (1982) An excursion into large rotations. Comput Methods Appl Mech Eng 32(1–3):85–155. https://doi.org/10.1016/0045-7825(82)90069-x
Argyris J, Dunne P, Scharpf D (1978) On large displacement-small strain analysis of structures with rotational degrees of freedom. Comput Methods Appl Mech Eng 14(3):401–451. https://doi.org/10.1016/0045-7825(78)90076-2
Argyris J, Balmer H, Doltsinis J, Dunne P, Haase M, Kleiber M, Malejannakis G, Mlejnek HP, Müller M, Scharpf D (1979) Finite element method–the natural approach. Comput Methods Appl Mech Eng 17–18:1–106. https://doi.org/10.1016/0045-7825(79)90083-5
Başar Y, Krätzig WB (1990) Introduction into finite-rotation shell theories and their operator formulation. In: Atluri SN, Krätzig WB, Oñate E (eds) Computational mechanics of nonlinear response of shells. Springer, New York, pp 3–30. https://doi.org/10.1007/978-3-642-84045-6_1
Basar Y, Krätzig WB (2013) Mechanik der flächentragwerke: theorie. Springer-Verlag, Berechnungsmethoden, Anwendungsbeispiele. https://doi.org/10.1007/978-3-322-93983-8
Kj Bathe, Bolourchi S (1980) A geometric and material nonlinear plate and shell element. Comput Struct 11(1–2):23–48. https://doi.org/10.1016/0045-7949(80)90144-3
Beck T (1994) Automatic differentiation of iterative processes. J Comput Appl Math 50(1):109–118. https://doi.org/10.1016/0377-0427(94)90293-3
Belytschko T, Lin JI, Chen-Shyh T (1984) Explicit algorithms for the nonlinear dynamics of shells. Comput Methods Appl Mech Eng 42(2):225–251. https://doi.org/10.1016/0045-7825(84)90026-4
Belytschko T, Wong BL, Chiang HY (1992) Advances in one-point quadrature shell elements. Comput Methods Appl Mech Eng 96(1):93–107. https://doi.org/10.1016/0045-7825(92)90100-X
Benson D, Bazilevs Y, Hsu M, Hughes T (2010) Isogeometric shell analysis: the reissner–mindlin shell. Comput Methods Appl Mech Eng 199(5–8):276–289. https://doi.org/10.1016/j.cma.2009.05.011
Betsch P, Gruttmann F, Stein E (1996) A 4-node finite shell element for the implementation of general hyperelastic 3d-elasticity at finite strains. Comput Methods Appl Mech Eng. https://doi.org/10.1016/0045-7825(95)00920-5
Betsch P, Menzel A, Stein E (1998) On the parametrization of finite rotations in computational mechanics a classification of concepts with application to smooth shells. Comput Methods Appl Mech Eng. https://doi.org/10.1016/S0045-7825(97)00158-8
Bischoff M, Ramm E, Irslinger J (2017) Models and finite elements for thin-walled structures. Encyclopedia of computational mechanics, 2nd edn. Wiley, New Jersey, pp 1–86. https://doi.org/10.1002/9781119176817.ecm2026
Boumal N (2020) An introduction to optimization on smooth manifolds. Available online, http://www.nicolasboumal.net/book
Brouwer L (1912) Über Abbildung von Mannigfaltigkeiten. Math Ann 71:97–115
Büchter N (1992) Zusammenführung von degenerationskonzept und schalentheorie bei endlichen rotationen. PhD thesis, Institut für Baustatik, Universität Stuttgart
Büchter N, Ramm E (1992) Shell theory versus degeneration–a comparison in large rotation finite element analysis. Int J Numer Methods Eng 34(1):39–59. https://doi.org/10.1002/nme.1620340105
Chien WZ (1944) The intrinsic theory of thin shells and plates. I. General theory. Q Appl Math 1(4):297–327. https://doi.org/10.1090/qam/9744
Conn AR, Gould NI, Toint PL (2000) Trust region methods. Siam, Philadelphia. https://doi.org/10.1137/1.9780898719857
Crisfield MA, Jelenić G (1999) Objectivity of strain measures in the geometrically exact three-dimensional beam theory and its finite-element implementation. Proc Math Phys Eng Sci 455(1983):1125–1147. https://doi.org/10.1098/rspa.1999.0352
Dadvand P, Rossi R, Oñate E (2010) An object-oriented environment for developing finite element codes for multi-disciplinary applications. Arch Comput Methods Eng 17:253–297. https://doi.org/10.1007/s11831-010-9045-2
Dornisch W, Klinkel S, Simeon B (2013) Isogeometric reissner-mindlin shell analysis with exactly calculated director vectors. Comput Methods Appl Mech Eng 253:491–504. https://doi.org/10.1016/j.cma.2012.09.010
Dornisch W, Müller R, Klinkel S (2016) An efficient and robust rotational formulation for isogeometric reissner-mindlin shell elements. Comput Methods Appl Mech Eng 303:1–34. https://doi.org/10.1016/j.cma.2016.01.018
El-Abbasi N, Meguid SA (2000) A new shell element accounting for through-thickness deformation. Comput Methods Appl Mech Eng 189(3):841–862. https://doi.org/10.1016/S0045-7825(99)00348-5
Frisvad JR (2012) Building an orthonormal basis from a 3D unit vector without normalization. J Graph Tools. https://doi.org/10.1080/2165347X.2012.689606
Gilbert JC (1992) Automatic differentiation and iterative processes. Optim Methods Softw 1(1):13–21. https://doi.org/10.1080/10556789208805503
Griewank A, Juedes D, Utke J (1996) Algorithm 755: Adol-c: a package for the automatic differentiation of algorithms written in c/c++. ACM Trans Math Softw 22(2):131–167. https://doi.org/10.1145/229473.229474
Grohs P (2011) Finite elements of arbitrary order and quasiinterpolation for data in riemannian manifolds. Tech. Rep. 2011-56, Seminar for applied mathematics, ETH Zürich, https://www.sam.math.ethz.ch/sam_reports/reports_final/reports2011/2011-56.pdf
Grohs P, Hardering H, Sander O (2015) Optimal a priori discretization error bounds for geodesic finite elements. Found Comput Math 15(6):1357–1411. https://doi.org/10.1007/s10208-014-9230-z
Grohs P, Hardering H, Sander O, Sprecher M (2019) Projection-based finite elements for nonlinear function spaces. SIAM J Numer Anal 57(1):404–428. https://doi.org/10.1137/18M1176798
Gruttmann F, Stein E, Wriggers P (1989) Theory and numerics of thin elastic shells with finite rotations. Arch Appl Mech 59(1):54–67. https://doi.org/10.1007/BF00536631
Gruttmann F, Sauer R, Wagner W (2000) Theory and numerics of three-dimensional beams with elastoplastic material behaviour. Int J Numer Methods Eng 48(12):1675–1702. https://doi.org/10.1002/1097-0207(20000830)48:12<1675::AID-NME957>3.0.CO;2-6
Guennebaud G, Jacob B, et al (2010) Eigen v3. http://eigen.tuxfamily.org
Hardering H (2015) Intrinsic discretization error bounds for geodesic finite elements. PhD thesis, Mathematisches Institut, Fachbereich Mathematik und Informatik, Freie Universitat Berlin, https://doi.org/10.17169/refubium-15367
Hardering H (2018) \(L^2\)-discretization error bounds for maps into Riemannian manifolds. Numer Math (Heidelb) 139(2):381–410. https://doi.org/10.1007/s00211-017-0941-3
Hardering H, Sander O (2020) Geometric finite elements. In: Grohs P, Holler M, Weinmann A (eds) Handbook of variational methods for nonlinear geometric data. Springer, Cham, pp 3–49. https://doi.org/10.1007/978-3-030-31351-7_1
Hughes TJ, Liu WK (1981) Nonlinear finite element analysis of shells: Part I. three-dimensional shells. Comput Methods Appl Mech Eng 26(3):331–362. https://doi.org/10.1016/0045-7825(81)90121-3
Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194(39–41):4135–4195. https://doi.org/10.1016/j.cma.2004.10.008
Ibrahimbegovic A, Taylor RL (2002) On the role of frame-invariance in structural mechanics models at finite rotations. Comput Methods Appl Mech Eng. https://doi.org/10.1016/S0045-7825(02)00442-5
Jelenić G, Crisfield M (1999) Geometrically exact 3D beam theory: implementation of a strain-invariant finite element for statics and dynamics. Comput Methods Appl Mech Eng 171(1–2):141–171. https://doi.org/10.1016/S0045-7825(98)00249-7
Kiendl J, Bazilevs Y, Hsu MC, Wüchner R, Bletzinger KU (2010) The bending strip method for isogeometric analysis of kirchhoff-love shell structures comprised of multiple patches. Comput Methods Appl Mech Eng 199:2403–2416. https://doi.org/10.1016/j.cma.2010.03.029
Kuo-Mo H (1987) Nonlinear analysis of general shell structures by flat triangular shell element. Comput Struct 25(5):665–675. https://doi.org/10.1016/0045-7949(87)90159-3
Kuo-Mo H, Yeh-Ren C (1989) Nonlinear analysis of shell structures by degenerated isoparametric shell element. Comput Struct 31(3):427–438. https://doi.org/10.1016/0045-7949(89)90390-8
Leal AMM, et al (2018) Autodiff, a modern, fast and expressive C++ library for automatic differentiation. https://autodiff.github.io, https://autodiff.github.io
Long Q, Burkhard Bornemann P, Cirak F (2012) Shear-flexible subdivision shells. Int J Numer Methods Eng 90(13):1549–1577. https://doi.org/10.1002/nme.3368
Magisano D, Leonetti L, Garcea G (2017) How to improve efficiency and robustness of the newton method in geometrically non-linear structural problem discretized via displacement-based finite elements. Comput Methods Appl Mech Eng 313:986–1005. https://doi.org/10.1016/j.cma.2016.10.023
Makowski J, Stumpf H (1995) On the symmetry of tangent operators in nonlinear mechanics. Z Angew Math Mech 75(3):189–198. https://doi.org/10.1002/zamm.19950750303
Martins JRRA, Sturdza P, Alonso JJ (2003) The complex-step derivative approximation. ACM Trans Math Softw 29(3):245–262. https://doi.org/10.1145/838250.838251
Miehe C, Schröder J (2001) Energy and momentum conserving elastodynamics of a non-linear brick-type mixed finite shell element. Int J Numer Methods Eng 50(8):1801–1823. https://doi.org/10.1002/nme.95
Misner CW, Thorne KS, Wheeler JA, Kaiser DI (2017) Gravitation. Macmillan, UK
Münch I (2007) Ein geometrisch und materiell nichtlineares cosserat-modell - theorie. Numerik und Anwendungsmöglichkeiten. https://doi.org/10.5445/IR/1000007371
Müller A (2022) Implementation of a non-linear Reissner-Mindlin shell formulation in Matlab. Version V1. DaRUS. https://doi.org/10.18419/darus-1255
Neff P (2004) A geometrically exact Cosserat shell-model including size effects, avoiding degeneracy in the thin shell limit. Part I: formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Contin Mech Thermodyn 16(6):577–628. https://doi.org/10.1007/s00161-004-0182-4
Nour-Omid B, Rankin C (1991) Finite rotation analysis and consistent linearization using projectors. Comput Methods Appl Mech Eng 93(3):353–384. https://doi.org/10.1016/0045-7825(91)90248-5
Oesterle B, Sachse R, Ramm E, Bischoff M (2017) Hierarchic isogeometric large rotation shell elements including linearized transverse shear parametrization. Comput Methods Appl Mech Eng 321:383–405. https://doi.org/10.1016/j.cma.2017.03.031
Oliver J, Onāte E (1984) A total Lagrangian formulation for the geometrically nonlinear analysis of structures using finite elements. Part I. Two-dimensional problems: shell and plate structures. Int J Numer Methods Eng 20(12):2253–2281. https://doi.org/10.1002/nme.1620201208
Ramm E (1976) Geometrisch nichtlineare Elastostatik und finite Elemente. University of Stuttgart, Habilitation
Ramm E (2000) From reissner plate theory to three dimensions in large deformation shell analysis. Z Angew Math Mech 80(1):61–68. https://doi.org/10.1002/(SICI)1521-4001(200001)80:1<61::AID-ZAMM61>3.0.CO;2-E
Rankin CC, Nour-Omid B (1988) The use of projectors to improve finite element performance. Comput Struct 30(1):257–267. https://doi.org/10.1016/0045-7949(88)90231-3
Ray D (2015) Computation of nonlinear structures: extremely large elements for frames. Wiley, New Jersey
Romano G, Diaco M, Sellitto C (2005) Tangent stiffness of elastic continua on manifolds. In: Rionero S, Romano G (eds) Trends and applications of mathematics to mechanics. Springer, Milanon, pp 155–184. https://doi.org/10.1007/88-470-0354-7_14
Romero I (2004) The interpolation of rotations and its application to finite element models of geometrically exact rods. Comput Mech. https://doi.org/10.1007/s00466-004-0559-z
Romero I, Armero F (2002) An objective finite element approximation of the kinematics of geometrically exact rods and its use in the formulation of an energy-momentum conserving scheme in dynamics. Int J Numer Methods Eng 54(12):1683–1716. https://doi.org/10.1002/nme.486
Romero I, Arnold M (2017) Computing with rotations: algorithms and applications. In: Stein E, de Borst R, Hughes TJR (eds) Encyclopedia of computational mechanics, 2nd edn. pp 1–27 https://doi.org/10.1002/9781119176817.ecm2119
Rosen JB (1960) The gradient projection method for nonlinear programming. Part I.linear constraints. J Soc Ind Appl Math 8(1):181–217. https://doi.org/10.1137/0108011
Rosen JB (1961) The gradient projection method for nonlinear programming. Part II. nonlinear constraints. J Soc Ind Appl Math 9(4):514–532. https://doi.org/10.1137/0109044
Sander O (2010) Geodesic finite elements for cosserat rods. Int J Numer Methods Eng 82(13):1645–1670. https://doi.org/10.1002/nme.2814
Sander O (2012) Geodesic finite elements on simplicial grids. Int J Numer Methods Eng 92(12):999–1025. https://doi.org/10.1002/nme.4366
Sander O (2015) Geodesic finite elements of higher order. IMA J Numer Anal. https://doi.org/10.1093/imanum/drv016
Sander O (2015b) Interpolation und simulation mit nichtlinearen daten. GAMM Rundbrief 1
Sander O (2016) Test function spaces for geometric finite elements. arXiv e-prints arXiv:1607.07479
Sander O, Neff P, Bîrsan M (2016) Numerical treatment of a geometrically nonlinear planar Cosserat shell model. Comput Mech 57(5):817–841. https://doi.org/10.1007/s00466-016-1263-5
Sansour C, Wagner W (2003) Multiplicative updating of the rotation tensor in the finite element analysis of rods and shells - a path independent approach. Comput Mech 31(1):153–162. https://doi.org/10.1007/s00466-002-0401-4
Seidel J (1973) Beitrag zur geometrisch nichtlinearen theorie dünner schalen unter annahme kleiner verzerrungen und grosser rotationen. PhD thesis, Institut für Baustatik
Simo J, Vu-Quoc L (1986) A three-dimensional finite-strain rod model. Part II: computational aspects. Comput Methods Appl Mech Eng 58(1):79–116. https://doi.org/10.1016/0045-7825(86)90079-4
Simo JC (1985) A finite strain beam formulation. the three-dimensional dynamic problem. Part I. Comput Methods Appl Mech Eng 49(1):55–70. https://doi.org/10.1016/0045-7825(85)90050-7
Simo JC (1992) The (symmetric) Hessian for geometrically nonlinear models in solid mechanics: intrinsic definition and geometric interpretation. Comput Methods Appl Mech Eng 96(2):189–200. https://doi.org/10.1016/0045-7825(92)90131-3
Simo JC, Fox DD (1989) On a stress resultant geometrically exact shell model. Part I: formulation and optimal parametrization. Comput Methods Appl Mech Eng 72(3):267–304. https://doi.org/10.1016/0045-7825(89)90002-9
Simo JC, Fox DD, Rifai MS (1989) On a stress resultant geometrically exact shell model. Part II: the linear theory; computational aspects. Comput Methods Appl Mech Eng 73(1):53–92. https://doi.org/10.1016/0045-7825(89)90098-4
Simo JC, Fox DD, Rifai MS (1990) On a stress resultant geometrically exact shell model. Part III: computational aspects of the nonlinear theory. Comput Methods Appl Mech Eng 79(1):21–70. https://doi.org/10.1016/0045-7825(90)90094-3
Simo JC, Rifai MS, Fox DD (1992) On a stress resultant geometrically exact shell model. Part VI: conserving algorithms for non-linear dynamics. Int J Numer Methods Eng 34(1):117–164. https://doi.org/10.1002/nme.1620340108
Smith M (2009) ABAQUS/standard user’s manual, Version 6.9. Dassault Systèmes Simulia Corp, United States
Spink M, Claxton D, de Falco C, Vázquez R (2020) Octave nurbs toolbox. http://octave.sourceforge.net/nurbs/index.html
Sprecher M (2016) Numerical methods for optimization and variational problems with manifold-valued data. PhD thesis, ETH Zurich. https://doi.org/10.3929/ethz-a-010686559
Steinmann P (2015) Geometrical foundations of continuum mechanics: an application to first- and second-order elasticity and elasto-plasticity. Lect Notes Appl Math Mech. https://doi.org/10.1007/978-3-662-46460-1
Suetake Y, Iura M, Atluri S (2003) Variational formulation and symmetric tangent operator for shells with finite rotation field. Comput Model Eng Sci. https://doi.org/10.3970/cmes.2003.004.329
Sze KY, Liu X, Lo SH (2004) Popular benchmark problems for geometric nonlinear analysis of shells. Finite Elem Anal Des 40(11):1551–1569. https://doi.org/10.1016/j.finel.2003.11.001
Waltersdorf KP (1971) Beitrag zur frage konsistenter geometrisch nichtlinearer theorien dünner elastischer Flächentragwerke. PhD thesis, Lehrstuhl für Massivbau, Teschnische Universität Hannover
Wong W, Pellegrino S (2006) Wrinkled membranes Part I: experiments. J Mech Mater Struct 1:3–25. https://doi.org/10.2140/jomms.2006.1.3
Wong W, Pellegrino S (2006) Wrinkled membranes. Part III: numerical simulations. J Mech Mater Struct 1:63–95. https://doi.org/10.2140/jomms.2006.1.63
Wriggers P, Gruttmann F (1993) Thin shells with finite rotations formulated in biot stresses: theory and finite element formulation. Int J Numer Methods Eng 36(12):2049–2071. https://doi.org/10.1002/nme.1620361207
Wriggers P, Simo JC (1990) A general procedure for the direct computation of turning and bifurcation points. Int J Numer Methods Eng 30:155–176. https://doi.org/10.1002/nme.1620300110
Wriggers P, Wagner W, Miehe C (1988) A quadratically convergent procedure for the calculation of stability points in finite element analysis. Comput Methods Appl Mech Eng 70:329–347. https://doi.org/10.1016/0045-7825(88)90024-2
Ziegler H (1977) Principles of structural stability, vol 35. https://doi.org/10.1007/978-3-0348-5912-7
Zienkiewicz O, Taylor R, Fox D (2014) Chapter 14 - a nonlinear geometrically exact shell model. In: The finite element method for solid and structural mechanics, 7th Edn. Butterworth-Heinemann, pp 519 – 588, https://doi.org/10.1016/B978-1-85617-634-7.00014-4
Acknowledgements
We would like to thank Oliver Sander, Ekkehard Ramm, Hanne Hardering, Anton Tkachuk and Simon Bieber for their comments and helpful discussions. Furthermore, we are deeply in debt to Tobias Teschemacher for his help with the implementation in KRATOS.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Recovery of Stress Resultants
In the following, we show how to
obtain the Cauchy stress resultants from the coefficients of the effective second Piola Kirchhoff stress resultants, as specified in Eq. (4.12). This is done using and extending the results from [84, 11]. We start by introducing the midsurface volume map as
and using it to map the effective second Piola Kirchhoff stress resultants to effective Cauchy stress resultants as
The effective Cauchy stress resultants can be calculated from the Cauchy stress \(\sigma ^{ij}\) as follows
where we introduced
Furthermore, the true/physical Cauchy stress resultants can be obtained as
The introduced quantities are defined as
Since we neglected second order effects of the moments in the internal energy, they simplify to
With this we can simplify Eq. (A.5), using Eq. (A.7) and (A.3), to
Since \({\textbf {a}}_1\) and \({\textbf {a}}_2\) do not form a Cartesian coordinate system, we have to convert the quantities of Eq. (A.8) to get the physical components \(\langle (\cdot )\rangle \).
These definition are similar to ([11], Eq. 3.2.24).
Appendix 2: Algorithms for Updating the Nodal Director
In this section we show two different update schemes, stemming from the retractions of Eqs. (8.2) and (8.3). Both of them are presented in Algo. 2. Particularly, care is taken for the possibility of nodal directors that do not have unit length.

Appendix 3: Construction of a Basis for the Tangent Space
1.1 Appendix 3.1: Constructing the Reference Tangent Basis
The tangent space \(T_{{{\textbf {t}}}_{I}} {{\mathcal {S}}}^2 \) and its basis are needed for the increment of the inextensible director. Due to the non-trivial kernel of the stiffness matrix, see Eq. (5.24), we need a basis that excludes the part normal to the sphere. Alternatively, a rank-aware sstates that there is no non-vanishingolver can also be used. Nevertheless, a useful construction of this basis is non-trivial. The Hairy Ball Theorem [21] tangent vector field on \({{\mathcal {S}}}^2\).
The first version is from ([86], Box 2, p. 35) where the singularity of the tangent vector field is circumvented in an incremental approach. An incremental approach needs an initialization which can be constructed as follows. Another solution to the problem of finding an orthonormal basis from a given vector can also be found in [31].
For the reference basis \(\varvec{{\Lambda }}^0_{{{\textbf {t}}}_{I}}\) we use the solution of the tangent base vectors from the Algorithm in [28], which we denote by \({\bar{{{\textbf {h}}}}}_{\alpha }\). As for a general reference surface these vectors are neither orthogonal to \({{\textbf {t}}}^0\) nor to each other, we project one of them into the tangent space by using \(P_{{{\textbf {t}}}^0}={\textbf {I}}-{{\textbf {t}}}^0\otimes {{\textbf {t}}}^0\) normalize it and construct the other one by using the cross product. Formally, we have
The construction of this reference base is only needed for the following incremental algorithms. In contrast to this the stereographic projection algorithm does not need an initialization.
1.2 Appendix 3.2: Tangent Basis by Incremental Update Using Parallel Transport
We assume that we have in an increment k a nodal director \({{\textbf {t}}}^k_I \in {{\mathcal {S}}}^2 \) and its increment \(\Updelta {{\textbf {t}}}^k_I \in T_{{\textbf {t}}}{{\mathcal {S}}}^2 \). Using these definitions, we can update \(\varvec{{\Lambda }}^k_I \), using a rotation matrix. It is constructed by a unit quaternion \( {{\textbf {q}}}= w +x~i + y~j + z~k\in {\mathbb {H}}_{||1||} \). The entries can be calculated as shown in Algo. 3. Essentially, this algorithm can be interpreted as incremental parallel transport (IncPT) of tangent vectors on the unit sphere. Several versions exist, e.g. the version in [86]. In Algo. 3 we first construct quaternion from the old and the new director. From this quaternion a rotation matrix is constructed. The algorithm to construct a rotation matrix from two vectors can be partially found in the implementation of the C++ library for linear algebra EIGEN [39]. This algorithm uses no trigonometric functions.

1.3 Appendix 3.3: Tangent Basis by Incremental Update Using Generalized Vector Transport
The following algorithm is motivated by the generalization of parallel transport, which is called vector transport in [2]. Since this vector transport is not an isometry, the tangent base vectors will not stay orthogonal to each other and will not preserve unit length. Therefore, we apply this vector transport only to one base vector and construct the other one by using the cross product w.r.t the director. Formally, this is summarized in Algo. 4. This construction follows the same reasoning as the initialization of the reference base in Eq. (C.1).

1.4 Appendix 3.4: Tangent Basis by Stereographic Projection
An alternative construction is proposed in ([74], Eq. 31). This approach circumvents an incremental update and does not require storage of the tangent space at every node. Instead, the tangent space is constructed directly from the current director. The procedure is described in Algorithm 5. The inverse stereographic mapping is differentiated to obtain a tangent space at the point on the unit sphere.
This definition of the tangent base cannot be smooth, it has to be used with care since, e.g. the tangent space parametrization has a discontinuity along the equator line, where \(|{{\textbf {t}}}_I(3)| =0 \) holds. If a moment load is defined at this node in the two dimensional director tangent space, one has to recalculate the external load vector, if \(|{{\textbf {t}}}_I(3)|\) passed through zero since the orientation of the parametrization of the tangent space changes. This is not needed, if the moment load is defined in the embedding space similar to Appendix 6. This seems to be the only drawback of using this singularity. This is due to the fact that the construction of the residual or Hessian does not include derivatives w.r.t. to that base and therefore the singularity along \(|{{\textbf {t}}}_I(3)| =0 \) does not hurt (Fig. 24).

Appendix 4: Derivatives of the Projector
These derivatives are only needed for the derivation of the quantities \(\varvec{{{\mathcal {Q}}}}_{\alpha },\varvec{{{\mathcal {S}}}}_{\alpha }\) and \(\varvec{{{\mathcal {X}}}}_{{\alpha }{\beta }} \). They do not explicitly appear in the implementation.
here \({\delta }_{ij} \) denotes the Kronecker delta.
Appendix 5: Solving the Local GFE Minimization Problem
For the geodesic finite element implementation the interpolation minimization problem of Eq. (10.5) has to be solved at every integration point. Therefore, we reformulate Eq. (10.5) as
where we introduced the function \({\alpha }(x)=\arccos ^2(x)\) for a compact notation, similar to [74, 78]. For the solution of Eq. (E.1) we use a Riemannian Newton-Raphson scheme as proposed in ([2], Table 4.1, Chapter 6.2, Chapter 6.4.1) and we use a base transformation into the tangent space using stereographic projection, as shown in Algo. 5.
For the construction of the Riemannian gradient and Riemannian Hessian [2, 3] we need the Euclidean gradient and Euclidean Hessian, which can be straightforwardly constructed as
here \({{\bar{f}}}: \mathbb {R}^3 \rightarrow \mathbb {R}\) is the Euclidean extension of the function \(f: {{\mathcal {S}}}^2 \rightarrow \mathbb {R}\). The derivatives of \({\alpha }(x)\) are
Near \(x=1\) these expressions are unstable, and the Taylor expansions
are used instead. We took a tolerance of \(1{\textrm {E}}-8\) to switch between the expansion and the exact formula. In this region, the error of both Taylor expansions is within machine precision.
These Euclidean quantities are then projected onto the tangent space \({\varvec{\Lambda }}\) of the director \({{\textbf {t}}}\). This matrix corresponds to the tangent space of the director at the integration point, in contrast to, e. g. Eq. (5.26), where the tangent space corresponds to the nodal directors. We end up with the following equations
These can then be used for the Riemannian Newton-Raphson scheme
where \(R_{{{\textbf {t}}}^k} (\Updelta {{\textbf {t}}}^k) \) is again one of the retractions defined in Eq. (8.2) or Eq. (8.3). As predictor of the GFE director we set the projection-based director, since these interpolations are close to each other, if the difference of the nodal directors is small. More formally, if the nodal directors \({{\textbf {t}}}_I\) are contained in a ball of radius \(h\ll 1 \), the distance of the projection-based and GFE-based director can be bounded by \(h^3\), as done in ([90], Chapter 1.4.3). Therefore, we set the first iterate in Eq. (E.9) to
Moreover, for the strains we need the partial derivatives of the director w.r.t \(\xi ^{\alpha }\) for the curvature terms. Following a similar reasoning as in [74], we can recast the gradient function in Eq. (E.8), evaluated at the converged state as
Taking the total derivative, we get
here we can identify several quantities and end up with
This can then be summarized as
This \(2 \times 2\) linear system of equations can be solved for \({{\textbf {t}}}_{\text {GFE},{\alpha }}\). Note, that \({{\textbf {t}}}_{\text {GFE},{\alpha }}\) has only two components in the \({\varvec{\Lambda }}\) base and therefore we need to reconstruct the three-dimensional representation with \({\varvec{\Lambda }}\).
Appendix 6: Linearization of the External Virtual Work
For the external virtual work we have the following continuous and discrete formulae,
here \({\partial }{{\mathcal {B}}}_0^N\) denotes the part of the boundary which is subjected to Neumann boundary conditions. The quantities \({{\hat{{{\textbf {n}}}}}}\) and \({{\hat{{{\textbf {m}}}}}}\) are the applied force and moment loads. We are interested in the linearization of the algebraic external virtual work \(\updelta {\varPi }_{\text {ext}}(\varvec{{\Phi }}) \), which can be expressed as
Plugging in Eq. (6.11) we get
For \({{\hat{{{\textbf {m}}}}}} \cdot {{\textbf {t}}}=0\) this contribution to the stiffness matrix is zero. Additionally, in [8, 81, 100] it was shown that a load for which this quantity does not vanish is considered non-conservative. Vice versa, if the moment load is defined w.r.t. a fixed axis and not w.r.t. the tangent space of the director, the load is non-conservative. The non-conservative property of such a fixed-axis moment load is not proven here.
Appendix 7: C++ Routines for the PBFE Element
To further clarify the implementation and for convenient usage we summarize the needed routines to obtain the strain-displacement operator \({{\mathcal {B}}}^{\text {riem}}\) of Eq. (7.19) and the geometric tangent matrices \({\textbf {K}}^{ {\textrm {g}},\text {riem} } \) and \( {\textbf {K}}^{ {\textrm {g}}2,\text {riem}} \) for one element. The strain-displacement operator can be found in Eq. (7.19) and the geometric tangent matrices are the second and third term in Eq. (7.18). We use for the element routines the linear algebra library Eigen [39], version 3.3.7. As input parameters of the function we defined two structs where KinematicVariables contains all kinematic quantities \({{\textbf {t}}},\varvec{{{\mathcal {P}}}}',{\textbf {a}}_1,{\textbf {a}}_2,{{\textbf {t}}}_{,1},{{\textbf {t}}}_{,2}\) and VariationVariables contains \(\varvec{{{\mathcal {Q}}}}_{1},\varvec{{{\mathcal {Q}}}}_{2},\varvec{{{\mathcal {S}}}}_{1},\varvec{{{\mathcal {S}}}}_{2},\varvec{{{\mathcal {X}}}}_{11},\varvec{{{\mathcal {X}}}}_{12},\varvec{{{\mathcal {X}}}}_{21}\) and \(\varvec{{{\mathcal {X}}}}_{22}\). Furthermore, the class IntegrationPoint contains the vector and matrix for the shape functions and its derivatives in physical space for all nodes. The member variables _num_node and _num_dof denote the number of nodes and number of degrees of freedom of the element. node is a std::vector member variable, which contains the nodes of the element. In the comments, \((\cdot )_{,\text {disp}}\) denotes a variation w.r.t. the displacements and \((\cdot )_{,\text {dir}}\) w.r.t. the director. For the geometric stiffness matrix in Listing 2 the stress resultants are stored in S in the following order: \(N_{11},N_{22},N_{12},M_{11},M_{22},M_{12},Q_1,Q_2\).


Appendix 8: Geometric and Physical Interpretation of the Additional Stiffness Contribution
In the following we want to provide insight into the geometric and physical nature of the additional stiffness contribution \({\textbf {K}}^{{\textrm {g}}2,\text {riem}}\) that appears due to the extrinsic derivative calculation of [3]. In order to provide an illustrative interpretation of this term, we start with a little digression by repeating the definition Eq. (5.12)
For the subsequent considerations, this equation is modified as follows: We replace \({{\textbf {x}}}\) with the algebraic configuration space \({\varvec{{\Phi }}}\) for a given discretization. Additionally, for the first expression in the brackets we use the identity \({\varvec{\eta }}= {\textbf {P}}_{\varvec{{\Phi }}} {\varvec{\eta }}\) to obtain directly the projected first part of the Hessian. This means \([{\textbf {P}}_{\varvec{{\Phi }}} {{\,\textrm{Hess}\,}}{\bar{{\varPi }}}({\varvec{{\Phi }}})] \) can be replaced by \([{\textbf {P}}_{\varvec{{\Phi }}} {{\,\textrm{Hess}\,}}{\bar{{\varPi }}}({\varvec{{\Phi }}}) {\textbf {P}}_{\varvec{{\Phi }}}]\), which is the quantity of interest we want to reason about in the following,
The nodal configurations contained in \( \varvec{{\Phi }} \) are \([\varvec{{\Phi }}_1,\ldots ,\varvec{{\Phi }}_n ]^T \) are six-dimensional geometry representations including three degrees of freedom for the midsurface position and three for the director. For a physical and geometric interpretation we introduce the Riemannian and Euclidean internal forces as \({\textbf {F}}\) and \({\bar{\textbf {{\textbf {F}}}}}\) as well as the Riemannian and Euclidean stiffness matrices as \({\textbf {K}}\) and \({\bar{\textbf {{\textbf {K}}}}}\) to obtain
Equation (H.3) is the covariant directional derivative of the internal forces in the direction of \({\varvec{\eta }}\in T_{\varvec{{\Phi }}} M\), highlighting the fact that, physically, stiffness is the change of force upon a change of configuration. For our goal to interpret the additional stiffness contribution, we are interested in a particular linearization direction \({\varvec{\eta }}\), namely the direction of a linearized rigid body motion \({\varvec{\eta }}\in {\textrm {L}}{\textrm {R}}{\textrm {B}}{\textrm {M}}({\varvec{{\Phi }}}) \subset T_{\varvec{{\Phi }}} M\), where \({\textrm {L}}{\textrm {R}}{\textrm {B}}{\textrm {M}}({\varvec{{\Phi }}}) \) is the space of linearized rigid body motions at the current configuration \({\varvec{{\Phi }}}\).
In order to discuss effects of different stiffness contributions, we rewrite Eq. (H.3) as
where \({\bar{\textbf {{\textbf {K}}}}}_{\text {mat}}\) is the material Euclidean stiffness matrix from Eq. (7.3) and \({\bar{\textbf {{\textbf {K}}}}}_{\text {g}}\) is the geometric Euclidean stiffness matrix from Eq. (7.13). For the considered case of \({\varvec{\eta }}\) being a linearized rigid body motion, the material stiffness matrix does not contribute to the change of internal forces \(\nabla _{\varvec{\eta }}{\textbf {F}}\), such that \({\textbf {P}}_{\varvec{{\Phi }}} {\bar{\textbf {{\textbf {K}}}}}_{\text {mat}} {\textbf {P}}_{\varvec{{\Phi }}}{\varvec{\eta }}= {\textbf {P}}_{\varvec{{\Phi }}} {\bar{\textbf {{\textbf {K}}}}}_{\text {mat}}{\varvec{\eta }}= {\varvec{0}}\).
This leads to the following equation without the material part.
This intermediate result reproduces the known fact that only the geometric stiffness matrix contributes to the change of internal forces in a rigid body motion.
At a given node I the quantities \( \nabla _{\varvec{\eta }}{\textbf {F}}_I[1 \dots 3]\), referring to the displacement degrees of freedom, are generally non-zero if the geometric stiffness matrix is non-zero. In the engineering literature, this phenomenon is denoted as P-Delta effect. The change of internal forces can be traced back to the fact, that for a stretched material fiber under rotation, the change of lever arm of the normal stress in direction of the fiber produces a change of moment and thus a change of the vector of internal forces. For transverse material fibers, represented by the director \({{\textbf {t}}}\), this effect is not present, as transverse normal stress is assumed to be zero. Therefore, the change of forces referring to the director degrees of freedom has to be zero at each node,
We use this fact in the following to discuss the significance of the second term of the geometric stiffness in Eq. (H.5). This can be done by focusing on nodal contributions. Therefore, we rewrite Eq. (H.5) as
Similar to Eq. (5.21) the off-diagonal contributions of the second part vanish, since the directional derivative \({\textrm {D}}_{{\varvec{\eta }}_J} {\textbf {P}}_{\varvec{{\Phi }}_I} \) is zero for \(I \ne J\). Accordingly, Eq. (H.7) reduces to
here it is obvious that the second part only contains diagonal blocks. Therefore, we can restrict our attention further to a single node. Using the following expansion
we can identify the contribution of node 1—or more generically of node I—as
here we exploited the identities of the midsurface \({\textbf {P}}_{\varvec{\varphi }}= {\textbf {I}}\) and \({\textrm {D}}_{{\varvec{\eta }}_I} {\textbf {P}}_{{\varvec{\varphi }}_I}={\varvec{0}}\) and the identities related to the director similar to Eq. (5.15) namely \({\textbf {P}}_{{{\textbf {t}}}_I} ({\textrm {D}}_{{\varvec{\eta }}_I} {\textbf {P}}_{{{\textbf {t}}}_I}) {\bar{\textbf {{\textbf {F}}}}}_I^{4..6} = -{{\textbf {t}}}_{I}\cdot {\bar{\textbf {{\textbf {F}}}}}_I^{4..6}\). Moreover, \({\bar{\textbf {{\textbf {K}}}}}_{\textrm {g}}^{II,{\varvec{\varphi }},{\varvec{\varphi }}}\) and \({\bar{\textbf {{\textbf {K}}}}}_{\textrm {g}}^{II,{{\textbf {t}}},{{\textbf {t}}}}\) denote the contributions of node I to the stiffness matrix referring to the midsurface and the director, respectively. Similarly, \({\bar{\textbf {{\textbf {K}}}}}_{\textrm {g}}^{II,{{\textbf {t}}},{\varvec{\varphi }}}\) and \({\bar{\textbf {{\textbf {K}}}}}_{\textrm {g}}^{II,{\varvec{\varphi }},{{\textbf {t}}}}\) denote the stiffness matrices coupling the midsurface and the director.
As we are only interest in the parts that interact with the additional stiffness contribution, we can restrict our attention to the lower right block of Eq. (H.10),
In an abuse of notation, in order to keep a compact notation, we rewrite Eq. (H.11) as
As argued earlier, this expression has to be zero. This fact is related to the definition of covariant derivatives along with the canonical Levi-Civita connection, requiring a vanishing derivative of a vector subject to parallel transport.
The first term in Eq. (H.12) can also be written as
with \({\textbf {P}}_{{\textbf {t}}}{\varvec{\eta }}= {\varvec{\eta }}\) and by introducing the notation \({\bar{\textbf {{\textbf {K}}}}}_{{\textrm {g}}}^{\textrm {T}}:={\textbf {P}}_{{\textbf {t}}}{\bar{\textbf {{\textbf {K}}}}}_{{\textrm {g}}}\) to define the tangential part of the geometric stiffness, we can rewrite the geometric stiffness contribution as
where \( {\bar{\textbf {{\textbf {K}}}}}_{{\textrm {g}}}^{\textrm {T}}{\varvec{\eta }}\in T_{{\textbf {t}}}{{\mathcal {S}}}^2 \). Since the force \({\bar{\textbf {{\textbf {F}}}}}\) is constant on the geodesic generated from \({\varvec{\eta }}\), the derivative of its tangential part \(\frac{{\partial }{\bar{\textbf {{\textbf {F}}}}}^{\textrm {T}}}{{\partial }{{\textbf {t}}}} \) produces the normal part of the stiffness \({\bar{\textbf {{\textbf {K}}}}}_{{\textrm {g}}}^{\textrm {N}}\) and the derivative of its normal part \(\frac{{\partial }{\bar{\textbf {{\textbf {F}}}}}^{\textrm {N}}}{{\partial }{{\textbf {t}}}} \), in turn, produces the tangential part \({\bar{\textbf {{\textbf {K}}}}}_{{\textrm {g}}}^{\textrm {T}}\). With this we can write
This is visualized on the right in Fig. 25. The normal part \({\bar{\textbf {{\textbf {F}}}}}^{\textrm {N}}\) of the internal force related to the director degrees of freedom is not included in the actual physical model, but only comes into play due to the extrinsic construction of the derivative. Eq. (H.15) reveals that this artificial transverse normal force introduces a tangential force component, which, given the geometric significance of the director degrees of freedom, actually constitutes a pair of forces, i.e. a moment. In other words, \({\bar{\textbf {{\textbf {F}}}}}^{\textrm {N}}\) introduces a transverse prestress of the director and thus a non-physical P-delta effect. \({\bar{\textbf {{\textbf {K}}}}}_{{\textrm {g}}}^{\textrm {T}}\) is an artificial geometric stiffness, resulting from this effect. This parasitic contribution is eliminated by the second term in brackets in Eq. (H.12) and it is shown in the following, why this is the case.
By definition, \({\textbf {P}}_{{\textbf {t}}}\frac{{\partial }{\bar{\textbf {{\textbf {F}}}}}^{\textrm {N}}}{{\partial }{{\textbf {t}}}}\) in Eq. (H.15) stems from the covariant derivative of [2, 3], which can be written as
Additionally, we can write
as \({{\textbf {t}}}\) is the normal on the unit sphere. With this, Eq. (H.16) simplifies to
Since the magnitude of \({\bar{\textbf {{\textbf {F}}}}}^{\textrm {N}}\) is constant this boils down to the problem of calculating \(\nabla _{\varvec{\eta }}{{\textbf {t}}}\). The directional derivative of the normal is also known as shape operator or Weingarten map. For the sphere, it is trivially computed as
where the second step results from the fact that the radius r of the unit sphere is one. The first part in brackets in Eq. (H.12) can thus be written as
From the definition of the scalar product and the collinearity of \({\bar{\textbf {{\textbf {F}}}}}^{\textrm {N}}\) and \({{\textbf {t}}}\) we can also write
We eventually see that the difference in Eq. (H.12) vanishes identically in the considered case of parallel transport of a vector, as required.
Mechanically speaking, the extrinsic construction of the derivative introduces an artificial P-delta effect on the director increments in the standard geometric stiffness matrix \({\bar{{{\textbf {K}}_{\textrm {g}}}}}\). It emanates from a parasitic transverse normal stress and is eliminated by the additional contribution \({\textbf {K}}^{{\textrm {g}}2,\text {riem}}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Müller, A., Bischoff, M. A Consistent Finite Element Formulation of the Geometrically Non-linear Reissner-Mindlin Shell Model. Arch Computat Methods Eng 29, 3387–3434 (2022). https://doi.org/10.1007/s11831-021-09702-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-021-09702-7