1 Introduction

Over the years, researchers have approached the study of assembly complexity in different ways. The main issue was to define an objective and easily computable algorithm able to provide a tool to assess assembly complexity. In this paper we consider the concept of assembly complexity proposed by Samy and ElMaraghy [1]. They defined product assembly complexity as the “the degree to which the individual parts/subassemblies contain physical attributes that cause difficulties during the handling and insertion processes in manual or automatic assembly”. A high degree of assembly complexity results in more effort required from the human operator, which can lead to longer assembly times [2]. Therefore, understanding assembly complexity allows an a-priori identification of potential time-consuming processes and thus allows designers to take corrective actions aimed at improving cost efficiency and process quality. In this regard, several studies showed that assembly complexity also affects the occurrence of defects and thus the economic performance of companies [3,4,5,6]. Given the relevance of this topic for the manufacturing field, a wide variety of methodologies have been proposed to assess the complexity of a product, of a process and, more generally, of an entire system. To this purpose, a common practice in the literature is to adapt information theory concepts and models [7, 8] to industrial contexts. Information theory is concerned with mathematically analysing the quantification and transmission of an information, (e.g., a message or a signal). In manufacturing, complexity can be linked to three factors: the quantity of information, the diversity of information and the content of information [9,10,11]. Therefore, variety or lack of information causes uncertainty that increases perceived complexity of product, processes or systems [12]. To address complexity of manufacturing systems, many researchers used a key concept of information theory, i.e., “information entropy” defined as the measure of the uncertainty of a random variable [7, 13]. Specifically in assembly processes, information may refer to quantity and variety of parts or fasteners, assembly sequences, product variants, type of machines and tools to be used, etc. In this context, Samy and ElMaraghy [1] developed a novel method to measure assembly complexity of products, modifying the MCAT initially proposed by ElMaraghy and Urbanic [10]. Samy and ElMaraghy H.’s method [1] combines information entropy with the well-established theory of the Design For Assembly (“DFA”) [14], resulting in an effective, quantitative and easy-to-use method. However, in some specific cases it presents some limitations, potentially leading to questionable results. To the best of authors’ knowledge, no previous studies investigated such limitations and thus this work sheds light on some crucial aspects of this method. The document is organized as follows. A brief literature review on assembly complexity assessment methods is presented in Sect. 2. In Sect. 3, the complexity assessment method proposed by Samy and ElMaraghy is discussed. Section 4 provides a thorough conceptual analysis on the Samy and ElMaraghy approach. The final section summarizes the effects of these critical issues on the assessment of assembly complexity.

2 Literature review

Over the years several studies investigated the topic of assembly complexity, adopting various approaches. A brief review of the literature showed that some researchers considered certain product characteristics (e.g. size, shape, material type, product architecture, etc.) as the only sources of assembly complexity; others, in addition to product characteristics, considered the amount and diversity of information to be handled (e.g., quantity and variety of assembly sequences, of parts, of fasteners and of necessary tools, etc.) as a cause of greater operator effort, and thus greater assembly complexity. Finally, others also included external environmental factors, such as availability of work instructions, ergonomics, workstation features, etc. This framework led to the identification of three main approaches [15]:

  • Product-based approach: methods belonging to this class focus primarily on geometrical and physical features of products. Many methods belonging to this category are derived from design-for-assembly techniques [14]. Some examples are the methods proposed by Alkan et al. [2, 16]; Hinckley [17]; Shibata [18]; Sinha [19] and Su et al. [20]. A significant method belonging to this approach was first proposed by Sinha [19] and then modified by Alkan [2, 16], who introduced a quantitative model of assembly complexity based on three contributions: complexity of individual components (i.e., \({C}_{1}\)), complexity of assembly liaisons (i.e., \({C}_{2}\)) and topological complexity (i.e., \({C}_{3}\)). The complexity of a product can thus be computed as follows. Alkan [16] estimated \({C}_{1}\) through the handling times of each component, \({C}_{2}\) through the joining times necessary to complete a liaison between two components, while \({C}_{3}\) is a dimensionless parameter considering the architecture of the product (specifically, it can be calculated through the so-called “energy” of the product adjacency matrix as shown by Sinha [19]).

    $$C = C_{1} + C_{2} C_{3}$$
    (1)

  • Entropy-based approach: these methods assume that the quantity and variety of information to be managed represent crucial variables influencing operators’ choice and thus assembly complexity. Most of these quantitative techniques make use of the concept of information entropy introduced by Shannon [7]. Examples of these methods are those proposed by ElMaraghy and Urbanic [10]; Samy and ElMaraghy [1]; Wang et al.[21]; Zhu et al.[21]. A representative method of this approach is the so-called ‘MCAT’ initially proposed by ElMaraghy and Urbanic [10] and later adapted to measure assembly complexity of products [1]. The modified version by Samy and ElMaraghy [1] will be discussed in detail in the following sections.

  • System-based approach: these methods provide a holistic view of complexity, including variables such as work organization, ergonomics, layouts, mental and physical workload. Given the large number of variables involved, these methods provide more qualitative models that make use of questionnaires and interviews. Examples of these methods are those by Falck et al. [22]; Jenab and Liu [23]; Mattsson et al. [24]; Zaeh et al. [25]. As an example, Mattsson et al. [24, 26] define the so-called “Complexity Index” (i.e., CXI). This method aims at measuring perceived assembly complexity, interviewing workers on five topics (i.e. product variants, layout, work content, tools and information). The questionnaire consists of 26 statements to be rated on a Likert-type scale from 1 to 5. The various answers are then aggregated into an overall index, i.e., the aforementioned CXI.

This paper will focus its attention specifically on the method of Samy and ElMaraghy [1]. This method is widely known in the manufacturing field and fully embodies the peculiarities of the entropy-based approach. Although this heuristic method made a major contribution in this area, some limitations arise from its implementation, especially when comparing different products.

3 Conceptual background

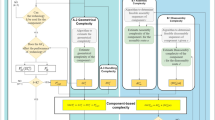
In proposing a Manufacturing Complexity Assessment Tool (MCAT), ElMaraghy and Urbanic linked complexity to three main elements: quantity of information, variety of information and information content [10]. In any given product, process or system, the greater the quantity and diversity of information to be understood and managed, the greater its complexity. This method was based on the concept of information entropy, originally introduced by Shannon [7, 8]. The entropy of a random variable \(X\) can be seen as “a measure of the average uncertainty in the random variable” [13]. The information entropy \(H\left(X\right)\) was defined as follows [8]:

$$H(X) = - k\sum\limits_{{i = 1}}^{n} {p_{i} \log _{2} } p_{i}$$
(2)

Where:

  • \(k\) is a constant (depending on the choice of the unit of measurement);

  • \({p}_{i}\)represents the probability associated to the random variable \(X\);

  • \(n\) is the total number of observed events.

Samy and ElMaraghy [1] adapted the MCAT [10] to measure specifically product assembly complexity. In this model, the quantity and diversity of information encountered in an assembly process is represented through the quantity and diversity of components and fasteners composing a product. Mathematically, they defined product assembly complexity as follows [1]:

$$C_{{product}} = \left[ {\frac{{n_{p} }}{{N_{p} }} + CI_{{product}} } \right][{\text{log}}_{2} (N_{p} + 1)] + \left[ {\frac{{n_{s} }}{{N_{s} }}} \right]\left[ {{\text{log}}_{2} \left( {N_{s} + 1} \right)} \right]$$
(3)

Where:

  • \({n}_{p}\) is the number of unique parts and \({N}_{p}\) is the total number of parts

  • \({n}_{s}\) is the number of unique fasteners and \({N}_{s}\) is the total number of fasteners

  • \(C{I}_{product}\) is a complexity index (calculated using the “difficulty factors” obtained from Design for Assembly analysis [14]).

The calculation of \(C{I}_{product}\) is summarized in the following steps (for further details refer to Samy and ElMaraghy work [1]):

  • Calculation of average handling factor \(C_{h} = \frac{{\sum\nolimits_{1}^{J} {C_{{h,f}} } }}{J}\) and average insertion factor \(C_{i} = \frac{{\sum\nolimits_{1}^{K} {C_{{i,f}} } }}{K}\). \({C}_{h,f}\) and \({C}_{i,f}\) represent respectively the handling and the insertion complexity factor, derived from Design for Assembly analysis [14]. For each potential attribute of a part, there are several difficulty levels (expressed on ordinal scales) to which specific numerical values correspond. Experts assess \(J\) handling attributes and \(K\) insertion attributes suitable for each component and compute a respective average value (i.e., \({C}_{h}\) and \({C}_{i}\)).

  • Calculation of weighted average (handling and insertion) complexity factor.

$$C_{{part}} = \frac{{C_{h} \sum\nolimits_{1}^{J} {C_{{h,f}} + C_{i} \sum\nolimits_{1}^{K} {C_{{i,f}} } } }}{{\sum\nolimits_{1}^{j} {C_{{h,f}} + \sum\nolimits_{1}^{K} {C_{{i,f}} } } }}$$
(4)

  • Calculation of the product complexity index \(CI_{{product}} = \sum\nolimits_{{p = 1}}^{n} {x_{p} C_{{part}} }\) as a composition of the single parts, where \({x}_{p}\) is the percentage of dissimilar parts and \(n\) the number of unique parts.

The contribution of this method, in fact, consists in the definition of a measure of assembly complexity that takes into account both the physical-geometric characteristics of the components (referring to the DFA theory) and the information content to be managed, which affects the effort required to perform the assembly process [1]. The amount and diversity of information is respectively described by the total number of parts (\({N}_{p})\), the total number of fasteners (\({N}_{s})\), and with the variety of parts (\(\frac{{n}_{p}}{{N}_{p}}\)) and fasteners (\(\frac{{n}_{s}}{{N}_{s}}\)). As the quantity and diversity of components and fasteners increase, assembly complexity increases.

4 Conceptual analysis

Based on Samy and ElMaraghy model, complexity (see Eq. 3) is as an a-dimensional value, defined in the set of positive real numbers as follows:

$${C_{{product}} = f\left( {n_{p} ,N_{p} ,n_{s} ,N_{s} ,CI_{{product}} } \right),C_{{product}} \in \left] {0; + \infty } \right[}$$
(5)

where:

$$1 \le n_{p} \le N_{p}, \qquad n_{p} ,N_{p} \in \mathbb{N}$$
$$1 \le n_{s} \le N_{s} , \qquad n_{s} ,N_{s} \in \mathbb{N}$$
$$CI_{{product}} \in \left[ {0;1} \right]$$

Some principles from the representational theory of measurements and indicators [27, 28] were used to analyse the properties of \({C}_{product}\). This theory deals with the formal analysis of the properties of measurement and indicator scales [28]. In this context, \({C}_{product}\) can be interpreted as a derived indicator obtained from a composition of basic indicators. A derived indicator is obtained by an aggregation of a set of indicators (or sub-indicators), while a basic indicator is obtained from the direct observation of an empirical system (in this case, \({n}_{p},{N}_{p},{n}_{s},{N}_{s}\)) [27]. It is worth noticing that \({CI}_{product}\) is also a derived indicator since it is obtained from a weighted average of the insertion and handling difficulty factors.

Samy and ElMaraghy assembly complexity can be rewritten isolating three main contributions: the first considering the diversity between parts, the second taking into account the geometric characteristics of parts, and the third taking into account the diversity between fasteners:

$$C_{{product}} = \frac{{n_{p} }}{{N_{p} }}[{\text{log}}_{2} (N_{p} + 1)] + CI_{{product}} [{\text{log}}_{2} (N_{p} + 1)] + \left[ {\frac{{n_{s} }}{{N_{s} }}} \right]\left[ {{\text{log}}_{2} \left( {N_{s} + 1} \right)} \right]$$
(6)

From Eq. 6, it can be deduced that the dependence of assembly complexity on \({n}_{s},{n}_{p}\) and \(C{I}_{product}\)is a linear dependence. However, the behaviour of \({C}_{product}\) as \({N}_{p}\) and \({N}_{s}\) change is different.

Let assume to analyse the end behaviour of \({C}_{product}\) as each single basic indicator increases, while keeping the others fixed. Due to the contribution of the second term of Eq. 6, it results that \(\mathop {{\text{lim}}}\limits_{{N_{p} \to + \infty }} C_{{product}} = + \infty\). On the other hand, the same behaviour is not observed as \(N_{s} \to + \infty\), since \(\mathop {{\text{lim}}}\limits_{{N_{s} \to + \infty }} C_{{product}} = \gamma = \frac{{n_{p} }}{{N_{p} }}[{\text{log}}_{2} (N_{p} + 1)] + CI_{{product}} [{\text{log}}_{2} (N_{p} + 1)]\), with \(\gamma \in \mathbb{R}\).

Table 1 summarizes the limit values of \({C}_{product}\) as \({n}_{p},{N}_{p},{n}_{s},{N}_{s}\to +\infty\) separately.

Table 1 Limit values of assembly complexity (fixed the other basic indicators)
Full size table

The end behaviour as \({n}_{p}, {n}_{s}\) and \({N}_{p}\) approach positive infinity seems reasonable, since, as the quantity or variety of components and fasteners increase, assembly complexity may also increase. However, the same behaviour is not observed for “low values” of \({N}_{p}\) and \({N}_{s}\), as it will be discussed in Sect. 4.1. In this regard, the following critical issues emerged:

  • Non-monotonicity of \({C}_{product}\),

  • Dependence of \({C}_{product}\) on subjective evaluations,

  • Compensation effect between basic indicators in the \({C}_{product}\) formula.

Each single issue will be analysed in detail in the following subsections.

4.1 Non-monotonicity of Cproduct

The monotonicity of a function \(f\left(x\right)\) can be defined as follows [29]: “Let \(f\left(x\right)\) have an interval \(I\) of \({\mathbb{R}}^{1}\) as its domain and a set in \({\mathbb{R}}^{1}\) as its range. We say that \(f\left(x\right)\) is increasing on \(I\) if \(f\left({x}_{2}\right)\) > \(f\left({x}_{1}\right)\) whenever \({x}_{2}\)> \({x}_{1}\); the function \(f\left(x\right)\) is nondecreasing on \(I\) if \(f\left({x}_{2}\right)\ge f\left({x}_{1}\right)\) whenever \({x}_{2}\)> \({x}_{1}\). The function \(f\left(x\right)\) is decreasing on \(I\) if \(f\left({x}_{2}\right)<f\left({x}_{1}\right)\) whenever \({x}_{2}\)> \({x}_{1}\). The function\(f\left(x\right)\) is nonincreasing on \(I\)if \(f\left({x}_{2}\right)\le f\left({x}_{1}\right)\) whenever \({x}_{2}\)> \({x}_{1}\). A function that has any one of these four properties is called monotone.”

Similarly, a derived indicator is said to fulfil the property of (strict) monotony with respect to a specific sub-indicator if an increase/decrease of the sub-indicator corresponds to an increase/decrease of the derived indicator [27]. The derived indicator \({C}_{product}\) developed by Samy and ElMaraghy H. does not respect this property. As an example, assume a set of products composed of only five types of unique components and fasteners (\({{n}_{p}=n}_{s}=5\)). Figure 1 shows the graph of \({C}_{product}\) as \({N}_{p}\), \({N}_{s}\) and \(C{I}_{product}\) change, respectively for \(C{I}_{product}=\left\{0.5;0.6;0.7;0.8;0.9;1\right\}.\) For each value of \(C{I}_{product}\), a specific complexity surface is defined. The value of \({CI}_{product}\) mainly translates the surface upward. This is a reasonable behaviour since higher values of \({CI}_{product}\) increase the overall assembly complexity. From a preliminary analysis of the surfaces, it can be seen that, counter-intuitively, complexity is not monotonically increasing as the number of components or fasteners grow. This result can be partially explained by the fact that, given the number of unique parts and fasteners \(\left({n}_{p}={n}_{S}=5\right)\), the degree of diversity decreases as \({N}_{p}\)and \({N}_{s}\) increase. Figures 2 and 3 show the graph of \({C}_{product}\) as function of \({N}_{p}\) and \({N}_{s}\) with different values of \({n}_{p}\) and \({n}_{s}\) (respectively \({n}_{p}={n}_{s}=1\) and \({n}_{p}={n}_{s}=20\)). As shown, the three response surfaces not only exhibit non-monotonic behaviour, but as the initial conditions change, they also present different concavities. These unexpected results are mainly due to compensation issues between the terms of \({C}_{product},\) as it will be further discussed in Sect. 4.3. On the same topic, let us consider the following case: a product consisting of two types of parts and only one type of fastener. A practical example of such a product might be the drive chain of a bicycle. A drive chain is in fact made up of a set of links connected by two pins. Each link consists of four plates of two types, the inner plates and the outer plates (see Fig. 4).

Fig. 1
figure 1

Assembly complexity as function of Np and Ns with: ns=5, np=5 and CIproduct = [0.5;1]

Full size image
Fig. 2
figure 2

Assembly complexity as function of Np and Ns with: ns=1, np=1 and CIproduct = [0.5;1]

Full size image
Fig. 3
figure 3

Assembly complexity as function of Np and Ns with: ns=20, np=20 and CIproduct = [0.5;1])

Full size image
Fig. 4
figure 4

Front view scheme of a bicycle chain

Full size image

Let \(C{I}_{product}=0.5\) computed using average difficulty coefficients for manual assembly proposed by Samy and ElMaraghy [1]. The whole assembly process of a bicycle chain can be broken down into shorter assembly tasks, each consisting of adding progressively a couple of plates to previous ones using one pin. In this case, assembly complexity can be expressed as a function of \({N}_{p}\), given that \({N}_{s}={(N}_{p}-2)/2\). Hence, from Eq. 3, \({C}_{product}\left({N}_{p}\right)\) can be formulated as follows:

$$C_{{product}} \left( {N_{p} } \right) = \left[ {\frac{2}{{N_{p} }} + 0.5} \right]\left[ {{\text{log}}_{2} \left( {N_{p} + 1} \right)} \right] + \left[ {\frac{1}{{(N_{p} - 2)/2}}} \right]\left[ {{\text{log}}_{2} \left( {\frac{{N_{p} - 2}}{2} + 1} \right)} \right]$$
(7)

Similarly, \({C}_{product}\) can be expressed as a function of \({N}_{s}\) since \({N}_{p}=2{N}_{s}+2\).  Figs. 5 and 6 show the curve of \({C}_{product}\) as a function of \({N}_{p}\) and of \({N}_{s}\). Note that \({C}_{product}\) under these conditions is not monotonic and has a minimum value. This behaviour can be easily shown, assuming, as a first approximation, that \({C}_{product}\) is a continuous function (\({\forall N}_{p}\in \mathbb{R}\)), setting the first derivative to zero:

$$\frac{{dC_{{product}} }}{{dN_{p} }} = \frac{1}{{N_{p} {\text{ln}}\left( 2 \right)\left( {\frac{{N_{p} }}{2} - 1} \right)}} - \frac{{{\text{ln}}\left( {\frac{{N_{p} }}{2}} \right)}}{{2{\text{ln}}\left( 2 \right)\left( {\frac{{N_{p} }}{2} - 1} \right)^{2} }} + \frac{{\frac{2}{{N_{p} }} + \frac{1}{2}}}{{{\text{ln}}\left( 2 \right)\left( {N_{p} + 1} \right)}} - \frac{{2{\text{ln}}\left( {N_{p} + 1} \right)}}{{N_{p}^{2} {\text{ln}}\left( 2 \right)}} = 0$$
(8)

In this specific case, the Eq. 8 admits a minimum for \({N}_{p}=\text{13,93}\) (stationary point). Similar considerations can be made for \({N}_{s}\) (see Fig. 6).

Fig. 5
figure 5

Bicycle chain complexity as function of Np (Ns=(Np-2)/2, ns=1, np=2 and CIproduct= 0.5)

Full size image
Fig. 6
figure 6

Bicycle chain complexity as function of Ns (Np= 2Ns+2, ns= 1, np= 2 and CIproduct = 0.5)

Full size image

For a fixed value of \(C{I}_{product}\), from Fig. 5 we observe about the same assembly complexity of 3.32 for products respectively composed of 4 and 58 parts (the two values are not exactly the same since \({C}_{product}\) is computed for discrete values of \({N}_{p}\)). Hence, in this specific case, the Samy and ElMaraghy H.’s method is unable to distinguish between the assembly complexity of a chain with \({N}_{p}=4\) and \({N}_{s}=1\) from a chain composed of \({N}_{p}=58\) and \({N}_{s}=28\) elements. It can be noted that the \({C}_{product}\) function (see Figs. 5 and 6) presents a decreasing trend for “low values” of \({N}_{p}\) and \({N}_{s}\) closer to 0, i.e., for values of \({0<N}_{p}<14\) and for \(0<{N}_{s}<6\). However, it is not possible to define intervals of \({N}_{p}\) and \({N}_{s}\), generalisable to all products, where the stationary point may occur. In fact, although the existence of this minimum does not seem to be exclusively linked to this example, the position of the minimum points vary as \({n}_{p}\), \({n}_{s}\) and \(C{I}_{product}\) change. As a second example, let us consider a set of products with the following characteristics \(\left( {{n}_{p}{\text{ = 5, }} {n}_{p} {\text{ = 10, }} {n}_{s} {\text{ = 5, }} {n}_{s} {\text{ = 10}}} \right)\). Let the value of \(C{I}_{product}=0.8\) and assume that each part is connected to another by two screws. Mathematically, this condition can be expressed as \({N}_{s}=2({N}_{p}-1)\). Figure 7 shows the related graphs of assembly complexities considering different values of \({n}_{p}\) and \({n}_{s}\).

Fig. 7
figure 7

Assembly complexities as function of Np and Ns (CIproduct=0.8, Ns=2(Np−1))

Full size image

From a conceptual point of view, as the number of parts of a product increases, it would be expected that the assembly complexity presents a monotonous trend. On the contrary, one can observe (see Figs. 5, 6 and 7) the presence of a stationary point thus preventing the ability to distinguish the complexity of different products. The same \({C}_{product}\) can in fact be referred to products with very different \({N}_{p}\) values, leading to debatable results.

4.2 Dependence of Cproduct on subjective evaluations

Another critical issue of the methodology by Samy and ElMaraghy H. is the use of \({CI}_{product}\). With reference to the bicycle chain (\({n}_{p}=2, {n}_{s}=1)\), Fig. 8 shows assembly complexities for different values of \({N}_{p}\) (see Eq. 6), when \({CI}_{product}\) varies from 0.3 to 1. For different values of \({CI}_{product}\), different behaviours of the complexity curves are observed. In particular, as \({CI}_{product}\) increases, a point of minimum is shown. Consequently, again the same value of \({C}_{product}=3.09\) may refer simultaneously to a bicycle chain with \({N}_{p}=4\) and \({CI}_{product}=0.4\), or with \({N}_{p}=30\) and \({CI}_{product}=0.5\). Although \({N}_{p}\) and \({CI}_{product}\) increase simultaneously, the assembly complexity does not change.

Fig. 8
figure 8

Assembly complexity as function of Np (ns=1, np=2, Ns=(Np−2)/2, CIproduct= [0.3;1])

Full size image
Fig. 9
figure 9

Assembly complexity as function of Np (ns=5, np=5, Ns=2(Np−1), CIproduct= [0.3;1])

Full size image

The effect of \({CI}_{product}\) on assembly complexity is even more noticeable if the initial values of \({n}_{p}\) and \({n}_{s}\) change. Figure 9 shows assembly complexity curves for \({n}_{p}=5, {n}_{s}=5\) and \({N}_{s}=2({N}_{p}-1)\). For values of \({CI}_{product}\) less than 0.4, the curve decreases and then flattens in the interval \(N_{p} \in [0;100]\). As \({CI}_{product}\) increases, the minimum point shifts progressively to the left (smaller values of \({N}_{p}\)). The reason of this behaviour can be attributed to the original formulation of the model by ElMaraghy and Urbanic [10]. The first two terms of Eq. 6, derived from ElMaraghy and Urbanic’s previous proposal [10], can be expressed as follows:

$$C^{'} _{{product}} = \frac{{n_{p} }}{{N_{p} }}{\text{log}}_{2} \left( {N_{p} + 1} \right) + CI_{{product}} {\text{log}}_{2} \left( {N_{p} + 1} \right)$$
(9)

Already for this formulation of the model, the additive composition of these two terms can lead to the occurrence of a stationary point. This anomalous behaviour of the complexity function is due to the introduction of the term “\(C{I}_{product}\)” in the original formulation of information entropy (see Eq. 2). As further evidence, note the graphs in Fig. 10 showing the trend of \(C^{\prime}_{{product}}\) with \({n}_{p}=2\) and \(N_{p} \in [0;100]\). Figure 10a shows the behaviour of \(C^{\prime}_{{product}}\) with \(C{I}_{product}=0\), and Fig. 10b with \(C{I}_{product}=0.5\). It can be inferred how the introduction of the term \(C{I}_{product}\) leads the function to switch from a monotonous decreasing to a non-monotonous trend.

Fig. 10
figure 10

C′product as function of Np with: (a) \(C{I}_{product}=0\) and (b) \(C{I}_{product}=0.5\)

Full size image

Moreover, \(C{I}_{product}\), although based on objective values, is influenced by the competence of the experts. The so-called “difficulty factors” used to compute \(C{I}_{product}\) are objective, reliable and widely used in the literature. Subjectivity issues may emerge depending on the assessor’s level of experience. Hence, in assessing the insertion and handling attributes of the same product, different experts might provide different assessments. In general, an indicator is said to be subjective when the mapping of empirical manifestation into symbolic manifestation depends on subjective judgements [27]. In conclusion, the introduction of \(C{I}_{product}\) may generate some drawbacks, reducing the robustness of this method.

4.3 Compensation issues between basic indicators in the Cproduct formula

The nonmonotonic trend of \({C}_{product}\) may be mainly due to a compensation phenomenon. In general, consider a derived indicator \(D\) obtained through additive aggregation of two sub-indicators \({I}_{1}\) and \({I}_{2}\). The derived indicator \(D\) is said to satisfy the compensation property if the following two conditions are fulfilled [27]:

  • a variation of \({I}_{1}\) (i.e., \({\varDelta I}_{1}\)) determines a variation \(\left( {\Delta {{D}}} \right)\) of the derived indicator \(D\)

  • there exists a variation of \({I}_{2}\) \(\left( {\Delta I_{2} } \right)\) that compensates the previous \(\Delta {{D}}\)

If a derived indicator fulfils the property of compensation, then a substitution rate can be calculated. The substitution rate is defined as the variation of the sub-indicator \(\left( {\Delta I_{1} } \right)\) that compensates a second variation in the other sub-indicator \(\left( {\Delta I_{2} } \right)\) such that the derived indicator (D) remains constant [27]. As an example, let us consider three different products (A,B,C) with the characteristics shown in Table 2.

Table 2 Values of basic indicators for the three different products (A,B,C)
Full size table

The application of Samy and ElMaraghy model (Eq. 6) provides respectively the following results:

$$C_{{product,A}} = {\text{6,46}}$$
$${C}_{product,B}=\text{6,72}$$
$${C}_{product,C}=\text{5,84}$$

Compared with A, product B is characterized by a greater number of unique and total parts and fasteners and by a greater value of \(C{I}_{product}\). In this case, the model indicates that the complexity of B is higher than the complexity of A (\({C}_{product,B}>{C}_{product,A}\)).

On the opposite, if we compare product C and product A, even though: \({n}_{p,C}>{n}_{p,A}; {N}_{p,C}>{N}_{p,A}; {n}_{s,C}>{n}_{s,A}\); \({N}_{s,C}>{N}_{s,A}\) and \(C{I}_{product,C}>C{I}_{product,A}\), the assembly complexity of product C is less than that of product A (\({C}_{product,A}>{C}_{product,C}\)). These questionable results are due to the compensation issues between the contribution of the basic indicators, composing \({C}_{product}\).

Even though degrees of variety of parts and fasteners decrease, i.e., \(\frac{{n}_{p,C}}{{N}_{p,C}}<\frac{{n}_{p,A}}{{N}_{p,A}}\), it appears controversial that the assembly complexity of a product consisting of 25 components and 100 screws \(({N}_{p,C}=25, {N}_{s,C}=100)\) is less complex than that of a product consisting of 5 components and 5 screws \(({N}_{p,A}=5, {N}_{s,A}=5)\).

For further verification, suppose to calculate the substitution rate between \({n}_{p}\) and \({n}_{s}\). Since \({n}_{p}\) and \({n}_{s}\) are natural numbers, the substitution rate between \({n}_{p}\) and \({n}_{s}\) is calculated using the finite difference method [27]. Hypothesising a contemporary variation of \({n}_{p}\) and \({n}_{s}\), for \({C}_{product}\) constant, Eq. 3 can be rewritten as:

$$C_{{product}} = \left( {\frac{{n_{p} + \Delta n_{p} }}{{N_{p} }} + CI_{{product}} } \right){\text{log}}_{2} (N_{p} + 1) + \left( {\frac{{n_{s} + \Delta n_{s} }}{{N_{s} }}} \right){\text{log}}_{2} (N_{s} + 1)$$
(10)

Replacing the expression of \({C}_{product}\) with Eq. 3, it results that:

$$\left[\frac{{n}_{p}}{{N}_{p}}+C{I}_{product}\right][{\text{log}}_{2}({N}_{p}+1)]+\left[\frac{{n}_{s}}{{N}_{s}}\right][{\text{log}}_{2}\left({N}_{s}+1\right)=\left(\frac{{n}_{p}+\varDelta {n}_{p}}{{N}_{p}}+C{I}_{product}\right){\text{log}}_{2}({N}_{p}+1)+\left(\frac{{n}_{s}+\varDelta {n}_{s}}{{N}_{s}}\right){\text{log}}_{2}({N}_{s}+1)$$
(11)
$$\frac{{\Delta n_{p} }}{{N_{p} }}{\text{log}}_{2} (N_{p} + 1) + \frac{{\Delta n_{s} }}{{N_{s} }}{\text{log}}_{2} \left( {N_{s} + 1} \right) = 0$$
(12)
$$\Delta n_{p} = - \frac{{N_{p} }}{{N_{s} }}\frac{{{\text{log}}_{2} (N_{s} + 1)}}{{{\text{log}}_{2} (N_{p} + 1)}}\Delta n_{s}$$
(13)

As can be observed, the substitution rate is not a constant. It depends strongly on values of \({N}_{p}\) and \({N}_{s}\). Thus, it can be stated that the substitution rate of \({C}_{product}\) is influenced by the so-called “operating point”, i.e., initial values of basic indicators [27].

With reference to the example of a bicycle chain, assume a chain composed of 40 plates (i.e., \({N}_{p}=20\) and \({N}_{s}={(N}_{p}-2)/2=9\) elements). The substitution rate between \({n}_{p}\) and \({n}_{s}\) is \(\Delta {n}_{p} { = - 1}{\text{.68}}\Delta {n}_{s}\). Now, consider the same bicycle chain of a different length (i.e., \({N}^{'}_{p}=80\) and \({N}^{'}_{s}=39\)). In this second case, the substitution rate between \({n}_{p}\) and \({n}_{s}\) is \(\Delta {n}_{p} { = - 1}{\text{.72}}\Delta {n}_{s}\). Due to the dependence on \({N}_{p}\) and \({N}_{s}\), variations in \({n}_{p}\) and \({n}_{s}\) impact the assembly complexity differently, even though the reference product is the same. Hence, conceptual difficulties may arise while comparing even similar products with different \({N}_{p}\) and \({N}_{s}\).

5 Conclusions

Samy and ElMaraghy method has proven to be very easy to implement, thus providing product and process designers with an effective quantitative method to assess the product assembly complexity. A great advantage of this method lies in its merging of two aspects that impact the perceived complexity and thus the effort required to assemble a product, i.e., the physical–geometric characteristics of a product and its so-called information content. However, from a theoretical point of view, it presents some critical issues. The main weaknesses identified can be summarized as follows:

  • The additive model is defined as the sum of three contributions. This model structure can give rise to compensation problems that may lead to occurrences of stationary points. The presence of minimum points leads to assign the same complexity to very different products (see Sect. 4.1). Contrary to what might be expected, assembly complexity is not defined on a monotonically increasing scale as the number of components or fasteners increases.

  • The substitution rate between couple of basic indicators (i.e., \({n}_{p},{N}_{p},{n}_{s},{N}_{s}\)) is not constant and generally depends on their initial values. However, this model does not fully explain why variations in one basic indicator are compensated differently as operating point changes. In light of what has been shown (see Sect. 4.3), this method might not be entirely reliable when comparing even similar products.

  • Another weakness lies in the introduction of the term “\(C{I}_{product}\)” that partly derives from experts’ subjective judgements (see Sect. 4.2). This does not guarantee that results will be the same if the assessor changes.

All these aspects may result in the possibility of obtaining questionable results, especially while comparing multiple products. As shown in Sect. 4.2, the introduction of \(C{I}_{product}\) led to the occurrence of questionable stationary points, whose position depends also on \({n}_{p}\) and \({n}_{s}\) values.

A possible improvement would be to evaluate \(C{I}_{product}\) and \({C}_{product}^{*}\) separately: on the one hand, \(C{I}_{product}\), and on the other hand, a new product complexity value, i.e., \({C}_{product}^{*}=\frac{{n}_{p}}{{N}_{p}}[{\text{log}}_{2}({N}_{p}+1)]+\left[\frac{{n}_{s}}{{N}_{s}}\right][{\text{log}}_{2}\left({N}_{s}+1\right)]\), obtained by removing the \(C{I}_{product}\) term from Eq. 3. In this way, both the physical-geometrical characteristics of the product and the quantity and variety of parts and fasteners would be taken into account, excluding the possibility that the new \({C}_{product}^{*}\) may present minimum points. A conceptual map of assembly complexity may be defined (see Fig. 11), basing on the values assumed by \({C}_{product}^{*}\) and \(C{I}_{product}\).

Fig. 11
figure 11

Assembly complexity conceptual map as \({C}_{product}^{*}\) and \(C{I}_{product}\) vary

Full size image

Four main areas can be identified:

  • Low complexity (low \(C{I}_{product}\)−low \({C}_{product}^{*}\)) : This area includes products that are relatively simple to assemble, e.g., products consisting of equal, symmetrical and light parts. Such products do not require excessive physical or cognitive effort from the assembly operator. Small shelving units may represent an example of this category, since they’re mainly composed of equal rectangular pieces.

  • Morphology-intensive complexity (high \(C{I}_{product}\)−low \({C}_{product}^{*}\)): products falling in this area are composed of parts that share equal characteristics (hence with a reduced variety of information). However, due to their physical/geometrical features (e.g., difficult to manipulate, tight tolerances, resistance to insertion, poor accessibility etc.), they can demand significant physical effort from the assembly operator. The bicycle drive chain discussed in this paper could be categorized as an example of “morphology-intensive complexity”. The inner and outer plates are indeed small, difficult to handle and align. This raises the value of \(C{I}_{product}\). However, since it is composed of only two type of parts and one type of fasteners, considering typical chain lengths (approximately 114 links), the value of \({C}_{product}^{*}\) will be low, close to 0.

  • Information-intensive complexity (low \(C{I}_{product}\)−high \({C}_{product}^{*}\)): products belonging to this area are characterised by various different components. Although they are not difficult to handle and join, the variety of parts and fasteners results in a greater cognitive effort required to correctly assemble them. Some electro-mechanical products, such as small water pumps, belong to this category.

  • High complexity (high \(C{I}_{product}\)−high \({C}_{product}^{*}\)): this area includes products consisting of a great variety of parts and fasteners and also having physical characteristics that make their handling and joining process difficult. This results in greater both physical and cognitive effort. An example of this kind of products could be electronic boards, since they’re made of various small wires, resistors, buttons to be assembled in restricted accessibility conditions.

Obviously, the proposed preliminary map requires appropriate numerical thresholds identifying univocally the four areas of complexity. Future research will focus both on the empirical definition of such thresholds and on developing a way to effectively aggregate \(C{I}_{product}\) and \({C}_{product}^{*}\) to further improve Samy and ElMaraghy method.