1 Introduction

High technological innovations, which are radically changing the manufacturing industries, are strictly related to the increasing level of complexity of new products as well as the possibility of a push customization [1]. In addition, the world is facing with the need to create circular economies, reducing material waste, and breathing new life into seemingly end-of-life products or components [2].

For these reasons, being able to assess the product's complexity and direct its design towards multi-life cycle is a crucial step in supporting the designers in choosing the most suitable manufacturing technology and the most efficient planning of assembly and disassembly [3].

To be competitive, companies need to modify the approach to their business; moreover, selecting the best production technologies for the specific product is a significant decision-making process, involving the consideration and the evaluation of different aspects [4, 5].

Several research in the literature addressed the problem of technology selection and assembly/disassembly operations, dealing with various aspects such as product complexity, costs, assembly and disassembly issues, and more. Complexity has been recognized as a critical issue in manufacturing systems due to the difficulty to understand it and, as a result, to measure it [6].

So, identifying, analyzing and understanding complexity factors represent the first step to manage the complexity at a strategic level to improve company competitiveness, especially in terms of technology selection and order response time [7].

The state of the art about the complexity in science is considered multidimensional and it has been explored from three points of view: (i) Design and Product Development Complexity, (ii) Manufacturing and Manufacturing System Complexity, (iii) Business and Marketing Complexity [8]. Another way of looking at product complexity is to relate it to both the individual component and the whole assembly.

A literature gap has been found for what concerns the development of a methodological approach that brings together all the problematics related to individual parts and to the whole assembly as well. The study proposed here-in tackles the challenge of bridging this gap by presenting a novel methodological framework for assessing product complexity with an overall view, integrating every aspect of product life cycle.

This paper continues an earlier work [9] in which the authors investigated the problem of determining a geometrical complexity index of a CAD part, to be used in conjunction with assembly complexity, costs, and production volume to select the most suitable production technology. Building on this, the present paper proposes a novel methodological framework useful for supporting both the technology selection process and the assembly/disassembly operations based on the combination of component-based complexity and system-based complexity. Specifically, the procedure combines geometrical aspects with manufacturing, technical aspects, and additional aspects related to both assembly and disassembly, with the prospect of future remanufacturing. The approach is based on two main information: the CAD model of parts and the product’s Assembly Structure Matrix (ASM).

However, it was decided to divide the study into two parts as it is necessary to make the evaluation procedures as objective as possible in order to streamline and make decision support effective. In fact, although several studies in the literature have investigated the issues of product complexity, from a geometrical point of view there is no established metric. A comprehensive definition of geometrical complexity, related to the stand-alone component, as defined in the proposed methodology, is crucial, especially when selecting the production technology for a given product. This paper deals with the first part of the overall study. In addition to the proposal and detailed description of the novel methodological framework for the assessment of the overall product complexity index, the main focus is on the geometrical complexity. Indeed, an index, more comprehensive than the one previously defined in [9], was defined through both experimental and numerical surveys, involving CAD modelling experts and implementing an interactive routine in Grassoppher plug-in for Rhinoceros®, able to evaluate geometrical features from CAD models of parts.

The second part of the research, addressed in a subsequent article, deals with the overall complexity of the entire assembly and propose the application of the methodological framework to a real application case.

The reminder of the article is described as follows: in Sect. 2, the state of the art about product complexity is presented; the methodological framework is proposed and described in Sects. 3; 4 describes methods and tools to define a geometrical complexity index, which is the focus of this article; Sect. 5 concludes the paper.

2 Literature review

Exhaustive reviews about the historical approaches to the design and manufacturing complexity, which are considered in this study, can be found in the literature [8, 10].

Individual part complexity may be generally related to its geometry. Since the 1980s, several methodologies for evaluating geometrical (or shape) complexity have been introduced. In the first decade of 1980s, the technique of expert systems was widespread, and there were mathematical programs that provided complexity indexes based on operators’ input. In the 1990s, mathematics has been simplified, leaving the assessment of certain parameters to the subjective judgment of experts by means of questionnaires. Additionally, there are also several more rigorous approaches based on objective system data.

In applications such as computer graphics and Finite Element Analysis, polygonal meshes are defined in terms of the geometry and connectivity of the nodes. The shape complexity measures how entrapped the polygon is and it is closely associated with geometry, organizational and operational aspects of CAD software. Indeed, often it is also called CAD-complexity [11]. The complexity of CAD modelling is subjective and varies individual to individual, depending also on the strategic use of the functionalities provided by the CAD software. Current parametric feature-based CAD software facilitates the creation of fully parameterized products, and the user can manage how the model can vary thanks to a set of (even complex) relationships among variables. So, it is reasonable pointing out that the complexity of the design activity is related to the complexity of the product geometry, that has implications not only on the design but especially in the production phase. In fact, in the mechanical field there is a need to produce increasingly complex and multi-functional parts, so the need for the development of a model to estimate complexity as in additive as in the traditional manufacturing is essential.

In the literature, several evaluation metrics have been proposed for objectively assessing the geometrical complexity of the part, based on the geometrical features of its CAD model. These metrics were defined in different ways, considering features such as: surface area, part volume and its bounding box volume [12, 13]; convex envelope of the part [14]; number of cored features and thickness of the part [12, 15]; number of surfaces [16]; curvature for curved shapes [17]; number of triangles representing an.stl file [18]. The metrics are described in detail in Sect. 3. Other factors affecting the geometrical complexity of a CAD model can be addressed to Systems Engineering [19], not in the scope of this research, which will be increasingly present in the products of the future.

Considering other aspects related to the product complexity, those that concern product development, and its manufacturability cannot be separated from the consideration of the whole assembly and the interaction between its parts.

Most studies addressed the design and the manufacturing complexity through the information-theoretic approach. MacDuffie et al. [20] demonstrated that part complexity measure, in terms of part variation or commonality among other product family models, negatively impacts the productivity. Static complexity measures for quantifying manufacturing complexity have been already proposed. Deshmukh et al. [21] linked the manufacturing complexity to the processing times of a component mix for every task at a defined machine. Entropy theory has been adopted by Fujimoto et al. [22] to measure the manufacturing complexity of a product family. Authors assessed the impact of product variety on the assembly processes. Park et al. [10] demonstrated that static design and static manufacturing complexity negatively impact on production cost and lead time. Samy & ElMaraghy proposed models to measure product assembly complexity in manual and automated assembly lines [23, 24]. Authors build a univocal complexity index to quantitatively measure the complexity of assembly a component on the basis of its handling and insertion attributes. Su et al. [25] build a function based on four evaluation criteria, i.e. assembly angle, assembly direction, reorientation and stability, to automatically select the optimal assembly sequence. The fuzzy set theory and clustering analysis have been adopted to allocate criteria and weights. The link between perceived assembly complexity and product complexity has been firstly addressed by Alkan [26]. The author provided an empirical prediction model. Complexity was measured by considering handling and insertion features of the parts and the connectivity patterns as well; whereas perceived complexity was represented by the subjective interpretation of the participant on the feeling and difficulty connected to the assembly tasks. Conner et al. [15] tried to facilitate product development decisions by proposing a manufacturability map based on the key attributes of a product: complexity, customization, and production volume. Contextually, they proposed also the so-called Modified Complexity Factor (MCF) based on geometrical attributes of the part. However, this study is still unfinished since it does not correlate numerical data with subjective judgments and does not include any reference on assembly and disassembly issues. Soh et al. [27] included both assembly and disassembly aspects in a design framework, although from a purely remanufacturing perspective. They dealt with Design for Assembly (DfA) and Design for Disassembly (DfD) simultaneously and proposed a complexity index for the second one. However, they did not consider any geometrical feature, except the characteristic sizes (larger dimensions in both longitudinal and transverse directions) useful to assess the disassembly feasibility. In [28], the authors investigated parts consolidation issues, in perspective of Design for AM (DfAM), by proposing a double level approach: the study of Design Structure Matrix (DSM) for identifying possible candidates for consolidation (i.e. merging of multiple parts); the evaluation of geometrical complexity, by means of MCF, for checking the manufacturability. This research limited only to this aspect. Instead, Buecher et al. [29] changed perspective and developed an Artificial Intelligence (AI) based predictive model for estimating production costs by comparing several technologies, to select the most suitable for each component of the system. About costs estimation for machining parts, Armillotta [30] proposed a model which combines product complexity and additional information able to predict machining time with average errors of 25%. However, also this research is not exhaustive and limited to the only subtractive manufacturing technologies.

An exhaustive review has been conducted by Hamzeh and Xu [5]. They provided a taxonomy of research works published between 1990 and 2017 about the trends in technology selection. The results of the analysis suggest there has been a significantly growth in the use of Multi-Attributes Decision Making (MADM) methods for selecting the technology in manufacturing, as actually done in other subsequent research [31, 32].

3 Methodological framework

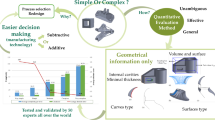
The proposed methodological framework, reported in Fig. 1, aims to support designers during the early design phase, which strongly influences operations during manufacturing and assembly. As compared to the previous literature on this topic, the proposed approach considers all the phase of the product life cycle to determine a univocal measure of the product complexity. It is argued that the implementation of such integrated approach is justified by the need to go beyond the limits of the design and manufacture phases of the company and look at the Life Cycle Thinking [33]. The methodology is designed for speeding up the decision process about the product configuration through a well-defined procedure that is able to provide a quantitative measure to compare alternative designs. However, human interaction is always necessary for the definition of the manufacturing technologies, the design of the alternative components’ configurations, the identification of assembly/disassembly routes and during the assessment phase [23]. In a variable and unpredictable environment, this approach could have an operative and strategical value.

Fig. 1
figure 1

Methodological framework. The A.2 block is in-depth investigated in the next Sect.  4

Full size image

Typically, products have several configurations, due to strategic business choices. In addition, as-is design can change over time to accommodate the customer’s requirements (mass customization) or to facilitate end-of use operations, such as remanufacturing. Measuring product complexity in such contexts becomes crucial to enhance the Company's competitiveness, tending towards the detection of the product configuration with the minimum value of overall complexity.

The starting information of the methodology are the components’ CAD models and the Assembly Structure Matrix (ASM) of the considered product design. The expected production volume and the cardinality of the essential components in the Bill of Material (BOM) are extra information that might be useful to estimate the manufacturing complexity and to determine feasible assembly routes [5].

Design complexity has been associated to geometrical complexity of the component in this study, meaning that the design complexity is derived from the geometrical features of the component. The overall complexity index of the product configuration c is an aggregated index based on the Geometrical Complexity, the Manufacturing Complexity and Assembly/Disassembly Complexity of its parts. The product configuration c represents a product variant within a product family. The framework in Fig. 1 shows the logical flow that allows determining a univocal Product Complexity Index (\({PCI}_{c}\)) for the product configuration c, according to the following Equation:

$${PCI}_{c}={MC}_{c}+{\sum }_{i=1}^{{N}_{c}}SAC{I}_{i}^{ c} +\left({\sum }_{i=1}^{{N}_{c}}OGC{I}_{iad,opt}^{ c}\right)\times TC{I}_{ASM}^{ c}$$
(1)

where:

  • \(SAC{I}_{i}^{ c}\) is the Stand-Alone component Complexity Index of component i in the product variant c,

  • \(OGC{I}_{iad}^{ c}\) is the On-Grid component Complexity Index of component i in product variant c for the assembly route a and the disassembly route d,

  • \(TC{I}_{ASM}^{ c}\) is the Topology Complexity Index of the product variant c,

  • \({MC}_{c}\) Manufacturing Complexity of product configuration c,

  • Nc is the number of essential components corresponding to the part variants for the product variant c,

  • ASM is the Assembly Structure Matrix.

All these contributions will be described in detail below.

The essential components (Nc) within the product configuration c are the part variants that appear in the minimal Liaison diagram [34] of the product configuration c, meaning that quasi-component (screw, bolts, nuts) and virtual components (soldered and welded joints) are excluded from the assessment.

The mathematical formulation to derive the Product Complexity Index (PCI) is inspired by Alkan et al. [34], who used the physical Huckel’s theory [35], to model an overall complexity index that considers component complexity, interface complexity and topological complexity.

The methodology resumes this formulation defining a product complexity index starting from the measurement of two component-based complexity indexes:

  1. A.

    Stand-Alone component Complexity Index (\(SAC{I}_{ik}^{ c}\)),

  2. B.

    On-Grid component Complexity Index (\(OGC{I}_{iad}^{ c}\)).

As shown in the framework, components’ CAD models are the main inputs for the blocks in the box A which refers to the Stand-Alone component Complexity, while the ASM of the product is utilized to estimate the complexity associated to assembly and disassembly operations (box B in the framework). Moreover, information within the ASM can be used to calculate the Topology Complexity (\(TC{I}_{ASM}\)) of the product [34].

3.1 Stand-alone component complexity index

This metric measures the component complexity looking at the component as a stand-alone part. In [34], the Stand-Alone component Complexity Index was only made up of the part Handling Complexity (\(H{C}_{i}^{c}\), A.3 block) that can be obtained by using the handling attributed tables provided by the Lucas’ method [36] or by Samy & ElMaraghy [24]. Since the methodological framework here-in proposed aims to provide a screening index that describes the product complexity by considering all the production steps, other two stages have been added to characterize this complexity. Thus, the component’s design, the handling efforts and the performance of the production technology in processing component i all contribute to define a univocal index for the complexity of the component i in the product configuration c (\({SACI}_{i}^{c}\)), as is shown in Eq. 2.

$${SACI}_{i}^{c}= {{GC}_{i}^{c}+HC}_{i}^{c}+{P}_{i,opt}^{c}$$
(2)

where, \({GC}_{i}^{c}\), \({HC}_{i}^{c}\) are respectively the Geometrical Complexity Index, the Handling Complexity Index associated to the component i in the product configuration c. The last term \({P}_{i,opt}^{c}\) is a performance measure linked to the technology adopted to produce the component i (see section A.1). Since terms in Eq. 2 have different unit of measure and scales, normalization is needed. Moreover, the complexity regarding the manufacturing, the geometry and the handling of the specific component i is not an absolute value but it is always relative to standard/reference values that are established by the experts. Normalization of complexity factors can be performed according to reference values set by the decision maker(s). These reference values could be the minimum/maximum admissible manufacturing cost, or time, the minimum/maximum value of design complexity (see Sect. 4) associated to a specific component variant, the minimum/maximum feasible handling effort.

3.1.1 Technology selection & manufacturing complexity

Manufacturing complexity in a product family is a measure of uncertainty linked to the attainment of commonality of manufacturing process to produce a product family. Thus, the information content that describe the process variety related to a product variant can be used as a measure of the manufacturing complexity. According to Park et al. [10], the static Manufacturing Complexity of the product configuration (or product variant) c is:

$${MC}_{c}= \sum_{k}{I}_{kc}=\sum_{k}(-{log}_{2}({\gamma }_{kc}))$$
(3)

In Eq. 3, \({I}_{kc}\) is the information content of the production technology k for the product variant c and \({\gamma }_{kj}\) is the probability (commonality) of sharing the technology k for product variant c (Eq. 4):

$${\gamma }_{kc}=\frac{{n}_{kc}}{{N}_{c}}$$
(4)

where \({n}_{kc}\) is the number of components in product variant c that are processed by the technology k.

Performance of the production technology k can, or cannot, be affected by the component’s Geometrical Complexity. The methodology considers this aspect and distinguishes between these two cases. In the view of the technology selection, this consideration is discriminant. Indeed, some free-form fabrication technologies, such as Additive Manufacturing, have reached the technological maturity to be used in traditional manufacturing contexts for producing very complex end-usable parts and for enabling the part consolidation within critical assemblies [37]. While the link between Design and Geometrical Complexity is straightforward, the same cannot be said for the connection between the production technology and geometrical complexity. However, it was demonstrated that the combination of Geometrical Complexity and technological parameters can be adopted to estimate the completion time or the production cost of the manufacturing process [30, 38].

The set of technologies (processes) into the production system is known (\(K\)). At each iteration, the procedure firstly checks if the technology k can process the component i. Then, there is another check to establish if the performance of the production process (performance can be measured in terms of production time, cost, resource consumption) is affected by the Geometrical Complexity of the parts. The output is the performance \({P}_{ik}^{c}\) of technology k when component i is processed. When all the available and feasible technologies are checked, the performance measure that enters Eq. 2 will be the value associated to the best performing technology for the specific component and regarding a defined performance measure of the production. The procedure counts how many times each technology enters the formula. Once all components are examined, the term \({n}_{kc}\) are calculated for every technology k in order to measure \({MC}_{c}\). Therefore, the block A.1 provides two information: the ‘best’ technology to process the component i among those available, and the number of times the technology k is adopted to produce the product variant c.

However, it is not said that adopting the best performing technologies for each part variant ensures the minimum Manufacturing Complexity of the product configuration. In fact, the formula presents a trade-off between choosing of the best performing technologies and the scenario representing the maximum commonality.

3.2 On-grid component complexity

Measuring the complexity of assembly is useful for designers who want to realize assembly-oriented products with low assembly complexity. The metric On-Grid Component Complexity represents the complexity associated to the component i assembled according with the assembly route a and disassembled according with the disassembly route d. Here, the component is intended as part of a system. The metric is obtained by summing the Assembly Complexity (AC)\(,\) and the Disassembly Complexity (DC), according to the following Equation:

$${OCGI}_{iad}^{ c}= {AC}_{ia}^{c}+\left({DC}_{id}^{c}|a\right)$$
(5)

Assembly (\({AC}_{ia}^{c}\), B.1 block) and Disassembly Complexity (\(({DC}_{id}^{c}|a)\), B.2 block) can be calculated once the number of feasible assembly and disassembly routes (a and d respectively) are defined. The work by Soh et al. [27] specifically treated this topic suggesting a way to derive the disassembly complexity of a component given the disassembly route d. Determining the feasible assembly routes and estimating the corresponding complexity for the component i is a prerequisite for estimating the disassembly complexity. Feasible disassembly sequences d are given for a defined assembly route a. It is worth noting that minimizing the number of components may reduce the assembly efforts, and assembly cost as well.

Nevertheless, minimizing the product cardinality could make assembly more challenging; an efficient DfA is not necessarily a suitable DfD [3]. Disassembly routes, as well as disassembly complexity, strictly depend on assembly route a. Let it be \({N}_{a}^{ i}\) the number of suitable assembly routes, and \({N}_{a}^{ i} | a\) the number of disassembly routes for each assembly route a, the number of values that the \(OGC{I}_{iad}^{ c}\) can assume is:

$${N}_{a}^{ i} \times \left({N}_{d}^{ i} | a\right)$$
(6)

Since the approach is oriented towards the identification of the configuration at minimum complexity, the minimum value (\(OGC{I}_{iad,min}^{ c}\)) for each component i will enter Eq. (1).

The part accessibility metric is one of the most adopted metrics to quantify the assembly complexity. It is a way to measure the difficulty of grasping a part during disassembly operations and measures the easiness of accessing a sub-assembly [39, 40].

4 Geometrical complexity index

As mentioned in Sect. 2, the evaluation of geometrical complexity is still an open issue. In this first paper about our research on product complexity, a strong contribution is intended to be made to the evaluation of stand-alone complexity by proposing a geometrical complexity metric that is a combination of those already existing in the literature, described in the next section. To this end, both experimental and numerical surveys were carried out. A certain number of CAD models, characterized by different geometrical features, were submitted to the judgement of CAD modelling experts. The results were compared and correlated with those from a numerical survey, in which the considered complexity metrics were evaluated for each of the CAD models analyzed.

4.1 Geometrical complexity metrics

In literature there are several CAD features-based definitions about geometrical complexity and several metrics have been defined for an objective quantification of it. About objective metrics, Joshi and Ravi [12] proposed both Sphere Ratio (SR) and Part Volume Ratio (PVR) for quantifying the complexity. SR represents the ratio between the surface area of a sphere with the same volume of the part and the surface area of the part itself; PVR is the ratio between the volume of the part and the volume of its minimum Bounding Box. Lian et al. [14] defined the complexity as the ratio between the volume of the part and the volume of its convex envelope. They talk about Convex Envelope Complexity (CEC) and this probably is the most used metric. Always linked to geometric characteristics, Chougule and Ravi [13] quantified the complexity by proposing the Cube Ratio (CR), defined as the ratio between the surface area of a cube with the same volume of the part and the surface area of the part itself. Other metrics are reported in [12, 15], mainly related to any tooling operations: Number of Cores (NC), related to the number of cored features, which influence the tooling cost; Core Volume Ratio (CVR), defined as the ratio between the sum of cores volumes and the volume of part’s Bounding Box; Thickness Ratio (TR), defined as the ratio between minimum and maximum thickness of the part.

Table 1 describes the mathematical definition of these metrics.

Table 1 Geometrical complexity metrics
Full size table

Other metrics, proposed by literature, appear to be linked also to other information characterizing a CAD model, not always related to geometrical properties. Qamar et al. [41] estimate complexity as function of the ratio of the perimeter of a cross-sectional area to be extruded and the round bar perimeter having same cross-sectional area. Bodein et al. [16] suggest examining the complexity based on the number of surfaces (NS) composing a part. Lastly, Valentan et al. [18] associated the complexity to the number of triangles (NT) required for representing an object in a.stl file.

From the analysis, it is possible to point out that: (i) none of these metrics, taken individually, seems to be exhaustive in describing geometrical complexity, since they consider only partial features; (ii) only a few studies tried to compare them with each other, but based on small samples of models [42, 43]; (iii) a weighted combination of these metrics, correlated with experts’ judgements, could provide more comprehensive results than those provided by individual metrics.

These considerations mean that a step forward is necessary, tending towards the proposal of increasingly comprehensive metrics.

4.2 Survey for the definition of the geometrical complexity index

Figure 2 shows the adopted framework for the definition of the geometrical complexity index of CAD parts.

Fig. 2
figure 2

Workflow for geometrical complexity index definition

Full size image

The goal is to develop an analytical formulation of the geometrical complexity index as a function of objective metrics extrapolated from the available CAD model of the component under investigation:

$$GC=f\left\{{g}_{1}, {g}_{2}, \dots ,{g}_{n}\right\}$$
(7)

where GC is the Geometrical Complexity Index and \({g}_{i}\) is the i-th complexity metric. The approach herein adopted to perform this task is delegated to a regression model aimed at finding a relationship between objective (computable) geometrical complexity metrics and subjective (non-computable) perception of the modelling complexity of several, different components. Such defined index is not restricted to a specific production process and represents a general-purpose information to be used for characterizing further decision metrics.

To demonstrate how achieving the estimator for the geometrical complexity index, a set of 13 CAD models, shown in Table 2, have been investigated. All the components are made of polymeric materials, and they have no structural function.

Table 2 Investigated components
Full size table

4.2.1 Experimental survey

Subjective judgements have been collected by means of an experimental survey involving 39 CAD modelling experts, selected from academy and industry. Participants were asked to navigate the 3D PDF CAD models and to fill in a module where assigning a geometrical complexity judgement based on Likert scale [44] going from 1 (not complex at all) to 5 (very complex).

Figure 3 reports the results of the experimental survey shown through histogram plots.

Fig. 3
figure 3

Experimental survey results

Full size image

Although it is reasonable to think that experts involved in the decision-making team of a company could have comparable sensitivity toward a kind of component, it is also right to say that experts’ judgments can be influenced by their technological background and experience. There are several approaches to consider these aspects during the judgement; one of them consists in weighting the judgments according to the experience of experts [45]. However, the assignment of such weights could in turn be affected by uncertainty. Issues regarding the uncertainty can be faced by adopting fuzzy logic methods [46].

Regarding the objective metrics reported in Sect. 2, the measurement has been conducted through an interactive routine, implemented in Grasshopper plugin for Rhinoceros®.

4.2.2 Numerical survey

The plug-in Grasshopper for Rhinoceros® is a visual programming interface that uses a Lego-like approach: combining different blocks within a Canvas, a designer can create parametric CAD models that can be easily modified by interactively changing the value of any desired user-defined input parameter.

In general, the tool can be adopted to build up a parametric model from scratch and to modify and analyze any CAD geometry as well. In this work, Grasshopper has been used to implement a visual algorithm for analyzing CAD models imported in Rhinoceros environment. Figure 4 shows the overall structure of the routine.

Fig. 4
figure 4

The implemented workflow for computing geometrical complexity metrics

Full size image

Starting from geometry as input, it provides all the objective metrics reported in Sect. 2. The Galapagos Evolutionary Solver [47] routine available in Grasshopper is used to find the minimum Bounding Box, necessary to compute the Part Volume Ratio and the Core Volume Ratio of any model. To this end, Galapagos is employed to minimize the Bounding Box volume (fitness function) by automatically detecting its optimum orientation, defined by the rotations around the coordinate axes (parameters to optimize). By using this procedure, and with reference to Fig. 4, the user can easily import a CAD model in Rhinoceros, link it as input geometry in the Grasshopper routine (Step 1), start the Galapagos optimization engine (Step 2), and finally obtain all the objective metrics. The modularity of the algorithm allows user to get additional useful information as well as to compute new complexity metrics. The routine works with all CAD formats supported by Rhinoceros, including neutral CAD formats such as STEP and IGES and SOLIDWORKS® native format as well. However, it is intended to operate only with analytically defined geometries, i.e., Boundary REPresentation (BREP), and not with tessellated ones (meshes).

4.3 Results

Once values of both objective metrics and subjective judgments are available for each part of a given dataset, the functional link can be obtained using regression analysis technique.

Outputs of the survey (experts’ judgment) and the calculus by Grasshopper are summarized in Table 3. The final dataset contains 9 objective metrics (predictors) and one dependent variable (judgment of complexity) for each item. The 39 experts’ judgments have been aggregated using the geometric mean to have a single univocal score. According to [45, 48], the geometrical mean method is one of the most common group preference aggregation methods as it reduces the inconsistency of the judgments. Here, no weighting has been given to the judgments.

Table 3 Experimental and numerical surveys results
Full size table

A dataset like this can be used as training set to derive a multivariate regression model that explains the link between predictors and complexity. The XLSTAT [49] by Addinsoft® add-on for Microsoft® EXCEL 365 has been used to perform the analysis.

The correlation matrix (Pearson coefficients) for the predictors is reported in Fig. 5. It is evident that the implemented metrics are averagely low correlated between each other, exception done for some correlations such as between NS and NT.

Fig. 5
figure 5

Correlation matrix

Full size image

Table 4 shows the goodness of fit statistics provided by the Best Model method with adjusted R2 as optimization criterion. The confidence interval is 95%. Table 6 highlights the outcomes of the Analysis of Variance (ANOVA) and sum of squares.

Table 4 Statistics of the regression model
Full size table

Using the Best Model variables selection method, 7 variables have been retained in the model. Using the Adjusted R2, 99% of the variability of the dependent variable (complexity-geometric mean) is explained by 7 metrics. Looking at the p-value of the F statistic computed in the ANOVA (Table 5), with a significance level of 5%, the information brough by the predictors is significantly better than what a basic mean would bring. Based on sum of square, the following predictors bring significant information to explain the variability of the dependent variable: Number of Surfaces (NS), Number of Triangles (NT), Sphere Ratio (SR), Cube Ratio (CR), Number of Cores (NC), Core Volume Ratio (CVR) and Thickness Ratio (TR). Among all, the predictors number of surfaces is the most influential.

Table 5 ANOVA results
Full size table

The Geometrical Complexity index, obtained by the regression model, is given by the following Equation:

$$ \begin{aligned} GC = & - 12.65 + 0.0086NS + 0.000084NT + 71.53SR \\ & \quad - 57.49CR - 0.61NC - 2.35CVR + 1.95TR \\ \end{aligned} $$
(8)

Model’s predictions and corresponding residuals are shown in Table 6, while the plots of prediction vs standardized residuals and predictions vs actual (complexity) are reported in Fig. 6.

Table 6 Residuals
Full size table
Fig. 6
figure 6

Prediction vs standardized residuals (A) and predictions versus actual (B) plots

Full size image

Standardized residuals are used to identify outliers in a regression model. Any standardized residual that presents an absolute value greater than 3 is considered an outlier or may suggest that the normality assumptions are wrong. Sometimes, the threshold is set to 2. From the plot in Fig. 6A, it is evident that none of the standardized residuals goes beyond an absolute value of 3.

Regarding residuals, two main assumptions must be verified for linear regression models: residuals must follow a normal distribution and must be independent. The independence of the residuals has been tested and verified by adopting the Durbin-Watson test [50]. Moreover, the hypothesis that residuals follow a normal distribution cannot be rejected according to the Jarque–Bera test [51].

4.4 Discussion

The regression model has been achieved using a semi-automatic procedure. The result is a linear regression that links the objective geometrical features of a component to a subjective judgment of complexity. Although the set used for the analysis contains few components, it gives the opportunity to show how implementing the frameworks described in previous Sects. 3 and 4 (Figs. 1 and 2). The dataset of components could be expanded to have enough observations to split the dataset into a training set and a test set. Best Model method is not the only method implemented to derive the regression model.

Table 7 shows the statistics provided by other investigated regression methods: Stepwise, LASSO 1-FOLD and LASSO 5-FOLDS.

Table 7 Statistics for all investigated regression methods
Full size table

The regression models resulting from such methods are listed in Table 8.

Table 8 Results for all investigated regression methods
Full size table

The Stepwise method, as well as LASSO methods, provides too low values of adjusted R2 and higher values of MSE, if compared to the Best Model method (Table 4). Moreover, these models do not have adequate predictive capabilities (Fig. 7). Only the PVR should enter the regression model provided by the Stepwise method. LASSO method is very useful in a high-dimensional context, where there is a very large number of predictors compared to the number of observations.

Fig. 7
figure 7

Predictions versus actual plots for Stepwise (A), LASSO 1-FOLD (B) and LASSO 5-FOLD (C) methods

Full size image

Two-way interactions have also been investigated. Since there are 9 potential main effects, there are 45 potential two-way interactions. Table 9 shows the statistics provided by both Stepwise and Best Model regressions methods, while Table 10 reports the results of the regressions.

Table 9 Statistics for regression models with two-way interactions
Full size table
Table 10 Results for regression models with two-way interaction
Full size table

With reference to Fig. 5, it is worth noting that high-correlated metric pairs do not enter in the two-way interaction models (except for the pair NS-NT), since their influence would be neglectable. The interactions improve the statistics of the regression model (better fit of the data) and help to understand the effect of an independent predictor over another. However, a significant interaction term involves uncertainty about the relative importance of main effects, meaning the relative importance of predictors is more difficult to understand. Moreover, in an explanatory modeling, where one is interested about the coefficients of the predictors, it makes sense to simplify the model including only the most important effects.

Finally, the regression model described in the previous Sect. 4.3 should be a candidate to be used for explaining the geometrical complexity index of a component. It is worth noting that the generalization of the model strongly depends on the numerosity of the dataset as well as the type and number of geometrical features considered. However, fuzzy theory and fuzzy regression methods [52] can be exploited to be aware of the uncertainty introduced by subjective judgments, poor dataset and the bias or distortion due to the linearization.

5 Conclusions

The analysis of the literature about the complexity-based model for facing with design and manufacturability issues, although substantial, shows that there is a lack of methods that consider all the influential factors. This research proposed a novel methodological framework for evaluating the overall product complexity by combining geometrical, manufacturing, assembly and disassembly contributions starting from CAD models of product configurations and Assembly Structure Matrix, integrating several aspects of product’s life cycle.

However, the major focus pointed towards the definition of an exhaustive Geometrical Complexity index, trying to fill a significant gap in the literature that proposes several evaluation metrics, but not enough effective to describe the problem when considered individually. By means of a regression model, the (objective) metrics and subjective metric, obtained by numerical and experimental surveys, respectively, have been correlated and a new Geometrical Complexity index has been defined.

A numerical survey has been conducted on 13 CAD models by implementing an interactive algorithm in the Rhinoceros/Grasshopper environment that provides all the considered metrics. The same CAD models have been used for an experimental survey, involving 39 users with a long experience in CAD modeling.

The Geometrical Complexity index combines most of the considered metrics, unlike the index defined in our previous work, and can be applied to any kind of CAD model. Future attempts will be made to refine the model even more by increasing the number of CAD parts to be judged and the number of participants in the experimental survey. In a future study on geometrical complexity, modelling experts will be asked to weight some proposed features, related to both part geometry and modelling strategy, influencing their personal judgement on the complexity of a part. Moreover, the uncertainty factor linked to the judgments will be considered.