Modeling the Residence Time of Metal Droplets in Slag During BOF Steelmaking

Abstract

The ejection of metal droplets into slag due to top-blowing is characteristic of the BOF process. The residence time of the metal droplets in the slag plays a significant role in the kinetics of the metal–slag reactions. In this study, the residence time of ejected metal in slag during BOF steelmaking is investigated and various approaches, based on the blowing number theory and mass balances are compared. Previously published blowing number theories are evaluated in comparison with physically based upper and lower boundaries. The results illustrate that only some of the laboratory-scale blowing number correlations apply to industrial blowing conditions. A mathematical model is developed to predict mass fraction return rates and thus the residence time of droplets in the slag emulsion. Combined with a previously published model for ejected droplet size distribution, it is possible to predict dynamic changes in the interfacial area and mass transfer conditions for metal–slag reactions.

Introduction

Refining reactions in basic oxygen steelmaking (BOS) occur mainly at the gas-jet impingement zone, at the emulsion-metal interface and in the slag-metal emulsion. The significance of the refining processes taking place in the emulsion are explained based on the observation that the carbon and phosphorous contents in the metal droplets of the emulsion were considerably lower than those in the bulk.^[1] Efforts to estimate the mass ejection rate of droplets participating in the refining were made using cold and hot models.^[2,3] Formulas linking the gas jet momentum and the lance distance to the ejected metal mass were then proposed.^[4,5,6,7] Due to the complex interactions of the oxygen jet with the foam and the expanded jet with the liquid metal surface, accurate prediction of mass ejection rates proved difficult. To determine the emulsion refining kinetics, three parameters have to be considered: the total mass ejected into the slag, the size distribution of ejected droplets and the droplet residence time. Combining these quantities, emulsion properties can be deducted assuming that the size distribution and shape of the metal droplets remain unaffected during their residence time in the slag. Although studies already presented fracturing of Fe–C droplets during refining reactions,^[8,9] and proved bloating or swelling of droplets^[10] in nearly stagnant slag, it is possible to use the dense droplet theory for very small droplets and even for larger droplets when considering a one-step emulsion decarburization reaction path. Proposed models can be applied to estimate reaction rates as such or used a basis for more comprehensive process models involving further phenomena.

This research aim to develop a computationally efficient modeling approach that can be used to estimate the metal–slag interfacial area in BOF process models. The model is validated using experimental data from industrial BOF converters.

Considering today’s economic and ecological challenges, it becomes increasingly imperative for researchers to focus on and gain new insight into the presently existing refining processes. To optimize the understanding of steelmaking phenomena, researchers require innovative approaches and new insight into the ongoing development of new refining processes.

Model Formulation

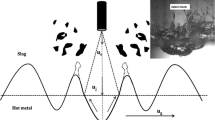
A thought model for the mass ejection procedure and the emulsion refining is shown in Figure 1. A certain hot metal mass is ejected per time interval ${\dot{m}}_{\rm ej}$. Various correlations have been proposed to predict the ejection rate,^[5,6,7,11] but the Blowing number theory by Subagyo et al.^[7] and the modification proposed by Rout et al.^[11] are arguably the most popular ones in recent literature. The ejected mass is transferred as metal droplets of varied sizes into the slag. The surface-to-volume ratio of the ejected mass is relevant for refining kinetics when droplets do not reach equilibrium with the slag during their residence time. Recently, it was shown that the weight distribution of ejected droplets ${f}_{\rm ej}$, also termed the mass density function of the ejected droplet population, can be predicted well using a mass-spring oscillator model.^[12] The mass of hot metal emulsified at a specific time into the blow ${m}_{\rm st}$ depends on the blowing conditions and slag properties. The residence time ${t}_{\rm R}$ of a droplet fraction between droplets of radius ${R}_{1}$ and ${R}_{2}$ can be evaluated for steady-state conditions of emulsion in- and outflow through the Eq. [1].

$${\dot{m}}_{\rm ej} {\int }_{{R}_{1}}^{{R}_{2}}{{ f}_{\rm ej} t}_{R} \text{d}R = {m}_{\rm st} {\int }_{{R}_{1}}^{{R}_{2}}{ f}_{\rm st} \text{d}R$$

(1)

${f}_{\rm st}$ is taken as the mass density function of the droplet population held up by the slag under static conditions. ${R}_{1}$ and ${R}_{2}$ are the limits of the considered fraction of the mass density function. The separation driving force is directly proportional to the mass of a single droplet. Droplets with a higher mass are expected to have a shorter residence time in the slag than smaller droplets. This phenomenon can be described using the specific droplet return rate ${\dot{f}}_{\rm r}$, which is the fraction of the droplets being lost from the emulsion to the bulk hot metal per time unit. For this to apply, it is assumed that the droplets have a constant density and are homogeneously distributed in the slag at all times. Therefore, it is expected that if samples of sufficient size are taken at arbitrary positions of the emulsion, the metal droplet size distribution in the sample remains constant. The droplet return rate is a key element in accurately describing the metal–slag emulsion. A validated modeling approach is presented in this paper.

Fig. 1

A schematic Illustration of the Ejection of Metal Droplets at the Cavity Area

It was observed that around a liquid iron droplet in the oxidizing slag, a gas halo is formed.^[13] Usually calculating emulsion decarburization, a two-step reaction path is assumed, shown in Figure 2(a). Initially oxygen is transferred over the slag-gas interface, oxidizing carbon monoxide to carbon dioxide. The carbon dioxide then is transferred to the gas-metal interface providing oxygen for the subsequent oxidation of the carbon dissolved in the iron droplet. This mechanism is expected to be valid for small droplets in stagnant slag, which have a low terminal velocity and thus behave similarly to rigid spheres. However, if the slag is highly agitated or the droplets are large enough to fall such that a rear wake is formed, the iron–carbon droplets may decarburize through a one-step reaction path (depicted in Figure 2(b)). At the stagnation point of the liquid iron droplet on the slag-metal interface, oxygen is transferred from the slag to the metal droplet resulting in a locally oversaturated solution of carbon monoxide. This oversaturated layer follows the assumed internal streamlines^[14] and flows towards the second stagnant point on the gas-iron interface. When the oversaturated layer of liquid within the droplet reaches the triple-fluid line (gas-slag-iron) the decarburization reaction takes place.

Fig. 2

Emulsion decarburization via (a) indirect^[15] and (b) direct reaction path

There is still speculation regarding the exact reaction mechanism during decarburization in the metal–slag emulsion. The newly introduced reaction model serves as a further possibility for agitated emulsion conditions and lacks any experimental evidence.

The Correlation Assessment for the Mass Ejection Rate

Various empirical equations are used to calculate the mass ejection rate of hot metal into the emulsion. These equations were usually derived from water models using bulk volume scales of about 1:1000 to today’s industrial converters. To validate the model, methods for estimating the upper and lower limits of ejection rates were studied.

The lower limit of the mass ejection rate can be estimated via a phosphorus mass balance assuming that the dephosphorization only takes place in the emulsion. Resch^[6]mentions that the hot metal mass flux turnover through the slag can be calculated by sampling the bulk and emulsion at two specific points in the blow ${t}_{1}$ and ${t}_{2}$. The mass flow of droplets through the slag can be estimated using a phosphorus balance assuming that the bulk mass does not change significantly during the two sampling times ${t}_{1}$ and ${t}_{2}$. Under steady-state conditions, the mass ejection rate can be approximated as follows:

$${\dot{m}}_{\rm ej}\approx \frac{{m}_{\rm b }\left({\left[P\right]}_{\rm b}^{t1}-{\left[P\right]}_{\rm b}^{t2}\right)}{\left({\left[P\right]}_{\rm d,ej}^{t1,t2}-{\left[P\right]}_{\rm d,r}^{t1,t2}\right)\left({t}_{2}-{t}_{1}\right)},$$

(2)

where ${m}_{\rm b}$ is the mass of the metal bath, while ${[P]}_{\rm b}^{t1}$ and ${[P]}_{\rm b}^{t2}$ are the weight fractions of phosphorus in the metal bath at the mentioned points $t1$ and$t2$, ${\left[P\right]}_{\rm d,ej}^{t1,t2}$ and ${\left[P\right]}_{\rm d,r}^{t1,t2}.$ The time average of the phosphorus weight fraction between $t1$ and $t2$ of the droplets being ejected from and returning to the bulk.

The anticipated error of the numerator in Eq. [2] is low because the bulk phosphorous is assumed to be homogenously distributed due to the thorough mixing of the hot metal bulk. The mass of the bulk can be assumed to be constant or can be amended via mass balance. When samples are taken within a short period, the rate of hot metal mass change is negligible. The average of the ejected phosphorous content can be estimated as the average of the bulk phosphorus between ${t}_{1}$ and ${t}_{2}$. The phosphorous content of the bulk is thus accurately estimated in comparison to the time average phosphorus concentration of the ejected mass. The greatest ambiguity with these quantities is the phosphorous content of the droplet when it returns to the bulk. It can be assumed that during the sampling procedure (20 seconds^[6]) of the emulsion, the dephosphorization reaction continues. This results in a considerable fraction of droplet refining being attributed to the sampling procedure rather than to the process itself. The residence time according to the calculation by Resch^[6] was found to be close to two seconds. Therefore, the analyzed phosphorous content of metal droplets retrieved from slag-metal emulsion can and should be disregarded. As mentioned by Resch,^[6] the phosphorous content of the droplets was already close to a state of equilibrium. Instead of mass ejection prediction, only an estimation of the lower ejection limit is possible assuming that the BOF dephosphorization is found in the emulsion refining.

$${\dot{m}}_{\rm ej,lower limit}= \frac{{m}_{\rm b }({[P]}_{\rm b}^{t1}-{[P]}_{\rm b}^{t2})}{({\left[P\right]}_{\rm b}^{t1}-0)({t}_{2}-{t}_{1})}$$

(3)

Equation [3] provides an estimation of the minimal mass ejection rate assuming that the phosphorous content of droplets falling back into the bulk is zero and that the average ejected phosphorus content is equivalent to that of the bulk at ${t}_{1}$. This leads to an upper estimate of the phosphorous difference in the denominator. Since the physical quantities in the numerator are known to a higher degree of accuracy, the resulting quantity is a lower limit of the desired physical variable.

The cause of hot metal mass ejection is the impingement of the gas jet on the surface of the hot metal. The nozzles on the lance are designed to deliver a jet with high kinetic energy, thus allowing continuous gas-metal contact during the blow. The power of the gas jet exiting the nozzle can be approximated using equations of isentropic flow. The power of the directed kinetic energy of the jet remaining at the lance height is calculated using the free turbulent jet theory. The power $P$ of a fluid flow with velocity $v$ and mass flux $\dot{m}$ is presented in Eq. [4]

$$P=\frac{1}{2}\dot{m}{v}^{2}$$

(4)

To estimate the upper limit of the droplet mass ejection rate it is assumed that, the power of the hot metal mass flow exiting the bulk must be less than the power of a similar gas jet under free turbulent conditions at a distance from the nozzle similar to the lance height. The power of the mass flow exiting the bulk is calculated according to

$$P=\frac{1}{2} {\dot{m}}_{\rm ej} {\int }_{R1}^{R2}{ f}_{\rm ej}{v}_{\rm ej}^{2} dR$$

(5)

where ${v}_{\rm ej}$ represents the initial velocity of a spherical droplet with radius $R$ exiting the hot metal bulk. For small droplets, this velocity is influenced mostly by the boundary layer momentum. In larger droplets, the governed influence is taken as the oscillation velocity of a similar mass before takeoff. This oscillation velocity of the droplet is estimated using the mass-spring substitution model proposed by Mitas et al.^[12] Then the exit velocity of a spherical droplet with radius $R$ was calculated by the momentum weighted velocity of the two discussed velocities. A comparison between the calculated droplet exit velocities for the experimental setup of Koria and Lange^[2] and corresponding calculations using the model by Subagyo^[16] are shown in Figure 3. For very small droplets the exiting momentum is governed by the momentum of the liquid boundary layer. To larger droplets, a transition period is entered visible in Figure 3 through the strong curvature of the function. To even larger droplet diameter the momentum of the droplet when exiting the cavity gets increasingly independent of the boundary layer momentum.

Fig. 3

Exit velocity of metal droplets as a function of droplet size with different supply pressures (4, 5, 6, and 7 bar) using a dimensionless lance height of 37.5. Comparison of values calculated by Subagyo et al.^[16] using experimental values by Koria and Lange^[2] (markers) with values calculated using the oscillator model by Mitas et al.^[12] (continues lines)

The calculated values for the drop exit velocities shown in Figure 3 are in the same order of magnitude as the values reported by Subagyo et al.^[16] For very small droplets the exit velocity approaches the momentum boundary layer velocity of the hot metal. For droplets in the range of 20–40 mm in diameter, the gradient of calculated values is similar to the gradient of calculated values by Subagyo et al.^[16]

To estimate the upper limit of liquid mass ejection, Eq. [5] is combined with Eq. [4] resulting in Eq. [6]. The upper limit of the ejection rates is calculated using Eq. [6] applicable for a 200-ton BOF converter are shown in Figure 4. It is observed that lowering the lance height increases the maximum power of the gas jet acting on the surface. The droplet size distribution shifts towards larger droplets and the exit velocities of the droplets increase resulting in a higher kinetic energy requirement per ejected mass. This specific energy is the dominating influence resulting in lower maximum ejection values associated with lower lance heights.

Fig. 4

Mass ejection rates according to various blowing number theories and lower- and upper mass turnover limit according to Eqs. [3] and [6], applied to data from a 200-ton converter.^[6]

$${\dot{m}}_{\rm ej,upper limit}=\frac{2 {P}_{\rm g}}{{\int }_{R1}^{R2}{ f}_{\rm ej}{v}_{\rm ej}^{2} dR}$$

(6)

The ejection rates observed are so elevated that the lance height could not be sustained despite low residence time as seen in Figure 4. Despite this fact the lance height was not corrected when presenting an overview. This enabled the evaluation of the applicability of certain mass ejection models, no corrections of lance height were done. The models by Block et al.^[5] and Subgyo et al.^[7] lead to results which conflict with the proposed limits which means that they are not suitable for predicting the ejection rate in the studied 200-ton BOF based on the studied case, it appears likely that the models by Block^[5] and Subagyo et al.^[7] describe the ejection behavior of metal droplets in industrial converters only qualitatively. The model by Rout et al. ^[11] is in essence a modification of the blowing number correlation by Subagyo et al.^[7] for high-temperature environments, yields ejection rates that fall well between the lower and upper limits and are thus quantitatively plausible.

Estimating the Residence Time

The residence time ${t}_{\rm R}$ of a metal droplet population consisting of equal-sized droplets under steady-state conditions, can be calculated as follows:

$${t}_{\rm R}=\frac{{m}_{\rm st}}{{\dot{m}}_{\rm ej}}$$

(7)

where ${m}_{\rm st}$ is taken as the metal mass suspended in the slag and ${\dot{m}}_{\rm ej}$ represents the metal mass ejection rate into the slag. As noted in Reference 17 the expression given in Eq. [7] corresponds to Little’s law,^[18] which is valid for any stable and preemptive system.

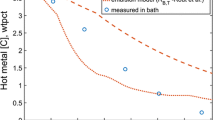
Provided a metal–slag emulsion sample $\Omega$ is given and the weight fraction of metal to slag in the sample $\frac{{m}_{\Omega,{\rm M}}}{{m}_{\Omega,{\rm S}}}$ is evaluated, the total mass of metal in the emulsion can be estimated. The prediction of the slag mass is expected to be more accurate than that of the metal fraction. When samples were taken by interrupting the blow and tilting the converter, droplets of higher mass segregated and could not be retrieved. The heaviest droplets are responsible for the largest weight fraction in the ejected distribution. Considering the sampling procedure, the sampling retrieval time mentioned by Resch^[6] was 20 seconds, which is remarkably fast, but still too slow to retrieve a representative size distribution. As further mentioned by Resch^[6] this led to an underestimation of the emulsified hot metal mass ${m}_{\rm st}$ and therefore the mass weighted residence time ${t}_{\rm R}$. Residence time as calculated by Resch^[6] via Eq. [7] is shown in Figure 5.

Fig. 5

Residence time according to Resch using Eq. [7] (line) compared with residence times using Eq. [8] for various droplet size fractions (markers) for a 200-ton industrial converter

If the size distribution of ejected and emulsion droplet population is known, the residence time of a droplet having Radius $R$ can be calculated as follows:

$${t}_{\rm R}\left(R\right)=\frac{{{\frac{{m}_{\rm S}}{{m}_{\Omega,{\rm S}}}m}_{\Omega,{\rm M}} \;f}_{\Omega }(R)}{{\dot{m}}_{\rm ej}\;{ f}_{\rm ej}\;(R)}$$

(8)

where the total slag weight ${m}_{\rm s}$ can be estimated through a phosphorus mass balance. The ejected size distribution ${f}_{\rm ej}$ was calculated using the model proposed by Mitas et al.,^[12] while the static size distribution ${f}_{\Omega }$ was taken from experimental data from Resch.^[6] For comparable results, the mass ejection rate ${\dot{m}}_{\rm ej}$ was calculated according to Resch.^[6]

The weight fraction of droplets in the size ranges of Figure 5 is much lower than the analyzed values of the physically retrieved samples. Only a few large droplets would shift the weight fractions to lower values leading to a much lower residence time as shown in Figure 5. Exactly these droplets returned to the bulk hot metal before the emulsion samples were taken. This is believed to be the dominating factor and the reason why the shown residence time in Figure 5. is seemingly high. The mass ejection rates ${\dot{m}}_{\rm ej}$ as calculated by Resch are probable although it is possible that the actual values are even higher. The emulsified mass under static conditions is certainly higher than the values taken for the calculations. This effect, rather than the previous two would lead to longer residence durations.

Modeling the Droplet Size Dependent Residence Time

The hot metal mass flow from the emulsion into the bulk can be described assuming that all droplet sizes are homogeneously distributed throughout the slag. Using this assumption, it is possible to calculate an emulsion volume-based droplet return rate $\dot{{f}_{\rm r}}$. If a volume element of the emulsion $\Delta {V}_{\rm e}$ is emptied of its Radius $R$ droplets each duration $dt$, then the droplet mass flow out of the emulsion of Volume ${V}_{\rm e}$ is given as shown in Eq. [9].

$$\frac{{\Delta V}_{\rm e}(R)}{{V}_{\rm e} \text{d}t}=\frac{\text{d}{m}_{\rm st}(R)}{{m}_{\rm st}\left(R\right) \text{d}t}:=\dot{{f}_{\rm r}}$$

(9)

This is the proposed definition of the droplet return rate in the metal–slag emulsion. The inverse of this physical quantity is the residence time.

$${t}_{\rm R}(R)=\frac{1}{\dot{{ f}_{\rm r}}(R)}$$

(10)

During the BOF process, the slag emulsion is perfused with purging gas as well as decarburization products which are partly generated in the emulsion itself. To describe this emulsion foam, the converter domain was modeled as a battery of bubble columns with a diameter equal to the converter vessel radius. The analytical model of Zehner^[19,20] was chosen for characterizing the bubble column. Figure 6 illustrates a bubble column of diameter $D$ in a converter. Here the upward flow in the column axis center and the downward flow on the outer edge of the bubble column are indicated. The eddy velocity ${v}_{\rm F}$ according to this model is shown in Eq. [11].

Fig. 6

A schematic illustration of the residence time model

$${v}_{\rm F}=\sqrt[3]{\frac{ {(\rho }_{\rm e}- {\rho }_{\rm g}) g D {v}_{\rm go}}{\zeta {\rho }_{\rm e}}}$$

(11)

The bubble column geometry restricts the magnitude of the largest eddy. Given the eddy velocity ${v}_{\rm F}$ and the eddy dimension $L$, the calculation of angular speed as well as the time necessary for quarter rotations is achieved. For each droplet size, it is assumed that the distribution along the radial component of the two-dimensional eddy is homogeneous. After a quarter rotation of the eddy, a certain fraction of droplets has exited the emulsion. This fraction is represented by Eq. [12] and is used to describe the volume fraction of the emulsion losing the droplets during the mentioned quarter rotation.

$$\frac{\Delta L(R)}{L}=\frac{{\Delta V}_{\rm e}(R)}{{V}_{\rm e}}$$

(12)

Using the previous Eqs. [9], [10], and [12], the residence time can be calculated according to Eq. [13].

$${t}_{\rm R}(R)=\frac{2\pi {L}^{2}}{4 {{v}}_{\rm{F}}\Delta L}$$

(13)

Here, $L-\Delta L$ represents the distance from the eddy rotation origin to the beginning of the emulsion’s droplet void area. A droplet at this position will move in relation to the slag, the distance $\Delta L$ during a quarter rotation, therefore being the limiting instance. Droplets initially placed further from the center will be consumed by the hot metal bulk whereas droplets closer to the rotation center will not reach the slag-metal interface.

The movement of the droplets can be calculated by solving the second-order nonlinear ordinary equation of motion considering the gravity and centrifugal force as driving forces and drag and viscosity force acting against them. For a droplet population ejected during the blow of an 200t converter (e.g. analyzed by Resch^[6]) neither viscosity nor drag forces can be safely disregarded.

It is less calculation intensive to disregard the acceleration phase of the droplets and calculate the sedimentation velocity^[21] S.106 (6.1) as shown in Eq. [14].

$${v}_{\rm d}=\sqrt{\frac{8 R g ({\rho }_{\rm d}- {\rho }_{\rm s})}{3\Phi (Re){ \rho }_{\rm s}}}$$

(14)

This equation is slightly modified to include the centrifugal acceleration as seen in Eq. [15].

$${v}_{\rm d}=\sqrt{\frac{8 R (g+{\omega }^{2}{s}_{0}) ({\rho }_{\rm d}- {\rho }_{\rm s})}{3\Phi (Re){ \rho }_{\rm s}}}$$

(15)

By implementing Eq. [13] in a numerical minimization routine for $\Delta L$, the residence time for each droplet diameter can be calculated.

Modeling the Residence Time of the Droplet Population $\overline{{{\varvec{t}} }_{{\varvec{R}}}}$

The previous section presented the modeling of the residence time of a droplet of the given radius R. Considering the residence time of a droplet population multiple quantities could be significant. Figure 7 depicts a hypothetical droplet distribution being ejected. It consists of two droplet sizes. One large and one small droplet is ejected into the slag each second. The large droplets return on average after 2 seconds to the bulk, while the smaller droplets have a four times higher residence time, leading to their accumulation in the slag-metal emulsion. The displayed arrows do not indicate a trajectory only the exiting and returning to the bulk.

Fig. 7

Hypothetical ejected population consisting of two droplet sizes: a smaller droplet with a residence time of 8 s and a three times larger droplets with a residence time of 2 s

A mass weighted residence time of the droplet population $\overline{{t }_{\rm R}^{m}}$ can be calculated by Eq. [16]. This residence time would prove relevant when reaction kinetics is limited by mass supply.

$$\overline{{t }_{\rm R}^{m}}=\frac{{m}_{1}{ {t}_{\rm R}}_{1}+{m}_{2} {t}_{{\rm R}_{2}}}{{m}_{1}+{m}_{2}}=\frac{{R}^{3} 8+{\left(3R\right)}^{3}2 }{28 {R}^{3}}=2.2s$$

(16)

An interfacial area weighted residence time $\overline{{t }_{\rm R}^{\rm A}}$ can be calculated analog to Eq. [16]. using the individual surface area of the droplets. This physical quantity is useful when the reaction speed is significantly dependent on the exchange area.

$$\overline{{t }_{\rm R}^{\rm A}}=\frac{{A}_{1}{ {t}_{\rm R}}_{1}+{A}_{2} {t}_{{\rm R}_{2}}}{{A}_{1}+{A}_{2}}=\frac{{R}^{2} 8+{\left(3R\right)}^{2}2 }{10 {R}^{2}}=2.6\,\text{s}$$

(17)

Results

The calculations are performed using dense droplet assumption, and that the characteristic drop sequestration eddy is defined by the vessel geometry and quantities shown in Table I. The empty pipe speed ${v}_{\rm go}$ is calculated using the emulsion decarburization efficiency ${\eta }_{\rm S}$ to calculate the carbon monoxide volume generated per the converters cylindrical surface. The slag viscosity is calculated using the measured chemical composition of the slag^[6] and Mudersbach modification of the Urbain viscosity model.^[22] It was assumed that the temperature of the slag is 100 °C higher than the temperature of the hot metal. The influence of the chemical composition and temperature on the slag viscosity is considered while the influence of the solid fraction and the slag density is neglected.

Table I Physical Properties Employed in the Model Calculations

The principles depicted in Eqs. [16] and [17] are applied to the 200-ton BOF converter analyzed by Resch^[6] and this leads to the results shown in Figure 8. The 200-ton converter implemented lime co-injection using the oxygen lance. The author^[6] does not mention the use of bottom blowing technique, which is known to increase the mass ejection rate.^[3] The effect of bottom blowing on the mass ejection rate was therefore not considered in following calculations.

Fig. 8

The residence time ${t}_{\rm R}$ of ejected droplet population compared to calculations from Sarkar^[23] and measurements performed by Price^[24] for different values of the upper droplet distribution limit factor ${K}_{\rm r1}$: (a) 1, (b) 1/4, (c) 1/16, and (d) 1/64

The gas flow permeating the slag was linked to the oxygen supply using the emulsion decarburization efficiently ${\eta }_{\rm S}$ as a constant quantity overall calculations. The effect of reduced decarburization at the end of the blow on the residence time is therefore not seen in Figure 8. Nonetheless, there is still attenuation in residence time attributed to the change in slag viscosity. It can be observed in Figure 8 that the mass-weighted residence time depends significantly on the upper droplet distribution limit and therefore on the Constant ${K}_{\rm r1}$. While varying this model constant from 1 to 1/64 the mass-weighted residence time varies disproportionately. As expected, the interfacial-area-weighed residence time varies comparatively little. This is attributable to the fact that the smaller droplets, which form most of the overall surface area, remain unchanged. The residence time for small droplets can exceed the converter’s overall refining time and they are therefore lost in the slag from the viewpoint of mass balance calculations for the BOF process. Figure 9 depicts the residence time for 9.2 minutes into the blow. It can be observed that the droplets near the lower size limit have a residence time of over 10,000 seconds. To visualize droplet population residence times that are relevant when refining is proportional to the interface area, the interfacial-area-weighted residence time of the ejected droplet population was calculated for the condition that only droplets with residence times shorter than 1000 seconds are considered. In other words, only droplets that can return to the hot metal bulk under otherwise invariant conditions further in the blow were accounted for. The quantity of droplets lost in the slag is predominantly dependent on the end phase of the blow where the residence times are lower. This could also mean that droplets that had been entrapped almost permanently in the slag can return to the metal due to changes in slag properties.

Fig. 9

The residence time of ejected metal droplets at 9.2 minutes into the blow. The upper droplet distribution limits are shown for ${K}_{\rm r1}=1/64$, ${K}_{\rm r1}=1/16$, ${K}_{\rm r1}=1/4$ and ${K}_{\rm r1}=1$

Figure 9 depicts the residence time as a function of droplet diameter. The residence time is larger than 1000 seconds for submillimeter droplets. The residence time is lower for larger droplets since the presented model yields a higher fraction of slag void of droplets when having passed the metal–slag boundary. The upper end of the ejected droplet population is denominated for various values of ${K}_{\rm r1}$. It is observed that between ${K}_{\rm r1}=1/4$ and ${K}_{\rm r1}=1/16$ a point is reached where the model does not yield residence times anymore. This point marks the diameter of a droplet, which when starting at the origin of the considered emulsion eddy, reaches the slag metal interface during the time of a quarter rotation of the eddy.

Figure 10. depicts the residence time of individual droplets with diameters of 2 mm (a) and 0.5 mm (b). The modeled residence time is compared with calculations performed by Dogan et al.,^[25] as well as by a mass balance based method given in Eq. [8]. Larger values for ${K}_{\rm r1}$ result in a smaller mass fraction for a given radius. Since the mass density function ${f}_{\rm ej}(R)$ is in the denominator in Eq. [8], larger values for ${K}_{\rm r1}$ result in larger residence times. The estimated residence times of the half millimeter diameter droplets are higher than the 2 mm diameter droplet for the present model and mass balance model. When comparing the residence times for equal values of ${K}_{\rm r1}$ using Figures 10(a) and (b) it is observed that for each value of ${K}_{\rm r1}$ the residence time presented for the smaller droplets in Figure 10(b) is larger. The estimated residence times via. Equation 8 proved sensitive to the upper droplet distribution limit. On the other hand, it can be observed that the model by Dogan et al.^[25] and the present model fall within the range of realistic residence times validated through the bass balance approach. However, it is also possible to assess the ejected drop size distribution constant in relation to the modeled results. To obtain valid results for this case, it would be necessary to assume values of ${K}_{\rm r1}$ between 1 and 1/4 for the present model and between ¼ and 1/64 for the model by Dogan et al.^[25] For two-millimeter droplets, all presented formulations predict a reduced residence time at the end of the blow. For the half-millimeter droplets, the residence durations change significant toward the end of the blow when using the model by Dogan et al.^[25] This phenomenon is less pronounced when using the present model and the mass balance approach presented in Eq. [8]. The residence time attenuation for two-millimeter droplets is larger than for half-millimeter droplets when using the mass balance approach.

Fig. 10

Residence time dependent on blowing time of individual droplets of diameter (a) 2 mm and (b) 0.5 mm Eq. [8]

Figure 11 illustrates quantities for droplets moving relative to the slag for the blowing conditions at 9.2 minutes into the blow (Resch^[6] “Schmelzengruppe 1”). For visualization, the drop distribution is divided into seven fractions where each point show in Figure 11 represents the relative weight of the displayed drop fraction. A rather large share of the weight is found outside the region of rigid sphere behavior. Therefore internal circulation in the droplet and outer droplet shape variations during the movement of the droplet through the slag play a role in the mass transfer of droplet constitutions with the surrounding. Small droplets experience low relative velocities to the slag. Therefore the deformation force of the droplets is less compared to large droplets. The surface tension strive towards minimization of surface area and leads to nearly spherical droplets at nearly stagnant slag conditions. Figure 11 indicates that the areas where spherical-cap formations occur were not reached by droplets of the calculated droplet population for upper population factors of ${K}_{\rm r1}$ =1/16 under present calculation conditions.

Fig. 11

Shape regimes for bubbles and droplets in unhindered gravitational motion through liquids^[26] with superimposed values for metal droplets assuming ${K}_{\rm r1}$ =1/16

Since the ejected droplet sizes vary over magnitudes and according to Figure 11 several shape regimes are to consider, various mass transfer models have to be implemented when the relative refining importance of droplet size fractions is unknown.

Measured refining rates can be used to validate the model. Since dephosphorization only takes place at the slag-metal interface this refining reaction was chosen for model validation. The change of phosphorous in the metal bulk can be calculated using Eq. [18]. Where the concentration $c$ of a species in the droplets is in general a function of the droplet radius $R$ and the reaction time $t$, therefore $c(R,t)$. More specifically, the reaction time is also a function of the droplet radius.

$$\frac{\rm{d}{m}_{[P]}}{\rm{d}t}={m}_{\rm ej}{\int }_{{R}_{0}}^{{R}_{1}}\frac{\rm{d}{w}_{\rm ej}(R)}{\rm{d}R} \left({c}_{0}-c\left(R,{t}_{R}(R)\right)\right) \frac{1}{{t}_{R}(R)}\rm{d}R$$

(18)

Evidently, the refining rate depends on a product of three terms. The logarithm of the in Eq. [18] presented product for the test case (9.2 minutes into the blow, “Schmelzengruppe 1”) is shown in Figure 12.

Fig. 12

Importance of the factors: relative mass fraction of population ($\Delta {w}_{\rm ej}$), concentration change during residence time ($\Delta c$), and the inverse of the residence time $\frac{1}{{t}_{\rm R}}$: (a) whole droplet population, (b) droplet sizes 6–11 mm

It is evident that the refining contribution of the smallest droplets is negligible due to their high residence time and therefore poor mass exchange rates between the slag and metal bulk. The logarithm of the inverse of the residence time, i.e., log₁₀(1/t_R), is the largest element of the stack at small droplet diameters. Therefore it is also the largest inhibitor of refining performance. When considering a distribution fraction regarding larger droplets, the effect of their poorer dephosphorization is compensated by shorter residence times and higher mass fractions. From smaller to larger droplets the orange stack element reduces its size while the green stack element increases its size. From droplet diameters of around 5 mm to larger diameters the overall refining inhibition seems nearly constant. Figure 12(b)) indicates that the displayed function exhibits a minimum. An mathematical analysis of the presented phenomena is displayed in Appendix. The droplet return concentration depends on the kinetic model applied. Since ejected droplets vary greatly in size and relative velocity to the slag—various models have been implemented.

Figure 13 illustrates the relative and cumulative dephosphorization over the ejected drop population for various implemented mass transfer models. The models chosen for describing internal limited mass transfer are Handlos and Baron,^[14] Calderbank and Korchinski^[27] and diffusion-controlled mass transfer. The models from Frössling,^[28] Higbie^[29] and Wakao and Kagei^[30] were applied to explore the external limited case. Reading Figures 13 and 11 it can be concluded that droplets which are sufficiently small have virtually no contribution to the refining rate. Therefore the implementation of pure diffusion controlled models can be, in good approximation, disregarded. The model by Calderbank and Korchinski^[27] describes mass transfer in the oscillating droplet region of the droplet regimes (see Figure 11). Due to the consideration of the internal fluid circulation, the mass transfer rates predicted using the model by Calderbank and Korchinski^[27] are considerably faster than those in a diffusion-controlled case. The differences in the refining rates predicted using the models of Wakao and Kagei,^[30] Handlos and Baron^[14] and Higbie^[28] are minor (see Figure 13(d)), indicating that mass transfer in all models is sufficiently similar compared to remaining influencing factors in Eq. [18], although the influence of the external mass transfer on the estimated overall mass transfer is for all calculated states < 5 pct.

Fig. 13

Relative importance of droplets of diameter d on refining of whole drop population (solid line) and cumulative phosphorus removal of bulk metal due to emulsion refining (dotted line) for different values of the emulsion decarburization efficiency ${\eta }_{\rm S}$: (a) 0.1, (b) 0.25, (c) 0.75 and (d) 1

A certain fraction of the total decarburization of bulk hot metal occurs in the emulsion. This fraction is called the emulsion decarburization efficiency ${\eta }_{\rm S}$. Using foaming index models the foamy emulsion height can be calculated under the assumption that gas is generated at random positions. Therefore, on average half, the slag volume is perfused with decarburization products. Figure 13 depicts that when decarburization takes purely place in the emulsion (${\eta }_{\rm S}=1$) the foam height would need to be five times the available height for the foam in the converter. Even at 25 pct emulsion decarburization slopping is occurring.

Using the modeled residence time per droplet radius and the mass fraction of ejected metal the calculation of the overall interaction area or interfacial area of metal droplets in slag is achieved. Results for the test conditions of an industrial 200t converter are shown in Figure 14. The calculated interfacial area proves to be comparable in magnitude to other researchers. For example, Lytvynyuk et al.^[31] conducted their calculations for a 200-ton converter assuming an interfacial area of 1000 m², while Bundschuh^[32] applied values between 1000 and 5000 m² for the duration of the main blow.

Fig. 14

Total interfacial area of liquid metal droplets in the slag

Discussion

The magnitude of physical challenges faced in converter research compel experts to explore and rely on complex simulations. It is however necessary to state that a simulation using reduced complexity can lead to interesting and sufficiently accurate results.

In this work, the residence time of the droplets in the slag is calculated under BOF steelmaking conditions. A bubble column model by Zehner^[19,20] is used to describe the metal–slag foamy emulsion. The Droplet sequestration phenomenon is modeled by a force balance resulting in derived dynamic equations. This enables the calculation of the residence time of various droplet populations as well as the residence times of individual droplets of any given size. The residence durations proved comparable with the results obtained from numerous dynamic BOF models. The residence time model proves adaptable and can be integrated into an online dynamic BOF converter model.

When analyzing the available literature, it became apparent that models for mass ejection, due to the oxygen jet impingement, prove ambiguous. The current scientific formulations for mass ejection rates proposed in published literature prove vastly diverse when applied to industrial size converters. In this paper, calculated values have been compared and validated by relating them to formulated physical based limits. The blowing number correlations available in the literature were found to be partly in conflict with these boundaries.

It is mentioned in the available literature that droplet refining in the emulsion is one of the crucial aspects to be considered in overall refining. The droplets retrieved via slow sampling methods (> 10 seconds) are perceived as the cause of this emulsion refining. Using a residence time model developed with this thought in mind it is shown that droplets that are sufficiently accessible using slow sampling methods are exactly the droplets that don’t play a role in droplet refining. It is therefore concluded that only droplets larger than 2 mm in diameter are capable of contributing to emulsion refining. Regarding the significantly larger droplets, the assumption that droplets are homogeneously distributed is not valid. This fraction of large droplets could still play a vital role in the refining process due to elevated mass exchange rates (low residence time) and to a high mass fraction of the total ejected metal mass is attributed to the larger droplets. On the other hand, the small and finely dispersed droplets which led to the terminology “emulsion refining”, contribute negligibly towards the total refining. There is an emulsion of small iron droplets dispersed in slag but no relevant inherent refining.

The results by Resch^[6] and Schürmann et al.^[33] are of interest as they estimated droplets residence durations based on the mass balance of phosphorous. This supports the results in this research where the large droplets contribute mainly to the refining process as only they have sufficient short residence times. The existence of large droplets was forecast by mathematical models^[12] and shown through CFD calculations.^[34] If droplet refining proves sufficiently relevant in future research, it would be recommended to use the presented model for medium-mass droplets combining this with a trajectory-based model, e.g., that by Brooks et al.,^[35] for larger droplets.

Whether calculations are made with dense or bloated drops is irrelevant, the small drops have poor refining performance due to their low mass exchange rates with the bulk. This also applies to the hypothetical situation where the droplets “explode” into very small droplets. After droplets have suffered irreversible fragmentation their mass fragments have not sufficient small residence time to account for significant refining. The bloating time is minor compared to the residence time. The relative velocity of large droplets is too high to allow a gas halo (see Figure 2(a)). Internal nucleation seems unlikely for large droplets with sufficient internal circulation but could be more relevant than classical nucleation theory would suggest.^[36] The reaction mechanism shown in Figure 2(b) seems plausible but needs to be validated experimentally.

When comparing the various models for internal limiting mass transfer used in this research with the Wakao^[30] model for external limiting mass transfer, it is of interest to note that external mass transfer has little influence over total mass transfer. Consequently, the internal mass transfer is the rate-controlling factor (> 95 pct) during the mass exchange.

Droplet mass changes due to chemical reactions or coalescence are not considered in this work. The large residence times of small droplets lead to the accumulation of these droplets during the blow in the slag. Calculations show that the emulsion can contain significant volume fractions of metal. The modeling of coalescence phenomena is therefore required when modeling emulsion refining. It is expected that the residence time shortens significantly with a rising metal fraction in the emulsion. The unification of droplets leads to their accelerated sequestration into the bulk.

The presence of surface active components can enhance mass exchange.^[37] The influence of this phenomenon on overall mass transfer is not investigated in this work.

The upper droplet distribution Factor ${K}_{\rm r1}$ is calculated based on Kemminger’s^[34] published simulation results. The largest droplets in published figures are measured and the value of ${K}_{\rm r1}$ for equal blowing conditions is calculated resulting in ¼. By further validating the residence time of the ejected population with data retrieved from experiments using a radioactive tracer method perform by Price, ${K}_{\rm r1}$ would be expected to be between ¼ and 1/16 for the first 2/3 of blowing time. Using a phosphorous balance and the presented model ${K}_{\rm r1}$ is expected to be between 1 and ¼. Therefore the calculated ${K}_{\rm r1}$ of ¼ is considered to be feasible and can be implemented in the droplet size distribution model for full scale converters instead of 2.7^[12] (small-scale validation).

Conclusions

This work aimed to study the residence time of metal droplets in the slag during BOF processing. To this end, a mathematical model for the residence time was developed and coupled with the blowing number theory by Rout et al. and a previously proposed model for the droplet size distribution. The main conclusions of the study can be summarized in the following.

For the study of industrial BOF converters, the mass ejection models by Resch^[6] and Rout et al.^[11] are preferable over the models by Subagyo et al.^[7] and Block et al.^[5] The droplet exit velocities were predicted using the model developed in this work and that by Subagyo et al.^[16] are improbably low in comparison to the CFD results available in the literature.^[34] The model constant ${K}_{\rm r1}$ of the droplets size distribution model^[12] was revised to ¼. The influence of the bloating phenomena on residence time was found to be negligible.

Regarding the kinetics of decarburization, the contribution of emulsion to the overall rate was estimated to be less than 25 pct. The refining contribution of small droplets (< 2 mm) was estimated to be negligible. Under the conditions of the calculations, the reaction rate of metal droplets was found to be limited by internal mass transfer irrespective of droplet size.

Appendix

The influence of viscosity regarding the movement of droplets, close to the upper droplet distribution limit, through the slag, is negligible. For similar trajectory lengths, the residence time is estimated to be proportional to the inverse of the square root of the droplet diameter.

$$F=m\times g=\frac{1}{2}A {v}^{2}{C}_{\rm v}\rho \ge {d}^{3}\propto {d}^{2}{v}^{2} \ge d\propto {v}^{2} \ge d\propto \frac{1}{{t}_{{R}^{2}}}$$

(A1)

$${t}_{\rm R}\propto \frac{1}{\sqrt{d}}$$

(A2)

Using the Model of Calderbank^[27] the concentration of species in the droplet after a defined residence time is calculated.

$${c}_{\rm r}={c}_{\rm eq}+\left({c}_{0}-{c}_{\rm eq}\right) \times \left(1-\sqrt{1-\rm{exp}\left(-\frac{4{\pi }^{2}{t}_{\rm R}KD}{{d}^{2}}\right)}\right)$$

(A3)

Considering species with sufficient refining potential which could not be utilized due to the short residence time ${c}_{\rm r}\gg {c}_{\rm eq}$ Eq. [A3] is simplified to [A4].

$$\Delta c={c}_{0}-{c}_{\rm r}\approx {c}_{0} \times \left(1-\sqrt{1-\rm{exp}\left(-\frac{4{\pi }^{2}{t}_{\rm R}KD}{{d}^{2}}\right)}\right)$$

(A4)

Large droplets experience short residence times. Using the Taylor series up to the linear term $\rm{exp}\left(x\right)\approx 1+x$ Eq. [A4] is simplified to Eq. [A5].

$$\Delta c\approx {c}_{0} \times \left(1-\sqrt{\frac{4{\pi }^{2}{t}_{\rm R}KD}{{d}^{2}}}\right)$$

(A5)

$$\frac{d\Delta c}{dd}\propto \frac{\sqrt{{t}_{\rm R} }}{{d}^{2}}$$

(A6)

$$\Delta c\propto \frac{\sqrt{{t}_{\rm R} }}{d}$$

(A7)

When using a trajectory-based model for large droplets the residence time in Eq. [A7] is expressed using Eq. [A2] leading $\Delta c\propto {d}^{-\frac{5}{4}}$ and therefore

$$\Delta c \times \frac{1}{{t}_{\rm R}}\approx {d}^{-\frac{5}{4}} {d}^\frac{2}{4}={d}^{-\frac{3}{4}}$$

(A8)

Equation [A8] shows already a weaker than linear dependence of the product of two of three terms regarding Eq. [18] for large droplets. Considering the cumulative mass of the droplet size distribution equation [A9] and the relative mass fraction equation [A10]. The estimation of the dependence of relative mass fraction is possible.

$${w}_{\rm ej}=\rm{exp}\left(-{\left(\frac{d}{{d}^{^{\prime}}}\right)}^{n}\right)$$

(A9)

$$\frac{d{w}_{\rm ej}}{dd}= -\frac{n {d}^{n-1}}{{d}^{{\prime} n}}\rm{exp}\left(-{\left(\frac{d}{{d}^{{\prime}}}\right)}^{n}\right)$$

(A10)

The distribution exponent $n$ was calculated and measured to 1.25.^[12] Close to d′ the diameter dependence of the mass density function is estimated to $\frac{d{w}_{\rm ej}}{dd}\propto {d}^\frac{1}{4}$. Therefore reducing the dependence of emulsion refining on the droplet diameter for large droplets even further as presented in Eq. [A11].

$$\Delta {w}_{\rm ej}\times \Delta c\times \frac{1}{{t}_{\rm R}}\approx {d}^\frac{1}{4}{d}^{-\frac{5}{4}} {d}^\frac{2}{4}={d}^{-\frac{1}{2}}$$

(A11)

In reference to Figure 12, it is noted that the modeled mass density function does not follow an RRS distribution. The diameter dependence is stronger for large droplets. The residence time in Eq. [A7] is modeled and not estimated using [A2].