Mathematical Modeling of the Ejected Droplet Size Distribution in the Vicinity of a Gas–Liquid Impingement Zone

Abstract

The controlled splashing of metal droplets plays a decisive role in the kinetics of the basic oxygen furnace (BOF) process. In this work, a mathematical model was developed for predicting the size distribution of spherical droplets ejected at an impingement zone. Harmonic oscillators are used to describe the ejection sites, and the upper limit for the droplet population is calculated through a force balance. The model was validated against literature data from high-temperature crucible experiments involving different supply pressures and lance heights as well as both single-hole and multihole lances. The predicted size distribution of the metal droplets was found to be in good agreement with the droplet size distributions measured from outside the crucible. The model was also applied for predicting the size distribution parameters of the Rosin–Rammler–Sperling (RRS) size distribution function. The model developed is computationally light and is suitable to be used as a part of offline and online simulation tools for the BOF process.

Introduction

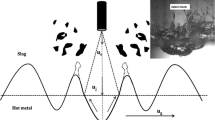
The basic oxygen furnace (BOF) is the main refining process for hot metal produced using blast furnace ironmaking. Modern basic oxygen furnaces are fitted with a multihole supersonic top lance for oxygen injection as well as porous plugs for bath stirring using inert gases. Upon impact to the bath surface, the top-blown gas jet creates a cavity. Molloy^[1] identified three cavity modes: dimpling, splashing, and penetrating. The dimpling mode is characteristic of low gas injection rates and denotes the mild deformation of the surface. As the gas flow rate is increased or the lance height is decreased, the cavity enters the splashing mode, which is characterized by the ejection of large quantities of outwardly directed droplets. With a further increase in the gas flow rate or a decrease in lance height —the penetrating mode is reached. In this mode, the penetration becomes much deeper and the amount of outwardly directed splashing is reduced.

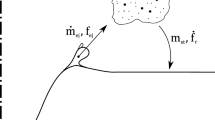
The generation of metal droplets and the resulting metal-gas-slag foam, which play a decisive role in the high decarburization rates, are characteristic of the BOF process. For example, Meyer et al.^[2] suggested that the metal-slag interfacial area may reach 2000 ft² (186 m²) per ton. Consequently, a significant amount of experimental and computational research effort has been directed at investigating the droplet generation phenomenon. Two key areas of interest can be identified: (1) the generation rate of metal droplets, which, together with the residence time of the droplets, defines the volume of metal in the foam; and (2) the size distribution of the droplets, which, together with the volume of metal in the foam, defines the surface area available for metal-slag reactions. The size distribution of the metal droplets also affects the residence time of those droplets.

Different approaches have been proposed to predict the droplet generation rate. The blowing number ($B$) proposed by Block et al.^[3] provides a criterion for the onset of splashing (Eq. [1]) considering the gas flow rate $\dot{V}$, the lance height $h$, the nozzle diameter ${d}_{n}$, and the cavity depth ${t}_{\mathrm{cav}}$. The squared deviation of the blowing number to the critical blowing number was found to be directly proportional to the mass ejection rate of liquid exiting the bulk (Eq. [2]). The proportional constant ${K}_{l}/\frac{\mathrm{kg s}^2}{{\mathrm{m}}^{5}}$ was found to be dependent on the liquid properties and was determined to be 2.88 for water and 23 for hot metal.

$$B=\frac{\dot{V}}{{d}_{n}(x+{t}_{\mathrm{cav}})}\ge 4.646 {\sigma }^{0.432}$$

(1)

$$\dot{m}={K}_{l} \dot{V }{(B-{B}_{\mathrm{crit}})}^{2}$$

(2)

He and Standish^[4] linked the onset of splashing to the Weber number. The blowing number theory proposed by Subagyo et al.^[5] relates the onset of splashing formation to a dimensionless number also called the Blowing number ${N}_{B}$, which itself is a modified Weber number (Eq. [3]). It is the ratio between the drag force of the gas acting on the liquid surface and the geometric mean of surface tension and gravitational force.

$${N}_{B}=\frac{{{u}_{c}^{2}\rho }_{g}}{2\sqrt{\sigma g{\rho }_{l}}}\ge 1$$

(3)

where ${\rho }_{g}$ is the density of the gas at the impingement site, $\sigma$ is the surface tension, $g$ is the gravitational constant, and ${\rho }_{l}$ is the density of the liquid. The critical gas velocity ${u}_{c}$ was defined to be directly proportional to the axial velocity of the free turbulent jet ${u}_{t}$ at the position of the cavity so that Eq. [3] holds. The proportional constant was found to be 0.44721. Based on computational fluid dynamic (CFD) simulations, Alam et al. found that the constant was dependent on the lance angle^[6] and lance height.^[7] The original correlation for droplet generation by Subagyo et al. was later revised by Rout et al.^[8] to account for the volume expansion of gas in the converter atmosphere. Sabah and Brooks^[9] noted that because the original correlation by Subagyo et al. was derived for a fixed lance height, it could not reproduce their results for different lance heights. Owing to its simplicity and reasonable predictive capability, the blowing number theory has been used extensively to describe the droplet generation rate in various mathematical models for the BOF,^{[10,11,12,13,14]} argon-oxygen decarburization,^[15,16] and CAS-OB processes.^[17,18]

Meanwhile, several studies have been devoted to measuring or predicting the droplet size distribution. Table I shows a compilation of experimental and numerical studies focused on the droplet size distribution. An early study on the physical modeling of droplet generation was published by Kleppe and Oeters.^[19] They conducted low-temperature splashing experiments using both water and dibromoethane (CH₂Br₂) as the liquid phase. Kleppe and Oeters also used their measurements to estimate the foaming^[20] and droplet generation rate in a full-scale BOF converter.^[21] Perhaps the most elaborate experimental work on the dependency of droplet size distribution on the operating parameters was published by Koria and Lange,^[22] who suggested that the droplet size distribution can be described using the Rosin–Rammler–Sperling (RRS) function. Based on an extensive number of high-temperature measurements, they conducted a statistical analysis to relate dimensionless momentum numbers to the parameters of the RRS distribution. As the metal droplets were collected at their place of origin, the metal droplet size distributions reported by Koria and Lange^[22] extended to larger droplet sizes than those reported for slag samples taken from industrial vessels.

Another important study was carried out by Standish^[23] and He and Standish,^[24] who also studied the interaction of top and bottom blowing, reporting that the mean droplet size was increased by bottom blowing. While Subagyo et al.^[5] successfully related the Blowing number to the parameters of the RRS distribution function, their approach, similar to that of Koria and Lange,^[22] provides only a statistical explanation for the mechanisms affecting the dependency of droplet size distribution on the blowing parameters. Ji et al.^[25] measured droplet size distribution in a crucible larger than those employed by Koria and Lange and found that the RRS approach predicted large metal droplets that could not be found in the emulsion. The deviation was proposed to be associated with the fact that the RRS approach considers the emulsion as a homogeneous system and does not account for the coalescence and breakup of the droplets.

Recently, Haas et al.^[26] employed the shadowgraphy method for the direct measurement of the direction, size, and velocity of droplets generated by top blowing in a physical model. In keeping with earlier studies,^[25,27] the results by Haas et al.^[26] confirmed that the droplet properties depend strongly on the sampling position. Unlike in the study by Koria and Lange,^[22] the distribution exponent of the RRS distribution was found to depend strongly on the lance height. The splashing angle was reported to be less dependent on the cavity mode than what would be expected based on the changes in the cavity modes.

In the study by Li et al.,^[37] CFD calculations using a three-phase volume of fluid method were used to predict cavity geometries and, qualitatively, the ejection phenomena up to three seconds of blowing time. The required fine grid between the lance tip and the liquid surface led to the choice of the coarse grid resolution at ejection sites in order to achieve acceptable calculation durations.^[37] Predicted ejected mass fragments were classified as large droplets and splashed sheets. Here, the underlying splashing mechanism was attributed to the traveling of generated ripples or instabilities from inside the cavity to its boundaries. This led to instable fingers, which broke up to droplets. A consecutive study was made by Li et al.^[38] calculating one half of the converter domain. Using a longer initial time step and increased computational effort, the calculation of the blowing number under splashing conditions was attained.^[38] As mentioned by Li et al.^[38] the calculation method was unable to predict the droplet ejection phenomena of the size range found in experimental hot models. Thus, it may be concluded that while modern CFD models can capture the formation of splash sheets during top blowing, tracking the splashing of individual droplets is still computationally too expensive to replace simplistic approaches such as the blowing number theory.

To the authors’ knowledge, there is no simple modeling approach that would relate the blowing parameters to the size distribution of the metal droplets in a physically sensible way. Consequently, the aim of this work was to develop a mathematical model that can be incorporated as part of phenomena-based process models for the BOF process and other unit processes involving splashing due to top blowing.

Materials and Methods

Model Description: Relative Mass Ejection Rate

For high ratios of jet momentum compared to lance height, the ejection phenomena are predominantly stochastic. The droplets vary in mass over four to five orders of magnitude.^[27] If an ejection of a certain mass is triggered at a defined location on the cavity circumference, then this site is blocked for further ejection of a similar mass for the period of time needed to restore the pre-ejection state. The schematics of droplet generation, as calculated by Li et al.,^[38] are shown in Figure 1.

Fig. 1

(a) Excitation or finger, (b) the narrowing neck occurs while the mass center of the forming droplet travels further, and (c) the droplet separation leaves the crest at the ejection site behind

Fig. 2

(a) Oscillation site of radius R at displacement s = 0, ${E}_{\gamma }=0$, ${E}_{\sigma }={R}^{2}\pi \sigma$ and (b) displacement s = R, ${E}_{\gamma }=\left(\frac{3}{8}R\right)\frac{1}{2}\left(\frac{4}{3}{R}^{3}\pi \right)\rho g, {E}_{\sigma }={2 R}^{2}\pi \sigma$

The size of the crest created after droplet formation is proportional to the droplet size. The high surface area per volume, as well as gravity, accelerates the crest downward, leading to an unlikely further ejection of a droplet of similar mass at this position directly after ejection. This is due to the inertia of the liquid mass flowing opposite to the ejection direction shortly after the previous ejection. Therefore, a duration of time exists between the initial crest formation and a liquid state at the ejection site where further droplet ejection becomes far more probable again.

This duration determines the ejection rate if the condition of sufficient activation energy for droplet ejection is always met right after an ejection-capable state is regained. It provides a measure for relative ejection rates of different droplet sizes for the case where the time between two ejections is shorter than the time needed for damping the oscillations caused by the first ejection, thus re-establishing a stagnant liquid. It is assumed that in each period, an ejection favorable geometrical condition is passed with a certain probability of ejection. This probability depends on the energy of eddies of the same magnitude and the work necessary for droplet creation. The ratio of the number of oscillators of given radii on the circumference of the cavity is taken as inversely proportional to their ratio of radii, thus allowing superpositions. A cavity circumference of 1 m manages to hold 50 potential oscillation sites of 2-cm d. and 500 potential oscillation sites of 2-mm d. If, at every upswing, an ejection occurs for both ejection site sizes oscillating with equal frequency, 10 times more 2-mm-d. droplets are formed than 2-cm-d. droplets. Despite this ratio, the 2-cm-d. droplets weigh 1000 times more than the 2-mm-d. droplets and, therefore, represent 100 times more ejected mass. It is important to model the influence of the mentioned frequency in order to successfully predict the relative mass of generated droplet sizes.

Let a half-sphere of liquid be placed on the surface of a stagnant liquid of the same kind or removed from it with its midpoint at the undisturbed surface. The subsequent motion of the fluid shall be defined over a simple harmonic oscillator given by a spring-mass system, with the spring constant determined by the energy of the initial protrusion stored as path-independent work over the displacement taken as the radius of the half-sphere. The resulting energy balance is given by

$$\Delta E={\int }_{0}^{R}k s ds=\left(\frac{1}{2}4-1\right){R}^{2}\pi \sigma +\left(\frac{3}{8}R\right)\frac{1}{2}\left(\frac{4}{3}{R}^{3}\pi \right)\rho g$$

(4)

where R is the radius of the considered protrusion, k is the spring constant, s is the displacement of the spring from the equilibrium position, $\sigma$ is the surface tension, $\rho$ is the density of the liquid, and $g$ is the gravitational constant. The position of the half-sphere’s center of gravity is at a distance of $\frac{3}{8}R$ from the base. The added surface area of a considered oscillation site of ${R}^{2}\pi$ is half the surface area of a sphere subtracting the base (${R}^{2}\pi$) surface. It is assumed that the indistinct oscillating mass $m$ is equal to the mass of a sphere having the same radius. The frequency $f$ of a one-dimensional simple harmonic oscillator described by a spring-mass system with the spring obeying Hooks law is given by

$$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}} $$

(5)

The frequency of an oscillating site with a given radius R and a spring constant defined by Eq. [4] can be calculated by

$$f=\frac{1}{2\pi }\sqrt{\frac{\frac{1}{2}{\rho }_{l}gR{^{2}}+2\sigma }{\frac{4}{3}R{^{2}}{\rho }_{l}}}$$

(6)

The mass flux rate $\dot{m}$ of a given droplet size exiting the cavity is proportional to the probability $X$ of an oscillating mass gaining sufficient excess energy, during one period, for ejection. The mass ejection rate is also proportional to the number of oscillators fitting on the cavity circumference ($\propto \frac{1}{R})$, the mass of a single droplet $m$, and the frequency of the oscillation sites:

$$\dot{m}\propto X\left(R\right)\frac{1}{R}m\left(R\right)f\left(R\right)$$

(7)

Eddies of the same magnitude as the droplets contribute to the energy available for ejection. By using Kolmogorov’s energy spectra, an eddy’s energy in a completely turbulent field is given as $\propto {L}^\frac{5}{3}$, with $L$ being the characteristic length of an eddy. Considering the droplet separation mechanism shown in Figure 1, the energy necessary for successful separation was assumed to be predominately dependent on surface energy and, therefore, $\propto R^2$. A possibility for taking the gravitation influence on ejected liquid mass into account would be to apply the geometric mean of the volume and the area therm, ${\left(R^2 R^2\right)}^\frac{1}{2}$. A relationship for the mass flow rate can be calculated.

$$X\left(R\right)\propto \frac{{R}^\frac{5}{3}}{{R}^{2}}$$

(8)

$$\dot{m}\propto \frac{1}{\sqrt[3]{R}}\frac{1}{R}m\left(R\right)f\left(R\right)$$

(9)

With this equation, it is already possible to calculate the relative mass flows of given droplet radii. In order to calculate the stochastic fraction of the ejected droplet size distribution, the definition of the upper and lower limits of the population is necessary. The lower limit is modeled over the liquid momentum boundary layer.^[19]

The main assumptions for the relative mass ejection rate can be summarized as follows.

• (1) Periodic favorable droplet ejection conditions are occurring for droplet generation along the circumference of the outer cavity. The probability of an ejection occurring during favorable conditions depends on the energy of turbulent eddies being of the same size as the droplet to be produced.

• (2) Droplet ejection is further dependent on the surface tension that has to be overcome for successful separation. Viscosity effects are considered negligible.

• (3) The frequency of the ejection favorable conditions occurring at a cavity position can be described using a spring-mass system. The spring constant and, therefore, the force acting against ejection are described by using a protruded half-sphere as the defining state. The force acting on the protruding liquid is described using this spring constant for sufficient protrusion lengths.

Validation Data

When studying gas–liquid impingement phenomena, most authors focused on the mass flow rates exiting the bulk metal phase and the metal fraction momentarily in the emulsion. Few authors provided sufficient data regarding the size distribution of the generated droplets. Often, the sampling methods led to the alteration of the measured distribution due to slow sample removal and retrieval in a carrier phase. The focus of this research was the calculation of the ejected distribution. The work of Koria and Langes^[27] was the only research that met the criteria needed where a gas–liquid impingement experiment was set up under simulated steelmaking conditions. Their research provided sufficient data concerning ejected droplet distribution, measured without slag interaction, where the droplets had no significant energy barrier to overcome.

Upper Limit of the Droplet Distribution r₁

For a radius equal to an infinitesimal diminished upper droplet distribution limit r₁, there is a positive ejection probability for a specific system of gas–liquid jet impingement (Figure 2). To predict this boundary value, a force balance has to be defined. Given the momentum flow of the gas exiting the cavity, the calculation of the highest possible force acting on a droplet of radius R is possible considering the fraction of the cavity circumference occupied by the droplet. If a spherical liquid element protrudes into the cavity, the area blocked for the exiting gas relative to the maximum blocked area for equal intrusion depth is 4/π. In Figure 3, the cavity is seen from above (gray) with a droplet protruding at the circumference into the cavity (orange). The entering and exiting jet momentums are assumed to be perfectly and symmetrically distributed. The shown sector exhibits an influx and outflow of $\frac{2R}{2\pi {r}_{\mathrm{cav}}}$ times the total gas flux.

Fig. 3

(a) Cavity from above (gray) and protruding droplet (orange); (b) Detailed sketch for area ratio constant 4/π (half-circle per square)

The maximum force acting on the protrusion opposite to gravity would then be

$${F}_{\mathit{max}}={F}_{tot}\frac{2R}{2\pi {r}_{cav} }\frac{\pi }{4}$$

(10)

where r_cav is the cavity radius. For the limiting instance, this force would be the gravitational force of the droplet and the force of surface tension, leading to the equation for the upper limit r₁ of the droplet distribution.

$${F}_{\mathrm{max}}={F}_{\gamma }+{F}_{\sigma }$$

(11)

$${F}_{\gamma }=\frac{4}{3}{R}^{3}\pi g{\rho }_{l}$$

(12)

$${F}_{\sigma }=4\pi R\sigma $$

(13)

$${r}_{1}=\sqrt{\frac{3 }{4{\rho }_{l}g\pi }\left(\frac{{F}_{tot}}{4{r}_{cav}}-4\sigma \pi \right)}$$

(14)

The assumptions to be considered in the model upper distribution limit.

• (1) The empirical cavity geometry formulas of Koria and Lange^[39] are applicable for the experiments.

• (2) The cavity shape can be approximated as a paraboloid of revolution.

• (3) The hydrostatic force calculated from the paraboloid can be taken as a conservative upper limit of the vertical component of the jet exiting the cavity.

• (4) The flow inward and outward of the cavity is symmetrical.

• (5) The upper droplet distribution limit is modeled using the state of a droplet protruding halfway horizontally into the cavity.

• (6) The maximal force acting on the protruded droplet is proportional to the ratio of the area blocked for the exiting jet. This is relative to the rectangle defined by the maximum intrusion point and the droplet diameter.

• (7) The drag force acting on the protrusion counteracts the full gravitational force of the sphere defined by the protrusion radius.

• (8) The generated surface, per spatial deviation of the protrusion, can be modeled by the axial extension of a liquid cylinder out of the same fluid, leading to a force of ${F}_{\sigma }=2\pi R\sigma$.

• (9) The relevant retaining force attributed to surface tension effects considering droplet separation phenomena can be taken as twice the modeled force (${F}_{\sigma }=4\pi R\sigma$).

Results and Discussion

In the following, the cumulative weights of metal droplets measured in the experimental setups of Koria and Lange^[22] were compared with the calculated values for the same experimental setups. For the calculation, the following adaptations of the model were applied. The calculated graphs were shown to be insensitive to a further reduction of the lower droplet limit; therefore, in demonstrated calculations, the lower population boundary is zero. For single- and multihole lances, a correction of the upper droplet distribution limit was applied.

$${\mathrm{r}}_{1,\mathrm{calculated}}=2.7\cdot {r}_{1,\mathrm{model}}$$

(15)

The surface tension was taken as 1.5 J/m², and the liquid density was assumed to be 6580 kg/m³.^[40] The cavity profile was calculated as a parabola with the characteristic measurements taken from empirical correlations given in the work of Koria and Langes.^[39] The cavity exiting gas jet momentum was calculated in accordance with the capability of the jet maintaining the cavity shape. A summary of the test conditions applied to the model is shown in Table II.

Figure 4 shows the cumulative weight of the droplets for four different dimensionless lance heights (x/d_e) as a function of droplet size. The ratios of the mass ejection rates are in good agreement for the majority of the blowing parameters. The most significant deviations are exhibited for the 5 bar backpressure and a dimensionless lance distance of 50. For all published single-hole cumulative weight data sets with zero wall height, the Pearson R² is 0.979, indicating a very good statistical agreement with the predicted and measured values. The two-tailed p-value is on the order of 10^–262, which is the probability that the correlation of the validation data to the model would have been caused randomly.

Fig. 4

Predicted and measured^[27] cumulative mass of ejected droplet population for a single-hole lance

Figure 5 shows the cumulative weight fraction of droplets for three- and four-hole lances at different lance heights as a function of droplet diameter. The predictions are, in all cases, less accurate than those with the one-hole lance. The change in cumulative mass increase to smaller droplets is tendentially smaller than predicted, thus underpredicting the smaller size fractions of droplets. The R² value was calculated as 0.983, and the two-tailed p-value was on the order of 10^–39.

Fig. 5

Predicted and measured^[27] cumulative mass of ejected droplet population for multihole lances

Figure 6 shows the average prediction deviation for a fraction of the droplet population close to a diameter on the abscissa. For example, it is seen that with single-hole experiments at 4 bar and multihole experiments at 6 bar, the model predictions for the weight fraction of droplets with diameters close to 10 mm are less than the experimental readings indicated by the blue color in the plot. For the droplets smaller than 6 mm, an overprediction tendency for the multihole blowing experiments and an underprediction tendency for the single-hole blowing experiments, independent of the back pressure, are indicated. The largest deviation was found in the region of the largest droplets. The model for the upper droplet distribution limit is responsible for this deviation.

Fig. 6

Qualitative prediction error. Overprediction is red and underprediction is blue for single-hole lance data (left) and multihole lance data (right). Validation data from Koria and Lange.^[27] (Color figure online)

Single- and Multihole Correction (Correction Factor r₁)

The gas exiting the cavity is subjected to momentum variations.^[41] This gas momentum is not uniform along the circumference of the cavity and in time. If we let the calculated effective momentum be the expectation of a random variable, then we conclude that the effective local momentum for ejection leading to the 2.7-fold value of the upper droplet distribution limit has a negligible probability of occurrence. Further deviations could originate from the empirical equations used for the cavity geometry predictions.

Size Distribution Function

Koria and Lange^[22] proposed that the size distribution of metal droplets can be described well using the RRS distribution function, defined as follows:

$$R=100\mathit{exp}\left[-{\left(\frac{d}{{d}^{{\prime}}}\right)}^{n}\right]$$

(16)

where $R$ is the cumulative weight of droplets (in percentage), $d$ is the droplet diameter, ${d}^{{\prime}}$ is a fineness parameter that is equal to the statistical droplet size for R = 36.8 pct, and n is the distribution exponent that is a parameter for the homogeneity of the size distribution. The results for the RRS function parameters reported by Koria and Lange^[22] and those calculated using the model presented in this work are shown in Table III. As for the fineness parameter d', the predicted values are, on average, slightly larger than those measured by Koria and Lange.^[22] The mean absolute percentage error is 19 pct, but despite the scatter, the statistical agreement (R² = 0.89) is reasonably good. In fact, the predicted direction of change in the value of d' following a change in dimensionless lance height or backpressure is correct for all the cases given in Table III. The predicted distribution exponent n is in close agreement with the measured values: the predicted average value of n = 1.22 matches the measured average value of n = 1.22, while the mean absolute percentage error and mean absolute error are only 5 pct and 0.06, respectively. However, the model predicts more variation in the value of the parameter n than what was reported experimentally by Koria and Lange^[22]; consequently, the statistical agreement is poor (R² = 0.05). All in all, it can be concluded that while the accuracy of the model for determining the RRS distribution parameters is only satisfactory, it can still reliably estimate their correct order of magnitude.

Further Use of the Model

This work aimed to develop a mathematical model that can be incorporated as part of the phenomena-based BOF process models. Short calculations are needed in online prediction software; therefore, it is preferable to have submodels that are computationally light. The typical calculation time for the cases presented in this article was 200 ms using python 3.9 on an intel i7-8750H without any considerations regarding performance optimization. This indicates that the model is sufficiently fast for online applications, especially if the fluid flow field is assumed to be steady state.

Conclusions

A mathematical model was developed that can be used as a part of phenomena-based process models for unit processes involving splashing due to top blowing. Considering the basic nature of the model, these depictions provide interesting insight into the possible mechanisms involved in droplet formation and their creation. The prediction accuracy for single-hole setups is high, and that for multihole setups is acceptable. Additional model adaptations could increase the multihole prediction accuracy. There are no defined criteria for successful mass escape, and all the experimental data used for evaluation originated from setups performed with a container wall height near zero. The model was applied for predicting the size distribution parameters of the RRS size distribution function. The distribution parameters obtained were in close agreement with those reported in the literature. Finally, it can be concluded that the model is sufficiently fast to be integrated as a part of fundamental mathematical models for the BOF process also in online use.

Table I Experimental Studies on the Size Distribution of Metal Droplets Generated by Top Blowing

Table II The Conditions Used for Model Testing

Table III Comparison of Predicted and Measured RRS Size Distribution Parameters

Appendix

The calculation of mass fraction of droplets greater than R = 2.5 mm from a droplet population ejected using a single-hole lance operated at 4 bar and 37.5 dimensionless lance height (Figure 4(a), 4 bar):

$${p}_{0}=4 \mathrm{bar}$$

$$\frac{x}{{d}_{e}}=37.5$$

$${d}_{e}=1.2 \mathrm{mm}$$

The cavity depth and diameter are calculated according to Koria and Lange:^[39]

$${t}_{\mathrm{cav}}=37.7 \mathrm{mm}$$

$${r}_{\mathrm{cav}}=30.955\mathrm{ mm}$$

Therefore, the hydrostatic force of the paraboloid can be computed as

$${F}_{\mathrm{tot}}=3.63 \mathrm{N}$$

Using Eq. [14] and the conditions in Table II, the upper distribution limit is found:

$${r}_{1}=17 \mathrm{mm}$$

(R1 = 16.889 mm)

Incorporating Eq. [9] in Eq. [A1], the calculation of the weight fraction of droplets with radii greater than 2.5 mm is achieved.

$$w\left(R\right)= \frac{{\int }_{R}^{r1}\dot{m dr}}{{\int }_{r0}^{r1}\dot{m dr}}$$

(A1)

With $R=2.5\times 10^{-3}$, we calculate numerically, using scipy.integrate.quad, that 92 wt pct of the ejected droplets are bigger than 5 mm in diameter. All droplets smaller than 5 mm in diameter account for only 8 wt pct of the total ejected mass.

The weight fractions of droplets $R0<R< R1$ can be evaluated using Eq. [A2]:

$$w\left(R\right)= \frac{{\int }_{R0}^{R1}\dot{m dr}}{{\int }_{r0}^{r1}\dot{m dr}}$$

(A2)

For a lower droplet class bound $R0$ of 1 mm and upper droplet class bound of $R1$ of 2.5 mm, results show that this size class amounts to 5 wt pct of all droplets ejected at this blowing condition.