Modeling and Energy Efficiency Analysis of the Steelmaking Process in an Electric Arc Furnace

Abstract

This paper presents a comprehensive model of an industrial electric arc furnace (EAF) that is based upon several rigorous first-principles submodels of the heat exchange in the EAF and practical experience from an industrial melt shop. The model is suited for process simulation, optimization, and control applications. It assumes that the energy demand of the process is satisfied by six sources, the electric arc, the oxy-fuel burners, the oxygen lances, the combustion of coal, and the oxidation of metal in the liquid and in the solid phase. The energy exchange between the liquid and the solid phase due to liquid metal splashing is also considered. The different mechanisms of heat exchange are represented in the model as follows: (a) the radiative heat exchange from the arc to the other phases is computed using the DC circuit analogy, where the view factors are calculated using exact formulae and Monte-Carlo algorithms. (b) The energy input from the oxy-fuel burner is modeled using simplified geometries for which heat transfer relationships are known. (c) The amount of heat released by the oxidation of solid metal is described by the quadratic corrosion formula. (d) The energy exchange from the bath to the solid phase due to splashing is modeled using relationships and experimental data that are available in the literature. The model contains the melting rates and the efficiency of the oxygen lancing as free parameters; their values were computed by a least squares fit to process data of an industrial Ultra-High-Power EAF. In comparison with existing EAF models, the model presented here describes the dynamic behavior of the melting process more realistically. Based on the model, time-dependent energy efficiency curves for the various contributions and for the overall process are computed and discussed.

Introduction

Carbon Steel vs Stainless Steelmaking Processes

Steel production via electric arc furnaces (EAFs) is a very energy-intensive process that accounts for almost 25 pct of the total crude steel production worldwide.^[1] Although the technology has a history of over 100 years, a full understanding of the process has not yet been accomplished, and industrial operations still rely strongly on empirical models and on the experience of the operating crews. A modern EAF can be viewed as a batch reactor in which metal scrap is melted, and its composition is partially or completely refined. The latent and sensible heat that is required for the phase transition of the metal is mainly provided by electric energy and supported by chemical energy. On the one hand, the electric energy is used to generate plasma jets that can reach temperatures of up to 17,500 K.^[2,3,4] On the other hand, natural gas burners and oxygen lances are used for two purposes. First, to create oxy-fuel flames with temperatures over 3,000 K^[5,6] that aid the melting of the solid scrap and second, to inject oxygen in the liquid metal pool, promoting its decarbonization.

The way in which steel is produced in EAFs depends on the geographical location and the type of steel produced. Some of the most influential factors in the operations are the costs of the raw materials and of electric power. EAFs in countries with high electricity and scrap costs tend to use more chemical energy and to use more direct reduced iron (DRI) as raw material. This is because industrial gases and DRI are cheaper than electricity and scrap. Furthermore, the operational practices to produce a batch of steel also vary considerably from meltshop to meltshop and are strongly dependent on whether carbon steel or stainless steel is produced. It can be said that stainless steels tend to be produced with more scrap than carbon steel. One of the main differences in the operative practices between carbon and stainless steels is that in carbon steels, large quantities of oxygen and carbon are injected toward the end of the batch with the target of creating a foamy slag layer on the top of the liquid metal which can be sufficiently deep to cover the electric arc. On the other hand, stainless steel is produced without carbon injections, and the arc mostly remains uncovered throughout the batch time.

One of the most important challenges in modern EAF steelmaking is how to operate the processes such that its environmental impact is reduced, and its economics are improved. In an earlier work,^[7] we demonstrated that for the EAF process, dynamic optimization can be employed to compute an optimal group of setpoints that reduces the electrical losses of the process, thus improving its economics and reducing its environmental footprint. Dynamic optimization requires an accurate mathematical model of the process under study because in the presence of process model mismatches, the optimization algorithm may compute pseudo-optimal operating policies that can be distant from the true optimum of the plant.

Developing an accurate EAF process model is a very challenging task due to several reasons. First, a complete EAF model should consider many phenomena such as plasmas, oxy-fuel combustion, chemical reactions, heat exchange due to conduction, convection, radiation, and many others. Second, to build an EAF process model, many assumptions that cannot be validated have to be made, e.g., the selection of an appropriate mechanism of heat exchange from the arc to the other phases in the EAF, which is a fundamental assumption in any EAF model. Third, the lack of online measurements of the most important dynamic variables in the process makes it very difficult to validate the performance of EAF models in a rigorous manner.

While a significant number of EAF process models have been developed with the aim of predicting the dynamic evolution of steelmaking processes with foamy slag slayers (carbon steel), see e.g., References 8,9,10, through 11, these models can hardly be employed in a model-based optimization framework of the production of stainless steel because the predictions that they provide regarding the trajectories of critical state variables are unrealistic. In particular, the extremely fast melting rates that these models predict do not match our observations and process data from industrial-scale furnaces and lead to a dramatic mismatch between the predicted and the observed amount of unmolten metal over the course of the batch. This mismatch is problematic because the energy fluxes, and hence the energy efficiency of the process over the course of the batch, are not computed accurately. The considerable process model mismatches can be attributed mainly to the assumptions made regarding the heat exchange in the interior of the EAF. In the presence of the foamy slag layer in an EAF producing carbon steel, it is assumed that the slag absorbs a substantial amount of the energy emitted by the arc, and that a large fraction of this energy is then transmitted to the solid scrap, promoting its melting. For the case of the stainless steelmaking process, this assumption does not hold because the arc remains mostly uncovered throughout the batch.

Contributions of This Work

In this work, we present an EAF process model that was employed for the optimization of the stainless steelmaking process as reported in Reference 7. The application of the optimized operational policy led to a reduction of up to 4.5 pct in the energy consumption of one of the operative EAFs at Acciai Speciali Terni (AST) in Terni, Italy, the largest integrated plant producing stainless steel in the European Union.

The importance of re-evaluating the fundamental assumptions on which EAF process models have been built during the last 20 years is justified by the transition that the steelmaking sector is experiencing toward a more environmentally friendly mode of operation. First, it has been projected that by 2050, almost half of the global production of steel will take place in EAFs—as a measure to decarbonize the steelmaking sector.^[12] Secondly, to reduce its environmental impact, the steelmaking sector will embrace a circular economy approach where the use of metallic scrap will be increased.^[13] For an EAF that currently operates with significant amounts of DRI/HBI, this will result in an operation with shorter batch times (assuming no changes in the energy input) and a delay of the entry point of the oxygen lances. For operations with large shares of scrap, the oxygen lancing is ideally initiated when sufficient material has melted and the jet can reach the pool of liquid metal. Otherwise, the remaining solid material will impede the oxygen jet from reaching its target, causing significant oxygen losses. This implies that the pre-foaming period of the batch will have a larger impact on the energy demand of the process than it currently has. This paper focuses on developing a model for the energy exchange of the current operational practice of the stainless steel production process, which is similar to the pre-foaming period of carbon steelmaking.

The novel EAF model presented here is tailored to predict the evolution of the masses and temperatures of the different phases in the EAF and of the energy fluxes between these, the arc, and the containment, for EAFs that operate with thin slag layers and that employ large amounts of metallic scrap as raw material. For operations with large shares of scrap, the oxygen lancing can only be initiated at a very late stage of the melting process, when sufficient material has been molten—otherwise, the remaining solid material will impede the oxygen jet from reaching the pool of liquid metal. Our model was successfully validated using process data of an Ultra-High-Power EAF (UHP-EAF) producing stainless steels, and we conjecture that it can also be used to predict the behavior of EAFs producing carbon steels that are operated using large shares of scrap material and a late oxygen lancing strategy, because for this mode of operation, the electric arc will also remain uncovered during most of the batch.

The EAF model introduced in this work differs from its predecessors in several aspects:

• (a) In earlier modeling works, a cone frustrum geometry was used to model the shape of the solid metal phase. Here, a novel hollowed cylinder geometry is employed. Based on our observations of the process, this geometry approximates better the real shape of the solid metal over the course of the batch, especially during the boredown period of the electrodes.

• (b) Earlier EAF process models have assumed that radiation is an important mechanism of heat exchange. However, its contribution to the process has been limited to a maximum of approximately 70 pct of the total electrical power input to the process. Based on recent findings,^[2] we assume in this work that radiation is the dominant mechanism of heat exchange from the arc to the other the phases and the EAF enclosure, and that the electric arc converts 100 pct of its electrical power to radiation.

• (c) In this work, custom-developed Monte-Carlo algorithms are employed to compute the view factors that characterize the radiative exchanges. The use of these algorithms enables one to deal for the first time with the shadings and view lines blockages in the radiative exchanges, which earlier works have ignored. Furthermore, the heat exchange problem is solved using the DC circuit analogy. The topology of the proposed electric circuit is designed to change over time according to the changes in the geometry of the participating surfaces, and the energy fluxes are controlled using switching variables.

• (d) Earlier works have assumed that the oxidation of solid metals can take place at all times and that they are only limited by the presence of oxygen in the atmosphere—which until today has been the prevailing modeling assumption. Here, we have considered that the energy contribution from the oxidation of solid metals is governed by the corrosion phenomena of solid metals in oxidizing atmospheres. This assumption sets an upper limit to the energy contribution from the oxidation of solid metals, which is much lower than that established by the presence of oxygen in the atmosphere of the furnace.

• (e) The heat exchange that occurs due to the splashing of liquid metal onto the solid metal is considered for the first time. Although its overall contribution to the evolution of the process is small, this mechanism of heat exchange is fundamental in the melting process toward the end of the batch, when the radiation from the arc to the solid metal is not contributing much anymore.

• (f) The structure of the model proposed here focuses on providing a comprehensive description of the mechanisms of heat exchange of the process, making it possible to identify what sources contribute when to the melting of the solid metal. This provides the basis for estimating dynamic efficiency curves for each energy input and for the overall process, as well as for the computation of optimal modes of operation of the process—which is discussed in other papers of the authors, e.g. References 7 and 14

This manuscript is organized as follows: Section II provides a short overview of the most influential EAF process models in the scientific literature, and the main modeling assumptions in these works are briefly discussed. Section III introduces the full system of Differential Algebraic Equations (DAE) that describes the dynamics of the metal melting process as well as the mechanisms of heat exchange, considering all the elements mentioned above. In Section IV, the predictions of the model are compared with those obtained by the models of Logar et al.^[10] and Opitz et al.^[15,16] In Section V, the time-varying energy efficiency of a typical EAF process is analyzed and discussed. The paper is concluded with final remarks and conclusions in Section VI.

Brief Overview of EAF Process Models

Two of the most influential EAF dynamic models in the literature are those developed by Bekker et al.^[8] and MacRosty et al.^[9] In Reference 8, a first-principles non-linear model with 14 states that describes the chemical composition of the flue gas and the molten metal was developed. The study assumed that 100 pct of the power of the arc was transferred to the liquid phase and from there, via conductive mechanisms, to the solid phase. This obviously is a quite drastic simplification of reality where the electric arc also heats up the solid metal and the enclosure of the furnace. The heat transfer parameters used in the study were indicated, but no reference or arguments for their selection were given. Nonetheless, most of the research in advanced process control strategies (APC) to improve the process conditions^[17,18] and the economics of the process^[19,20,21] relied on this model to predict the trajectory of the state variables during the batch.

Based on the ideas formulated in Reference 8, MacRosty et al.^[9] developed a first-principles model based on the mass and energy balances of four assumed phases in an EAF: the gas zone, the slag zone, the solid metal zone, and the molten metal zone. This work considered for the first time the radiation mechanisms from the arc to the other phases in the EAF enclosure and introduced the cone-frustum geometry to model the shape of the solid phase in the furnace. The model was parameterized by the heat transfer constants which were adapted using an estimation procedure from available process data of the temperature and the chemical composition of the flue gases, as well as the final temperature of the molten steel. Although the model predicted the chemical composition of the flue gases, the slag and the liquid metal well, many heuristic approximations were made to compute the view factors in the radiation model of the EAF. Furthermore, the results of the parameter estimation procedure reduced by almost 45 pct the enthalpy of fusion of the solid metal compared to the usually assumed values. This implies that the raw materials needed to be modeled with unrealistically low enthalpies of fusion to obtain realistic batch times. APC work that utilized this model to optimize the economics of the process was reported in Reference 22 and 23.

In a series of papers, Logar et al.^[10,24] treated in detail the heat and mass transfer phenomena occurring in the EAF melting process. In these works, special attention was paid to the radiative heat exchange mechanisms, and a detailed description of the view factors for the cone-frustum geometry was provided.^[25] The model, however, yielded some debatable results as the oxidation reactions of solid metals provided energy contributions that were twice as large as that of the electric arc. This excessive energy contribution led to ultra-fast melting rates that according to our experience, are unachievable in practice. Recent research efforts focused on refining the works of Bekker et al., MacRosty et al., and Logar et al., in terms of improving the predictions of the chemical compositions of the slag,^[26] the liquid metal,^[27] and the radiative heat exchange.^[11] Nonetheless, these efforts did not address the problem of the too fast melting rates and the overestimation of the energy contributions of the oxidation reactions of solid metal. To our knowledge, these models have not yet been employed in APC studies.

Opitz et al.^[15,16] published two papers were the electric system, the regulation of the position of the electrodes, the vessel and the off-gas systems were included. The solid metal phase was discretized and a simplified version of the dynamical behavior of the melting, based on first-principles modeling, was developed. The two works differ from each other as one considered radiative heat exchanges and the other did not. In the first model, the influence of the participating media in the radiative exchange was also included. Industrial data were not used to validate the results, but the temperature and melting profiles were compared to those predicted by Logar et al.^[10] Interestingly, Opitz et al. argued that the addition of radiative mechanisms in the process had only a minor enhancing effect of the heat transfer phenomena. Detailed overviews of the state of the art and open issues in the area of EAF process modeling can be found in References 28 and 29.

Derivation of the Mathematical Model of an EAF

The model derived in this paper describes the melting process of solid scrap in an industrial Ultra-High-Power AC EAF producing stainless steels with a capacity of 150 Tons. The electrical power input is manipulated via the control system of the electrodes. The chemical input is provided using oxy-fuel burners and oxygen lances. The loading practices (number of charges, materials employed, etc.) and the power inputs (electrical and chemical) vary according to production needs.

The model presented here can be used to simulate the melting process in larger or smaller furnaces by modifying the geometrical parameters of the furnace (radius and height, and the diameter of the electrodes), the length of the electric arc (which can be determined from the electrical melting profile using the arc model^[2]), and the free parameters of the model (the geometrical constant of the furnace, the melting adjustment constant, and the oxygen distribution constants). The geometrical constant of the furnace depends on the dimensions of the EAF and the amount of charged material in each load, the melting adjustment constant on the scrap density, and the oxygen distribution constants on the oxygen practices. All these constants are described in detail in the following section.

Modeling Assumptions

Number and type of considered phases

The model assumes that only three phases exist in the interior of the furnace: the solid metal, the liquid metal, and a gaseous atmosphere.

• The solid metal is divided into two parts; one is the solid material that still not melted (i.e., the temperature is below the melting temperature), the other is the fraction of solid metal that is in the melting state (i.e., its temperature is the phase change temperature of the metal). The first will be called the solid metal in heating state, and the second the solid metal in melting state.

• The molten metal and the slag are modeled together as the liquid phase of the process for two reasons. First, in the production of stainless steels, the slag layer is formed only toward the end of the batch and is only few centimeters thick. Second, the energetic contribution of the chemical reactions in the slag and the liquid metal to the melting the process can be studied from a macro perspective without the need of considering in detail the chemical composition of the slag and the liquid metal. This simplification is described in more detail in Section III–H.

• The gas phase is assumed to be composed only of the combustion products from the oxy-fuel burners and the oxygen lances. This assumption is realistic for EAFs that operate during most of the melting process with the de-slagging door closed, as the flow of air from the atmosphere and into the interior of the furnace is minimized.

Geometry

The hollowed cylinder geometry that was introduced in earlier work by the authors^[30] is used to model the solid phase. From our observations of the process at various stages and for a large number of batches, this geometry approximates better than the cone-frustum geometry the real shape of the solid scrap during 60 to 70 pct of the total batch time. Observations of the geometry of the solid metal were carried out when there was an opportunity to observe the interior of the EAF, e.g., when an electrode replacement took place or when, due to anomalies, visual inspections of the interior of the furnace were needed.

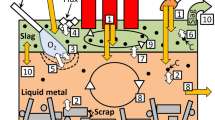
For convenience and as a model simplification, we concentrate the total power of the AC arcs into one arc. Therefore, only one electrode is considered in the modeling of the radiative heat exchange. The assumed simplified geometry of the EAF is presented in Figure 1.

Fig. 1

EAF model geometry: hollowed cylinder

Boredown, melting, and refining period of the batch

To process one batch of steel, the EAF has to be loaded several times (normally two or three times). In industry, the loading procedure of the EAF is called a charge. Throughout the process, each charge undergoes two main stages: the boredown period of the electrodes and the normal melting stage. At the end of the last charge, a final stage, the refining period of the batch, is executed. These stages are modeled making the following assumptions:

Boredown period of the electrodes

The boredown period of a batch is the period that the electrodes take to dig into the scrap until they reach the bottom of the furnace. See Figures 2(a) through (d). It is assumed that during this time, the radius of the created cavity in the scrap remains constant at a value that is equal to the radius of the electrode plus the length of the arc. During the boredown, the arc melts the cylindric volume of solid scrap that is immediately under the electrode, as observed in the studied EAF. At any point in time, the depth of the cavity depends on the amount of metal that has melted. It can be estimated using the melting rate equations presented in Section III–C.

Fig. 2

Various stages during the melting of a charge (not at scale). (a) through (d) Boredown, (e) through (g) Melting, (h) Refining

Melting stage

When the electrode reaches the bottom of the furnace, it locks into its position, and the hollowed cylinder starts to increase in its internal radius and its height decreases due to the reduction of the volume of the scrap. See Figures 2(e) through (g). The geometry of the hollowed cylinder is computed for any point in time based on the melting rates and geometrical relationships detailed in Section III–C.

Refining stage

The refining stage takes place after most of the metal scrap has melted. Depending on the type of metal produced and on the operational practices of the specific meltshop, it can last only few minutes or can take as long as half an hour. During this period, alloying metals, carbon, and oxygen are injected into the liquid metal with the aim to refine its chemical composition. See Figure 2(h).

Energy Streams and Energy Balances

It is assumed that the energy demand of the process is provided by six energy inputs: the heat irradiated by the electric arc, the thermal heat from the oxy-fuel flames, the heat released by the combustion of coal, and the heat from the oxidation of solid and liquid metal. The oxygen demanded by the oxidation reactions of carbon and metals is supplied via the oxy-fuel burners. The splashing of liquid metal onto the solid metal during the oxygen lancing stage of the melt is also considered. The assumed energy streams from each energy input are presented in Figure 3.

Fig. 3

The energy flows within the EAF model

In Figure 3, the blue streams represent the net energy content of each input. Each input is characterized by an efficiency parameter that is computed from first principles, from empirical formulae, or using a parameter estimation technique. The fraction of usable energy from each energy input can contribute to:

• (a) the melting of solid metal (${\dot Q_{{\text{net}}\_{\text{s}}{{\text{m}}_{\text{m}}}}}$)—represented by the yellow streams

• (b) the heating of solid metal (${\dot Q_{{\text{net}}\_{\text{s}}{{\text{m}}_{\text{h}}}}}$)—represented by the green streams

• (c) the heating of the liquid metal (${\dot Q_{{\text{net}}\_{\text{m}}{{\text{m}}_{\text{h}}}}}$)—represented by the red streams

• (d) be lost to the environment—represented by brown streams.

The energy streams (a) to (c) are computed as in Eqs. [1] through [3]:

$${\dot Q_{{\text{net}}\_{\text{s}}{{\text{m}}_{\text{m}}}}} = \;{\dot Q_{{\text{arc}}\_{\text{ra}}{{\text{d}}_{{\text{sm}}}}}} + \;{\dot Q_{{\text{bur}}\_{\text{rad}}}}\; - \;{\dot Q_{{\text{smm}}\_{\text{con}}{{\text{d}}_{{\text{sm}}\_{\text{h}}}}}}$$

(1)

$${\dot Q_{{\text{net}}\_{\text{s}}{{\text{m}}_{\text{h}}}}} = \;{\dot Q_{{\text{smm}}\_{\text{con}}{{\text{d}}_{{\text{sm}}\_{\text{h}}}}}} + \;{\dot Q_{{\text{mm}}\_{\text{con}}{{\text{d}}_{{\text{sm}}\_{\text{h}}}}}} + \;{\dot Q_{{\text{bur}}\_{\text{conv}}}} + \;{\dot Q_{{\text{o}}{{\text{x}}_{{\text{sm}}}}}} + \;{\dot Q_{{\text{coal}}}} + \;{\dot Q_{{\text{s}}{{\text{p}}_{{\text{sm}}}}}}$$

(2)

$${\dot Q_{{\text{net}}\_{\text{m}}{{\text{m}}_{\text{h}}}}} = \;{\dot Q_{{\text{arc}}\_{\text{ra}}{{\text{d}}_{{\text{mm}}}}}}\; + \;{\dot Q_{{{\text{L}}_{{{\text{O}}_2}}}}} - \;{\dot Q_{{\text{mm}}\_{\text{con}}{{\text{d}}_{{\text{sm}}\_{\text{h}}}}}} - \;{\dot Q_{{\text{s}}{{\text{p}}_{{\text{sm}}}}}}\; - \;{\dot Q_{{\text{s}}{{\text{p}}_{{\text{w/r}}}}}}\; - \;{\dot Q_{{\text{loss}}}}$$

(3)

In the real process, we observed that the metal melts at a higher rate than it heats up. Because of this behavior, we assume that while the dominant mechanism of radiation promotes the melting of the solid metal, the weaker conduction and convection mechanisms between the other phases in the EAF and the solid phase, promote its heating. The melting is assumed to take place in a thin film on the surface of the solid scrap. It absorbs radiative energy from the arc (${\dot Q_{{\text{arc}}\_{\text{ra}}{{\text{d}}_{{\text{sm}}}}}}$) and from the flame of the oxy-fuel burner (${\dot{Q}}_{\text{bur}\_\text{rad}}$), and transmits heat to the bulk of the solid scrap (${\dot Q_{{\text{smm}}\_{\text{con}}{{\text{d}}_{{\text{sm}}\_{\text{h}}}}}}$), see Eq. [1].

In Eq. [2], ${\dot Q_{{\text{mm}}\_{\text{con}}{{\text{d}}_{{\text{sm}}\_{\text{h}}}}}}$ accounts for the power transmitted via conduction mechanisms from the liquid phase to the solid phase for heating purposes, ${\dot{Q}}_{\text{bur}\_\text{conv}}$ is the convective power from the oxy-fuel burner, ${\dot{Q}}_{\text{coal}}$ is the energy from the combustion of coal, and ${\dot{Q}}_{{\text{sp}}_{\text{sm}}}$ is the power transferred from the bath to the solid steel due to splashing.

The energy streams that drive the heating process of the liquid metal are the radiative power from the arc to the molten metal (${\dot Q_{{\text{arc}}\_{\text{ra}}{{\text{d}}_{\text{mm}}}}}$) and the oxidation of carbon and liquid metals during the oxygen lancing stage of the process (${\dot{Q}}_{\text{L}_{\text{O}_{2}}})$. The energy balance in the liquid metal phase (Eq. [3]) is completed by subtracting from the energy gains the losses due to the splashing of liquid metal that lands on the solid metal (${\dot{Q}}_{{\text{sp}}_{\text{sm}}}$), the walls and the roof of the furnace (${\dot{Q}}_{{\text{sp}}_{\text{w/r}}}$), and due to the losses to the environment at the bottom of the EAF (${\dot{Q}}_{\text{loss}}$). These heat losses were computed as a conductive heat flow from the pool of liquid metal to the environment, using the known geometry (area and depth) and the thermal properties of the refractory material protecting the bottom the furnace, and the temperature difference between the highest temperature reading of the refractory bed and the ambient temperature. They were estimated to be around 500 kW for most operative conditions.

The power transmitted from both the film in the melting state and the liquid metal to the solid metal for heating purposes in Eqs. [2] and [3] is assumed to be equivalent to the flow of conductive heat through the scrap, from the surface that is in contact with each of the liquid phases. Only for the purpose of the computation of this conductive heat exchange, it is assumed that the solid scrap is a perfectly uniform solid material. The conductive flows of energy can be quantified in terms of the temperature of the solid metal (${T}_{\text{sm}}$), the molten metal (${T}_{\text{mm}}$), the melting temperature of the metal (${T}_{\text{f}}$), and on the contact areas between the two liquid metal surfaces and the solid metal, as in Eqs. [4] and [5]:

$${\dot{Q}}_{{\text{smm}\_\text{cond}}_{\text{sm}\_\text{h}}}=\frac{{k}_{\text{sm}}\,(2\,\pi\,{{R} }_{\text{eff}}\,{h }) }{{({R}}_{\text{fur}}-{{R}}_{\text{eff}})}\,({T}_{\text{f}}-{T}_{\text{sm}}),$$

(4)

$$\dot{Q}_{{\text{mm}}\_{\text{cond}}_{{\text{sm}}\_{\text{h}}}} = \frac{k_{{\text{sm}}} \, \pi \, ({R_{{\text{fur}}}}^2 - {R_{{\text{eff}}}}^2)} {h} \, (T_{{\text{mm}}} - T_{{\text{sm}}}).$$

(5)

In Eqs. [4] and [5], ${{R} }_{\text{fur}}$ represents the radius of the furnace, and ${{R} }_{\text{eff}}$, and ${h }$ are the internal radius and the height of the pile of solid metal.

Dynamic Model

We model the process of melting metal in an EAF as a sequence of several processes. First, a fraction of the total solid mass (${\dot{m}}_{\text{smm}}$) is melted due to the melting power ${\dot{Q}}_{{\text{net}\_{\text{sm}}}_{\text{m}}}$. See Eq. [6]. The rate of change of the solid mass (${\dot{m}}_{\text{sm}}$) is given by the difference between the fraction of splashed liquid metal that lands on the solid scrap and is due to the oxygen lancing (${\dot{R}}_{\text{B}}\,{\zeta }_{\text{sm}}$) and the amount of molten liquid metal that is transferred from the solid phase to the liquid phase (${\dot{m}}_{\text{smm}}$), see Eq. [7].

$$\dot{m}_{\text{smm}} = \frac{\dot{Q}_{\text{net}\_{\text{sm}}_{\text{m}}}}{k_{\text{m}_{\text{sm,k}}} \, (c_{\text{p}_{\text{sm}}} \, (T_{\text{f}} - T_{\text{sm}}) + \Updelta H_{\text{f}})}$$

(6)

$${\dot{m}}_{\text{sm}}= {\dot{R}}_{\text{B}}\,{\zeta }_{\text{sm}}-{\dot{m}}_{\text{smm}}, \;{\text{for}}\; k = 1,2,3.$$

(7)

A batch of steel is normally produced from two or three charges of different solid materials, and each charge can melt at different rates. To account for these variations, the melting rate during each charge is adjusted using the tuning parameter ${k}_{\text{m}_{\text{sm},k}}$. These parameters can be estimated for each charge or for each batch using process data. We discuss the estimation procedure in detail in the Appendix B.

The second process is the heating of the bulk of remaining solid scrap due to the energy flow ${\dot{Q}}_{{\text{net}\_\text{sm}}_{\text{h}}}$. It can be computed using the energy Eq. [8]:

$${\dot{T}}_{\text{sm}}= \frac{{\dot{Q}}_{{\text{net}\_{\text{sm}}}_{\text{h}}}}{{c}_{\text{p}_{\text{sm}}}\,{m}_{\text{sm}}}.$$

(8)

Third, the rate of change of the mass of the liquid phase (${\dot{m}}_{\text{mm}}$) is computed as in Eq. [9] as the difference between the mass of molten metal transferred from the solid phase (${\dot{m}}_{\text{smm}}$) and the fraction of splashed liquid metal that lands on the walls, the roof, and the solid metal. The splashing phenomena and the splashing fractions ${\zeta }_{\text{sm}}$ and ${\zeta }_{\text{w/r}}$ are discussed in detail in Section III–H.

$${\dot{m}}_{\text{mm}}= {\dot{m}}_{\text{smm}}- \dot{{R}_{\text{B}}}\,{(\zeta }_{\text{sm}}+{\zeta }_{\text{w/r}})$$

(9)

Lastly, the temperature change of the molten metal due to the heating power ${\dot{Q}}_{{\text{net}\_\text{mm}}_{\text{h}}}$ is computed from the energy balance as shown in Eq. [10]:

$${\dot{T}}_{\text{mm}}= \frac{{\dot{Q}}_{{\text{net}\_{\text{mm}}}_{\text{h}}}- {\dot{m}}_{\text{smm}}\,{c}_{\text{p}_{\text{mm}}} \, \left({T}_{\text{mm}}-{T}_{\text{f}}\right)}{{c}_{\text{p}_{\text{mm}}} {m}_{\text{mm}}}.$$

(10)

In Eqs. [6] through [10], ${c}_{{\text{p}}_{\text{sm}}},$ ${c}_{{\text{p}}_{\text{mm}}}$ , and $\Delta {H}_{\text{f}}$ are the heat capacities of the solid metal, the molten metal, and the enthalpy of fusion of the solid metal. The polynomial approximations of the thermophysical properties of the steel used in this work were obtained from Reference 31.

The dynamic behavior of the solid metal is modeled as follows. During the normal melting stage of a charge, Eqs. [11] through [14] describe how the internal radius and the height of the hollow cylinder change over time.

$$\alpha = \frac{{{m_{{\text{sm}}}}}}{{{m_{{\text{s}}{{\text{m}}_{0,k}}}}}}, $$

(11)

$${{R} }_{\text{eff}}= {k}_{\text{geo}}\left({{R} }_{\text{fur}} (1-\alpha ) + ({{R} }_{\text{ele}}+{{l} }_{\text{arc}}) \alpha \right),$$

(12)

$${V}_{\text{sm}} = \frac{{m}_{\text{sm}}}{{\rho }_{\text{sm}}},$$

(13)

$${h } = \frac{{V}_{\text{sm}}}{\pi ({{{R} }_{\text{fur}}}^{2} - {{{R} }_{\text{eff}}}^{2})}.$$

(14)

Equation [12] determines how large the internal radius of the hollowed cylinder is, governed by the varying fraction of the remaining solid metal ($\alpha$). In Eq. [11], the term $m_{\text{sm}_{0,k}}$ represents the total weight of the solid material loaded into the furnace during each charging procedure k. Equation [12] must satisfy an initial and a terminal condition. At the beginning of the melting period of a charge, the internal radius of the hollowed cylinder must be equal to that of the boredown period (${{R} }_{\text{eff}} = {{R} }_{\text{ele}}+{{l} }_{\text{arc}}$). At the end of the batch, this radius equals the radius of the furnace. The correction term ${k}_{\text{geo}}$ is a parameter that can be tuned to ensure that at the end of the melting stage, the height of the solid metal is zero. It depends exclusively on the amount of charged material and the geometry of the EAF. For various loading conditions and furnace geometries, we estimated that its value ranges from 0.95 to 0.98. In this study, its value is set to 0.96.

During the boredown period of a charge, the height of the pile of metal under the electrode can be computed using the geometrical relationship for the volume of a cylinder and using the instantaneous mass of metal (${m}_{\text{sm}}$), and Eqs. [13] through [14].

Flows of Radiative Energy from the Electric Arc

In earlier work,^[2] we have demonstrated that a steelmaking arc can be modeled as a thin plasma column that exchanges heat with the surrounding via radiation mechanisms only. Because the absorption bands of the gases that compose the assumed atmosphere of the furnace do not overlap with those of the emitted radiation by the electric arc,^[32,33,34] the radiative heat exchange is computed assuming a transparent atmosphere. The effect of the dust particles is neglected.

The radiative heat exchanges for the electric arc are computed using the DC circuit analogy.^[35] Solving the radiative heat exchange problem in the EAF using this strategy has been suggested in earlier works,^[36,37] but obtaining a solution was not attempted. In Reference 30, we addressed in detail the construction of a radiative circuit for the EAF enclosure and computed the radiative energy exchanges between the involved surfaces and proposed four different circuit topologies that model the various stages that take place during a single batch. These stages occur because depending on the amount of unmolten solid metal, exchanges between the arc, the roof, and the walls of the furnace occur or do not occur. A novel radiative circuit that uses time-controlled switches (controlling variables) that open and close according to the state of the batch is employed here. The radiative circuit is presented in Figure 4, where the electric arc is modeled as a source of electrical current that delivers a current equal to the power of the arc ($P_{\text{arc}}$). The main advantage of this approach—which can be employed if the assumption of a radiation dominated arc holds—is that the heat exchanges in the circuit can be computed without making assumptions regarding the values of the surface emissivity and the temperature of the arc,^[10,15] or the fractions of energy that the arc dissipates through radiation, convection, and other mechanisms.^{[8,9,11,16,37]}

Fig. 4

Radiative circuit with energy flow controlling switches

Assuming that all surfaces that exchange heat behave as gray-bodies, the circuit in Figure 4 can be solved in terms of the radiosities ($J$) of each participating surface (i) using the Node-Voltage method.^[38] The matrix representation of the resulting linear system is given in Eq. [15]. Here, the switches are represented as resistors of very large resistance for open states (10⁷ times larger than the largest resistor in the circuit) or as resistors of zero resistance for closed states. A detailed description of every voltage source (${\text{VT}}_{{i}}$), radiosity resistor (${{Rr}}_{{i}}$), view factor resistor (${Rx}$), and switch (${Sw}_{{y}}$) is provided in the Appendix A.

$$A= \left[\begin{array}{c}\begin{array}{cccccccc}\frac{1}{Ra} + \frac{1}{Rb} + \frac{1}{Rc+Sw_2} + \frac{1}{Rd} + \frac{1}{Re+Sw_3} + \frac{1}{Rw+Sw_4},& -\frac{1}{Ra},& -\frac{1}{Rb},& -\frac{1}{Rc+Sw_2},& -\frac{1}{Rd},& 0,& -\frac{1}{Re+Sw_3},& -\frac{1}{Rw+Sw_4}\end{array}, 0, 0\\ \begin{array}{cccccccc}-\frac{1}{Ra},& \frac{1}{Rl} + \frac{1}{Rk} + \frac{1}{Rf} + \frac{1}{Ra} + \frac{1}{Rg} + \frac{1}{Rr_{\text{sm}}},& -\frac{1}{Rg},& -\frac{1}{Rf},& -\frac{1}{Rk},& -\frac{1}{Rl},& 0,& 0, \end{array} 0, 0\\ \begin{array}{c}-\frac{1}{Rb}\begin{array}{cccccccc},& -\frac{1}{Rg},& \frac{1}{Rb} + \frac{1}{Rj} + \frac{1}{Rg} + \frac{1}{Rh} + \frac{1}{Rm} + \frac{1}{Ri+Sw_5}+ \frac{1}{Rr_{\text{mm}}},& -\frac{1}{Rh},& -\frac{1}{Rj},& -\frac{1}{Rm},& -\frac{1}{Ri+Sw_5},& 0\end{array}\end{array}, 0, 0 \\ \begin{array}{c}-\frac{1}{Rc+Sw_2}\begin{array}{cccccccc},& -\frac{1}{Rf},& -\frac{1}{Rh} ,& \frac{1}{Rh}+ \frac{1}{Rc+Sw_2} + \frac{1}{Rt} + \frac{1}{Rf} + \frac{1}{Rn} + \frac{1}{Ru}+ \frac{1}{{Rr}_{roof}},& 0,& -\frac{1}{Rn},& -\frac{1}{Rt},& -\frac{1}{Ru}\end{array}, 0, 0\end{array}\\ -\frac{1}{Rd}\begin{array}{cccccccc},& -\frac{1}{Rk},& -\frac{1}{Rj} ,& 0,& \frac{1}{Rd}+ \frac{1}{Rk} + \frac{1}{Rj} + \frac{1}{Ro+Sw_6} + \frac{1}{Rx+Sw_7} + \frac{1}{Rr_{\text{eleh}}},& 0,& -\frac{1}{Ro+Sw_6},& -\frac{1}{Rx+Sw_7}, 0, 0\end{array}\\ \begin{array}{c}0\begin{array}{cccccccc},& -\frac{1}{Rl},& -\frac{1}{Rm} ,& -\frac{1}{Rn},& 0,& \frac{1}{Rl} + \frac{1}{Rm} + \frac{1}{Rn}+ \frac{1}{Rp} + \frac{1}{Rq}+ \frac{1}{Rr_{\text{elev}}},& -\frac{1}{Rp},& -\frac{1}{Rq}\end{array}\end{array}, 0, 0\\ -\frac{1}{Re+Sw_3}\begin{array}{cccccccc},& 0,& -\frac{1}{Ri+Sw_5} ,& -\frac{1}{Rt},& -\frac{1}{Ro+Sw_6},& -\frac{1}{Rp} ,& \frac{1}{Re+Sw_3} + \frac{1}{Ri+Sw_5} + \frac{1}{Rt}+ \frac{1}{Ro+Sw_6} + \frac{1}{Rp}+ \frac{1}{Rs}+ \frac{1}{Rr_{\text{wall}}},& -\frac{1}{Rs}\end{array}, 0, 0\\ -\frac{1}{Rw+Sw_4}\begin{array}{cccccccc},& 0,& 0,& -\frac{1}{Ru},& -\frac{1}{Rx+Sw_7},& -\frac{1}{Rq} ,& -\frac{1}{Rs},& \frac{1}{Rw+Sw_4} + \frac{1}{Ru}+ \frac{1}{Rx+Sw_7} + \frac{1}{Rq}+ \frac{1}{Rs}+ \frac{1}{{Rr}_{sm2}}\end{array}, 0, 0\\ \begin{array}{cccccccc}0,& 0,& 0,& 0,& 0,& 0,& 0,& 0\end{array}, \frac{1}{Rg\_s} + \frac{1}{{Rr}_{sm3}}, -\frac{1}{Rg\_s}\\ \begin{array}{cccccccc}0,& 0,& 0,& 0,& 0,& 0,& 0,& 0\end{array}, -\frac{1}{Rg\_s}, \frac{1}{Rg\_{s}} + \frac{1}{{Rr}_{mm2}}\end{array}\right]$$

(15)

$$\begin{aligned}&b =\left[\begin{array}{cc}P_{\text{arc}}\begin{array}{cccccccc},& \frac{{\text{VT}}_{\text{sm}}}{Rr_{\text{sm}}},& \frac{{\text{VT}}_{\text{mm}}}{Rr_{\text{mm}}} ,& \frac{{\text{VT}}_{\text{roof}}}{Rr_{\text{roof}}},& \frac{{\text{VT}}_{\text{eleh}}}{Rr_{\text{eleh}}},& \frac{{\text{VT}}_{\text{elev}}}{Rr_{\text{elev}}},& \frac{{\text{VT}}_{\text{wall}}}{Rr_{\text{wall}}},& \frac{{\text{VT}}_{\text{sm}}}{Rr_{\text{sm2}}}\end{array}, \frac{{\text{VT}}_{\text{sm}}}{Rr_{\text{sm3}}}, \frac{{\text{VT}}_{\text{mm}}}{Rr_{\text{mm2}}}\end{array}\right] \\ & \qquad \qquad \qquad \qquad \qquad \qquad J ={A}^{-1}{b}^{T}\end{aligned}$$

Equation [15] requires a computation of the view factors of the heat exchanging surfaces. The view factors are computed using either (a) Monte-Carlo algorithms for those exchanges with blockages in the lines of sight,^[30] (b) the formulae provided in the view factor library^[39] when possible, or (c) employing the summation and complementarity rules.^[35] A detailed discussion of these computations as well as a comparison of our approach with others can be found in Reference 40.

The net power that enters or leaves a surface due to radiation can be computed as in Eq. [16]:

$${\dot{Q}}_{{{\text{arc}}\_\text{rad}}_{i}}= \frac{{J}_{i}- \text{VT}_i}{Rr_i}.$$

(16)

The radiative energy streams that arrive at the surfaces of the solid metal and the liquid metal coming from the arc are defined as the useful fraction of energy from the arc (${\dot{Q}}_{\text{arc}\_\text{gain}}$). The efficiency of the electric input is computed as the useful power over the total power of the electric arc:

$${\dot Q_{{\text{arc}}\_{\text{gain}}}} = \;{\dot Q_{{\text{arc}}\_{\text{ra}}{{\text{d}}_{{\text{sm}}}}}} + \;{\dot Q_{{\text{arc}}\_{\text{ra}}{{\text{d}}_{{\text{mm}}}}}}$$

(17)

$${\eta }_{\text{ele}}= \frac{{\dot{Q}}_{\text{arc}\_{\text{gain}}}}{{P}_{\text{arc}}}.$$

(18)

Energy Flows from the Oxy-Fuel Burner

The energy exchange from the flames of the burner is computed employing the first-principles model presented in Reference 41, which describes the oxy-fuel flame as a fluid that undergoes four processes: combustion, radiation, expansion, and convection, see Figure 5. First, the fuel (methane) and pure oxygen combust forming a fluid of cylindrical shape, which extends for 13 times the diameter of the burner. In this section of the flame, it is assumed that heat exchange occurs only via radiation mechanisms. After emitting radiative heat, the flue gases expand adiabatically to atmospheric pressure until they occupy a volume equivalent to that of 80 pct the void space of the scrap.^[42] After expansion, the cooled flue gases move through the void spaces in the solid scrap, exchanging heat with the metal via forced convection mechanisms. The total energy contribution from the burner to the process is quantified as the sum of the flows due to radiation (${\dot{Q}}_{\text{bur}\_\text{rad}}$) and convection (${\dot{Q}}_{\text{bur}\_\text{conv}}$). See Eq. [19]. The efficiency of the burners is quantified with respect to the total energy content in the fuel, in terms of its low heating value ($\text{LHV}_{\text{CH}_4}$), as in Eq. [20]:

Fig. 5

Geometry of the flames and heat transport

$${\dot{Q}}_{\text{bur}}={\dot{Q}}_{\text{bur}\_{\text{rad}}}+ {\dot{Q}}_{\text{bur}\_{\text{conv}}}$$

(19)

$${\eta }_{\text{bur}}=\frac{{\dot{Q}}_{\text{bur}}}{\dot{{m}_{\text{CH}_4}}\,{\text{LHV}}_{\text{CH}_4}} .$$

(20)

Chemical Energy from Oxidation Reactions on the Surface of the Solid Phase

When pieces of solid metal interact with oxygen, a thin layer of solid metal oxides forms on its surface. The amount of energy released by these oxidation reactions depends on the surface area of the scrap and the amount of oxygen available in the atmosphere. Because the metal oxides remain in solid state on the surface of the scrap, we assume that 100 pct of the heat released by these reactions (${\dot{Q}}_{{\text{ox}}_{\text{sm}}}$) is spent on raising the temperature of the solid metal:

$${\eta }_{{\text{ox}}_{\text{sm}}}= 100.0\, \text{pct}.$$

(21)

Corrosion of stainless steels can be quantified using the parabolic approximation (22).^[43,44] Here, $\Delta M$ [mg] represents the mass gain of the oxidized material, ${k}_{\text{p}}$ is an experimental constant, $t$ is time, and ${A}_{\text{sc}}$ is the total area of the scrap [cm²] that is in contact with the oxidizing gas. The factor 0.8 accounts for the fact that the oxygen injected will expand to occupy a maximum of 80 pct of the void space in the scrap.^[42]

$$\frac{{\Delta M}}{0.8\,{A}_{\text{sc}}}= (k_{\text{p}}\,t)^{0.5}$$

(22)

In this study, we have assumed that ${k}_{\text{p}}=2.5\times{10}^{-12} \;{\text{g}}^{2}\; \text{cm}^{-4} \;{\text{s}}^{-1}$.^[45] The available area for oxidation of the scrap (${A}_{\text{sc}}$) depends on the surface to volume ratio of the scrap. Assuming that the bulk of scrap is composed of metal sheets of thickness $\text{Sh}_{\text{tk}}$, the surface area for oxidation can be approximated as

$${A}_{\text{sc}}= 2\left(\frac{\pi \left({{R}_{\text{fur}}}^{2}-{{R}_{\text{eff}}}^{2}\right)\,h\, {\rho }_{\text{sc}}}{\text{Sh}_{\text{tk}} \, {\rho }_{\text{sm}}}\right).$$

(23)

Because the formed oxide layer is composed almost entirely of iron oxides,^[45] we will assume that the heat released by the oxidation of solid metals can be approximated well by the heat released by the formation of ferritic oxide. The total energy released by the oxidation reaction (${\dot{Q}}_{{\text{ox}}_{\text{sm}}}$) is calculated from the energy balance between the sensible heat required to raise the mass of reacting iron to the assumed reaction temperature (T = 1127°K), the energy released by the oxidation reaction (${\Delta H}_{\text{Fe}_{2}\text{O}_{3}}$), and the heat consumed by two cooling processes: the cooling of the resulting oxides (from the reaction temperature to the temperature of the bulk of solid scrap) and the cooling of the reacting oxygen (from the temperature at the outlet of the convective zone of the burner to the reaction temperature). See Eq. [26]. The mass balance (Eq. [25]) for the oxidation reaction assumes a perfect stoichiometry as in Eq. [24].

$$ \frac{4}{3}{\text{Fe}} + {\text{O}}_{2} \rightarrow \frac{2}{3} {\text{Fe}}_{2} {\text{O}}_{3}, $$

(24)

$$\Delta \dot{M} = \;{\dot m_{{{\text{O}}_{2_{\text{ox}}}}}}\; \to \;{\dot m_{{\text{F}}{{\text{e}}_2}{{\text{O}}_3}}} = \frac{{106.4}}{{32}}\;{\dot m_{{{\text{O}}_{2_{\text{ox}}}}}}$$

(25)

$${\dot Q_{{\text{o}}{{\text{x}}_{{\text{sm}}}}}} = \;{\dot m_{{\text{F}}{{\text{e}}_2}{{\text{O}}_3}}}\left( {\Delta {H^{{T^o}}}_{{\text{F}}{{\text{e}}_2}{{\text{O}}_3}} - \mathop \smallint \limits_{{T^o}}^{{T_{sm}}} C{p_{{\text{F}}{{\text{e}}_2}{{\text{O}}_3}}}\;\;{\text{d}}T\;} \right) - \;{\dot m_{{\text{F}}{{\text{e}}_{2{\text{ox}}}}}}\left( {\mathop \smallint \limits_{{T_{{\text{sm}}}}}^{{T^o}} C{p_{{\text{F}}{{\text{e}}_2}}}\;\;{\text{d}}T} \right) - \;{\dot m_{{{\text{O}}_{2_{\text{ox}}}}}}\left( {\mathop \smallint \limits_{{T_{{\text{burn}}\_{\text{out}}}}}^{{T^o}} C{p_{{{\text{O}}_{2}}}}\;\;{\text{d}}T} \right)$$

(26)

Chemical Energy from the Combustion of Coal

The instantaneous amount of coal consumed during the process is calculated from the stoichiometry formula [27], where $a$ is the number of oxygen moles that remain in the gaseous phase after the combustion in the burner and the oxidation of solid metals:

$$ a{{C}} + a{\text{O}}_{2} \rightarrow a{\text{CO}}_{2}, $$

(27)

$${\dot{m}}_{\text{coal}}= 12 a.$$

(28)

The fraction of the energy released by the combustion of coal that is transferred to the solid metal is uncertain and no reference about it was found in the literature. In the same fashion as in Reference 10, we assume that the flue gases from the combustion of coal experience similar heat exchanging processes to those of the oxy-fuel burners during the periods of time when the burners are on; therefore, their efficiencies are the same. On the other hand, if the burners are off, we assume a constant energy efficiency of 28 pct, which corresponds to the lowest value of the efficiency of an oxy-fuel burner as computed in Reference 46.

$$ \begin{aligned} \eta _{{{\text{coal}}}} & = \eta _{{{\text{burn}}}} ,\,{\text{if}}\,{\text{burner}}\,{\text{is}}\,{\text{on}} \\ \eta _{{{\text{coal}}}} & = 0.28,\,{\text{if}}\,{\text{burner}}\,{\text{is}}\,{\text{off}} \\ \end{aligned} $$

(29)

The energy contribution of coal to the melting process (${\dot{Q}}_{\text{coal}}$) in Eq. [2] can be computed considering the LHV of the coal, the amount of combusted carbon, and the efficiency of the heat exchange from the combustion gases to the solid metal:

$${\dot{Q}}_{\text{coal}}= {\eta }_{\text{coal}} \left(0.85 {\dot{m}}_{\text{coal}}\right)\,\text{LHV}_{\text{coal}}.$$

(30)

In Eq. [30], the factor 0.85 accounts for the fact that about 85 pct of the total mass in anthracite coal is carbon.

Energy exchange due to oxygen lancing

During the lancing stage of the batch, oxygen at supersonic speed is injected in the direction of the liquid bath. When the oxygen jets reach the surface of the liquid bath, two phenomena occur:

• (a) The lanced oxygen reacts with the metals and the carbon dissolved in the liquid bath. Despite the relatively small area of contact between the oxygen and the metal phase, it is known that the energy provided by these oxidation reactions to the process is significant.^[47]

• (b) A part of the momentum of the gas is transferred to the liquid metal particles around the impingement point, splashing liquid metal onto the solid metal, the roof and the walls of the furnace.^[48]

Chemical energy from oxidation reactions in the liquid phase

We assume that the oxidation reactions in the liquid phase take place during the oxygen lancing stage only. When oxygen is lanced into the bath, it is consumed mainly by the oxidation reactions of liquid metals and the carbon dissolved in it. The heat released by these reactions—the oxidation of liquid metals (${\dot{Q}}_{{\text{L}}_{\text{M}}}$) and the oxidation of carbon dissolved in the liquid metal (${\dot{Q}}_{{\text{L}}_{\text{C}}}$)—can be quantified in terms of the volumetric flow rate (${\dot{F}}_{\text{O}_{2}}$) of the lanced oxygen, the efficiency of the oxygen lancing (${\eta }_{{\text{L}}_{\text{O}_{2}}}$), and the fraction of oxygen spent on the oxidation of liquid metals ($x_{{\text{O}}_{2{\text{m}}}}$), as given by Eqs. [31] and [32]:

$$\dot{Q}_{L_M} = \dot{F}_{\text{O}_2} \ \eta_{\text{L}_{\text{O}_2}} \ x_{{\text{O}_2}_m} \ \Delta H_{{\text{L}_{\text{O}_{2{\text{M}}}}}},$$

(31)

$$\dot{Q}_{\text{L}_\text{C}} = \dot{F}_{\text{O}_2} \ \eta_{\text{L}_{\text{O}_2}} \ (1-x_{{\text{O}_{2\text{m}}}}) \ \Delta H_{{\text{L}_{\text{O}_{2{\text{C}}}}}}.$$

(32)

The heat released by the oxidation of dissolved carbon (${\dot{Q}}_{{\text{L}}_{\text{C}}}$) is taken up by two processes. The first uses a fraction of ${\dot{Q}}_{{\text{L}}_{\text{C}}}$ to heat up the resulting CO₂ gases to the temperature of the liquid bath (${\dot{Q}}_{{\text{L}}_{\text{CO}_2}}$) as in Eq. [33]. The other consumes the remaining fraction of ${\dot{Q}}_{{\text{L}}_{\text{C}}}$ to increase the temperature of the liquid metal (${\dot{Q}}_{\text{L}_{\text{C}_\text{mm}}}$). We assume that ${\dot{Q}}_{\text{L}_{\text{CO}_2}}$ is lost, as the generated CO₂ gases are quickly removed from the furnace via the gas extraction system. In Eq. [33], ${\dot{m}}_{\text{L}_{\text{CO}_2}}$ can be computed from the volumetric flowrate of lanced oxygen ($\dot{{F}_{\text{O}_2}}$) and assuming a complete oxidation of the carbon dissolved in the bath.

$$\dot{Q}_{\text{L}_{\text{CO}_2}} = \dot{m}_{{\text{L}}_{\text{CO}_2}} \ \int_{T_{\text{ref}}}^{T_{\text{mm}}} c_{p_{\text{CO}_2}} \text{d}T$$

(33)

The net energy contribution from the oxygen lancing to the process (${\dot{Q}}_{{\text{L}}_{\text{O}_{2}}}$) is computed as the sum of ${\dot{Q}}_{{\text{L}}_{\text{M}}}$ and ${\dot{Q}}_{{\text{L}}_{{\text{C}}_{\text{mm}}}}$:

$${\dot{Q}}_{\text{L}_{\text{O}_{2}}}= {\dot{Q}}_{\text{L}_{\text{M}}}+{\dot{Q}}_{\text{L}_{\text{C}_{\text{mm}}}}={\dot{Q}}_{\text{L}_{\text{M}}}+{\dot{Q}}_{\text{L}_{\text{C}}}- {\dot{Q}}_{\text{L}_{\text{CO}_2}}.$$

(34)

In this work, ${\eta _{\text{L}{_{{{\text{O}}_2}}}}}$ and ${x}_{\text{O}_{2_\text{m}}}$ are used as tuning parameters and their values are estimated from process data in subsection B of Appendix B. The enthalpies of reactions here considered ($\Delta H_{{\text{L}_{\text{O}_2}}_{\text{M}}}$ and $\Delta H_{{\text{L}_{\text{O}_2}}_{\text{C}}}$) were obtained from Pfeifer et al.^[47]

Energy transfer due to liquid metal splashing

When oxygen is lanced into the furnace, the momentum of the jet generates large amounts of liquid metal drops that are splashed onto the solid scrap, the roof, the walls, and back into the metal pool. Overall, the splashing of liquid metals constitutes a mechanism that reduces the net mass and the energy efficiency of the process because the splashed material that lands on the walls, the roof, or that escapes from the furnace, is lost. On the other hand, the fraction of splashed liquid metal that lands on the solid scrap constitutes a beneficial mechanism that transfers heat from the liquid bath to the solid metal phase, supporting the melting of solid metal toward the end of the batch.

Because a detailed study of the splashing phenomena in EAFs is missing in the literature, we performed an educated guess to the value of the amount of liquid metal that lands into the solid metal.

Splashed liquid metal using empirical relationships

The total amount of flying liquid metal generated by the oxygen lancing ($\dot{{R}_{\text{B}}}$) can be estimated using the empirical relationship in Eq. [35].^[49,50] The calculation of $\dot{{R}_{\text{B}}}$ depends on the parameter known as the blowing number (${{N}_{\text{B}}}$), which in this study is set to five (${{N}_{\text{B}}}=5$). For different EAF configurations (location of the lances and geometries of the furnace), an appropriate value of ${{N}_{\text{B}}}$ can be obtained from the CFD results presented in Reference 5.

$$\frac{\dot{{R}_{\text{B}}}}{{\dot{F}}_{\text{O}_{2}}}= \frac{{{N}_{\text{B}}}^{3.2}}{{(2.6 \times {10}^{6}+2 {\times 10}^{-4}{{ N}_{\text{B}}}^{12})}^{0.2}}$$

(35)

Observations of the splashing phenomena in the industrial EAF

In the studied EAF, we observed that during the initial one to three minutes of the oxygen lancing stage, no liquid metal drops escaped the shell of the furnace. As the batch progressed and more metal melted, the amount of liquid metal that flew out from the EAF through the orifices in the roof and the de-slagging door increased considerably. We estimate that toward the end of the batch, a reasonable upper bound to the number of metallic drops that escape the EAF via the de-slagging door is 5000 per second. We observed that most of the drops that escaped from the furnace had a diameter lower than 3 mm. Assuming that the drops are spherical and mainly composed of slag (density = 2700 kg m⁻³), the total mass that escaped from the furnace through the de-slagging door is 0.19 kg s⁻¹. Considering the location of the oxygen lances in the furnace, we estimate that the total area of the walls where most of the spilled drops lands is 12 times that of the area of the de-slagging door. Consequently, the total amount of liquid mass that lands on the walls of the furnace is approximately 2.3 kg s⁻¹. These values align well with those reported in the literature.^[48]

For the operational conditions of the studied EAF, the computation of Eq. [35] led to values of $\dot{{R}_{\text{B}}}$ in the range from 1 to 4 kg s⁻¹ per lance, or 6.6 kg s⁻¹ in total. Due to protection of IP, we cannot disclose the number of lances installed in the EAF, nor the actual flow rates of oxygen employed during the process. The estimated amount of liquid metal that lands on the walls of the furnace after all the solid metal has melted (2.3 kg s⁻¹) is approximately 35 pct of the total amount of splashed liquid metal (6.6 kg s⁻¹), as computed from Eq. [35].

On the basis of the above considerations, we propose to approximate the amount of liquid metal that lands on the various surfaces of the EAF as follows: At the beginning of the oxygen lancing stage, 90 pct of the splashed metal will land on the solid metal (${\zeta }_{\text{sm}}$), 5 pct on the roof and the walls of the EAF (${\zeta }_{\text{w/r}}$), and 5 pct will fall into the liquid metal pool (${\zeta }_{\text{mm}}$). As the batch progresses, the amount of splashed metal that falls on the solid metal reduces linearly until the point where all the solid metal has melted. At this point, 35 pct of the splashed metal falls onto the walls and the roof, and the remaining 65 pct falls back into the liquid bath. The instantaneous values of ${\zeta }_{\text{sm}}$, ${\zeta }_{\text{w/r}}$, and ${\zeta }_{\text{mm}}$ can be computed in terms of the internal radius of the hollowed cylinder by means of the following approximations:

$${\alpha }_{\text{sp}}= \frac{{{R} }_{\text{eff}}- {{R} }_{\text{eff}_0}}{{{R} }_{\text{fur}}\,{k}_{\text{geo}}- {{R} }_{\text{eff}_0}},$$

(36)

$${\zeta }_{\text{sm}}= 0.9\,\left(1-{\alpha }_{\text{sp}}\right),$$

(37)

$${\zeta }_{\text{mm}}= 0.05\,\left(1-{\alpha }_{\text{sp}}\right)+0.35\,{\alpha }_{\text{sp}},$$

(38)

$${\zeta }_{\text{w/r}}= 1- {\zeta }_{\text{sm}}-{\zeta }_{\text{mm}}.$$

(39)

In Eq. [36], ${{R} }_{\text{eff}_0}$ represents the internal radius of the hollowed cylinder at the time when the oxygen lancing begins.

The energy transferred from the liquid metal to the solid metal due to splashing (${\dot{Q}}_{{\text{sp}}_{\text{sm}}}$), and the energy lost in the fraction of liquid metal that lands on the roof and walls of the furnace (${\dot{Q}}_{{\text{sp}}_{\text{w/r}}}$) are quantified as

$${\dot{Q}}_{{\text{sp}}_{\text{tot}}}= \dot{{R}_{\text{B}}} \left({\int }_{{T}_{\text{ref}}}^{{T}_{\text{f}}}{Cp}_\text{sm}\, \text{d}T+\Delta {H}_{\text{f}}+ {\int }_{{T}_{\text{f}}}^{{T}_{\text{mm}}}{Cp}_{\text{mm}} \, \text{d}T\right),$$

(40)

$${\dot{Q}}_{{\text{sp}}_{\text{sm}}}= {\dot{Q}}_{{\text{sp}}_{\text{tot}}} {\zeta }_{\text{sm}},$$

(41)

$${\dot{Q}}_{{\text{sp}}_{\text{w/r}}}= {\dot{Q}}_{{\text{sp}}_{\text{tot}}} {\zeta }_{\text{w/r}} .$$

(42)

The efficiency of the oxygen lancing is given by:

$${\eta }_{\text{LT}_{\text{O}_{2}}}=\frac{{\dot{Q}}_{\text{L}_{\text{O}_{2}}}-{\dot{Q}}_{{\text{sp}}_{\text{w/r}}}}{{\dot{Q}}_{{\text{L}}_{\text{M}}}+{\dot{Q}}_{{\text{L}}_{\text{C}}}}.$$

(43)

Numerical Solution of the EAF Model

Solution Strategy and Description of the Numerical Case Study

The mathematical model was implemented and solved in MATLAB^®. A two-time scale simulation structure was used to avoid the need of using a DAE solver to simulate the batch and to overcome the convergence issues that the integrator had with the Monte-Carlo algorithms that are used to compute the view factors in the radiative system.

On the coarse grid that consists of 1-minute intervals, the energy contributions from each source are computed. Within each 1-minute interval, the dynamic model is solved using the $\mathtt{ode45}$ algorithm assuming the computed energy contributions from each energy source as constant. The time resolution is automatically set by the integrator, thus generating the fine time grid of the simulation. The simulation time depends on the batch size and the energy inputs. For all the cases presented in this paper, it varied from 7 to 12 seconds for a batch of approximately 65 minutes.

Well known models that describe the evolution of the process in terms of the masses and temperatures of the solid and metal phases are those of Logar et al.^[10] and by Opitz et al.^[15,16] Here, we compare the predictions of our model with those presented in Reference 10, 15, and 16. Even though these models are used to simulate EAFs producing steel with foamy slags layers, while our model was tailored to the production of steel with thin slag layers, the comparisons presented are useful to illustrate how the different assumptions regarding the mechanisms of heat exchange impact the melting rates and the temperatures of the metal phases before the lancing stage of the batch is initiated.

The simulations presented in References 10, 15, and 16 describe the production of a batch of steel with an operative practice of three charges. In the simulations, the authors used the same furnace geometry, scrap properties, simulation timeline, but different electrical power inputs. While Logar et al. use an electric power input of approximately 50 MW throughout the batch, Opitz et al. simulate the batch with an electric power of almost 75 MW. For comparison purposes, we ran two simulations, at 50 and 75 MW. In our simulations, we set the arc length to the values reported in the other studies. The free parameters of the models were set to the values reported in Table I.

Table I Free Parameters of the Model

The values in Table I are the result of a parameter estimation that employed the process data of over two weeks of production in one of the UHP-EAFs at Acciai Speciali Terni in Italy. The EAF model presented in this paper was validated against process data of over three years of production of the same EAF, and accurate predictions for the boredown periods, the charging times, the batch time, the energy demand, and the final temperature of the molten metal were obtained. A detailed and extensive discussion of the methods and results of the parameter estimation procedure and the model validation are provided in the Appendices B and C.

Melting Rate and Solid Metal Mass

The results of the computations of the mass of solid metal and the temperature of the solid and liquid metal phases during the batch are presented in Figures 6 through 8. The figures show that the different models predict quite different process trajectories and terminal states. In these simulations, we assumed ${k}_{{\text{m}}_{\text{sm,2}}}={k}_{{\text{m}}_{\text{sm,3}}}$.

Fig. 6

Evolution of the mass of solid scrap over time for different models

Fig. 7

Evolution of the solid metal temperature

Fig. 8

Evolution of the liquid metal temperature

In terms of the melting rate, the model of Logar et al. predicts that 80 pct of the solid metal in a single charge can be melted in a little over 6 minutes, whereas our model and the model proposed by Opitz et al. predict that it takes 15 minutes to melt between 70 and 88 pct of the solid material in a single charge (see Figure 6). The extremely fast melting rates predicted by the model of Logar et al. are the result of very large energy contributions from the oxidation of carbon and solid metals. For example, in Reference 24, Logar et al. estimated that the energy contribution from the oxidation reactions was 50 pct larger than that provided by the electric arc during the periods when the oxy-fuel burners were on. To achieve such a large energy contribution, the process should be provided with an average of approximately 45 kg s⁻¹ of operational gases (oxygen, methane, and air), with peaks of up to 80 kg s⁻¹ when the burners are operated. These mass flow of flue gases seem unrealistic based on the facts that (a) large oxy-fuel injectors can provide only few kilograms of combustion gases per second, (b) that air entrainment into the furnace is limited during the early stages of the batch when the furnace is almost full of scrap and the de-slagging door is closed, and (c) that reported measurements in a large EAF cap the total mass flow rate of flue gases to less than 10 kg s⁻¹ at all times.^[51,52]

The prediction that 80 pct of the total metal can be melted in just under 6 minutes also seems exaggerated based on the widely accepted conjecture that the arc is the largest contributor of thermal energy to the process and on the observation that during the boredown period of the electrodes, which typically lasts between 3 and 5 minutes, less than 15 pct of the total metal is molten. Therefore, it can be concluded that the melting rates during the early stage of each charge are better predicted by our model and by the model of Opitz et al. than by the model of Logar et al.

Both our model and that of Opitz et al. exhibit similar melting curves. The melting behavior of the two models is, however, different after the 33rd minute of the simulation, as the melting rate of our model slows down considerably. The difference in the melting rates predicted by our model and by that of Opitz et al. toward the end of the batch is a consequence of the large amounts of energy that are transferred from the liquid to the solid phase via conductive mechanisms as considered by Opitz et al. In our model, the melting of solid metal toward the end of the batch is slow because: (a) the energy transferred from the arc to the solid metal for melting purposes is small (this is because the view factor that characterizes this exchange is small toward the end of the batch); (b) the heat exchange coefficient from the molten metal to the solid metal for heating purposes as computed by Eq. [5] is also small (it varies from 15 to 45 W m⁻¹ K⁻¹ as the batch progresses) compared to the values assumed by Logar et al. (200 W m⁻¹ K⁻¹) and Opitz et al. (9000 W m⁻¹ K⁻¹).

In the melt shop, the operational crews describe the last few hundred kilograms of solid metal as the hardest to melt. In fact, it is common to extend the batch time of the process, as required, until any unmelted solid material fuses. This is a clear indication that the melting efficiency of the process is much lower at the end than at the beginning of the process. On the basis of this observation and considering the trends described by the various models in Figure 6, we argue that the melting rate toward the end of the batch in the studied EAF is better predicted by our model and that of Logar et al. than by that of Opitz et al.

The different melting rates in the models lead to different simulated batch times. For the electrical input of 50 MW, the predicted batch times for our model and that of Logar et al. are 49 and 40 minutes. On the other hand, the predicted batch times for our model and that of Opitz et al. with and without radiation are 38, 35, and 39 minutes, using 75 MW of electrical power.

Temperature of the Solid and Liquid Metal Phases

Figure 7 shows the temperature profiles of the solid metal reported by Logar et al. and those obtained with our model for both electrical power inputs (50 and 75 MW). Both models predict that the temperature of the solid metal increases more rapidly when the oxy-fuel burners are operating than when they are off. However, while our model predicts a moderate temperature increase of the bulk of the solid material from 295 K to nearly 400 K in the first 5 minutes of processing of a charge, the temperature increase predicted by the model of Logar et al. is more significant and raises the temperature of the solid material to over 1000 K during the same period. Although it is not possible to obtain measurements of the temperature of the solid metal for the process, after months of observations of the process, we did not observe that the solid phase ever reached the characteristic red-glowing color of steel above 800 K after 10 to 18 minutes of operation in a single charge. These observations were carried out for about ten batches in a non-systematic fashion and mostly took place when an electrode replacement took place during the first melting or before the loading of the second charge. In the same fashion as for the melting rate, the rapid increase in the temperature of the solid metal in the model proposed by Logar et al. can be attributed to the large energy contributions from the operational gases.

The rapid increase in the temperature of the solid metal predicted by our model toward the end of the last charge is explained by the fact the energy absorption rate of the solid metal is larger than the rate at which metal melts.

Figure 8 shows the temperatures of the liquid phase predicted by the three models. Among these, the temperatures computed by Opitz et al. present the most dramatic changes: falling from 1800 K to 1500 K in 3 minutes and then increasing from 1500 K to over 2500 K in 4 minutes. Then, after the 7th minute, the temperature of the liquid metal decreases during most of the batch time. These results are debatable with respect to both the 2500 K and 1500 K temperature levels. On the one hand, operational experience suggests that the liquid metal reaches its highest temperature only at the end of the refining stage and very rarely surpasses 2000 K (regardless of the energy intensity of the operation and the type of steel produced). On the other hand, a crossing of the 1600 K temperature level from above is problematic as this is the phase change temperature of steel.

In contrast to the results of Opitz et al., both our model and that of Logar et al. predict a smooth increase of the temperature of the liquid metal during most of the batch, except during the boredown period of the electrodes. This is because during this period, the liquid metal loses heat to the solid metal but it does not receive any radiation from the electric arcs. After the boredown period of the electrodes, the temperature of the liquid metal is strongly dependent on the electrical power level during the melting of the first charge, see Figure 8. On the other hand, the influence of the electrical power become less evident during the second and the third charge because, during these stages, the oxygen lancing provides the most energy to the liquid metal. This is discussed in more detail in the following section.

Energy Efficiency Analysis

In this section, the different exchanges of energy as well as the dynamic efficiencies for the various energy inputs are studied. Because the batch simulation presented by Logar et al. considers the oxygen input due to lancing, while Opitz et al. neglected it, the results in this section correspond to a batch that is simulated using the inputs according to Logar et al.^[10]

Radiative Energy Flows and Electrical Energy Efficiency

The flows of radiative energy that arrive at each surface are presented in Figure 9.

Fig. 9

Radiative power arriving at each participating surface. sm-solid metal. mm-molten metal. ele_v-electrode vertical. ele_h-electrode horizontal

Figure 9 shows that the solid metal is the largest absorber of radiative energy within the EAF enclosure. For all charges, the solid metal absorbs the largest amount of radiative energy during the boredown period of the batch (43 MW or around 87 pct of the total energy irradiated by the arc). As time progresses, the amount of energy absorbed by the solid metal decreases rapidly, until the moment when the walls of the furnace become the largest absorber of radiative energy (at around 2700 s). This is due to the fact that toward the end of the batch, a large fraction of the area of the walls is no longer covered by solid metal, thus the electric arc can exchange large amounts of energy with them. At the end of the batch, the losses through the walls reach almost 30 MW (nearly 60 pct of the total power of the arc). So clearly, the radiative heating is much less efficient than the oxygen lancing during this stage (see the oxygen lancing efficiency in Table I).

The energy absorbed by the molten metal exhibits two different trends. During the boredown stage, the liquid metal loses considerable amounts of radiative energy to the solid metal. This flow reaches a maximum of 8 MW (almost 20 pct of the total energy irradiated by the arc). The second trend takes place immediately after the electrodes have completed the boredown and the arc starts exchanging heat with the liquid metal. Throughout the melting stages of the three charges, the liquid metal absorbs a constant heating power of approximately 3 MW, which is less than 10 pct of the total electrical power input.

The energy losses through the walls and the roof of the EAF exhibit similar behaviors. They are small at the beginning of each charge and increase rapidly as the solid metal melts. During the first and the second charge, the losses through the walls increase twice as fast as those to the roof and reach values of 10 and 6 MW (20 and 12 pct of the total power of the arc), respectively. The losses through the roof reach smaller peaks of 4 and 3 MW approximately (8 and 6 pct of the total power of the arc) at the end of the first and the second melting phase. Interestingly, the roof of the furnace transfers a few hundred kW of thermal power to the solid metal during the boredown stage of the batch.

The energy losses through the horizontal and the vertical surfaces of the electrodes remain almost constant throughout the whole batch, except during the boredown period of the batch. They reach values of 12 and 3 pct of the total power irradiated by the arc. In previous works,^[48,53] the losses through the horizontal surface of the electrodes were estimated at 14 pct of the total power irradiated by the arc. An interesting observation from the results in Figure 9 is that the power absorbed by the horizontal electrode surface is almost twice as large as that absorbed by the pool of liquid metal. This counterintuitive finding results from the fact that when considering the net heat exchange among all the surfaces in the radiative enclosure, the pool of liquid metal loses large amounts of heat to the solid metal, the roof, the walls, and the vertical surface of the electrode. These losses reduce considerably the amount of energy that the liquid metal absorbs from the arc. On the other hand, the horizontal surface of the electrode does not lose energy to these surfaces because throughout the batch, they do not face each other.

Figure 10 shows the dynamic electrical energy efficiency (η_ele)—as defined in Eq. [18]—and the power losses throughout the batch. The electrical efficiency of the EAF process changes significantly over time. It peaks at over 80 pct immediately after every loading procedure and decreases as the batch progresses. Still, the instantaneous electrical efficiency remains above 60 pct for over 70 pct of the duration of the batch. On the other hand, the electrical losses are larger than the gains during the last 20 pct of the processing time. Even though the solid metal receives the most radiative energy from the arc during the boredown period (see Figure 9), Figure 10 also suggests that the boredown periods are not the most energy-efficient ones. This is because during this stage of the batch, the horizontal surface of the electrode also absorbs the largest amount of radiative energy (see Figure 9). This result has an important practical implication as it suggests that the boredown should be performed with the longest possible arc, as this will help to reduce the energy losses to the electrode surface.

Fig. 10

EAF dynamic electrical efficiency and losses

Dynamic Efficiency of the Energy Inputs

In Figure 11, the energy efficiency of the various energy inputs to the process, as defined in Figure 3 and quantified in Eqs. [18], [20], [21], [29], and [43] are presented. The results in Figure 11 suggest that in comparison with the other energy inputs, the oxy-fuel burners and the combustion of coal are not very efficient. This is in contrast to the results in our earlier work,^[41] where the efficiency of the oxy-fuel burners was as high as 65 pct at the beginning of the melting stage of a single charge. The difference between these two results is due to the different loading practices, furnace geometries, and raw material densities considered. While in Reference 41, the simulation was performed for a furnace with an operational practice where a full loading of the EAF after each charge is done, here, almost half of the furnace remains empty after one charge. This result is in line with one of our conclusions in Reference 41, where we argued that the efficiency of the burner is strongly dependent on the amount of solid metal charged in the furnace and not exclusively on the melting progress of the batch, as it has until now been assumed. This is because the smaller the amount of solid metal, the lower the residence time of the combustion gases in the scrap, and the smaller the energy exchange between these and the solid material.

Fig. 11

Efficiencies of the energy inputs

The efficiency trends for the oxidation of solid metals, the oxygen lancing, and the combustion of coal are presented from second 1050 onwards, because only from this point onward, oxygen is available in the atmosphere of the EAF to promote these mechanisms. This is a result of our modeling assumption that no air is flowing into the furnace, and from the fact that the oxy-fuel burners are operated at stoichiometric conditions at all times. When there is oxygen available in the atmosphere, the efficiency of the oxidation mechanisms of the solid metal remains constant at 100 pct and that of the combustion of coal equals the efficiency of the oxy-fuel burners (see the modeling assumptions in Eqs. [21] and [29]). On the other hand, the efficiency of the oxygen lancing mechanism remains at all times between 62 and 58 pct, but it decreases slightly as the batch time progresses. The reasons for this behavior are discussed in the following subsection.

Overall Energy Efficiency of the Process

The overall energy efficiency of the process is computed with respect to the total instantaneous power input to the furnace, which is given by the sum of all the inputs:

$${Q_{{\text{TOT}}}} = \;{P_{\text{arc}}} + {\dot{m}_{\text{CH}_4}}\;{\text{LH}}{{\text{V}}_{\text{CH}_4}} + \;{\dot m_{{\text{coal}}}}\;{\text{LH}}{{\text{V}}_{{\text{coal}}}} + \;{\dot Q_{{\text{o}}{{\text{x}}_{{\text{sm}}}}}} + {\dot F_{{\text{O}}_2}}\;\left( {0.32\;\Delta {H_{{\text{L}}_{{\text{O}_{2{\text{M}}}}}}}\; + \;0.68\;\Delta {H_{{\text{L}}_{{\text{O}_{2{\text{C}}}}}}}} \right).$$

(44)

In Eq. [44], the energy transfer due to the splashing of liquid metal is neglected as it occurs within the thermodynamic boundary established at the exterior of the shell of the furnace.

In Figure 12, the energy flows that arrive at the solid and the liquid metal phases due to each mechanism of heat exchange, including the splashing of liquid metal, are presented in a normalized fashion with respect to the total energy input according to Eq. [45].

Fig. 12

Normalized energy flows and net energy efficiency of the process

$${\widehat{Q}}_{j}= \frac{\dot{{Q}_{j}}}{{Q}_{\text{TOT}}}.$$

(45)

As Figure 12 shows, the instantaneous total energy efficiency of the process is strongly dependent on how the power sources are operated. The process exhibits the highest total efficiency between 300 and 900 seconds because during this period, only the electric arc provides energy to the process. The instantaneous energy efficiency of the process reduces significantly during the periods when the oxy-fuel burners and the combustion of coal are turned on, i.e., between 0 and 300 seconds, 900 and 1200 seconds, and 1500 to 1750 seconds.

Throughout most of the batch and until 2900 seconds (90 pct of the duration of the batch), the electrical energy from the arc is the main contributor to the melting and heating process. After this point and until the end of the batch, the heat released by the oxidation reactions of liquid metal and the carbon dissolved in it become the largest source of energy to the process.

Some important observations can be made from the results shown in Figure 12. First, the splashing phenomenon (share of energy of the oxygen lancing to the melting of the solid metal) accounts for almost 10 pct of the total energy demand of the process immediately after a charge has been performed. As time passes and the solid metal melts, it progressively decreases to zero. On the other hand, the contribution of power by the oxygen lancing to the heating of the liquid metal increases, as the energy transferred from the liquid metal to the solid metal via the splashing decreases. These two mechanisms combined account for the total energy contribution of the oxygen lacing to the process, which remains constant at approximately 20 pct.

Second, it demonstrates the importance of including physically meaningful limiting factors into the mechanisms of heat exchange. For the case of the oxidation of solid metals, the quadratic corrosion formula limits these contributions to a maximum of 200 kW. Although the instantaneous energy contributions from both the oxidation of metals and the liquid metal splashing (during the last stages of the batch) are small, they are important for the overall process efficiency. For example, we found that the batch time extended by 2 minutes if these sources were not considered.

Third, with respect to the total energy input, the energy contribution from the oxy-fuel burners to the process is between 16 and 9 pct during the periods of time when the burner is on.

Finally, the results in Figure 12 also suggest that the melting of metal in the EAF is a highly efficient process that operates at energy efficiencies between 80 and 60 pct most of the time. However, it deteriorates toward the end of the batch when most of the solid metal has melted. This aligns well with intuition as (a) the smaller the amount of unmolten scrap, the larger the energy losses to the roof and to the walls via radiation and the amount of liquid metal splashed to the walls of the furnace, and (b) the smaller the areas of heat exchange, the smaller the heat exchange due to conduction and convection mechanisms, as well as the residence time of the combustion gases in the void spaces of the solid scrap.

From an operational perspective, the above results point at a mode of operation that can lead to an improved energy performance of the EAF. Because the energy efficiency of the EAF changes significantly over time and considering that industrial processes should operate when they are most efficient—both to improve their economic and environmental performances—steelmakers should aim at operating at a higher energy intensity when the process is more energy efficient and at a low energy intensity when the efficiency deteriorates.

Conclusions

In this work, a comprehensive model of an EAF for the production of steel using large shares of scrap and an operational practice of a late oxygen lancing (as in stainless steel production) was presented and validated. It predicts accurately several of the most important parameters of the process: the batch time, the final temperature of the melt, and the amount of solid metal that remains unmolten after the termination of each intermediate melting stage. The model was constructed using first principles and accommodating empirical observations that until today have not been considered. We made well-founded assumptions regarding the efficiencies of the process when first-principles reasoning was not sufficient to explain satisfactorily the nature of the process.

We proposed to model the heat exchange from the electrical input via radiation mechanisms only. In contrast to conduction-convection dominated models that require (a) to relax usual assumptions regarding the value of many of the heat exchange constants, and (b) the use of complex parameter estimation approaches to compute them, a radiation dominated model is much simpler and allows for an straightforward computation of the heat exchange. For the computation of the radiative heat exchange, we proposed novel Monte-Carlo algorithms to accurately estimate (errors below 0.5 pct^[40]) the view factors in the system. The use of the DC circuit analogy led to a better understanding of the energy fluxes in the EAF and to a series of findings that challenge many of the long-accepted hypotheses regarding the energy exchanges between the arc, the electrode, and the liquid metal. For example, we found that for a radiation dominated arc, the electrode absorbs much more heat from the arc than the pool of liquid metal, and that less than 5 pct of the power of the electric arc is absorbed by the pool of liquid metal. These results are in contrast to those reported in Reference 53 in the late 1970s and that until now have remained unchallenged.

The inclusion of the oxidation mechanisms of the solid metal and of the splashing of liquid metal makes it possible to understand better the impacts of the injection of oxygen. Traditionally, it has been accepted—and modeled—that larger quantities of oxygen would in general be beneficial to the melting process as these will promote the oxidation of iron and carbon, even during the early and intermediate stages of a batch. However, if the quadratic corrosion formula is valid, large contributions of thermal energy cannot result, regardless of the amount of oxygen that is available in the gaseous atmosphere of the EAF. In addition, the modeling of the effects of the oxygen lancing revealed that they are important not only for the purposes of decarbonizing or increasing the temperature of the liquid metal phase, but they also play an important role in the heat exchange from the liquid phase to the solid phase during the lancing stage of the batch.

To our knowledge, dynamic energy efficiency curves for the various inputs to the process as well as the overall energy efficiency of the process are shown here for the first time. Our computations suggest that the melting of the solid metal in an EAF is a highly efficient process during the early stages of the batch and that its performance deteriorates over time. Based on this observation, one can employ dynamic optimization to find the optimal electrical inputs that maximize the electrical energy efficiency of the process. In Reference 7, we used dynamic optimization and the EAF model presented here to compute an optimal group of setpoints for the electrical input that reduced by more than 4 pct the energy demand of the EAF process at Acciai Speciali Terni.

In a series of additional numerical studies, we found out that for a given batch of steel, the optimal control policy depends on the required final temperature of the liquid metal and the batch time. For example, to achieve an optimal operation, a batch of steel of 90 tons, with the requirement of a high final temperature of the liquid metal (around 1950 K) and a short batch time (around 50 minutes), should be operated using a constant electrical input, throughout the batch, that is close to the maximum operative power of the EAF (75 MW). On the other hand, for a batch with a batch time and a final temperature of around 60 minutes and 1860 K, respectively, the optimal control policy is in line with the arguments discussed earlier in Section V: the optimal melting profile uses large quantities of electrical power immediately after each charge when the electrical efficiency of the process is high and reduces the power input when a large fraction of the solid metal has melted and the energy efficiency deteriorates. Detailed discussions on the impact that various operational requirements have on the computation of an optimal control policy for a batch of steel (i.e., the length of the electric arc, a given the final temperature, the total batch time, or operational electrical power level) can be found in References 14 and 54.

While the model presented here was tailored and validated using process data of an UHP-EAF producing stainless steels, it can be expected that the model can also predict well the behavior of any EAF that uses large shares of scrap material and that operates the oxygen lancing only at a late stage of the batch. Because the future electrical steelmaking will be more reliant on the use of scrap, this model can be used to evaluate feasible strategies for future demand side management applications (DSM) where the EAF can operate as a flexible load that balances the electrical grid in the presence of intermittent energy from non-conventional renewable energy sources.^[55]

A possible refinement of the model is that the thermal inertia of the furnace could be modeled to describe satisfactorily the dynamic evolution of the water temperature of the cooling water in the walls and the roof of the furnace. The results of our model overestimate the temperature of the cooling water significantly compared to measurements and the values in the literature. In preliminary estimations, we found out that the error can be reduced to less than 10 pct if (a) the entrainment of air through the de-slagging door is considered and (b) the energy balance is closed considering also the time-off periods of the batch (and not only the time-on period of the batch as it is the standard practice). In this manner, the heat removed from the walls of the furnace during the time-off periods—which is clearly visible from the measurements—is included. We intend to explore these issues in more detail in future work.

Appendices

Appendix A: Radiative Circuit Switches and Resistors Descriptions

The DC circuit analogy is a strategy that simplifies the computation of the radiative heat exchange among various surfaces in geometrically complex arrangements. It employs (a) voltage sources to represent the potential of the surfaces to exchange heat ($\text{VT}_i$). Their values depend on the Stefan-Boltzmann constant is ${\sigma }_\text{b}=5.670367\times{10}^{-8}\,\text{W}\,{\text{m}}^{-2}\,{\text{K}}^{-4}$ and on the temperature of each participating surface in the exchange (${T}_{i}$) (see Eq. [A1]). (b) Resistors to model two types of radiative phenomena. On the one hand, radiosity resistors ($Rr_i$) represent the opposition of a given surface ($i$) to absorb radiative energy. Their values depend on the emissivity (${\varepsilon }_{i}$) and the area (${A}_{i}$) of the exchanging surface, as in Eq. [A2]. On the other hand, view factor resistors ($Rx$) determine how much of the energy that leaves the emitting surface “$i$” reaches the receiving surface “j.” Their values depend on the view factor from the surface $i$ to the surface j ($\text{VF}_{i-j}$), and on the area of the emitting surface, as in Eq. [A3].

$$\text{VT}_i= {\sigma }_\text{b} {{T}_{i}}^{4}$$

(A1)

$$Rr_i = \frac{1 - {\varepsilon }_{i}}{{\varepsilon }_{i}\,{A}_{i}}$$

(A2)

$$Rx= \frac{1 }{\text{VF}_{i-j}\,{A}_{i}}$$

(A3)

A detailed description of the required parameters to solve the radiative circuit in Section III–D is given in Tables AI through AIV.

Table AI State of the Controlling Switches (Sw_y) in the Radiative Circuit. 0: No Flow of Energy–Switch Open, 1: Flow of Energy–Switch Closed. (See Fig. 4)

Table AII List of View Factor Resistors ($Rx$) in the Radiative Circuit (See Fig. 4)

Table AIII List of Radiosity Resistors ($Rr_i$) in the Radiative Circuit (See Fig. 4)

Table AIV List of Assumed Surface Temperatures for Computing $\text{VT}_i$. (See Figure 4)

In Table AII, the elemental geometries A to D refer to the five basic geometrical configurations that can be used to describe the exchanges in the EAF radiative circuit. These are presented in Figures A1 through A5.

Fig. A1

Primitive A: cylinder to disk

Fig. A2

Primitive B: cylinder to ring with a gap

Fig. A3

Primitive C: concentrically off-set cylinders

Fig. A4

Primitive D: distant rings

Fig. A5

Primitive E: ring to the external cylinder

Appendix B: Estimation of the Free Model Parameters from Process Data

Formulation of the Problem

The free parameters of the model are estimated for a batch of two charges, which goes through three stages: the first melting, the second melting, and a refining stage.

In the EAF process, the boredown time of the electrodes during the first (${t}_{\text{b1}}$) and the second melting (${t}_{\text{b2}}$), the batch time (${t}_{\text{b}}$), and the final temperature of the melt (${T}_{\text{mm}}{|}_{t = {t}_{b}}$) are measurable parameters that can be used to estimate the free parameters of the model. The amount of metal that was melted during the first melting (${m}_{\text{mm}}{|}_{t = t_{m1}}$) and during the second melting (${m}_{\text{mm}}{|}_{t = t_{m2}}$) can be approximated from process observations and operational experience.

${m}_{\text{mm}}{|}_{t = t_{m1}}$ can be estimated from the mass balance between the first charge (${m}_{\text{sm}_1}$), the second charge (${m}_{\text{sm}_2}$), the maximum mass capacity of the furnace, and considering that during normal batches, approximately 10 pct of the total volume of the furnace remains voided after the second charge.

$${m}_{\text{mm}}{|}_{t = t{m}_{1}}= {m}_{\text{sm}_1}+ {m}_{\text{sm}_2}- 0.9 \pi\,{{R}_{\text{fur}}}^{2}\,{H}_{\text{fur}}\,{\rho }_{\text{sm}}$$

(B1)

During normal operations, the state of the batch is controlled visually after the second melting stage before initiating the refining stage. The operative personal estimates that the amount of solid metal that remains unmolten after the second melting and is floating on top of the pool of liquid metal can be as high as 5 pct of the total mass of charged material. Furthermore, it is also known that at this stage solid pieces of metal remain unmolten under the surface at the bottom of the furnace. Although it is impossible to measure this fraction of unmolten metal, operators and plant engineers conjecture that the fraction of unmolten metal under the surface should be equal or larger than that of the unmolten metal above the liquid pool. Based on these considerations, we assume that the total amount of unmolten material before the refining stage is 12 pct of the total mass loaded in the furnace.

$${m}_{\text{mm}}{|}_{t = t{m}_{2}}= 0.88 ({m}_{s{m}_{1}}+ {m}_{s{m}_{2}})$$

(B2)

Based on the above observations ${p}_{i} =\left\{{t}_{b1}, { t}_{b2},{ t}_{b}, {T}_{mm}{|}_{t = {t}_{b}},{m}_{mm}{|}_{t = t{m}_{1}}, {m}_{mm}{|}_{t = t{m}_{2}}\right\}$, the free parameters of the model ${x_j} = \left\{ {{k_{{{\text{m}}_{{\text{sm}}1}}}},{\text{\;}}{k_{{{\text{m}}_{{\text{sm}}2}}}},{\text{\;}}{\eta_{\text{L} _{{{\text{O}}}_2}}},\;\;{\text{and}}\;\;{x_{{{\text{O}}_{2{\text{m}}}}}}} \right\}$ can be estimated using a least square approximation.

$$\begin{aligned} &\min_{x_j}\quad f(x) = \sqrt{\sum_{i=1}^{I} \delta_i \ \left( \dfrac{p_i - {p_i(x_j)}^*}{p_i} \right)^2} \\& \text{s.t.} \quad \text{EAF process model} \\& \qquad x_l \,< x\,< x_u \end{aligned}$$

(B3)

In Eq. [B3], ${p}_{i}$ represents the measured data, ${p_i(x_j)}^*$ is the prediction of the measured data computed by the model, and ${\delta }_{i}$ are the weights associated to each approximated parameter. Because the calculated parameters are associated to phenomena that mostly take place in different time windows, the estimation can be carried out by dividing the original problem (Eq. [B3]) into simpler sequential problems where only relevant process data is considered. For a two charges batch, these intervals are the three stages of a normal batch of steel: the first extends from the beginning of the first boredown until the moment when the first melting stage is terminated. The second lasts from the beginning of the second boredown until the moment when all the solid metal has melted. The last interval extends from the beginning of the refining stage until the end of the batch.

In the first and the second problem, which correspond to the first and the second stage of a batch, the melting rates of the first (${k}_{{\text{m}}_{\text{sm1}}}$) and the second melting stage (${k}_{{\text{m}}_{\text{sm2}}}$) are computed. In the third problem, the efficiency of the oxygen lancing (${\eta }_{L_{\text{O}_{2}}}$) and the oxygen distribution in the metal pool (${x_{{{\text{O}}_{2_{\text{m}}}}}}$) are estimated. For the estimation of ${k}_{{\text{m}}_{\text{sm2}}}$ in the second estimation problem, we assume that the influence of the oxygen lancing and the oxygen distribution on the speed of the second melting is negligible. This is justified by the fact that the oxygen lancing is initiated only toward the end of the second melting, thus its average energy contribution to the melting process—via the splashing mechanisms—is small in comparison with the total energy provided by the arc.

The oxygen lancing efficiency is estimated from the recorded batch time because the final temperature of the melt (${T}_{\text{mm}}{|}_{t = {t}_{b}}$) is used as the termination condition in the simulator. Therefore, there is no error in its computation. As a rule of thumb, the batch time in the real process is extended by one or two minutes after visual controls through the de-slagging door confirm that all the metal has melted. Here, we assumed that the time of completion of the melting (${t}_{{\text{sm}}_{\text{c}}}$) is 1 minute less than the batch time:

$${t}_{\text{sm}_c}={t}_{b}-1.$$

(B4)

In the first and second estimation problems, the weights associated to the boredown times and the amount of metal melted during each stage are set to 0.4 and 0.6. This is because despite the fact that it is more important to predict accurately the mass of molten metal during each melting stage, if the weight associated to the boredown period is too low, the model will overestimate the melting rates at the beginning of each charge. This, in fact, is one of the weak points in existing EAF process models.

For the computation of the parameters that are associated to the oxygen lancing, weights of 0.7 and 0.3 were chosen. This is because from an energy perspective, it is more important to predict more accurately the batch time than the melting time of the solid metal—the energy demand of the process is determined mostly by the batch time. In Table BI, the employed process data, the estimated parameters and the weights employed in each of the three estimation problems are summarized.

Table BI Parameters Estimation Table

Considered Process Data

For the estimation procedure described above, the process data of two weeks of production were considered. During normal operations, many unpredicted events that extended the processing time can occur. i.e., the need for extending the refining period when solid pieces of metal remain unmolten at the end of the batch, or when the process needs to be stopped (time-off) due to the lack of processing availability in any of the downstream assets in the meltshop (AOD, Ladle, Continuous Caster). For the estimation, abnormal batches, defined as those with batch times or time-off times that are 1.5 times their standard deviation larger than the average value of the whole campaign, are excluded. The collected data consider batches producing two different types of steels A and B, from different raw materials and using different charging practices.

Results

Given the simplicity of the estimation problems, they can be solved by performing a graphical analysis over the feasible domain. Bounds of the domain of the melting rates are imposed to match realistic enthalpies of fusion of various metals, from 261 to 290 KJ kg⁻¹. These limits are established by adopting the enthalpy of fusion of 304 stainless steel (290 KJ kg⁻¹) as a reference and varying the melting rates between 0.9 and 1.0. On the other hand, the parameters associated with the oxygen lancing are bounded to the physically meaningful range from 0.2 to 0.9. The results of these computations for the family of steel A are presented in Figure B1. The curves for family of steel B are not presented as the cost surfaces are very similar to those of steel A. The optimal values of the estimated parameters for the steels A and B are summarized in Table BI.

Fig. B1

Graphical depiction. (a) f(x) vs.${\text{k}}_{{\text{m}}_{\text{sm}1}}$. (b) f(x) vs.${\text{k}}_{{\text{m}}_{\text{sm}_2}}$. (c) f(x) vs. ${\eta }_{\text{L}_{\text{O}_{2}}}$ and ${\text{x}}_{{\text{O}_{2}}_m}$

The results in Figures B1(a) and (b) show that the optimal values for ${{k}}_{{\text{m}}_{\text{sm}1}}$ and ${{k}}_{{\text{m}}_{\text{sm}_2}}$ are 0.92 and 0.9, respectively. Figure B1(c) shows that within the region bounded by $0.55<{\eta }_{\text{L}_{\text{O}_{2}}}<0.9$ and $0.2<{ x}_{{\text{O}}_{2_m}}<0.5$, various parameter combinations provide an error between 1 and 2 pct according to Eq. [B3]. The fraction of oxygen and the oxygen lancing efficiency are negatively correlated, implying that in order to maintain the energy contribution needed to obtain a low error in the estimation, the oxygen lancing efficiency must decrease as more oxygen is consumed by the oxidation of liquid metal. We chose the values of ${\eta }_{\text{L}_{\text{O}_{2}}}=0.72$ and $x_{{{\text{O}}_{{2_m}} }} = 0.3$ for two reasons. First, these values are located centrally in the subdomain where the error is very small. Second, in earlier work, Pfeifer et al.^[47] estimated these values as ${\eta }_{\text{L}_{\text{O}_{2}}}=0.7$ and $x_{{{\text{O}}_{{2_m}} }} = 0.3$.

Appendix C: Validation of the Model

The accuracy of the model in terms of the predictions of (a) the melting time of the first charge, (b) the total batch time, (c) the energy demand, (d) the final temperature of the liquid metal, and (e) the digging time of the electrodes during the first and the second charge, is evaluated by comparing the predictions of the adjusted model against the process data of 3 years of production and for two types of steels. Available process data were cleaned according to the criteria described in Appendix B, and the information of over 1000 batches of each type of steel remained.

Because the cleaned data corresponds to batches with significantly different loading practices (amount and type of material charged in the EAF), the model was run for three different loading scenarios: the first corresponds to the average value of the mass loaded in the 1000 batches for each type of steel (Sim. Center), and the second and third are simulations carried out with an initial mass that corresponds to the upper (Sim. Upper Limit) and lower (Sim. Lower Limit) 2-sigma limits of the loaded mass. In all three simulations, the density of the initial solid scrap was kept constant and the value of the free parameters of the model were set to the computed values in Appendix B (See Table BI).

Because the model requires as input parameters the electrical power and the length of the arc, and because in practice only the voltage and the impedance setpoints of the arc known, the electric arc model presented in Reference 2 was employed to transform, at each point in time of the simulation, the operative voltage, and impedance points into an electrical power and arc length. The employed electrical setpoints cannot be disclosed as they represent confidential information. The results of these simulations are presented in Figure C1.

Fig. C1

Process data vs simulation results for steels A and B. 1-Melting time of the first charge. 2-Batch time. 3-Electrical energy demand of the process. Normalized representation

The results in Figure C1 show that the model predicts the melting time of the first charge, the total batch time, and the energy demand of the process well for both types of steel—for most of the cases, the predictions lie within the 2-sigma interval of the process data. The predictions of the time parameters are slightly more accurate than those of the energy demand of the process. Also, the model captures the correlation that exists among the amount of charged material, the batch time, and the energy demand well. The significantly different batch times and energy demands between the two types of steels can be explained by the wider variety of raw materials used in the process. This also explains why the 2-sigma intervals of the batch time and the energy demand of the process are larger for steel B (see Figure C1(b)), than for steel A.

The boredown time of the electrodes was estimated from electrical process data. During this period, the arc power constantly increases, its currents exhibit a very erratic behavior, and the control system maintains the electrodes moving downwards. The end of this period can be estimated as the moment at which the power reaches its setpoint, the current stabilizes, and the control signal (the voltage to a servo-valve of the hydraulic system of the supporting columns of the electrodes) becomes zero. At the end of the boredown period, the electrodes have melted an amount of steel that is equivalent to that of the volume occupied by the electrodes plus an additional space equal to the arc length (see the modeling assumptions). In the simulation, the boredown period is automatically computed by the simulator as the point where the arc reaches the pool of liquid metal (see Figure 2(d)). Figure C2 shows the computed vs measured boredown times of the electrodes, for both families of steel, A and B.

Fig. C2

Boredown time of the electrodes. 1- Fist charge steel A. 2- Second charge steel A. 3- Fist charge steel B. 4- Second charge steel B. Normalized representation

Figure C2 suggests that for both types of steel, the model predicts the boredown time of the electrodes in the first charge well. On the other hand, the predictions are less accurate for the second charge. The results also show a coherent relationship between the amount of loaded material and the digging times—the more/less material is loaded in the furnace, the longer/shorter the boredown period of the electrodes is. Although the accuracy of the predictions of these parameters could be improved by increasing their corresponding weights in the estimation parameters in problem (Eq. [B3]), this is not done for two reasons. (1) Higher weights will increase the error in the prediction of the batch time and thus in the prediction of the energy demand of the process. (2) The error in the computations of the boredown times is in fact small as compared to the batch time—while the boredown lasts less than 4 minutes, the batch time is always larger than 50 minutes.

The model was also validated for the final temperature of the melt. Temperature measurements of the molten steel were taken manually by an operator at the end of three random batches from the group of batches employed during the parameter estimation in Section II–A. for each family of steel. The comparisons of the measured values and the predictions of the model are presented in Figure C3.

Fig. C3

Final melt temperature. 1-Steel A. 2-Steel B. Normalized data

Figure C3 shows that our model predicts an approximately 3.5 pct higher temperature of the melt for both steel families. In the case of the stainless steel making process, a prediction of the final temperature of the liquid metal with an error of up to 4 pct is acceptable because downstream the EAF, the temperature of the liquid steel is corrected in the Argon-Oxygen-Decarburization (AOD) unit and in the Ladle (LD) furnace, before it enters the temperature critical casting process. The error probably results from the fact that energy losses via convection mechanisms to the gaseous phase during the off periods and during the refining stage of the batch (due to the infiltration of air from the atmosphere) have been neglected.