1 Introduction

Low-alloy martensitic steels tempered at high temperatures are often employed in the energy industry for applications requiring mechanical strength and hydrogen embrittlement (HE) resistance.[1,2] As the study of any HE phenomenon involves the ingress, diffusion, and trapping of hydrogen into the exposed metallic structure,[3] it is essential for improved steel design to characterize the impact of alloying elements and metallurgical defects on the kinetics of hydrogen diffusion and hence on the embrittlement mechanisms.

Since the first observation of an impediment of hydrogen diffusion inside cold-worked steels,[4] many authors have proposed hydrogen diffusion models. They consider the existence of two sites for hydrogen occupancy: normal lattice sites and trapping sites, where the occupancy is energetically favorable.[5,6,7,8,9,10] In carbon martensitic steels, without alloying elements additions, the main possible trapping sites are carbon in solid solution, dislocation, vacancy, boundaries (prior austenite grain, packet, block, sub-block and lath), cementite, inclusions, and retained austenite. In general, the diffusivity increases, and the solubility decreases with increasing the tempering temperature and/or reducing the carbon content.[11,12] Wei and Tsuzaki suggested that dislocations are the main traps in a Fe-0.2C martensitic steel after observing that the detrapping activation energy was constant (around 34 kJ/mol or 0.35 eV) over the range of tempering temperatures up to 700 °C. Since the martensitic boundaries do not evolve significantly during tempering and the dislocations density decreases considerably with tempering, the trapping and annihilation of dislocations could explain the decrease of hydrogen solubility with tempering. It also explains the increase of the solubility due to carbon, as the dislocation density in martensite increases with carbon content. Additionally, at the onset of cementite precipitation (around 300 °C), no considerable increase on hydrogen solubility was observed, which indicates that the cementite–matrix interfaces are not the primary trapping sites of tempered martensite[13] despite the complex nature of this interface.[14,15]

Substitutional alloying elements are added to martensitic steels to improve their properties. Their addition usually results in a reduction of diffusivity and an increase in solubility shifting the solubility peak toward higher tempering temperatures.[12] The diffusion of hydrogen is affected by both the elastic and the chemical interactions between hydrogen and the alloying atoms. Hagi found the following order for the effect of substitutional solute elements on reducing the hydrogen diffusivity in iron Co < Si < Cr < Al < Ni < Mo < V based on electrochemical permeation results.[16] Counts et al. performed density functional theory (DFT) calculations of the binding energy between hydrogen and several solute elements and found that among the usual alloying elements, Ti and Nb have the strongest binding energy around 0.08 eV similar to carbon-hydrogen binding energy of 0.09 eV.[17] According to their calculations, the common alloying elements Mo, Cr, Mn, and Si do not trap hydrogen significantly.

Alloying elements also precipitate as carbides which can trap hydrogen. Their binding energies depend on their nature, their coherency with the matrix, and the location of the trap sites.[18] Hydrogen atoms may be weakly bonded to the strain field around (semi-) coherent carbides. They can also be trapped at the misfit dislocations or carbon vacancies at the carbide interface.[18,19] In general, coherent, semi-coherent, and incoherent interfaces of the same carbide have distinct trapping energies and their values may vary considerably from very weak traps to strong irreversible ones.[20] If enough energy is provided, hydrogen can also move into the precipitates and be strongly trapped at their vacancies.[19] The MC precipitates with NaCl-type crystal structures are the strongest trapping sites. It was observed from thermal desorption spectroscopy (TDS) spectra that the trapping ability of usual precipitates varies in the descending order of NbC > TiC >  > VC > Mo2C. The first three precipitates present NaCl-type crystal structure, whereas Mo2C has a hexagonal crystal structure.[18] Directly observations of hydrogen trapping sites for TiC, VC, and NbC precipitates have been performed using deuterium charging and atom probe tomography (APT),[21,22] and small-angle neutron scattering.[23] It was observed that hydrogen is trapped in the broad interface between the matrix and the TiC carbides,[21] whereas for the vanadium carbides, their results indicate that hydrogen is strongly trapped at the carbon vacancies at the (001) broad interface.[22] These results are supported by ab initio calculations of binding energies between hydrogen and the coherent strain, carbon vacancy, and coherent interface of Ti and V carbides.[19]

Despite all the research on hydrogen diffusion in steels, there is still a scatter in trap binding energies reported in the literature.[13,17,22,24,25,26,27,28,29,30,31] Experimental errors, the difficulty to correlate the measured hydrogen to specific microstructural elements, the differences in the nature of trapping sites and microstructural defects, e.g., grain boundary type and misorientations, screw or edge dislocation, elastic strain, or dislocation core, can explain this discrepancy. Additionally, there is a lack of data of hydrogen diffusion and trapping for martensitic steels tempered at very high temperatures in the range between 650 °C and the transformation temperature Ac1. The present work completes this gap by providing an in-depth investigation of hydrogen diffusion into ten low-alloy (additions of Cr, Mo, Mn, and V) martensitic steels with carbon contents from 0.3 to 0.6 wt pct tempered at temperatures between 580 °C and 740 °C. The diffusion and trapping behavior of the steels are characterized by electrochemical charging and permeation, and thermal desorption spectroscopy analysis. The apparent diffusion coefficient is related to their mechanical strength and analyzed in terms of their dislocation density. For the four steels with higher hydrogen solubility, other trapping sites besides dislocations are required to explain their trap ability. Trapping at MC carbides is investigated as a possible source of extra reversible and irreversible trapping.

2 Experimental Procedures

2.1 Material and Characterization

The present work studied ten quenched and tempered martensitic steels (QTM1 to 10), which simplified chemical composition is given in Table I. The steels also contain similar small amounts (less than 0.04 wt pct) of Cu, Ni, Nb, N, Ti, Ca, and Al. Table I also presents equivalent carbon contents (CEQ) calculated by Eq. [1] adapted from Yurioka et al. work[32] by increasing the contribution of vanadium in agreement to its greater effect on hardening at high tempering temperatures.[33] Calculation of carbon equivalent was extensively developed in the context of steel welding to assess the risk of cold-cracking[32] and it is only used here to give a roughly comparison of the extent of the alloying additions.

$$ C_{{{\text{EQ}}}} = C + \frac{{{\text{Si}}}}{24} + \frac{{{\text{Mn}}}}{6} + \frac{{{\text{Cr}} + {\text{Mo}}}}{5} + \frac{{\text{V}}}{3} $$
(1)
Table I Chemical Composition and Carbon Equivalent in Weight Pct; Transformation Points, Austenitization, and Tempering Temperatures in Degree Celsius for the Studied Steels
Full size table

Samples of all the studied steels with dimensions 180 × 120 × 15 mm were austenitized for 15 min and then water (C = 0.3 wt pct) or oil (C > 0.3 wt pct) quenched. Thereafter, tempering was conducted for 30 min. Table I displays the transformation points Ac1 and Ac3 measured by dilatometric analysis as well as the austenitization and tempering temperatures.

Optical microscopic images of etched samples confirmed the presence of the desired tempered martensitic microstructure with prior austenite grain (PAG) sizes estimated by the intercept method. Intra-lath statistically stored dislocation (SSD) density was estimated by the line-intercept method using five TEM images for each steel.[34] Lath boundaries geometrically necessary dislocation (GND) density was estimated by an approach similar to the works of Persicka et al.,[35,36] considering that low-angle boundaries have simple planar dislocation structures and using misorientation data from EBSD maps. Precipitates were identified by synchrotron X-ray diffraction spectra (beam line ID31 at the European Synchrotron Radiation Facility with a beam of 67.77 keV, wavelength of 0.0292961 nm, and size of 100 μm) and/or TEM diffraction patterns (TEM JEOL JEM 2011, 200 kV). Vacancy concentration was evaluated using differential scanning calorimetry (DSC) measurements by considering the exothermic peaks between 60 and 200 °C related to vacancies annihilation and their areas corresponding to the vacancy-stored energy.[37] Energy-dispersive X-ray diffraction (EDXRD) technique was employed to verify the absence of retained austenite. Figure 1 shows images of the main structural features (grain boundaries, precipitates, and dislocations), whereas Table II summarizes the structural characterization results along with yield strength values (at the Lüders plateaus) from tensile tests performed at strain rate of 10–5 s−1.

Fig. 1
figure 1

(a) Optical microscope image after Bechet-Beaujard etching revealing PAG, (b) TEM images showing (b.i) precipitates and (b.ii) intra-lath dislocations, (c) EBSD (c.i) IPF and (c.ii) IQ maps with red (1–5°), blue (6–15°), black (16°-50°) and green (51–90°) boundaries for the QTM8 steel (Color figure online)

Full size image
Table II Structural Parameters of the Studied Steels
Full size table

2.2 Hydrogen Diffusion and Trapping

2.2.1 Experimental setups

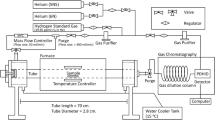
Hydrogen diffusion and trapping characterization were performed using Devanathan-Stachurski electrochemical permeation (EP) and thermal desorption spectroscopy (TDS). The employed EP cell contained charging and detection compartments equipped with SSE (Hg/HgSO4/K2SO4) reference electrodes inside Luggin capillaries filled with saturated K2SO4 solution and platinum counter electrodes. A floating ground Radiometer galvanostat PGP201 was used for the charging side, whereas a BioLogic potentiostat VSP was employed for the detection. Steel membranes of 1.05 ± 0.15 mm thickness were placed in a Teflon holder with an opening of 1 cm diameter, where a platinum wire provides the electrical connection between the sample and the permeation device. The steel membranes were not coated with palladium, resulting in a passive film formation at the exit surface. Deionized water circulated in the double jacket thorough a cryothermostat Lauda RK8 CS in order to maintain a constant temperature of 20, 30, 40, or 50 ± 0.5 °C. Before the test, both cells were deaerated by argon for 1 h. This deaeration was kept throughout the tests. At the beginning of the permeation tests, the detection sides of the membranes were maintained at a constant potential of − 300 mV/SSE in a 0.1 mol/L NaOH solution for around 20 h in order to stabilize the anodic current density to approximately 0.1 µA/cm2. During the next step, the charging side of the samples was polarized at a constant cathodic current density between 5 and 100 mA/cm2 in a 1 mol/L H2SO4 solution. The anodic potential at the detection side allows the oxidation of the hydrogen atoms that cross the membrane, consequently the anodic current gave a direct measure of the hydrogen flow rate. This current gradually increased until reaching a stationary state. Then the cathodic polarization at the hydrogen entry surface was stopped and the charging side was emptied. Lastly, hydrogen desorption was monitored following the decrease of the anodic current at the detection side.

For the TDS measurements, steel samples of 4 × 4 × 10 mm were cold mounted, polished , and cathodic polarized at one side (other faces masked with mounting resin) with current density of 20 mA/cm2 inside a cell with 1 mol/L H2SO4 solution, SSE (Hg/HgSO4/K2SO4) reference and platinum counter electrodes. The temperature was set to 20 °C and the cell was continuously deaerated with argon. After the samples were charged for 24 h, the resins were removed, and they were quickly polished with grinding paper #2400 for the thin oxide layer removal and then rinsed with acetone. Afterward, hydrogen concentration was measured by the TDS machine with a Jobin Yvon Horiba EMGA-621 W hydrogen analyzer. In this machine, samples were placed in a chamber continuously purified with argon and heated up to 2000 °C using seven heating rates from 75 to 280 °C/min. The degassed hydrogen was then detected and analyzed using thermal conductivity detector (TCD). The time between the end of the hydrogen charging and the sample insertion into the TDS chamber was around 7 min. A more detailed description of these methodologies has already been published in previous works.[31,38,39]

2.2.2 Analyses of the experimental data

The experimental apparent diffusion coefficient (Dapp) was obtained by the numerical adjustment of the experimental charging transient curve (permeation current density j as a function of time t) with the theoretical Eq. [2], where l is the membrane thickness. This equation was derived from the analytical solution of Fick’s law calculated by Laplace transform considering a constant hydrogen sub-surface concentration at the entry side and a concentration equal to zero at the exit side. This methodology is based at the beginning of the transient as better described in a previous work, in which it is referred as “Regime 1 technique”.[38] At the equilibrium, the C0app at the entry surface was calculated by Eq. [3], where jmax is the steady-state permeation current density, MH is the molar mass of hydrogen, ρFe is the density of iron (7.87 × 106 g/m3), and F is the Faraday constant (96,485 C/mol).

$$ \frac{\partial \ln \left( j \right)}{{\partial t}} = \frac{1}{2t} + \frac{{l^{2} }}{{4D_{{{\text{app}}}} t^{2} }} $$
(2)
$$ C_{{0{\text{app}}}} = \frac{{j_{\max } lM_{{\text{H}}} }}{{D_{{{\text{app}}}} F\rho_{{{\text{Fe}}}} }} $$
(3)

By fitting the decays of the anodic current density during the desorption steps using the theoretical Eq. [4] (Fick’s law solution), it was possible to obtain the concentrations of lattice and reversible trapped hydrogen.[38] The area defined by the theoretical equation corresponds to the lattice hydrogen (CL), whereas the one between the theoretical and the experimental curves provides the amount of reversible trapped hydrogen (CTr). The irreversible trapped concentration (CTir) was then calculated as the difference between the C0app and the sum of CL and CTr, since C0app is similar to the average concentration in the permeation membrane.

$$ j = j_{\max } \left( {1 - \frac{2L}{{\sqrt {\pi D_{{{\text{app}}}} t} }}\mathop \sum \limits_{n = 0}^{\infty } e^{{\left( { - \frac{{\left( {2n + 1} \right)^{2} l^{2} }}{{4D_{{{\text{app}}}} t}}} \right)}} } \right) $$
(4)

The partial derivatives of these concentrations (CL, CTr, and CTir) with respect to the average concentration in the membrane C ≈ C0app were then employed in the calculation of the lattice diffusion coefficient (DL) according to the Eq. [5].[38]

$$ D_{{{\text{app}}}} = \frac{{D_{{\text{L}}} }}{{\left( {1 + \frac{{\partial C_{{\text{T}}} }}{{\partial C_{{\text{L}}} }}} \right)}} = \frac{{D_{{\text{L}}} }}{{\left\{ {1 + \left[ {\left( {\frac{{\partial C_{Tr} }}{\partial C} + \frac{{\partial C_{{{\text{Tir}}}} }}{\partial C}} \right)*\frac{\partial C}{{\partial C_{{\text{L}}} }}} \right]} \right\}}} $$
(5)

Thereafter, the permeation charging transients were used for the estimation of the number density of trapping sites (NT) according to the method described in a previous paper[38] based on the works of Kumnick and Johnson, and McNabb and Foster.[5,40] This approach estimates NT by correlating the average hydrogen concentration inside the membrane (C) with the experimental breakthrough time for 10 pct of jmax (tb10 pct) using Eq. [6], where tL is the exit time for a membrane without trapping sites and M is a coefficient equal to 15.3.

$$ \frac{{t_{{{\text{b}}10{\text{\% }}}} }}{{t_{{\text{L}}} }} - 1 = \frac{{3N_{{\text{T}}} }}{C} \;{\text{where}} \;t_{{{\text{L}} }} = \frac{{l^{2} }}{{MD_{{\text{L}}} }} $$
(6)

Arrhenius-type linear relationships of diffusivity (Dapp) from the charging permeation transients performed at the four employed temperatures provided the pre-exponential factor D0app and the diffusion activation energy ∆Ea.

TDS spectra were adjusted using the sum of four Gaussian distributions following the previous work of Frappart et al.[31] Thereafter, the variation of the temperature of the center of each peak with the heating rate allowed the calculation of their trapping energies according to the Kissinger equation.[41] The first peaks had energy around 0.1 to 0.2 eV for all the steels corresponding to interstitial lattice hydrogen. The second and third peaks presented energy slightly higher than the first ones (0.2 to 0.3 eV) related to reversible trapping. Finally, the fourth peaks were the ones with the highest energy (> 0.40 eV) possibly acting as irreversible trapping sites.

3 Results and Discussion

3.1 Hydrogen Diffusion Kinetics

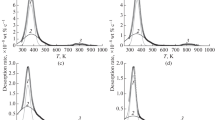
The EP and TDS results revealed differences in the hydrogen diffusion kinetics of the studied steels. Figure 2, for example, illustrates these differences for the QTM3 and QTM8 steels, revealing slower hydrogen diffusion kinetics and greater solubility for the more highly alloyed QTM8 steel.

Fig. 2
figure 2

Normalized charging (a.i) and desorption (a.ii) permeation transients with cathodic polarization of 100 mA/cm2 at 20 °C; (b) TDS spectra with the heating rate of 230 °C/min

Full size image

Table III provides a summary of the diffusion and trapping parameters obtained from EP and TDS experiments for all the studied steels, as previously explained in Section II–B–2.

Table III Summary of Diffusion and Trapping Parameters for the Studied Steels
Full size table

The Dapp max, DL, and NT were calculated from the analysis of charging and desorption transients at 20 °C, whereas D0app and ∆Ea were calculated from the transients at four temperatures, except for the QTM1 steel in which permeations were performed only at 20 °C and these parameters were not obtained. Finally, ∆EL and ∆ETir are the trapping energies estimated from the first and fourth Gaussian peaks of TDS spectra, corresponding to lattice (CL) and irreversible trapped (CTir) hydrogen, respectively.

Figure 3(a) summarizes the obtained Dapp values as a function of the apparent sub-surface concentration (C0app) for the ten studied martensitic steels. As all the tests were performed without palladium coating, oxide layers formed at the exit surfaces acting as barriers to hydrogen diffusion due to their significantly lower hydrogen diffusion coefficient compared to the steels. The hydrogen profiles throughout the membrane are then expected to be almost homogeneous, with the apparent sub-surface concentrations similar to the average hydrogen concentrations inside the samples.[42] Therefore, Figure 3(a) shows important differences between the diffusion kinetics and solubility of the steels. In general, solubility increases with the decrease of Dapp, indicating that the differences observed in diffusion kinetics between the steels are related to some extent to the hydrogen-trapping phenomenon in their microstructural features. For the QTM 1, 2, and 3 steels, there is a clear dependence of Dapp on the severity of the cathodic polarization and consequently on the sub-surface concentration C0app. For the other steels, it is difficult to observe evolutions of Dapp with C0app (Figure 3(a)). The Dapp values are similar across the range of cathodic current densities tested (from 5 to 100 mA/cm2). According to diffusion models,[5,6] the differences of the Dapp values can be related to a variation of the lattice hydrogen diffusion coefficient (DL) and/or to the trapping phenomenon. It is possible to see from the chart of the Figure 3(b) that Dapp max (average of the highest values, i.e., plateau values) is related to the density of trapping sites, decreasing when NT increases. On the other hand, the differences of Dapp do not seem to be linked to the lattice diffusion. The dispersion of DL values, ranging between 1 and 2 × 10–9 m2/s for most steels, could not be related to the Dapp values. This is coherent with similar ΔEL values, which are in the range of the experimental error of the TDS technique (≈ 0.1 eV). Additionally, from the Table III, it is possible to see that most of the steels have detrapping energy around 0.5 eV. All these information together indicate that the key differences between the hydrogen kinetics of the steels are mostly related to the density of trapping sites. Permeation data also provided similar partition of hydrogen concentration for all the steels as can be seen in Figure 3(c). Lattice hydrogen concentration (CL) stayed below 0.09 wppm for all the steels (Figure 3(c.i)). CTr increases with C0app up to values below 0.25 wppm, except for two samples of the QTM8 steel in which the highest value was 0.5 wppm (Figure 3(c.ii)). For all the studied steels, the hydrogen concentration that did not leave the membranes during the desorption step (CTir) corresponds to around 86 pct of the hydrogen concentration (C0app), as shown in Figure 3(c.iii), with the trend just below the CTir = C0app line.

Fig. 3
figure 3

Evolutions of (a) hydrogen apparent diffusion coefficient with apparent sub-surface concentration (C0app ≈ average concentration);(b) maximum (or plateau) apparent diffusion coefficient (Dapp max) with number density of trapping sites (NT); (c.i) lattice (c.ii) reversible trapped, and (c.iii) irreversible trapped hydrogen concentrations with C0app for the ten studied steels (QTM1 to 10)

Full size image

Finally, regarding the Arrhenius relationships, it was not possible to relate the differences of the Dapp values with the activation energies of diffusion (∆Ea), agreeing with the idea that these differences are not primarily associated with the interstitial diffusion. Instead, they seemed to be related to the pre-exponential factor (D0app), which can be explained by changes in the mean free path of hydrogen diffusion due to the presence of trapping sites.

Yield strength is often one of the most important parameters of steel products for the energy sector, determining the product grade. The yield strength of martensitic steels is mostly controlled by their tempering temperature and composition (contents of carbon and alloying elements). Figure 4(a) displays the studied steels (numbered from 1 to 10 corresponding to QTM1 to QTM10 of Tables I, II, and III) according to their yield strength (σYS) and tempering temperature. The QTM 4, 9, and 10 steels (red circles in Figure 4) have the same composition (0.3C0.9Cr1.2Mo) and their yield strengths are strongly affected by the choice of the tempering temperature, varying in a linear way as observed in previous works.[43,44,45] The yield strengths of the other steels are more similar, although they are tempered over a wider range of temperatures. In this case, yield strength is strongly related to the steel compositions, as suggested by the black arrow indicating an increase of the carbon-equivalent values toward high tempering temperatures. Interestingly, a decrease in Dapp with σYS could be observed as shown in Figure 4(b). This indicates that the structural features that harden the studied steels retarding the tempering softening also act to some extent as trapping sites. This result agrees with previous data from permeation tests of other low-alloy tempered martensitic steels hydrogen charged in acid solution containing 1 bar partial pressure of H2S gas,[46] as can be seen in Figure 4(b). Although σYS and Dapp are linked, the graph of Figure 4(b) shows that it is still possible to design high-strength low-alloy martensitic steels with similar σYS and different Dapp (e.g., QTM 7 and 8) or with similar Dapp and distinct σYS (e.g., QTM8 and QTM10), as highlighted by the dashed blue arrows. Therefore, the choices of composition and tempering temperature in the steel design for applications in hydrogenating environments could aim not only at achieving a YS value for a specific steel grade, but also a desired hydrogen diffusion kinetics.

Fig. 4
figure 4

Plots of (a) yield strength (σYS) according to tempering temperature showing the direction of increase of carbon equivalent and (b) maximum (or plateau) apparent diffusion coefficient (Dapp max) according to σYS for the QTM studied steels and previous data in 1 bar H2S environment from Thébault et al. [46] The QTM 4, 9, and 10 steels, which have same composition, are represented by red circles. Blue dashed arrows illustrate a certain flexibility in the design (Color figure online)

Full size image

3.2 Hydrogen Trapping at Martensitic Structure

As the previous comparison of the diffusion and trapping parameters suggests that the hydrogen diffusion kinetics of the steels is mainly related to the number density of trapping sites (NT), this section analyzes the nature of such sites. This investigation firstly considers irreversible trapping sites at dislocation cores. Figure 5(a) shows the ratio of NT to the theoretical density of lattice sites of Fe-α (5 × 1029 m−3)[47] plotted as a function of the total density of dislocations (sum of ρSSD and ρGND from Table II). Additionally, an estimation of the density of deep trapping sites in dislocation cores is shown in this figure as a black dotted line named “Model”. Dislocation cores are well-known deep trapping sites with binding energies up to 0.5 eV for edge and 0.3 eV for screw dislocation cores calculated by atomistic simulations for the Fe-α.[28] These values being similar to the binding energies found in the present work (differences between ∆ETir and ∆EL in Table III). The density of trapping sites is very dependent on the dislocation core structure and was estimated in this work through Eq. [7] considering that the dislocation core has a simplified cylinder structure of radius r0 equal to the Bürgers vector (b = 0.25 nm) multiplied by a coefficient α.[48] It is difficult to know which value of α leads to a good prediction of the density of trapped hydrogen atoms at the dislocation core. Taketomi et al. have extensively investigated the trapping energies around the {112} <111> edge dislocations in Fe-α using molecular statics and dynamic simulation.[49] In one of the works of the same research group, the estimated average number of hydrogen atoms trapped at 1 nm of edge and screw dislocations was about 23 and 18 at 0 K.[50] These numbers of trapped hydrogen atoms give α around 0.5. Al-Nahlawi found a core structure with α equal to 0.7 given hydrogen concentrations close to what was obtained by small-angle neutron scattering measurements.[51] Due to the difficulty of obtaining α, it is considered here as 0.6 around the two values of the previously mentioned works.

$$ N_{\rho } = \pi r_{0}^{2} N_{{\text{L}}} \rho \;{\text{where}}\; r_{0} = \alpha b $$
(7)
Fig. 5
figure 5

(a) Evolution of the number density of trapped sites normalized by the NL of Fe-α (5 × 1029 m−3) with the total measured dislocation density (GND + SSD) and (b) difference of measured NT and NT at dislocation cores (Nρ of Eq. [7]) as a function of the maximum concentration at the permeation membrane for the ten studied QTM steels

Full size image

It can be seen from Figure 5(a) that four steels (QTM 4, 8, 9, and 10) have considerably higher trapping sites than predicted by the trapping at the dislocation cores, given their measured dislocation density (ρTOTAL). Figure 5(b) shows the differences between the measured densities of trapping sites and the ones predicted by Eq. [7] as a function of the maximum sub-surface concentration (≈ average concentration) of the permeation membrane shown in Figure 3(a). According to this graph, the differences in NT are associated with the solubilities of the steels, being larger for the four steels that possess hydrogen concentration higher than 1.5 wppm.

The second considered trapped hydrogen site are the vacancies, which possess binding energies around 0.4–0.6 eV according to ion implantation/channeling technique[52] and DFT calculations[17,28] in iron (Fe-α). A vacancy can trap up to six hydrogen atoms in Fe-α,[53] with the decrease of the trapping energy as the number of hydrogen atoms in the cluster increases.[28] It has been shown by DFT calculations that the most stable cluster in Fe-α is the one with two atoms of hydrogen per vacancy with trapping energy similar to the 1H-vacancy complex (around 0.6 eV).[28,53,54] Considering that all vacancies trap two hydrogen atoms, we can obtain the minimum vacancies concentration necessary (CV) to increase the NT by the ΔNT = NT-NTdislocation of Figure 5(b). The values of vacancies measured by DSC without hydrogen and the ones calculated are shown in Figure 6. For the QTM 4, 8, 9, and 10 steels, which possess hydrogen solubility higher than 1.5 wppm, considerable superabundant vacancies (SAV) production would be necessary to be able to justify the amount of trapping sites and hydrogen solubility.

Fig. 6
figure 6

Vacancies concentration from DSC measurements and calculated considering the ΔNT of Fig. 5(b) for all the ten QTM steels

Full size image

From Figures 3 and 5, it can be noticed that among all the steels, the QTM8 presents the most remarkable density of trapping sites (NT) and hydrogen solubility. An additional analysis described below was then performed for this steel, also considering trapping at vanadium carbides.

3.2.1 Further analysis for the QTM8 steel

Both the electrochemical permeation and the thermal desorption spectroscopy provided considerably higher solubility of trapped hydrogen for the QTM8 steel. EP indicates that it comprises mostly irreversible trapped hydrogen, i.e., the trapped concentration that did not leave the membranes during the permeation desorption steps (Figure 3(c)). On the other hand, TDS provides greater reversible trapped concentration. The TDS spectra for all steels were adjusted using the sum of four Gaussian distributions, except for the QTM8 in which the first peak was divided into a small CL Gaussian peak and the rest is considered as very weakly trapped as can be seen in the example of Figure 7(a.i). This division was performed due to the high concentration of the first peak for this steel (≈ 0.5 wppm), which is incompatible with the theoretical values of concentration in interstitial sites. Figure 7(a.ii) shows the average total concentration as well as the average concentration in each of the peaks for the QTM8 along with the similar yield strength (around 920 MPa) QTM7 steel for comparison. The values were obtained considering the average of the area of the Gaussian peaks for the spectra obtained at the seven employed heating rates. According to this analysis, the extra hydrogen solubility of the QTM8 is mostly related to the weakly trapped hydrogen of the second TDS peak (CTr-2).

Fig. 7
figure 7

(a.i) Example of Gaussian distributions used to fit a TDS spectrum at 180 °C/min for the QTM8 steel and (a.ii) total experimental TDS and each of the Gaussian peaks’ average hydrogen concentrations for the QTM7 and 8 steels

Full size image

The differences between the hydrogen distribution from EP and TDS are probably linked to the fact that during the TDS measurements the temperature increases in a certain rate modifying the equilibrium between trapped and diffusible hydrogen. Evidence of this heating rate influence is seen as a more pronounced difference between EP and TDS results for lower heating rates. For example, for the test at 75 °C/min for the QTM8 steel, irreversible trapped hydrogen (CTir) corresponded to only 6 pct of the total spectrum, whereas for the 230 K/min spectrum, it corresponded to 20 pct. Additionally, the overlapping of Gaussian peaks in TDS spectra analyses probably has also contributed to the observed differences, complicating the estimation of hydrogen concentration in each state (lattice, reversibly and irreversibly trapped).[55]

The last remaining question of this work is which structural feature could have provided extra strong and weak trapping sites for the QTM8 steel. Synchrotron XRD and TEM diffraction analyses revealed a volume fraction of 0.8 pct of VC-FCC carbides with lattice parameter around 0.42 nm for the QTM8 steel as shown in Figure 8. Two populations were identified: one is with few-nanometers size and another is with sizes between 10 and 20 nm as can be seen in the TEM images of Figure 8(b). As previously summarized in Table II, the only other steel with V carbides was the QTM7. However, for this steel, the around 0.4 pct volume fraction of VC carbides identified consisted only of a larger population above 20 nm in size. Cementite and Mo2C were also detected in the QTM8 synchrotron XRD spectrum of Figure 8(a). Cementite has not considerable trapping ability.[13] Mo2C carbides can contribute more significantly to hydrogen trapping. However, the volume fraction of Mo2C carbides in the QTM8 steel was below the quantification limit of 0.1 pct and they could not be observed in the TEM diffraction patterns. Therefore, only vanadium carbides are considered in the following detailed analysis.

Fig. 8
figure 8

Vanadium carbides in the QTM8 steel identified using (a) Rietveld analysis of XRD peaks and (b) bright field TEM image with red circle where a dark field image was taken showing a population of few-nm size precipitates and bright and dark field images of 10–20 nm size precipitate. Both dark field images were taken of the diffraction spot indicated with the red arrow in the diffraction pattern consistent with the [001] zone axis of the BCC matrix and FCC VC carbides (Color figure online)

Full size image

VC precipitates presents the NaCl-type crystal structure typically found in precipitates with strong trapping ability, such as TiC and NbC.[18] Several works agree that hydrogen trapping at VC carbides occurs mostly at their interfaces.[19,22,56,57] The detrapping energies of these carbides obtained by TDS are around 34 kJ/mol (0.35 eV) according to Asahi et al.[29] On the other hand, Takahashi et al.[22] obtained slightly smaller values (25 kJ/mol or 0.26 eV) for precipitates with an atomic ratio of C/V higher than 0.9 and significantly higher (60 kJ/mol or 0.612 eV) for atomic ratios C/V next to 0.75. In fact, according to their chemical composition, vanadium carbides are often written as V4C3 with considerable amount of carbon vacancies.[58] By observing deuterium atoms through atom probe tomography (APT) on the (001) interface between the precipitate and the matrix combined with the rare observation of misfit dislocations by high-resolution TEM, Takahashi et al.[22] concluded that strong trapping occurs at the surface carbon vacancies of V4C3 precipitates. This result is supported by atomistic calculations, which found detrapping energies of 116 kJ/mol (1.2 eV)[19] and 63 kJ/mol (0.645 eV)[57] for the surface carbon vacancies. Additionally, Restrepo et al. also calculated the detrapping energy of perfect VC-Fe interfaces as 19 kJ/mol (0.2 eV), which is a bit smaller than the obtained by Asahi et al.[29] and the lower trapping energy from Takahashi et al.[22]

The combination of all these works presents evidence that strong trapping at vanadium carbides occurs at carbon vacancies (especially surface ones). In view of these results, we estimated through Eq. [8] the number density of trapping sites associated with surface carbon vacancies (NVS). In this equation, NoVS is the number of surface carbon vacancies per precipitate, Nop is the number, rp is the radius, and fv is the volume fraction of the precipitates, aVC and aFe are the lattice parameters of the carbides and the matrix, ρFe is the density of the steel, MFe is the molar mass of iron, NA is the Avogadro number, and α is the fraction of surface vacancies among all the sites occupied by C atoms. This equation considers the precipitates as spheres and only vacancies at the first atomic layer at the surface.

$$ N_{{{\text{VS}}}} = {\text{No}}_{{{\text{VS}}}} \frac{{{\text{No}}_{{\text{p}}} }}{{{\text{No}}\;{\text{Fe}}\;{\text{atoms}}}}\frac{{{\text{No}}\;{\text{Fe}}\;{\text{atoms}}}}{{m^{3} }} = 3\alpha f_{v} \frac{{a_{{{\text{Fe}}}}^{3} }}{{a_{{{\text{VC}}}}^{2} }}\frac{1}{{r_{{\text{p}}} }}\frac{{\rho_{{{\text{Fe}}}} }}{{M_{{{\text{Fe}}}} }}{\text{N}}_{{\text{A}}} $$
(8)

Similarly, Eq. [9] estimates the density of trapping sites provided by bulk carbon vacancies within the precipitates (NVB), where β is the fraction of bulk vacancies among all the sites occupied by C atoms.

$$ N_{{{\text{VB}}}} = {\text{No}}_{{{\text{VB}}}} \frac{{{\text{No}}_{p} }}{{{\text{No}}\;{\text{Fe}}\;{\text{atoms}}}}\frac{{{\text{No}}\;{\text{Fe}}\;{\text{atoms}}}}{{m^{3} }} = 2\beta f_{v} \frac{{a_{{{\text{Fe}}}}^{3} }}{{a_{{{\text{VC}}}}^{3} }}\frac{{\rho_{{{\text{Fe}}}} }}{{M_{{{\text{Fe}}}} }}N_{{\text{A}}} $$
(9)

We considered the volume fraction of VC obtained by synchrotron of 0.8 pct, an average diameter of 10 nm (between the two sizes observed by TEM), and the measured lattice parameters by TEM of 0.418 and 0.292 nm for the VC and the matrix, respectively.

Figure 9(a) shows the experimental and estimated NT values obtained by strong trapping at dislocations using Eq. [7], at the initial matrix vacancy concentrations (CV-Fe), at the surface (CV-S) and bulk (CV-B) carbon vacancies of the vanadium carbides. Besides the surface vacancies considering one atomic layer (CV-S1), the calculations were also performed with 2 (CV-S2) and 3 atomic layers (CV-S3), which represent surfaces with thickness equal to 0.5aVC and aVC, respectively. For the surface vacancies, the results are plotted considering the fraction of vacancies (α) of 0.25 and 0.5. For the bulk one, we used β of 0.25 representing the composition of V4C3 carbide.

Fig. 9
figure 9

Values for the QTM8 steel of (a) experimental and calculated NT at dislocation cores, matrix vacancies, surface, and bulk carbon vacancies of V carbides and (b) excess of hydrogen concentration outside V carbides of 5 and 10 nm in diameter as a function of the distance r from the precipitate–matrix interface, with a schematic illustration of the VC and Fe-α interface

Full size image

In addition to strong trapping at C vacancies, elastic strain fields around dislocations and (semi) coherent precipitates can weakly trap hydrogen. The ratios of the reversible trapped hydrogen concentration to the lattice concentration associated with the local strain fields can be estimated by the Eqs. [10] and [11] for edge dislocations and precipitates, respectively. For a certain edge dislocation density (ρ), the calculation considerers the excess of hydrogen due to the lattice distortions,[59,60] where ν is the Poisson’s ratio (0.3), \(\overline{{V }_{H}}\) is the partial molar volume of hydrogen (2 × 10–6 m3/mol), b is the Burgers vector (0.25 nm), μ is the shear modulus (79 GPa), kB is the Boltzmann constant, and T is the temperature (293 K).

$$ \frac{{C_{{\text{Tr,dislo}}} }}{{C_{{\text{L}}} }} = \frac{{\pi \beta^{2} }}{{2k_{{\text{B}}}^{2} T^{2} }}\rho \ln \left( {\frac{1}{b\sqrt \rho }} \right)\;{\text{with}}\; \beta = \left( {\frac{\mu b}{{3\pi }}} \right) \left( {\frac{1 + v}{{1 - v}}} \right)\overline{{V_{{\text{H}}} }} $$
(10)

Considering the total dislocation density values (sum of SSD and GND) of the Table II, the calculated ratio CTr,dislo/CL is smaller than 0.1 for all the steels. Therefore, dislocation strain fields have a negligible impact on the reversible trapped concentration. The major impact of dislocations is in the irreversible trapping as previously estimated by Eq. [7].

For the (semi-) coherent precipitates, the calculation considers the mismatch (δ) between the precipitate and the matrix,[38,60,61,62] where σm and εm are the hydrostatic stress and strain, E is the Young’s modulus (210 GPa), ∆r = r – rp is the radius, and ∆V is the volume of the elastic distortion. Finally, Vp is the precipitate volume considered as a sphere.

$$ \frac{{C_{{\text{Tr,prec}}} }}{{C_{{\text{L}}} }} = f_{{\text{p}}} \frac{\Delta V}{{V_{{\text{p}}} }}\frac{1}{\Delta r}\mathop \smallint \limits_{{r_{{\text{p}}} }}^{{r_{{\text{p}}} + \Delta r}} \frac{s\left( r \right)}{{s_{0} }}d{\text{r}} \;{\text{with}}\; \frac{s\left( r \right)}{{s_{0} }} = e^{{\left( {{\raise0.7ex\hbox{${\sigma_{{\text{m}}} \overline{{V_{{\text{H}}} }} }$} \!\mathord{\left/ {\vphantom {{\sigma_{{\text{m}}} \overline{{V_{{\text{H}}} }} } {Tk_{{\text{B}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${Tk_{{\text{B}}} }$}}} \right)}} ,\;\sigma_{{\text{m}}} = \left( {\frac{E}{1 - 2v}} \right)\varepsilon_{{\text{m}}} \;{\text{and}}\;\varepsilon_{{\text{m}}} = \frac{2}{3} \delta \left( {\frac{{r_{{\text{p}}} }}{r}} \right)^{3} $$
(11)

To use Eq. [11] for the VC carbides of the QTM8 steel, we first obtained the mismatch value based on the strain tensor generated by the accommodation of the VC-FCC crystal with the BCC matrix. Figure 9(b) illustrates the interface of the VC and Fe-α. The optimal coincidence of this interface with the highest strain accommodation happens when three unit cells of Fe-α are linked to two unit cells of the VC with the following orientation relationship (100)α||(100)VC and [010]α||[011]VC.[19] We then calculated the mismatch by using Eq. [12] based on the strain tensor generated by this interface, obtaining the value of 0.0237.

$$ \delta = \frac{{\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} } \right)}}{3} = \frac{1}{3}\left[ {\frac{{2\left( {d_{{{\text{Fe}}010}} - d_{{{\text{VC}}011}} } \right)}}{{d_{{{\text{Fe}}010}} }} + \frac{{\left( {3d_{{{\text{Fe}}100}} - 2d_{{{\text{VC}}100}} } \right)}}{{3d_{{{\text{Fe}}100}} }}} \right] $$
(12)

Figure 9(b) illustrates the excess of hydrogen around a precipitate with rp equal to 2.5 and 5 nm as a function of the distance r from the precipitate–matrix interface. The integral of these curves up to r equal to 10 and 20 nm (∆r = 7.5 and 15 nm) was used in the calculation of the ratio of trapped to lattice hydrogen of Eq. [11]. The results are 76 for the carbide with 10 nm diameter and 18 for the one with 5 nm. The larger the size of the carbides, larger the volume of the elastic distortion and the excess of hydrogen. However, Eq. [12] is valid only for coherent and semi-coherent precipitates, and larger precipitates are likely to lose their coherence.

The results of Figure 9 indicate that the high experimental value of NT for the QTM8 steel can be only achieved with irreversible trapping at V carbides when considering the hydrogen trapping at the bulk carbon vacancies, which is energetically unfavorable.[19] On the other hand, trapping at the elastic strain field of VC carbides could explain the considerably higher CTr concentration observed in the TDS analysis for this steel (CTr/CL ≈ 50).

Although improvement in hydrogen embrittlement due to trapping at carbides has been reported in the past few years,[63,64,65,66] our recent fracture testing results with the QTM 6, 7, and 8 steels have not shown any clear improvement in the HE resistance of the QTM8 due to its slower hydrogen diffusion kinetics and enhanced trapping.[2] The discrepancy in these results is probably linked to the experimental conditions. In our work,[2] we chose to evaluate cracking nucleated at surfaces under continuous hydrogen permeation flux while applying uniaxial tensile loading, approaching the sulfide stress cracking (SSC) morphology of sour service applications. In contrast to the improvements in HE resistance due to trapping at carbides observed previously with SSRT specimens fully (pre-)immersed in hydrogen charging solutions[63,64,66] and under cyclic loading.[65] Another possible origin of the differences in these results is that carbides can also improve HE resistance through microstructural refinement in addition to trapping.[67] In our previous HE comparison,[2] this potential carbide refining effect had little influence on the results, since the three QTM steels evaluated presented similar very fine prior austenite grain size (5 μm or less).

4 Conclusions

We have combined the hydrogen diffusion and trapping data of ten high-temperature tempered martensitic steels. The differences between the steels are summarized in terms of their apparent diffusion coefficient and concentration. Thereafter, these differences were explained mainly by the number density of trap sites and the pre-exponential factor related to the mean free path of diffusion. The distinct Dapp values do not seem to be significantly related to the lattice diffusion or to the trap binding energies. The results were discussed in terms of the deeply trapping at dislocation cores and matrix vacancies. Without considering the creation of superabundant vacancies, the density of trapping sites for all the steels with solubility up to 1.5 wppm could be explained only by trapping at dislocation and vacancies. For the steel, which has the highest solubility and density of trapping sites, trapping at carbon vacancies of vanadium carbides was also investigated. For the reversible trapped concentration, estimates of the effect of the elastic strain fields around edge dislocations and few-nanometers size VC carbides were performed, showing a minor impact of dislocations but considerable contributions of the VC carbides to the reversible trapped concentration. Finally, a relationship between the apparent diffusion coefficient and yield strength was established. Besides the strength, the tempering temperature and composition also affect the hydrogen diffusion kinetics. A combination of alloying elements and tempering temperatures can result in steels with similar yield strengths, but with distinct diffusion kinetics.