1 Introduction

Austenitic steel and Ni-based superalloy are promising materials for many high-temperature applications, thanks to their unique mechanical properties. Ni-based superalloys have excellent mechanical properties such as high strength and resistance to corrosion and oxidation at elevated temperatures. These properties make this type of superalloy to be the first candidate in aero engines and power plants. The distinguishing features of Ni-based superalloy are inherited from its particular microstructure that consists of \(\gamma ^{\prime}\) phase (precipitate) embedded coherently in \(\gamma \) phase (solid solution matrix). Austenitic steel also has good mechanical properties at lower costs than superalloys, making it a favorable choice in aeroengine, nuclear, and petrochemical industries. In the aerospace industry, Ni-based alloys and stainless steels are the key materials of turbine blades as they can endure a wide range of stresses and temperatures.

As both austenitic steel and Ni-based superalloy are exposed to high temperatures and long-term intermittent mechanical loads in many of the mentioned applications, understanding and being able to model their isothermal fatigue and TMF behavior are mandatory for future innovations.

Many experimental studies have been performed on the austenitic steel 316L under low-cycle and high-cycle fatigue tests to study fatigue properties,[1] fatigue life and type of crack nucleation,[2] temperature effects,[3] change in chemical composition,[4] environmental conditions,[5,6] microstructure properties,[7] and the influence of mean stress.[8] The cyclic mechanical properties of 316L austenitic steel have been studied at medium temperature (650 °C) by experimental tests and the development of a numerical model based on a constitutive law that considers the evolution of cyclic stress amplitudes.[9] In this work, the authors have investigated the influence of strain amplitude, strain rate, and loading sequences on the hardening/softening behavior and showed that the hardening/softening behavior depends on the strain rate under displacement-controlled condition loading. Based on their proposed constitutive law that incorporates a hardening factor into Chaboche kinematic hardening equation to consider plastic strain memory surface and the maximum plastic strain rate, they could reproduce the cyclic stress amplitude and hysteresis loops. The cyclic behavior of two types of 316L steel with different strain amplitudes has also been studied by developing a constitutive model taking into account hardening and softening behavior and the strain range memory effect.[10] The authors of this work applied the Armstrong and Frederick hardening model, revealing the hardening and softening effect in the back stress and relating it to the accumulated plastic strain. Then by calibrating the material parameters using the identification process, they could obtain comparable numerical results with experimental data. The ratcheting failure of 316L steel under the low-cycle fatigue tests has been studied numerically and experimentally.[11] In their work, the authors developed a numerical model based on Chaboche kinematic hardening equation and calibrated its parameters based on hysteresis and post-stabilized monotonic stress plastic–strain curves from experimental tests. They identified the Chaboche parameters by adopting two optimization approaches using particle swarm optimization and Genetic algorithms. Results could predict the ratcheting behavior of the material based on the identified parameters, in good agreement with experimental data. Ratcheting and mean stress relaxation in 316L have been investigated under cyclic loading with different stress ratios and considering nonlinear kinematic and isotropic hardening models.[12] Based on the hardening models in the numerical model, the authors of that work could predict the cyclic behavior, accumulation of plastic strain, and fatigue life with good precision. A modified Chaboche-type hardening model has been proposed to study strain-controlled vs stress-controlled isothermal and thermomechanical low-cycle fatigue tests of 316L steel.[13] The authors defined an internal variable in the modified kinematic hardening relation based on the experimental test observations, which led to good numerical results compared to strain-controlled ratcheting experiments. The cyclic plastic behavior of 316L steel induced by the hysteresis loop has also been evaluated by developing a damage evolution model based on the flow stress.[11] The proposed damage model could mimic the life cycle curve behavior obtained from experimental tests well.

Microstructural features of 316L have a significant effect on the fatigue behavior of this material. Low-cycle and high-cycle fatigue tests have been performed on 316L steel samples produced by laser powder bed fusion technique, and a correlation between microstructure and cyclic mechanical behavior has been obtained.[14] 316L revealed a good performance under low-cycle fatigue tests, but surface defects on the sample have shown to be detrimental to the fatigue limit in the high-cycle fatigue regime. Microstructure observations of samples under low-cycle fatigue tests have revealed that local plastic deformations influence material behavior by slip steps but lack-of-fusion defects limit the high-cycle fatigue resistance.

Extensive studies have also been performed on Ni-based superalloys to investigate the effect of microstructure,[15] fatigue and fracture parameters,[16] and strain amplitude[17] under low-cycle, high-cycle, and TMF tests. As the microstructural properties play an important role in micromechanical modeling, many investigations have focused on the extraction of suited microstructural features for the generation of realistic RVEs. Optimal numerical domains for statistically equivalent RVEs have been developed for intergranular microstructures of Ni-based superalloys.[18] These authors generated RVEs based on microstructure morphologies and convergence of material properties and obtained good agreement between the morphological properties and response variable based on the two developed RVEs and from the literature. In another study, a unit-cell mesh has been used to represent the microstructure of \(\gamma \) and \(\gamma ^{\prime}\) in CMSX-4.[19] The numerical results have highlighted the significant effect of lattice mismatch between \(\gamma \) and \(\gamma ^{\prime}\) leading to a tension–compression asymmetry in the material behavior. Micromechanical analysis of Ni-based superalloys based on microstructure properties has been performed to study their behavior near to the yield limit that is compared with experimental results under uniaxial tensile loading.[20] These authors have generated a micromechanical model with high spatial resolution using the Voronoi tessellation technique based on a periodic field which could represent the intergranular strain evolution during elastic–plastic deformation.

The creep fatigue and low-cycle fatigue behavior of two types of Ni-based superalloy have been studied experimentally, and the results have been compared.[21] The authors of that work found out that the fatigue life of CMSX-8 and CMSX-4 superalloys, both, depends on the crystal orientation, cycle type, and range of temperature. Furthermore, the creep fatigue behavior of Ni-based superalloy (GH4169) under strain-controlled conditions at 650 °C has been investigated experimentally,[22] and it was found that cyclic softening and mean stress relaxation are affected mainly by the evolution of back stress and effective stress.

The effects of different variables such as strain rates, strain ratio, temperature range, and strain/temperature phase angle have been studied on Ni-based superalloy by performing low-cycle and TMF tests.[23] The authors of that work proposed micromechanical models that take the microstructure of Ni-based superalloy into account to predict the fatigue life of this material. Dislocation evolution of Ni-based superalloys under low-cycle fatigue deformation has been studied, and cyclic behavior with different strain amplitudes has been obtained.[24] The authors evaluated the sample's microstructure during fatigue deformation and concluded that a reduction of the volume fraction of \(\gamma ^{\prime}\) precipitates leads to a degradation of strength and to uneven slip patterns. An isotropic elastic–plastic model based on the Ohno–Wang relation has been developed to simulate the isothermal low-cycle fatigue behavior of Ni-based superalloy.[25] The authors obtained the material response in terms of hysteresis loops with different strain amplitudes and load ratios within a wide temperature range. Results of the maximum and minimum stress, the plastic strain range, and hysteresis loops from numerical models have been validated with experimental tests. The cyclic behavior of Ni-based superalloy has also been studied by developing a physics-based model for the isotropic and kinematic hardening behavior and considering the microstructure evolution during the cyclic hardening.[26] This model could reproduce the material behavior with different aging conditions and strain amplitudes.

The cyclic mechanical behavior of a Ni-based superalloy under multiaxial loading conditions has been investigated considering orthotropic material properties and a Hill plasticity model.[27] The proposed constitutive model could capture the cyclic elastic–plastic behavior under complex loading conditions. In another study, a visco-plastic constitutive model with the Chaboche hardening relation has been used to obtain the mechanical behavior of a Ni-based superalloy under cyclic anisothermal loads.[28] The authors found the relation of the constitutive model parameters with the cyclic behavior through a sensitivity study and showed that the mean stress evolution parameter primarily influences the results.

Based on the extensive studies performed on the austenitic steel 316L and Ni-based superalloys, it is seen that the kinematic hardening behavior used in numerical modeling plays a crucial role in predicting the behavior of both materials under cyclic loading at different temperatures. In the current work we introduce a constitutive law for austenitic steel (316L) which considers thermal effects in the flow rule together with nonlinear kinematic hardening law. Furthermore, a consistent parameter set is derived that is valid to describe cyclic plasticity at various temperatures. In a second step, the isothermal fatigue behavior of two materials commonly used for high-temperature applications, 316L austenitic steel and CMSX-4 superalloy, is investigated numerically, and their cyclic behavior is compared based on the developed constitutive model for each material with a special focus on their kinematic hardening behavior. In Section B, the numerical models used for these two materials, including their microstructure properties and constitutive relations, are introduced. In Section C, the isothermal fatigue behavior of 316L and CMSX-4 are compared with corresponding experimental data and, finally, in Section D, the cyclic behavior of these two materials is investigated within a wide temperature range and with two different strain amplitudes, and their deformation behavior in terms of cyclic plasticity and strain hardening are compared.

2 Numerical Modeling

This section describes the microstructure properties and finite element models of both 316L and CMSX-4.

2.1 Microstructural Features

For the micromechanical analysis of these two materials under isothermal cyclic loading, their microstructures are analyzed for the generation of RVEs to be implemented in the finite element models for further analyses.

2.1.1 Austenitic steel

The microstructural features of the austenitic steel 316L have been extracted from electron backscatter diffraction (EBSD) map of the specimens after isothermal fatigue tests. Specimens have been produced using laser powder bed fusion technique and prepared to be tested under low-cycle fatigue tests at different temperatures. The detail of the sample preparation and experimental tests procedure will be provided in a forthcoming paper.

An EBSD map of one of the 316L sample is represented in Figure 1(a) indicating the existence of rather equiaxed grains along the given axis of view. It is noted here that this material from additive manufacturing exhibits elongated grains with an aspect ratio between 1:2 and 1:3 along the axes orthogonal to this view. However, in Reference 29, it has been shown that the influence of the aspect ratio of the grains on the resulting mechanical behavior of the material as quite small compared to the influence of the crystallographic texture. Hence, in the present study, we approximate the grain geometry as being equiaxed and take into account the realistic crystallographic texture of the material as obtained from EBSD analyses. Consequently, an RVE with a regular pattern of cubic grains is created for 316L on the basis of the crystallographic orientation of its grains, by systematically down sampling the orientation distribution function (ODF) obtained from the EBSD map to the given number of grains in the RVE, as described in Reference 30; see Figure 1(b) for a graphical representation of the RVE. Figures 1(c) and (d) represent the pole figures of the reduced ODF used in the micromechanical simulations and the ODF based on the original EBSD map. As the difference is negligible, it is seen that the reduced ODF represents the crystallographic orientations of the grains in the polycrystals with a high quality and can be applied to obtain the material response under cyclic loading. The number of grains has been set to 216, according to the sensitivity analysis of isothermal fatigue behavior on the number of grains, shown in Figure 2(a). In Figure 2(b), the cyclic behavior of the generated RVE along different loading directions is seen highlighting the quasi-isotropic behavior of the model material along different loading directions. As the effect of grain shape on the macroscopic cyclic response of 316L is minor, the generated RVEs are just based on the reduced and optimized number of crystallographic orientations from the real material. Hence, the effects of grain size and shape have been neglected in this study, following Reference 31, and RVEs have been created based on the reduced number of crystallographic orientations from the real material.

Fig. 1
figure 1

Microstructure representation of 316L material from additive manufacturing, (a) EBSD map in inverse pole figure color code, (b) generated RVE with 216 grains, pole figure of (c) reduced ODF, and (d) ODF based on the EBSD map (Color figure online)

Full size image
Fig. 2
figure 2

Generated RVE evaluation by (a) sensitivity analysis on number of grains, (b) loading along different directions

Full size image

2.1.2 Single crystal Ni-based superalloy

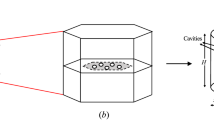
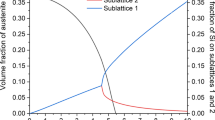
Scanning electron microscopy (SEM) images of single crystal Ni-based superalloy reveal that it consists of narrow matrix channels (\(\gamma \)-phase) surrounding coherent precipitates (\(\gamma ^{\prime}\)-phase). Therefore, an RVE has been developed in Reference 32 to capture this microstructure for constitutive modeling. This RVE includes one central cube of \(\gamma ^{\prime}\) precipitate enclosed with six half-channels of \(\gamma \) matrix to resemble the three-dimensional representation of a single crystal Ni-based superalloy microstructure.[32] In the present work, we adopt this RVE for CMSX-4, see Figure 3, and apply it in the finite element model for further analyses. In the current study, the volume fraction changes in the precipitate and matrix channels at different temperatures are taken into account according to the model presented in Reference 32. The relation between the \(\gamma ^{\prime}\) and \(\gamma \) volume fractions is described by

$${f}_{x}+{f}_{y}+{f}_{z}+{f}_{p}=1,$$
(1)

where \({f}_{p}\) is the precipitate volume fraction and \({f}_{x}\), \({f}_{y}\) , and \({f}_{z}\) are volume fractions of the matrix along x, y, and z directions, respectively.

Fig. 3
figure 3

RVE for CMSX-4 consisting of the precipitate and six matrix channels.[32]

Full size image

2.2 Constitutive Modeling and Material Parameters Calibration

The finite element models of both 316L and CMSX-4, together with their constitutive laws and material parameters calibration, are described in the following.

2.2.1 Austenitic steel

To investigate the isothermal fatigue behavior of the austenitic steel 316L, the polycrystalline RVE including the realistic description of the material’s crystallographic texture will be used in a finite element model. To make a scale-bridging approach between microstructure and macroscopic response, a homogenization technique is used by applying periodic boundary conditions.[33] Figure 4 represents the finite element model of 316L to which periodic boundary conditions are applied on four reference points at the model corners. The other boundary nodes follow the kinematics of these reference nodes during the deformation. Mimicking experimental isothermal fatigue tests, the simulations are performed under displacement-controlled conditions, where the load is applied on one reference node along y direction with R = –1 with two different strain amplitudes, 0.3 and 0.5 pct. As demonstrated above, the mechanical behavior of the material is quasi-isotropic such that in the following only one loading direction is evaluated. A sensitivity analysis has been done on the number of elements per grain as visualized in Figure 5. The cyclic response for different numbers of elements per grain is almost overlapping except at the maximum and minimum stresses, where the differences, however, still can be neglected. Hence, to reduce the computational cost, the RVE discretized with 216 elements and one element per grain is used in the numerical analyses which the type of element is 8-node brick element (C3D8).

Fig. 4
figure 4

Finite element model (a) including mesh discretization, (b) schematic view of four reference nodes to apply the periodic boundary condition

Full size image
Fig. 5
figure 5

Sensitivity analysis of generated RVE for austenitic steel with number of elements

Full size image

The material model in the numerical analysis is described by a local crystal plasticity model, which is implemented as a user-defined material (UMAT) subroutine in ABAQUS 2016.[34]

Kinematic relations follow a large strain theory, which is based on the assumption of the multiplicative decomposition of the deformation gradient (F) into elastic and plastic components, as

$$\mathrm{F}={\mathrm{F}}^{e}{\mathrm{F}}^{p},$$
(2)

where \({F}^{e}\) and \({F}^{p}\) correspond to elastic and plastic parts of the deformation gradient, respectively. The rate of the deformation gradient is described based on the plastic deformation gradient and its velocity gradient tensor (\({L}^{p}\)) as.

$$\dot{\mathrm{F}}={\mathrm{L}}^{p}{\mathrm{F}}^{p}.$$
(3)

Within this crystal plasticity model, it is assumed that plastic deformation occurs only due to dislocation slip on crystallographic slip planes. Since the crystal structure of the austenitic steel 316L is face-centered cubic (FCC), \({N}_{s}=12\) slip systems contribute to its plastic deformation. Hence, the velocity gradient tensor is described by

$${\mathrm{L}}^{p}=\sum_{\alpha =1}^{{N}_{s}}{\dot{\gamma }}^{\alpha }\left({d}^{\alpha }\otimes {n}^{\alpha }\right),$$
(4)

where \({\dot{\gamma }}^{\alpha }\) is the slip rate on slip system \(\alpha \). The normal vectors \({d}^{\alpha }\) and \({n}^{\alpha }\) indicate the slip direction and the normal direction to the slip plane, respectively, and their dyadic product (\(\otimes \)) defines the Schmid tensor for slip system \(\alpha \). According to the large deformation theory, the second Piola–Kirchhoff stress tensor, \(\widetilde{\mathrm{S}}\) in the intermediate configuration is related to the elastic strain, \({E}^{e}\) by the fourth-rank stiffness tensor, \({\mathbb{C}}\) as

$$\widetilde{S}=\frac{1}{2}{\mathbb{C}}:{E}^{e}=\frac{1}{2}{\mathbb{C}}\left({{\mathrm{F}}^{e}}^{T}{\mathrm{F}}^{e}-I\right).$$
(5)

Therefore, the Cauchy stress \(\sigma \) in the current configuration is obtained based on the second Piola–Kirchhoff stress and the elastic part of the deformation gradient:

$$\sigma =\frac{1}{det\left({\mathrm{F}}^{e}\right)}{\mathrm{F}}^{e}\widetilde{\mathrm{S}}{{\mathrm{F}}^{e}}^{T},$$
(6)

and assuming only small elastic strains for the metallic materials considered here, the resolved shear stress for each slip system is approximated as

$${\tau }^{\alpha }\approx \widetilde{\mathrm{S}}:\left({d}^{\alpha }\otimes {n}^{\alpha }\right).$$
(7)

Thus, the flow rule governing plastic deformation by dislocation slip is written as

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_{0}\cdot {\text{exp}}\left(-\frac{Q}{RT}\right)\cdot {\left|\frac{{\tau }^{\alpha }-{\chi }_{b}^{\alpha }}{{\tau }_{c,0}^{\alpha }}\right|}^{{p}_{1}}\mathrm{sign}\left({\tau }^{\alpha }-{\chi }_{b}^{\alpha }\right),$$
(8)

where the Arrhenius term with activation energy \(Q\), gas constant \(R\) , and temperature \(T\) considers thermal effects. The pre-factor \({\dot{\gamma }}_{0}\) refers to the reference shear rate. The term \({\tau }^{\alpha }\) is the resolved shear stress on slip system \(\alpha \) and the stress exponent \({p}_{1}\) is the inverse value of the strain rate sensitivity. \({\tau }_{c,0}^{\alpha }\) and \({\chi }_{b}^{\alpha }\) correspond to the critical resolved shear stress and the resolved back stress of each slip system, respectively.

To capture the kinematic hardening behavior during cyclic plasticity and the resulting Bauschinger effect, the nonlinear kinematic hardening model proposed by Ohno–Wang is used to describe the evolution of the back stress.[35] The empirical relation of Ohno–Wang model for kinematic hardening is an extension of Chaboche kinematic hardening[36] and is formulated as

$$ \dot{\chi }_{b}^{\alpha } = A\dot{\gamma }^{\alpha } - B\left( {\frac{{\left| {\chi _{b}^{\alpha } } \right|}}{{A/B}}} \right)^{M} \chi _{b}^{\alpha } \left| {\dot{\gamma }^{\alpha } } \right| ,$$
(9)

where \(A\) and \(B\) are fitting parameters, and the ratio \(A/B\) is considered as saturation level of the back stress such that once the back stress reaches this level, the dynamic recovery term controlled by exponent \(M\) becomes active.

Isothermal fatigue tests of 316L reveal that the stress amplitude with respect to the number of cycles remains stable and does not reflect any isotropic hardening or softening behavior during the test cycles. Hence, in the current study, isotropic hardening is neglected in the flow rule, and exclusively kinematic hardening is considered during cyclic plasticity deformation.

The elastic constants given in Table I have been calculated based on the Young’s modulus measured during experimental tests at different temperatures and the relation between the Young’s modulus and anisotropic elastic constants provided in Reference 37. The constitutive parameters for thermal activation of plastic slip have been determined by Reference 38, see Table II.

Table I Temperature-Dependent Elastic Constants of 316L
Full size table
Table II Constitutive Parameters for Thermal Activation of Plastic Slip of 316L
Full size table

The remaining constitutive parameters are two parameters of the flow rule: \({\tau }_{c,0}^{\alpha }\) and \({p}_{1}\), and three parameters of the kinematic hardening relation: \(A\), \(B\) , and \(M\), where \({\tau }_{c,0}^{\alpha }\) and \(A\) are considered to be temperature dependent. The material parameter identification by the inverse procedure is based on the first cycle of the experimental fatigue test at two different temperatures: 21 °C (room temperature, RT) and 750 °C. The material identification process is done using the trust-region-reflective algorithm for the minimization of the loss function that quantifies the difference between experimental and numerical results, where the latter are a function of the variable material parameters that are optimized iteratively.[39] For a detailed description of the identification procedure, the reader is referred to previous publications.[1, 39] The identified material parameters using this optimization process are listed in Table III.

Table III Identified Material Parameters Based on the Inverse Analysis
Full size table

2.2.2 Single crystal Ni-based superalloy

The similar finite element model visualized in Figure 4 based on the RVE for single crystalline Ni-based superalloy CMSX-4 is used to obtain the overall cyclic response of the material in terms of the stress–strain curve. For CMSX-4, the numerical model has been discretized with 8 elements and consists of 27 nodes totally. To accomplish this, cyclic load under displacement-controlled conditions with the strain amplitude ratio \(R=-1\) is applied to the finite element model. A phenomenological constitutive law based on different mechanisms activated at different temperatures has been developed for CMSX-4 before.[40] In this model, the elastic behavior for two phases of the matrix and precipitate is described by temperature-dependent anisotropic elastic constants neglecting the effect of lattice mismatch in the elastic regime due to small elastic strains. The flow rule during plastic deformation is governed by dislocations in various slip systems of matrix, precipitate, and their interface (cube slip). Different mechanics which are activated at different temperature ranges are taken into account in the developed phenomenological constitutive model, following other studies that also used those mechanisms in the flow rules for Ni-based superalloys.[41, 42]

Considering the thermal effect during plastic deformation, the flow rule for 〈112〉 {111} slip in the precipitate, for 〈110〉 {111} slip in the matrix, and for 〈110〉 {100} cube slip along the interface is written as

$${\dot{\gamma }}_{\alpha }={\dot{\gamma }}_{0}\cdot {\text{exp}}\left(-\frac{Q}{RT}\right)\cdot {\left|\frac{{\tau }_{\alpha }+{\tau }_{\alpha }^{\text{INT}}}{{\widehat{\tau }}_{\alpha }^{\text{slip}}+{\tau }_{\alpha }^{add}}\right|}^{{p}_{1}}\cdot {\text{sgn}}\left({\tau }_{\alpha }+{\tau }_{\alpha }^{\text{INT}}\right),$$
(10)

where the activation energy \(Q\) differs for precipitate, matrix, and cube slip.[40] \({\tau }_{\alpha }^{\text{INT}}\) is the internal stress between matrix and the coherent precipitates due to their lattice mismatch and \({\widehat{\tau }}_{\alpha }^{\text{slip}}\) describes the slip resistance. \({\tau }_{\alpha }^{add}\) considers additional stresses due to different mechanisms in the precipitate and matrix slip systems. The remaining parameters have already been introduced in Eq. [8].

In Eq. [10], the resolved shear stress, the internal stress due to lattice mismatch, and the evolution of the slip resistance are described by

$${\tau }_{\alpha }=\mathbf{S}\cdot \left({d}^{\alpha }\otimes {n}^{\alpha }\right),$$
(11)
$${\tau }_{\alpha }^{\mathrm{INT}}={\mathbf{S}}^{\mathrm{INT}}\cdot \left({d}^{\alpha }\otimes {n}^{\alpha }\right),$$
(12)
$${\dot{\widehat{\tau }}}_{\alpha }^{\text{slip}}={\sum }_{\beta =1}^{{N}_{\text{slip}}}{h}_{0}{\chi }_{\alpha \beta }{\left(1-\frac{{\widehat{\tau }}_{\beta }^{\text{slip}}}{{\widehat{\tau }}^{\text{sat}}}\right)}^{{p}_{2}}\left|{\dot{\gamma }}_{\beta }\right|,$$
(13)

where \(\mathbf{S}\) is the applied stress, \({\mathbf{S}}^{\mathrm{INT}}={\mathbb{C}}\mathbb{^{\prime}}\mathbb{^{\prime}}:\overline{\varepsilon }\) in which \({\mathbb{C}}\mathbb{^{\prime}}\mathbb{^{\prime}}\) is the effective stiffness matrix that relates the internal stress to total strain \(\overline{\varepsilon }\) that is sum of misfit strain and plastic strain. The full derivation of internal stress and calculation of effective stiffness matrix are described in References 1 and 43. In Eq. [12], \({h}_{0}\) and \({\chi }_{\alpha \beta }\) are the reference hardening parameter and the cross-hardening matrix, respectively. \({\widehat{\tau }}^{\text{sat}}\) is the saturated slip resistance and \({p}_{2}\) is a fitting parameter.

For the precipitate, \({\tau }_{\alpha }^{add}\) consists of two terms: \({\widehat{\tau }}_{\alpha }^{m}+{\widehat{\tau }}_{\alpha }^{kw}\), where the former is a softening stress due to the relaxation of matrix stress in the filled channels, which reduces the hardening of the precipitate. The constitutive model for the latter considers Kear–Wilsdorf (KW)-locks at medium temperatures (700 °C – 850 °C). These shear stresses are obtained as

$${\widehat{\tau }}_{\alpha }^{m}=-{a}_{1}{\left({\gamma }_{\alpha }^{\text{form}}\right)}^{{p}_{3}}\cdot {\text{exp}}(-{a}_{2}\left|{\gamma }_{\text{tot}}^{m110}\right|,$$
(14)
$${\widehat{\tau }}_{\alpha }^{kw}={a}_{3}{\left|{\gamma }_{\alpha }^{p112}\right|}^{{p}_{4}}\cdot {\text{exp}}\left(-{a}_{4}\left|{\gamma }_{\alpha }^{p112}\right|\right),$$
(15)

where \({a}_{1}\) is the reference parameter, \({p}_{3}\) and \({a}_{2}\) are fitting parameters. \({\gamma }_{\alpha }^{\text{form}}\) and \({\gamma }_{\text{tot}}^{m110}\) refer to shear strains caused by channel dislocations on 〈112〉{111} slip systems and the total shear strain in the matrix, respectively. \({a}_{3}\) is the KW hardening parameter and \({p}_{4}\) and \({a}_{4}\) are fitting parameters. \({\gamma }_{\alpha }^{p112}\) refers to the shear strain in the precipitate for a certain slip system.

For the matrix, \({\tau }_{\alpha }^{add}\) also consists of two terms: \({\tau }^{\text{oro}}+{\widehat{\tau }}^{\mathrm{soft}}\). The Orowan stress \({\tau }^{\text{oro}}\) is described by \(\sqrt{2/3}\mu b/w\), where \(\mu \), \(b\) , and \(w\) are shear modulus, the magnitude of Burgers vector, and the width of the matrix channel, respectively. The softening stress \({\widehat{\tau }}^{\mathrm{soft}}\) is described by

$${\widehat{\tau }}^{\mathrm{soft}}=-{s}_{1}\cdot \mathrm{tanh}\left({s}_{2}\cdot {\varepsilon }^{\upgamma -\mathrm{channels}}\right),$$
(16)

where \({s}_{1}\) and \({s}_{2}\) are the softening stress and the softening rate parameter. \({\varepsilon }^{\upgamma -\mathrm{channels}}\) collects shear strains of all matrix channels for all slip systems. For the cube slip system, \({\tau }_{\alpha }^{add}\) is equal to zero.

The material parameters defined in the constitutive law are taken from Reference 32, and all material parameters for CMSX-4 are listed in Table IV.

Table IV The Material Parameters for CMSX-4 Defined in the Flow Rule.[32]
Full size table

3 Validation of Constitutive Models with Experimental Data

3.1 Austenitic Steel

The comparison of the numerical model results under cyclic load with the strain amplitude ratio \(R=-1\) with the parameterized constitutive model and experimental test data is represented in Figure 6. These results refer to the temperatures RT, 550 °C, and 750 °C and strain amplitudes of 0.3 and 0.5 pct. The results indicate a good agreement between model and experimental data. In particular, it is seen that the Bauschinger effect in the austenitic steel under cyclic load is rather significant and captured quite well by the Ohno–Wang kinematic hardening model. As numerical results at different temperatures reveal, the Arrhenius term defined in the flow rule, together with the material dependent parameters \(A\) and \({\tau }_{c,0}^{\alpha }\), describes the temperature-dependent materiel response in a quantitative way.

Fig. 6
figure 6

Comparison of numerical and experimental results for cyclic behavior of 316L at (a) RT, (b) 550 °C, and (c) 750 °C

Full size image

As seen in Figure 6, at RT, the material exhibits a significant strain hardening rate, which decreases with raising temperatures until the material response is close to an ideal plastic behavior at the highest temperature. Furthermore, the results also indicate that increasing the temperature significantly reduces the material's initial yield strength. It is seen that the temperature-dependent constitutive model introduced in this work captures this complex thermal behavior of the material with a high reliability.

3.2 Single Crystal Ni-Based Superalloy

The hysteresis loop of stress–strain curves of the superalloy CMSX-4 along two different loading directions, [111] and [100], obtained from the numerical model at different temperatures, is compared with the relevant experimental data[44] in Figure 7. Only the data for the cyclic response at 850 °C have been used to identify the material parameters using inverse analysis. Then, the cyclic responses at 750 °C and 950 °C have been predicted based on those identified material parameters for validation purposes and it is seen that the quality of the prediction compared to experimental results is very accurate for the [100] direction and acceptable for the [111] direction as no further calibration has been done on the identified material parameters. As visualized in Figure 7(a), the behavior of the material at 700 °C along both loading directions is linear, and the plastic deformation is negligible. At higher temperatures, 850 °C and 950 °C in Figures 7(b) and (c), the material experiences more plastic deformation, particularly for the [111] loading direction. Even for [100] load cases where the applied strain amplitude is higher, the cyclic behavior of the material is less dominated by plastic deformation compared to the [111] loading direction. At higher temperatures, 850 °C and 950 °C, the maximum and minimum stresses for both loading directions, [111] and [100], are the same, but the amount of plastic deformation is different depending on the loading direction, which is due to the severe elastic anisotropy of the material and the activation of special slip systems in the 〈110〉 and 〈112〉 directions.

Fig. 7
figure 7

Comparison of numerical and experimental[38] results for cyclic behavior of CMSX-4 at (a) 700 °C (prediction), (b) 850 °C (reference for parameter calibration), and (c) 950 °C (prediction)

Full size image

4 Application to Isothermal Fatigue

Using numerical models developed for 316L and CMSX-4, the cyclic behavior of these two materials at different temperatures is compared for two strain amplitudes of 0.3 and 0.5 pct. Figure 8 visualizes the behavior of both 316L and CMSX-4 under cyclic load at 550 °C, 750 °C, and 850 °C. To simulate the cyclic behavior numerically, adopting a proper kinematic hardening model in the constitutive law plays an important role. The kinematic hardening for 316L was modeled based on the Ohno–Wang relation, which updates the back stress during plastic deformation, while for CMSX-4, the kinematic hardening is captured by the calculation of internal stresses due to the lattice mismatch between \(\gamma \) and \(\gamma ^{\prime}\) phase.

Fig. 8
figure 8

Comparison of isothermal fatigue behavior of 316L with CMSX-4 at strain amplitudes of 0.3 pct (left column, subfigures (a), (c), (e)) and 0.5 pct (right column, subfigures (b), (d), (f)) at different temperatures (top row) 550 °C, (middle row) 750 °C and (bottom row) 850 °C

Full size image

Figure 8 compares the hysteresis loops for 316L and CMSX-4 for two different strain amplitudes at various temperatures. It is seen that for 550 °C, 316L already undergoes a rather large plastic deformation, while CMSX-4 exhibits an almost linear response along both loading directions due to its microstructure properties leading to a higher strength at these temperatures. However, for the smaller strain amplitude, the stress amplitudes of 316L and CMSX-4 are still comparable. At higher temperatures, both alloys experience increasingly more plastic deformation, which is particularly pronounced for 316L and CMSX-4 loaded along the [111] direction. In particular, the response of 316L varies from a rather significant strain hardening at low temperatures to an increasingly ideal plasticity at elevated temperatures, thus reducing the stress amplitude significantly. In contrast, the [100] loading direction of CMSX-4, which is elastically the most compliant of all test cases, reveals very little plastic relaxation at all temperatures and, hence, maintains a rather constant stress amplitude.

As can be seen from this analysis, the internal stresses on the microstructural level play an important role for the kinematic hardening behavior. The model for CMSX-4 that includes these internal stresses in a scale-bridging approach consequently does not require an additional term for kinematic hardening. The model for 316L, in contrast, employs a purely empirical kinematic hardening model which is agnostic of internal stresses. In future work, the role of deformation gradients and the resulting geometrically necessary dislocation (GND) densities in kinematic hardening will be investigated.

5 Conclusions

The mechanical behavior of the austenitic steel 316L and the single crystal Ni-based superalloy CMSX-4 has been studied in terms of cyclic plasticity at different temperatures. An RVE has been developed based on the microstructure of the 316L and we used the RVE generated in a former study for CMSX-4.[32] These two RVEs have been used in finite element simulations to obtain the macroscopic material response to cyclic loads in form of hysteresis loops that can be directly compared with experiment. A phenomenological constitutive model based on the activation of different deformation and creep mechanisms at different temperatures has been used for CMSX-4 and the behavior of 316L during plastic deformation has been described by a temperature-dependent crystal plasticity model, including terms for nonlinear kinematic hardening. Material parameters of the 316L have been calibrated using an inverse analysis based on experimental data for isothermal fatigue at various temperatures. The results have been validated by comparison to independent experimental data. The constitutive parameters for CMSX-4 have been obtained from a former study.[32]

The results highlight that the cyclic plasticity of these two materials can only be captured if proper microstructure-specific kinematic hardening models are considered in the constitutive law. In the case of 316L, the empirical Ohno–Wang kinematic hardening model could reproduce the hardening behavior during cyclic loading and even reflect the Bauschinger effect in the results correctly. In contrast to that, as already reported before,[32] a physical model for the kinematic hardening arising through internal stresses due to the mismatch between the precipitate and matrix in the superalloy CMSX-4 is found to capture the kinematic hardening behavior under cyclic load with high precision such that there is no need to consider additional terms in the flow rule.

Comparing the fatigue behavior of these two materials in a quantitative way has revealed that CMSX-4 has a higher mechanical strength compared to 316L at all investigated temperatures. As temperature increases from 550 °C to 850 °C, CMSX-4 behavior changes from a linear-elastic regime to a nonlinear cyclic regime. This behavior is more pronounced for loading along the crystallographic [111] axis, which exhibits a higher elastic stiffness and undergoes more plastic strains than the [100] load case. In contrast, for 316L, cyclic plasticity at 550 °C is characterized by a significant strain hardening that gradually vanishes with increasing temperatures, such that at 850 °C, almost ideal plastic behavior with a negligible hardening rate is observed.