Three-dimensional constraint-based void-growth model for high temperature hydrogen attack

Abstract

High temperature hydrogen attack (HTHA) is degradation of steels exposed to hydrogen gas at high temperatures and pressures. Hydrogen in steels reacts with carbon from carbides to produce methane gas bubbles typically on grain boundaries which grow and coalesce, leading to loss of strength and fracture toughness. Current design practice against HTHA is based on the Nelson curves which define the conditions for safe operation in a temperature/hydrogen-partial-pressure diagram. Nelson curves are phenomenological in nature and do not account for the underlying failure mechanism(s), material microstructure, carbide stability, and applied stresses. In light of experimental evidence of predominant cavitation ahead of cracks reported by Martin et al. (Acta Mater 140:300–304, 2017), it is expected that void growth is accelerated by the triaxial stresses associated with microstructural flaws. To this end, we propose a three-dimensional, axisymmetric, constraint-based void-growth model extending the “one-dimensional” model of Dadfarnia et al. (Int J Fract 219:1–17, 2019). The present model is shown to yield satisfactory agreement with the available experimental data from hydrogen attack of 2¼Cr–1Mo steel at temperatures ranging from 500 to 600 °C. In addition, the model is used to construct Nelson type curves in the temperature/hydrogen-partial-pressure diagram. These curves represent failure times for given applied stresses and triaxiality. The proposed methodology can be viewed as providing a step toward improving the current design practice against HTHA while maintaining the simplicity of the original Nelson curve approach.

Appendices

Appendix A: Constitutive model for the of 2¼Cr–1Mo steel

Dadfarnia et al. (2019) studied the creep response data of 2¼Cr–1Mo steel from Klueh (1980) and Viswanathan (1974) and observed that the creep exponent, $n$, and the activation energy, $Q_{v}$, vary significantly with temperature. Accordingly, the experimental data of Viswanathan (1974) can be fit at different temperatures¹ by the power-law equation

$$ \dot{\varepsilon } = \underbrace {{\dot{\varepsilon }_{0} \exp \left( {\frac{{ - Q_{v} }}{R\Theta }} \right)}}_{{ = \dot{\varepsilon }(\Theta )}}\left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{n} , $$

(A1)

in which the reference stress $\sigma_{0}$ is taken equal to 1 MPa the reference strain rate $\dot{\varepsilon }_{0}$ equal to $5.69 \times 10^{ - 4} /{\text{s}}$, and R is the universal gas constant equal to 8.31 J/mol.K. The creep exponent $n$ and the activation energy $Q_{v}$ are estimated from the experimental data as shown in Fig. 

Fig. 21

Experimental data for creep of 2¼Cr–1Mo steel at four different temperatures by Viswanathan (1974) shown as log of normalized strain rate vs log of normalized stress along with the corresponding power law function fit (dashed lines)

21 The values of the fitted parameters are listed in Table

Table 2 Fitted creep parameters of the experimental data for 2¼Cr–1Mo steel by Viswanathan (1974) for various temperatures

2, and linear interpolation, as shown in Fig. 

Fig. 22

Linear interpolation of the Table 2 data for a creep exponent and b creep activation energy for 2¼Cr–1M steel as function of temperature

22, yields

$$ \begin{gathered} n(\Theta ) = - 0.0585\Theta + 56.397 \hfill \\ Q_{v} (\Theta ) = - 2.2137\Theta + 2205.8 \hfill \\ \end{gathered} $$

(A2)

where the temperature $\Theta$ is measured in Kelvin and the activation energy $Q_{v}$ in kJ/mole. In the computations, the creep response of the material, in both cavitated and uncavitated regions, at any given temperature in between range 500–600 °C, is described by the power law creep equation (6) in which $n\left( \Theta \right)$ and $\dot{\varepsilon }\left( \Theta \right) = \dot{\varepsilon }_{0} \exp \left( { - Q_{v} \left( \Theta \right)/R\Theta } \right)$ are calculated through Eqs. (A2).

Appendix B: Void growth model of Van Der Giessen et al. (1995)

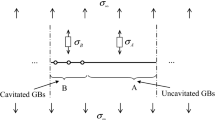
The deformation of the imbedded $C$ cylinder given in Fig. 4b is studied in this section. The mean and effective macroscopic stress associated with this state of stress in cylinder $C$ are

$$ \begin{gathered} \sigma_{m}^{C} = \frac{{(S_{app}^{B} + 2T)}}{3} + p \hfill \\ \sigma_{e}^{C} = |S_{app}^{B} - T|. \hfill \\ \end{gathered} $$

(B1)

Void growth model of Van Der Giessen et al. (which is based on the previous studies by Sham and Needleman 1983 and Needleman and Rice 1980), provides the volumetric growth rate as the summation of void growth due to creep and grain boundary diffusion:

$$ \dot{V} = max[(\dot{V}_{cr}^{L} + \dot{V}^{L}_{diff} ),(\dot{V}_{cr}^{H} + \dot{V}^{H}_{diff} )] $$

(B2)

Here, ^L and ^H denote low and high triaxiality ratios, respectively.

Void growth rate due to creep is given by

$$ \begin{gathered} \dot{V}^{L}_{cr} = \frac{3}{2}V\dot{\varepsilon }_{m}^{C} sign(\sigma_{m}^{C} ) \times \left\{ {\begin{array}{*{20}c} {\left(\alpha_{n} + \beta_{n} \left| {\frac{{\sigma_{e}^{C} }}{{\sigma_{m}^{C} }}} \right|\right)^{n} ,\left| {\frac{{\sigma_{m}^{C} }}{{\sigma_{e}^{C} }}} \right| \ge 1} \\ {(\alpha_{n} + \beta_{n} )^{n} \left| {\frac{{\sigma_{e}^{C} }}{{\sigma_{m}^{C} }}} \right|^{n - 1} ,\left| {\frac{{\sigma_{m}^{C} }}{{\sigma_{e}^{C} }}} \right| < 1} \\ \end{array} } \right. \hfill \\ \dot{V}^{H}_{cr} = \frac{3}{2}V\dot{\varepsilon }_{m}^{C} sign(\sigma_{m}^{C} )\left( {\frac{1}{{1 - (0.87 \times a/b)^{3/n} }}} \right)^{n} \times \left\{ {\begin{array}{*{20}c} {(\alpha_{n} + \frac{m}{n}\left| {\frac{{\sigma_{e}^{C} }}{{\sigma_{m}^{C} }}} \right|)^{n} ,\left| {\frac{{\sigma_{m}^{C} }}{{\sigma_{e}^{C} }}} \right| \ge 1} \\ {(\alpha_{n} + \frac{m}{n})^{n} \left| {\frac{{\sigma_{e}^{C} }}{{\sigma_{m}^{C} }}} \right|^{n - 1} ,\left| {\frac{{\sigma_{m}^{C} }}{{\sigma_{e}^{C} }}} \right| < 1} \\ \end{array} } \right., \hfill \\ \end{gathered} $$

(B3)

where $\dot{\varepsilon }_{m}^{C} = \dot{\varepsilon }(\Theta )\left| {\frac{{\sigma_{m}^{C} }}{{\sigma_{0} }}} \right|^{n} ,\alpha_{n} = \frac{3}{2n},\beta_{n} = \frac{(n - 1)(n + 0.4319)}{{n^{2} }},m = \frac{{sign(S_{app}^{B} - T)}}{{sign(\sigma_{m}^{C} )}}$.

For the contribution of diffusion

$$ \begin{gathered} \dot{V}^{L}_{diff} = \dot{V}_{diff} (f),f = \max [(a/b)^{2} ,(a/(a + 1.5L_{NR} ))^{2} ] \hfill \\ \dot{V}^{H}_{diff} = \dot{V}_{diff} (f),f = (a/b)^{2} \hfill \\ \end{gathered} $$

(B4)

Here,

$$ \dot{V}_{diff} = 4\pi D(\Theta ) \times \frac{{S_{app}^{B} + p - \sigma_{s} }}{{\ln \frac{1}{f} - (3 - f)(1 - f)/2}}, $$

(B5)

where $p$ is the pressure due to gas in cavity, $\sigma_{s} = \left( {1 - f} \right)2\gamma_{s} \sin \psi /a$ is the sintering stress, $\gamma_{s}$ is the surface free energy, $D\left( \Theta \right) = D_{B} \delta_{B} \Omega /k\Theta$ is the grain boundary diffusion parameter, $D_{B} \delta_{B}$ is the boundary diffusion coefficient, $\Omega$ is the atomic volume, $k$ is the Boltzmann’s constant and $L_{NR} = \left( {D(\Theta )\sigma_{e}^{C} /\dot{\varepsilon }_{e}^{C} } \right)^{1/3}$ is the diffusion length parameter introduced by Needleman and Rice (1980), $\sigma_{e}^{C}$ is the effective stress in the imbedded cylinder C given by (B1), and $\dot{\varepsilon }_{e}^{C}$ is the effective strain rate in the imbedded cylinder C given by

$$ \dot{\varepsilon }_{e}^{C} = \dot{\varepsilon }(\Theta )(\sigma_{e}^{C} /\sigma_{0} )^{n} . $$

(B6)

Appendix C: Cavity pressure

Grabke and Martin (1973) proposed the kinetics of methane formation on iron surface as

$$ \frac{{dN_{{CH_{4} }} }}{dt} = A\left( {K_{1} C_{C} f_{{H_{2} }}^{3/2} - K_{2} f_{{CH_{4} }} /f_{{H_{2} }}^{1/2} } \right), $$

(C1)

where $N_{{CH_{4} }}$ is the number of methane molecules, $A$ is the reaction area, $C_{C}$ is the concentration of carbon atoms at the reaction surface area, $f_{{H_{2} }}$ and $f_{{CH_{4} }}$ are the fugacities of hydrogen and methane gas, respectively, $K_{1}$ and $K_{2}$ are the reaction rate constants for formation and dissociation reactions of methane, respectively, which are given by

$$ \begin{gathered} K_{1} = 1.64 \times 10^{ - 3} \exp \left( {\frac{ - 56,900}{{R\Theta }}} \right) \, \frac{{\text{m}}}{{{\text{s MPa}}^{{3/2}} }} \hfill \\ K_{2} = 4.08 \times 10^{7} \exp \left( {\frac{ - 213,400}{{R\Theta }}} \right) \, \frac{{{\text{mol}}}}{{{\text{m}}^{2} {\text{s MPa}}^{{1/2}} }}, \hfill \\ \end{gathered} $$

(C2)

where $R = 8.314$ J/mol K is the universal gas constant and $\Theta$ is the temperature in Kelvins. Dadfarnia et al. (2019) showed that under typical HTHA conditions, the kinetics of methane formation, based on the Grabke and Martin (1973) model, are such that carbon and hydrogen gas can very well be assumed to be in chemical equilibrium. Thus, Eq. (C1) provides

$$ f_{{CH_{4} }} = \frac{{K_{1} }}{{K_{2} }}f_{{H_{2} }}^{2} C_{C} . $$

(C3)

The fugacity of hydrogen gas is assumed to be the same as the hydrogen partial pressure. The concentration of carbon, in mol/m³, is calculated by

$$ C_{C} = 6577.85 \,a_{C} \,C_{gr} , $$

(C4)

where, $a_{C}$ is the activity of carbon in steel and $C_{gr} = 66.79\exp \left( { - 68,700/R\Theta } \right)$ is the solubility of graphite in ferrite in percent weight. Based on the carbon concentration and hydrogen fugacity, equilibrium methane fugacity at a given temperature can be calculated using Eq. (C3). Odette and Vagarali (1982) proposed the relationship between methane fugacity, $f_{{CH_{4} }}$, and methane partial pressure, $p_{{CH_{4} }}$, as

$$ f_{{CH_{4} }} = p_{{CH_{4} }} \exp \left( {C(\Theta )p_{{CH_{4} }} } \right), $$

(C5)

where $C(\Theta )$ is given by

$$ C(\Theta ) = \left\{ \begin{gathered} \begin{array}{*{20}c} {0.005{\text{ MPa}}^{ - 1} } & {,f_{{CH_{4} }} < 10^{3} {\text{ MPa}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{1.1875}{\Theta } + 3.0888 \times 10^{ - 3} {\text{ MPa}}^{ - 1} } & {,10^{3} {\text{ MPa}} < f_{{CH_{4} }} < 10^{4} {\text{ MPa}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\frac{2.375}{\Theta } + 1.1716 \times 10^{ - 3} {\text{ MPa}}^{ - 1} } & {,f_{{CH_{4} }} > 10^{4} {\text{ MPa}}{.}} \\ \end{array} \hfill \\ \end{gathered} \right. $$

(C6)

Finally, the total pressure is assumed to be the sum of partial pressures of hydrogen gas and methane gas,

$$ p = p_{{H_{2} }} + p_{{CH_{4} }} . $$

(C7)

It should be noted that Eq. (C7) is a simplified assumption which has been conventionally adopted by researchers for modeling the void-growth during HTHA (Van der Burg et al. 1996; Dadfarnia et al. 2019).