Abstract
Genotype by environment interaction (G×E) refers to the comparative performances of genotypes differing among environments, representing differences in genotype rankings or differences in the level of expression of genetic differences among environments. G×E can reduce heritability and overall genetic gain, unless breeding programmes are structured to address different categories of environments. Understanding the impact of G×E, the role of environments in generating G×E and the problems and opportunities is vital to efficient breeding programme design and deployment of genetic material. We review the current main analytical methods for identifying G×E: factor analytic models, biplot analysis and reaction norm. We also review biological and statistical evidence of G×E for growth, form and wood properties in forest species of global economic importance, including some pines, eucalypts, Douglas-fir, spruces and some poplars. Among these species, high levels of G×E tend to be reported for growth traits, with low levels of G×E for form traits and wood properties. Finally, we discuss possible ways of exploiting G×E to maximise genetic gain in forest tree breeding. Characterising the role of environments in generating interactions is seen as the basic platform, allowing efficient testing of candidate genotypes. We discuss the importance of level-of-expression interaction, relative to rank-change interaction, as being greater than in many past reports, especially for deployment decisions. We examine the impacts of G×E on tree breeding, some environmental factors that cause G×E and the strategies for dealing with G×E in tree breeding, and the future role of genomics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The phenotype of an individual is controlled by its genotype, the environment and any interactions between genotype and environment (G×E interactions, or G×E). Such interactions are said to exist when the comparative performances of genotypes vary according to the environment. The performance of one genotype that is superior in one environment might be inferior in another environment (de Jong 1990; Falconer and Mackay 1996). In forestry, G×E can lead to unpredictability of some genotypes’ performance across certain sets of environments. Characterising and understanding G×E in order to reduce or even remove such unpredictability has, therefore, been an overarching goal. Where it occurs, G×E complicates the design of breeding programmes but it also provides opportunities for matching the most appropriate planting stocks to targeted deployment conditions to optimise forest health, growth and wood quality in intensively managed forests.
G×E can be categorised into two major types (Lynch and Walsh 1998; White et al. 2007): (1) rank-change interaction, whereby genotypes are ranked in different orders in different environments; and (2) level-of-expression interaction,Footnote 1 whereby the expression of genotypic differences (e.g. the spread of the breeding values) varies across environments, not necessarily with any change in the order of the genotype rankings. Breeders, therefore, need to determine the patterns and magnitude of G×E in order to obtain the best genetic gain for the forest industry (Muir et al. 1992; Raymond and Namkoong 1990). Since breeders are primarily concerned with evaluation and selection among candidate genotypes, rank-change interaction will generally be of greater interest for them. While level-of-expression interaction is generally less important for breeding, it may be of major interest for helping to decide what genetic material is chosen for deployment in particular growing environments and for particular end-products.
In forest tree breeding, G×E can often be substantial and create problems in finding consistently superior genotypes, especially for broad adaptation. Breeders often address G×E either by selecting stable genotypes that are not sensitive to environmental changes, or selecting genotypes for specific environments in order to maximise genetic gain on that site (Raymond and Namkoong 1990). In trees, significant G×E has been reported in almost all commercially important species such as radiata pine (Pinus radiata D. Don; Raymond 2011; Wu and Matheson 2005), loblolly pine (Pinus taeda L.; McKeand et al. 1997; Paul et al. 1997), Scots pine (Pinus sylvestris L.; Gullberg and Vegerfors 1987; Haapanen 1996), slash pine (Pinus elliottii Englem. var. elliottii; Hodge and White 1992; Roth et al. 2007), eucalypts (Eucalyptus spp.; e.g. Costa e Silva et al. 2006; Hardner et al. 2010), Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco; Campbell 1992; Dungey et al. 2012), spruces (Picea spp.; Bentzer et al. 1988) and poplars (Populus spp.; Rae et al. 2008; Yu and Pulkkinen 2003).
Increased awareness of the magnitude and nature of G×E helps tree breeders and foresters to see the opportunities to increase genetic gain in the forests (Cullis et al. 2014; Ivković et al. 2013a, b). With this awareness comes a transition from thinking about G×E mainly in relation to selection and structuring of breeding populations to thinking more about G×E also in relation to deployment. For breeding, the expected benefits of capturing additional genetic gain may not outweigh the complexity and additional costs of a multi-environment breeding programme (Carson 1991). For deployment, however, concern among tree-growing businesses in New Zealand over the realisation of genetic gain on some sites led to a reappraisal of the situation by the Radiata Pine Breeding Company (RPBC) (Butcher, 2015, personal communication). Application of multi-environment factor analytic models has also given a new level of statistical efficiency and evidence that there are additional genetic gains possible by deploying the right genotypes on the right sites (Cullis et al. 2014).
In this review, we examine the available analytical methods for identifying G×E and their properties, the empirical evidence of the importance and pattern of G×E in forest trees for selected commercially important species, information on the environmental variables that drive G×E in forestry and strategies for dealing with G×E in tree breeding programmes. Based on this information, the implications and challenges in exploring G×E to optimise genetic gain in forest tree breeding are discussed. The importance of genomic selection in identifying G×E in forest tree breeding is also discussed. Our focus in reviewing the statistical methodology is on the analysis of data from existing trials for selection and other breeding decisions. The aspect of identifying the environmental drivers of G×E for future choices of screening environments is given only limited attention, being seen as a topic for separate review.
Analytical methodology for the estimation of G×E interactions
A number of analytical methods have been proposed to measure the extent of G×E for traits in tree breeding, including ratio of interaction to genetic variance, stability analysis, type-B genetic correlation biplot analysis, factor analytic models and reaction norm. All these methods can be implemented as special cases of mixed linear models. The ratio of interaction to genetic variance can be estimated using analysis of variance (e.g. Shelbourne 1972). Stability analysis has been used to identify stable or sensitive genotypes across multiple environments (e.g. Eberhart and Russell 1966; Finlay and Wilkinson 1963; Huehn 1990). Type-B genetic correlation (Burdon 1977) and factor analytic models characterise patterns of ranking changes of genotypes across multiple environments (Cullis et al. 2014). Likelihood ratio tests now provide robust tests of interaction in departures from perfect type-B correlations. Biplot analysis combines analysis of variance (ANOVA) and principal component analysis (PCA) and allows visualisation of results (Gauch 1992; Mandel 1971; Yan et al. 2007). Reaction norm describes a range of responses or phenotypes produced by a single genotype across a range of environments (Lynch and Walsh 1998; Pierce 2005; Woltereck 1909). The first three methods have well been covered in books or review articles for G×E in crop and forest tree breeding (Freeman 1973; Kang and Gauch 1996; Zobel et al. 1988). This review will cover biplot analysis, factor analytic models and reaction norm.
Biplot analyses
Biplot analysis is most commonly applied in plant breeding, with the aim of developing crops with high yield and good quality. Cultivars selected from one environment might not maintain their high performance in another environment due to G×E. Identifying cultivars with high performance and wide adaptability in multiple environments is the ultimate aim. A biplot analysis uses singular-value decomposition to break down data into a component matrix and displays both column and row information simultaneously (Gabriel 1971). The additive main effects and multiplicative interaction (AMMI) and the genotype main effects and G×E effects (GGE) are the two main biplot analysis methods to identify G×E patterns in plant and forest tree breeding. AMMI and GGE biplot analyses test the significance of G×E and the relative size of G×E variance to genetic variance and visualise stability of genotypes and environments where genotypes are best performed.
AMMI is a statistical approach that combines ANOVA and PCA (Gauch 1992; Mandel 1971; Mrode 2014). It decomposes the source of variation, first into the additive effects of genotypes and environments using ANOVA, and then into multiplicative effects for G×E using PCA (Zobel et al. 1988). The interaction effects are decomposed into a portion representing real responses to G×E and a portion due to random variation (Crossa et al. 1990). The linear model used for the AMMI analysis is as follows (Gauch 1992):
where y ij is the observed phenotype of genotype i in environment j, μ is the grand mean, α i is the genotype main effects as deviations from μ, β j is the environment main effects as deviation from μ, λ k is the singular value for the interaction principal component (IPC) axis k, ξ ik and η jk are the genotype and environment IPC scores (i.e. the left and right singular vectors) for axis k, and ρ ij is the interaction residual containing all multiplicative terms that are not included in the model; n is the number of axes or principal components retained by the model, and ε ij is the residual associated to the genotype i at environment j, assumed independent with identical distribution. The additive part of the AMMI model (μ, α i and β j ) is estimated from ANOVA and the multiplicative part (λ k , ξ ik and η jk ) from PCA.
The GGE methodology is also based on ANOVA and PCA, using a sites regression model (SREG) with two principal components. The linear model used in GGE analysis is as follows (Yan and Hunt 2001):
where y ij is the average performance of genotype i in environment j, β j is the average performance of all genotypes planted at environment j, λ k is the singular value for the principal component k, ξ ik and η jk are the scores for genotype i and environment j for principal component k, respectively, and ε ij is the residual associated to genotype i and environment j. The GGE methodology removes the environmental main effects through ANOVA and retains the genotypic main effect (G) and interaction effect (G×E) in the environment-centred data (Yan et al. 2000). It allows direct visualisation of the performance and stability of genotypes across multiple environments through PCA. This model is recommended when the environments are the main source of variation in relation to the contributions of the genotypes and the G×E with respect to the total variability (Kandus et al. 2010). In the GGE biplot, the lines that connect the biplot origin and the markers for the environments are environment vectors. The angle between the vectors of two environments is related to the correlation coefficient between them. The cosine of the angle approximates the correlation coefficient (Yan 2002), which is equivalent to the type-B genetic correlation in the study carried out by Ding et al. (2008b). A limitation of the GGE biplot is that it may explain only a small proportion of the total GGE when the genotype main effect is considerably smaller than the interaction effects or when the G×E pattern is complex (Ding et al. 2008b). The GGE biplot approach is not amenable to rigorous hypothesis testing, so it is better as a hypothesis-generator rather than as a decision-maker (Ding et al. 2008b).
Both the AMMI and GGE methods use linear models and treat the main and interaction effects as fixed effects (Crossa 2012). The residual variance has a normal distribution and is homogeneous and independent across environments (Gauch 1992; Kang and Gauch 1996; Piepho 1995). A biplot procedure is used to provide a graphical interpretation of results through plotting PCA scores of interaction effects for each genotype and environment (Crossa 1990; Crossa et al. 1990; Kempton 1984; Yan et al. 2000). The difference between them is that GGE biplot analysis is based on environment-centred PCA, whereas AMMI analysis refers to double-centred PCA (Kroonenberg 1995; Rad et al. 2013). The GGE biplot has many visual interpretations that AMMI does not have when presenting for ‘which-won-where’, particularly when visualising any crossover G×E (Ding et al. 2008b).
The AMMI analysis methodology has been extensively applied in the statistical analysis of multi-environment cultivar trials in crop breeding (Annicchiarico 1997; Crossa et al. 1990, 1999; Table 1; Gauch and Zobel 1989; Gauch and Zobel 1997; Hassanpanah 2010). AMMI has also been used for characterising G×E in forest trees, e.g. in Eucalyptus (Baril et al. 1997a; Karuntimi 2012; Lavoranti et al. 2007), pines (Pinus spp.; Chambel et al. 2008; Falkenhagen 1996; Kim et al. 2008), poplars (Populus spp.; Rae et al. 2008), white spruce (Picea glauca (Moench) Voss; Rweyongeza 2011), birch (Betula spp.; Zhao et al. 2014) and lodgepole pine (Pinus contorta Douglas; Wu and Ying 2001).
The GGE method has been used to investigate G×E in many agronomic trials (Yan et al. 2000, 2007) and also in tree breeding (Correia et al. 2010; Ding et al. 2008b; Sixto et al. 2011). Correia et al. (2010) used GGE biplot analysis to study G×E for total height, diameter, stem form and survival of 30 maritime pine (Pinus pinaster Aiton) populations sourced from Portugal, Spain, France and Australia, in a multiple environment provenance trial in Spain. The GGE biplot analyses were used to analyse the biomass production and stability of poplar clones, which were ranked according to mean performance and stability in southwest Europe (Sixto et al. 2011). Ding et al. (2008b) used GGE biplot to investigate G×E of 216 radiata pine families across five environments in Australia. The biplot analysis allowed different groups of clones to be identified according to their performance and degree of interaction displayed, thus providing useful information for the selection process in radiata pine.
Factor analytic models
Factor analytic (FA) models can provide a reliable, parsimonious and holistic approach for estimation of genetic correlations between all pairs of trials (Cullis et al. 2014; Smith et al. 2015) and provide a natural framework for modelling G×E patterns in complex multi-environment experiments (Meyer 2009). The FA model is the most useful for making decisions of selection for breeding populations and decisions of deployment for production populations.
The use of FA models in multi-environment trials is based on the use of eigenvectors from PCA (Jolliffe 1986; Smith et al. 2001) and extended to accommodate both additive and non-additive effects (Oakey et al. 2006a, b). Cullis et al. (2014) used FA models to accommodate a large number of environments and poor connectivity between environments with a reduced animal model. The FA models aim to identify the statistical common factors that give rise to correlations between variables (Mrode 2014). They represent traits assessed under multiple environments as linear combinations of a few latent variables (Cullis et al. 2014; Smith et al. 2001), referred to as common factors (Hardner et al. 2010; Meyer 2009), thereby reducing the dimensionality of the among-sites variation with respect to G×E. The number of factors is called the order of the model and an FA model of order k is denoted as FAk. Assuming a linear mixed model
where y is the vector of observations for t sites; β is the vector of fixed effects; u is the vector of random additive genetic effects with u ∼ N(0, G ⊗ A), where \( \boldsymbol{G}=\left[\begin{array}{ccc}{\sigma}_{a_1}^2& \cdots & {\sigma}_{a_1{a}_t}\\ {}\vdots & \ddots & \vdots \\ {}{\sigma}_{a_t{a}_1}& \cdots & {\sigma}_{a_t}^2\end{array}\right] \), where \( {\sigma}_{a_i}^2 \)is the additive genetic variance for site i, \( {\sigma}_{a_i{a}_j} \) is the additive genetic covariance between site i and site j, A is the numerical relationship matrix and ⊗ denotes the Kronecker product; and e is the vector of random residual effects with \( \boldsymbol{e}\sim N\left(0,\left[\begin{array}{ccc}{\sigma}_{e_1}^2& \cdots & 0\\ {}\vdots & \ddots & \vdots \\ {}0& \cdots & {\sigma}_{e_t}^2\end{array}\right]\right) \), where \( {\sigma}_{e_i}^2 \) is the residual variance for site i, X and Z the design matrices associated phenotypes with β and u, and t is the number of trials. The FAk model for the additive genetic effects of m genotypes in t trials can be modelled as u = (Λ ⨂ I m )f + δ (Costa e Silva et al. 2006; Cullis et al. 2014), where Λ is the t × k matrix of trial loadings, f is the mk × 1 vector of scores and δ is the mt × 1 vector of genetic regression residuals. Var(u)=(ΛΛ′ + Ψ) ⨂I m with assumptions of var(f) = I mk , var(δ) = ψ ⨂ I m , where ψ is a t × t diagonal matrix with a variance (called a specific variance) for each environment, and the vectors of random effects f and δ are mutually independent as multivariate Gaussian distribution with zero means. The between-environment genetic variance matrix is defined as G e = (ΛΛ ′ + ψ). G e can be estimated with the REML algorithms as \( {\widehat{\boldsymbol{G}}}_{\boldsymbol{e}}=\left(\widehat{\boldsymbol{\varLambda}}{\widehat{\boldsymbol{\varLambda}}}^{\boldsymbol{\prime}}+\widehat{\boldsymbol{\psi}}\right) \) and can be converted to a correlation matrix \( {\widehat{\boldsymbol{C}}}_{\boldsymbol{e}}={\widehat{\boldsymbol{D}}}_{\boldsymbol{e}}{\widehat{\boldsymbol{G}}}_{\boldsymbol{e}}{\widehat{\boldsymbol{D}}}_{\boldsymbol{e}} \), where \( {\widehat{\boldsymbol{D}}}_{\boldsymbol{e}} \) is a diagonal matrix with elements given by the inverse of the square roots of the diagonal elements of \( {\widehat{\boldsymbol{G}}}_{\boldsymbol{e}} \). The FA models outlined above are equivalent to the extended factor analytic models specified by Meyer (2009).
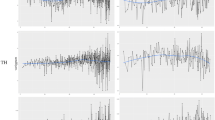
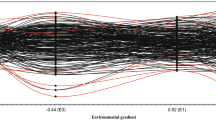
Latent regression plots were used to show genetic responses to trial loadings, indicating the magnitude of G×E (or stability) of selection candidates across multiple environments in the FA models (Chen et al. 2017; Cullis et al. 2014; Smith et al. 2015; Table 1). A latent regression of a selection candidate with a higher slope means that the candidate is more sensitive to the environment. A latent regression with a zero slope indicates that the performance of the candidate is stable across multiple environments.
This approach has been applied to investigate G×E across multiple environments in barley (Smith et al. 2001), potato (Burgueño et al. 2011), maize (Burgueño et al. 2011) and wheat (Burgueño et al. 2011; Oakey et al. 2006a, b), and also in livestock breeding (Meyer 2009). In tree breeding, this approach has been successfully applied to the studies of G×E in Khasi pine (Pinus kesiya Royle ex Gordon; Costa e Silva 2007), radiata pine (Cullis et al. 2014; Ivković et al. 2015), loblolly pine (Zapata-Valenzuela 2012), Eucalyptus and Eucalyptus hybrid clones (Costa e Silva et al. 2006; Hardner et al. 2010) and Norway spruce (Picea abies (L.) H. Karst.; Chen et al. 2017). Despite its statistical power, the FA approach has not yet delivered in identifying the roles of specific environmental factors in driving G×E (B. Cullis, 2016, personal communication).
Reaction norm
Reaction norm, also called a norm of reaction, describes a range of responses or phenotypes produced by a single genotype across a range of environments (Lynch and Walsh 1998; Pierce 2005; Woltereck 1909). It is suitable for analysing data on traits that vary gradually and continuously over an environmental gradient (e.g. temperature) (Kolmodin and Bijma 2004). A linear reaction norm for a single trait has a model (Kolmodin and Bijma 2004; Strandberg et al. 2000):
where y ik is the phenotypic value of genotype i in environment k; b 0 and b 1 are the fixed effects of the intercept and slope of the reaction norm for genotype, respectively; \( {\boldsymbol{a}}_{0_{\boldsymbol{i}}} \) and \( {\boldsymbol{a}}_{1_{\boldsymbol{i}}} \) are the random additive genetic effects of the intercept (corresponding to the classical EBV for performance potential) and the slope (equivalent to the EBVs for environmental sensitivity) of the reaction norm for genotype i, respectively; \( {\boldsymbol{e}}_{0_{\boldsymbol{i}}} \) and \( {\boldsymbol{e}}_{1_{\boldsymbol{i}}} \) are the random residual effects of the intercept and slope of the reaction norm for genotype i; and x k is the effect of environment k on the phenotype. The random additive genetic effects a 0 and a 1 were assumed to be normally distributed with expectation zero and variances \( {\boldsymbol{\sigma}}_{{\boldsymbol{a}}_0}^2 \) and \( {\boldsymbol{\sigma}}_{{\boldsymbol{a}}_1}^2 \), respectively, and covariance \( {\boldsymbol{\sigma}}_{{\boldsymbol{a}}_0{\boldsymbol{a}}_1}. \)
The advantage of the reaction norm is that selection response can be predicted not only in the phenotypic expression in any environment but also in quantifying the environmental sensitivity of the trait through the slope of a linear reaction norm (robustness or responsiveness to changes in the environment) (Kolmodin and Bijma 2004). Disease exposure, stocking density and nutrient quality are thought to be included as environmental factors affecting livestock production when conducting reaction norm analysis (Rauw and Gomez-Raya 2015). Similarly, environmental factors related to forest tree breeding, such as temperature, rainfall and soil nutrition, can be applied to reaction norm analysis to identify the drivers of G×E in forest tree breeding. The limitations of the reaction norm are that any environmental variables included in the analysis need to clearly identified and the G×E patterns identified are valid only within the range of the modelled environmental conditions (Gregorius and Kleinschmit 2001). The stability of a given genotype in the reaction norm model can be visualised by plotting observed phenotypic values against one or more environmental variables. A flat slope of the reaction norm means that the phenotype produced over the entire range of environments is constant. Any divergence between a genotype’s reaction norm and that of the population as a whole constitutes a component of G×E. For instance, a particularly steep reaction norm slope for a given genotype means that its phenotype is more sensitive to environments, and the genotype will contribute strongly to G×E. The level of G×E can also be expressed as the ratio of variances in the additive genetic slope (\( {\boldsymbol{\sigma}}_{{\boldsymbol{a}}_1}^2 \)) to the additive genetic intercept (\( {\boldsymbol{\sigma}}_{{\boldsymbol{a}}_0}^2 \)) (Kolmodin and Bijma 2004) or by genetic correlation (r g ) between the additive genetic slope and intercept with \( {\boldsymbol{r}}_{\mathbf{g}}=\frac{{\boldsymbol{\sigma}}_{{\boldsymbol{a}}_0{\boldsymbol{a}}_1}}{\sqrt{{\boldsymbol{\sigma}}_{{\boldsymbol{a}}_0}^2{\boldsymbol{\sigma}}_{{\boldsymbol{a}}_1}^2}} \) (Strandberg et al. 2000).
The reaction norm approach has been applied in forest trees (Gregorius and Kleinschmit 2001), including species that are widely distributed with clinal ranges, notably Norway spruce (Oleksyn et al. 1998) and Scots pine (Abraitiene et al. 2002) in Sweden, and lodgepole pine (Rehfeldt et al. 1999; Wang et al. 2006) and its hybrids (Wu and Ying 2001) in Canada. Oleksyn et al. (1998) examined plant growth, partitioning, net CO2 exchange rate, tissue chemistry and phenology of 54 Norway spruce populations to quantify differences in growth and associated plant traits among populations from altitudinal gradients and better understand their relationships. This study showed that Norway spruce populations from cold mountain environments can be characterised by several potential adaptive features, such as mean annual temperature and altitude. Abraitiene et al. (2002) studied genetic variation of pollen viability and susceptibility to ozone in Scots pine. Significant genetic variation in susceptibility of pollen to increased ozone concentration was found, but only 5% of variation was attributed to G×E.
A reaction norm concept was used to derive response functions for incorporating climate variables into analytic models, and considerably improved their reliability in lodgepole pine populations (Wang et al. 2006) and structure of the specific combining ability between two species of Eucalyptus (Baril et al. 1997b). Response functions predicted that small changes in climate greatly affected growth and survival of forest populations and that maintaining contemporary forest productivities during global warming requires a wholesale redistribution of genotypes across the landscape (Rehfeldt et al. 1999). Significant population by site interactions among 10 natural lodgepole pine populations sampled from three lodgepole pine subspecies (Pinus contorta ssp. contorta, ssp. latifolia and ssp. murrayana) were found for 20-year heights measured in 57 provenance test sites across interior British Columbia (Wu and Ying 2001).
Evidence of G×E in forest trees
In forest trees, G×E has been studied in various economically important species, notably in New Zealand, Australia, USA, Europe, Asia and Africa (Table 1). Most studies investigated G×E for growth and form traits with some investigation of G×E for wood density traits and wood property traits. Table 1 presents examples of evidence of G×E in various forest tree studies in the literature. The criteria to measure the magnitude of G×E in forest tree breeding were proposed in two studies. Robertson (1959) suggested as a guideline that a genetic correlation of 0.8 or higher could be interpreted as G×E with less biological importance. Shelbourne (1972) suggested that interactions have a serious effect on genetic gains from selection and testing when the interaction variance reaches 50% or more of the genetic variance.
High G×E is normally found for tree growth (e.g. radiata pine; Carson 1991; Johnson and Burdon 1990; Table 1; Wu and Matheson 2005). The ratio of estimated interaction to genetic variance for diameter-at-breast-height (DBH) was above 0.50 in a diallel experiment covering 10 sites in Australia (Wu and Matheson 2005). The genetic correlation estimate between pairs of environments for DBH was 0.39 (Wu and Matheson 2005), 0.34–0.38 (Ding et al. 2008a) and −0.60 to 1.0 (Raymond 2011). Type-B genetic correlations were 0.27–0.84 for volume (Dieters and Huber 2007; Li and Mckeand 1989; Roth et al. 2007; Sierra-Lucero et al. 2003), 0.18–0.95 for height (Gwaze et al. 2001; Li and Mckeand 1989; Owino et al. 1977; Paul et al. 1997) and 0.27 for mean annual increment for volume per hectare (Sierra-Lucero et al. 2003). Baltunis and Brawner (2010) reported high G×E for growth traits in clonal trials among Australian sites but not among New Zealand sites. Nearly two-thirds of genetic correlation estimates for DBH between paired sites were below 0.6 in an analysis using data covering 76 sites across the whole of New Zealand (McDonald and Apiolaza 2009). Ivković et al. (2015) reported that pairwise genetic correlations for DBH among 20 control-pollinated trials ranged from −0.51 to 0.98, 48% of which were significantly different from the perfect genetic correlation of 1 with an average of 0.35. Estimates of type-B genetic correlations between trials increased with age, indicating that the importance of G×E appears to decline with age and early growth data may be unreliable for evaluating G×E at maturity (Dieters et al. 1995; Gwaze et al. 2001; Roth et al. 2007; Zas et al. 2003).
Tree form is often an important trait in tree breeding programmes. Traits such as stem straightness and branching confer value in trees at rotation age (Cown et al. 1984; Ivković et al. 2006). The extent of G×E in these traits varies much more among studies. Low levels of G×E have been reported in most studies for stem straightness (Carson 1991; Gapare et al. 2012b; Johnson and Burdon 1990; Pederick 1990), branch angle (Gapare et al. 2012b), branch size (Gapare et al. 2012b; Pederick 1990), branch habit (Carson 1991; Johnson and Burdon 1990) and malformation (Johnson and Burdon 1990). This contrasts with some evidence of G×E in form traits for branch size, numbers of forks and ramicorn branches (Wu and Matheson 2005) and for stem straightness and branch quality among some sites across Australia and New Zealand (Baltunis and Brawner 2010). Similarly, Gwaze et al. (2001) reported high levels of G×E for stem straightness in Zimbabwe for stem straightness and Suontama et al. (2015) reported high levels of G×E for branching in New Zealand. Conflicting G×E was found in two New Zealand studies: Dungey et al. (2012) reported a high level of provenance × site interaction for stem straightness but a low level of family-within-provenance × site interaction in Douglas-fir; Kennedy et al. (2011) found a high type-B genetic correlation (over 0.80) for straightness and form score and a low type-B genetic correlation (0.49) for malformation.
Traits associated with wood structure and quality generally appear to have low G×E in conifers, e.g. wood basic density (Apiolaza 2012; Baltunis et al. 2010; Gapare et al. 2010, 2012a; Johnson and Gartner 2006; Muneri and Raymond 2000), acoustic velocity or modulus of elasticity (Dungey et al. 2012; Gapare et al. 2012a; Jayawickrama et al. 2011; Johnson and Gartner 2006), wood chemical properties (Sykes et al. 2006), wood specific gravity (Jett et al. 1991) and resin canal traits (Westbrook et al. 2014). Osorio et al. (2001) reported minimal G×E for wood density in Eucalyptus grandis in Colombia. Eucalypt hybrid clones (Eucalyptus grandis × Eucalyptus urophylla) in Brazil were, however, found to have significant G×E for wood basic density across four sites (Lima et al. 2000).
Statistically significant type-B genetic correlations may not reflect the true magnitude of G×E. Good experimental design is essential at all stages of testing when estimating genetic parameters. The lack of randomization for the seedling population apparently resulted in a problem with partitioning of the genetic variance, causing among-family variance to be inflated (Baltunis et al. 2007). Poor (i.e. very imprecise) estimates of genetic correlations between environments are often related to a limited number of parents in common between environments (Apiolaza 2012; Raymond 2011). A propagation effect may be relating to the season when cuttings are rooted. The worst genetic correlations were observed between the trial established with rooted cuttings from the winter setting and any of the other trials, while the best genetic correlations were obtained from the field trials that included rooted cuttings originating from the spring settings (Baltunis et al. 2005, 2007).
Impacts of G×E in tree breeding
The overall impact that G×E has for tree breeders is to complicate breeding programme design. The efficiency of selecting for a trait in one environment in pursuing genetic gain in another environment is proportional to the genetic correlation between the two environments and the overall heritability of the trait across the two environments (Falconer and Mackay 1996). Overall heritability across environments is calculated as \( {\boldsymbol{h}}^2=\frac{{\boldsymbol{\sigma}}_{\boldsymbol{a}}^2}{{\boldsymbol{\sigma}}_{\boldsymbol{a}}^2+{\boldsymbol{\sigma}}_{\boldsymbol{ge}}^2+{\boldsymbol{\sigma}}_{\boldsymbol{e}}^2} \) , where \( {\boldsymbol{\sigma}}_{\boldsymbol{a}}^2 \) is the additive genetic variance, \( {\boldsymbol{\sigma}}_{\boldsymbol{ge}}^2 \) is the interaction variance and \( {\boldsymbol{\sigma}}_{\boldsymbol{e}}^2 \) is the residual variance. High G×E, therefore, reduces overall heritability across sites in two aspects. Firstly, large G×E variance in the denominator directly reduces the overall heritability. Secondly, G×E also compromises the estimation of genetic variance across multiple environments, further reducing the size of the heritability estimate. For example, heritability of mean annual increment in volume was 0.08 in an analysis across seven sites, whereas it was over 0.20 within each of two regions (Sierra-Lucero et al. 2003). G×E can also inflate estimation of heritability if estimated in one environment. When G×E is present and the estimates from a single location test are used for a general genetic prediction, the heritability estimate is inflated as part of G×E variance is partitioned into the additive genetic variance. For example, the additive G×E was found to be large enough to cause upward biases on heritability estimates and genetic gain predictions of up to 60–100% (Owino et al. 1977). Family-mean heritability was over-estimated by about 15% when estimated from a single site, compared with that estimated from across-site analysis, and even a type-B genetic correlation for acoustic velocity was 0.85 among sites.
G×E can affect estimation of predicted genetic gain in scenarios for testing and selection as it reduces overall heritability or accuracy across environments. Sierra-Lucero et al. (2003) found that selecting families in region 1 for deployment in region 2 resulted in a 4–8% reduction in mean annual increment in volume per hectare. Loss of genetic gain reached more than 10% in a scenario ignoring G×E when compared with a scenario considering G×E when type-B genetic correlation between sites was less than 0.80 (Diaz Solar et al. 2011). Leksono (2009) reported that genetic gains resulting from direct selection were apparently greater than those resulting from indirect selection, with a decrease of 24–60% in genetic gains if breeding populations were transferred between breeding zones. Diameters at the northern-most site in Queensland, Australia, were poorly correlated with those at other sites (r g = 0.39), and if individual selection was based on this site for planting at any other sites, the estimated genetic gain was only 29–57% as efficient as a selection programme based on the plantation site (Woolaston et al. 1991).
Xie (2003) found considerable G×E for height in interior spruce, a white spruce (Picea glauca (Moench) Voss) and Engelmann spruce (Picea engelmannii Parry ex Engelm.) complex (Xie and Yanchuk 2002), among five seed planning zones located in north-central interior British Columbia with an average between-sites genetic correlation of 0.64. The five seed planning zones were clustered into two new seed zones, with genetic correlations within the new seed zones of 0.97 and 0.84, respectively, and a genetic correlation between the two new zones of 0.41. When selecting the best 25% of tested parents within each zone, the expected genetic gain was 19% when considering the entire region as one zone, 24% when considering the five original zones and 26% when consolidating the five original zones into the two new zones. Despite the apparently modest enhancements of expected gains from regionalised breeding, failure to evaluate genotypes on sites where performance is poorly correlated with that elsewhere would inevitably sacrifice around half or more of the potential genetic gain on such sites.
Significant G×E does not always result in considerable loss of genetic gain. Jett et al. (1991) found significant G×E for specific wood gravity in loblolly pine. Four of 18 families were classified as unstable for the trait, accounting for half the observed G×E variance. However, this G×E only caused a negligible effect on potential genetic gain. Dieters et al. (1996) reported that type-B genetic correlations were over 0.67 for fusiform rust resistance and G×E did not appear to be important in the rust resistance of slash pine in the USA. Carson (1991) found significant G×E for diameter in radiata pine but genetic gains predicted for several regionalisation options suggested the size of G×E in radiata pine in New Zealand appeared to be too small to warrant regionalised breeding populations.
A measure of loss of potential gain (C) has been used as a criterion to evaluate the impact of G×E on breeding programmes for family selection (Matheson and Raymond 1984, 1986) with
\( \boldsymbol{C}=\left(1-{\left[\left({\boldsymbol{V}}_{\mathbf{f}}+\frac{{\boldsymbol{V}}_{\mathbf{e}}}{\boldsymbol{NBS}}\right)/\left({\boldsymbol{V}}_{\mathbf{f}}+\frac{{\boldsymbol{V}}_{\mathbf{i}}}{\boldsymbol{S}}+\frac{{\boldsymbol{V}}_{\mathbf{e}}}{\boldsymbol{NBS}}\right)\ \right]}^{\frac{1}{2}}\right)\times 100 \),
where V f is the phenotypic variance, V i is the variance due to interaction and V e is the error mean square; S is the number of sites, B is the number of replications at each site and N is the number of trees per plot. This assumes that the intensities of selection remain the same and that the residual and genetic components remain the same in the models including or not including the interaction term. Using the preceding relationships, a 2% loss of potential gain corresponds to an approximate reduction of 5% of the numerical value of heritability.
Drivers of G×E in tree breeding
Identifying what environmental factors are the key drivers of G×E is important for both breeding and deployment purposes. It informs the choice of environments in which the candidate genotypes are to be tested and evaluated. It is also important for knowing what the performance of genotypes in a particular environment can tell us about their expected performance in other environments, which may have their attributes characterised, but not necessarily by empirical G×E data.
Various studies have been conducted for characterising the roles of environments in generating G×E in radiata pine. G×E has often been found to reflect differential stress responses among genotypes when an environmental factor is at either a sub-optimal or a strongly sub-optimal level for at least some genotypes (Kang 2002). Stress may be either biotic (diseases or pests) or abiotic (e.g. temperature, salinity and excess or deficiency of water or nutrients). For a given set of genotypes, the more diverse the environments are, the larger the magnitude of possible G×E (Li et al. 2015). G×E may result from different adaptability of subraces or individual genotypes to environmental conditions promoting water and light stresses during the summer and, in some extent, from differential susceptibility to the biotic factors observed (Costa e Silva et al. 2006).
Johnson and Burdon (1990) obtained excellent discrimination between two site categories in New Zealand, representing Northland clays (which are naturally phosphorus-deficient) and pumiceland sites, a pattern that parallels some earlier results in both Australia (Fielding and Brown 1961) and New Zealand (Burdon 1971; Burdon 1976). Wu and Matheson (2005) found that prior land use created some grouping of sites according to interactive behaviour. Since then, the study by Raymond (2011) of G×E for diameter growth in radiata pine in New South Wales found elevation to be the prime driver of G×E, with lesser roles for prior land use and geological parent material. Elevation, however, was associated with a suite of important bioclimatic factors, including rainfall, its seasonality and temperature variables. High-latitude provenances and sites with cool winters and dry summers and high-elevation provenances and sites with high precipitation and short growing seasons contributed the greatest to G×E for height and DBH in white spruce (Rweyongeza 2011).
Wu and Matheson (2005) reported that a large genotype by region interaction in radiata pine was attributed to the extensive snow loading at the two higher-elevation sites. G×E for DBH was found to be possibly driven by extreme maximum temperatures in an analysis of data collected from 76 radiata pine trials across the whole of New Zealand (McDonald and Apiolaza 2009) and by minimum temperature in both provenance and progeny levels (Gapare et al. 2015). A mean daily temperature less than 3.2 °C in May and June explained 27.8% G×E interaction, and it was moderately correlated with the first factor in the FA model, indicating that spring or autumn frost weather conditions could be a main driver for G× E in Norway spruce (Chen et al. 2017). Ivković et al. (2013a) reported that high rainfall and cold temperature explained 25% of G×E variance and they are likely drivers of G×E in New Zealand, based on breeding values of DBH estimated by Cullis et al. (2014).
On the other hand, biotic factors such as foliage diseases, which tend to be strongly related to rainfall and its seasonality, are an obvious potential driver of G×E for stem diameter and volume growth (cf. Ades and Garnier-Géré 1997). G×E caused by differential exposure to Swiss needle cast in Douglas-fir is also a good example, as the needle disease is more prevalent in warmer temperatures and sites can have radically different disease loads and differential growth responses in the host tree population as a result (Dungey et al. 2012).
Li et al. (2015) reported that G×E levels for growth traits were significantly associated with site differences in soil nutrient levels of nitrogen and total phosphorus and mean annual temperature and that G×E levels for foliar calcium content and fascicle weight were significantly associated with site differences in soil levels of magnesium and potassium, respectively. At the broadest scale (across New Zealand and Australia), climatic variables such as temperature and rainfall were the most significant factors driving observed G×E; however, at a local regional scale, soils and topographical factors were of more significance (Ivković et al. 2013a).
Strategies for dealing with G×E in tree breeding programmes
Two main strategies have been proposed for dealing with the presence of strong G×E (Kang 2002; Raymond 2011): (1) select individuals that perform stably across sites; or (2) select individuals that are well suited to each individual environment to maximise genetic gain. The first strategy is applicable when no obvious source of the observed G×E can be found and the interactions are regarded as essentially ‘noise’. The strategy aims to select genotypes with broad adaptation which would be expected to yield dependably across a wide range of environments. Selection for stability is the approach that has been recommended in G×E studies for radiata pine in Australia (Ding 2008; Matheson and Raymond 1984), New Zealand (Carson 1991) and Spain (Codesido and Fernández-López 2009); for loblolly pine in the USA (Owino 1977; Paul et al. 1997); and for Norway spruce in Sweden (Bentzer et al. 1988). This approach aims to eliminate the genotypes that are the most interactive with environments. However, for this to succeed well, the breeder needs to use an appropriate set of test environments that exposes both the interactive and stable genotypes.
The second strategy is to exploit the interactions by analysing and interpreting genetic and environmental differences (Raymond 2011). This strategy would be expected to maximise heritability and genetic gain within each environment individually, and accordingly, this requires the creation of separate breeding populations and seed production with consequent problems of cost, management, recording and ancestry control (Barnes et al. 1984). This strategy might be impracticable when the number of environments is large and spans different climatic and geographic regions and different soil types. A practical adaptation of this strategy is to group similar environments into regions. Application of this strategy relies on the ability to identify which site or environmental factors are causing the interaction (Raymond 2011). Regionalisation is commonly used for Northern Hemisphere species growing in their natural range where a single environmental factor, usually related to temperature gradients, determines seedlot performance. As an example, for Scots pine in Sweden, breeding and seed zones have been established based on the latitudinal temperature gradient, and G×E within these zones for growth traits is very low (Hannrup et al. 2008; Raymond 2011).
Research results from a diallel mating design experiment in radiata pine seem to favour regionalisation of radiata pine breeding for DBH into two main regions in Australia: the high-elevation Tumut region in New South Wales, and regions of Victoria, South Australia and Western Australia (Wu and Matheson 2005). In New Zealand, however, Carson (1991) had reported that the magnitude of G×E in radiata pine appeared to be too small to warrant regionalised breeding populations. Matheson and Raymond (1984) proposed that a better solution to the G×E problem is not to attempt to regionalise the breeding but to omit families that seem to be particularly susceptible to environmental variation. Trade-offs need to be fully evaluated as these approaches have serious implications for operational breeding and a cost/benefit analysis may be needed. A regionalised breeding programme with separate breeding populations might have smaller breeding populations in each environment, lower selection intensities and therefore lower genetic gains than one national programme of the same size (Carson 1991). While extra gain might be available through regionalisation, further costs for land use, operation of multiple seed orchards, additional records and extension in the progeny-testing would increase proportionally (Barnes et al. 1984; Carson 1991).
Towards applications and future research
The multi-trait context
We have reviewed statistical methodologies for studying G×E primarily in relation to the single-trait case. However, quantitative geneticists and breeders almost always have to consider G×E in the context of multiple traits for selection and deployment. Among the methodologies, the study of type-B genetic correlations (Burdon 1977) can readily be extended to multiple traits between multiple environments. With multiple traits, several more complicated manifestations of G×E can arise. Different traits may exhibit different patterns of G×E. Moreover, genetic and phenotypic between-trait (type-A) correlation matrices can differ between environments as another form of G×E. Correlations between different traits expressed in different environments (for which the term type-AB correlations is proposed) can differ between pairs of environments, in a complex manifestation of G×E, likely to be relevant for traits related to health and frost or drought tolerance.
The multi-trait case creates interplays between rank-change and level-of-expression G×E for both selection and deployment. As indicated above, level-of-expression interaction can generate rank-change interaction, some classic examples being the effects of disease expression which, by influencing tree growth or tree form, can certainly influence genotypic rankings for the latter traits, with obvious implications for stability of genotype performance. One such example involves provenance trials of radiata pine in New Zealand, where the Cambria provenance, which is less resistant to needle-cast diseases, gave much worse relative performance for growth on disease-prone sites (Burdon et al. 1997). Another involves provenance trials of coastal Douglas-fir in New Zealand, in which comparative growth performance was strongly affected by Swiss needle cast (caused by Phaeocryptopus gaeumannii), with the susceptible lowest-latitude native provenance doing comparatively better at a highest-latitude site (46° S), where disease risk was much lower than at the lower-latitude site (38° S) (Dungey et al. 2012). Such disease-related influences are of interest for both breeding and deployment.
Level-of-expression interaction
Level-of-expression G×E does not cause rank change of selection candidates and is generally less important for breeding (Muir et al. 1992), but it is important for deployment across multiple environments (Burdon et al. 2017). If there is no rank-change interaction, testing in one environment should be sufficient. If selection for deployment involves a range of environments and multi-trait selection, level-of-expression interaction may require deployment of quite different sets of genotypes to different environments without there necessarily being rank-change interaction. In this situation, evaluation on several environments may be needed to give good resolution of genetic differences for all the traits of interest. Classic examples of level-of-expression interaction can arise with disease resistance, in which resolution of genotypic differences can depend greatly on disease incidence (e.g. Dieters et al. 1996; Sohn and Goddard 1979). Typically, resolution tends to be best at moderate to severe levels of disease, especially among the most resistant genotypes. Nevertheless, there may be cases in which a disease may be present at levels that are of no direct practical importance, but resolution of genetic differences in that environment may still be good. Resistance to that disease does not need to figure as a deployment criterion in such an environment, yet disease resistance expressed there may still be a valuable selection criterion for deployment in other environments, where the disease is troublesome but incidence not highly heritable because of high levels of ‘noise’ variation.
Genomics will help tackle G×E
Genomic selection is being increasingly explored as a major tool for selection in forest tree breeding (Grattapaglia and Resende 2011; Isik et al. 2011, 2016; Lexer and Stölting 2012; Ratcliffe et al. 2015; Resende et al. 2011, 2012a, b). The major benefit of genomic selection is that selection can be undertaken well before the normal age of phenotyping—around age 8 in radiata pine. DNA can be extracted and genotyping undertaken on only a few needles, before the age of 6 months. This means that generation intervals for breeding can be greatly reduced and the expected genetic gains per unit of time can be increased (Grattapaglia and Resende 2011; Isik 2014).
G×E in genomic selection has been studied for several forest species. When G×E interactions exist for a trait, observed SNP effects for the trait changed across environments, and their association with the trait might be significant in one environment but not significant in other environments, as shown in radiata pine (Li et al. 2016). Significant QTL by environment interaction was found for QTLs associated with DBH, basic wood density, Kraft pulp yield, and wood chemical compounds of cellulose, klason lignin and extractives, and lignin syringyl to guaiacyl ratio using 663 individuals of one F2 family and three F1 families of Eucalyptus globulus planted in Tasmania, Victoria and Western Australia (Freeman et al. 2011, 2013). Accuracies of genomic selection, however, have been shown to decline drastically when a model was developed using a dataset of one population to predict phenotypes of another population in Eucalyptus (Resende et al. 2012a). In loblolly pine in the USA, G×E severely affects the transferability of models across breeding zones (Resende et al. 2012b). In interior spruce planted in the western coast of Canada, genomic selection accuracy for growth and wood attributes was higher in a multi-site model (where the G×E term was fitted) than in a single-site model when predicting phenotypes for different sites (El-Dien et al. 2015).
To characterise the roles of genotypes and environments in driving G×E in forest tree breeding, we may need to collect data of genotypes at the molecular level, assess even broader number of phenotypes and collect climatic and geographical data together with edaphic data across all seasons and all years during which tested genotypes grow. Functional genomics (Pevsner 2009), genome sequence annotation (Ouzounis and Karp 2002; Wolf et al. 2001) and high-resolution phenotyping (Crowell et al. 2016) can be useful for characterising the roles of genotypes and environments in driving G×E. Developing environment-specific genomic breeding values is the next challenge to maximise genetic gain in multiple environments when using genomic selection in forest tree breeding. Among the analytical methodologies mentioned above, factor analytic models (Cullis et al. 2014; Smith et al. 2015) are a parsimonious and holistic approach for estimation of genetic correlations between all pairs of environments and can eventually play an important role to develop the environment-specific genomic breeding values for a large number of environments.
Overview
Statistical methods, AMMI, GGE biplot analysis, FA and reaction norm, are reviewed in this paper. Table 2 summarises the strengths and weaknesses of these methods. They are tools for identifying the patterns and magnitude of G×E in forest tree breeding. The first three methods infer groupings of environments and genotypes, based purely on phenotypic data and using PCA to reduce dimensionality. AMMI and GGE biplot analyses test the significance of G×E and the relative size of G×E variance to genetic variance and allow visualisation of stability and environments where genotypes are best performed. These methods are most suitable for making decisions around the deployment of genotypes across multiple environments. They would certainly be useful in the visualisation of forest data to help make informed decisions for deployment.
The FA model has the ability to estimate the unstructured genetic variance-covariance matrix for a large number of environments without the use of an excessive number of variance parameters. This type of model can be easily used to explain the nature and the extent of G×E. Type-B genetic correlations estimated from FA models can clearly show if there are rank changes of genotypes among environments. FA models are statistically efficient for breeding value estimations and provide a reliable, holistic approach to estimate genetic correlations between all pairs of environments (Cullis et al. 2014). FA models are most useful for making decisions of selection for breeding populations and decisions of deployment for production populations. The reaction norm approach uses a combination of phenotypic and environmental data to make inferences on the environmental drivers of G×E. It is suitable for analysing traits that vary gradually and continuously over an environmental gradient and needs environmental variables included to be clearly defined. Stability analysis has intuitive appeal in forest tree breeding, helping forest growers identify stable genotypes and reduce long-term risks.
All of these statistical methods provide solutions to the identification of high-performing stable genotypes in forest tree breeding programmes. However, pursuing stability of performance does not take full advantage of potential genetic gain in specific environments. In order to maximise potential genetic gains for all environments, selecting the right individuals best adapted to specific environments is likely to be the best approach.
Most G×E studies in forest tree breeding investigated the patterns and magnitude of G×E for growth traits. High levels of G×E were reported for these traits, especially in radiata pine, loblolly pine, Eucalyptus and Populus species. Some studies also investigated the patterns and magnitude of G×E for form traits and wood property traits. Half the studies included in this review reported a high level of G×E for form traits whereas no G×E or minimal G×E was reported for wood property traits.
In summary, G×E can be quantified in a number of ways, and taking several different approaches will likely give complementary insights to help understand the interactions involved, and ensure the best outcome. For New Zealand and for forestry in general, breeding value estimation is clearly most effective using new methods such as factor analytic models. For understanding and quantifying the detailed roles of environments, more work is still required. We believe that genomics technologies (e.g. Elshire et al. 2011; Neves et al. 2013) and genome sequence annotation (Ouzounis and Karp 2002; Wolf et al. 2001) will provide more information and help unravel the cause and effect at the genetic level. To maximise genetic gains and economic benefits from forest plantations, the strategy of selecting individuals for specific and known environments should be applied. The end result will be advances in forest productivity and forest management systems that will ensure the long-term sustainability and enhanced profitability of the forest industry.
Notes
We distinguish between level-of-expression and scale-effect interaction, reserving the latter term for the subset of cases in which interaction can be eliminated simply by data transformation.
References
Abraitiene A, Kairiukstis L, Pliura A, Girgzdiene R, Abraitis R (2002) Variation in germination of Scots pine (Pinus sylvestris L.) pollen exposed to ozone. Baltic For 8:2–7
Ades PK, Garnier-Géré PH (1997) Making sense of provenance × environment interaction in Pinus radiata. Paper presented at the IUFRO ‘97 Genetics of Radiata Pine, pp. 113–119. Rotorua, New Zealand 1–4 December 1997
Annicchiarico P (1997) Joint regression vs AMMI analysis of genotype-environment interactions for cereals in Italy. Euphytica 94:53–62. doi:10.1023/A:1002954824178
Apiolaza LA (2012) Basic density of radiata pine in New Zealand: genetic and environmental factors. Tree Genet Genomes 8:87–96
Baltunis BS, Brawner JT (2010) Clonal stability in Pinus radiata across New Zealand and Australia. I. Growth and form traits. New For 40:305–322
Baltunis BS, Huber DA, White TL, Goldfarb B, Stelzer HE (2005) Genetic effects of rooting loblolly pine stem cuttings from a partial diallel mating design. Can J For Res 35:1098–1108. doi:10.1139/x05-038
Baltunis BS, Huber DA, White TL, Goldfarb B, Stelzer HE (2007) Genetic analysis of early field growth of loblolly pine clones and seedlings from the same full-sib families. Can J For Res 37:195–205
Baltunis BS, Gapare WJ, Wu HX (2010) Genetic parameters and genotype by environment interaction in radiata pine for growth and wood quality traits in Australia. Silvae Genet 59:113–124
Baril CP, Verhaegen D, Vigneron P, Bouvet JM, Kremer A (1997a) Structure of the specific combining ability between two species of Eucalyptus. II. A clustering approach and a multiplicative model. Theor Appl Genet 94:804–809
Baril CP, Verhaegen D, Vigneron P, Bouvet JM, Kremer A (1997b) Structure of the specific combining ability between two species of Eucalyptus. I. RAPD data. Theor Appl Genet 94:796–803. doi:10.1007/s001220050480
Barnes RD, Burley J, Gibson GL, Garcia de Leon JP (1984) Genotype-environment interactions in tropical pines and their effects on the structure of breeding populations. Silvae Genet 33:186–198
Bentzer BG, Foster GS, Hellberg AR, Podzorski AC (1988) Genotype × environment interaction in Norway spruce involving three levels of genetic control: seed source, clone mixture, and clone. Can J For Res 18:1172–1181. doi:10.1139/x88-180
Burdon RD (1971) Clonal repeatabilities and clone-site interactions in Pinus radiata. Silvae Genet 20:33–37
Burdon RD (1976) Foliar macronutrient concentrations and foliage retention in radiata pine clones on four sites. NZ J For Sci 5:250–259
Burdon RD (1977) Genetic correlation as a concept for studying genotype-environment interaction in forest tree breeding. Silvae Genet 26:168–175
Burdon RD, Firth A, Low CB, Miller MA (1997) Native provenances of Pinus radiata in New Zealand: performance and potential. NZ J For 41:32–36
Burdon RD, Li Y, Suontama M, Dungey HS (2017) Genotype × site × silviculture interactions in radiata pine: knowledge, working hypotheses and pointers for research. NZ J For Sci 47(6). doi: 10.1186/s40490-017-0087-1
Burgueño J, Crossa J, Miguel Cotes J, San Vicente F, Das B (2011) Prediction assessment of linear mixed models for multienvironment trials. Crop Sci 51:944–954. doi:10.2135/cropsci2010.07.0403
Bush D, Marcar N, Arnold R, Crawford D (2013) Assessing genetic variation within Eucalyptus camaldulensis for survival and growth on two spatially variable saline sites in southern Australia. For Ecol Manag 306:68–78. doi:10.1016/j.foreco.2013.06.008
Campbell RK (1992) Genotype × environment interaction: a case study for Douglas-fir in western Oregon. Res. Pap. PNW-RP-455. Portland, OR: U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station. 21p
Carson SD (1991) Genotype × environment interaction and optimal number of progeny test sites for improving Pinus radiata in New Zealand. NZ J For Sci 21:32–49
Chambel MR, Climent J, Alía R (2008) A dissection of the provenance × site interaction of three Iberian pines using the AMMI method. In: Workshop on Plasticity Adaptation in Forest Trees, Madrid, Spain, 27–29 February 2008.
Chen Z-Q, Karlsson B, Wu HX (2017) Patterns of additive genotype-by-environment interaction in tree height of Norway spruce in southern and central Sweden. Tree Genet Genomes 13:25. doi:10.1007/s11295-017-1103-6
Codesido V, Fernández-López J (2009) Implication of genotype × site interaction on Pinus radiata breeding in Galicia. New For 37:17–34
Correia I, Alía R, Yan W, David T, Aguiar A, Almeida MH (2010) Genotype × environment interactions in Pinus pinaster at age 10 in a multi-environment trial in Portugal: a maximum likelihood approach. Ann For Sci 67:612
Costa e Silva J (2007) Evaluation of an international series of Pinus kesiya provenance trials for adaptive, growth and wood quality traits, vol no. 22-2007. University of Copenhagen, Forest and Landscape Denmark
Costa e Silva J, Borralho NMG, Wellendorf H (2000) Genetic parameter estimates for diameter growth, pilodyn penetration and spiral grain in Picea abies (L.) Karst. Silvae Genet 49:29–36
Costa e Silva J, Potts B, Dutkowski G (2006) Genotype by environment interaction for growth of Eucalyptus globulus in Australia. Tree Genet Genomes 2:61–75
Cown DJ, McConchie DL, Treloar C (1984) Timber recovery from pruned Pinus radiata butt logs at Mangatu: effect of log sweep. NZ J For Sci 14:109–123
Crossa J (1990) Statistical analyses of multilocation trials. Adv Agron 44:55–85
Crossa J (2012) From genotype × environment interaction to gene × environment interaction. Current Genomics 13:225–244. doi:10.2174/138920212800543066
Crossa J, Gauch HG Jr, Zobel RW (1990) Additive main effects and multiplicative interaction analysis of two international maize cultivar trials. Crop Sci 30:493–500
Crossa J, Vargas M, van Eeuwijk FA, Jiang C, Edmeades GO, Hoisington D (1999) Interpreting genotype × environment interaction in tropical maize using linked molecular markers and environmental covariables. Theor Appl Genet 99:611–625. doi:10.1007/s001220051276
Crowell S, Korniliev P, Falcão A, Ismail A, Gregorio G, Mezey J, McCouch S (2016) Genome-wide association and high-resolution phenotyping link Oryza sativa panicle traits to numerous trait-specific QTL clusters. Nat Commun 7:10527. doi:10.1038/ncomms10527
Cullis BR, Jefferson P, Thompson R, Smith AB (2014) Factor analytic and reduced animal models for the investigation of additive genotype-by-environment interaction in outcrossing plant species with application to a Pinus radiata breeding programme. Theor Appl Genet 217:2193–2210
Dean CA (2009) Short note: Genotype-environment interactions for coastal Douglas-fir grown to 21 years across western Washington State, USA. Silvae Genet 58:39–42
Diaz Solar I, de Oliveira HN, Bezerra LAF, Lobo RB (2011) Genotype by environment interaction in Nelore cattle from five Brazilian states. Genet Mol Biol 34:435–442
Dieters MJJ (1996) Genetic parameters for slash pine (Pinus elliottii) grown in south-east Queensland, Australia: growth, stem straightness and crown defects. For Genet 3:27–36
Dieters MJ, Huber DA (2007) Genotype × environment interaction in Florida sources of loblolly pine across the lower coastal plain of the southeastern USA. In: Byram TD, Rust ML (eds) Tree improvement in North America: past, present, and future, WFGA/SFTIC Joint Meeting, Galveston, TX. June 19–22, 2007
Dieters MJ, White TL, Hodge GR (1995) Genetic parameter estimates for volume from full-sib tests of slash pine (Pinus elliottii). Can J For Res 25:1397–1408
Dieters MJ, Hodge GR, White TL (1996) Genetic parameter estimates for resistance to rust (Cronartium quercuum) infection from full-sib tests of slash pine (Pinus elliottii), modelled as functions of rust incidence. Silvae Genet 45:235–242
Ding M (2008) Increasing the accuracy of analysing G×E interaction and integrating the information to P. radiata breeding program. PhD thesis, University of New England, Armidale, Australia
Ding M, Tier B, Dutkowski GW, Wu HX, Powell MB, McRae TA (2008a) Multi-environment trial analysis for Pinus radiata. NZ J For Sci 38:143–159
Ding M, Tier B, Yan W, Wu HX, Powell MB, McRae TA (2008b) Application of GGE biplot analysis to evaluate genotype (G), environment (E) and G×E interaction on Pinus radiata: a case study. NZ J For Sci 38:132–142
Dungey HS, Low CB, Lee J, Miller JT, Fleet K, Yanchuk AD (2012) Developing breeding and deployment options for Douglas-fir in New Zealand: breeding for future forest conditions. Silvae Genet 61:104–115
Eberhart SA, Russell WA (1966) Stability parameters for comparing varieties. Crop Sci 6:36–40
El-Dien OG, Ratcliffe B, Klápště J, Chen C, Porth I, El-Kassaby YA (2015) Prediction accuracies for growth and wood attributes of interior spruce in space using genotyping-by-sequencing. BMC Genomics 16:1–16. doi:10.1186/s12864-015-1597-y
Elshire RJ, Glaubitz JC, Sun Q, Poland JA, Kawamoto K, Buckler ES, Mitchell SE (2011) A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS One 6:e19379
Falconer DS, Mackay TFC (1996) Introduction to quantitative genetics (4th ed.). Longmans Group Ltd. Pearson Education Ltd. Harlow, Essex, England
Falkenhagen E (1996) A comparison of the AMMI method with some classical statistical methods in provenance research: the case of the south African Pinus radiata trail. For Genet 3:81–87
Fielding JM, Brown AG (1961) Tree-to-tree variations in the health and some effect of superphosphate on the growth and development of Monterey pine on a low quality site. Forest and Timber Bureau of Australia, Canberra, Leaflet No. 79
Finlay WK, Wilkinson GN (1963) The analysis of adaptation in a plant breeding program. Aus J Agric Res 14:742–754
Freeman GH (1973) Statistical methods for the analysis of genotype-environment interactions. Heredity 31:339–354
Freeman J, Potts B, Downes G, Thavamanikumar S, Pilbeam D, Hudson C, Vaillancourt R (2011) QTL analysis for growth and wood properties across multiple pedigrees and sites in Eucalyptus globulus. BMC Proc 5:O8
Freeman JS, Potts BM, Downes GM, Pilbeam D, Thavamanikumar S, Vaillancourt RE (2013) Stability of quantitative trait loci for growth and wood properties across multiple pedigrees and environments in Eucalyptus globulus. New Phytol 198:1121–1134. doi:10.1111/nph.12237
Gabriel KR (1971) The biplot graphic display of matrices with application to principal component analysis. Biometrika 58:453–467
Gapare WJ, Ivković M, Baltunis BS, Matheson CA, Wu HX (2010) Genetic stability of wood density and diameter in Pinus radiata D. Don plantation estate across Australia. Tree Genet Genomes 6:113–125. doi:10.1007/s11295-009-0233-x
Gapare WJ, Ivković M, Dillon SK, Chen F, Evans R, Wu HX (2012a) Genetic parameters and provenance variation of Pinus radiata D. Don. ‘Eldridge collection’ in Australia 2: wood properties. Tree Genet Genomes 8:895–910. doi:10.1007/s11295-012-0475-x
Gapare WJ, Ivković M, Dutkowski GW, Spencer DJ, Buxton P, Wu HX (2012b) Genetic parameters and provenance variation of Pinus radiata D. Don. ‘Eldridge collection’ in Australia 1: growth and form traits. Tree Genet Genomes 8:391–407
Gapare W, Ivković M, Liepe K, Hamann A, Low C (2015) Drivers of genotype by environment interaction in radiata pine as indicated by multivariate regression trees. For Ecol Manag 353:21–29
Gauch HG Jr (1992) Statistical analysis of regional yield trials: AMMI analysis of factorial designs. Elsevier, Amsterdam
Gauch HG Jr, Zobel RW (1989) Accuracy and selection success in yield trial analyses. Theor Appl Genet 77:473–481. doi:10.1007/BF00274266
Gauch HG, Zobel RW (1997) Identifying mega-environments and targeting genotypes. Crop Sci 37:311–326. doi:10.2135/cropsci1997.0011183X003700020002x
Grattapaglia D, Resende MDV (2011) Genomic selection in forest tree breeding. Tree Genet Genomes 7:241–255
Gregorius HR, Kleinschmit JRG (2001) Norms of reaction and adaptational value considered in a tree breeding context. Can J For Res 31:607–616. doi:10.1139/cjfr-31-4-607
Gullberg U, Vegerfors B (1987) Genotype-environment interaction in Swedish material of Pinus sylvestris. Scand J For Res 2:417–432
Gwaze DP, Wolliams JA, Kanowski PJ, Bridgwater FE (2001) Interactions of genotype with site for height and stem straightness in Pinus taeda in Zimbabwe. Silvae Genet 50:135–140
Haapanen M (1996) Impact of family-by-trial interaction on the utility of progeny testing methods for Scots pine. Silvae Genet 45:130–135
Hallingbäck HR, Jansson G, Hannrup B (2008) Genetic parameters for grain angle in 28-year-old Norway spruce progeny trials and their parent seed orchard. Ann For Sci 65:301–308. doi:10.1051/forest:2008005
Hannrup B, Säll H, Jansson G (2003) Genetic parameters for spiral grain in Scots pine and Norway spruce. Silvae Genet 52:215–220
Hannrup B, Jansson G, Danell Ö (2008) Genotype by environment interaction in Pinus sylvestris L. in southern Sweden. Silvae Genet 57:306–311
Hardner CM, Dieters M, Dale G, DeLacy I, Basford K (2010) Patterns of genotype-by-environment interaction in diameter at breast height at age 3 for eucalypt hybrid clones grown for reafforestation of lands affected by salinity. Tree Genet Genomes 6:833–851. doi:10.1007/s11295-010-0295-9
Hardner C, Dieters M, DeLacy I, Neal J, Fletcher S, Dale G, Basford K (2011) Identifying deployment zones for Eucalyptus camaldulensis × E. globulus and × E. grandis hybrids using factor analytic modelling of genotype by environment interaction. Aus For 74:30–35
Hassanpanah D (2010) Analysis of G×E interaction by using the additive main effects and multiplicative interaction in potato cultivars. Int J Plant Breed Genet 4:23–29
Hodge GR, White TL (1992) Genetic parameters for growth traits at different ages in slash pine and some implications for breeding. Silvae Genet 41:252–262
Huehn M (1990) Nonparametric measures of phenotypic stability. Part 1: theory. Euphytica 47:189–194. doi:10.1007/BF00024241
Isik F (2014) Genomic selection in forest tree breeding: the concept and an outlook to the future. New For 45. doi:10.1007/s11056-014-9422-z
Isik F, Whetten R, Zapata-Valenzuela J, Ogut F, McKeand S (2011) Genomic selection in loblolly pine—from lab to field. BMC Proc 5:I8
Isik F, Bartholomé J, Farjat A, Chancerel E, Raffin A, Sanchez L, Plomion C, Bouffier L (2016) Genomic selection in maritime pine. Plant Sci 242:108–119. doi:10.1016/j.plantsci.2015.08.006
Ivković M, Wu HX, McRae TA, Powell MB (2006) Developing breeding objectives for radiata pine structural wood production. I. Bioeconomic model and economic weights. Can J For Res 36:2920–2931. doi:10.1139/x06-161
Ivković M, Dutkowski G, Jefferson P, Gapare W, Wu H, Jovanovic T, McRae T (2013a) Matching genotypes to current and future production environments to maximise radiata pine productivity and profitability. Paper presented at the Forest Genetics 2013. A Joint Meeting of WFGA and IUFRO, Whistler, British Columbia, Canada, 22–25 July 2013
Ivković M, Gapare W, Wu H, Espinoza S, Rozenberg P (2013b) Influence of cambial age and climate on ring width and wood density in Pinus radiata families. Ann For Sci 70:525–534
Ivković M, Gapare W, Yang H, Dutkowski G, Buxton P, Wu H (2015) Pattern of genotype by environment interaction for radiata pine in southern Australia. Ann For Sci 72:391–401. doi:10.1007/s13595-014-0437-6
Jayawickrama KJS, Ye TZ, Howe GT (2011) Heritabilities, intertrait genetic correlations, G × E interaction and predicted genetic gains for acoustic velocity in mid-rotation coastal Douglas-fir. Silvae Genet 60:8–18
Jett JB, McKeand SE, Weir RJ (1991) Stability of juvenile wood specific gravity of loblolly pine in diverse geographic areas. Can J For Res 21:1080–1085. doi:10.1139/x91-148
Johnson GR, Burdon RD (1990) Family-site interaction in Pinus radiata: implications for progeny testing strategy and regionalised breeding in New Zealand. Silvae Genet 39:1990
Johnson GR, Gartner BL (2006) Genetic variation in basic density and modulus of elasticity of coastal Douglas-fir. Tree Genet Genomes 3:25–33
Jolliffe I (1986) Principal component analysis. Springer, New York
de Jong G (1990) Genotype-by-environment interaction and the genetic covariance between environments: multilocus genetics. Genetica 81:171–177. doi:10.1007/BF00360862
Kandus M, Almorza D, Ronceros RB, Salerno J (2010) Statistical models for evaluating the genotype-environment interaction in maize (Zea mays L.) ΦYΤΟΝ 79:39–46
Kang MS (2002) Genotype-environment interaction: progress and prospects. In: Kang MS (ed) Quantitative genetics, genomics and plant breeding. CABI, Cambridge, pp 221–243
Kang M, Gauch H (1996) Genotype by environment interaction. CRC, Florida
Karlsson B, Wellendorf H, Roulund H, Werner M (2001) Genotype × trial interaction and stability across sites in 11 combined provenance and clone experiments with Picea abies in Denmark and Sweden. Can J For Res 31:1826–1836
Karuntimi SM (2012) Modeling genotype by environment interaction of Eucalyptus using additive main effects and multiplicative interaction approach. University of Narobi, Narobi
Kempton RA (1984) The use of biplots in interpreting variety by environment interactions. J Agric Sci 103:123–135
Kennedy SK, Dungey H, Yanchuk AD, Low CB (2011) Eucalyptus fastigata: its current status in New Zealand and breeding objectives for the future. Silvae Genet 60:259–266
Kim I-S, Kwon H-Y, Ryu K-O, Choi WY (2008) Provenance by site interaction of Pinus densiflora in Korea. Silvae Genet 57:131–139
Kolmodin R, Bijma P (2004) Response to mass selection when the genotype by environment interaction is modelled as a linear reaction norm. Genet Sel Evol 36:435–454. doi:10.1051/gse:2004010
Koo YB, Yeo JK, Woo KS, Kim TS (2007) Selection of superior clones by stability analysis of growth performance in Populus davidiana Dode at age 12. Silvae Genet 56:93–101
Krakowski J, Stoehr MU (2009) Coastal Douglas-fir provenance variation: patterns and predictions for British Columbia seed transfer. Ann For Sci 66:811
Kroonenberg PM (1995) Introduction to biplots for G×E tables. Leiden University Research Report #51, University of Queensland, Brisbane, Australia
Lavoranti OJ, Dias CTS, Kraznowski WJ (2007) Phenotypic stability via AMMI model with bootstrap re-sampling. Pesq Flor bras, Colombo 54:45–52
Leksono B (2009) Breeding zones based on genotype-environment interaction in seedling seed orchards of Eucalyptus pellita in Indonesia. Indones J For Res 6:74–84
Lexer C, Stölting KN (2012) Whole genome sequencing (WGS) meets biogeography and shows that genomic selection in forest trees is feasible. New Phytol 196:652–654. doi:10.1111/j.1469-8137.2012.04362.x
Li B, McKeand SE (1989) Stability of loblolly pine families in the southeastern US. Silvae Genet 38:96–101
Li B, Wu R (1997) Heterosis and genotype × environment interactions of juvenile aspens in two contrasting sites. Can J For Res 27:1525–1537. doi:10.1139/97-110
Li Y, Xue J, Clinton PW, Dungey HS (2015) Genetic parameters and clone by environment interactions for growth and foliar nutrient concentrations in radiata pine on 14 widely diverse New Zealand sites. Tree Genet Genomes 11:1–16. doi:10.1007/s11295-014-0830-1
Li Y, Wilcox P, Telfer E, Graham N, Stanbra L (2016) Association of single nucleotide polymorphisms with form traits in radiata pine in the presence of genotype by environment interactions. Tree Genet Genomes. doi:10.1007/s11295-016-1019-6
Lima JT, Breese MC, Cahalan CM (2000) Genotype-environment interaction in wood basic density of Eucalyptus clones. Wood Sci Tech 34:197–206
Lu P, Charrette P (2008) Genetic parameter estimates for growth traits of black spruce in northwestern Ontario. Can J For Res 38:2994–3001. doi:10.1139/X08-133
Lynch M, Walsh JB (1998) Genetics and analysis of quantitative traits. Sunderland, Sinauer Associates Inc
Mandel J (1971) A new analysis of variance model for non-additive data. Technometrics 13:1–18
Matheson AC, Raymond CA (1984) The impact of genotype × environment interactions on Australian Pinus radiata breeding programs. Aus For Res 14:11–25
Matheson AC, Raymond CA (1986) A review of provenance x environment interaction: its practical importance and use with particular reference to the tropics. Comonw Forest Rev 65:283–302
McDonald TM, Apiolaza LA (2009) Genotype by environment interaction of Pinus radiata in New Zealand. In: the Second Australasian Forest Genetics Conference, Perth, Australia, 20–22 April 2009.
McKeand SE, Eriksson G, Roberds JH (1997) Genotype by environment interaction for index traits that combine growth and wood density in loblolly pine. Theor Appl Genet 94:1015–1022. doi:10.1007/s001220050509
Meyer K (2009) Factor-analytic models for genotype × environment type problems and structured covariance matrices. Genet Sel Evol 41:21. doi:10.1186/1297-9686-41-21
Mrode RA (2014) Linear models for the prediction of animal breeding values, 3rd edn. CABI, Cambridge
Muir W, Nyquist WE, Xu S (1992) Alternative partitioning of the genotype-by-environment interaction. Theor Appl Genet 84:193–200. doi:10.1007/BF00224000
Muneri A, Raymond C (2000) Genetic parameters and genotype-by-environment interactions for basic density, pilodyn penetration and stem diameter in Eucalyptus globulus. For Genet 7:317–328
Neves LG, Davis JM, Barbazuk WB, Kirst M (2013) Whole-exome targeted sequencing of the uncharacterized pine genome. Plant J 75:146–156
Oakey H, Verbyla A, Cullis BR, Pitchford W, Kuchel H (2006a) Joint modelling of additive and non-additive genetic line effects in single field trials. Theor Appl Genet 113:809–839
Oakey H, Verbyla A, Cullis BR, Wei X, Pitchford W (2006b) Joint modelling of additive and non-additive (genetic line) effects in multi-environment trials. Theor Appl Genet 114:1319–1332
Oleksyn J, Modrzynski J, Tjoelker MG, Zytkowiak R, Reich PB, Karolewski P (1998) Growth and physiology of Picea abies populations from a broad elevational transect: common garden evidence for altitutinal econtypes and cold adaptation. Funct Ecol 12:573–590
Osorio LF, White TL, Huber DA (2001) Age trends of heritabilities and genotype-by-environment interactions for growth traits and wood density from clonal trials of Eucalyptus grandis Hill ex Maiden. Silvae Genet 50:30–37
Ouzounis CA, Karp PD (2002) The past, present and future of genome-wide re-annotation. Genome Biol 3:Comment2001
Owino F (1977) Genotype × environment interaction and genotypic stability in loblolly pine. Silvae Genet 26:21–26
Owino F, Killison RC, Zobel BJ (1977) Genotype × environment interaction and genotypic stability in loblolly pine. Silvae Genet 26:131–134
Paul AD, Foster GS, Caldwell T, McRae J (1997) Trends in genetic and environmental parameters for height, diameter, and volume in a multilocation clonal study with loblolly pine. For Sci 43:87–98
Pederick LA (1990) Family × site interaction in Pinus radiata in Victoria, Australia, and implications for breeding strategy. Silvae Genet 39:3–4
Pevsner J (2009) Bioinformatics and functional genomics, 2nd edn. Wiley-Blackwell, Hoboken
Piepho HP (1995) Robustness of statistical tests for multiplicative terms in the additive main effects and multiplicative interaction model for cultivar trials. Theor Appl Genet 90:438–443. doi:10.1007/BF00221987
Pierce BA (2005) Genetics: a conceptual approach. Freeman, New York
Rad MRN, Kadir MA, Rafii MY, Jaafar HZE, Naghavi MR, Ahmadi F (2013) Genotype × environment interaction by AMMI and GGE biplot analysis in three consecutive generations of wheat (Triticum aestivum) under normal and drought stress conditions. Aus J Crop Sci 7:956–961
Rae AM, Pinel MPC, Bastien C, Sabatti M, Street NR, Tucker J, Dixon C, Marron N, Dillen SY, Taylor G (2008) QTL for yield in bioenergy Populus: identifying G × E interactions from growth at three contrasting sites. Tree Genet Genomes 4:97–112
Ratcliffe B, El-Dien OG, Klápště J, Porth I, Chen C, Jaquish B, El-Kassaby YA (2015) A comparison of genomic selection models across time in interior spruce (Picea engelmannii × glauca) using unordered SNP imputation methods. Heredity 115:547–555. doi:10.1038/hdy.2015.57
Rauw WM, Gomez-Raya L (2015) Genotype by environment interaction and breeding for robustness in livestock. Front Genet 6:310. doi:10.3389/fgene.2015.00310
Raymond CA (2011) Genotype by environment interactions for Pinus radiata in New South Wales, Australia. Tree Genet Genomes 7:819–833. doi:10.1007/s11295-011-0376-4
Raymond CA, Namkoong G (1990) Optimizing breeding zones: genetic flexibility or maximum value? Silvae Genet 39:110–113
Raymond CA, Volker PW, Williams ER (1997) Provenance variation, genotype by environment interactions and age-age correlations for Eucalyptus regnans on nine sites in South Eastern Australia. For Genet 4:235–251
Rehfeldt GE, Ying CC, Spittlehouse DL, Hamilton DA (1999) Genetic responses to climate in Pinus contorta: niche breadth, climate change, and reforestation. Ecol Monogr 69:375–407. doi:10.1890/0012-9615(1999)069[0375:GRTCIP]2.0.CO;2
Resende M, Munoz Del Valle P, Acosta J, Resende M, Grattapaglia D, Kirst M (2011) Stability of genomic gelection prediction models across ages and environments. BMC Proc 5:O14
Resende MDV, Resende MFR Jr, Sansaloni CP, Petroli CD, Missiaggia AA, Aguiar AM, Abad JM, Takahashi EK, Rosado AM, Faria DA, Pappas GJ Jr, Kilian A, Grattapaglia D (2012a) Genomic selection for growth and wood quality in Eucalyptus: capturing the missing heritability and accelerating breeding for complex traits in forest trees. New Phytol 194:116–128
Resende MFR, Muñoz P, Acosta JJ, Peter GF, Davis JM, Grattapaglia D, Resende MDV, Kirst M (2012b) Accelerating the domestication of trees using genomic selection: accuracy of prediction models across ages and environments. New Phytol 193:617–624
Riemenschneider DE, Berguson WE, Dickmann DI, Hall RB, Isebrands JG, Mohn CA, Stanosz GR, Tuskan GA (2001) Poplar breeding and testing strategies in the north-central U.S.: demonstration of potential yield and consideration of future research needs. Forest Chron 77:245–253
Robertson A (1959) The sampling variance of the genetic correlation coefficient. Biometrics 15(3):469
Roth BE, Jokela EJ, Martin TA, Huber DA, White TL (2007) Genotype × environment interactions in selected loblolly and slash pine plantations in the southeastern United States. For Ecol Manag 238:175–188. doi:10.1016/j.foreco.2006.10.010
Rweyongeza DM (2011) Pattern of genotype-environment interaction in Picea glauca (Moench) Voss in Alberta, Canada. Ann For Sci 68:245–253
Shelbourne CJA (1972) Genotype-environment interaction: its study and its implications in forest tree improvement. In: the IUFRO Genetics and SABRAO Joint Symposium, Tokyo, Japan, 1972. pp 1–28
Sierra-Lucero V, Huber DA, McKeand SE, White TL, Rockwood DL (2003) Genotype-by-environment interaction and develoment considerations for families from Florida provenances of loblolly pine. For Genet 10:85–92
Sixto H, Salvia J, Barrio M, Ciria MP, Cañellas I (2011) Genetic variation and genotype-environment interactions in short rotation Populus plantations in southern Europe. New For 42:163–177
Smith A, Cullis B, Thompson R (2001) Analyzing variety by environment data using multiplicative mixed models and adjustments for spatial field trend. Biometrics 57:1138–1147. doi:10.1111/j.0006-341X.2001.01138
Smith AB, Ganesalingam A, Kuchel H, Cullis BR (2015) Factor analytic mixed models for the provision of grower information from national crop variety testing programs. Theor Appl Genet 128:55–72. doi:10.1007/s00122-014-2412-x
Sohn SI, Goddard RE (1979) Influence of infection percent on improvement of fusiform rust resistance. Silvae Genet 28
Stoehr M, Woods J, Yanchuk A (2011) Selection approaches in high-elevation coastal Douglas-fir in the presence of G×E interactions. Silvae Genet 60:79–84
Stonecypher RW, Piesch RF, Helland GG, Chapman JG, Reno HJ (1996) Results from genetic tests of selected parents of Douglas-fir (Pseudotsuga menziesii [Mirb.] Franco) in an applied tree improvement program. For Sci Monogr 32:1–35
Strandberg E, Kolmodin R, Madsen P, Jensen J, Jorjani H (2000) Genotype by environment interaction in Nordic dairy cattle studied by use of reaction norms. In: Interbull Meeting, Bled, Slovenia, May 14–15 2000. pp 41–45
Suontama M, Low CB, Stovold GT, Miller MA, Fleet KR, Li Y, Dungey HS (2015) Genetic parameters and genetic gains across three breeding cycles for growth and form traits of Eucalyptus regnans in New Zealand. Tree Genet Genomes 11:1–14. doi:10.1007/s11295-015-0957-8
Sykes R, Li B, Isik F, Kadla J, Chang H-M (2006) Genetic variation and genotype by environment interactions of juvenile wood chemical properties in Pinus taeda L. Ann For Sci 63:897–904
Wang T, Hamann A, Yanchuk A, O’Neill GA, Attken SN (2006) Use of response functions in selecting lodgepole pine populations for future climates. Glob Change Biol 12:2404–2416
Westbrook JW, Walker AR, Neves LG, Munoz P, Resende MFR, Neale DB, Wegrzyn JL, Huber DA, Kirst M, Davis JM, Peter GF (2014) Discovering candidate genes that regulate resin canal number in Pinus taeda stems by integrating genetic analysis across environments, ages, and populations. New Phytol 205:627–641
White TL, Adams WT, Neale DB (2007) Forest genetics. CAB International, Cambridge
Wolf YI, Rogozin IB, Kondrashov AS, Koonin EV (2001) Genome alignment, evolution of prokaryotic genome organization, and prediction of gene function using genomic context. Genome Res 11:356–372. doi:10.1101/gr.161901
Woltereck R (1909) Weitere experimentelle Untersuchungen über Artveränderung, speziell über das Wesen quantitativer Artunterschiede bei Daphniden. Verhandlungen der Deutschen zoologischen Gesellschaft:110–172
Woolaston RR, Kanowski PJ, Nikles DG (1991) Genotype-environment interactions in Pinus caribaea var. hondurensis in Queensland, Australia. Silvae Genet 40:228–232
Wu HX, Matheson AC (2005) Genotype by environment interactions in an Australia-wide radiata pine diallel mating experiment: implications for regionalized breeding. For Sci 51:29–40
Wu HX, Ying CC (2001) Variation on reaction norm in lodgepole pine natural populations. Theor Appl Genet 103:331–345. doi:10.1007/s001220100540
Xie CY (2003) Genotype by environment interaction and its implications for genetic improvement of interior spruce in British Columbia. Can J For Res 33:1635–1643. doi:10.1139/x03-082
Xie CY, Yanchuk AD (2002) Genetic parameters of height and diameter of interior spruce in British Columbia. For Genet 9(1):1–10
Yan W (2002) Singular-value partitioning in biplot analysis of multienvrionment trial data. Agron J 94:990–996
Yan W, Hunt LA (2001) Interpretation of genotype × environment interaction for winter wheat yield in Ontario. Crop Sci 41:19
Yan W, Hunt LA, Sheng Q, Szlavnics Z (2000) Cultivar evaluation and mega-environment inverstigation based on the GGE Biplot. Crop Sci 40:597–605
Yan W, Kang MS, Ma B, Woods S, Cornelius PL (2007) GGE biplot vs. AMMI analysis of genotype-by-environment data. Crop Sci 47:641–653
Yu Q, Pulkkinen P (2003) Genotype-environment interaction and stability in growth of aspen hybrid clones. For Ecol Manag 173:25–35. doi:10.1016/S0378-1127(01)00819-2
Zapata-Valenzuela J (2012) Use of analytical factor structure to increase heritability of clonal progeny tests of Pinus taeda L. Chil J Agric Res 72:309–315
Zas R, Merlo E, Diaz R, Fernandez-Lopez J (2003) Stability across sites of Douglas-fir provenances in northern Spain. For Genet 10:71–82
Zhao XY, Bian XY, Li ZX, Wang XW, Yang CJ, Liu GF, Jiang J, Kentbayev Y, Kentbayeva B, Yang CP (2014) Genetic stability analysis of introduced Betula pendula, Betula kirghisorum, and Betula pubescens families in saline-alkali soil of northeastern China. Scand J For Res
Zobel RW, Eright MJ, Gauch HG Jr (1988) Statistical analysis of a yield trial. Agron J 80:388–393
Data archiving statement
This review manuscript does not use any data. There are no data uploaded to any database.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by S. C. González-Martínez
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, Y., Suontama, M., Burdon, R.D. et al. Genotype by environment interactions in forest tree breeding: review of methodology and perspectives on research and application. Tree Genetics & Genomes 13, 60 (2017). https://doi.org/10.1007/s11295-017-1144-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11295-017-1144-x