1 Introduction

Climate change on a global scale has led to spatial and temporal variation of precipitation on a regional and local scale. Accordingly, the frequency of the drought and flood disasters and abrupt change in the natural event has occurred and will continue in the future. Fang et al. (2017) claimed that the changes in the hydrological cycle can affect society and the environment. As a critical hydroclimatic variable, precipitation will directly affect floods, droughts, and water resources (Tian et al., 2016). Many researchers studied the spatial and temporal variability of rainfall within the last decades, among them were Zarghami et al. (2011), Wang et al. (2013), Chen et al. (2018), Huang et al. (2019), and Aydin and Raja (2020). They concluded that precipitation characteristics had changed considerably in which climate warming leads to an increase in rainfall, affects the quality and quantity of the water resources, and threatens the ecosystem. In general, Kurdistan Region has a semi-arid climate type. To adapt to the upcoming water shortage, the farmers and stakeholders seek to find alternative strategies to supply water. Hence, constructing small ponds and medium-sized dams seems to be the optimum choice. Rainwater harvesting (RWH) structures decrease the runoff rate and increase the groundwater efficiency and aquifer recharge (Adham et al., 2018; Kadam et al., 2019). Based on Tauer and Prinz (1993), the main challenges faced by implementing the RWH technique are primarily related to rainfall, intensity and distribution, runoff properties, soil water storage, reservoir capacity, agroforestry system, accessible technology, and socioeconomic situations. Environmental and hydrological conditions indicate that the Kurdistan Region of Iraq is an adequate area for RWH and can play a vital role in augmenting water for various purposes in order to achieve self-sufficiency (Zakaria et al., 2013).

Qaradaqh is one of the rural and touristic areas in the region confronting water shortage. This area provides water for irrigation and domestic uses mainly from springs, ephemeral streams, and well waters. The water scarcity and fertility of soils are significant constraints affecting socio-economic and agricultural developments in the area of interest. Drought events over the past two decades have caused most springs and streams to dry up, leading to a decline in groundwater levels and soil fertility. Although the region receives more than 600 mm/annum of precipitation, the mismanagement of this natural resource led to the loss of most of this input as a surface runoff outside the area of interest. The feasibility of constructing RWH can augment the water supply (Rajasekhar et al., 2020). Therefore, evaluating and selecting the appropriate sites for RWH during the rainy season is crucial to maintaining sustainable water management. The procedures required for collecting and analyzing thematic maps are mainly related to natural and artificial factors. They integrated with multi-criteria decision-making (MCDM) and GIS tools to investigate the potential sites for RWH by applying several methods, including AHP, simple additive weighting method (SAWM), and FBI methods. The validation and sensitivity analysis are performed to evaluate and validate the findings.

2 Study Area

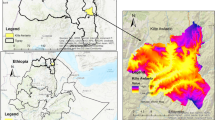
The Qaradaqh basin is located in the southern part of the Sulaimaniyah city and covers an area of 605 km2 (Fig. 1). The region has a semi-arid environment with a mean annual precipitation of 650 mm. The average temperature ranges from 18 °C in January–February to 40 °C in July–August for the last 30 years. The area consists geologically of sedimentary rock units. The stratigraphic sequence ranges in age from the Paleogene to Holocene. The lithological formations and hydrogeological setting of the area were studied by many researchers, including Bellen et al., (1959), Stevanovic & Markovic, (2003), Jassim & Goff, (2006), Mian et al., (2017), Nejad et al., (2021), Mohammed et al., (2020), etc. The characteristics and outcropping area of these stratigraphic units are summarized in Table 1. The dominant land use/land cover types of the basin are grassland and cropland with 55.8% and 26.0%, respectively, moderate shrubland (10.5%), as well as bare land and forest with 4.6% and 2.6%, while impervious surface and water bodies comprise the lowest ratio (< 1.0%) covering the catchment respectively. Geomorphologically, the area of interest is dominated by a mountainous landscape. The majority of the folds and faults are located in a northwest-to-southwest direction (Mohammed et al., 2020). Based on the isotopic study carried out by Hamamin & Ali (2013), the δ18O–altitude effect was − 0.79‰/100 m for the area. The output of the tritium concentrations in the springs and water well samples revealed the conclusion that the values closely resemble the present time tritium concentration in precipitation. Based on the pumping test analysis conducted by Hamamin, (2011), the hydraulic conductivity of the carbonate rocks in the vicinity of the site is more than 40 m/day, while for the intergranular aquifers it ranges between 0.05 and 0.2 m/day.

Fig. 1
figure 1

Location site with LULC types of the study area

Full size image
Table 1 Lithology and total exposed area overall the Qaradaqh catchment
Full size table

Recently, drought and water shortage led to numerous socio-economic problems for the region. Based on Table 1, the dominant geological formation of the area is the Injana Formation which is composed mainly of a high level of fine claystone, siltstone, and clayey sandstone. It occupies an area of 282 km2 or 46.6% of the catchment. This formation’s large thickness and lithologic properties show a higher water storage capacity and provide a suitable medium for building water-collecting structures. Accordingly, constructing RWH, especially in this formation, is crucial and may serve this purpose.

3 Materials and Methods

Ten necessary affecting factors were considered to analyze the potential of RWH sites. All data were retrieved from international organizations and various government sources (Table 2). The methodology framework of the constructed model includes the preparation of thematic maps, construction of rainwater harvesting maps, validation of the proposed sites, and sensitivity analysis of the outputs (Fig. 2).

Table 2 Source of the criteria map
Full size table
Fig. 2
figure 2

Methodology flowchart and procedures applied in the current study

Full size image

3.1 Preparation of Thematic Maps

The selection of factors and preparation of corresponding thematic layers are important components of any model (Crozier, 1986). For the current work, several conditioning parameters related to natural environmental and artificial factors were prepared (Fig. 3). The first level in the proposed model represents identifying the factors affecting the potential target model. The second level contains six primary criteria: lithology and structure, topographical, land, hydrology, accessibility, and social-cultural factors. The third level involves all ten criteria used in the present research to determine suitable sites as the optimum solution for drought management. The hierarchical scheme was designed according to the relations between each criterion and the decision process for RWH site selection. All these thematic layers were changed to the UTM WGS-1984 coordinate system with the same pixel size of 12.5-m resolution cells.

Fig. 3
figure 3

Hierarchical scheme of the decision process for drought management

Full size image

3.2 Suitable RWH Site Selection Methods

The spatial analysis tools in GIS were used to create the abovementioned criteria as layers, each criterion consisting of a database of a digital map created in GIS. Following these main processes, the datasets were utilized to integrate the AHP model:

  1. 1.

    Creation of mapping constraints utilizing regions of exclusion and developing a digital GIS database (spatial information).

  2. 2.

    Creating appropriate buffer zones or special constraints around significant regions of artificial criteria to fit each criterion map.

  3. 3.

    Determine the weighting of each criterion based on the priority of the study objective and use the MCDA model to identify the most preferable alternative. Swing weighting considers the criteria levels for determining criteria weights, which measures the relative significance of each criterion compared to others. Decision-makers begin with a worst-case scenario in which all criteria are set to the lowest potential levels. Then they choose the most crucial criterion by choosing the one that, if improved, would have the most impact on the total situation (Sayl et al., 2021).

  4. 4.

    Sub-criteria weightings based on scientific research, expert opinion, and environmental standards and legislation.

  5. 5.

    Incorporate all weighted criteria derived from the (AHP, SAWM, and FBI) methods into a GIS to create a suitable index map and choose the optimal dam-building location.

  6. 6.

    Compare the results by combining fuzzy membership raster data based on the selected overlay type.

  7. 7.

    Determine the area and volume water storage capacity for each selected dam to manage water shortage in the study area.

3.2.1 Criteria Restriction

Specific geographic features are created using buffer zones around each criterion by GIS spatial analysis tools. A buffer zone is a neutral area that can be separated by grade to decrease or eliminate the impact of land-use practices on delicate regions or natural characteristics. To determine the proper distance from RWH locations, each criterion should be characterized by the recommended distance according to the potential environmental risks and excess cost by considering the requirements of government regulations (Kara & Doratli, 2012; Siddiqui et al., 1996).

3.2.2 Sub-criteria Rating Values

Each criterion was classified into sub-criteria and assigned a suitability rating value from 0 to 10 (Saaty, 1980). Due to the associated legislation, limitations, and regulations, the criteria and variables are determined and assessed for their suitability for the research region, together with experience and information from literature reviews and scientific experts in this field. This was done to collect more information about category priorities for the study area and to rate the categories’ importance regarding RWH site selection. Several steps were followed to evaluate the rating value for each criterion and sub-criteria using the GIS spatial analysis tools in a sequence (buffer, clip, extract, overlay, proximity, convert, reclassify, and map algebra). Sub-criteria buffer zone and rating values are shown in Table 3.

Table 3 Layer buffer zone with sub-criteria ratings
Full size table

3.3 Predictive Factors

3.3.1 Lithology and Structure Factors

In general, stratigraphic units have a significant role in the surface runoff and/or infiltration potential from the input waters. In the current study, this criterion was adopted to protect the study area from geological hazards by understanding the engineering properties of the formations for settlements and other large structure buildings (Jassim & Goff, 2006). The “Geological formations” sub-criteria included nine formations divided into four categories and were given ratings of 2, 4, 6, and 8 respectively (Fig. 3). The suitability index is classed in these categories based on the formation suitability with lithology and the permeability of the sediments due to grain size distribution, which affects infiltration rate.

The analytic hierarchy process (AHP) is a multi-criteria decision-making approach in which all criteria are allocated to different levels in the matrix utilizing pairwise comparison to establish the relative weights for criteria (Saaty, 1980). It generates the judgment matrix by comparing the degree of relevance of the relative element and the weight of each index that is relevant to the overall objective, simplifying decision-making. Nowadays, AHP is the widely applied method for weighting criteria using a pairwise comparison for individual or group factors. In a pairwise, each criterion is evaluated with all the others by assigning it an important value between 1 and 9. The description of compared factors is shown in Table 4.

Table 4 Scales for pairwise comparisons (Saaty, 1980)
Full size table

Lineaments represent the potential weakness of any construction; accordingly, they should be avoided. Based on Noori et al., (2019), the dam sites should be located at least 100 m away from lineaments and active faults (Othman et al., 2020). As a result, all parameters were implemented accordingly, and the result was prepared and modified using the ArcGIS environmental toolboxes. The “Lineament” criterion is classified based on the distance of the weakness and risks from the suggested dam. Buffer zones ranging from 0 to 400 m received a rating value of 10, while buffer zones greater than 400 m received a score of 0 (Al-Ruzouq et al., 2019; Ramakrishnan et al., 2009; Singhai et al., 2019).

3.3.2 Hydrology Factors

Climate change significantly impacts rainfall scarcity due to changes in annual precipitation amounts, while excess rainwater causes floods (Gezie, 2019; Lema & Majule, 2009). In this category, the focus was on the precipitation and distance from the permanent stream. The rainfall data were gathered from the Directory of Sulaymaniyah weather Forecasting using the interpolation Thiessen polygon method in ArcGIS. The rainfall map is classified into four categories (< 650, 650–670, 670–690, and 690–720 mm) (Fig. 3). Rainfall was given a higher rating (4–10) in this study due to the importance of rainfall for water harvesting (Critchley et al., 2013; Rockström et al., 2010). The highest score of 10 was assigned to buffer zones from streams of 0–100 m in the “Stream” criteria due to the relevance of the planned dam existing near the stream (Fig. 3). More than 100-m buffer zones obtained a 0 rating (Shao et al., 2020). The runoff map was prepared in the form of CN benefitting from the geological map and soil, and geological formations in the area. The “CN” criterion was used to predict direct runoff. The CN for a watershed can be estimated as a function of land use, soil type, and antecedent watershed moisture using tables published by the United States Soil Conservation Service (Walega et al., 2020). To construct the runoff map of the case area, suitable topographical, geological, and soil maps, with the assistance of the experts and field trips, were achieved for dividing the basin into various zones with different curve numbers. In respect to the soil texture, it varies from clay to silty loam, while most of the mountain areas that exhibit high infiltration rates and soils could be classified under sandy loam, thin, or absent soil cover type (Fig. 4G). The most challenging issue in using SCS method is to find a suitable curve number for areas covered by limestone (such as Khurmala-Sinjar and Pilaspi formations); such sites are not given in the booklet of SCS Service. With a few exceptions, those terrains are put into hydrologic group B which have moderately low runoff or when thoroughly wet, while the soils of most parts of the plain sites are placed under group C, which are characterized by the high potential to yield runoff. Finally, curve numbers for each zone are determined. As can be noted from Fig. 3, the Qaradaqh watershed is divided into five subzones. The predicted lowest CN of 57 and 60 is within locations dominated by Sinjar and Pilaspi formations because those areas are characterized by joint and fracture networks system which provide excellent paths for percolating the precipitation. In addition to that, the undulated surfaces of the mountains lessen the opportunity for the flooded water to flow downward the lower elevated lands before finding its way to the existing discontinuities. In contrast, most formations characterized by low infiltration rate (such as Kolosh, Gercus, Injana and Fat'ha formations) with CN of 86 have the highest runoff potentials. High CN values indicate more rainfall and a greater volume of runoff. However, soil type and slope have a considerable impact on runoff and later, water harvesting. Curve numbers 57 and 60 were given a rate of 3 because they have the same soil classes, as lower values for certain correspond to an increased ability of the soil to retain rainfall and will produce much less runoff. Curve number 62 was given a rate of 6 because it had a different soil class than the other classes, and curve numbers 83 and 86 were given an 8 as they have relatively the same soil classification (Al-Abadi et al., 2017; Al-Ruzouq et al., 2019; Rajasekhar et al., 2020; Ramakrishnan et al., 2009; Rejani et al., 2017; Tiwari et al., 2018).

Fig. 4
figure 4

G–J Rating value for sub-criteria soil, DEM, slope, and villages

Full size image

3.3.3 Accessibility and Socio-cultural Factors

The “land use” criterion was adopted according to the land use classification and land specification due to the priority of land use and the distance between the dam site and other categories in the land use classification like factories, pasture, and forests, also considering the cost of unused land and ownership of agriculture land (Alkaradaghi et al., 2018). LULC criteria, which determines the approximate distance between dam sites, are influenced by a variety of variables, including government laws and scientific recommendations. The main goal of the dam proposed for the study region is to supply the stored water for irrigation. Dams should be built close to agricultural regions to reduce distances between crops while also considering flood risk (Mugo & Odera, 2019). The approximate distance should, in general, be acceptable for urban planning and potential future expansion. Furthermore, the economic concerns of transportation costs must assure water transportation costs will be reduced by the proximity of roads, settlements, and villages near the planned sites (Othman et al., 2020). The land-use classification was prepared using Landsat 8 Enhanced Thematic Mapper plus images that were downloaded from the United States Geological Survey (available at https://earthexplorer.usgs.gov) and processed by remote sensing software (ENVI 5.4). As a result, seven sub-criteria were recognized using pre-processed classified images from the training data, region of interest, or ROI, and considering the maximum likelihood of estimating probabilistic model parameters in a supervised classification technique based on Bayesian theory. Almost all MCDA studies on land use and land cover classification rely on specialists in the field and the degree of importance in each subcategory to the specific project aim. Forest and shrubland received a rating of 4 due to the suitability degree of these areas for dam implementation, while cropland, water body, and grassland received ratings of 2, 6, and 8, respectively, while impervious surface and bare land received ratings of 10 according to land availability for water harvesting without constraints (Alkaradaghi et al., 2019) (Fig. 4H).

3.3.4 Topography and Land Factors

The soil criterion was used since soil texture and structure influenced soil infiltration rates and runoff volume (Jha et al., 2014). The layer of the soil type was obtained from Buringh, (1960). Two main groups of soil are found in the area of interest: vertisols and aridisols. These soil types were rated 6 and 4 respectively (Fig. 4G). The vertisol soil type which contains 43% clay is more suitable for RWH building structures. The topography parameters are considered an essential part of controlling infiltration and runoff prevention. Altitude above the mean sea level in addition to the slope angle was derived from the digital elevation model (DEM) which was collected from the ALOS (ALOS PALSAR sensor: High-Resolution Observation Mode) accessed through ASF DAAC: 11 June 2015 Source. The extracted altitude of the catchment ranges between 373 and 1870 m, while the mean elevation is 905 m. The raster elevation model was divided into five categories, whereby 373–700, 700–850, 1325–1870, 1000–1325, and 850–1000 m above mean sea level (a.m.s.l.) were given ratings of 2, 4, 6, 8, and 10, respectively (Fig. 4H). In this research, appropriate elevations for dam suggestion sites were given grading values of 8 and 10 according to transportation cost and flood risk (Tiwari et al., 2018). The criterion of the slope was selected in respect of the potential for floods in the area (Prahl et al., 2018). Runoff drainage would be affected by excessively flat slopes (Javaheri et al., 2006; Yesilnacar et al., 2012). Landslides are more possible on steeper slopes, placing additional stress on infrastructural foundations. The steeper the slope on the building site, the less water storage and sediment accumulation, whereas lower slopes have a greater storage capacity (Ahmad & Verma, 2018). Four categories have been identified for land slope, less than 5°, 5°–10°, 10°–30°, and 30°–70°, and these were given ratings of 4, 8, 10, and 6 respectively (Fig. 4I). According to the literature, the slope range of 10°–30° is considered the best slope for implementing a dam due to flood risk and best water accumulation as a reservoir (Grum et al., 2016; Sayl et al., 2017). Here, we can use the same ranges of RWH as suggested by the abovementioned authors because both structures are more or less applied in the same environment. Buffer zones of higher than 1 km were provided with the rating of 10 in the “village” layers, while the zones with less than this value were given 0 grading values (Alkaradaghi et al., 2019) (Fig. 4J).

3.4 Multi-criteria Decision-making Methods

3.4.1 Analytical Hierarchy Process

AHP is a multi-criteria decision-making strategy where all criteria are assigned to different levels using pairwise comparison in the matrix to derive the relative weights for criteria. The elements of a row (i = 1, 2…, m) and column (j = 1, 2…, n) of xij are used to express the performance values in a matrix in terms of the (i) and (j) rows and columns, respectively. The values of the comparison criterion above the diagonal were used to fill the top triangle of the matrix. The inverse values of the top diagonal are then used to fill the lower triangle of the matrix, using Eq. (1) (Şener et al., 2011; Teknomo, 2006). The elements of a row (i = 1, 2,…,m) and column (j = 1, 2,…,n) of xij are used to express the performance values in a matrix in terms of the (i) and (j) rows and columns, respectively. The values of the comparison criterion above the diagonal were used to fill the top triangle of the matrix. The inverse values of the top diagonal are then used to fill the lower triangle of the matrix, using Eq. (1) (Şener et al., 2011; Teknomo, 2006).

$$\left({x}_{j1}=1/{x}_{ij}\right)$$
(1)

where xij is the element of row i and column j of the matrix.

In a decision matrix, the usual comparison matrix for every question and the relative relevance of the criteria could be described as follows (Eryiğit & Sulaiman, 2022):

(2)

The eigenvectors for each row are produced using geometric principles by multiplying the value for each criterion in each column in the same row of the original pairwise comparison matrix and then applying it to each row, as formulated below (Pecchia et al., 2011; Sayl et al., 2021).

$${\mathbf{E}\mathbf{g}}_{{\varvec{i}}}=({{x}_{11}\times {x}_{12 }\times {x}_{13 }\times {x}_{14 }{\dots }\times {x}_{1{\varvec{n}} })}^{{~}^{1}\!\left/ \!{~}_{{\varvec{n}}}\right.}$$
(3)

where Egi is the eigenvalue for row i, and n is the number of criteria in a row (i).

The priority vector is calculated by dividing the eigenvalues by their total and normalizing them to 1. The maximum lambda (max) is calculated by adding the products of each element of the priority vector and the sum of the reciprocal matrix’s columns, as indicated in the formula below (Eryiğit & Sulaiman, 2022; Pecchia et al., 2011; Sayl et al., 2021).

$${{\varvec{W}}}_{{\varvec{i}}}= \frac{{\mathrm{Eg}}_{i}}{{\sum }_{{\varvec{i}}=1}^{{\varvec{m}}}{\mathrm{Eg}}_{i}}$$
(4)
$$\left[\begin{array}{c}\begin{array}{c}{ P}_{1 }\\ { P}_{2 }\\ .\\ :\\ :\\ { P}_{n }\end{array}\\ \end{array}\right] = \left[\begin{array}{c}\begin{array}{ccccc}\frac{\frac{{x}_{11 }}{\sum {x}_{i1 }}}{n}+& \frac{\frac{{x}_{12 }}{\sum {x}_{i2 }}}{n}& \cdots & +& \frac{\frac{{x}_{in }}{\sum {x}_{in }}}{n}\\ .& \cdots & \cdots & \cdots & .\\ .& \cdots & \cdots & \cdots & .\\ \frac{\frac{{x}_{n1 }}{\sum {x}_{i1 }}}{n}+& \frac{\frac{{x}_{n2 }}{\sum {x}_{i2 }}}{n} & \cdots & +& \frac{\frac{{x}_{nn }}{\sum {x}_{in }}}{n}\end{array}\\ \end{array}\right]$$
$$\left[\begin{array}{c}\begin{array}{c}{W}_{1 }\\ {W}_{2 }\\ .\\ .\\ .\\ {W}_{n }\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{ P}_{1 }\\ { P}_{2 }\\ .\\ .\\ .\\ { P}_{n }\end{array}\\ \end{array}\right] \times \left[\begin{array}{c}\begin{array}{ccccc}{x}_{11 }& {x}_{11}& \dots & \dots & {x}_{1n }\\ {x}_{21 }& {x}_{22 }& \dots & \dots & {x}_{2n }\\ .& .& .& \dots & .\\ .& .& .& \dots & .\\ .& .& .& \dots & .\\ {x}_{m1 }& {x}_{m2 }& \dots & \dots & {x}_{mn }\end{array}\end{array}\right]$$
(5)

The maximum lambda (λmax) is calculated by adding the products of each element of the priority vector and the sum of the reciprocal matrix’s columns, as illustrated in the following formula (Alkaradaghi et al., 2019; Pecchia et al., 2011; Sayl et al., 2021):

$$\mathrm{\lambda max}= \frac{1}{{\varvec{n}}} \sum_{{\varvec{i}}=1 }^{m}\frac{{{\varvec{W}}}_{{\varvec{i}}}}{{{\varvec{P}}}_{{\varvec{i}}}}$$
(6)
$${\varvec{C}}{\varvec{R}}=\frac{({\varvec{\uplambda}}\mathbf{m}\mathbf{a}\mathbf{x}\boldsymbol{ }-\boldsymbol{ }{\varvec{n}})/({\varvec{n}}\boldsymbol{ }-\boldsymbol{ }1)}{{\varvec{R}}{\varvec{I}}}$$
(7)

The consistency ratio (CR) is obtained by dividing the consistency index value (CI) by the random index value, here (RI = 1.56), and n is the size of the matrix (n = 10). Table 5 shows the mean random index value RI for a matrix with different sizes (Saaty, 1980).

Table 5 Random inconsistency indices for different values of (n) (Chang & Davila, 2008; Isalou et al., 2013)
Full size table

The consistency index \(CI=(\lambda \mathrm{max }- n)/(n - 1)\) represents the equivalent of the mean deviation of each comparative element and the standard deviation of the evaluation error from the true ones (Sólnes, 2003), which will frequently turn out to be larger than the value describing a fully consistent matrix to provide a measure of severity of this deviation (Belton & Stewart, 2002). If CR is less than 0.1, the ratio indicates a reasonable consistency level in the pairwise comparison. CR should, therefore, be less than 0.1. In this study, CR = 0.027 < 0.1 and RI10 = 1.49. For any matrix, the judgments are completely consistent if a CR equals 0 (Musingwini & Minnitt, 2008).

In addition, multi-criteria decision-making (MCDM) methods were used to obtain the comparative weights for each criterion using different methods including AHP, SAWM, and FBI.

3.4.2 Suitability Index

By using ESRI’s ArcGIS Spatial Analyst to execute a weighted overlay analysis, all of the criteria were classed into a similar assessment scale with the same cell size (Gutzwiller et al., 2017). In this approach, four levels of appropriateness were used: “Most Suitable,” “Suitable,” “Relatively suitable,” and “Unsuitable.” The weighted linear combination (WLC) method was used in this study, which is based on a weighted average and is easy to grasp and apply in ArcMap using map algebra operations and cartographic modeling; to obtain the suitability index value for the potential areas, the WLC method was used based on the following formula (Alfy et al., 2010; Charnpratheep et al., 1997).

$${S}_{i}=\sum_{j=1}^{n}{W}_{j} \times {G}_{ij}$$
(8)

where Si is the suitability index, Wj is the relative importance weight of the criterion, Gij is the grading value (i) under criterion (j), and n is the total number of criteria.

The WLC method was applied to all criteria using the special analysis tools “map algebra” GIS to assess the suitability index map. This is achieved by summing up the products by multiplying the sub-criteria rating values for each criterion (based on expert opinion in this sector) by the corresponding relative importance weight.

3.4.3 Simple Additive Weighting Method

SAWM is a basic ranking method and is specified as a weighted linear combination or scoring method using a multi-attribute decision approach (Yildirim, 2012). The approach is based on weighted averages, with the weights of comparative significance directly allocated by the decision-maker to assess the weight for each criterion and to select the significance and weight of each criterion relative to the other criterion. The normalization of the relative weight of importance is done by dividing the weight of the criterion by their summation. The simple additive weighting method evaluates each alternative using the following formula (ŞENER 2004, Afshari et al, 2010).

$${W}_{i}= \frac{{A}_{i }}{{\sum }_{j=1}^{n}{A}_{j}} j=\mathrm{1,2},\dots n$$
(9)

where Wi is the normalized weight of each criterion by its sum; Ai is the weight of each criterion in the row (i); Aj is the weight of each criterion in the column (j); n is the number of criteria.

3.4.4 Fuzzy-Based Index

Weights can be applied to many input layers, combined into a single output, and favored locations within that output based on distribution and form attributes using overlay analysis techniques. These tools are widely used for suitability modeling. Overlay analysis may be done in a variety of ways. Regardless of methodology variations, they all follow the same approaches for handling multi-criteria problems. Weighted overlay in overlay analysis categorizes and weights multiple input rasters. Fuzzy logic is utilized in the fuzzy overlay and fuzzy membership tools to reconcile discrepancies in geographic information features and geometry.

4 Results and Discussion

4.1 Pairwise Comparison of Criteria

The relevance and weight of each criterion were compared in the weight evaluation approach. This was done by taking into account the views of local experts who have worked in this profession as well as the opinions of decision-makers. Each parameter specifies a value for the weight it deserves by assuming the method of straightforward additive weighting. These weights are then used to revise the right weight for each parameter in the comparison matrix for every criterion. Thus, a matrix comparison with weights for the 10 criteria was produced (Table 6).

Table 6 Pairwise comparison matrix for selecting a suitable dam site
Full size table
$$\mathrm{In}\;\mathrm{this}\;\mathrm{study},\;n=10,\;{\mathrm\lambda}_{max}=10.55,\;\mathrm{RI}\;\left(10\right)=1.49,\;\mathrm{and}\;\mathrm{CR}=0.02$$

Since CR obtained was less than 0.1, the experts’ judgments were considered consistent because, if CR is less than 0.1, the ratio indicates a reasonable consistency level in the pairwise comparison (Saaty, 1980).

4.2 Suitability Map

A suitability map for the dam/reservoir in the semi-arid zone of the province was produced together with a different map of suitability and classified into four classes of suitability levels predefined to be unsuitable, relativity suitable, suitable, and most suitable obtained from the AHP, SAWM, and fuzzy overlay methods. Seven locations were selected within the study area with the most suitable class in all methods as resulted in Fig. 5, Fig. 6, and Fig. 7, to compare the suitability in all MCDM method areas in a percentage calculated for all classes to determine the most reliable method (Fig. 8).

Fig. 5
figure 5

Suitability index map for RWH using AHP method

Full size image
Fig. 6
figure 6

Suitability index map for RWH using SAWM method

Full size image
Fig. 7
figure 7

Suitability index map for RWH using fuzzy overlay method

Full size image
Fig. 8
figure 8

Comparison of suitability in MCDM method

Full size image

Water accumulation in all selected dams/reservoirs was determined to undertake water management in the study area. The surface volume tool calculates a raster’s area and volume, DEM, or terrain dataset surface above or below a specified reference plane. To compute reservoir volumes and surface areas while taking into account varied elevations in the watershed, 3D Analyst Tools in Arc Toolbox were utilized to calculate surface volume using input raster watershed DEM to obtain the computed volume and surface area as shown in Table 7; if all seven candidate dams are built, the total water accumulation will be 377,260.8 m3.

Table 7 All suggested dam/reservoir with area and volume calculation
Full size table

4.3 The Model Results in Accuracy and Validation

4.3.1 Consistency in the Analytic Hierarchy Process

In the analytic hierarchy process, in the statistical criterion for accepting or rejecting the pairwise reciprocal comparison matrices, the matrix’s consistency in random matrices is the introduction of flexibility in the acceptance criterion, as well as the simplicity of the index, the eigenvalue, and the criterion are all advantages of the consistency method.

The random index is the average value of the consistency index for random matrices using the Saaty scale, which accepts a matrix as consistent when CR is less than 0.1 (Saaty, 1980). As a result, the normalized eigenvector can be read as the relative importance of each alternative. For all pairwise comparisons, the comparison matrix satisfies the transitivity property in this situation. Since the observed consistency ratio was less than 0.1, the expert assessments were considered consistent because a consistency ratio of less than 0.1 creates a significant degree of consistency in pairwise comparisons.

4.3.2 Receiver Operating Characteristics

There are various approaches for estimating the accuracy of any model’s expected output. The receiver operating characteristics (ROCs) and its area under the curve (AUC) were used. For this purpose, each pixel value in the expected suitability map was classified based on the validity of suitable classes by overlaying and comparing this classified map with the existing selected dams. The AUC value was calculated using the ArcSDTM software package of ArcGIS. According to Chen et al. (2016), this AUC represents the accuracy of the predicted results. In this research, AUC values ranging from 0.5 to 1 mean that all MCDM results are good or are correctly selected, while values below 0.5 are randomly selected.

In prediction rate curve for the suitability index map produced by AHP, SAWM, and fuzzy overlay method, the AUC value calculated for all MCDM and the results found in this study are 0.72, 0.57, and 0.59 for the method AHP, SAWM, and fuzzy overlay, respectively, which means that the prediction accuracies in all methods are 72%, 57%, and 59% respectively. This moderate accuracy is due to the currently implemented sites used in the validation process. However, these traditional current dam sites are located in inappropriate areas (Fig. 7).

To examine the present and recommended sites in the research area, a total of seven locations were checked in the field. The suitability map was overlaid with the georeferenced points of the prospective sites to examine the level of coincidence between these data sources that provide an overview of the region’s water infrastructure.

As depicted in Fig. 8, the unsuitable ratio over the study area in all methods AHP, SAWM, and fuzzy overlay occupied 14.6%, 12.7%, and 14.2%, respectively. The “most suitable” class occupies (18%, 29.3%, and 24.7%) all methods. Geology, stream, and lineament after rain criteria affected the “relatively suitable” and “suitable” classes. Thus, the suitability index in the study area occupied the north and around the study area. In contrast, the unsuitable site cover the northeastern and zones in the middle due to restriction of geology, distance to stream with the villages, and slope criteria. However, the highest coverage of suitable areas is in contrast to the north part of the study area to reserve for rainwater.

In the research region, four concrete and mortar stone dams/reservoirs are currently operating. Two implemented small dams were in the most suitable areas, while the others were in an unsuitable site due to weight weaknesses in geology, lineament criteria, and high slope. Seven places within the study area are suggested as the most suitable candidates to increase the number of dams/reservoirs and improve water supply to local people during the dry season (Fig. 9).

Fig. 9
figure 9

Prediction rate curve for the suitability map produced by AHP, SAWM, and fuzzy overlay method

Full size image

5 Conclusion

This paper contributes with a case study for locating the best places for building small dams/reservoirs in a semi-arid region of northern Iraq using a GIS-based and different MCDM approaches. Identifying appropriate locations for small dams/reservoirs is essential for the study area, a semi-arid region with significant water deficits. The approach used in this study, which was based on GIS-based MCDM and AHP method, allowed us to obtain information about the relevant variables (rain, geology, stream, lineament, LULC, CN, soil, DEM, slope, villages) to create a suitable dam/reservoir map for the Qaradagh region. We found that the suitability map influenced by all selected criteria and sub-criteria in MCDM is determined by the matrix’s priority and judgment for each certation, as well as the importance of the criteria influenced by the research area’s property. The dam implementation matrix field includes decision-makers and field experts. The study also examined the suitability map produced by different MCDM approaches for choosing dams/reservoirs. The most dependable approach, according to this research, is AHP, which has a higher AUC value ratio than SAWM and fuzzy overlay.

This study reveals several critical unmeasurable predictions, such as a suitability map for dams/reservoirs and scientific valuable failed criteria to appear necessary before implementing a dam. The suitability map reveals that the majority of locations match these crucial criteria and scientific evaluation in this field. This study identified the most critical suitability factors to consider when deciding whether or not to build dams or reservoirs. This information raises questions about the infrastructure’s long-term performance, which planners should extensively examine to manage the region’s water demands effectively. The approach is adaptable enough to consider other criteria, experts/stakeholders, and up-to-date data when selecting where to put these facilities in semi-arid regions or other areas with water shortage crises.