1 Introduction

In recent years, quantum computing has been considered one of the most promising technologies to overcome the physical limitations of current computers, in what is known as the post-Moore era. Although it has not been definitively determined which types of problems can be solved more efficiently through quantum computing, more and more examples are emerging that demonstrate the advantages of quantum computing over classical computing [1, 2].

Quantum computing seeks to harness the principles of quantum mechanics to gain advantages in the realm of computation. This opens the door to significant advancements in various fields such as environmental systems, healthcare, energy, and security [3]. However, the programming paradigm of quantum computers differs from the traditional approach and requires the modification of conventional algorithms to adapt to the counterintuitive rules of quantum mechanics. The primary model used in quantum computing is based on quantum circuits, where traditional logic gates are replaced by quantum gates. These quantum gates must abide by the laws of quantum physics and, therefore, are always reversible.

Nowadays, we are in the era of Noisy Intermediate-Scale Quantum (NISQ) computing, and the main challenges in the design of quantum circuits and algorithms are the scarcity of resources (numbers of qubits in platforms) and the difficulty in implementing fault-tolerant circuits [4]. Nowadays, quantum computers have a moderate number of qubits but are still not large enough to solve relevant problems without being affected by noise. After NISQ era, it is expected that we will have access to a greater number of quantum resources, which will put emphasis on achieving fast circuits. Therefore, it is essential to build highly optimised circuits.

Time is also a crucial factor, since the longer the circuit’s computation, the greater the exposure to noise. In fact, the state of the system becomes less pristine, leading to the degradation of the coherence responsible for phenomena such as interference (decoherence) and quantum parallelism, even in the absence of operations [5]. Therefore, noise represents a physical challenge that can be partially addressed through careful circuit design. The aim is to reduce both the computation time of the circuit and the number of operations. Additionally, error detection and correction codes can be employed to mitigate the effects caused by noise. It is important to design circuits as compactly as possible.

The circuits used to perform arithmetic operations play a fundamental role in many quantum algorithms that achieve significant acceleration compared to well-known classical methods [6,7,8]. However, designing the arithmetic component requires a thoughtful approach to minimise the number of gates used and reduce operational error, especially since the operations must be reversible, making real implementations non-trivial [8]. Currently, small circuits for the implementation of arithmetic operations, such as quantum comparators, the operation under study in this work, are of great interest [9]. They can be invoked from much more complex circuits, considering the resource limitation on quantum platforms. It is important to note that although these circuits may not offer a speed advantage due to the use of quantum computing [10], they remain valuable for various algorithms and applications, including quantum image processing, where quantum comparators play a crucial role in feature extraction and classification of quantum images [11], as well as in quantum machine learning.

In this study, with the aim of achieving an efficient design of quantum comparators, we have examined the implementation of three comparator circuits from existing literature. Our goal is to introduce novel comparator circuits composed exclusively of gates from the Clifford+T set, leveraging both the inherent advantages of these gates and the fact that the Clifford+T set holds the advantage that its constituent gates are readily available on current quantum computing platforms. These proposed circuits are then compared to the ones previously analysed. Additionally, we propose optimisations of various gates to reduce the number of T-gates needed, recognising that although T-gates are essential for mitigating the effects of internal and external noise, they come at a high cost. These optimised gates (in terms of T-gates) are integrated into our implementations. T-gates are advantageous for implementing error detection codes, facilitating their use in a quantum environment, albeit at a higher cost compared to other quantum gates [9, 12, 13].

As a result of our efforts, the new comparators have successfully reduced the number of T-gates by more than half, representing a significant improvement in terms of efficiency and computational cost.

The remainder of the paper is structured as follows. Section 2 introduces fundamental concepts related to quantum gates and the metrics we have used to analyse all the circuits studied and implemented. Additionally, in this section, we propose new optimised versions of the TR, Peres, and GN gates. These enhanced versions are designed to address the inherent limitations and challenges of quantum computing. These innovative proposals can be seen in the context of their practical application in the following section. In Sect. 3, we present the study of three different quantum comparators and introduce three new quantum comparators built exclusively with Clifford+T gates. Section 4 summarises the results obtained in this paper and offers a comparison with three quantum comparators present in the state of the art. Finally, in Sect. 5, we present the general conclusions of this research.

2 Quantum gates and metrics

Quantum gates have been intricately designed for utilisation within quantum computers [14]. While some quantum gates perform operations akin to their classical counterparts, there are also quantum gates without equivalents in classical circuits. Quantum gates can be represented as invertible matrices, serving as unitary operators on either a single qubit or multiple qubits, thereby transforming their initial states into different configurations. It is pertinent to mention that the invertibility of quantum gates is a consequence of their nature as unitary operators.

The possibilities offered by quantum computing are vast, with an infinite collection of quantum gates available for individual qubit manipulation. This consequently opens up an infinite spectrum of possibilities for cases involving two or more qubits [15]. Fortunately, there are specific sets of quantum gates that enable us to approximate this boundless variety. One of these sets, though not the sole option, is commonly referred to as the Clifford+T set [16].

The Clifford group, which is generated by the H, S, and CNOT gates, boasts a broad range of applications due to its unique ability to convert Pauli operations into other Pauli operations [17]. However, it does not achieve universality, meaning it cannot fully encompass any quantum functionality with an arbitrarily small error by itself; it requires the inclusion of the T-gate to form the Clifford+T set and achieve universality [18].

The T-gate, also known as the \(\pi /8\) phase gate (due to the appearance of the RZ (\(\pi /4\)) matrix), is widely used in quantum computing to counterbalance the impact of both internal and external noise. Nevertheless, it comes at a higher computational cost compared to other basic quantum gates, such as the Hadamard gate or Pauli gates [13, 19,20,21]. This heightened cost arises from the T-gate’s requirement for more intricate operations and a greater number of elementary steps for its implementation. Consequently, its incorporation into quantum circuits can exert a substantial impact on the overall computational cost of the circuit, underscoring the need for careful control over its usage.

Hence, the primary objective of this study has been to propose novel quantum comparator circuits that exclusively use Clifford+T gates. This choice is not solely based on its universality but also because various studies have demonstrated that a widespread technique for building fault-tolerant quantum circuits is to design them using only Clifford+T gates [22, 23]. Research has shown that a circuit built exclusively with these gates allows the incorporation of error correction codes [16, 24, 25], which will improve its error tolerance. Additionally, the Clifford+T set holds the advantage that its constituent gates are readily available on current quantum computing platforms. Furthermore, there is a deliberate effort to control the utilisation of T-gates to maximise circuit efficiency.

The quantum gates used in this work are as follows:

  • The Hadamard gate or H gate is used to put the qubit into a superposition state [26]. The matrix that defines its behaviour is given by:

    $$\begin{aligned} H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 &{} 1\\ 1 &{} -1 \end{pmatrix} \end{aligned}$$
    (1)

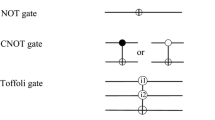
  • The CNOT gate performs an operation on two qubits, referred to as the control qubit and the target qubit. If the control qubit is in state \(|0\rangle \), the target qubit remains unchanged; however, if the control qubit is in the state \(|1\rangle \), the CNOT gate flips the state of the target qubit [12, 27]. Its behaviour is determined by the matrix presented as follows:

    $$\begin{aligned} \text {CNOT} = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{} \quad 0 &{} \quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{pmatrix} \end{aligned}$$
    (2)

  • The Pauli-X gate is equivalent to the classical NOT-gate, flipping the base state of a qubit. The matrix delineating its behaviour is specified as follows:

    $$\begin{aligned} \text {Pauli}\; X = \begin{pmatrix} 0 &{}\quad 1\\ 1 &{}\quad 0 \end{pmatrix} \end{aligned}$$
    (3)

  • The T-gate induces a phase shift of \(\pi /4\) and provides universality to the Clifford group. However, it is computationally expensive due to its complex operations, which can significantly affect circuit costs, necessitating cautious utilisation. The matrix outlining its behaviour is given by:

    $$\begin{aligned} T = \begin{pmatrix} 1 &{} \quad 0\\ 0 &{} \quad e^{\frac{i\pi }{4}} \end{pmatrix} \end{aligned}$$
    (4)

    Adjacent to this gate is its inverse, denoted as \(T^\dagger \) [28]. This gate induces a phase change of \(-\pi /4\) and shares the same characteristics of high cost and the inability to be efficiently simulated in a classical environment, similar to the T gate [13]. Its behaviour is defined by the matrix:

    $$\begin{aligned} T^\dagger = \begin{pmatrix} 1 &{} \quad 0\\ 0 &{} \quad e^{-\frac{i\pi }{4}} \end{pmatrix} \end{aligned}$$
    (5)

  • The S gate is equivalent to applying two consecutive T-gates. The defining matrix for its behaviour is given by:

    $$\begin{aligned} S = \begin{pmatrix} 1 &{}\quad 0\\ 0 &{}\quad i \end{pmatrix} \end{aligned}$$
    (6)

  • The Pauli-Z gate leaves the initial state \(\vert 0\rangle \) unchanged and assigns \(\vert 1\rangle \) to \(-\vert 1\rangle \). Its behaviour is defined by the matrix:

    $$\begin{aligned} \text {Pauli}\;Z = \begin{pmatrix} 1 &{}\quad 0\\ 0 &{}\quad -1 \end{pmatrix} \end{aligned}$$
    (7)

  • The Peres gate, given three qubits A, B, and C, returns \(A, B \oplus A\), and \(C \oplus AB\). The most standard implementation requires one CNOT gate, two Controlled-V gates, and one Controlled-\(V^\dagger \) gate [29]. However, it is important to note that this implementation will be optimised, and the details of this optimisation will be explained in the following subsection (see Subsection 2.1.2).

  • The TR gate, presented in [30], given three qubits A, B, and C, returns \(A, A \oplus B\), and \(A\bar{B} \oplus C\). An optimised version was proposed in [31] and can be seen in Fig. 1. This optimised version, also working with three qubits A, B, and C, produces outputs \(B, A \oplus C\), and \(A\bar{B} \oplus C\). However, it is important to note that in [32], a different implementation of the TR gate is used. This version consists of two Controlled-V gates, one Controlled-\(V^\dagger \) gate, and one CNOT gate, and it is this particular version of the TR gate that we propose optimising to reduce it cost in terms of T-gates.

  • The Temporary logical-AND gate is an alternative to the Toffoli gate, introduced in [33], focused on reducing the cost of T-gates. It performs the AND operation on two qubits and stores the result in an auxiliary qubit. It uses four T-gates, while the Toffoli gate uses seven T-gates, achieving an optimised converter. However, it should be noted that, unlike the Toffoli gate, the Temporary logical-AND gate cannot be applied to just any qubit C when one wants to perform the operation \(C \oplus AB\). Instead, this gate can only perform the AB operation on a qubit that has previously been prepared in a specific state of \(\frac{1}{\sqrt{2}} \left( |0\rangle + e^{\frac{i\pi }{4}} |1\rangle \right) \), called \(|T\rangle \). The aim of preparing the qubits in the state \(|T\rangle \) is to minimise the impact of the T gate on the overall circuit time. This is because the T gate is not only more resource-intensive than other gates but also takes longer to execute [13, 33]. The Temporary logical-AND gate functions on qubits that have already been readied in this specific state, ensuring these states are ready right from the beginning of the circuit. This accelerates the preparation of qubits in the required state, reducing the workload at the moment the gate is applied and ultimately enhancing the efficiency of the quantum circuit. Its implementation can be seen in Fig. 2.

  • The Controlled-V and Controlled-\(V^\dagger \) gates [14] have the same properties as the V and \(V^\dagger \) gates, but they represent a controlled version of the V gates. Taking into account that in this work, standard bases \(|0\rangle \) and \(|1\rangle \) will be used, and the possible outcomes of the gates V and \(V^\dagger \) are shown below:

    $$\begin{aligned} V(0) = \frac{1+i}{2} \begin{pmatrix} 1 &{}\quad -i \\ -i &{} \quad 1 \end{pmatrix} \begin{pmatrix} 1\\ 0 \end{pmatrix} = \frac{1+i}{2}\begin{pmatrix} 1\\ -i \end{pmatrix} \end{aligned}$$
    (8)
    $$\begin{aligned} V(1) = \frac{1+i}{2} \begin{pmatrix} 1 &{} \quad -i \\ -i &{} \quad 1 \end{pmatrix} \begin{pmatrix} 0\\ 1 \end{pmatrix} = \frac{1+i}{2}\begin{pmatrix} -i\\ 1 \end{pmatrix} \end{aligned}$$
    (9)
    $$\begin{aligned} V^\dagger (0) = \frac{1-i}{2} \begin{pmatrix} 1 &{} \quad i \\ i &{}\quad 1 \end{pmatrix} \begin{pmatrix} 1\\ 0 \end{pmatrix} = \frac{1-i}{2}\begin{pmatrix} 1\\ i \end{pmatrix} \end{aligned}$$
    (10)
    $$\begin{aligned} V^\dagger (1) = \frac{1-i}{2} \begin{pmatrix} 1 &{} \quad i \\ i &{} \quad 1 \end{pmatrix} \begin{pmatrix} 0\\ 1 \end{pmatrix} = \frac{1-i}{2}\begin{pmatrix} i\\ 1 \end{pmatrix} \end{aligned}$$
    (11)

    Taking these possibilities into account, there are three important properties that can be derived from the gates V and \(V^\dagger \):

    • \(V(A) \times V(A) = \bar{\text {A}}\)

    • \(V^\dagger (A) \times V^\dagger (A) = \bar{\text {A}}\)

    • \(V(A)\times V^\dagger (A) = V^\dagger (A) \times V(A) = \text {A}\)

    These properties are widely used in various works to simplify and reduce quantum circuits [7, 34, 35]. The matrices that define the behaviour of the Controlled-V and Controlled-\(V^\dagger \) gates are given by:

    $$\begin{aligned} \text {Controlled}\; V = \frac{1+i}{2} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{} \quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -i\\ 0 &{}\quad 0 &{}\quad -i &{} \quad 1 \end{pmatrix} \end{aligned}$$
    (12)
    $$\begin{aligned} \text {Controlled}\; V^\dagger = \frac{1-i}{2} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{} \quad 0\\ 0 &{} \quad 0 &{}\quad 1 &{} \quad i\\ 0 &{}\quad 0 &{}\quad i &{}\quad 1 \end{pmatrix} \end{aligned}$$
    (13)

  • The GN gate was proposed in [36] and is made up of two Controlled-V gates, one Controlled-\(V^\dagger \) gate, and one CNOT gate. This gate returns \(A \oplus C\), \({\overline{A}}C \oplus B\), and C. This implementation will be optimised and the details of this optimisation will be explained in the following subsection (see Sect. 2.1.3).

Fig. 1
figure 1

Most standard version of the TR gate proposed in [31]

Full size image
Fig. 2
figure 2

Implementation of Temporary logical-AND gate

Full size image

To assess the efficiency of the circuits analysed and proposed, the following established metrics will be followed:

  • T-count: total number of T-gates used in a quantum circuit. A lower T-count is generally considered better because it implies that fewer of these gates are being used in the circuit.

  • T-depth: the number of layers of T-gates in the circuit, where a layer consists of quantum operations that can be performed simultaneously. Therefore, a lower T-depth implies that the circuit can be executed in fewer stages, which can be beneficial in reducing execution time. In general, a lower T-depth is more efficient in terms of quantum resources and can execute more quickly on quantum hardware.

  • Ancillary qubits: inputs that have a constant value (for example, 0) used for auxiliary operations.

The metrics of the gates mentioned above are presented in Table 1. Furthermore, the gates belonging to the Clifford+T set have been indicated.

Table 1 Metrics of the described gates and membership in the Clifford+T set
Full size table

2.1 Proposed implementations of quantum gates

In our work, we introduce innovative implementations for three fundamental quantum gates: the Peres gate, the TR gate, and the GN gate. These proposed optimisations aim to reduce the number of T-gates needed.

2.1.1 TR Gate

A new implementation of the TR gate is proposed to minimise the utilisation of T-gates. This innovative approach is based on the use of a Temporary logical-AND gate, along with two Pauli-X gates and two CNOT gates (see Fig. 3).

Fig. 3
figure 3

New implementation of the TR gate, where A, B, and C are the qubits on which the operation is performed, and T is the auxiliary qubit initialised with the special state for the Temporary logical-AND gate

Full size image

In this version, the following can be observed:

  • The first Pauli-X gate negates qubit B before the Temporary logical-AND gate performs the qubit multiplication.

  • Next, the Temporary logical-AND gate performs the \(A{\overline{B}}\) multiplication and stores the result in the ancillary qubit.

  • A CNOT gate acts on the ancillary qubit, that is, \(A{\overline{B}}\) performing an \(\oplus \) operation with qubit C, resulting in \(A{\overline{B}}\oplus C\).

  • The second Pauli-X gate restores qubit B to its non-negated state so that the second CNOT gate can perform the \(A\oplus B\) operation.

2.1.2 Peres gate

The new version of the Peres gate uses a Temporary logical-AND gate and two CNOT gates (see Fig. 4).

Fig. 4
figure 4

Proposed new optimised version of the Peres gate, where A, B, and C are the qubits on which the operations are performed, and T is the auxiliary qubit initialised with the special state for the Temporary logical-AND gate

Full size image

In this version, it can be observed that:

  • The Temporary logical-AND gate performs the multiplication operation AB and stores the result in the ancillary qubit.

  • A CNOT gate acts on the ancillary qubit, that is, on AB performing an \(\oplus \) operation with qubit C, resulting in \(AB\oplus C\).

  • The second CNOT gate performs the \(A\oplus B\) operation.

2.1.3 GN Gate

An improved version of the GN gate is proposed, which reduces the T-count and T-depth. This version uses a Temporary logical-AND gate, two CNOT gates, and two Pauli-X gates. The implementation of this proposal can be seen in Fig. 5.

Fig. 5
figure 5

Proposed version of the GN gate, where A, C, and B are the qubits on which the operations are performed, and T is the auxiliary qubit initialised with the special state for the Temporary logical-AND gate

Full size image

In this optimised version, it can be observed that:

  • The first Pauli-X gate negates qubit A before the Temporary logical-AND gate performs the multiplication of the qubits.

  • Next, the Temporary logical-AND gate performs the multiplication \({\overline{A}}C\) and stores the result in the auxiliary qubit.

  • A CNOT gate acts on the ancillary qubit, i.e., on \({\overline{A}}C\), performing an \(\oplus \) operation with qubit B, resulting in \({\overline{A}}C\oplus B\).

  • The second Pauli-X gate returns the qubit A to its non-negated state so that the CNOT gate can perform the operation \(A\oplus C\).

The T-count for all proposed gates is 4, with a consistent T-depth of 2 for each gate. This uniformity arises because the Temporary logical-AND gate is the sole contributor to the T-gate cost. Moreover, it is important to observe that the number of auxiliary qubits has increased by one in all cases.

3 Proposed comparator circuits

In the realm of quantum computing, various quantum comparators have been explored in the literature [9, 31, 32, 36,37,38,39,40]. In [9], two comparators have been developed as part of their work. The first comparator focuses on reducing the T-count, while the second one is oriented towards minimising the T-depth. In pursuit of these objectives, authors make use of the Temporary logical-AND gate to diminish the number of involved T-gates. In [37,38,39], Toffoli gates are employed. However, these circuits are not considered in this study, as their optimisation is straightforward (replacing the Toffoli gate with a Temporary logical-AND gate and adding auxiliary qubits). We have focused on the comparator circuits presented in [31, 32, 36, 40]. These comparators utilise three specific gates (GN, Peres, and TR gates) with a high cost in terms of T-gates. These gates have not undergone optimisation in terms of T-gates or could potentially benefit from various optimisation techniques. Specifically, we have selected three of them [32, 36, 40], because they employ several types of gates from the others and best illustrates the methodology being followed. Furthermore, it is worth noting that reference [31] could be optimised using the same techniques applied to the others. Based on the studies of these three selected comparator circuits found in the literature, in this work, three new comparator circuits are presented. These circuits serve two primary objectives: first, to construct them by exclusively utilising Clifford+T gates, and second, to minimise the dependence on T-gates, thereby optimising overall circuit efficiency. Furthermore, it is worth noting that all of these circuits, both those that have been analysed and those newly proposed, have been successfully implemented in IBM Quantum Platform (https://quantum-computing.ibm.com/). These implementations are available upon request to the authors, allowing for on-demand access to the circuits for further study and experimentation.

These new implementations follow the same methodology, which involves a thorough analysis of the circuits and the use of the newly proposed gates outlined in Sect. 2.1.

3.1 Thapliyal et al. comparator and optimised proposal

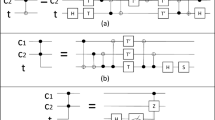
The first circuit on which we have based our proposal is the one described in [32]. This 2-bit half-comparator is made up of two R-Bcomps modules, two CNOT gates, and two TR gates (see Fig. 6). In Fig. 6a, it can be observed the gates that form each module R-Bcomp, which are two TR gates and one CNOT gate. The relevant outputs of this circuit are Z and Y, Y becomes 1 when the condition \(x>y\) is satisfied, and Z becomes 1 when \(x<y\).

Fig. 6
figure 6

Implementation of a an R-Bcomp module and b a 2-bit half-comparator proposed by Thapliyal et al.  [32]

Full size image

Following the implementation outlined in [32] and the metrics of the gates presented in Table 1, the resulting metrics for both the R-Bcomp modules and the overall circuit are consolidated in Table 2. The table provides a comprehensive overview, including T-count, T-depth, and ancillary qubits for each R-Bcomp module as well as the 2-bit half-comparator.

Table 2 Quantum circuit metrics for the R-Bcomp module and Thapliyal’s 2-bit half-comparator [32]
Full size table

Upon examination of the circuit, it can be seen that the large number of T-gates comes from the TR gate. Therefore, using the new version of the TR gate proposed in Sect. 2.1.1, a new comparator circuit is proposed, as shown in Fig. 7. Changes made to the TR gates in the R-Bcomp modules and the comparator circuit, which have been replaced by the new proposed version of the gate, can be observed.

Fig. 7
figure 7

Optimised proposed circuit, labelled optimised proposed circuit 1, where x1 and x0 represent a two-bit number, as well as y1 and y0, while the qubits labelled with T represent ancillary qubits with the specific initial state for the Temporary logical-AND gate

Full size image

To calculate the metrics of this circuit, it has been considered that two consecutive identical gates cancel each other (as shown in Fig. 7). It is important to note that this cancellation property holds specifically for Hermitian gates. Therefore, when TR gates are replaced with the proposed implementation, several Pauli-X and CNOT gates are eliminated, given that they are Hermitian gates [41]. After reducing the circuit, we have:

  • Six TR gates, in which the duplicate sequential gates have been removed when substituted in the original circuit.

  • Four H gates that initialise the qubits that form the numbers to be compared.

  • One CNOT gate.

Looking at Fig. 7, it can be determined that the circuit contains 6 TR gates, resulting in a total of \(6 \times 4 = 24\) T-gates. To calculate the T-depth, we need to observe the number of T-gates that are performed in parallel. It is evident that the two TR gates are executed in parallel two times, resulting in a T-depth of 4 (sequential TR gates) \(\times 2 = 8\). However, it should be noted that the initialisation of the auxiliary qubit for the Temporary logical-AND gate was performed only once; thus, the T-depth of the circuit is 5.

The metrics can be observed in Table 3. When comparing these results with Table 2 (2-bit half-comparator), it can be observed that both the T-count and T-depth are reduced significantly.

Table 3 Metrics calculated of the half-comparator Optimised proposed circuit 1
Full size table

3.2 Maity’s comparator and optimised proposal

The next comparator that has been studied was proposed by Maity [40]. This full 2-qubit comparator uses several Peres gates. This comparator can be seen in Fig. 8. The relevant outputs of this circuit are X, Y and Z, X becomes 1 when the condition \(x<y\) is met, Y becomes 1 when \(x=y,\) and Z becomes 1 when \(x>y\).

Fig. 8
figure 8

Full 2-bit comparator proposed by Maity in [40]

Full size image

Thus, the metrics of this comparator can be observed in Table 4.

Table 4 Metrics calculated of full 2-bit comparator proposed by Maity [40]
Full size table

Following the version of the Peres gate proposed in Sect. 2.1.2, the optimised circuit proposed can be seen in Fig. 9.

Fig. 9
figure 9

Proposed optimised circuit, labelled optimised proposed circuit 2 where x1 and x2 represent a 2-bit number, same as y1 and y2, while the qubits labelled T represent ancillary qubits that have the specific initial state for the Temporary logical-AND gate

Full size image

Regarding T-count and T-depth, each Peres gate has a T-count of 4, so the number of T-gates in this circuit is \(4 \times 4 = 16\), while the T-depth is \(4 \times 2 = 8\). Nevertheless, it is important to note that the auxiliary qubit initialisation for the Temporary logical-AND gate occurred only on a single occasion, resulting in a T-depth of 4 for the circuit. The metrics of the proposed comparator can be summarised in Table 5.

Table 5 Metrics calculated of the proposed full-comparator Optimised proposed circuit 2
Full size table

Comparing these results with Table 4, once again, the T-count and T-depth are reduced by more than half.

3.3 Kalita et al. comparator and optimised proposal

The last comparator on which we rely is the one proposed by Kalita et al. [36], specifically their 1-bit version (see Fig. 10).

Fig. 10
figure 10

Full 1-bit comparator proposed in [36], where A and C are the qubits to be compared

Full size image

The metrics of this comparator can be observed in Table 6.

Table 6 Metrics of full-comparator proposed in [36]
Full size table

Following the implementation of the GN gate proposed in Sect. 2.1.3, we propose a new circuit that uses this gate, as shown in Fig. 11.

Fig. 11
figure 11

Proposed optimised circuit, labelled Optimised proposed circuit 3, where x and y are the digits to be compared

Full size image

Regarding the calculation of the metrics of this circuit, the only gate that includes T-gates is the proposed GN gate, so the total T-count is 4, while the T-depth is 2. The metrics of the proposed comparator can be seen in Table 7. When these results are compared to Table 6, it can be observed that both the T-count and the T-depth are reduced by more than half.

Table 7 Metrics calculated of the full-comparator Optimised proposed circuit 3
Full size table

4 Results

Table 8 presents a summary of the metrics associated with the various circuits studied and proposed. These metrics encompass the T-count, T-depth, the number of ancillary qubits employed in each circuit, the comparator type, and the number of digits being compared.

Table 8 Comparison of the studied circuits and proposed circuits in terms of T-count, T-depth, ancillary qubits, comparator type, and the number of digits being compared
Full size table

As shown in Table 8, the proposed circuits, namely Optimised proposed circuit 1, Optimised proposed circuit 2, and Optimised proposed circuit 3, demonstrate significant improvements in terms of both T-count and T-depth when compared to their original counterparts. This clear reduction in the T-count and T-depth metrics indicates a substantial enhancement in the efficiency and computational performance of these circuits.

Optimised proposed circuit 1 exhibits the most remarkable improvements, with a T-count reduction from 54 to 24 and a T-depth reduction from 24 to 5 compared to the circuit by Thapliyal and Ranganathan [34]. Similarly, Optimised proposed circuit 2 and Optimised proposed circuit 3 also show significant reductions in both T-count and T-depth when compared to the circuits by Maity [40] and Kalita and Saikia [36], respectively. These improvements suggest that the optimisations introduced for the TR, Peres, and GN gates have had a highly positive impact on the overall performance of the circuits.

Significant improvements in computational efficiency are achieved by optimising circuits to reduce both T-count and T-depth. While the optimised circuits do require a slightly increased number of ancillary qubits, the trade-off between the utilisation of auxiliary qubits and the improved computational efficiency is apparent. These enhancements are exclusively implemented using Clifford+T gates, emphasising a focus on efficiency and precision in quantum computations. This underscores the potential practical applications of our proposed optimisations in the field of quantum circuit design.

5 Conclusions

In this study, we delve into the exploration of three distinct quantum comparator circuit designs from existing literature, focusing on their reliance on T-gates, which are currently receiving considerable attention in the design of quantum circuits. It is crucial to acknowledge that T-gates are associated with substantial computational costs.

One of the primary contributions of our work lies in optimising the quantum gates employed within these circuits (the TR, Peres and GN gates), as we propose three new quantum comparators using them. This approach allows us to use a methodology to design quantum circuits that can be transpiled onto real quantum platforms. In doing so, we harness the inherent advantages in the Clifford+T set. This entails efficiently using the available gates on current quantum computing platforms and, notably, acknowledging their potential to be converted into fault-tolerant configurations through the implementation of error-correcting codes, harnessing the potential of future quantum hardware capable of supporting such fault-tolerant designs. Furthermore, we have taken into account the cost of T-gates to avoid the computational overhead associated with their usage.

As part of our future work, we plan to scale up the proposed circuits so that they can effectively compare the number of desired digits. This expansion will contribute to practical applications in quantum computing, allowing for more complex and meaningful computations.