1 Introduction

Quantum computing emerges as a computing paradigm that tries to reproduce the characteristics of quantum mechanics to obtain computational advantages. While it is currently under study to define what kind of problems can be solved more efficiently with a quantum computer than with a classical computer, it has been shown that there are problems that can be solved more efficiently with quantum computing [1]. Quantum computing uses the concept of the quantum bit (qubit) as a basic unit of information representing not one of two states as a bit does, but a quantum state consisting of a combination of two values taken as the basis of the space in which it is operating. Through this superposition of values, qubits make it possible to represent and operate with probabilistic amplitudes, which with some ingenuity can lead to results with fewer operations than a classical computer. Other advantages offered by this disruptive are the possibility of representing information more efficiently, and the design of genuinely quantum models that allow problems to be addressed in ways never seen before in classical computation [2].

The most common way to programme a quantum computer is through the circuit paradigm. Since quantum mechanics is apparently reversible, these circuits must be reversible. Small circuits are a valuable resource. This is due to the limitations of current quantum computers and the high computational cost associated with quantum simulators. Small circuits are of great interest even when they do not offer any quantum advantage, since they can be used as part of larger algorithms that take advantage of quantum computation [3]. One of the best examples to illustrate this need for optimized circuits is Grover’s algorithm. This algorithm makes it possible to speed up a search problem compared to existing classical algorithms, if the search problem fulfils certain conditions [4]. An indispensable element of Grover’s algorithm is the so-called oracle, which, to simplify its definition, consists of a circuit that checks whether an element of the search fulfils a condition or not. The oracle is customizable to each problem (assuming that the problem is susceptible to be solved by such an algorithm), and the optimization of its design is fundamental to maintain the advantage achieved by the main algorithm. A slow oracle with many operations would weigh down the reduction in search iterations achieved by Grover’s algorithm, making the algorithm slower overall than the classical alternatives [5].

Focusing on the optimization of quantum circuits, adders receive special interest from the scientific community [6]. This is because adders are used to perform modular exponentiation in Shor’s algorithm [7]. Shor’s algorithm is undoubtedly the most famous quantum algorithm, since it manages to factor numbers and compute discrete logarithms in polynomial time (something that has not been achieved to date in classical computing) [8]. The algorithm consists of several operations that can be summarized in an inverse quantum Fourier transform and a modular exponentiation, as it is shown in Fig. 1. The most computationally intensive part of Shor’s algorithm is precisely the modular exponentiation. It is intuitive to solve this operation using circuits that perform multiplication or exponentiation. However, such circuits are currently too resource-intensive for current quantum computers [9, 10]. Instead, adders are commonly used to perform this operation in a more resource-efficient way [11]. Achieving more optimized adders will allow the acceleration of this part of Shor’s algorithm, as well as scaling its applicability to larger number sizes. With the implications that this algorithm has on such matters as cryptographic protocols [12], the interest in achieving such optimization is real and tangible [13]. However, it would be a mistake to limit the interest of adders to Shor’s algorithm, as there is a plethora of algorithms that use addition as part of their computational process [13,14,15,16].

Fig. 1
figure 1

Circuit for Shor’s algorithm. \(n=2(log_2 N)\) qubits are initialized to \({\left| {0}\right\rangle }\), and \(m=2(log_2 N)\) qubits to \({\left| {1}\right\rangle }\). A Hadamard transform is applied to the first n qubits, and then the second m qubits are multiplied by \(f(x)=a^x mod N\) for some random \(a < N\) that has not common factors with N. Finally, the inverse quantum Fourier transform on the first n qubits is applied [17]

Full size image

In classical computer structure theory, there are several types of adders that can be classified in two main groups: ripple carry adders and carry lookahead adders [18]. As a rule, circuits of the first type are cheaper but slower. Circuits of the second type are faster but more expensive since the increase in speed is achieved at the cost of involving more resources [19]. They are faster as they are focused on computing the carries of each pair of digits as soon as possible. Achieving a faster circuit will always be desirable, but it is subject to being able to perform this operation efficiently with the available resources. Classical computing has not the hard resource constraints existing in quantum computing, so “fast and expensive” adders are the most common option used to speed up the computation of the sum and the many sum-dependent operations [20]. However, the choice is not trivial in quantum computing. If this choice is based solely on the aforementioned resource limitation, the most obvious choice would be to use a ripple carry adder. But in quantum computing there is an even bigger problem: noise [21]. Because of this noise, each extra operation increases the probability of errors, so fewer operations also mean less exposure to noise and a consequent reduction in errors. Of course, this also benefits ripple carry adders, as they involve fewer operations. However, time is also a crucial factor—the longer the circuit duration, the greater the exposure to noise. In fact, current qubits slowly lose their state over time even in the absence of operations [21]. Therefore carry lookahead adders must also be valued in today’s quantum computing, although in this case the need for resource optimization is even greater than in the other type of adders. Moreover, it is also useful to keep them in mind for the future. After the so-called Noisy Intermediate-Scale Quantum (NISQ) era (the name given to the era in which computers have a moderate number of qubits, but not large enough to solve significant problems free of noise effects), it can be assumed that the focus of interest will be on achieving fast circuits [22]. Hence, the focus of this paper is on carry lookahead adders.

Back to the noise problem, this is a physics problem that can be partially solved by proper circuit design to reduce, as mentioned above, the circuit lifetime and the number of circuit operations. It is also possible to use error detection and correction codes to reduce the effects caused by noise. So-called T gate is widely used as it enables the use of such codes in a quantum environment. However, this gate has a high cost that can exceed by a factor of 100 the cost of other gates [23,24,25]. Thus, the problem comes from the need to use T gates to allow the use of error detection codes, but minimizing their use so that the total cost of the circuit is not excessive. The use and optimization of these gates is so widespread that two metrics have emerged in the scientific community focused on measuring the number of T gates a circuit has, as well as the number of consecutive T gates that make up the critical path of the circuit. They are called T-count and T-depth, respectively. Although initially the quantum cost and delay metrics were used, which contemplate all the gates involved in the circuit, the high cost of the T gates makes the cost of the rest of the gates negligible [26]. Therefore, the T-count and T-depth metrics are increasingly displacing these other metrics [9, 27, 28].

We have developed three reversible quantum adders that are focused on reducing the T-depth and the T-count. The reduction of the number of required qubits has also been prioritized, according to the imperative need to reduce resources that has been discussed. Generic designs for any quantum computer are presented, and the feasibility of optimally transposing these designs to the real 20-qubit IBM Q Tokyo quantum computer has been studied as an example of how our circuits should be mapped in a real quantum computer. In addition to the problems already mentioned, the qubits of today’s quantum computers are not all connected to each other. The architecture of such computers is organized as a graph with these qubits being the nodes and relationships being established only between certain nodes. In this way, two qubits participating in the same operation will have to perform extra operations (with the consequent increase in slowness and resources) to move their information to related nodes (qubits) and bring that information back to the original nodes. An initial optimized design that assigns to each physical qubit the appropriate circuit qubit will reduce these swap operations and reduce time and resources.

The main contributions of this paper are the following: (1) it presents three reversible quantum carry lookahead adders focused on reducing the T-depth and the T-count, and the number of ancilla qubits; (2) it demonstrates the proper way to construct the proposed adders in a real quantum computer using the most efficient techniques available in the literature; and (3) it compares the proposed adders with the existing state-of-the-art circuits and shows the superiority of the proposed ones for the case of addition between 4-digit numbers.

The rest of the paper is organized as follows. The basic concepts about quantum circuits necessary to understand the proposed implementations are presented in Section 2. Section 3 explains the methodology used to build the adders. The three proposed circuits are presented and detailed in Sect. 4. A real implementation in the specific quantum computer is presented in Sect. 5. In Section 6, an analysis of the proposed adders and a comparison between them and the state-of-the-art adders is carried out. Finally, Section 7 presents the conclusions.

2 Quantum circuits and gates

The most common way to program a quantum computer is by means of circuits. Analogous to classical circuits, quantum circuits are built using gates. These “quantum gates” can be expressed mathematically by complex unitary matrices that operate on qubits. There are an infinite number of gates, but there is a small set of them that allows us to approximate the rest [5]. Only four different gates are used in the circuits of this paper: the CNOT gate, the Toffoli gate, the Temporary logical-AND gate, and its uncomputation. However, these gates (except the CNOT gate) are built using other smaller gates (Z, T, S, and Hadamard gates, only Clifford+T gates are considered in this work), so it is also necessary to describe these other gates. Among these gates, we highlight the T gate, which is of vital importance in this work and whose usefulness has already been explained in the previous section. The symbols used to represent such gates in this work are shown in Fig. 2. A simple description of them is given below. For the sake of simplicity, it is assumed that the measuring devices will be fixed and that only the standard bases will be used for measuring.

Fig. 2
figure 2

Symbol of the gates used in the proposed circuits: a CNOT gate, b Toffoli gate, c Temporary logical-AND gate, and d Peres gate. Moreover, other gates are used to build the Toffoli gate and the Temporary logical-AND gate and its uncomputation: e Hadamard gate, f Z gate, g T gate, and h S gate

Full size image

  • The Z gate leaves the amplitude of \({\left| {0}\right\rangle }\) intact, but changes the sign of the amplitude of \({\left| {1}\right\rangle }\).

  • The Hadamard gate creates an equal superposition of the two basis states.

  • The T gate performs a \(\pi /4\) phase.

  • The S gate performs a \(\pi /2\) phase.

  • The CNOT gate operates on two qubits. One of them acts as a control, and the other as a target, so that the gate exchanges base amplitudes if and only if the control qubit is in state \({\left| {1}\right\rangle }\). Mathematically, let \({\left| {q}\right\rangle }= r{\left| {00}\right\rangle } + s{\left| {01}\right\rangle } + t{\left| {10}\right\rangle } + u{\left| {11}\right\rangle }\) a random quantum state. Then, the result of applying a CNOT on this state q will be \(r{\left| {00}\right\rangle } + s{\left| {01}\right\rangle } + u{\left| {10}\right\rangle } + t{\left| {11}\right\rangle }\).

  • The Toffoli gate is a generalization of the CNOT gate, but involving two control qubits. The most optimized implementation of this gate in terms of T-cost is shown in Fig. 3 [24].

  • The temporary logical-AND gate was presented by Gidney in [29] (Fig. 4). This gate performs an AND operation on the value of two qubits and stores it in a third qubit that needs to be initialized to a specific value of \(\frac{1}{\sqrt{2}}({\left| {0}\right\rangle } + e^{\frac{i\pi }{4}}{\left| {1}\right\rangle })\).

  • Given qubits A, B, and C, the Peres gate produces an effect similar to that of applying a Toffoli gate with A and B acting as control qubits and C as the target, and then applying a CNOT gate with A as the control qubit and B as the target.

Fig. 3
figure 3

Symbol of the Toffoli gate and its implementation. It has a T-count of 7 and a T-depth of 3

Full size image
Fig. 4
figure 4

Symbol of the temporary logical-AND gate and its implementation. It has a T-count of 4 and a T-depth of 2. The S gate counts as a T gate to compute these metrics

Full size image
Fig. 5
figure 5

Symbol of the uncomputation of the temporary logical-AND gate. No T gates are used

Full size image

For the reasons stated in the introduction, this work aims to minimize the number of T gates. Of the gates used (CNOT, Toffoli, Temporary logical-AND, and its uncomputation), the CNOT gates and the uncomputation of the temporary logical-AND operation do not involve the use of T gates. The Toffoli and Temporary logical-AND gates have a T-count of 7 and 4, respectively, as can be seen in Figures 3 and 4 (it is important to note that the S gate also counts as a T gate). Similarly, we set their T-depth as 3 and 2, respectively. However, the second gate requires preparing a specific quantum state and cannot be applied on a qubit already in use.

On the other hand, it is necessary to revert qubits that have been used to perform auxiliary operations and no longer have a useful value to their initial value. This is called uncomputation of garbage outputs. In the case of wanting to revert a Toffoli operation, another Toffoli gate will be necessary with the corresponding expense in T gates [30]. However, in the case of a temporary logical-AND construction, reversing such an operation by means of its uncomputation gate has no extra cost in terms of T gates, as it is shown in Fig. 5.

2.1 Fault-tolerance

It has been mentioned before that current quantum computers suffer from external and internal noise, which causes errors in their computation. Reducing the number of operations and the depth of the circuit reduces the noise exposure of the circuits and therefore, also the errors. It is equally important to consult the current state of the quantum computer to choose which physical qubits to work on, since depending on the current calibration, not all qubits offer the same stability at all times [31]. It is also essential to adapt the designs to the specific topologies of the devices to be operated on in order to reduce the number of SWAP operations, which will have a positive impact on the number of resulting operations and the depth of the circuit. However, using these strategies alone is insufficient.

A widespread technique for building fault-tolerant quantum circuits is to design them using only Clifford+T gates [30, 32, 33]. A circuit built exclusively with these gates will allow the use of error correction codes [34,35,36], which together with the aforementioned strategies will improve its error tolerance. In reality, the use of CNOT, S and H gates is sufficient to implement an error correction strategy in a quantum device. However, the Clifford group is not sufficient to implement any function in such devices. This is why the T gate is often added to the Clifford group (forming the Clifford+T group) to achieve a universal group of quantum gates. However, the high cost of the T gate (it is obvious from its name that it is included in the Clifford+T group) is a subject of special care, giving rise to the aforementioned T-count and T-depth metrics as explained above.

At the beginning of Section 2, it was stated that there is a set of gates that allows all the others to be approximated. For the sake of accuracy, it is useful to clarify that with a finite set of quantum gates it is impossible to reproduce exactly the infinite possible quantum gates. However, the group of gates that constitutes the Clifford+T set does allow to approximate any other function. For this reason, this group is labelled as “universal” [5].

3 Methodology to design carry look-ahead adders

Let \(S=A+B\) be the operation to be performed, where \(A = a_{N-1},...,a_0\) and \(B=b_{N-1},...,b_0\) are two positive numbers expressed in binary notation, and N is the maximum size of binary digits (bits) handled. Quite intuitively, addition will begin with the sum of the least significant pair of digits, i.e. \(a_0\) and \(b_0\). This operation produces two results: the sum of the digits, which we can express as \(s_0 = a_0 \oplus b_0\), and the carry output, which we mathematically represent as \(C_{i+1} = a_0 b_0\). Circuits capable of performing the addition of two digits and returning their sum and carry output are commonly called half adders. From here on, we continue computing the sum of the digits \(a_i\) and \(b_i\), with \(i=1\) up to \(N-1\), but now taking into account the carry generated by the previous pair \(a_{i-1}\) and \(b_{i-1}\). To account for the previous carry (formally named carry input), the operations \(s_i\) and \(C_{i+1}\) are rewritten as \(s_i=a_i \oplus b_i \oplus C_i\) and \(C_{i+1}=(a_i \oplus b_i)C_i \oplus a_i b_i\). Circuits capable of performing the addition of three digits and returning their sum and carry output are commonly called full adders. As a rule, an adder can be constructed to allow the addition of numbers of size N by connecting one half adder and \(N-1\) full adders. For the sake of clarity, it is mentioned that it is also common to use N full adders, allowing an input carry to be incorporated even at the beginning.

Although constructing a circuit in the manner indicated in the previous paragraph is simple, the complexity will be O(N) since the sum of each pair of digits needs to wait until the sum of the previous pair has been calculated. In order to reduce this delay and to parallelize the computation of the sums of pairs, carry lookahead adders anticipates their carries by a recurrence relation. In particular, they are based in the computation of two signals, \(G_i\) and \(P_i\) (commonly named carry generation and carry propagation, respectively), which can be calculated as follows [19]:

$$\begin{aligned} \begin{array}{cc} G_{i}=a_i b_i;&P_{i}=a_i + b_i \end{array} \end{aligned}$$
(1)

using such signals, the computation of the carries can be redefined as follows:

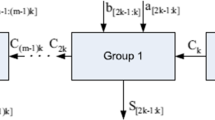
$$\begin{aligned} \begin{array}{c} C_{i+1}=G_i + P_i C_{i} \end{array} \end{aligned}$$
(2)

Although the methodology described above is the most widely used for constructing carry lookahead adders, other alternatives have been proposed in the literature [37, 38]. Some of these alternatives have been used in the construction of adders for quantum computing, as we discussed in [13]. Particularly interesting is the work presented by Bahadori et al. [38], where the authors use a hybrid methodology for the calculation of the sum, whereby modules called carry lookahead sub-tree (CLST) are constructed to allow a quick calculation of the carries. In turn, these modules are combined in a linear way to calculate the sum as a whole. In our work, the focus is on the methodology used to build the CLST blocks, whose conversion to a quantum circuit can be done by minimizing the T-count with respect to the implementation of a circuit based on \(G_{i}\) and \(P_i\) signals.

CLST blocks define two new signals called Alive (Al) and Generate (Gn) to calculate the carry outputs. Initially, such signals are computed for each i-pair according to these expressions:

$$\begin{aligned} \begin{array}{cc} Al_i=a_i + b_i;&Gn_i=a_i b_i \end{array} \end{aligned}$$
(3)

Then, they are redefined as:

$$\begin{aligned} \begin{array}{cc} Al_k=Al_i Al_j;&Gn_k=Gn_i + Gn_j Al_i \end{array} \end{aligned}$$
(4)

where i and j are related to a pair of consecutive outputs from the previous level, and k with the output at the new level. Figure 6 shows the structure of a CLST block of size \(N=4\), which is the size used in the present work. In the figure, the white squares represent the first level where each pair of digits (\(a_0b_0\) to \(a_3b_3\)) computes the signals according to Eq. 3. Once the value for each pair is computed, a tree structure is followed, computing the successive signal values using equation 4.

Fig. 6
figure 6

Structure of the CLST block proposed in [38], for the \(N=4\) case. White boxes computes Eq. 3, whereas black boxes computes Eq. 4

Full size image

However, the CLST block does not calculate some intermediate carries that are necessary to calculate partial results of the sum. In the work of Bahadori et al. [38], such values are calculated by other circuits, which are not of interest in the present work.

As far as our adders are concerned, the carries can be computed as follows:

$$\begin{aligned} C_k=Gn_i + Gn_j Al_i \end{aligned}$$
(5)

The proposed circuits use equations 3,4 and 5 to perform the addition, although they require some extra operation to complete the addition. Moreover, it is necessary to implement the circuits taking into account the peculiarities of quantum computing, such as reversibility. These extra operations are detailed in the next section.

4 Design of the quantum adders

Three circuits (adders) are presented in this section. They follow the same methodology but differ in the way they perform some operations. Initially, we describe the necessary steps to reproduce the first circuit, which of the three is the one that most directly implements the methodology explained in the previous section. Subsequently, we explain how to implement circuits two and three from this first circuit.

The first proposed circuit (will be referred to as Circuit 1) uses only three kinds of gates to implement equations 3, 4, and 5: the CNOT gate, the temporary logical-AND gate, and its uncomputation gate. The main objective of the circuit is to keep the T-count as small as possible, avoiding the use of the Toffoli gate, which, as explained above, has a higher cost both in the operation itself and later on by uncomputing the generated garbage outputs. The first level of \(Gn_i\) signals of Eq. 3, and the Al signals referred in Eq. 4 are computed using temporary-logical AND gates. Therefore, an extra qubit will be necessary for each of these operations. \(Gn_k\) of Eq. 4 is also partially computed using temporary-logical AND gates, in particular the product \(Gn_j Al_i\). All other operations of Eq. 3 and 4 are OR logic operations. However, due to the definition of the signals Gn and Al, the two entries of such OR operations cannot in any case be 1 at the same time (except as stated in Eq. 3 for \(Al_i\)). Therefore, such operations can be computed using CNOT gates. Regarding the carries of Eq. 5, they will be treated the same as \(Gn_k\) in Eq. 4, although it is necessary to calculate the signals not previously computed by means of Eqs. 3 and 4.

Once it became clear how each operation is implemented, the first step is to reproduce the CLST block of Fig. 6 using the quantum gates mentioned in the previous paragraph to compute Al and Gn. Once the signals are computed, the calculation of the digits of the sum, \(s_i=a_i \oplus b_i \oplus C_i\), is carried out. As it was mentioned, the carries \(C_i\) not included in the CLST block must be calculated in order to complete the sum. Of course, it is not necessary to wait for the CLST block to finish its calculations before starting the computation of these carries, but their computation can start as soon as the values they need are already available. The complete design of Circuit 1 is shown in Fig. 7 for the case \(N=4\). Although in this paper the proposal is focused on the case \(N=4\), the methodology is given below in detail to build the circuit for any size N:

Fig. 7
figure 7

First proposed quantum carry-lookahead adder, labeled as Circuit 1. It has a T-count of 36 and a T-depth of 10. The number of ancilla qubits is 9. \(a_i\) and \(b_i\) are the digits of the numbers to be added, and \(s_i\) are the digits of the result. The qubit marked as A are auxiliary qubits prepared in a special state. The vertical lines are used to separate the necessary steps for the construction of the circuit and are shown for the sake of clarity. However, to minimize the logical depth of the circuit, some intermediate uncomputations are made

Full size image

  • Step 0: The data are codified into the circuit using basis encoding. Two pairs of N qubits are required to represent each of the two N-digit numbers A and B.

  • Step 1: \(Gn_i=a_i b_i\) (Eq. 3) is computed for each pair of digits (that is, for \(i=0\) to \(N-1\)). To implement these operations, temporary-logical AND gates will be used. Such gates involve an ancilla qubit. Therefore, N extra qubits will be necessary in the circuit. All these calculations can be performed in parallel as there are no dependencies between them.

  • Step 2: \(Al_i\) is calculated for \(i=1\) to \(N-1\) according to Eq. 3. Since \(Al_0\) is not used in the CLST block, it is not computed. These operations are carried out using CNOT gates, being \(a_i\) the control qubits and \(b_i\) the target one.

  • Step 3: From this point on, Eq. 3 is no longer used for any calculations, but is replaced by Eq. 4. For \(u = 1\) to \(log(N) - 1\) and for \(v = 1\) to \(\frac{N}{2^u}-1\), \(Al_i Al_j\) and \(Al_j Al_k\) are computed using temporary logical-AND for indexes \(i=2^u v\), \(j=2^u v+2^u\), and \(k=2^u v+2^{u-1}\).

  • Step 4: For \(u = 1\) to log(N) and for \(v = 0\) to \(\frac{N}{2^u}-1\): to compute \(Gn_i + Gn_j Al_i\) and \(Gn_j + Gn_k Al_j\) for indexes \(i=2^u v\), \(j=2^u v+2^u\), and \(k=2^u v+2^{u-1}\). The products GnAl are computed using temporary-logical AND gates.

  • Step 5: For \(i = 0\) to \(\frac{N-2}{2}\), temporary-logical AND gates are applied to compute the carries not included in the CLST block. Such carries are used to calculate \(C_i \oplus b_i\), which is necessary to compute the digits of S. According to Eq. 5, the carries are computed using the Al and Gn signals of the one or two previous levels (i.e. \(C_{j-k}; k=1\) or 2) [38]. Due to such dependencies, they can not be computed in parallel. However, only two T-depth levels are required, avoiding a higher expansion in terms of T-depth presented in other adders.

  • Step 6: The circuit is uncomputed to revert all garbage outputs to the initial state of the qubits. Before their uncomputation, the carries are used to compute \(C_i \oplus b_i\) (using CNOT gates).

  • Step 7: S is completed performing \(a_i \oplus b_i\) for each pair \(a_i\) and \(b_i\) (using, again, CNOT gates).

The use of temporary-logical AND gates greatly reduces the T-count and T-depth of the circuit, but at the cost of increasing the required number of ancilla qubits. In particular, the circuit of Fig. 7 has 9 ancilla qubits. This number can be reduced by replacing temporary logical-AND gates by Toffoli ones. Performing these changes will increase the T-count and T-depth, but there are some operations in the circuit that can be carried out with Toffoli gates without increasing these values too much. For instance, in those operations where it is not necessary to uncompute the qubits since they are the values of the result. This is the case of \(s_4\). On the other hand, we can also replace the temporary logical-AND gates used to perform \(a_0b_0 \oplus b_1\) and \(a_2b_2 \oplus b_3\), which created a lattice of nested auxiliary qubits. These changes reduce the ancilla qubits from 9 to 5, with the counterpart of increasing the T-count from 36 to 51, and the T-depth from 10 to 11, respectively. The high increment in the T-count is due the Toffoli gate that performs \(a_0b_0 \oplus b_1\), since another Toffoli gate is necessary at the end to uncompute it. This new version of the circuit (will be referred to as Circuit 2) is shown in Fig. 8.

Fig. 8
figure 8

Second proposed quantum carry-lookahead adder, labeled as Circuit 2. It has a T-count of 51 and a T-depth of 11, but it saves 4 ancilla qubits. The numbers to the left of the circuit identify the position of each qubit, and are shown for ease of understanding in future explanations

Full size image

A third version of the circuit can be obtained at the cost of needing one more auxiliary qubit but significantly reducing the T-count. If the mentioned operation \(a_0b_0 \oplus b_1\) is computed using a temporary logical-AND gate instead of a Toffoli one, the following Toffoli gate (used to uncompute the previous one) can be also replaced by an uncomputation gate of the temporary logical-AND. This simple operacion will reduce the T-count from 51 to 41, keeping the T-depth invariant. At the cost, as mentioned above, of increasing the auxiliary qubits by one. This third version is shown in Fig. 9. It will be referred to as Circuit 3.

Fig. 9
figure 9

Third proposed quantum carry-lookahead adder, labeled as Circuit 3. It has a T-count of 41 and a T-depth of 11. The number of ancilla qubits is 6

Full size image

5 Mapping circuits on a real quantum computer

The three circuit designs, shown in Fig. 7, 8, and 9, respectively, represent the operations that must be applied to achieve \(S=A+B\). However, in a real quantum computer, these designs can hardly be directly applied since the available qubits on such a computer are not all connected to each other.

As an example, the topology of the IBM Q Tokyo computer is shown in Fig. 10. Let us suppose that we intend to implement Circuit 2, this circuit is taken as an example since it is the one that requires the least number of qubits. If we directly map Circuit 2 onto IBM Q Tokyo, qubit 0 of the computer will receive \(a_0\), qubit 1 will receive \(b_0\), qubit 2 will receive the first auxiliary qubit, and so on. The first quantum gate, a temporary logical-AND gate that performs the operation \(a_0 b_0\) and writes the result into the first auxiliary qubit, requires a connection of the first three qubits. However, as seen in Fig. 10, the first three qubits of the computer are not all connected to each other. Specifically, qubits 0 and 2 have no direct connection. Many other operations in Circuit 2 cannot be made directly as there is no real physical connection between the corresponding qubits.

Fig. 10
figure 10

Map for the IBM Q Tokyo architecture

Full size image

The way quantum computers solve this problem is to perform SWAP operations to exchange the values between physical qubits so that these values remain in qubits that do have a physical connection. The SWAP operation does not involve increasing the T-count or the T-depth. However, they do increase the overall quantum cost of the circuit and, obviously, make the circuit last longer. It has already been mentioned that longer lifetime means more noise exposure. Therefore, it is a priority to minimize the number of SWAP operations needed to implement the circuit in the real quantum computer.

The problem of efficiently mapping a circuit to a topology (i.e. minimizing SWAP operations) is widely addressed in the literature [31, 39, 40]. This problem is a general case of fitting a graph into a larger graph, and it is beyond the scope of this paper to study such a problem in its most general case. We have considered the work proposed by Bhattacharjee et al. [31] to develop the optimal implementations for each candidate machine minimizing losses caused by SWAP operations. Let a configuration \(C_t\) be a set of ordered tuples \((q_i, v)\), where qubit \(q_i\) is at location v in cycle t. The objective is to determine how many switch gates are needed to transform the location of the qubits of an initial configuration C and a topology graph T so that all pairs of qubits in the first level of operations (the first set of operations in the circuit, which we can denote as \(L_1\)) are neighbours, and then modify the location of the qubits again to be neighbours for the second level of operations (\(L_2\)) and so on, until the last level (\(L_k\)) is fulfilled and the combined delay of the switch gates and the gates present in the real circuit is minimal. Mathematically speaking, the target can be specified as follows:

$$\begin{aligned} Minimize \sum _{i=0}^{k}\sum _{t=0}^{T}t a_{i,t} \end{aligned}$$
(6)

being \(a_{i,t}\) 1 if there are gates in Level i that are scheduled in cycle t, and 0 otherwise.

Figure 11 shows, in matrix format, the relationships between the physical qubits of the quantum computer. It is equivalent to the diagram in Fig. 10. Figure 12 shows, also in matrix format, the necessary relationships to directly implement Circuit 2. Applying the algorithm of Bhattacharjee et al., it is obtained that the most optimal mapping of Circuit 2 in the machine is the one shown in Fig. 13. Although there is no direct implementation that totally eliminates the need for SWAP operations, it is only necessary to move the value of one qubit of the circuit (number 7 in the figure).

Fig. 11
figure 11

Map for the IBM Q Tokyo architecture

Full size image
Fig. 12
figure 12

Map with the necessary connections between qubits in Circuit 2

Full size image
Fig. 13
figure 13

(a) Circuit 2 mapped into the IBM Q Tokyo architecture. The numbers used correspond to the order of the qubits shown in Figure 8, starting from the top. SWAP operations are only required to move node 7 (\(b_2\) in Figure 8). (b) The connection between qubits in Circuit 2 is graphically shown for the sake of clarity

Full size image

There is one final consideration that must be taken into account. Not all connections between qubits are equally reliable, but the margin of error of each connection can be quantified. The algorithm of Bhattacharjee et al. also allows prioritizing qubit assignments taking into account these values so that quantum gates can be implemented while minimizing error. Since these values depend on the current calibration of the machine, we have not included them.

6 Results and discussion

The proposed and the state-of-the-art circuits have been designed and reproduced in Python and executed in IBM Quantum Experience devices and simulators. Once this reproduction has been carried out, the number of involved qubits, the number of T gates, and the number of T gates that must be executed sequentially, were counted using a simple Python routine (taking into account that some gates do not explicitly state their T-count and T-depth, and making the appropriate conversion), thus obtaining the metrics described below.

From the explanation of the circuit methodology, as well as the graphical designs shown in the corresponding section, it is clear that Circuits 1, 2, and 3 have a T-count of 36, 51, and 41, respectively; and a T-depth of 10, 11, and 11, respectively. In terms of ancilla qubit, they need 9, 5, and 6 qubits, respectively. None of the proposed circuits use non-valid operations for a quantum environment, nor do they contain garbage outputs. These values can be easily verified by knowing that a Toffoli gate has a T-count of 7, and a T-depth of 3, a temporary-logical gate has a T-count of 4 and a T-depth of 2 (and its uncomputation has no cost in terms of T gates), and no other gate involved in the circuits has T-count nor T-depth. In terms of T-count:

  • Circuit 1 has 9 temporary logical-AND gates: \(9 \times 4=36\).

  • Circuit 2 has 4 temporary logical-AND gates and 5 Toffoli gates: \(4 \times 4 + 5 \times 7=51\).

  • Circuit 3 has 5 temporary logical-AND gates and 3 Toffoli gates: \(5 \times 4 + 3 \times 7=41\).

In terms of T-depth:

  • Circuit 1 computes sequentially 5 temporary logical-AND gates: \(5 \times 2=10\).

  • Circuit 2 computes sequentially 1 temporary logical-AND gate and 3 Toffoli gates: \(1 \times 2 + 3 \times 3=11\). Figure 8 shows that the first temporary logical-AND gates are computed in parallel to the first Toffoli gate. The Toffoli gate is slower, so it is the gate that sets the speed (the T-depth in this case) in this first part.

  • Circuit 3 computes sequentially 1 temporary logical-AND gate and 3 Toffoli gates: \(1 \times 2 + 3 \times 3=11\).

In order to compare the proposed circuits with those available in the literature, we have mainly relied on two sources. The first source is an exhaustive review of quantum adders [13], which makes different comparisons between the various types of adders. One of these comparisons is devoted precisely to carry lookahead adders. The second source we have used is the paper by Thapliyal et al. [30], which presents four carry lookahead adders and also makes a complete comparison between adders in this category. Between the two papers, they analyse a very large number of adders. In order not to extend the comparison in this section too much by including information already collected in these papers, the comparison shown below only includes the best circuits collected in such sources.

Table 1 summarizes a comparison in terms of T-count, T-depth, and ancilla qubits between the best adders in the state-of-the-art and our three circuits. In terms of T-count and T-depth, the best options are the Out-FT-QCLA1 circuit and Circuit 1. Both circuits have the same T-count, 36, and the same T-depth, 10. However, Circuit 1 has one less ancilla input. The next best circuit in these terms is Circuit 3 with 41, but it involves only 6 ancilla qubits, that is 3 fewer qubits than Circuit 1 and 4 with respect to the Out-FT-QCLA1 circuit. However, it also increases the T-depth by 1 compared to both circuits. On the other hand, the best circuits in terms of ancilla qubits are the In-FT-QCLA1 circuit and Circuit 2, with only 5 ancilla qubits. Nevertheless, the circuit of [30] has a T-count and a T-depth of 76 and 22, respectively, whereas ours has values that outperform it greatly: 51 and 11, respectively.

Table 1 Depth and cost comparisons between the most optimized 4-digit adders in terms of T gates
Full size table

The methodology used to build the proposed circuit can be applied to build larger adders. In such sizes, the adders proposed by Thapliyal et al. [30] would be the most efficient in terms of T-count, T-depth, and ancilla inputs. It is due to the fact that intermediate carry calculations are increasingly omitted to compute the values indicated by Eq. 4. These uncomputed carries will have to be calculated using Eq. 5, causing an extra cost that does not occur in adders that use the classical methodology. This analysis focuses, as indicated, on the 4-digit size. For this size, our contributions are the most efficient in terms of T-count, T-depth, and ancilla qubits, as can be observed in Table 1.

7 Conclusions

We have presented three versions of a 4-digit carry lookahead adder optimized in terms of T-count, T-depth, and number of ancilla qubits. These adders use an alternative methodology that allows a fast calculation of the carries using operations with a lower associated T-count. Firstly, the design of the three adders, which have been based exclusively on Clifford+T gates, has been described in detail, showing the necessary steps, gates and qubits to build them. It has also been explained how the adders benefit from the temporary-logical AND and its capacity of optimizing resources in contrast to Toffoli gates to build the blocks defined in [38], adding several modifications to adapt it to a quantum environment. Secondly, it has been indicated the proper way to construct the circuits in a real quantum computer in order to avoid increases in their delay that make them more vulnerable to noise. We have also shown how this process does not lead in any case to an increase of the T-count or T-depth. Finally, we have carried out a comparison in terms of T-depth, T-count, and number of ancilla qubits between our circuits and the best adders available in the literature. From this comparison, it can be observed that the proposed adders outperform the state-of-the-art circuits in terms of T-depth, T-count, and number of ancilla qubits.

As future work, it is intended to study the implementation of this methodology for larger sizes. The extra operations necessary to calculate the carries and the sums that are not included in the CLST block increase as the size of the numbers A and B increases their size. But if a sufficiently efficient implementation is found for them, the T-count and T-depth values could be reduced with respect to the circuits studied in Table 1 for such sizes.