Deterrence, settlement, and litigation under adversarial versus inquisitorial systems

Abstract

In this paper, we compare deterrence, settlement, and litigation spending under adversarial and inquisitorial systems. We present a basic litigation model with three sequential stages—care, settlement, litigation—and we test the predictions on experimental data. In line with our theoretical expectations, we find that, compared with the adversarial system, the inquisitorial system is associated with lower litigation spending, lower rates of cases settled, and tends to strengthen deterrence.

1 Introduction

Scholars working across the fields of procedural rules and law and economics long have debated the differences between adversarial versus inquisitorial legal regimes (Kaplan, 1959; Posner, 1988; Tullock, 1988, 1997; Shin, 1998; Dewatripont & Tirole, 1999; Froeb & Kobayashi, 2001; Parisi, 2002; Damaska, 2008; Luppi & Parisi, 2012; Biser, 2014; Kim, 2014). The main disparity lies in the general role of the judge in the fact-finding phase of a trial. In the inquisitorial system—prevailing in the civil law countries of continental Europe, Japan and Latin America—a judge participates actively in the production of evidence. By contrast, in the adversarial system—prevailing in the Anglo-American common law tradition—a judge is prohibited from becoming actively involved in gathering evidence (but can rule on its admissibility), and is expected to reach a decision solely on the basis of the evidence presented by the parties (for an extensive review, see e.g., Froeb & Kobayashi, 2012).¹

Several theoretical contributions have shown that the different involvement of the judge in the two systems has crucial implications for legal procedure (Dewatripont & Tirole, 1999; Palumbo, 2001; Parisi, 2002; Parisi et al., 2017; Rizzolli & Saraceno, 2013; Shin, 1998; Thibaut et al., 1972). Indeed, alternative adjudicatory systems differently affect litigation efforts, their costs and outcomes, with the adversarial system being expected to reduce decision-making errors, albeit at the expense of larger rent dissipation (Parisi, 2002; Tullock, 1975, 1980, 1988, 1997). The latter effect is driven by litigants’ competition in the adversarial supply of evidence to prevail over the opponent, which is weaker or absent in the inquisitorial system, wherein the active role of the judge discourages the parties from dissipating scarce resources in swaying juries (Emons & Fluet, 2009; Kim, 2014; Palumbo, 2001; Rizzolli & Saraceno, 2013; Zywicki, 2008). In turn, it is possible that the adversarial system’s higher litigation costs may serve as threats to the parties before the bar, which might strengthen deterrence (Kim, 2014) and provide stronger incentives to settle disputes out of court to avoid costly trials (Baye et al., 2005). This likely produces a selection effect, with the mix of cases reaching the trial stage being more filtered under the adversarial—rather than the inquisitorial—process (Kim, 2014).

Overall, the theoretical models developed so far have shown formally that the adversarial and inquisitorial systems produce different levels of litigation spending and total trial costs (Emons & Fluet, 2009; Kim, 2014; Parisi, 2002; Tullock, 1988). Kim (2014) also discussed the possible effects of the two procedures on deterrence and settlement. Nonetheless, those predictions never have been evaluated formally, nor tested. The few experimental works of which we are aware—Thibaut et al. (1972), Block et al. (2000), Block and Parker (2004), Sevier (2014)—compared the two systems in terms of their relative fact-finding efficiency in adjudication, focusing on the revelation of relevant information and the accuracy of decisions. In doing so, those contributions have assumed that disputes are selected exogenously and have neglected comparative analysis of other crucial elements of procedural systems, namely trial costs, settlement, and deterrence. Nor have scholars questioned seriously the supposed superior professionalism and expertise of civil law judges.²

To the best of our knowledge, we report herein the first experimental analysis comparing the adversarial and inquisitorial systems in terms of deterrence, settlement, and litigation spending. We develop a basic litigation model to derive predictions that we test in a laboratory setting. Specifically, our model comprises three sequential stages—care, settlement, and litigation—and two players, a defendant and a plaintiff. In the care stage, the defendant can choose between being careful or careless. For example, a physician (defendant) can decide to exercise due care in performing surgery on a patient (plaintiff), or to be negligent. In absence of harm, the game ends, whereas in the event of harm, the game continues to the settlement stage, wherein the defendant (e.g., the physician) makes a settlement offer, and the plaintiff (e.g., the patient) chooses to accept or reject the offer.³ If the settlement fails, the parties go to court, wherein they can spend resources to increase their chances of winning the dispute. If the defendant wins, he does not have to compensate the plaintiff; otherwise, he must pay damages. Regardless of who wins the case, each of the parties must bear their own litigation costs (American rule).⁴

It is in the trial stage that we study the differences between adversarial and inquisitorial systems. We model the litigation phase as an all-pay auction with a head start. Conceptually, our setting is inspired by the rent-seeking approach of Tullock (1978, 1997) applied to litigation as in Parisi (2002). We look at the differences between the two procedural systems as an institutional change that reduces the costs of justice. Formally, we rely on the analytical framework proposed by Parisi (2002), in that we classify the procedural systems according to the allocation of control over the legal process. Specifically, we consider an institutional parameter, θ, which measures the weight attached to the inquisitorial arguments to win the award. A larger θ represents a more inquisitorial system rather than an adversarial one. It indicates that the judge—as opposed to the litigants—exercises more control over the process, or equivalently, that the evidence obtained by the judge is given greater weight than that presented by the parties. As discussed in Parisi (2002), the setup enables manipulating a single, continuous variable to compare the adversarial versus inquisitorial procedures. Our aim is to determine how care, settlement decisions, and litigation spending vary with θ.

We derive three main predictions: (1) aggregate litigation spending rises under the adversarial system (in line with Parisi, 2002); (2) parties always have incentives to settle, but the bargaining range is wider under the adversarial system, and the settlement amount depends upon the defendant’s behavior; (3) deterrence is stronger under the inquisitorial system.

We test the three predictions on a subset of the experimental data of Massenot et al. (2021) and supplementing it with new experimental sessions. While Massenot et al. (2021) studied deterrence and litigation spending under the American versus English rule while holding the procedural system constant, we compare the adversarial versus inquisitorial systems while keeping the fee-shifting rule constant (American rule). The experiment reproduces all theoretical assumptions that it is designed to test, which include designing the two regimes as an institutional parameter. The experimental results provide qualified support for the main theoretical predictions. At the trial stage we find that, compared with the adversarial system, the inquisitorial system is associated with less litigation spending, hence less rent-seeking. Furthermore, careful defendants win more often. We find that cases settle less frequently in the inquisitorial system than in the adversarial system. Finally, we find that potential defendants exercise more care in the inquisitorial system than in the adversarial system, but that the effect is not always statistically significant.

The remainder of the paper proceeds as follows. Section 2 briefly reviews prior experiments on adversarial versus inquisitorial systems, Sect. 3 presents our model, Sect. 4 describes the experiment, and Sect. 5 reports the results. Finally, Sect. 6 concludes.

2 Related experimental literature

Thibaut et al. (1972) provided an empirical test of Fuller’s claim that evidentiary presentation under the adversary model—versus the inquisitorial model—reduces significantly the effect of pretrial bias among decision makers on their ex-post decisions (Fuller, 1971). In their design, the facts were presented by two persons to simulate the adversary model, and by one person to simulate the inquisitorial model (for a critique, see Damaska, 1974). The experimental evidence confirmed the theoretical predictions (also see Froeb & Kobayashi, 1996).

Block et al. (2000) analyzed litigants’ incentives for revealing hidden facts to a decision maker and the accuracies of decisions across the two systems. In their experiment, the adversarial procedure was represented by a judge—referred to as the “referee”—who was completely passive until the decision, and two opposing parties with the complete control of both fact development and presentation. The opposite held for the inquisitorial procedure, under which the “referee” was granted complete control of both fact development and decision, while the parties were relegated to the status of interested witnesses. Block et al.’s findings reveal that the relative efficiencies of the two systems depend on the procedural rules governing the ex-ante information available to the parties. Specifically, under asymmetric and private information, “Mr. Wrong” (the party who should lose) is given private and discrediting information. In that case, the inquisitorial system is more revealing and accurate than the adversarial system. The result is reversed completely under asymmetric but correlated information, wherein “Mr. Right” (the party who should win) is given a clue about the content of discrediting information possessed by “Mr. Wrong”.

Block and Parker (2004) relied on a subset of Block et al.’s (2000) data to analyze the special case of non-revelation, i.e., when the proceedings fail to achieve explicit revelation of decisive information. Specifically, they tested two theoretical predictions: (1) adversarial decision making produces greater accuracy than inquisitorial decision making when one party has better information than the other (Shin, 1998); and (2) adversarial decision making tends to favor intermediate or moderate outcomes, i.e., an equal division of the contested stake, while inquisitorial decision making tends towards extreme outcomes (Dewatripont & Tirole, 1999). In contrast to Shin’s (1998) hypothesis, the experimental findings revealed that when explicit revelation failed, inquisitorial decision making was more accurate than adversarial decision making. In line with Dewatripont and Tirole’s (1999) prediction, the results showed further that adversarial decision makers had stronger tendencies than inquisitorial decision makers towards equal division of the disputed stake.

It also is worth mentioning Boudreau and McCubbins (2008), who studied experimentally whether competition between expert witnesses in a courtroom induces both experts to make truthful statements and enables jurors to trust those statements, hence improving their decisions. The results indicated that, contrary to critics of the adversarial system, competition between two experts induced truth-telling and improved decision making.

3 The litigation game

3.1 Setup

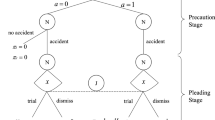
We now introduce the litigation game. It comprises three stages—care, settlement, and litigation—and two players, a defendant (D) and a plaintiff (P). Figure 1 depicts the game’s extensive form.

Fig. 1

Extensive form of the litigation game

3.1.1 Care stage

In the first stage, the defendant chooses between being careful ($c = 1$) or careless $(c = 0)$. Similar to Hirshleifer and Osborne (2001), we assume that the plaintiff knows the actual extent of the defendant’s fault.⁵ Being careful reduces the probability of causing harm $\delta$ to the plaintiff, but costs the defendant γ $(\gamma , \delta > 0).$ The probability of harm is ${\pi }_{1}$ if the defendant is careful, and ${\pi }_{0}> {\pi }_{1}$ if he is careless. In absence of harm, the game ends and the plaintiff’s utility is 0, while the defendant’s utility is $-c\gamma$. In the event of harm, the players proceed to the settlement stage.

3.1.2 Settlement stage

The settlement stage is modeled as a modified Nash demand game wherein both players choose thresholds for acceptance simultaneously. The defendant makes a settlement offer of ${s}_{D}$ and the plaintiff chooses a settlement request of ${s}_{P}$. If ${s}_{P}$ >${s}_{D}$, settlement fails and the game continues to the trial stage. If ${s}_{P}$ ≤${s}_{D}$, the two parties settle for an amount of $\overline{s }= \frac{{s}_{D}+ {s}_{P}}{\begin{array}{c}2\\ \end{array}}$and the final payoffs are $-\overline{s }-c\gamma$ for the defendant and $\overline{s } - \delta$ for the plaintiff.

3.1.3 Trial stage

The trial stage is modeled as an all-pay auction with a head start, wherein the winner earns a prize equal to the damages.⁶ The plaintiff receives the damages if he wins the case, while the defendant avoids paying the damages if he wins. Our setting is conceptually inspired by the rent-seeking approach of Tullock (1978, 1997) applied to litigation as in Parisi (2002).

The defendant spends $p \ge 0$ and the plaintiff spends $d \ge 0$. The indicator function $q()$ for a plaintiff’s win is given by (ties resolved at random):

$$q\left( {p,~d,~c} \right) = ~\left\{ {\begin{array}{*{20}l} {1~~if~\left( {1 - c} \right)\theta + p > d + c\theta ,~} \hfill \\ {\left\{ {0,1} \right\}~~if~\left( {1 - c} \right)\theta ~ + p = d + c\theta ,} \hfill \\ {~0~~if~\left( {1 - c} \right)\theta + p < d + c\theta .} \hfill \\ \end{array} } \right.$$

(1)

If the defendant loses at trial, he is ordered to pay damages of δ. If the defendant wins, he does not have to compensate the plaintiff. Whatever the outcome of the trial, the defendant must bear his own litigation costs d and the cost of care. Symmetrically, the winning plaintiff receives δ, and always bears his own costs of litigation p and the harm δ. Thus, the final payoffs after the trial stage are $-d - \delta q(p, d, c) - c\gamma$ for the defendant and $-p + \delta q(p, d, c) - \delta$ for the plaintiff. It is at the trial stage that we introduce the difference between adversarial and inquisitorial systems as an institutional parameter θ, $(0 < \theta <\delta ),$ which measures the judge’s involvement in evidence production.⁷ A larger value of $\theta$ (denoted as “I” in Parisi, 2002) represents a more inquisitorial or less adversarial system. It indicates that the evidence obtained by the judge is given greater weight than the evidence presented by the contending parties. Specifically, the parameter $\theta$ provides a head start to the party with a stronger case, who is either a careful defendant or a plaintiff facing a careless defendant. A careful defendant is given a head start because he wins the case even if he spends $\theta$ less than the plaintiff. By contrast, a careless defendant must spend at least $\theta$ more than the plaintiff to win the case.

3.2 Equilibrium

To derive theoretical predictions, we assume standard preferences and risk neutrality. We rely on backward induction to solve the game for subgame-perfect Nash equilibria. We start by studying the trial stage. We shall recall that all parameters are common knowledge, and that the plaintiff knows the level of care exercised by the defendant in the settlement and trial stages.

3.2.1 Trial stage

First, consider the case of a careless defendant. The maximum amount that the defendant can lose is $\delta$. Thus, the maximum amount that the defendant is willing to pay is $\delta$. Assuming that the defendant spends this maximum, the plaintiff can still win the case by spending ${p}^{*} = \delta - \theta$. Thus, the payoff of the plaintiff would be ${u}_{P}^{*} = \delta - {p}^{*} =\theta$.⁸ The best response of the defendant to this behavior is to spend 0 and lose $\delta$ for sure, namely ${u}_{D}^{*}=- \delta$. But then the plaintiff would win with probability 1 by also spending 0. Thus, as is standard in this class of problems, there exists no pure strategy Nash equilibrium. However, a mixed strategy equilibrium exists that delivers these expected payoffs:⁹

$$E\left[ {u_{P} } \right] = u_{P}^{*} = \theta$$

(2)

$$E\left[ {u_{D} } \right] = u_{D}^{*} = - \delta$$

(3)

Since damages are a transfer, they cancel out when summing the two utilities. As a result, the (negative of the) sum of these utilities is equal to the total litigation spending:

$$E\left[ {d + p} \right] = \delta {-} \theta$$

(4)

The aggregate litigation costs are thus increasing in $\delta$ and decreasing in $\theta$.

Let us now consider the case of a careful defendant. Assuming that the plaintiff spends the maximum that he is willing to pay—namely $\delta$— the defendant can win the case with probability 1 by spending ${d}^{*}= \delta - \theta$. In this case, the payoff of the defendant would be ${u}_{D}^{*} = -{d}^{*}= \theta - \delta$. The best response of the plaintiff to this behavior is to spend 0, which yields ${u}_{P}^{*} = 0$. As before, there exists a mixed strategy equilibrium that delivers these payoffs in expectation:

$$E\left[ {u_{P} } \right] = 0$$

(5)

$$E\left[ {u_{D} } \right] = \theta {-} \delta$$

(6)

As before, we compute the total expected litigation spending by taking the (negative of the) sum of these two utilities:

$$E\left[ {d + p} \right] = \delta {-} \theta$$

(7)

Whether the defendant is negligent or careful, expected aggregate litigation spending is the same. It increases with damages $\delta$ and decreases with $\theta$.

We can solve for the mixed strategy equilibrium. If the defendant is careless $(c = 0),$ then the head start of $\theta$ is with the plaintiff. Spending in the interval $d \in (0, \theta )$ is strictly dominated by $d = 0$. The maximum that the defendant is willing to spend is $\delta$. In equilibrium, the defendant draws from $F(d):$ with probability $\theta /\delta$ he spends zero, and with probability $1 - \theta /\delta$ he draws uniformly from the interval $[\theta ,\delta ].$ For the plaintiff—the player with the head start in this case—all pure strategies in $[0, \delta - \theta ]$ have the same expected payoff of $\theta$. For example, $p = 0$ leads to victory in $\theta /\delta$ percent of the cases, and thus expected damages are $\theta /\delta$ × $\delta$  = $\theta$. Increasing litigation spending increases the probability of winning but comes with higher litigation costs. The two effects balance such that the expected payoff is constant at $\theta$. Finally, $p = \delta - \theta$ ensures receiving damages of $\delta$ at a cost of $\delta - \theta$, which also yields a payoff of $\theta$. In equilibrium, the plaintiff plays $H(p):$ he spends zero with probability $\theta /\delta$ and draws uniformly from the interval $[0, \delta - \theta ]$ with probability $1 - \theta /\delta$. This in turn makes the defendant indifferent between all pure strategies in support of the mixed strategy as defined above. In expectation, the defendant and the plaintiff spend:

$$E\left( p \right) = E\left( d \right) - \left( {1 - \frac{\theta }{\delta }} \right) \theta = \frac{{(\delta - \theta )^{2} }}{2\delta }$$

(8)

The plaintiff wins the case if the defendant spends less than the expected amount spent by the plaintiff, $E(p),$ which happens with probability $(E(p) +\theta )/\delta$. A higher value of $\theta$ increases the winning probability of the plaintiff. In a purely adversarial system ($\theta$ = 0), the probability that the plaintiff wins is 50%, while it is 100% in a purely inquisitorial system ($\theta$ = 100).

If the defendant is careful, the equilibrium strategies are identical but the players switch role from the player with the head start to the player without the head start, and vice versa.

Prediction 1

The litigants spend less in the inquisitorial system than in the adversarial system. The rightful party—either a careful defendant or a plaintiff facing a careless defendant—has a higher probability of winning the case in the inquisitorial system than in the adversarial system.

3.2.2 Settlement Stage

In case of harm, the parties can bargain over a settlement offer that specifies a transfer from the defendant to the plaintiff. The players have reservation prices ${\widehat{s}}_{P}$ and ${\widehat{s}}_{D}$ equal to their expected utility of going to court, which we derived above. Table 1 summarizes these reservation prices.

Table 1 Reservation prices for out-of-court settlement

The assumption of $\theta < \delta$ ensures that there is always room for a settlement (i.e., ${\widehat{s}}_{D}$>${\widehat{s}}_{P}$). Since the settlement amount is defined by the average between the settlement claim $({s}_{P})$ and the settlement offer $\left({s}_{D}\right)$ a player’s best response is simply to match the other player’s action as long as it is below (above) the defendant’s (plaintiff’s) reservation price. This stage has an infinite number of Nash equilibria where both players state an identical number in the range of (${\widehat{s}}_{P}$, ${\widehat{s}}_{D})$.¹⁰ Predicting outcomes over the entire action space of the players is unsatisfactory. To obtain a precise prediction, we apply the Nash bargaining solution to this problem (Nash, 1953). Assuming risk-neutral players leads to an equal split of the surplus in the settlement stage. The two parties settle for $\frac{\delta -\theta }{2}$ if the defendant was careful and $\frac{\delta +\theta }{2}$ if the defendant was careless. Hence, the settlement amount either decreases or increases with $\theta$, depending on whether the defendant was careful or not.

Even if the Nash equilibrium predicts settlement in all cases, we see a number of reasons why this prediction might be unrealistic. First, players must assume equal bargaining power. Second, settlement might fail because it is difficult to compute the expected payoff of handling the case in court. If their perceived outside opportunities include a random term, out-of-court settlement might fail even if both players agree on an equal split of the surplus. A larger bargaining range —which decreases with $\theta$— may thus facilitate settlement.

Prediction 2

In equilibrium, the litigants always settle. The bargaining range is larger in the adversarial system, which may facilitate settlement if players do not play equilibrium strategies. The settlement amount is lower (higher) in the inquisitorial system if the defendant was careful (careless).

3.2.3 Care Stage

In the first stage, the defendant decides whether or not to exert care. He is careful if his expected payoff from being careless is lower than his expected payoff from being careful. We use the expected payoffs of the Nash bargaining solution of the settlement stage to derive the predictions for care:

$$\pi_{0} \left[ { - \frac{\delta + \theta }{2}} \right] < \pi_{1} \left[ { - \frac{\delta - \theta }{2}} \right] - \gamma$$

(9)

This gives us a threshold cost level ${\widehat{\gamma }}^{s}$ below which the defendant prefers to be careful:

$${\widehat{\gamma }}^{s}= \frac{\left({\pi }_{0}- {\pi }_{1}\right)\delta + \left({\pi }_{0}+ {\pi }_{1}\right)\theta }{2}$$

(10)

The threshold level is increasing in $\delta$ and $\theta$. This implies that a defendant who faces a random cost of care is more likely to be careful when $\theta$ increases.

In the next step, we want to investigate the care decision in a slightly modified game where we remove the settlement stage: in case of harm, the two parties directly proceed to the trial stage. We refer to this version as the Two-stage game, and to the version including the settlement stage as the Three-stage game. In the experiment, we implemented both versions of the game.

In the Two-stage game, the defendant’s condition for being careful depends on the expected utilities of the trial stage. The defendant prefers to be careful if:

$${\pi }_{0}\left[-\delta \right]< {\pi }_{1}\left[\theta -\delta \right]-\gamma$$

(11)

Which yields the critical cost level:

$${\widehat{\gamma }}^{NS} = ({\pi }_{0} - {\pi }_{1})\delta + {\pi }_{1}\theta$$

(12)

When settlement is not feasible, the threshold for care is also increasing in $\delta$ and $\theta$.

Prediction 3

The defendant is more careful in the inquisitorial system than in the adversarial system, whether settlement is feasible or not.

Being careful has a cost but yields two benefits for the defendant: (i) it lowers the probability of a legal dispute, and (ii) in case of a dispute it offers the defendant a head start in court. The expected cost of a dispute is higher in the inquisitorial system, whether the parties settle or go to court. As a result, defendants are more willing to avoid harm, which results in higher levels of care.

4 The experiment

This section describes the experimental design and procedures. We ran two versions of the game: in the Two-stage game the care stage is directly followed by the trial stage, while in the Three-stage game we add the settlement stage in between. Payoffs are measured in a fictitious currency (ECU).

4.1 Experimental design

4.1.1 Care Stage

There are two players, a defendant and a plaintiff. In the first stage, the defendant decides between being careful or not. The plaintiff does not act in this stage, but he observes whether the defendant is careful or not. If the defendant is not careful, the probability of harm of $\delta$ = 100 is ${\pi }_{o}=0.5$. If the defendant is careful, he incurs a cost $\gamma$, and the probability of harm decreases to ${\pi }_{1}$= 0.1. The cost of care is randomly drawn from the set {20, 30,..., 90} ECU, all values with equal probability. The wide range of costs allows us to observe both careful and careless defendants. Subsequently, the game either continues with the settlement stage (Three-stage game) or directly with the trial stage (Two-stage game).

4.1.2 Settlement Stage

(Three-stage game only). The settlement stage proceeds as follows:

• Simultaneously, the defendant specifies his maximum settlement offer and the plaintiff specifies his minimum request.

• If the maximum offer is greater than or equal to the minimum request, the case is settled. The defendant pays the average between the maximum offer and the minimum request.

• If the maximum offer is lower than the minimum request, settlement fails and the players proceed to the trial stage.

4.1.3 Trial Stage

• The plaintiff sues the defendant for damages equal to 100 ECU.

• The plaintiff and the defendant simultaneously decide how much to spend on their case.

• If the defendant was careless, then the plaintiff has a strong case. The defendant must spend at least $\theta$ ECU more than the plaintiff to win.

• If the defendant was careful, then the plaintiff has a weak case. The plaintiff must spend at least $\theta$ ECU more than the defendant to win.

• If there is a tie, the winner is determined by chance with equal probabilities.

4.1.4 Adversarial and Inquisitorial Systems

The two games only differ with respect to the parameter $\theta$:

• In the adversarial system, we set $\theta$ = 20.

• In the inquisitorial system, we set $\theta$ = 70.

The higher value of $\theta$ in the inquisitorial system captures the greater involvement of the judge. As a result, a careful defendant and a plaintiff facing a careless defendant receive a larger head start in the inquisitorial system than in the adversarial system.

4.1.5 Numerical predictions

Table 2 summarizes the numerical predictions of the model presented in Sect. 3 using the parameter values of the experiment: $\delta$ = 100, ${\pi }_{0}$ = 0.5, ${\pi }_{1}$ = 0.1, $\theta$ = 20 in the adversarial system, $\theta$ = 70 in the inquisitorial system.

Table 2 Numerical predictions using the experimental parameter values

4.2 Experimental procedures

In our experiment, we vary the parameter $\theta$ and the presence or absence of a settlement stage. We implement the main treatment variation (Adversarial versus Inquisitorial) on a between-subject basis, while we vary the inclusion of a settlement stage within subjects. For each treatment, we play 20 rounds of the game in a stranger matching protocol. The subjects in a session are allocated to matching groups of six to eight subjects. The matching groups remain constant throughout the session. In each round, we randomly allocate subjects to the role of defendant and plaintiff, ensuring that all matching groups contain the same number of each type. We then randomly allocate the subjects in a matching group into groups of two.

For each defendant, we randomly and independently draw the cost of care from the distribution described above. Subjects play a first sequence of 20 rounds in either the Two-stage game or the Three-stage game, followed by a second sequence of 20 rounds with a different treatment.¹¹ For the decisions in Stages 2 and 3, we apply a partial version of the strategy method (Selten, 1967). Independently of the realization of harm, all subjects proceed with the game.¹² The subsequent decisions only affect payoffs in case of harm. Participants are informed about this procedure. All reactions to players’ actions (as opposed to moves of nature) are elicited in the direct response method. In the settlement and trial stage, plaintiffs respond to the actual care decision of their defendant. In the Three-stage game, the game ends when settlement is successful, i.e., we do not observe litigation spending of participants who reach an agreement.¹³ To facilitate the understanding of the game, we use a rich framing and set the game in a medical malpractice context. The defendant is called the doctor and the plaintiff is called the patient.¹⁴

At the beginning of each treatment, we handed out written instructions explaining the procedures and rules of the game. After reading the instructions, participants had to answer control questions.¹⁵ At the end of the session, participants filled in a questionnaire with demographic and other questions. All profits that accrued through the experiment were counted in ECU and paid at the end of the experiment to the subjects in CHF, the local currency. To avoid overall losses, all subjects started each of the 40 games with a new endowment of 300 ECU. Participants were informed about the exchange rate (1000 ECU = 3.6 CHF).

We ran the experiment in z-Tree (Fischbacher, 2007). Participants were recruited using ORSEE (Greiner, 2015), from a pool of undergraduate students at the University of Lausanne and the Swiss Federal Institutes of Technology (EPFL). Participants’ mean age was 21, with a standard deviation of 3. The proportion of female participants was 42%. We report data from twelve sessions with 234 subjects. The sessions lasted around two hours. Participants received a show-up fee of 10 CHF and the average payoff amounted to 37 CHF (34 EUR).

5 Results

We follow the logic of backward induction and start with the results on litigation spending in Stage 3. We then present the results on the settlement claims and offers of Stage 2, followed by the care decision in Stage 1. Throughout the analysis, we cluster standard errors to account for the dependency of observations within matching groups; for all non-parametric tests we use matching group averages across the 20 periods as unit of observation.

5.1 Litigation spending

Figure 2 shows the average litigation spending in the adversarial and inquisitorial systems. We present the results separately for the Two-stage game and Three-stage game treatments. Spikes indicate standard errors, and horizontal lines show the theoretical prediction (Adversarial: 40; Inquisitorial: 15).¹⁶ The left panel shows the results in the Two-stage game. In line with Prediction 1, litigation spending is significantly higher in Adversarial than in Inquisitorial (53.1 vs. 40.6, p = 0.009).¹⁷ In all treatments, litigants spend more than the model predicted (all comparisons p < 0.01).

Fig. 2

Average litigation spending across treatments. Spikes indicate standard errors. Horizontal lines indicate predicted values

The right panel of Figure 2 shows the results in the Three-stage game. Note that unlike before, we observe a selected sample at Stage 3. Therefore, the effects discussed for this sample are not cleanly identified causal effects. Also in the Three-stage game we find that litigation spending is higher in Adversarial than in Inquisitorial (74.6 vs. 50.9, p = 0.017). Furthermore, litigation spending tends to be higher than in the Two-stage game, even though the presence of the settlement stage should not affect the actions in court in theory. This suggests that litigants become more competitive after failed settlement, which could be explained by an emotional response to settlement failure, or it could reflect selection of particularly tough negotiators.

In the next step, we use random effects estimates to study the determinants of litigation spending. For these and all following models, we estimate robust standard errors using the matching groups as clusters. Table 3 shows the results. Model (1) explains litigation spending by the treatment dummies Inquisitorial, Three-stage game, and whether the litigant is a defendant. In line with Figure 2, we find that litigants spend significantly less under the inquisitorial rule than under the adversarial rule. We also find that litigation is significantly higher after failed settlement in the Three-stage game. Finally, we find that defendants spend less than plaintiffs.

Table 3 Instrumental variable estimates for litigation spending

In Model (2) we investigate the differences between the plaintiffs’ and the defendants’ spending in court more closely. We interact Careful with dummies for the two roles because our theoretical model predicts that the effect of care on litigation differs for plaintiffs and defendants. When we control for care, we introduce an endogeneity problem, because defendants’ care decisions and litigation spending may be correlated. To address this concern, we use an instrumental variable approach. We use the cost of care to instrument the care decision. The costs are a valid instrument as they are randomly generated in each game and, as we discuss below, are highly predictive of the care decision. Careful defendants spend about 26 ECU less than careless defendants. This result is in line with our theoretical model, which predicts that careful defendants should spend less than careless defendants. Plaintiffs facing a careful defendant spend about 13 ECU less when facing a careful defendant. This result is inconsistent with the theory because plaintiffs facing a careful defendant are disadvantaged and are predicted to spend more than the plaintiffs facing a careless defendant.

Model (3) additionally controls for time effects with a variable identifying the period (1 to 20), and includes a dummy indicating whether the observation stems from the second sequence of 20 periods. As there is random rematching in every period the games are one-shot interactions. We can then interpret time effects as reflecting subjects’ increased experience with the environment. The coefficient for Period suggests decreasing spending over time. The dummy for the second sequence is significantly negative, suggesting that litigants spend less in the second sequence of 20 periods. In Model (4) we introduce an interaction with the dummy for the inquisitorial system to investigate whether the dynamics are treatment-dependent. We do not find a significant difference in the time trends.

Finally, Fig. 3 shows the winning rates of defendants for the adversarial and inquisitorial system and for careful and careless defendants. For expositional ease, we pool the results of the Two-stage and Three-stage game. Horizontal lines indicate the predicted winning probabilities (see Table 2). In the adversarial system, where the predicted probabilities depart only slightly from 50 percent, we find that defendants win more often than predicted when they were careful and less often when they were careless. The adversarial system yields more accurate verdicts than predicted by the theory. This reflects the results above that the plaintiffs facing a careful defendant tend to spend less on litigation, even though they are predicted to spend more. It is true that careful defendants also spend less than careless defendants, but this lower spending is more than compensated by the contribution of the judge. In the inquisitorial system, the winning rate of careless defendants is very close to the prediction of the model while the winning rate of careful defendants is slightly higher than predicted. Overall, the inquisitorial system yields more accurate verdicts than the adversarial system, because careful defendants win more often while careless defendants win less often.

Fig. 3

Average winning rates of careless and careful defendants in the adversarial and inquisitorial systems. Data from the Two-stage game and the Three-stage game combined. Spikes indicate standard errors. Horizontal lines indicate predicted values

Result 1

In line with Prediction 1, litigation spending is higher in the adversarial system than in the inquisitorial system. Careful defendants win more often in the inquisitorial system than in the adversarial system.

5.2 Settlement

The results of this section only concern the Three-stage game treatment. Overall, we observe that 47.6% of the cases are settled in Stage 2. This settlement rate is much lower than the agreement rates observed in Nash demand games (e.g. Fischer et al., 2006). The reason for the low settlement rate is presumably that the consequences of going to court are much more difficult to compute compared to the outside option in a standard Nash demand game. On average, defendants offer 57.3 ECU to settle the dispute, while plaintiffs ask for 67.3 ECU. Given that on average plaintiffs ask for more than defendants offer, it is unsurprising that settlement frequently fails. Figure 4 shows the settlement rate by treatment. In line with our theoretical considerations with respect to the bargaining range, we observe higher settlement rates in the adversarial than in the inquisitorial system (51.0 vs. 43.5 percent, p = 0.028).

Fig. 4

Average settlement rate across treatments with standard errors

We use random effects estimates to investigate treatment effects in the settlement stage. The results are presented in Table 4. The top set of coefficients reports results from models including only the treatment dummy Inquisitorial as the explanatory variable. The remaining coefficients show the results of the models with the full set of controls. As before, we instrument the care decision using the cost of care. Further controls are the interaction between Inquisitorial and Careful, and the two controls for time trends, Period and Second sequence.

Table 4 Instrumental variable estimates for the settlement stage

Models (1) and (2) explain the defendants’ offers and the plaintiffs’ claims, respectively. The simple linear regression shows that offers and claims are lower in Inquisitorial than in Adversarial systems. The multivariate estimates reveal that offers and claims are importantly affected by the care decision, as careful defendants offer 33 ECU less compared to careless defendants in the adversarial rule. Consistent with our prediction, the difference between careful and careless offers is larger in the inquisitorial system (weakly significant). Plaintiffs facing a careful defendant claim about 18 ECU less, with no significant differences across systems. Both offers and claims seem to decrease over time and in the second sequence. The interaction between Inquisitorial and Period suggests that for claims the negative time trend is strongest in adversarial systems, while for offers it is strongest in inquisitorial systems.

Model (3) explains settlement success in a linear probability model. Settlement rates are significantly lower in Inquisitorial than in Adversarial when estimated without controls. When we add the controls, the coefficient remains the same but loses significance. In the adversarial system, the cases that involve a careful defendant settle 34 percentage points less often than the cases that involve a careless defendant. The interaction term shows that this effect is significantly weaker in the inquisitorial system. Over the course of the 20 periods, the settlement rate increases in the adversarial system, while the interaction term indicates the opposite in the inquisitorial system. This means that the treatment differences in settlement rates tend to become more pronounced as subjects gain experience with the game.

Finally, we study the settlement amounts. Conditional on having reached an agreement, the average transfer is 37.6 ECU in the inquisitorial system and 58.1 ECU in the adversarial system if the defendant was careful. Both values are significantly higher than the equal split transfer of 15 ECU and 40 ECU, respectively (p < 0.01). If the defendant was careless, the average transfer is 79.5 (76.5) ECU in the adversarial (inquisitorial) system, which is significantly higher than predicted in the adversarial system (60 ECU, p < 0.01) but lower than predicted in the inquisitorial system (85 ECU, difference not significant). Model (4) in Table 4 explains the settlement amount. We find that settlement amounts are lower in inquisitorial systems, but the effect is mainly driven by the cases where the defendant was careful. Finally, there is some indication that settlement amounts decrease over time and in the second sequence.

Result 2

In line with Prediction 2, cases settle more often in the adversarial than in the inquisitorial system. Settlement amounts are mainly driven by the care decision.

5.3 Care

Figure 5 shows the frequency of care in the adversarial and inquisitorial system for the Two-stage game and Three-stage game, whereby spikes indicate clustered standard errors. The horizontal lines show the predicted levels of care.¹⁸ In all treatments, defendants exert more care than the model predicted (all comparisons p < 0.04).

Fig. 5

Bars show the frequency of careful defendants across treatments. Spikes indicate standard errors. Horizontal lines indicate predicted values

In the Two-stage game, we find evidence for Prediction 3 as we observe higher levels of care in Inquisitorial than in Adversarial (56.0% vs. 44.6%, p = 0.035, Wilcoxon rank-sum test). In the Three-stage game, we observe a qualitatively similar treatment effect, albeit not reaching significance (56.8% vs. 50.2%, p = 0.246).

Table 5 presents the results from linear probability models, which allow us to account for the cost of care and test for time effects. All models are random effects estimates. In Model (1), we include the treatment dummies and the cost of care. As expected, higher costs reduce the willingness to be careful. The effect is highly significant and large in size. At the lowest cost level (20), we observe 88 percent of defendants being careful, while at the highest level (90) the corresponding number is down to 19 percent.

Table 5 Linear probability estimates for care

However, the treatment effect between Adversarial and Inquisitorial does not reach significance. Likewise, the possibility of settlement does not seem to affect care. In Model (2), we add an interaction term between Inquisitorial and Three-stage game, which is insignificant, indicating that the results do not systematically differ in the Two-stage game and the Three-stage game. In Model (3), we add the controls for time effects. We observe a negative trend in care across time. Finally, in Model (4), we find again that the treatment differences do not significantly change over time.

Result 3

The defendant’s decision to be careful is strongly determined by the cost of care. In line with Prediction 3, care tends to be higher in the inquisitorial system, but the difference does not reach statistical significance when we control for the cost of care.

6 Conclusion

This paper analyzes deterrence, settlement, and litigation spending under alternative procedural systems, i.e., the adversarial versus inquisitorial systems. We have used a basic litigation model to derive three main hypotheses to be tested using experimental data. In line with our theoretical predictions, we find that the inquisitorial system is associated with lower litigation spending, but also lower rates of cases settled than in the adversarial system. We also show that care is higher in the inquisitorial system (with careful defendants winning more often), although this effect is not always statistically significant.

Our findings also indicate that under both procedural systems, the levels of litigation spending and care are higher than the predicted levels (see Figs. 2 and 5). What might be motivating this result? We provide possible interpretations based on the joint reading of two separate strands of the literature: experiments for contest theory, and experiments in the realm of tort law. Overbidding in lottery contests and all-pay auctions has been often observed in prior experiments, wherein the average effort level exceeds the equilibrium prediction (for reviews: Chowdhury et al., 2014; Dechenaux et al., 2015).¹⁹ Experiments in tort law further show that individuals tend to over-invest in care (e.g., Guerra & Parisi, 2022; for a review: Guerra, 2021). A number of plausible rationales may explain our consistent finding of over-spending in both litigation and care, including individual risk aversion and/or loss aversion, or distorted perceptions of probabilities. While falling beyond the scope of our experiment, identifying which specific factor(s) can explain non-equilibrium behavior remains an interesting question for future investigations.

As a first attempt at exploring deterrence, settlement, and litigation spending under adversarial versus inquisitorial systems, our setup has been intentionally kept simple and highly stylized. Inevitably, several aspects have been omitted, which are worth being discussed as avenues for future research. To start with, by using the rent-seeking framework proposed by Parisi (2002), we have modeled the differences between the two systems as a difference in the institutional component $\theta$ (low $\theta$: Adversarial; high $\theta$: Inquisitorial). We have treated $\theta$ as a parameter (as in Parisi, 2002, pp. 197–201), and not as a choice variable for the litigants and/or policy-makers. Our study can be extended to include a normative analysis on the optimal procedural choice, by treating $\theta$ as an institutional choice variable (as in Parisi, 2002, pp. 201–207). This would allow deriving—and experimentally testing—the “mix” of adversarial and inquisitorial systems that maximizes the net social benefit from litigation.

The purpose of this study was to conduct a quantitative analysis of the evidence production in court (as in e.g., Landeo et al., 2007). We have not analyzed the law of evidence per se, as it would have implicated qualitative assessments that our experiment was not designed to test. This calls for further investigations into the motivations driving litigation decisions under the two different systems. For example, it may be fruitful to conduct a qualitative analysis of the evidence production as factored in the parties’ decision to pursue litigation. To further assess the respective merit of each procedure, our analysis can be extended by weakening the common knowledge assumption about the defendant’s true degree of fault.

Overall, our research speaks to both theorists and practitioners. The results show that the theoretical predictions are robust to experimental validation, but also suggest the need to revisit the existing theory to account for the observed excessive litigation spending and care. From a policy perspective, our study identifies different pros and cons associated with the adversarial and inquisitorial systems. Neither system is uniformly better: it depends upon the relative importance of deterrence, litigation, and settlement. It is thus important for future research to advance our understanding of individuals’ behaviors under the two procedural systems, in a wider range of tort contexts.

Appendix: Instructions to participants

This is an English translation of the instructions for the Three-stage game and Inquisitorial. For the treatments Two-stage game we dropped the parts in ; for the treatments Adversarial the head start is 20 ECU instead of 70. The original instructions are in French and are all available upon request.

1.1 Instructions

Welcome to this experiment!

From now on, it is strictly forbidden to speak to the other participants. If you have a question, please contact the assistants. If you violate this rule, we will be forced to exclude you from the experiment.

During this experiment, you will make decisions that will allow you to earn some money. The rules determining your earnings are explained below. It is therefore very important that you read them attentively.

1.2 Description of the experiment

The experiment is a game that allows you to earn ECU (experimental currency unit). The conversion rate is as follows: 1000 ECU = 3.60 CHF.

The game is played in pairs and each player has a different role. You can be either the doctor or the patient.

The game consists of two stages that are further described below. During the first stage, the doctor treats the patient more or less carefully. During the second stage, the patient who is victim of a medical error can seek compensation in court.

You will play the game 20 times and your role (doctor or patient) will be randomly determined each time. Your partner is another participant of the experiment drawn randomly for each game.

At the beginning of each of the 20 games, you will receive an initial endowment of 300 ECU.

1.3 First stage of the game—medical consultation

The first stage is only played by the doctor.

The doctor treats the patient and decides to be either negligent or careful. If the doctor is careful, it reduces the risk of medical error but it costs him some ECU.

In case of medical error, the patient loses 100 ECU.

If the doctor is careful:

• The doctor loses a variable number of ECU. This number will be communicated to the doctor at the beginning of each game. This number will not be communicated to the patient.

• The patient has 1 in 10 chance (10 percent) of being victim of a medical error and thus of losing 100 ECU.

If the doctor is negligent:

• The doctor does not lose any ECU.

• The patient has 1 in 2 chance (50 percent) of being victim of a medical error and thus of losing 100 ECU.

1.4 Second stage of the game–Trial

The second stage of the game takes place in case a medical error has occurred and is played by both the patient and the doctor.

The patient learns whether the doctor was careful or negligent.

In case of medical error, the patient can take legal action to claim a compensation of 100 ECU to the doctor. .

1.5 Functioning of the trial

In case of trial, the patient tries to convince the judge to grant him a compensation of 100 ECU. By contrast, the doctor tries to convince the judge not to award this compensation. The role of the judge is played by the computer.

To convince the judge, the doctor and the patient must simultaneously spend ECU. The more they spend, the more they convince the judge. If the patient convinces the judge, he receives 100 ECU from the doctor.

If the doctor was careful, the patient must spend at least 70 ECU more than the doctor to convince the judge.

Example: The doctor was attentive and a medical error occurred. Assume the doctor spends 110 ECU to convince the judge:

• If the patient spends 130 ECU, he does not convince the judge. He therefore receives no compensation.

• If the patient spends 190 ECU, he convinces the judge. He therefore receives a compensation of 100 ECU from the doctor.

If the doctor was negligent, the doctor must spend at least 70 ECU more than the patient to convince the judge.

Example: The doctor was negligent and a medical error occurred. Assume the doctor spends 90 ECU to convince the judge:

• If the patient spends ECU 30, he convinces the judge. He therefore receives a compensation of 100 ECU from the doctor.

• If the patient spends 10 ECU, he does not convince the judge. He therefore receives no compensation.

In case of tie, the judge flips a coin to determine if the patient is compensated or not.

1.6 Functioning of the out-of-court settlement

The patient and the doctor can avoid the trial by settling their dispute out of court. The procedure works as follows:

• The doctor specifies the maximum amount he is willing to pay to the patient to avoid going to court.

• The patient specifies the minimum amount he is willing to receive from the doctor to avoid going to court.

If the players find an agreement, that is, if the doctor is willing to pay more than what the patient is willing to receive, then we take the mean between these two amounts, and the settlement takes place. The game is finished.

Example: the doctor is willing to pay a maximum of 100 ECU and the patient is willing to receive at least 50 ECU to avoid going to court. In this case, the players find an agreement and the doctor pays 75 ECU to the patient.

If players fail to reach an agreement, that is, if the doctor is willing to pay less than what the patient is willing to receive, the trial described above starts.

Example: the doctor is willing to pay a maximum of 70 ECU and the patient is willing to receive at least 150 ECU to avoid going to court. In this case, players fail to reach a settlement.

Remark

We will ask you at each of 20 rounds what would be your decisions for the legal process before telling you whether a medical error occurred. These decisions will only affect your earnings in case of medical error.