1 Introduction

Nonlinear partial differential equations are significant models to express the internal behaviour of intricate phenomena arise in applied mathematics, mathematical physics, elastic media, chemical kinematics, plasma physics, optical fibre, biology, solid-state physics, ocean dynamics, geochemistry, photonics, optics, shallow water waves, fiber optics, water optical metamaterials and so on (Oldham and Spanier 1974; Miller and Ross 1993; Fang et al. 2021; Wazwaz 2002; Wang et al. 2022; Bo et al. 2023). Many prominent mathematicians and physicists have recently become interested in the study of wave profiles which are illustrated through a family of nonlinear evolution equations (Kilbas et al. 2006; Hu et al. 2008; Wen 2023; Fang et al. 2023; Dai and Wang 2020). Several computational schemes have been established to analyze distinct obstacles of real-life by utilizing wave solutions extracted from relevant nonlinear models. Instantaneously, generalized projective Riccati equation method (Akram et al. 2021), Sardar sub-equation and modified Sardar sub-equation techniques (Ullah et al. 2022; Akinyemi et al. 2022a, b; Nasreen et al. 2023a), generalized exponential rational function scheme (Ghanbari et al. 2019; Rehman et al. 2022), distinct tanh approaches (Zulfiqar and Ahmad 2022; Islam et al. 2023a; Ahmad and Rani 2023; Ali et al. 2023; Mostafa et al. 2023), new extended direct algebraic method (Raddadi et al. 2021; Nasreen et al. 2023b, c), reduced differential transform and variational iteration techniques (Zulfiqar and Ahmad 2020), first integral approach (Akinyemi et al. 2022c), Hirota and Darboux methods (Ma 2022; Geng et al. 2023a, b; Chen 2023a, b; Chen and Zhu 2023; Chen and Xiao 2022; Dai et al. 2020; Rehman and Ahmad 2022a, b; Ismael et al. 2023), generalized exp \((-w(\xi ))\)-expansion and extended rational \(({G}{\prime}/{G}^{2})\)-expansion schemes (Owyed et al. 2022), improved auxiliary equation approach (Islam et al. 2023b), semi-inverse and fractional variation techniques (Fu et al. 2023), the rational \(({G}{\prime}/G)\)-expansion scheme (Islam et al. 2018), extended simplest equation and modified Khater methods (Khater 2021), \({\Phi }^{6}\)-model expansion tool (Seadawy et al. 2021), generalized auxiliary equation approach (Akinyemi et al. 2022d), various exp \((-\varphi (\xi ))\)-expansion techniques (Inan et al. 2022; Ahmad et al. 2023a), extended and modified rational expansion method (Nasreen et al. 2023d), extended Fan sub-equation scheme (Younis et al. 2020), F-expansion and improved F-expansion methods (Nasreen et al. 2018; Seadawy et al. 2019; Ahmad et al. 2023b) and so on.

In the field of wave profiles propagation, nonlinear Schrodinger equations concerning diverse intricate nonlinear phenomena have attracted profound attention of researchers. Schrodinger type partial differential equations bear specialty for explaining distinct intricate nonlinear phenomena arise in electromagnetism, photonics, fluid dynamics, quantum electronics, plasma physics etc. The coupled Schrodinger model that we consider is stated as follows:

$$\begin{gathered} iD_{t}^{\alpha } u + D_{x}^{2\beta } u + a\left( {\left| u \right|^{2} + b\left| v \right|^{2} } \right)u = 0 \hfill \\ iD_{t}^{\alpha } v + D_{x}^{2\beta } v + a\left( {b\left| u \right|^{2} + \left| v \right|^{2} } \right)v = 0 \hfill \\ \end{gathered}$$
(1)

where \(0<\alpha\), \(\beta \le 1\); \(u(x,t)\) and \(v(x,t)\) denote the complex-valued functions of spatial variable \(x\) and temporal variable \(t\). These functions are utilized to illustrate the envelopes of two individual and polarized optical signals. The free parameters \(a\) and \(b\) stand for the group velocity dispersion. Several studies of Eq. (1) alongside fractional order as well as integer order have extensively taken a major part of the literature after initiating in 1992 by Boyd (Boyd 1992). If we look back in the literature, then some works with integer orders could be mentioned accordingly such as in 1995, Wright had examined the modulation instability (Wright 1995); the effects of parameters on solitary waves had been explained and tested the stability at the same time (Yang 1997); Tan and Boyd had obtained exact analytic solutions, and analyzed single-mode and coupled-mode solitary waves (Tan and Boyd 2000); the stability of periodic waves for certain ranges of parameters had been studied by Tan and Boyd (Tan and Boyd 2001); the variational iteration method had been utilized by Sweilam and Al-Bar to study the same model which highlighted wave-wave interaction together with energy conservation (Sweilam and Al-Bar 2007). Eslami has considered the model due to only time fractional and obtained some analytic solutions by applying Kudryashov technique (Eslami 2016). Several recent studies of the mentioned nonlinear system with time and space fractional derivatives are noticeable. Instantly, Lakestani and Manafian have used extended trial equation, exp \((-\Omega (\eta ))\)-expansion, improved tan \((\phi (\eta )/2)\)-expansion and semi-inverse variational principle methods which provided some analytic solutions in characterizing different soliton shapes arise in nonlinear optics (Lakestani and Manafian 2018); extended sinh-Gordon equation expansion method has been applied by Esen et. al. to generate several soliton solutions (Esen et al. 2018); Wang et. al. have demonstrated the model by fractional Riccati and fractional dual-function schemes which delivered vector solitons and periodic solutions with the assistance of Mittag-Leffler function (Wang et al. 2020); modified generalized exponential rational function and Hirota bilinear techniques have been utilized by Rehman and Ahmad through which several analytical solutions have been constructed by balancing the nonlinear physical components (Rehman and Ahmad 2022a, b); optical solitons arise in optical fibers have been produced by Nasreen et. al. via new extended direct algebraic method (Nasreen et. al. 2023c); Ahmad et. al. have employed improved modified extended tanh-expansion method and achieved optical soliton solutions (Ahmad et al. 2023c).

The above study inspires us to choose the nonlinear system stated in Eq. (1) for investigating accurate wave solutions and analyzing the wave propagation related to nonlinear optics. The current exploration deals with two competent schemes, namely improved auxiliary equation and improved tanh. The inspection from earlier studies confirms that these two competent techniques haven’t been utilized by any researchers to extract wave solutions of the model Eq. (1). That is why, the authors claim that the outcomes throughout the present work are unique and distinct. The involved free parameters in achieved solutions are assigned with suitable numeric values which characterize the dynamic nature of nonlinear optical waves through graphical representations. Beyond 3D and 2D plots, contour plots are included to make visible the overhead view of dynamic waves. Diverse solitons for nonlinear dynamic waves are obtained which might be helpful to analyze the phenomena arise in optical communication systems.

2 Outline of schemes

Assume a nonlinear evolution equation of fractional order in the succeeding form.

$${\rm K}\left( {u,D_{x}^{\upsilon } u,D_{y}^{\upsilon } u, \ldots ,D_{t}^{\upsilon } ,D_{xx}^{\upsilon } u,D_{xy}^{\upsilon } u,D_{yy}^{\upsilon } u, \ldots ,D_{tt}^{\upsilon } u, \ldots } \right) = 0,$$
(2)

where \(0<\upsilon \le 1\). Implementing the transformation of wave variable as \(u\left(x,y,t,\dots \right)=U(\eta )\) reduces Eq. (2) into the following ordinary differential equation due to \(\eta\):

$${\Omega }\left( {U,U^{\prime},UU^{\prime},U^{\prime\prime}, \ldots } \right) = 0,$$
(3)

where primes in \(U\) specify the order of derivatives with respect to \(\eta\). Thereupon, the processes of instructed approaches are declared as below:

2.1 Improved auxiliary equation scheme

This approach announces the solution as follows:

$$U\left( \eta \right) = \frac{{\mathop \sum \nolimits_{i = 0}^{r} \iota_{i} a^{i\psi \left( \eta \right)} }}{{\mathop \sum \nolimits_{i = 0}^{r} \sigma_{i} a^{i\psi \left( \eta \right)} }},$$
(4)

where the included constraints are assessed under some procedures; homogenous balance rule grants the value of \(r\) and \({a}^{\psi (\eta )}\) satisfies the ODE.

$$\psi ^{\prime}\left( \eta \right) = \frac{1}{\ln a}\left\{ {\lambda a^{ - \psi \left( \eta \right)} + \mu + \tau a^{\psi \left( \eta \right)} } \right\}.$$
(5)

The solutions of Eq. (5) are noticeable in Ref. (Akbar et al. 2019). The operational rules with the improved auxiliary equation approach are accessible in earlier work (Islam et al. 2023b).

2.2 Improved tanh approach

This technique declares the solution to be the subsequent form.

$$U\left( \eta \right) = \frac{{c_{0} + \mathop \sum \nolimits_{i = 0}^{r} c_{i} {\Psi }^{i} \left( \eta \right) + d_{i} {\Psi }^{ - i} \left( \eta \right)}}{{e_{0} + \mathop \sum \nolimits_{i = 0}^{r} e_{i} {\Psi }^{i} \left( \eta \right) + f_{i} {\Psi }^{ - i} \left( \eta \right)}},$$
(6)

where the concerned free parameters are evaluated under some operations, homogenous balance rule supplies the value of \(r\) and \(\Psi \left(\eta \right)\) satisfies the ODE.

$$\Psi^{\prime}\left( \eta \right) = \delta + \Psi^{2} \left( \eta \right).$$
(7)

The solutions of Eq. (7) and the working rules alongside the improved tanh scheme are available in previous study (Islam et al. 2023a). Now, we utilize the recommended tools for celebrating the perfect solitary wave solutions of the pointed governing model Eq. (1).

3 Extraction of wave solutions

Consider the subsequent transformation of wave variables.

$$u\left( {x,t} \right) = U\left( \eta \right)e^{i\phi } ,\;v\left( {x,t} \right) = V\left( \eta \right)e^{i\phi } ,$$
(8)

where \(\eta =\frac{{x}^{\beta }}{\beta }-c\frac{{t}^{\alpha }}{\alpha }\) and \(\phi =-l\frac{{x}^{\beta }}{\beta }+m\frac{{t}^{\alpha }}{\alpha }+{\theta }_{0}\). This change is made in accordance with conformable fractional derivatives which follows chain rule and Leibniz rule (Khalil et al. 2014; Abdeljawad 2015). Equation (8) is inserted in Eq. (1) and thereupon separated into the following two ordinary differential equations due to the independent variable \(\eta\):

$$U^{\prime\prime} + aU^{3} + abV^{2} U - \left( {l^{2} + \mu } \right)U = 0,$$
(9)
$$V^{\prime\prime} + aV^{3} + abU^{2} V - \left( {l^{2} + \mu } \right)V = 0,$$
(10)

where \(c = - 2l\). Consider

$$V = kU.$$
(11)

Then Eq. (9) and Eq. (10) produce

$$U^{\prime\prime} + a\left( {1 + bk^{2} } \right)U^{3} - \left( {l^{2} + m} \right)U = 0.$$
(12)

Balancing theme provides \(r=1\). Now, the desired wave solutions are constructed throughout the succeeding section.

3.1 Solutions found by improved auxiliary equation approach

The solution of Eq. (12) is then appeared to be.

$$U\left( \eta \right) = \frac{{\iota_{0} + \iota_{1} a^{\psi \left( \eta \right)} }}{{\sigma_{0} + \sigma_{1} a^{\psi \left( \eta \right)} }},$$
(13)

where \({\iota }_{1}\) and \({\sigma }_{1}\) are not zero at a time. Create a polynomial in \({a}^{\psi (\eta )}\) from Eq. (12) by utilizing Eq. (13) and its essential derivatives together with Eq. (5). Coefficients of this polynomial are equated to zero and solve them for the subsequent results.

Case 1: \(\iota_{0} = \pm \frac{{2\lambda \sigma_{1} - \mu \sigma_{0} }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\), \(\iota_{1} = \pm \frac{{\mu \sigma_{1} - 2\tau \sigma_{0} }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\), \(m = \frac{1}{2}\left( {4\lambda \tau - \mu^{2} - 2l^{2} } \right).\)

Case 2: \(\iota_{0} = \pm \frac{{\sigma_{1} \left( {4\lambda \tau - \mu^{2} } \right)}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\), \(\iota_{1} = 0\), \(\sigma_{0} = \frac{{\mu \sigma_{1} }}{2\tau }\), \(m = \frac{1}{2}\left( {4\lambda \tau - \mu^{2} - 2l^{2} } \right).\)

Case 3: \(\iota_{0} = \pm \frac{{\mu \sigma_{0} }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\),\(\iota_{1} = \pm \frac{{2\tau \sigma_{0} }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\),\(\sigma_{1} = 0\), \(m = \frac{1}{2}\left( {4\lambda \tau - \mu^{2} - 2l^{2} } \right).\)

Case 4: \(\iota_{0} = \mp \frac{{\sigma_{1} \left( {\mu \mp \sqrt {4\lambda \tau - \mu^{2} } } \right)}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\), \(\sigma_{0} = \frac{{\sigma_{1} \left( {\mu \pm \sqrt {4\lambda \tau - \mu^{2} } } \right)}}{2\tau }\), \(m = \frac{1}{2}\left( {4\lambda \tau - \mu^{2} - 2l^{2} } \right).\)

A heap of accurate wave solutions of the governing model Eq. (1) may be accumulated with the assistance of above parameter’s values. Only the solutions for case 1 are presented here for simplicity while the readers might assess other results if necessary.

Solution group 1: The expression for traveling wave solutions due to Case 1 is found as follows:

$$u_{1} \left( \eta \right) = \pm \frac{{\left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)a^{\psi \left( \eta \right)} e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} a^{\psi \left( \eta \right)} } \right]}},$$
(14)

where \(\eta =\frac{{x}^{\beta }}{\beta }+2l\frac{{t}^{\alpha }}{\alpha }\) and \(\phi =-l\frac{{x}^{\beta }}{\beta }+\frac{1}{2\alpha }(4\lambda \tau -{\mu }^{2}-2{l}^{2}){t}^{\alpha }+{\theta }_{0}\).

Assigning \({\mu }^{2}-4\lambda \tau <0\) and \(\tau \ne 0\) provide

$$u_{1}^{1} \left( \eta \right) = \pm \frac{{2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu - \sqrt {4\lambda \tau - \mu^{2} } {\text{tan}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu - \sqrt {4\lambda \tau - \mu^{2} } {\text{tan}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(15)
$$u_{1}^{2} \left( \eta \right) = \pm \frac{{2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu + \sqrt {4\lambda \tau - \mu^{2} } {\text{cot}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {4\lambda \tau - \mu^{2} } {\text{cot}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(16)
$$v_{1}^{1} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu - \sqrt {4\lambda \tau - \mu^{2} } {\text{tan}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}} \right]}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu - \sqrt {4\lambda \tau - \mu^{2} } {\text{tan}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(17)
$$v_{1}^{2} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu + \sqrt {4\lambda \tau - \mu^{2} } {\text{cot}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}} \right]}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {4\lambda \tau - \mu^{2} } {\text{cot}}\left( {\sqrt {4\lambda \tau - \mu^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(18)

where \(\eta =\frac{{x}^{\beta }}{\beta }+2l\frac{{t}^{\alpha }}{\alpha }\) and \(\phi =-l\frac{{x}^{\beta }}{\beta }+\frac{1}{2\alpha }(4\lambda \tau -{\mu }^{2}-2{l}^{2}){t}^{\alpha }+{\theta }_{0}\).

For the assumptions \({\mu }^{2}-4\lambda \tau >0\) and \(\tau \ne 0\),

$$u_{1}^{3} \left( \eta \right) = \pm \frac{{2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right)} \right\}}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(19)
$$u_{1}^{4} \left( \eta \right) = \pm \frac{{2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right){ }} \right\}}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(20)
$$v_{1}^{3} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right)} \right\}} \right]}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(21)
$$v_{1}^{4} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right){ }} \right\}} \right]}}{{2\tau \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda \tau } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda \tau } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(22)

where \(\eta =\frac{{x}^{\beta }}{\beta }+2l\frac{{t}^{\alpha }}{\alpha }\) and \(\phi =-l\frac{{x}^{\beta }}{\beta }+\frac{1}{2\alpha }(4\lambda \tau -{\mu }^{2}-2{l}^{2}){t}^{\alpha }+{\theta }_{0}\).

Under the values \({\mu }^{2}+4{\lambda }^{2}<0\), \(\tau \ne 0\) and \(\tau =-\lambda\),

$$u_{1}^{5} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu - \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu - \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(23)
$$u_{1}^{6} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{cot}}\left( {\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} [\sigma_{0} + \sigma_{1} \{ \mu + \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{cot}}(\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2\} ]e^{ - i\phi } }},$$
(24)
$$v_{1}^{5} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu - \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu - \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(25)
$$v_{1}^{6} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{cot}}\left( {\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} [\sigma_{0} + \sigma_{1} \{ \mu + \sqrt { - \mu^{2} - 4\lambda^{2} } {\text{cot}}(\sqrt { - \mu^{2} - 4\lambda^{2} } \eta /2\} ]e^{ - i\phi } }},$$
(26)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {4\lambda^{2} + \mu^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

For the agreements \(\mu^{2} + 4\lambda^{2} > 0\), \(\tau \ne 0\) and \(\tau = - \lambda\),

$$u_{1}^{7} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(27)
$$u_{1}^{8} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(28)
$$v_{1}^{7} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(29)
$$v_{1}^{8} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \left( {\mu \sigma_{1} + 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} + 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(30)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {4\lambda^{2} + \mu^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

Assigning \(\mu^{2} - 4\lambda^{2} < 0\) and \(\tau = \lambda\) provide.

$$u_{1}^{9} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu - \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu - \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(31)
$$u_{1}^{10} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{cot}}\left( {\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} [\sigma_{0} - \sigma_{1} \{ \mu + \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{cot}}(\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2\} ]e^{ - i\phi } }},$$
(32)
$$v_{1}^{9} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu - \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\mu - \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{tan}}\left( {\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(33)
$$v_{1}^{10} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{cot}}\left( {\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} [\sigma_{0} - \sigma_{1} \{ \mu + \sqrt { - \mu^{2} + 4\lambda^{2} } {\text{cot}}(\sqrt { - \mu^{2} + 4\lambda^{2} } \eta /2\} ]e^{ - i\phi } }},$$
(34)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \frac{1}{2\alpha }\left( {4\lambda^{2} - \mu^{2} - 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

For the agreements \(\mu^{2} - 4\lambda^{2} > 0\) and \(\tau = \lambda\),

$$u_{1}^{11} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}},$$
(35)
$$u_{1}^{12} \left( \eta \right) = \pm \frac{{2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(36)
$$v_{1}^{11} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{tanh}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(37)
$$v_{1}^{12} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) - \left( {\mu \sigma_{1} - 2\lambda \sigma_{0} } \right)\left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]}}{{2\lambda \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\mu + \sqrt {\mu^{2} - 4\lambda^{2} } {\text{coth}}\left( {\sqrt {\mu^{2} - 4\lambda^{2} } \eta /2} \right)} \right\}} \right]e^{ - i\phi } }},$$
(38)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \frac{1}{2\alpha }\left( {4\lambda^{2} - \mu^{2} - 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

When \(\mu^{2} = 4\lambda \tau\),

$$u_{1}^{13} \left( \eta \right) = \pm \frac{{2\tau \eta \left( {2\lambda \sigma_{1} - \sqrt {4\lambda \tau } \sigma_{0} } \right) - \left( {\sqrt {4\lambda \tau } \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {2 + \mu \eta } \right\}}}{{2\tau \eta \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {2 + \mu \eta } \right\}} \right]e^{ - i\phi } }},$$
(39)
$$v_{1}^{13} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \eta \left( {2\lambda \sigma_{1} - \sqrt {4\lambda \tau } \sigma_{0} } \right) - \left( {\sqrt {4\lambda \tau } \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {2 + \mu \eta } \right\}} \right]}}{{2\tau \eta \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {2 + \mu \eta } \right\}} \right]e^{ - i\phi } }},$$
(40)

where \(\eta =\frac{{x}^{\beta }}{\beta }+2l\frac{{t}^{\alpha }}{\alpha }\) and \(\phi =-l\frac{{x}^{\beta }}{\beta }-\frac{{l}^{2}{t}^{\alpha }}{\alpha }+{\theta }_{0}\).

Under the values \(\tau \lambda <0\), \(\mu =0\) and \(\tau \ne 0\),

$$u_{1}^{14} \left( \eta \right) = \pm \frac{{2\lambda \sigma_{1} + 2\tau \sigma_{0} \left\{ {\sqrt { - \lambda /\tau } tanh\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\sqrt { - \lambda /\tau } tanh\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}} \right]}},$$
(41)
$$u_{1}^{15} \left( \eta \right) = \pm \frac{{2\lambda \sigma_{1} + 2\tau \sigma_{0} \left\{ {\sqrt { - \lambda /\tau } coth\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\sqrt { - \lambda /\tau } coth\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}} \right]}},$$
(42)
$$v_{1}^{14} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \sigma_{1} + 2\tau \sigma_{0} \left\{ {\sqrt { - \lambda /\tau } tanh\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}} \right]}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\sqrt { - \lambda /\tau } tanh\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}} \right]}},$$
(43)
$$v_{1}^{15} \left( \eta \right) = \pm \frac{{k\left[ {2\lambda \sigma_{1} + 2\tau \sigma_{0} \left\{ {\sqrt { - \lambda /\tau } coth\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}} \right]}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {\sqrt { - \lambda /\tau } coth\left( {\sqrt { - \tau \lambda } \eta } \right)} \right\}} \right]}},$$
(44)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \frac{1}{2\alpha }\left( {4\lambda \tau - 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

For the assumptions \(\mu = 0\) and \(\lambda = - \tau\),

$$u_{1}^{16} \left( \eta \right) = \pm \frac{{2\tau \sigma_{1} \left\{ {1 - e^{ - 2\tau \eta } } \right\} - 2\tau \sigma_{0} \left\{ {{ }1 + e^{ - 2\tau \eta } } \right\}}}{{e^{ - i\phi } \left\{ { - 1 + e^{ - 2\tau \eta } } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {1 + e^{ - 2\tau \eta } { }} \right\}} \right]}},$$
(45)
$$u_{1}^{17} \left( \eta \right) = \pm \frac{{2\tau \sigma_{1} \left\{ { - 1 + e^{2\tau \eta } } \right\} - 2\tau \sigma_{0} \left\{ {1 + e^{2\tau \eta } { }} \right\}}}{{e^{ - i\phi } \left\{ {1 - e^{2\tau \eta } } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {1 + e^{2\tau \eta } } \right\}} \right]}},$$
(46)
$$v_{1}^{16} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \sigma_{1} \left\{ {1 - e^{{\left( { - 2\tau \eta } \right)}} } \right\} - 2\tau \sigma_{0} \left\{ {{ }1 + e^{{\left( { - 2\tau \eta } \right)}} } \right\}} \right]}}{{e^{ - i\phi } \left\{ { - 1 + e^{ - 2\tau \eta } } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {1 + e^{ - 2\tau \eta } { }} \right\}} \right]}},$$
(47)
$$v_{1}^{17} \left( \eta \right) = \pm \frac{{k\left[ {2\tau \sigma_{1} \left\{ { - 1 + e^{2\tau \eta } } \right\} - 2\tau \sigma_{0} \left\{ {1 + e^{2\tau \eta } { }} \right\}} \right]}}{{e^{ - i\phi } \left\{ {1 - e^{2\tau \eta } } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {1 + e^{2\tau \eta } } \right\}} \right]}},$$
(48)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {4\tau^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

Assigning \(\lambda = \tau = 0\) provides

$$u_{1}^{18} \left( \eta \right) = \pm \frac{{ - \mu \sigma_{0} + \mu \sigma_{1} \left\{ {\cosh \left( {\mu \eta } \right) + {\text{sinh}}\left( {\mu \eta } \right)} \right\}}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\cosh \left( {\mu \eta } \right) + {\text{sinh}}\left( {\mu \eta } \right)} \right\}} \right]}},$$
(49)
$$v_{1}^{18} \left( \eta \right) = \pm \frac{{k\left[ { - \mu \sigma_{0} + \mu \sigma_{1} \left\{ {\cosh \left( {\mu \eta } \right) + \sinh \left( {\mu \eta } \right)} \right\}} \right]}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\cosh \left( {\mu \eta } \right) + {\text{sinh}}\left( {\mu \eta } \right)} \right\}} \right]}},$$
(50)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {\mu^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

For the agreements \(\lambda = \mu = K\) and \(\tau = 0\),

$$u_{1}^{19} \left( \eta \right) = \pm \frac{{K\left\{ {\left( {2\sigma_{1} - \sigma_{0} } \right) + \sigma_{1} \left( {e^{K\eta } - 1} \right)} \right\}}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {e^{K\eta } - 1} \right\}} \right]}},$$
(51)
$$v_{1}^{19} \left( \eta \right) = \pm \frac{{k\left[ {K\left\{ {\left( {2\sigma_{1} - \sigma_{0} } \right) + \sigma_{1} \left( {e^{K\eta } - 1} \right)} \right\}} \right]}}{{e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {e^{K\eta } - 1} \right\}} \right]}},$$
(52)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {K^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

Under the values \(\mu = \tau = K\) and \(\lambda = 0\),

$$u_{1}^{20} \left( \eta \right) = \pm \frac{{K\left\{ {\sigma_{0} \left( { - 1 + e^{K\eta } } \right) + \left( {\sigma_{1} - 2\sigma_{0} } \right)e^{K\eta } } \right\}}}{{e^{ - i\phi } \left( {1 - e^{K\eta } } \right)\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {e^{K\eta } } \right\}} \right]}},$$
(53)
$$v_{1}^{20} \left( \eta \right) = \pm \frac{{k\left[ {K\left\{ {\sigma_{0} \left( { - 1 + e^{K\eta } } \right) + \left( {\sigma_{1} - 2\sigma_{0} } \right)e^{K\eta } } \right\}} \right]}}{{e^{ - i\phi } \left( {1 - e^{K\eta } } \right)\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {e^{K\eta } } \right\}} \right]}},$$
(54)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {K^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

Assigning \(\mu = \lambda + \tau\) provides

$$u_{1}^{21} \left( \eta \right) = \pm \frac{{\left\{ {1 - \tau e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\left( {2\lambda \sigma_{1} - \lambda \sigma_{0} - \tau \sigma_{0} } \right) - \left( {\lambda \sigma_{1} + \tau \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {1 - \lambda e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}}}{{e^{ - i\phi } \left\{ {1 - \tau e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {1 - \lambda e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}} \right]}},$$
(55)
$$v_{1}^{21} \left( \eta \right) = \pm \frac{{k\left[ {\left\{ {1 - \tau e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\left( {2\lambda \sigma_{1} - \lambda \sigma_{0} - \tau \sigma_{0} } \right) - \left( {\lambda \sigma_{1} + \tau \sigma_{1} - 2\tau \sigma_{0} } \right)\left\{ {1 - \lambda e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}} \right]}}{{e^{ - i\phi } \left\{ {1 - \tau e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} - \sigma_{1} \left\{ {1 - \lambda e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}} \right]}},$$
(56)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left\{ {\left( {\lambda - \tau } \right)^{2} + 2l^{2} } \right\}t^{\alpha } + \theta_{0}\).

For the agreement \(\mu = - \left( {\lambda + \tau } \right)\),

$$u_{1}^{22} \left( \eta \right) = \pm \frac{{\left\{ {\tau - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\left( {2\lambda \sigma_{1} + \lambda \sigma_{0} + \tau \sigma_{0} } \right) - \left( {\lambda \sigma_{1} + \tau \sigma_{1} + 2\tau \sigma_{0} } \right)\left\{ {\lambda - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}}}{{e^{ - i\phi } \left\{ {\tau - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\lambda - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}} \right]}},$$
(57)
$$v_{1}^{22} \left( \eta \right) = \pm \frac{{k\left[ {\left\{ {\tau - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\left( {2\lambda \sigma_{1} + \lambda \sigma_{0} + \tau \sigma_{0} } \right) - \left( {\lambda \sigma_{1} + \tau \sigma_{1} + 2\tau \sigma_{0} } \right)\left\{ {\lambda - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}} \right]}}{{e^{ - i\phi } \left\{ {\tau - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\lambda - e^{{\left( {\lambda - \tau } \right)\eta }} } \right\}} \right]}},$$
(58)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left\{ {\left( {\lambda - \tau } \right)^{2} + 2l^{2} } \right\}t^{\alpha } + \theta_{0}\).

For the assumption \(\lambda = 0\),

$$u_{1}^{23} \left( \eta \right) = \pm \frac{{\mu \sigma_{0} \left\{ { - 1 + \tau e^{\mu \eta } } \right\} + \mu e^{\mu \eta } \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)}}{{e^{ - i\phi } \left\{ {1 - \tau e^{\mu \eta } } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \mu e^{\mu \eta } } \right]}},$$
(59)
$$v_{1}^{23} \left( \eta \right) = \pm \frac{{k\left[ {\mu \sigma_{0} \left\{ { - 1 + \tau e^{\mu \eta } } \right\} + \mu e^{\mu \eta } \left( {\mu \sigma_{1} - 2\tau \sigma_{0} } \right)} \right]}}{{e^{ - i\phi } \left\{ {1 - \tau e^{\mu \eta } } \right\}\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \mu e^{\mu \eta } } \right]}},$$
(60)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {\mu^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

Under the values \(\tau = \mu = \lambda \ne 0\)

$$u_{1}^{24} \left( \eta \right) = \pm \frac{{\lambda \left[ {2\left( {2\sigma_{1} - \sigma_{0} } \right) + \left( {\sigma_{1} - 2\sigma_{0} } \right)\left\{ {\sqrt 3 \tan \left( {\sqrt 3 \lambda \eta /2} \right) - 1} \right\}} \right]}}{{2e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\sqrt 3 \tan \left( {\sqrt 3 \lambda \eta /2} \right) - 1} \right\}} \right]}},$$
(61)
$$v_{1}^{24} \left( \eta \right) = \pm \frac{{k\lambda \left[ {2\left( {2\sigma_{1} - \sigma_{0} } \right) + \left( {\sigma_{1} - 2\sigma_{0} } \right)\left\{ {\sqrt 3 \tan \left( {\sqrt 3 \lambda \eta /2} \right) - 1} \right\}} \right]}}{{2e^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {\sqrt 3 \tan \left( {\sqrt 3 \lambda \eta /2} \right) - 1} \right\}} \right]}},$$
(62)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \frac{1}{2\alpha }\left( {3\lambda^{2} - 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

When \(\tau = \mu = 0\),

$$u_{1}^{25} \left( \eta \right) = \pm \frac{{2\lambda \sigma_{1} e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \lambda \eta } \right]}},$$
(63)
$$v_{1}^{25} \left( \eta \right) = \pm \frac{{2k\lambda \sigma_{1} e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \lambda \eta } \right]}},$$
(64)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{{l^{2} t^{\alpha } }}{\alpha } + \theta_{0}\).

Assigning \(\lambda = \mu = 0\) provides

$$u_{1}^{26} \left( \eta \right) = \pm \frac{{2\sigma_{0} e^{i\phi } }}{{\tau \eta^{2} \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left\{ {\sigma_{0} - \sigma_{1} } \right\}}},$$
(65)
$$v_{1}^{26} \left( \eta \right) = \pm \frac{{2k\sigma_{0} e^{i\phi } }}{{\tau \eta^{2} \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left\{ {\sigma_{0} - \sigma_{1} } \right\}}},$$
(66)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{{l^{2} t^{\alpha } }}{\alpha } + \theta_{0}\).

For the assumptions \(\tau = \lambda\) and \(\mu = 0\),

$$u_{1}^{27} \left( \eta \right) = \pm \frac{{2\lambda [\sigma_{1} - \sigma_{0} {\text{tan}}\left( {\lambda \eta } \right)]e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} {\text{tan}}\left( {\lambda \eta } \right)} \right]}},$$
(67)
$$v_{1}^{27} \left( \eta \right) = \pm \frac{{2k\lambda [\sigma_{1} - \sigma_{0} \left\{ {{\text{tan}}\left( {\lambda \eta } \right)} \right\}]e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {{\text{tan}}\left( {v\eta } \right)} \right\}} \right]}},$$
(68)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \frac{1}{2\alpha }\left( {4\lambda^{2} - 2l^{2} } \right)t^{\alpha } + \theta_{0}\).

Under the value \(\tau = 0\),

$$u_{1}^{28} \left( \eta \right) = \pm \frac{{n\left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \mu \sigma_{1} \left\{ {ne^{\mu \eta } - m} \right\}}}{{ne^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left( {ne^{\mu \eta } - m} \right)} \right]}},$$
(69)
$$v_{1}^{28} \;\left( \eta \right) = \pm \frac{{k\left[ {n\left( {2\lambda \sigma_{1} - \mu \sigma_{0} } \right) + \mu \sigma_{1} \left\{ {ne^{\mu \eta } - m} \right\}} \right]}}{{ne^{ - i\phi } \sqrt { - 2a\left( {bk^{2} + 1} \right)} \left[ {\sigma_{0} + \sigma_{1} \left\{ {ne^{\mu \eta } - m} \right\}} \right]}},$$
(70)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{1}{2\alpha }\left( {\mu^{2} + 2l^{2} } \right)t^{\alpha } + \theta_{0} .\)

3.2 Improved tanh method

The solution of Eq. (12) due to balancing value turns into the following form:

$$U\left( \eta \right) = \frac{{c_{0} + c_{1} {\Psi }\left( \eta \right) + d_{1} {\Psi }^{ - 1} \left( \eta \right)}}{{e_{0} + e_{1} {\Psi }\left( \eta \right) + f_{1} {\Psi }^{ - 1} \left( \eta \right)}}.$$
(71)

A polynomial in \(\Psi \left(\eta \right)\) is obtained by inserting Eq. (71) and its essential derivatives together with Eq. (7) into Eq. (12) whose coefficients are equated to zero for algebraic equations in used free parameters. Calculating these equations by Maple, a computer software, gives the succeeding outputs.

Case 1: \({c}_{0}=\mp \frac{2{f}_{1}}{\sqrt{-2a(b{k}^{2}+1)}}\), \({c}_{1}=\mp \frac{2{e}_{0}}{\sqrt{-2a(b{k}^{2}+1)}}\), \({d}_{1}=0\), \({e}_{1}=0\), \(m=2\delta -{l}^{2}\).

Case 2: \({c}_{0}=0\), \({c}_{1}=\mp \frac{2{e}_{0}}{\sqrt{-2a(b{k}^{2}+1)}}\), \({d}_{1}=\mp \frac{\delta {e}_{0}\sqrt{-2a}}{a\sqrt{(b{k}^{2}+1)}}\), \({e}_{1}=0\), \({f}_{1 }=0\),

$$l = \pm \sqrt {8\delta - m} .$$

Case 3: \({c}_{0}=\mp \frac{{2f}_{1}}{\sqrt{-2a(b{k}^{2}+1)}}\), \({c}_{1}=0\), \({d}_{1}=\pm \frac{2{e}_{0}\delta }{\sqrt{-2a(b{k}^{2}+1)}}\), \({e}_{1}=0\), \(m=2\delta -{l}^{2}\).

Case 4:\({c}_{0}=0\),\({c}_{1}=\mp \frac{2{e}_{0}}{\sqrt{-2a(b{k}^{2}+1)}}\), \({d}_{1}=\pm \frac{\delta {e}_{0}\sqrt{-2a}}{a\sqrt{(b{k}^{2}+1)}}\),\({e}_{1}=0\),\({f}_{1 }=0\),

$$l = \pm \sqrt { - 4\delta - m} .$$

Case 5: \({c}_{0}=0\),\({c}_{1}=\mp \frac{2{e}_{0}}{\sqrt{-2a(b{k}^{2}+1)}}\), \({d}_{1}=0\),\({e}_{1}=0\),\({f}_{1 }=0\), \(l=\pm \sqrt{2\delta -m}\).

Case 6: \({c}_{0}=0\), \({c}_{1}=0\), \({d}_{1}=\mp \frac{2{e}_{0}\delta }{\sqrt{-2a(b{k}^{2}+1)}}\), \({e}_{1}=0\), \({f}_{1 }=0\), \(m=2\delta -{l}^{2}\).

The found parameter’s values combined with Eq. (71) and the solutions of Eq. (7) generate six groups of wave solutions. For the simplicity, three groups of traveling wave solutions are presented in this present text as follows:

Group 1: Due to Case 1, the wave solution expressions are

$$u_{1} \left( { \eta } \right) = \frac{{ \mp 2e^{i\phi } {\Psi }\left( { \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},$$
(72)
$$v_{1} \left( { \eta } \right) = \frac{{ \mp 2ke^{i\phi } {\Psi }\left( { \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},$$
(73)

where \(\eta =\frac{{x}^{\beta }}{\beta }+2l\frac{{t}^{\alpha }}{\alpha }\) and \(\phi =-l\frac{{x}^{\beta }}{\beta }+(2\delta -{l}^{2})\frac{{t}^{\alpha }}{\alpha }+{\theta }_{0}\). Accordingly, the wave solutions are

$$u_{1}^{1} \left( \eta \right) = \pm \frac{{ 2\sqrt { - \delta } e^{i\phi } \tanh \left( {\sqrt { - {\updelta }} \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\,\delta < 0$$
(74)
$$v_{1}^{1} \left( \eta \right) = \pm \frac{{ 2k\sqrt { - \delta } e^{i\phi } \tanh \left( {\sqrt { - {\updelta }} \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(75)
$$u_{1}^{2} \left( \eta \right) = \pm \frac{{ 2\sqrt { - \delta } e^{i\phi } \coth \left( {\sqrt { - {\updelta }} \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(76)
$$v_{1}^{2} \left( \eta \right) = \pm \frac{{ 2k\sqrt { - \delta } e^{i\phi } \coth \left( {\sqrt { - {\updelta }} \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(77)
$$u_{1}^{3} \left( \eta \right) = \mp \frac{{ 2\sqrt \delta e^{i\phi } \tan \left( {\sqrt {\updelta } \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(78)
$$v_{1}^{3} \left( \eta \right) = \mp \frac{{ 2k\sqrt \delta e^{i\phi } \tan \left( {\sqrt {\updelta } \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(79)
$$u_{1}^{4} \left( \eta \right) = \pm \frac{{ 2\sqrt \delta e^{i\phi } \cot \left( {\sqrt {\updelta } \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(80)
$$v_{1}^{4} \left( \eta \right) = \pm \frac{{ 2k\sqrt \delta e^{i\phi } \cot \left( {\sqrt {\updelta } \eta } \right)}}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(81)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \left( {2\delta - l^{2} } \right)\frac{{t^{\alpha } }}{\alpha } + \theta_{0}\).

$$u_{1}^{5} \left( \eta \right) = \pm \frac{{2e^{i\phi } }}{{\eta \sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(82)
$$v_{1}^{5} \left( \eta \right) = \pm \frac{{2ke^{i\phi } }}{{\eta \sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(83)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{{l^{2} t^{\alpha } }}{\alpha } + \theta_{0}\).

Group 2: The solution expressions for Case 2 are

$$u_{2} \left( \eta \right) = \mp \frac{{2e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\left\{ {{\Psi }\left( \eta \right) - \delta {\Psi }^{ - 1} \left( \eta \right)} \right\},$$
(84)
$$v_{2} \left( \eta \right) = \mp \frac{{2ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }}\left\{ {{\Psi }\left( \eta \right) - \delta {\Psi }^{ - 1} \left( \eta \right)} \right\},$$
(85)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = \mp \sqrt {8\delta - m} \frac{{x^{\beta } }}{\beta } + m\frac{{t^{\alpha } }}{\alpha } + \theta_{0}\). Consequently, the wave solutions are.

$$u_{2}^{1} \left( \eta \right) = \mp \frac{{2{\updelta }e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{ tanh}}^{2} { }\left( {\sqrt { - {\updelta }} \eta } \right) + 1}}{{\sqrt { - {\updelta }} {\text{tanh}}\left( {\sqrt { - {\updelta }} \eta } \right)}},\;\delta < 0$$
(86)
$$v_{2}^{1} \left( \eta \right) = \mp \frac{{2{\delta k}e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{ tanh}}^{2} { }\left( {\sqrt { - {\updelta }} \eta } \right) + 1}}{{\sqrt { - {\updelta }} {\text{tanh}}\left( {\sqrt { - {\updelta }} \eta } \right)}},\;\delta < 0$$
(87)
$$u_{2}^{2} \left( \eta \right) = \mp \frac{{2{\updelta }e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{ coth}}^{2} { }\left( {\sqrt { - {\updelta }} \eta } \right) + 1}}{{\sqrt { - {\updelta }} {\text{coth}}\left( {\sqrt { - {\updelta }} \eta } \right)}},\;\delta < 0$$
(88)
$$v_{2}^{2} \left( \eta \right) = \mp \frac{{2{\delta k}e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{ coth}}^{2} { }\left( {\sqrt { - {\updelta }} \eta } \right) + 1}}{{\sqrt { - {\updelta }} {\text{coth}}\left( {\sqrt { - {\updelta }} \eta } \right)}},\;\delta < 0$$
(89)
$$u_{2}^{3} \left( \eta \right) = \mp \frac{{2{\updelta }e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{tan}}^{2} \left( {\sqrt {\updelta } \eta } \right) - 1}}{{\sqrt {\updelta } {\text{tan}}\left( {\sqrt {\updelta } \eta } \right)}},\;\delta < 0$$
(90)
$$v_{2}^{3} \left( \eta \right) = \mp \frac{{2{\delta k}e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{tan}}^{2} \left( {\sqrt {\updelta } \eta } \right) - 1}}{{\sqrt {\updelta } {\text{tan}}\left( {\sqrt {\updelta } \eta } \right)}},\;\delta < 0$$
(91)
$$u_{2}^{4} \left( \eta \right) = \pm \frac{{2{\updelta }e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{ cot}}^{2} \left( {\sqrt {\updelta } \eta } \right) - 1}}{{\sqrt {\updelta } {\text{cot}}\left( {\sqrt {\updelta } \eta } \right)}},\;\delta < 0$$
(92)
$$v_{2}^{4} \left( \eta \right) = \pm \frac{{2{\delta k}e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{{\text{ cot}}^{2} \left( {\sqrt {\updelta } \eta } \right) - 1}}{{\sqrt {\updelta } {\text{cot}}\left( {\sqrt {\updelta } \eta } \right)}},\;\delta < 0$$
(93)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = \mp \sqrt {8\delta - m} \frac{{x^{\beta } }}{\beta } + m\frac{{t^{\alpha } }}{\alpha } + \theta_{0}\).

$$u_{2}^{5} \left( { \eta } \right) = \frac{{ \pm 2e^{i\phi } }}{{\eta \sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(94)
$$v_{2}^{5} \left( { \eta } \right) = \frac{{ \pm 2ke^{i\phi } }}{{\eta \sqrt { - 2a\left( {bk^{2} + 1} \right)} }},\;\delta < 0$$
(95)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = \mp \sqrt { - m} \frac{{x^{\beta } }}{\beta } + m\frac{{t^{\alpha } }}{\alpha } + \theta_{0}\).

Group 3: Consistent with Case 3, the solution expressions are

$$u_{3} \left( \eta \right) = \frac{{ \mp e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{2f_{1} - 2e_{0} \delta {\Psi }^{ - 1} \left( \eta \right)}}{{e_{0} + f_{1} {\Psi }^{ - 1} \left( \eta \right)}},$$
(96)
$$v_{3} \left( \eta \right) = \frac{{ \mp ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{2f_{1} - 2e_{0} \delta {\Psi }^{ - 1} \left( \eta \right)}}{{e_{0} + f_{1} {\Psi }^{ - 1} \left( \eta \right)}},$$
(97)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \left( {2\delta - l^{2} } \right)\frac{{t^{\alpha } }}{\alpha } + \theta_{0}\). Therefore, the wave solutions are

$$u_{3}^{1} \left( \eta \right) = \frac{{ \mp 2e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt { - {\updelta }} \tanh \left( {\sqrt { - {\updelta }} \eta } \right) - e_{0} \delta }}{{e_{0} \sqrt { - {\updelta }} \tanh \left( {\sqrt { - {\updelta }} \eta } \right) - f_{1} }},\;\delta < 0$$
(98)
$$v_{3}^{1} \left( \eta \right) = \frac{{ \mp 2ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt { - {\updelta }} \tanh \left( {\sqrt { - {\updelta }} \eta } \right) - e_{0} \delta }}{{e_{0} \sqrt { - {\updelta }} \tanh \left( {\sqrt { - {\updelta }} \eta } \right) - f_{1} }},\;\delta < 0$$
(99)
$$u_{3}^{2} \left( \eta \right) = \frac{{ \mp 2e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt { - {\updelta }} \coth \left( {\sqrt { - {\updelta }} \eta } \right) - e_{0} \delta }}{{e_{0} \sqrt { - {\updelta }} \coth \left( {\sqrt { - {\updelta }} \eta } \right) - f_{1} }},\;\delta < 0$$
(100)
$$v_{3}^{2} \left( \eta \right) = \frac{{ \mp 2ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt { - {\updelta }} \coth \left( {\sqrt { - {\updelta }} \eta } \right) - e_{0} \delta }}{{e_{0} \sqrt { - {\updelta }} \coth \left( {\sqrt { - {\updelta }} \eta } \right) - f_{1} }},\;\delta < 0$$
(101)
$$u_{3}^{3} \left( \eta \right) = \frac{{ \mp 2e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt {\updelta } \tan \left( {\sqrt {\updelta } \eta } \right) - e_{0} \delta }}{{e_{0} \sqrt {\updelta } \tan \left( {\sqrt {\updelta } \eta } \right) + f_{1} }},\;\delta < 0$$
(102)
$$v_{3}^{3} \left( \eta \right) = \frac{{ \mp 2ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt {\updelta } \tan \left( {\sqrt {\updelta } \eta } \right) - e_{0} \delta }}{{e_{0} \sqrt {\updelta } \tan \left( {\sqrt {\updelta } \eta } \right) + f_{1} }},\;\delta < 0$$
(103)
$$u_{3}^{4} \left( \eta \right) = \frac{{ \mp 2e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt {\updelta } \cot \left( {\sqrt {\updelta } \eta } \right) + e_{0} \delta }}{{e_{0} \sqrt {\updelta } \cot \left( {\sqrt {\updelta } \eta } \right) - f_{1} }},\;\delta < 0$$
(104)
$$v_{3}^{4} \left( \eta \right) = \frac{{ \mp 2ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} \sqrt {\updelta } \cot \left( {\sqrt {\updelta } \eta } \right) + e_{0} \delta }}{{e_{0} \sqrt {\updelta } \cot \left( {\sqrt {\updelta } \eta } \right) - f_{1} }},\;\delta < 0$$
(105)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } + \left( {2\delta - l^{2} } \right)\frac{{t^{\alpha } }}{\alpha } + \theta_{0}\).

$$u_{3}^{5} \left( { \eta } \right) = \frac{{ \mp 2e^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} }}{{\left( {e_{0} - f_{1} \eta } \right)}},\;\delta < 0$$
(106)
$$v_{3}^{5} \left( { \eta } \right) = \frac{{ \mp 2ke^{i\phi } }}{{\sqrt { - 2a\left( {bk^{2} + 1} \right)} }} \times \frac{{f_{1} }}{{\left( {e_{0} - f_{1} \eta } \right)}},\;\delta < 0$$
(107)

where \(\eta = \frac{{x^{\beta } }}{\beta } + 2l\frac{{t^{\alpha } }}{\alpha }\) and \(\phi = - l\frac{{x^{\beta } }}{\beta } - \frac{{l^{2} t^{\alpha } }}{\alpha } + \theta_{0} .\)

Remarks

A variety of wave solutions of the governing model (1) are successfully constructed by means of the improved auxiliary equation and improved tanh schemes. The acquired solutions are figured out in contour, 2D and 3D outlines with the consideration of different parameter’s values. A noteworthy number of wave solutions stated in this exploration might play significant role to discuss the nature of wave propagation in nonlinear optics. The competency of the used techniques and finding outcomes throughout the present work are noteworthy due to the plenty and variation of achieved wave solutions than previous results (Nasreen et. al. 2023c; Ahmad et al. 2023c).

4 Graphical representations

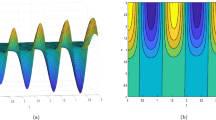
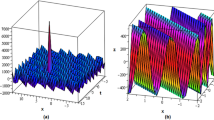
The significance of physical representations of wave solutions designated from nonlinear partial models are remarkable to make understand the underlying scenario of concerned intricate phenomena. In this consideration, it fascinates the researchers to depict dynamic nature of waves for bringing out the internal behavior of complex physical phenomena. This current work consists of a few contours, 3D and 2D sketches of some acquired wave solutions. The solitons in Kink, anti-kink, singular kink, periodic, singular periodic, bell, singular bell shapes are presented in this work. The different values of used parameters might provide diverse solitons. Kink type solitons are crucial in assorted arenas like nonlinear optics and condensed matter physics. They indicate steady, confined transitions between different positions in materials, vital in understanding defects in crystalline structures, phase changes, and optical communication systems. Various singular type solitons are appeared in this exploration. These type solitons signify abrupt, concentrated disturbances in physical systems, decisive in various domains like nonlinear optics and fluid dynamics. They characterize localized areas of extreme energy or diverse structures, offering understandings into complicated phenomena, shock waves, or compact information carriers in nonlinear dynamic wave equations. Subsequently, the significance and necessity of various solitons are unquestionable to explain nonlinear complex physical phenomena. Figure 1: The solution Eq. (19) represents anti-kink soliton for the values \(\alpha =\beta =1\), \(a=-1.5\), \(b=\tau ={\sigma }_{0}=0.5\), \(c=k={\sigma }_{1}=-1\), \(l=-2\), \(\lambda =0.7\), \(\mu =1.5\), \({\theta }_{0}=0\) within the interval \(-15\le x\), \(t\ge 15\) whereas 2D plot is found with \(t=0\). Figure 2: Periodic soliton for solution Eq. (33) is exhibited with the values \(\alpha =\beta =\mu ={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), \(b={\sigma }_{0}=0.5\), \(c=k=-1\), \(l=-2\), \(\lambda =0.9\) in the range \(-10\le x\), \(t\ge 10\) while 2D plot is drawn for \(t=0\). Figure 3: The solution Eq. (51) signifies singular kink shape soliton under the values \(\alpha =\beta ={\sigma }_{1}={\theta }_{0}=1\), \(a=c=k=l-1\), \(b={\sigma }_{0}=0.5\), \(K=0.8\), \(\lambda =-0.5\), \(\mu =1.4\) within the range \(-15\le x\), \(t\ge 15\) whereas 2D plot is shown with \(t=0\). Figure 4: The singular kink type soliton of Eq. (63) is revealed for the values \(\alpha =\beta ={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), c \(=k=l=-1\), \(b={\sigma }_{0}=0.5\), \(\lambda =-0.5\) in the interval \(-10\le x\), \(t\ge 10\) although 2D plot is displayed along with \(t=0\). Figure 5: The solution Eq. (65) provides singular bell shape soliton for the values \(\alpha =\beta =l={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), c \(=k=-1\), \(b={\sigma }_{0}=0.5\), \(\tau =-0.5\) within \(-4\le x\), \(t\ge 4\) where 2D plot is appeared alongside \(t=0\). Figure 6: Periodic type soliton is exhibited for the solution Eq. (67) under the values \(\alpha =\beta =\lambda ={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), c \(=k=-1\), \(b={\sigma }_{0}=0.5\), \(l=-2\) in the range \(-13\le x\), \(t\ge 13\) whereas 2D is plot is given for \(t=0\). Figure 7: The solution Eq. (74) represents ant-kink shape soliton for the values \(\alpha =\beta ={\theta }_{0}=1\), \(a=\delta =-0.8\), \(b=0.5\), \(k=l=-1\) within the interval \(-3\le x\), \(t\ge 3\) while 2D plot is provided along with \(t=0\). Figure 8: The solution Eq. (75) provides kink type soliton together with the values \(\alpha =\beta ={\theta }_{0}=1\), \(a=-0.8\), \(b=0.5\), \(k=l=-1\), \(\delta =-0.5\) in the range \(-10\le x\), \(t\ge 10\) whereas 2D plot is drawn for \(t=0\). Figure 9: Singular periodic shape soliton for the solution Eq. (79) is displayed under the values \(\alpha =\beta ={\theta }_{0}=1\), \(a=-0.8\), \(b=\delta =0.5\), \(k=l=-1\) within \(-3\le x\), \(t\ge 3\) while 2D plot is represented by considering \(t=0\). Figure 10: The solution Eq. (107) is in singular kink shape soliton for the values \(\alpha =\beta =\delta ={\theta }_{0}=1\), \(a=-0.8\), \(b={f}_{1}=0.5\), \(k=l=-1\), \({e}_{0}=0.7\) in the interval \(-13\le x\), \(t\ge 13\) whereas 2D plot is represented along with \(t=0\).

Fig. 1
figure 1

Anti-kink shape soliton of Eq. (19) for \(\alpha =\beta =1\), \(a=-1.5\), \(b=\tau ={\sigma }_{0}=0.5\), \(c=k={\sigma }_{1}=-1\), \(l=-2\), \(\lambda =0.7\), \(\mu =1.5\), \({\theta }_{0}=0\)

Full size image
Fig. 2
figure 2

Periodic shape soliton of Eq. (33) under \(\alpha =\beta =\mu ={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), \(b={\sigma }_{0}=0.5\), \(c=k=-1\), \(l=-2\), \(\lambda =0.9\)

Full size image
Fig. 3
figure 3

Singular kink type soliton of Eq. (51) with \(\alpha =\beta ={\sigma }_{1}={\theta }_{0}=1\), \(a=c=k=l-1\), \(b={\sigma }_{0}=0.5\), \(K=0.8\), \(\lambda =-0.5\), \(\mu =1.4\)

Full size image
Fig. 4
figure 4

Singular kink shape soliton of Eq. (63) for \(\alpha =\beta ={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), c \(=k=l=-1\), \(b={\sigma }_{0}=0.5\), \(\lambda =-0.5\)

Full size image
Fig. 5
figure 5

Singular bell shape soliton of Eq. (65) with \(\alpha =\beta =l={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), c \(=k=-1\), \(b={\sigma }_{0}=0.5\), \(\tau =-0.5\)

Full size image
Fig. 6
figure 6

Periodic type soliton of Eq. (67) under \(\alpha =\beta =\lambda ={\sigma }_{1}={\theta }_{0}=1\), \(a=-1.5\), c \(=k=-1\), \(b={\sigma }_{0}=0.5\), \(l=-2\)

Full size image
Fig. 7
figure 7

Anti-kink shape soliton of Eq. (74) for \(\alpha =\beta ={\theta }_{0}=1\), \(a=\delta =-0.8\), \(b=0.5\), \(k=l=-1\)

Full size image
Fig. 8
figure 8

Kink type soliton of Eq. (75) with \(\alpha =\beta ={\theta }_{0}=1\), \(a=-0.8\), \(b=0.5\), \(k=l=-1\), \(\delta =-0.5\)

Full size image
Fig. 9
figure 9

Singular periodic type soliton of Eq. (79) under \(\alpha =\beta ={\theta }_{0}=1\), \(a=-0.8\), \(b=\delta =0.5\), \(k=l=-1\)

Full size image
Fig. 10
figure 10

Singular kink shape soliton of Eq. (107) for \(\alpha =\beta =\delta ={\theta }_{0}=1\), \(a=-0.8\), \(b={f}_{1}=0.5\), \(k=l=-1\), \({e}_{0}=0.7\)

Full size image

5 Conclusions

The present study deals with a coupled of nonlinear Schrodinger equations signifying intricate phenomena connected to nonlinear optics, heat pulse, hydrodynamics, nonlinear acoustics, and quantum condensates. A variety of traveling and solitary wave solutions have been generated by the adaptation of advised schemes in different types of functions. The acquired solutions have been figured out in the outlines of 2D, 3D and contour shapes to illustrate the dynamic characteristics of nonlinear waves. Achieved distinct solitons might bear great importance to explain the dynamic nature of nonlinear wave propagation in optical communication systems. The abundance and generality of obtained solutions might be new aspects in the literature. The efficiency and competency of the directed schemes providing much more wave solutions claim to be used for future related research.