Optical soliton solutions in a distinctive class of nonlinear Schrödinger’s equation with cubic, quintic, septic, and nonic nonlinearities

Abstract

The Biswas–Mollivic equation is a special type of nonlinear Schrödinger equation, which explains the spatio-temporal behaviour of excitable media. In this paper, we investigate the optical soliton solutions of the Biswas–Mollivic equation with cubic–quintic–septic–nonic nonlinearities using the generalized Riccati equation mapping method. This method is efficient and provides new perspectives. It also provides novel insights into the dynamics of excitable media. Our findings add to a better understanding of the complex spatio-temporal patterns that develop in excitable media and have potential applications in the design of new technologies for controlling and manipulating pattern formation. To depict optical soliton solutions graphically, we use the MATLAB software.

1 Introduction

Excitable media are systems that display self-organized spatio-temporal patterns of activity. Typically, these patterns result from the combination of diffusive coupling with nonlinear excitable terms. Nerve fibers, heart tissue, and several types of chemical reaction–diffusion systems are examples of excitable media. In excitable media, waves that are either spatially homogeneous or exhibit complex spatio-temporal patterns mediate the propagation of activity. Excitable media can display a variety of dynamic behaviors, such as oscillations, waves, and patterns, depending on the unique characteristics of the excitable elements and the coupling between them. This is a key characteristic of excitable media. Due to their capacity to generate complex patterns and behavior from simple components, excitable media are of interest in a number of disciplines, including biology, physics, and chemistry. Numerous mathematical and computational methods, such as nonlinear dynamics, partial differential equations, and stochastic simulations, have been used to study them. All things considered, excitable media represent an exciting area of study in nonlinear science, with important implications for comprehending the dynamics of complex systems and creating new tools for guiding and controlling pattern development (Meron 1992; Zykov 1987; Tyson and Keener 1988; Keener 1980; Sakurai et al. 2002).

Nonlinear partial differential equations have been increasingly popular for studying physical processes over the past ten years. In order to comprehend how nonlinear waves behave, nonlinear evolution equations have been thoroughly explored. The study of the characteristics of solitons in optical fibers has recently been one of the most significant area of nonlinear optics research. Nonlinear Schrodinger’s equation, which determines how solitons move along an optical fiber, therefore this equation is essential to many fields of the physical, biological, and engineering sciences. It can be found in a wide range of practical domains, like nonlinear optics, protein chemistry, fluid dynamics and plasma physics (Biswas and Aceves 2001; Biswas and Milović 2010; Biswas et al. 2010, 2008, 2012; Biswas and Milovic 2010; Khalique 2011).

The Biswas–Mollivic equation, which has the form

$$\begin{aligned} i\left( {u}^{m}\right) _{t}+a\left( {u}^{m}\right) _{xx}+bF \left( \left| u \right| \right) ^{ 2}{u}^{m}=0 \end{aligned}$$

(1.1)

where $u = u(x, t)$ is a complex wave function. a and b are called group velocity dispersion(GVD) and nonlinearity coefficients, respectively. Equation (1.1) is a partial differential equation that is nonlinear but non-integrable, where non-integrability is not always related to the nonlinear term that is present in the equation. F is an algebraic function with real values, and it must be smooth for it to satisfy the criterion that the complex function $F(|u|^2)u$ must have smoothness. It is believed that the function $F(|u|^2)u$ is continuously differentiable k times, x and t, which usually represent in for the spatial and time parameters, respectively, are just the independent variables. Finally, this expression is just a generalized form of the NLSE due to a nonlinearity parameter m.

$$\begin{aligned} iu_{{t}}+au_{{{ xx}}}+bF \left( \left| u \right| \right) ^{2}u=0, \end{aligned}$$

(1.2)

The Biswas–Mollivic equation provides a genuine knowledge of optical solitons dynamics with a generalized nature. The factor of divergence from perfection is controlled by a generalization parameter. Consequently, the community of nonlinear fiber optics is particularly interested in the governing equation. In 2010 Biswas–Mollivic equation is firstly published. After that, numerous authors over years explored Biswas–Mollivic equation (Ebadi et al. 2011; Elsherbeny et al. 2023; Asghari et al. 2023; Neirameh and Eslami 2023; Asghari et al. 2024). This expression is a generalized form of the NLSE, which is predominantly researched in the framework of solitons in nonlinear fibre optics.

There have been several effective techniques suggested, including the F-expansion method (Seadawy et al. 2019), new simple integration technique (Arnous 2022), enhanced Kudryashov’s method (Arnous et al. 2023), enhanced algebraic method (Arnous et al. 2024), general projective Riccati equation technique (Arnous et al. 2023), generalized sine-Gordon equation method (Arnous et al. 2023), first integral method (Eslami and Rezazadeh 2016), generalized exponential rational function approach (Eslami et al. 2024) and so on. Here, we apply a powerful technique known as the generalized Riccati equation mapping technique to build a variety of exact solutions for the nonlinear partial differential equation.

2 Algorithm for generalized Riccati equation mapping method

In this section, the algorithm for generalized Riccati equation mapping method is introduced, see Zhu (2008), Naher and Abdullah (2012), Malwe et al. (2016), Naher and Abdullah (2012) and Zheng (2009). In the following we will outline the main steps of our method. Suppose we have the following nonlinear PDEs

$$\begin{aligned} P(u,u_{t},u_{x},u_{tt},u_{xx},u_{x t},\cdots ) =0, \end{aligned}$$

(2.1)

where $u=u(x,t)$ is an unknown function, P is a polynomial in $u=u(x,t)$ and its various partial derivatives in which the highest order derivatives and nonlinear terms are involved. Step 1 for traveling wave solutions, use the following wave transformation

$$\begin{aligned} u=U(z), \,\,\,\,\,\,\,\, z = x-v\,t, \end{aligned}$$

(2.2)

where v is the wave speed. Step 2 plugging Eq. (2.2) into Eq. (2.1) forms a nonlinear ordinary differential equation

$$\begin{aligned} O(U, U^{\prime }, U^{\prime \prime },U{\prime \prime \prime },\cdots )=0. \end{aligned}$$

(2.3)

Step 3 suppose that the traveling wave solution of Eq. (2.3) can be expressed

$$\begin{aligned} U \left( \zeta \right) =\sum _{j=0}^{n}\beta _{{j}} \Phi (\zeta )^{j}, \end{aligned}$$

(2.4)

where $\beta _{j}$ are real constants with $\beta _{M} \ne 0$ to be determined, M is a positive integer. The function $\varPhi (\zeta )$ expresses the solution of the following generalized Riccati equation

$$\begin{aligned} \Phi ^{'}\left( \zeta \right) = r + p \varPhi (\zeta ) + q \varPhi ^2(\zeta ), \end{aligned}$$

(2.5)

where r, p and q are arbitrary constants, such that $q\ne 0.$

Step 4 the highest order derivatives and the nonlinear terms found in Eq. (2.3) can be investigated in order to determine the value of the positive integer M.

Plugging Eq. (2.4) into Eq. (2.2) along with Eq. (2.5) will form a system of algebraic equations w.r.t. $\beta _{i},$ where $i = \pm 1,\pm 2,\cdots$.

Step 5 after solving the algebraic system of equations and plugging the results into Eq. (2.4), then we obtain the traveling wave solutions of Eq. (2.2). Equation (2.5) admits the following solutions. We have twenty seven solutions in the section below include four distinct families.

Family 1 whenever $p^2 - 4q r > 0$ as well as $p q \ne 0$ or $q r \ne 0,$ the result of (2.5) are:

$$\begin{aligned} \Phi {{1}}= & {} -\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{1}} \tanh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) \right) , \end{aligned}$$

(2.6)

$$\begin{aligned} \Phi {{2}}= & {} -\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{1}} \coth \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) \right) , \end{aligned}$$

(2.7)

$$\begin{aligned} \Phi {{3}}= & {} -\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{1}} \left( \tanh \left( \sqrt{\delta _{1}}\zeta \right) {\pm i{{\,\textrm{sech}\,}}\,\left( \sqrt{\delta _{1}}\,\zeta \right) }\right) \right) , \end{aligned}$$

(2.8)

$$\begin{aligned} \Phi {{4}}= & {} -\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{1}} \left( \coth \left( \sqrt{\delta _{1}}\zeta \right) {\pm i{{\,\textrm{csch}\,}}\,\left( \sqrt{\delta _{1}}\,\zeta \right) }\right) \right) , \end{aligned}$$

(2.9)

$$\begin{aligned} \Phi {{5}}= & {} -\frac{1}{4\,q}\,\left( 2p+ \sqrt{\delta _{1}} \left( \tanh \left( \frac{\sqrt{\delta _{1}}}{4}\zeta \right) \pm \coth \,\left( \frac{\sqrt{\delta _{1}}}{4}\,\zeta \right) \right) \right) , \end{aligned}$$

(2.10)

$$\begin{aligned} \Phi {{6}}= & {} \frac{1}{2\,q}\, \left( -p+{\frac{ \sqrt{ \left( {A}^{2}+{B}^{2} \right) \left( {\delta _{1}}\right) } -A \sqrt{\delta _{1}}\cosh \left( \sqrt{\delta _{1}}\zeta \right) }{ A \sinh \left( \sqrt{\delta _{1}}\zeta \right) +B}} \right) , \end{aligned}$$

(2.11)

$$\begin{aligned} \Phi {{7}}= & {} \frac{1}{2\,q}\, \left( -p-{\frac{ \sqrt{ \left( {B}^{2}-{A}^{2} \right) \left( {\delta _{1}}\right) } +A \sqrt{\delta _{1}}\cosh \left( \sqrt{\delta _{1}}\zeta \right) }{ A \sinh \left( \sqrt{\delta _{1}}\zeta \right) +B}} \right) , \end{aligned}$$

(2.12)

$$\begin{aligned} \Phi {{8}}= & {} {\frac{2\,r \cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }{\sqrt{ \delta _{1}} \sinh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) - p \cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }}, \end{aligned}$$

(2.13)

$$\begin{aligned} \Phi {{9}}= & {} {\frac{-2\,r \sinh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }{p\sinh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) - \sqrt{ \delta _{1}} \cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }}, \end{aligned}$$

(2.14)

$$\begin{aligned} \Phi {{10}}= & {} {\frac{2\,r \cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }{\sqrt{ \left( \delta _{1} \right) } \sinh \left( \sqrt{ \delta _{1} }\,\zeta \right) -p \cosh \left( \sqrt{ \delta _{1} }\,\zeta \right) \pm i\,\sqrt{\delta _{1}}}}, \end{aligned}$$

(2.15)

$$\begin{aligned} \Phi {{11}}= & {} {\frac{2\,r \sinh \left( \,\sqrt{\delta _{1}}\zeta \right) }{ -p\sinh \left( \sqrt{ \delta _{1} }\,\zeta \right) +\sqrt{ \left( \delta _{1} \right) } \cosh \left( \sqrt{ \delta _{1} }\,\zeta \right) \pm \sqrt{\delta _{1}}}}, \end{aligned}$$

(2.16)

$$\begin{aligned} \Phi {{12}}= & {} {\frac{4\,r \sinh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) \cosh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) }{ -2p\sinh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) \cosh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) +\Omega _{1} }}, \end{aligned}$$

(2.17)

where $\Omega _{1}=2\sqrt{\delta _{1}} \cosh ^2\left( \,\frac{\sqrt{\delta _{1}}}{4}\zeta \right) - \sqrt{\delta _{1}}$.

A and B two real, nonzero constants and $B^2 - A^2 > 0$.

Family 2 whenever $\delta _{2} = 4qr - p^2 > 0$ as well as $p q \ne 0$ or $q r \ne 0,$ the result of (2.5) are:

$$\begin{aligned} \Phi {{13}}= & {} \frac{1}{2\,q}\,\left( -p+\left( \sqrt{\delta _{2}} \right) \tan \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) \right) , \end{aligned}$$

(2.18)

$$\begin{aligned} \Phi {{14}}= & {} -\frac{1}{2\,q}\,\left( p+\left( \sqrt{\delta _{2}} \right) \cot \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) \right) , \end{aligned}$$

(2.19)

$$\begin{aligned} \Phi {{15}}= & {} \frac{1}{2\,q}\,\left( -p+ \sqrt{\delta _{2}} \left( \tan \left( \sqrt{\delta _{2}}\zeta \right) {\pm \sec \,\left( \sqrt{\delta _{2}}\,\zeta \right) }\right) \right) , \end{aligned}$$

(2.20)

$$\begin{aligned} \Phi {{16}}= & {} -\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{2}} \left( \cot \left( \sqrt{\delta _{2}}\zeta \right) {\pm \csc \,\left( \sqrt{\delta _{2}}\,\zeta \right) }\right) \right) , \end{aligned}$$

(2.21)

$$\begin{aligned} \Phi {{17}}= & {} \frac{1}{4\,q}\,\left( -2p+ \sqrt{\delta _{2}} \left( \tan \left( \frac{\sqrt{\delta _{2}}}{4}\zeta \right) - \coth \,\left( \frac{\sqrt{\delta _{2}}}{4}\,\zeta \right) \right) \right) , \end{aligned}$$

(2.22)

$$\begin{aligned} \Phi {{18}}= & {} \frac{1}{2\,q}\, \left( -p+{\frac{{{\pm }} \sqrt{ \left( {A}^{2}-{B}^{2} \right) \left( \delta _{1}\right) } -A \sqrt{\delta }_{1}\cos \left( \sqrt{\delta _{2}}\zeta \right) }{ A \sinh \left( \sqrt{\delta _{2}}\zeta \right) +B}} \right) , \end{aligned}$$

(2.23)

$$\begin{aligned} \Phi {{19}}= & {} \frac{1}{2\,q}\, \left( -p-{\frac{{{\pm }} \sqrt{ \left( {A}^{2}-{B}^{2} \right) \left( {\delta _{2}}\right) } +A \sqrt{\delta _{2}}\cos \left( \sqrt{\delta _{2}}\zeta \right) }{ A \sin \left( \sqrt{\delta _{2}}\zeta \right) +B}} \right) , \end{aligned}$$

(2.24)

$$\begin{aligned} \Phi {{20}}= & {} -{\frac{2\,r \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{\sqrt{ \delta _{2}} \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) + p \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }}, \end{aligned}$$

(2.25)

$$\begin{aligned} \Phi {{21}}= & {} {\frac{2\,r \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{-p \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) + \sqrt{ \delta _{2}} \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }}, \end{aligned}$$

(2.26)

$$\begin{aligned} \Phi {{22}}= & {} -{\frac{2\,r \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{\sqrt{ \left( \delta _{1}\right) } \sin \left( \sqrt{ \delta _{2}} \,\zeta \right) +p \cos \left( \sqrt{\delta }_{1}\,\zeta \right) \pm \,\sqrt{\delta _{2}}}}, \end{aligned}$$

(2.27)

$$\begin{aligned} \Phi {{23}}= & {} {\frac{2\,r \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{ -p\sin \left( \sqrt{ \delta _{1} }\,\zeta \right) +\sqrt{ \left( \delta _{1} \right) } \cos \left( \sqrt{ \delta _{1} }\,\zeta \right) \pm \sqrt{\delta _{2}}}}, \end{aligned}$$

(2.28)

$$\begin{aligned} \Phi {{24}}= & {} {\frac{4\,r \sin \left( \,\frac{\sqrt{\delta _{2}}}{4}\zeta \right) \cos \left( \,\frac{\sqrt{\delta _{2}}}{4}\zeta \right) }{ -2p\sin \left( \,\frac{\sqrt{\delta _{2}}}{4}\zeta \right) \cos \left( \,\frac{\sqrt{\delta _{2}}}{4}\zeta \right) +\Omega _{2}}}, \end{aligned}$$

(2.29)

A and B two real, nonzero constants and $A^2 - B^2 > 0$.

where $\Omega _{2} = 2\sqrt{\delta _{2}} \cos ^2\left( \frac{\sqrt{\delta _{2}}}{4}\zeta \right) - \sqrt{\delta _{2}}$.

Family 3 when $r = 0$ and $p q \ne 0,$ then result of (2.5) becomes:

$$\begin{aligned} \Phi {{25}}= & {} \frac{-p\, f_{1}}{q \left( f_{1}+\cosh (p\zeta )-\sinh (p\zeta )\right) }, \end{aligned}$$

(2.30)

$$\begin{aligned} \Phi {{26}}= & {} \frac{-p\left( \cosh (p\zeta )+\sinh (p\zeta )\right) }{q \left( f_{1}+\cosh (p\zeta )+\sinh (p\zeta )\right) }, \end{aligned}$$

(2.31)

where $f_1$, arbitrary constant.

Family 4 whenever $q \ne 0$ as well as $r = p = 0,$ the result of (2.5) becomes:

$$\begin{aligned} \Phi {{27}}= & {} \frac{-1}{q\zeta + l_1}, \end{aligned}$$

(2.32)

where    $l_1$ is an arbitrary constant.

3 Application of generalized Riccati equation mapping method

Consider the Biswas–Mollivic equation with cubic–quintic–septic–nonic nonlinearities

$$\begin{aligned} i{\frac{\partial u}{\partial t}} +a{\frac{\partial ^{2} u}{\partial {x}^{2}}} + \left( b_{{1}} |u| ^{2}+b_{{2}} |u|^{4}+ b_{{3}}| u |^{6}+b_{{4}} | u |^{8} \right) u=0 \end{aligned}$$

(3.1)

Now we split the wave profile into amplitude and phase components, respectively, as

$$\begin{aligned} u \left( x,t \right) = U \left( \zeta \right) {e}^{i\eta }. \end{aligned}$$

(3.2)

where     $\zeta = B(x-vt)$, and     $\eta = -k\,x+w\,t+\theta .$

Hence Eq. (3.2) becomes

$$\begin{aligned} u \left( x,t \right) = U [B( x-v\,t)] {e}^{i \left( -k\,x+w\,t+\theta \right) }. \end{aligned}$$

(3.3)

Nomenclature of the parameters In Eq. (3.3), $U (\zeta )$ is amplitude component, ${e}^{i\eta }$ is phase component, k represents the soliton frequency, w is the wave number and $\theta$ stands for phase constant, while B and v are the width and velocity of the soliton, respectively.

Substituting Eq. (3.3) into Eq. (3.1) and separating the real and imaginary parts. The imaginary part gives the following constraint condition

$$\begin{aligned} v = - 2 a k, \end{aligned}$$

(3.4)

and real part is

$$\begin{aligned} a{B}^{2} U^{\prime \prime } +b_{{4}} U ^{9}+b_{{3}} U^{7}+b_{{2}} U^{5}+b_{{1}} U^{3}- \left( \alpha \,{k}^{2} + w \right) U =0. \end{aligned}$$

(3.5)

Balancing the highest order derivative term and the nonlinear terms in Eq. (3.5), we get a balance constant $M =\dfrac{1}{4}$. In this case M is a fraction, now we make the transformation $U(\zeta ) = V(\zeta )^{\frac{1}{4}}$ then NODE is

$$\begin{aligned} 4\,a{B}^{2} V V^{\prime \prime }-3\,a{B}^{2} ( V^{\prime }) ^ {2}-16\,V \left( \alpha \,{k}^{2}+w \right) +16 b_{1} V^{\dfrac{5}{2}}+16 b_{3} V^{\dfrac{7}{2}}+16\,b_{{4}} V ^{4}+16\,b_{{2}} V^{3}=0. \end{aligned}$$

(3.6)

Setting $b_{1}$ = $b_{3} = 0$ reduces Equation (3.7) to

$$\begin{aligned} 4\,a{B}^{2} V V'' -3\,a{B}^{2} ( V ') ^ {2}-16\,V \left( \alpha \,{k}^{2}+w \right) +16\,b _{{4}} V ^{4}+16\,b_{{2}} V^{3}=0. \end{aligned}$$

(3.7)

It must be noted that in Eq. (3.6), $b_{1}$ and $b_{3}$ were set to zero simply for Eq. (3.6) to be rendered integrable since these would free (3.6) from all terms carrying fractional exponents of V. Thus, only $b_{2}$ and $b_{4}$ sustain to permit integrability of (3.6). This is equivalent to studying the governing model with only two non-zero terms, namely $b_{2}$ and $b_{4}$ terms. This is equivalent to saying that the governing NLSE is integrable with cubic-quintic nonlinear form of refractive index that is present in $\text {LiNbO}_{3}$ crystals (Samir et al. 2022, 2023; Arnous et al. 2023, 2024). Balancing the highest order derivative term and the nonlinear terms in Eq. (3.7), gives $M = 1$ then using Eq. (2.4)

$$\begin{aligned} V \left( \zeta \right) =\beta _{{0}}+\beta _{{1}}\varPhi \left( \zeta \right) \end{aligned}$$

(3.8)

Substituting Eq. (3.8) along with Eq. (2.5) into Eq. (3.6) and setting the coefficients of all powers of $\varPhi ^{i}, i = 0,1,\cdots ,n$ to zero, the following system of algebraic equations is obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} 5\,a{B}^{2}{\beta _{{1}}}^{2}{q}^{2}+16\,b_{{4}}{\beta _{{1}}}^{4}=0,\\ 8\,a{B}^{2}\beta _{{0}}\beta _{{1}}{q}^{2}+64\,b_{{4}}\beta _{{0}}{\beta _ {{1}}}^{3}+16\,b_{{2}}{\beta _{{1}}}^{3}+6\,a{B}^{2}{\beta _{{1}}}^{2}pq =0,\\ 96\,b_{{4}}{\beta _{{0}}}^{2}{\beta _{{1}}}^{2}+a{B}^{2}{\beta _{{1}}}^{2 }{p}^{2}+48\,b_{{2}}\beta _{{0}}{\beta _{{1}}}^{2}+12\,a{B}^{2}\beta _{{0 }}\beta _{{1}}pq+2\,a{B}^{2}{\beta _{{1}}}^{2}qr=0,\\ 8\,a{B}^{2}\beta _{{0}}\beta _{{1}}qr-16\,\beta _{{1}}\alpha \,{k}^{2 }+64\,b_{{4}}{\beta _{{0}}}^{3}\beta _{{1}}+4\,a{B}^{2}\beta _{{0}}\beta _ {{1}}{p}^{2}-16\,\beta _{{1}}w\\ +\,48\,b_{{2}}{\beta _{{0}}}^{2}\beta _{ {1}}-2\,a{B}^{2}{\beta _{{1}}}^{2}pr=0,\\ 4\,a{B}^{2}\beta _{{0}}\beta _{{1}}pr+16\,b_{{4}}{\beta _{{0}}}^{4}-16\, \beta _{{0}}\alpha \,{k}^{2}-16\,\beta _{{0}}w+16\,b_{{2}}{ \beta _{{0}}}^{3}-3\,a{B}^{2}{\beta _{{1}}}^{2}{r}^{2}=0.\\ \end{array}\right. } \end{aligned}$$

(3.9)

Solving the (3.9) system of algebraic equations with the aid of Mathematica, we have the following results:

$$\begin{aligned} {\left\{ \begin{array}{ll} \beta _0 = -\frac{5 b_2 \left( \sqrt{p^2-4 q r}-\sqrt{3} p\right) }{12 b_4 \sqrt{p^2-4 q r}},\,\,\,\, \beta _1 = \pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \left( p^2-4 q r\right) }},\,\,\, B = \pm \,{\frac{10\,b_{{2}}}{\sqrt{-15\,ab_{{4}}(p^2-4\,qr)}}}. \end{array}\right. } \end{aligned}$$

(3.10)

Substituting Eq. (3.10) along with Eq. (3.8) into Eq. (3.2), we get the following solitary wave solutions of Eq. (3.1).

Family 1 When $\delta _{1} = p^2-4qr >0$ and $pq \ne 0$ or $qr \ne 0$ then results of (2.5) are

$$ u_{1} \left( {x,t} \right) = \left[ { - \frac{{5b_{2} \left( {\sqrt {\delta _{1} } - \sqrt 3 p} \right)}}{{12b_{4} \sqrt {\delta _{1} } }} \pm \frac{{5b_{2} q}}{{2b_{4} \sqrt {3\delta _{1} } }}\left\{ { - \frac{1}{{2q}}\left( {p + \sqrt {\delta _{1} } \tanh \left( {\frac{{\sqrt {\delta _{1} } }}{2}\zeta } \right)} \right)} \right\}} \right]^{4} e^{{i\eta }} , $$

(3.11)

$$ u_{2} \left( {x,t} \right) = \left[ { - \frac{{5b_{2} \left( {\sqrt {\delta _{1} } - \sqrt 3 p} \right)}}{{12b_{4} \sqrt {\delta _{1} } }} \pm \frac{{5b_{2} q}}{{2b_{4} \sqrt {3\delta _{1} } }}\left\{ { - \frac{1}{{2q}}\left( {p + \sqrt {\delta _{1} } \coth \left( {\frac{{\sqrt {\delta _{1} } }}{2}\zeta } \right)} \right)} \right\}} \right]^{4} e^{{i\eta }} , $$

(3.12)

$$ u_{3} \left( {x,t} \right) = \left[ { - \frac{{5b_{2} \left( {\sqrt {\delta _{1} } - \sqrt 3 p} \right)}}{{12b_{4} \sqrt {\delta _{1} } }} \pm \frac{{5b_{2} q}}{{2b_{4} \sqrt {3\delta _{1} } }}\left\{ { - \frac{1}{{2q}}\left( {p + \sqrt {\delta _{1} } \left( {\tanh \left( {\sqrt {\delta _{1} } \zeta } \right) \pm i{\text{sech}}\left( {\sqrt {\delta _{1} } \zeta } \right)} \right)} \right)} \right\}} \right]^{4} e^{{i\eta }} , $$

(3.13)

$$u_{4} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{-\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{1}} \left( \coth \left( \sqrt{\delta _{1}}\zeta \right) {\pm i{{\,\textrm{csch}\,}}\,\left( \sqrt{\delta _{1}}\,\zeta \right) }\right) \right) \right \}\right ]^4 e^{i\eta },$$

(3.14)

$$\begin{aligned}{} & {} u_{5} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{-\frac{1}{4\,q}\,\left( 2p+ \sqrt{\delta _{1}} \left( \tanh \left( \frac{\sqrt{\delta _{1}}}{4}\zeta \right) \pm \coth \,\left( \frac{\sqrt{\delta _{1}}}{4}\,\zeta \right) \right) \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.15)

$$\begin{aligned}{} & {} u_{6} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}}\left \{\frac{1}{2\,q}\, \left( -p+{\frac{ \sqrt{\left( {A}^{2}+{B}^{2} \right) \left( {\delta _{1}}\right) } -A \sqrt{\delta _{1}}\cosh \left( \sqrt{\delta _{1}}\zeta \right) }{A \sinh \left( \sqrt{\delta _{1}}\zeta \right) +B}} \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.16)

$$\begin{aligned}{} & {} u_{7} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{\frac{1}{2\,q}\, \left( -p-{\frac{ \sqrt{\left( {B}^{2}-{A}^{2} \right) \left( {\delta _{1}}\right) } +A \sqrt{\delta _{1}}\cosh \left( \sqrt{\delta _{1}}\zeta \right) }{A \sinh \left( \sqrt{\delta _{1}}\zeta \right) +B}} \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.17)

$$\begin{aligned}{} & {} u_{8} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{{\frac{2\,r \cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }{\sqrt{ \delta _{1}} \sinh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) - p \cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }}\right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.18)

$$\begin{aligned}{} & {} u_{9} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}}\left \{{\frac{- 2\,r \sinh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }{\sqrt{ \delta _{1}} \sinh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) - \delta _{1}\cosh \left( \frac{\sqrt{\delta _{1}} }{2} \,\zeta \right) }} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.19)

$$\begin{aligned}{} & {} u_{10} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}}\left \{{\frac{2\,r \cosh \left( \,\sqrt{\delta _{1}}\zeta \right) }{\sqrt{ \left( \delta _{1} \right) } \sinh \left( \sqrt{ \delta _{1} }\,\zeta \right) -p \cosh \left( \sqrt{ \delta _{1} }\,\zeta \right) \pm i\,\sqrt{\delta _{1}}}} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.20)

$$\begin{aligned}{} & {} u_{11} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{{\frac{2\,r \sinh \left( \,\sqrt{\delta _{1}}\zeta \right) }{ -r\sinh \left( \sqrt{ \delta _{1} }\,\zeta \right) +\sqrt{ \left( \delta _{1} \right) } \cosh \left( \sqrt{ \delta _{1} }\,\zeta \right) \pm \sqrt{\delta _{1}}}} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.21)

$$\begin{aligned}{} & {} u_{12} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{{\frac{4\,r \sinh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) \cosh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) }{ -2r\sinh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) \cosh \left( \,\frac{\sqrt{\delta _{1}}\zeta }{4}\right) +\Omega _{1} }} \right \}\right ]^4 e^{i\eta }. \end{aligned}$$

(3.22)

where $\Omega _{1}=2\sqrt{\delta _{1}} \cosh ^2\left( \,\frac{\sqrt{\delta _{1}}}{4}\zeta \right) - \sqrt{\delta _{1}}$,

$\zeta =\pm \,{\frac{10\,b_{{2}}}{\sqrt{-15\,a{p}^{2}b_{{4}}+60\,aqrb_{{4}}}}}\left( x + 2 a k \, t \right) .$

Also $B^2 - A^2 > 0$.

Family 2 when $\delta _{2} = 4qr-p^2 > 0$ and $pq \ne 0$ or $qr\ne 0$ ,then

$$\begin{aligned}{} & {} u_{13} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{\frac{1}{2\,q}\,\left( -p+\left( \sqrt{\delta _{2}} \right) \tan \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.23)

$$\begin{aligned}{} & {} u_{14} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{-\frac{1}{2\,q}\,\left( p+\left( \sqrt{\delta _{2}} \right) \cot \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.24)

$$\begin{aligned}{} & {} u_{15} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{\frac{1}{2\,q}\,\left( - p+ \sqrt{\delta _{2}} \left( \tan \left( \sqrt{\delta _{2}}\zeta \right) {\pm \sec \,\left( \sqrt{\delta _{2}}\,\zeta \right) }\right) \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.25)

$$\begin{aligned}{} & {} u_{16} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{-\frac{1}{2\,q}\,\left( p+ \sqrt{\delta _{2}} \left( \coth \left( \sqrt{\delta _{2}}\zeta \right) {\pm \csc \,\left( \sqrt{\delta _{2}}\,\zeta \right) }\right) \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.26)

$$\begin{aligned}{} & {} u_{17} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{\frac{1}{4\,q}\,\left( -2p+ \sqrt{\delta _{2}} \left( \tan \left( \frac{\sqrt{\delta _{2}}}{4}\zeta \right) - \cot \,\left( \frac{\sqrt{\delta _{2}}}{4}\,\zeta \right) \right) \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.27)

$$\begin{aligned}{} & {} u_{18} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}}\left \{\frac{1}{2\,q}\, \left( -p+{\frac{{{\pm }} \sqrt{ \left( {A}^{2}-{B}^{2} \right) \left( \delta _{2}\right) } -A \sqrt{\delta }_{2}\cos \left( \sqrt{\delta _{2}}\zeta \right) }{ A \sin \left( \sqrt{\delta _{2}}\zeta \right) +B}} \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.28)

$$\begin{aligned}{} & {} u_{19} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{\frac{1}{2\,q}\, \left( -p+{\frac{{{\pm }} \sqrt{ \left( {A}^{2}-{B}^{2} \right) \left( {\delta _{2}}\right) } +A \sqrt{\delta _{2}}\cos \left( \sqrt{\delta _{2}}\zeta \right) }{ A \sin \left( \sqrt{\delta _{2}}\zeta \right) +B}} \right) \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.29)

$$\begin{aligned}{} & {} u_{20} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}} \pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{{\frac{-2\,r \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{\sqrt{ \delta _{2}} \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) + p\cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.30)

$$\begin{aligned}{} & {} u_{21} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{ {\frac{2\,r \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{-r\sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) + \sqrt{ \delta _{2}} \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.31)

$$\begin{aligned}{} & {} u_{22} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{ {\frac{-2\,r \cos \left( \,\sqrt{\delta _{2}}\zeta \right) }{\sqrt{ \left( \delta _{1}\right) } \sin \left( \sqrt{ \delta _{2}} \,\zeta \right) +p \cos \left( \sqrt{\delta }_{2}\,\zeta \right) \pm \,\sqrt{\delta _{2}}}}\right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.32)

$$\begin{aligned}{} & {} u_{23} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{{\frac{2\,r \sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }{-r\sin \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) + \sqrt{ \delta _{2}} \cos \left( \frac{\sqrt{\delta _{2}} }{2} \,\zeta \right) }} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.33)

$$\begin{aligned}{} & {} u_{24} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{{\frac{4\,r \sin \left( \,\frac{\sqrt{\delta _{2}}\zeta }{4}\right) \cos \left( \,\frac{\sqrt{\delta _{2}}\zeta }{4}\right) }{ -2r\sin \left( \,\frac{\sqrt{\delta _{2}}\zeta }{4}\right) \cos \left( \,\frac{\sqrt{\delta _{2}}\zeta }{4}\right) +\Omega _{2}}} \right \}\right ]^4 e^{i\eta }. \end{aligned}$$

(3.34)

where $\Omega _{2}=2\sqrt{\delta _{2}} \cos ^2\left( \frac{\sqrt{\delta _{2}}}{4}\zeta \right) - \sqrt{\delta _{2}}$.

Also $A^2 - B^2 > 0.$

Family 3 when $r = 0$ and $p q \ne 0,$ then results of (2.5) are:

$$\begin{aligned}{} & {} u_{25} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{\frac{-p\,f_1}{q \left( f_{1}+\cosh (p\zeta )-\sinh (p\zeta ) \right) } \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.35)

$$\begin{aligned}{} & {} u_{26} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{ \frac{p[\cosh (p\zeta )+\sinh (p\zeta )]}{q [ f_{1}+\cosh (p\zeta )+\sinh (p\zeta )]}\right \}\right ]^4 e^{i\eta }. \end{aligned}$$

(3.36)

where $f_1$, arbitrary constant.

Family 4 when $q \ne 0$ and $r = p = 0,$ then result of (2.5):

$$\begin{aligned} u_{27} \left( x,t \right) =\left [-\frac{5 b_2 \left( \sqrt{\delta _{1}}-\sqrt{3} p\right) }{12 b_4 \sqrt{\delta _{1}}}\pm \frac{5 b_2 q}{2 b_4 \sqrt{3 \delta _{1}}} \left \{ \frac{-1}{q\zeta + l_1} \right \}\right ]^4 e^{i\eta }, \end{aligned}$$

(3.37)

where    $l_1$ is an arbitrary constant.

3.1 Physical Implications

A regime in physics and engineering is usually a range of characteristics or conditions that a specific model or theory is expected to accurately represent the behaviour of a system inside. Depending on how closely the model’s assumptions and approximations match the system’s actual behaviour, a regime may or may not apply to a real physical system. Models are frequently designed to represent particular aspects of a system’s behaviour under particular circumstances, and they might not be useful in other conditions. For instance, there are various regimes in fluid dynamics, such as turbulent flow and laminar flow, each of which characterises the behaviour of fluids in various scenarios. When referring to optical solitons, a regime is a set of circumstances, such as the anomalous dispersion regime in optical fibres, under which soliton behaviour may be precisely described. Here, a balance between dispersion and nonlinearity allows solitons to maintain their shape and propagate across long ranges, which is important for applications such as fibre optic communication. For the nonlinear partial differential equations regulating optical solitons, we have constructed an infinite number of solutions, each of which depends on different constants and parameters. While analytical techniques offer a wide range of solutions, their applicability to real-world problems depends on the specific constraints and boundary conditions encountered in physical systems. Researchers are exploring both analytical and numerical approaches to bridge the gap between theoretical solutions and practical applications, aiming to connect these solutions to real-world scenarios by considering physical constraints and data.

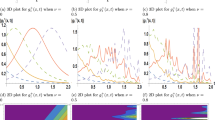
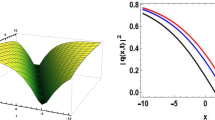
4 The graphical representations

See Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14, 15 and 16.

Fig. 1

Take $p=4.02,\, q=2.54,\, r=1.023,\, v=0.55,\, k=0.132,\, w=6.05, \, \theta =5.5,\, b_2=2.35,\, b_4=1.00$ for 3D and contour plots of Eq. (3.11)

Fig. 2

Select $p=2.02,\, q=0.054,\, r=0.023,\, v=0.05,\, k=2.00,\, w=6.05, \, \theta =0.005,\, b_2=5.35,\, b_4=5.03$ for 3D and contour plots of Eq. (3.13)

Fig. 3

Select $p=4.02,\, q=3.54,\, r=2.023,\, v=0.25,\, k=1.032,\, w=2.05, \, \theta =0.005,\, b_2=2.35,\, b_4=1.00$ for 3D and contour plots of Eq. (3.16)

Fig. 4

Select $p=4.02,\, q=3.54,\, r=2.023,\, v=0.25,\, k=1.032,\, w=2.05, \, \theta =0.005,\, b_2=2.35,\, b_4=1.00$ for 3D and contour plots of Eq. (3.17)

Fig. 5

Select $p=6.02,\, q=4.54,\, r=1.023,\, v=0.005,\, k=3.032,\, w=7.05, \, \theta =5.005,\, b_2=12.35,\, b_4=12.00$ for 3D and contour plots of Eq. (3.18)

Fig. 6

Select $p=3.02,\, q=1.054,\, r=1.023,\, v=0.005,\, k=0.4,\, w=10.05, \, \theta =0.15,\, b_2=22.35,\, b_4=43.00$ for 3D and contour plots of Eq. (3.19)

Fig. 7

Select $p=9.02,\, q=8.054,\, r=1.023,\, v=1.55,\, k=0.04,\, w=6.05, \, \theta =0.15,\, b_2=22.35,\, b_4=43.00$ for 3D and contour plots of Eq. (3.20)

Fig. 8

Select $p=0.0002,\, q=1.0054,\, r=0.023,\, v=1.25,\, k= 0.432,\, w=8.05, \, \theta =.005,\, b_2=70.35,\, b_4=60.00$ for 3D and contour plots of Eq. (3.23)

Fig. 9

Select $p=0.2,\, q=1.54,\, r=0.023,\, v=0.095,\, k=0.0432,\, w=12.05, \,\theta =0.005,\, b_2=70.35,\, b_4=60.00$ for 3D and contour plots of Eq. (3.25)

Fig. 10

Select $p=2.5,\, q=1.61,\, r=1.023,\, v=0.090,\, k=0.032,\, w=8.05, \, \theta =0.15,\, b_2=2.35,\, b_4=1.00$ for 3D and contour plots of Eq. (3.26)

Fig. 11

Select $p=10.06,\, q=4.22,\, r=5.99,\, v=6.095,\, k=0.0030,\, w=4.05, \, \theta =0.05,\, b_2=1.35,\, b_4=23.00$ for 3D and contour plots of Eq. (3.28)

Fig. 12

Select $\alpha _{1}=1.7,\alpha _{2}=1.2, \alpha _{3}=1.5, c=0.45,\sigma = - 0.007$ for 3D and contour plots of Eq. (3.32)

Fig. 13

Select $p=1.02,\, q=2.54,\, r=1.023,\, v=0.025,\, k=0.0032,\, w=5.05, \, \theta =8.55,\, b_2=20.35,\, b_4=20.00$ for 3D and contour plots of Eq. (3.33)

Fig. 14

Select $p=0.025,\, q=0.054,\, r=1.023,\, v=0.035,\, k= 0.02,\, w=6.05, \, \theta =0.055,\, b_2=2.35,\, b_4=1.00$ for 3D and contour plots of Eq. (3.34)

Fig. 15

Select $p=15.05,\, q=4.54,\, r=0,\, v=0.005,\, k= 3.32,\, w=5.05, \, \theta =3.5,\, b_2=35.35,\, b_4=45.00, \, f_1=2.5$ for 3D and contour plots of Eq. (3.35)

Fig. 16

Select $p=2.02,\, q=1.54,\, r=0,\, v=2.05,\, k= 0.032,\, w=6.05, \, \theta =1.5,\, b_2=15.35,\, b_4=15.00, \, f_1=12.5$ for 3D and contour plots of Eq. (3.36)

5 Results and discussion

In order to explain the physical behavior of the solutions and give insight into the formation of optical soliton solutions, we discuss the results from the graphical behavior of optical soliton solutions in this section, which is shown in the form of 3D and contour plots. The 3D graphs demonstrate how the wave fluctuates in space and time, while contour graphs depict the wave as a series of lines connecting points of equal amplitude. The characteristics of optical soliton solutions and how they interact with their surroundings can be better understood by researchers with the aid of these graphs. We can also learn more about the shape, amplitude, speed, and direction of optical soliton by viewing these graphs.

The Figs. 1, 2, 3, 4, 5, 6, and 7 display soliton and soliton-like solutions while Figs. 8, 9, 10, 11, 12, 13, and 14 display periodic optical soliton solutions. Similarly the Figs. 15 and 16, display singular optical soliton solutions.

Physically relevant parameter ranges ensure realism, such as ensuring non-negative values for quantities like light intensity in optics. Exploring specific parameter ranges reveals intriguing dynamics like soliton formation, while balancing computational efficiency by avoiding extreme values that may be computationally costly. Researchers employ various parameter values to understand parameter dependence, validate analytical solutions, explore parameter space boundaries for specific wave behavior, and compare simulations with simplified models, facilitating deeper insights and model accuracy validation.

6 Conclusion

This study uses the generalized Riccati mapping approach to thoroughly analyze the cubic-quintic-septic-nonic order nonlinearities in the Biswas–Mollivic equation in excitable media. The technique is demonstrated to be very successful for constructing optical soliton solutions. This study offers useful insights into the mechanics underlying the foundation of the solitary waves in excitable media by analyzing the physical behavior of the solutions with the aid of the 3D and contour plots. Overall, this study significantly advances our understanding of nonlinear dynamics and excitable media and highlights the generalized Riccati mapping method potential applications. Future research can concentrate on expanding this study to other excitable media models and investigating their dynamics with the generalized Riccati mapping method and other analytical techniques. Additionally, this study provides tantalising novel opportunities for future research, such as the use of this method for additional nonlinear partial differential equations, the development of more effective analytical methods, and practical investigations to confirm the theoretical predictions. Overall, this research makes a substantial contribution to the study of nonlinear dynamics and excitable media and highlight the potential of generalized Riccati mapping method for use in future studies.