New soliton molecules to couple of nonlinear models: ion sound and Langmuir waves systems

Abstract

In this paper, we will study two various nonlinear models: the Atangana–Baleanu fractional system of equations for the ion sound and Langmuir waves (ISALWs) and Hirota Ramani equation to obtain variety of solitary wave solutions. We will obtain bright, dark, periodic wave and solitory wave for ISALWs equation. We will also retreived bell type, kink type, singular, Jacbion elliptic function, Weierstrass-elliptic function, hyperbolic functions, periodic functions and other solitary wave solutions for Hirota Ramani equation using Sub ODE technique under some constraint conditions. At the end we will present our solutions with the help of graphs in distinct dimensions.

1 Introduction

Recently, the number of applications of fractional calculus is growing speedily. Fractional differential equations (FDEs) are used in various areas of nonlinear sciences like diffusion, electrical circuits, economy, control problem, etc. (Sheng et al. 2020). Nonlinear FDE (NLFDE) have gained high attention and interest for researchers. These equations possess huge network of applications in the subject of physics and engineering fields with the development of corresponding theories. In real life, the solution of these types of equations have significant effects in the form of traveling waves. The theory of fractional derivatives (FD) is also helpful in physiology, medical science, and epidemic diseases (Rezazadeh et al. 2021; Younas et al. 2021; Akram et al. 2021; Seadawy et al. 2021c, 2021d, 2021e; Bilal et al. 2021; Rizvi et al. 2021b, c; Seadawy et al. 2021a; Tariq et al. 2021; Ahmad et al. 2021; Bashir et al. 2021; Seadawy et al. 2021b). There are so many types of FDs like Reimann Liouville, Caputo-Fabrizio and the Atangana Baleanu fractional derivatives (ABFD) (Syama and Al-Refai 2019; Atangana 2018). Mittag Leffler function is used in ABFD as non local and non singular kernels accepting all properties of FD. Antangana and Koca (2016) used ABFD in nonlinear system and discussed the uniqueness and existence of the fractional order system. In the field of fractional calculus, ABFD is used to sort out many problems (Atangana and Baleanu 2016; Fernandez et al. 2019; Baleanu et al. 2018; Bas and Ozarslan 2018). Ghanbari and Atangana (2020) studied some applications of ABFD in image processing. Jarad et al. (2018) studied uniqueness and existence conditions for numerous ordinary differential equations with ABFD. Owolabi (2018) displayed relationship between dynamical system and ABFD. Peter et al. (2021) used AB Operator to analyse fractional order mathematical model of COVID-19 in Nigeria. Recently, many integration architectonics such as new extended auxiliary scheme (Rizvi et al. 2020a), $\frac{G^{\prime}}{G}$-expansion method (Abazari 2016), csch method, extended tanh-coth mechanism and extended rational sinh-cosh process (Rizvi et al. 2020b), generalized exponential rational function method (Ghanbari et al. 2019), Jacobi elliptic function expansion scheme (Kurt 2019), sub-ode method (Zayeda et al. 2019) and many other have been used to find exact solutions for different nonlinear evolution and FDEs(Ahmed et al. 2019b, Dianchen 2018, Khater et al. 2006, Seadawy et al. 2019b, c). Our aim is to obtain some new types of solitary waves for ISALWs with ABFD and Hirota Ramani model with the aid of sub ode scheme.

The ISLAWs with ABFD is given by Rezazadeh et al. (2021)

$$\begin{aligned} ^{ABR}_tD_{0^+}^\alpha J+\frac{1\partial ^2J}{2\partial x^2}-rJ=0, \end{aligned}$$

$t>0, 0<\alpha \le 1$

$$\begin{aligned} ^{ABR}_tD_{0^+}^\alpha r-\frac{\partial ^2r}{\partial x^2}-2\frac{\partial ^2(|J|^2)}{\partial x^2}=0, \end{aligned}$$

(1)

here normalised density, electric field and AB fractional operator are represented by r, $Je^{{-i\omega }_pt}$ and $^{ABR}_tD_{0^+}^\alpha$ respectively.

$$\begin{aligned} ^{ABR}_tD_{a^+}^\alpha g(t)=\frac{\varpi (\alpha )}{1-\alpha }\frac{d}{dt}\int _a^tg(x) \Omega \alpha \left( \frac{-\alpha (t-\alpha )^\alpha }{1-\alpha }\right) dx, \end{aligned}$$

(2)

where $\Omega _\alpha (.)$ is Mittag–Leffler function, which is given as

$$\begin{aligned} \Omega _\alpha \left( \frac{-\alpha (t-\alpha )^\alpha }{1-\alpha }\right) =\Sigma _{r=0}^\infty \frac{\left( \frac{-\alpha }{1-\alpha }\right) ^q(t-x)^ {\alpha q} }{\Gamma (\alpha q+1)}, \end{aligned}$$

normalization function defined by $\varpi (\alpha )$. Thus, we get the AB fractional operator

$$\begin{aligned} ^{ABR}_tD_{a^+}^\alpha g(t)=\frac{\varpi (\alpha )}{1-\alpha }\Sigma _{q=0}^\infty \left(\frac{-\alpha }{1-\alpha }\right)^q~RLI_a^{\alpha q}g(t) \end{aligned}$$

The second model is known as Hirota Ramani equations given by Roshid and Alam (2017)

$$\begin{aligned} \Theta _{t} -\Theta _{xxt} + A \Theta _{x} (1 - \Theta _{t}) = 0, \end{aligned}$$

(3)

where $\Theta =\Theta (x, t)$ is the amplitude of the wave mode and $A\ne 0$ is a real constant.

The paper is arranged as follows: in Sect. 2, we will describe sub ode scheme, in Sect. 3, we will apply our tehnique to ISLAWs with ABFD, in Sect. 4, we will find solitary wave solutions for Hirota Ramani equation with our scheme. In Sect. 5, we will discuss our results and at the end in Sect. 6, we will provide conclusion.

2 Sub-ODE method

To approach this sub ode, we suppose the following solution: (Rizvi et al. 2020c, 2021a)

$$\begin{aligned} G(\eta )=\mu M^m(\eta ),~~~~~\mu >0 \end{aligned}$$

(4)

here m is a parameter and $M(\eta )$ satisfies the equation:

$$\begin{aligned} M'^2(\eta )=\Upsilon M^{2-2p}(\eta )+\Delta M^{2-p}(\eta )+\Lambda M^2(\eta )+\Pi M^{2+p}(\eta )+\Psi M^{2+2p}(\eta ),~p>0, \end{aligned}$$

(5)

here $\Upsilon ,\Delta ,\Lambda ,\Pi ~ and ~\Psi$ are constants. By using homogeneous balance method we can find m in (4) given as ,

$$\begin{aligned} D(\phi _1)=m,~~ D(\phi ^2)=2m,\ldots \quad D(\phi ^{\prime})=m+p, ~ ~D(\phi ^{\prime\prime})=m+2p,... \end{aligned}$$

(6)

Thus Eq. (5) has following solutions cases:

Case 1

When $\Upsilon =\Delta =\Pi =0$, we have a bell type soliton solution for Eq. (5) as:

$$\begin{aligned} G(\eta )=\bigg [\sqrt{-\frac{\Lambda }{\Psi }}\sec h(\sqrt{\Lambda }p\eta )\bigg ]^\frac{1}{p} , ~~~\Lambda >0, ~~\Psi <0, \end{aligned}$$

(7)

a periodic solution

$$\begin{aligned} G(\eta )=\bigg [\sqrt{-\frac{\Lambda }{\Psi }}\sec (\sqrt{-\Lambda }p\eta )\bigg ]^\frac{1}{p} , ~~~\Lambda <0, ~~\Psi >0, \end{aligned}$$

(8)

and a rational solution

$$\begin{aligned} G(\eta )=\bigg [\frac{\varepsilon }{\sqrt{\Psi }p\eta }\bigg ]^\frac{1}{p} , ~~~\Lambda =0, ~~\Psi >0, ~~\varepsilon =\pm 1. \end{aligned}$$

(9)

Case 2

If $\Delta =\Pi =0$, $\Upsilon ={\frac{\Lambda ^{2}}{4\Psi }}$, then Eq. (5) has a kink type soliton:

$$\begin{aligned} G(\eta )=\bigg [\varepsilon \sqrt{-\frac{\Lambda }{\Psi }}\tanh (\sqrt{\Lambda }p\eta )\bigg ]^\frac{1}{p} , ~~~\Lambda >0, ~~\Psi <0, ~~\varepsilon =\pm 1, \end{aligned}$$

(10)

and a periodic solution

$$\begin{aligned} G(\eta )=\bigg [\varepsilon \sqrt{-\frac{\Lambda }{\Psi }}\tan (\sqrt{-\Lambda }p\eta )\bigg ]^\frac{1}{p} , ~~~\Lambda <0, ~~\Psi >0, ~~\varepsilon =\pm 1, \end{aligned}$$

(11)

Case 3

If $\Delta =\Pi =0$, then Eq. (5) has following three Jacbion elliptic function (JEF) solutions:

$$\begin{aligned} G(\eta )= & {} \bigg [\sqrt{-\frac{\Lambda m^{2}}{\Psi (2m^{2}-1)}}cn\bigg (\sqrt{\frac{\Lambda }{(2m^{2}-1)}}p\eta \bigg ) \bigg ]^\frac{1}{p} , ~~~\Lambda >0, ~~~\Upsilon ={\frac{\Lambda ^{2}m^{2}(m^{2}-1)}{\Psi (2m^{2}-1)^{2}}}, \end{aligned}$$

(12)

$$\begin{aligned} G(\eta )= & {} \bigg [\sqrt{-\frac{\Lambda }{\Psi (2-m^{2})}}dn\bigg (\sqrt{\frac{\Lambda }{(2-m^{2})}}p\eta \bigg ) \bigg ]^\frac{1}{p} , ~~~\Lambda >0, ~~~\Upsilon ={\frac{\Lambda ^{2}(1-m^{2})}{\Psi (2-m^{2})^{2}}}, \end{aligned}$$

(13)

and

$$\begin{aligned} G(\eta )=\bigg [\sqrt{-\frac{\Lambda m^{2}}{\Psi (m^{2}+1)}}sn\bigg (\sqrt{ -\frac{\Lambda }{(m^{2}+1)}}p\eta \bigg ) \bigg ]^\frac{1}{p} , ~~~\Lambda <0, ~~~\Upsilon ={\frac{\Lambda ^{2}m^{2}}{\Psi (m^{2}+1)^{2}}}. \end{aligned}$$

(14)

Case 6

For $\Delta =\Pi =0$, the Weierstrass-elliptic function (WEF) solutions are obtained for Eq. (5) as:

$$\begin{aligned} G(\eta )=\bigg [\frac{1}{\Psi }\wp (p\eta ,g_2,g_3)-\frac{\Lambda }{3}\bigg ]^\frac{1}{2p}, \end{aligned}$$

(15)

where $g_2=\frac{4\Lambda ^2}{3}$ and $g_3=\frac{4\Lambda (-2\Lambda ^2)}{27}$.

$$\begin{aligned} G(\eta )=\frac{3\sqrt{\Psi ^-1}\wp ^{\prime}(p\eta ,g_2,g_3)}{6\wp (p\eta ,g_2,g_3)+\Lambda }^\frac{1}{p}, \end{aligned}$$

(16)

where $g_2=\frac{\Lambda 2}{12}~ and~ g_3=0$.

Case 7

If $\Delta =\Pi =0$ and $\Upsilon ={\frac{5\Lambda ^{2}}{36\Psi }}$ the Eq. (5) has following WEF solutions :

$$\begin{aligned} G(\eta )=\bigg [\frac{\Lambda \sqrt{\frac{-15\Lambda }{2\Psi }}\wp (p\eta ,g_2,g_3)}{3\wp (p\eta ,g_2,g_3) +\Lambda }\bigg ]^\frac{1}{p}, \end{aligned}$$

(17)

where $g_2=\frac{2\Lambda ^2}{9}$ and $g_3=\frac{\Lambda ^3}{54}$. Here $g_2$ and $g_3$ are known as invariant WEF.

Case 8

For $\Upsilon =\Delta =0$, the following bell type and kink type solutions for Eq. (5) are obtained:

$$\begin{aligned} G(\eta )= & {} \bigg (\frac{1}{\cosh (\sqrt{\Lambda }p\eta )}\bigg )^\frac{1}{p} , ~~\Lambda >0, ~~\Pi =0, ~~\Psi =\frac{\Pi ^2}{4\Lambda }-\Lambda , \end{aligned}$$

(18)

$$\begin{aligned} G(\eta )= & {} \bigg (\frac{1}{2}\sqrt{\frac{\Lambda }{\Psi }}\bigg [1+\varepsilon \tanh \bigg (\frac{1}{2}\sqrt{\Lambda }p\eta \bigg )\bigg ]\bigg )^\frac{1}{p} ,~~\Lambda>0, ~~\Psi >0, ~~\Pi =0, ~~\varepsilon =\pm 1, \end{aligned}$$

(19)

and

$$\begin{aligned} G(\eta )=\bigg (\frac{1}{(\frac{1}{2}p\eta )^2-\Psi }\bigg )^\frac{1}{p} , ~~\Lambda =0, ~~\Pi =0, ~~\Psi =<0. \end{aligned}$$

(20)

Case 9

For$\Upsilon =\Delta =0,\Lambda >0$ ,then the following hyperbolic functions solutions for Eq. (5) are obtained:

$$\begin{aligned} G(\eta )= & {} \bigg [\frac{2\Lambda {{\,\mathrm{sech}\,}}^2(\frac{\sqrt{\Lambda }}{2}p\eta )}{[\sqrt{-4\Lambda \Psi }] {{\,\mathrm{sech}\,}}^2(\frac{\sqrt{\Lambda }}{2}p\eta )-2\sqrt{-4\Lambda \Psi }}]^\frac{1}{p},~~~\Pi ^2-4\Lambda \Psi >0 \end{aligned}$$

(21)

$$\begin{aligned} G(\eta )= & {} \bigg (\frac{2\Lambda {{\,\mathrm{csch}\,}}^2(\frac{\sqrt{\Lambda }}{2}p~\eta )}{[\sqrt{-4\Lambda \Psi }] {{\,\mathrm{csch}\,}}^2(\frac{\sqrt{\Lambda }}{2}p\eta )+2\sqrt{-4\Lambda \Psi }}\bigg )^\frac{1}{p},~~~\Pi ^2-4\Lambda \Psi >0 \end{aligned}$$

(22)

Case 10

For$\Upsilon =\Delta =0,\Lambda <0$ ,then the following periodic functions solutions for Eq. (5) are obtained:

$$\begin{aligned} G(\eta )= & {} \bigg (\frac{2\Lambda \sec ^2(\frac{\sqrt{-\Lambda }}{2}p~\eta )}{[\sqrt{-4\Lambda \Psi }]\sec ^2(\frac{\sqrt{-\Lambda }}{2}p~\eta ) -2\sqrt{-4\Lambda \Psi }}\bigg )^\frac{1}{p},~~~~\Pi ^2-4\Lambda \Psi >0 \end{aligned}$$

(23)

$$\begin{aligned} G(\eta )= & {} \bigg (\frac{2\Lambda \csc ^2(\frac{\sqrt{-\Lambda }}{2}p~\eta )}{[\sqrt{-4\Lambda \Psi }]\csc ^2(\frac{\sqrt{-\Lambda }}{2}p~\eta ) -2\sqrt{-4\Lambda \Psi }}\bigg )^\frac{1}{p},~~~\Pi ^2-4\Lambda \Psi >0 \end{aligned}$$

(24)

3 Solitary wave solutions for Eq. (1)

We use the following transformation for Eq. (1),

$$\begin{aligned} J(x,t)= & {} u(\eta )e^{i\mu },~~~ n(x,t)=v(\eta ),\nonumber \\ \mu= & {} kx+\frac{\omega (1-\alpha )t^{-q}}{B(\alpha )\Sigma _{q=0}^\infty (-\frac{\alpha }{1-\alpha })^q\Gamma (1-\alpha q)},~~\eta =\gamma x+\frac{\beta (1-\alpha )t^{-q}}{B(\alpha )\Sigma _{q=0}^\infty (-\frac{\alpha }{1-\alpha })^q\Gamma (1-\alpha q)}, \end{aligned}$$

(25)

here $\beta$ and $\omega$ are constants. By putting Eq. (25) into Eq. (1) we obtain

$$\begin{aligned}&\frac{1}{2}\gamma ^2u^{\prime\prime}+i(\beta +k\gamma )u^{\prime}-0.5(k^2+2\omega )u-uv=0, \end{aligned}$$

(26)

$$\begin{aligned}&(\beta ^2-\gamma ^2)v^{\prime\prime}+4\gamma ^2(u^{\prime 2}-uu^{\prime\prime})=0, \end{aligned}$$

(27)

Separating real and imaginary parts we get

$$\begin{aligned} \beta =-k\gamma \end{aligned}$$

(28)

By double integration Eq. (27) we have

$$\begin{aligned} v=\frac{2\gamma ^2}{\beta ^2-\gamma ^2}u^2=\frac{2}{k^2-1}u^2. \end{aligned}$$

(29)

substituting Eqs. (28) and (29) into Eq. (26) provide us

$$\begin{aligned} u^{\prime\prime}-\frac{4}{\gamma ^2(k^2-1)}u^3-\frac{(k^2+2w)}{\gamma ^2}u=0 \end{aligned}$$

(30)

By homogeneous balancing method we get $p=m$.

$$\begin{aligned} u(\eta )=\mu G^p(\eta ),~~~~~\mu >0 \end{aligned}$$

(31)

By putting Eq. (30) into Eq. (5), we get the following set of algebraic equations:

$$\begin{aligned}&G^{3p}(\eta ):2p^2\Psi \mu -\frac{4\mu ^2}{(-1+k^2)\gamma ^2}=0, \end{aligned}$$

(32)

$$\begin{aligned}&G^p(\eta ):\Lambda p^2\mu -\frac{k^2\mu }{\gamma ^2}-\frac{2\mu \omega }{\gamma ^2}=0, \end{aligned}$$

(33)

we have the following types of solutions:

Type 1a

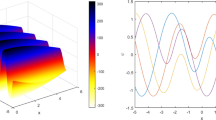
By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters (Fig. 1).

$$\begin{aligned} \mu =\sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~ \Lambda =\frac{k^2+w}{\gamma ^2p^2}, \end{aligned}$$

provided that

$$\begin{aligned} J_{1,1}(x,t)=\frac{\sqrt{(-1+k^2)(-k^2-2w)}{{\,\mathrm{sech}\,}}\bigg (\eta \sqrt{k^2+2w}\bigg )}{\gamma \sqrt{2}}. \end{aligned}$$

(34)

Fig. 1

The dynamical behavior of the solution $J_{1,1}(x,t)$ given by Eq. (34) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =15$, $\alpha = -1$, $\beta = 3$

Type 1b

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters (Fig. 2).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2},\nonumber \\ J_{1,2}(x,t)= & {} \frac{\sqrt{(-1+k^2)(-k^2-2w)}\tanh \bigg (\eta \sqrt{k^2+2w}\bigg )\epsilon }{\gamma \sqrt{2}}. \end{aligned}$$

(35)

Fig. 2

The dynamical behavior of the solution $J_{1,2}(x,t)$ given by Eq. (29) is shown at $p=1$, $T=5$, $\gamma =0.1$, $K=0.8$, $\omega = 0.6$, $r =0.1$, $\alpha = 0.3$, $\beta =0.7$, $\epsilon =1$

Type 1c

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtained the solitary wave solutions (Fig. 3).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};\quad \Lambda =\frac{k^2+w}{\gamma ^2p^2},\nonumber \\ J_{1,3}(x,t)= & {} \frac{\sqrt{-1+k^2} \gamma \epsilon }{\sqrt{2}~~\eta }. \end{aligned}$$

(36)

Fig. 3

The dynamical behavior of the solution $J_{1,3}(x,t)$ given by Eq. (30) is shown at $p=1$, $T=5$, $\gamma =0.1$, $K=0.8$, $\omega = 0.6$, $r =0.1$, $\alpha = 0.3$, $\beta =0.7$, $\epsilon =1$

Type 2a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the kink and anti-kink type soliton solutions (Fig. 4).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};\quad \Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{2,1}(x,t)= & {} \frac{\sqrt{(-1+k^2)(-k^2-2w)}\tanh \bigg (\eta \sqrt{k^2+2w}\bigg )\epsilon }{\gamma \sqrt{2}}. \end{aligned}$$

(37)

Fig. 4

The dynamical behavior of the solution $J_{2,1}(x,t)$ given by Eq. (31) at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 2b

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the kink and anti-kink type soliton solutions (Fig. 5).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{2,2}(x,t)= & {} \frac{\sqrt{(-1+k^2)(-k^2-2w)}\tanh \bigg (\eta \sqrt{-}{k^2-2w}\bigg )\epsilon }{\gamma \sqrt{2}}. \end{aligned}$$

(38)

Fig. 5

The dynamical behavior of the solution $J_{2,2}(x,t)$ given by Eq. (32) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 3a

m $\rightarrow$ 1 By substituting $\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the solitary wave solutions (Fig. 6).

$$\begin{aligned} \mu =\sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~ \Lambda =\frac{k^2+w}{\gamma ^2p^2}, \end{aligned}$$

provided that

$$\begin{aligned} J_{3,1}(x,t)=\frac{\sqrt{(-1+k^2)(-k^2-2w)}sech\bigg (\eta \sqrt{\frac{k^2+2w}{\gamma }}\bigg )}{\sqrt{2}}. \end{aligned}$$

(39)

Fig. 6

The dynamical behavior of the solution $J_{3,1}(x,t)$ given by Eq. (33) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =15$, $\alpha = -1$, $\beta = 3$

Type 3b

m $\rightarrow$1 By substituting $\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the bell type soliton solutions (Fig. 7).

$$\begin{aligned} \mu =\sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~ \Lambda =\frac{k^2+w}{\gamma ^2p^2}, \end{aligned}$$

provided that

$$\begin{aligned} J_{3,2}(x,t)=\frac{\sqrt{(-1+k^2)(-k^2-2w)}{{\,\mathrm{sech}\,}}\bigg (\eta \sqrt{\frac{\frac{k^2}{2}+w}{\gamma }}\bigg )}{2}. \end{aligned}$$

(40)

Fig. 7

The dynamical behavior of the solution $J_{3,2}(x,t)$ given by Eq. (34) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =15$, $\alpha = -1$, $\beta = 3$

Type 3c

m $\rightarrow$1 By substituting $\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the solitary wave solutions (Fig. 8).

$$\begin{aligned} \mu =\sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~ \Lambda =\frac{k^2+w}{\gamma ^2p^2}, \end{aligned}$$

provided that

$$\begin{aligned} J_{3,3}(x,t)=\frac{1}{2}\sqrt{(-1+k^2)}\sqrt{-(k^2+2\omega )} \tanh \bigg (\frac{\eta \sqrt{-\frac{k^2+2\omega }{\gamma ^2}}}{\sqrt{2}}\bigg ). \end{aligned}$$

(41)

Fig. 8

The dynamical behavior of the solution $J_{3,3}(x,t)$ given by Eq. (35) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =15$, $\alpha = -1$, $\beta = 3$

Type 6a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtained the WEF (Fig. 9).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{6,a}(x,t)= & {} \frac{\sqrt{(-1+k^2)p^2\Psi \gamma ^2-\frac{(k^2+2w)}{3p^2\gamma 2} +~~\wp \bigg (~p\eta ,\frac{4(k^2+2w)^2}{3p^4\gamma ^2},-\frac{8(k^2+2w)^3}{27p^6\gamma ^6}}}{\sqrt{2}}. \end{aligned}$$

(42)

Fig. 9

The dynamical behavior of the solution $J_{6,1}(x,t)$ given by Eq. (36) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =15$, $\alpha = -1$, $\beta = 3$

Type 6e

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the WEF (Fig. 10).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{6,e}(x,t)= & {} \frac{3\sqrt{(-1+k^2)~p^2~\Psi \gamma ^2} ~~\wp \bigg (~p\eta ,{\frac{(k^2+2w)}{12p^4\gamma ^4},0}\bigg )}{\sqrt{2}(\frac{k^2+2w}{p^2\gamma ^2} +~~6\wp \bigg (~p\eta ,\frac{(k^2+2w)}{12p^4\gamma ^4},0\bigg ))}. \end{aligned}$$

(43)

Fig. 10

The dynamical behavior of the solution $J_{6,2}(x,t)$ given by Eq. (37) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =15$, $\alpha = -1$, $\beta = 3$

Type 7

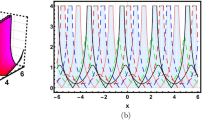
By substituting $\Delta =\Pi =0$, $\Upsilon =\frac{5\Lambda ^{2}}{36\Gamma }$ in Eq. (5) and we get values of following parameters and we obtained JEF (Fig. 11).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{7}(x,t)= & {} \frac{\sqrt{15}\sqrt{(-1+k^2)p^2\Psi \gamma ^2}(k^2+2\omega )\sqrt{ -\frac{k^2+2\omega }{p^2\Psi \gamma ^2}}\wp \bigg (p\eta ,{\frac{2(k^2+2\omega )^2}{9p^4\gamma ^4}, \frac{(k^2+2)^3}{54p^6\gamma ^6}}\bigg )}{2(k^2+2\omega +3p^2\gamma ^2\wp [p\eta ,{ \frac{2(k^2+2\omega )^2}{9p^4\gamma ^4},\frac{(k^2+2)^3}{54p^6\gamma ^6}}])}. \end{aligned}$$

(44)

Fig. 11

The dynamical behavior of the solution $J_{7}(x,t)$ given by Eq. (38) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$

Type 8a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtained the bell type soliton solutions (Fig. 12).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{8,1}(x,t)= & {} \frac{\sqrt{(-1+k^2)~p^2\gamma ^2}{{\,\mathrm{sech}\,}}\bigg (\eta \sqrt{k^2+2w}\bigg )}{\gamma \sqrt{2}}. \end{aligned}$$

(45)

Fig. 12

The dynamical behavior of the solution $J_{8,1}(x,t)$ given by Eq. (39) is shown at $p=1$, $T=5$, $\gamma =0.1$, $K=0.4$, $\omega = 0.6$, $r =0.1$, $\alpha = 0.3$, $\beta =0.7$, $\epsilon =1$

Type 8b

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the kink and anti-kink type soliton solutions (Fig. 13).

$$\begin{aligned} \mu =\sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{8,2}(x,t)=\frac{\sqrt{(-1+k^2)~p^2\Psi \gamma ^2}\sqrt{\frac{k^2+2w}{p^2\Psi \gamma ^2}}~(1+\epsilon ~ \tanh \bigg (\frac{1}{2}p~\eta \sqrt{\frac{k^2+2w}{p^2\gamma ^2}}\bigg ))}{2\sqrt{2}}. \end{aligned}$$

(46)

Fig. 13

The dynamical behavior of the solution $J_{8,2}(x,t)$ given by Eq. (40) is shown at $p=1$, $T=5$, $\gamma =0.1$, $K=0.4$, $\omega = 0.6$, $r =0.1$, $\alpha = 0.3$, $\beta =0.7$, $\epsilon =1$

Type 9a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the bell type soliton solutions (Fig. 14).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{9,1}(x,t)= & {} \frac{\sqrt{(-1+k^2)~p^2\Psi \gamma ^2}\sqrt{-\frac{\Psi (k^2+2w)}{p^2\gamma ^2}} {{\,\mathrm{sech}\,}}^2\bigg (\frac{1}{2}~p~\eta \sqrt{\frac{k^2+2w}{p^2\gamma ^2}}\bigg )}{\sqrt{2}~(2\Psi -\Psi {{\,\mathrm{sech}\,}}^2\bigg (\frac{1}{2}p\eta ~\sqrt{\frac{k^2+2w}{p^2\gamma ^2}}\bigg ))}. \end{aligned}$$

(47)

Fig. 14

The dynamical behavior of the solution $J_{9,1}(x,t)$ given by Eq. (41) is shown at $p=1$, $T=5$, $\gamma =0.1$, $K=0.3$, $\omega = 0.1$, $r =0.1$, $\alpha = 0.3$, $\beta =0.7$

Type 9b

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the following results (Fig. 15).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{9,2}(x,t)= & {} -\frac{\sqrt{(-1+k^2)~p^2\Psi \gamma ^2}\sqrt{-\frac{\Psi (k^2+2w)}{p^2\gamma ^2}} {{\,\mathrm{csch}\,}}^2\bigg (\frac{1}{2}~p~\eta \sqrt{\frac{k^2+2w}{p^2\gamma ^2}}\bigg )}{\sqrt{2}~(2\Psi +\Psi {{\,\mathrm{csch}\,}}^2\bigg (\frac{1}{2}p\eta ~\sqrt{\frac{k^2+2w}{p^2\gamma ^2}}\bigg ))}. \end{aligned}$$

(48)

Fig. 15

The dynamical behavior of the solution $J_{9,2}(x,t)$ given by Eq. (42) is at $p=1$, $T=5$, $\gamma =0.1$, $K=0.3$, $\omega = 0.1$, $r =0.1$, $\alpha = 0.3$, $\beta =0.7$

Type 10a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the bell type soliton solutions (Fig. 16).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{10,1}(x,t)= & {} -\frac{\sqrt{(-1+k^2)~p^2\Psi \gamma ^2}\sqrt{-\frac{\Psi (k^2+2w)}{p^2\gamma ^2}} \sec ^2\bigg (\frac{1}{2}~p~\eta \sqrt{-\frac{k^2+2w}{p^2\gamma ^2}}\bigg )}{\sqrt{2}~ \Psi (-2-\sec ^2\bigg (\frac{1}{2}p\eta ~\sqrt{-\frac{k^2+2w}{p^2\gamma ^2}}\bigg )~)}. \end{aligned}$$

(49)

Fig. 16

The dynamical behavior of the solution $J_{10,1}(x,t)$ given by Eq. (43) is at $p=1$, $T=5$, $\gamma =10$, $K=0.9$, $\omega = -1$, $r =1$, $\alpha =-1$, $\beta =0.1$

Type 10b

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the solitary wave solutions (Fig. 17).

$$\begin{aligned} \mu= & {} \sqrt{\frac{\gamma ^2p^2\Psi (k^2-1)}{2}};~~~\Lambda =\frac{k^2+w}{\gamma ^2p^2}, \nonumber \\ J_{10,2}(x,t)= & {} -\frac{\sqrt{(-1+k^2)~p^2\Psi \gamma ^2}\sqrt{-\frac{\Psi (k^2+2w)}{p^2\gamma ^2}} \csc ^2\bigg (\frac{1}{2}~p~\eta \sqrt{-\frac{~k^2+2w}{p^2\gamma ^2}}\bigg )}{\sqrt{2}~ \Psi (-2+\csc ^2\bigg (\frac{1}{2}p\eta ~\sqrt{-\frac{k^2+2w}{p^2\gamma ^2}}\bigg )~)}. \end{aligned}$$

(50)

Fig. 17

The dynamical behavior of the solution $J_{10,2}(x,t)$ given by Eq. (44) is shown at $p=1$, $T=5$, $\gamma =10$, $K=0.9$, $\omega = -1$, $r =1$, $\alpha =-1$, $\beta =0.1$

4 Sub-ODE method

By applying transformation in Eq. (3), $\zeta =k(x - \omega t), ~here ~k > 0$, we get

$$\begin{aligned} (A\omega )U_\zeta + k^2U_{\zeta \zeta \zeta } + Ak\omega U^2= 0, \end{aligned}$$

(51)

let $U_\zeta = V$ , it will give us

$$\begin{aligned} (A\omega )V + k^2\omega V^{\prime\prime} + Ak\omega V^2= 0, \end{aligned}$$

(52)

By balancing technique we get $2p=m$.

By putting Eq. (48) into Eq. (5), we get the following set of algebraic equations:

$$\begin{aligned}&G^{4p}(\eta ):6k^2p^2T\mu \omega +Ak\mu ^2\omega =0, \end{aligned}$$

(53)

$$\begin{aligned}&G^{2p}(\eta ):A\mu -\mu \omega +4Ck^2p^2\mu \omega =0, \end{aligned}$$

(54)

we have the following types of solutions:

Type 2a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the kink and anti-kink type soliton solutions (Fig. 18).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{2,1}(x,t)= & {} \frac{3\epsilon ^2(-A+\omega )\tanh \bigg (\frac{p\xi \sqrt{1+\frac{A}{\omega }}}{2kp}\bigg )^2}{2Ak\omega }. \end{aligned}$$

(55)

Fig. 18

The dynamical behavior of the solution $\Theta _{2,1}(x,t)$ given by Eq. (51) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 2b

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the kink and anti-kink type soliton solutions (Fig. 19).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};~~~~~~~~~~~~~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{2,2}(x,t)= & {} \frac{3\epsilon ^2(-A+\omega )\tan \bigg (\frac{p\xi \sqrt{1+\frac{A}{\omega }}}{2kp}\bigg )^2}{2Ak\omega }. \end{aligned}$$

(56)

Fig. 19

The dynamical behavior of the solution $\Theta _{2,2}(x,t)$ given by Eq. (52) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 3a

(m $\rightarrow$1) By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain periodic solutions (Fig. 20).

$$\begin{aligned} \mu =-\frac{6kp^2T}{A};~~~~~~~~~~~~~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{3,1}(x,t)=\frac{-3A+3\omega }{Ak\omega +Ak\omega \cosh \bigg (\frac{p\xi \sqrt{\frac{-A+\omega }{\omega }}}{kp}\bigg )}. \end{aligned}$$

(57)

Fig. 20

The dynamical behavior of the solution $\Theta _{3,1}(x,t)$ given by Eq. (53) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 3b

(m $\rightarrow$ 1) By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the periodic solutions (Fig. 21).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{3,1}(x,t)= & {} \frac{-3A+3\omega }{2Ak\omega +2Ak\omega \cosh \bigg (\frac{p\xi \sqrt{\frac{-A+\omega }{\omega }}}{\sqrt{2}kp}\bigg )}. \end{aligned}$$

(58)

Fig. 21

The dynamical behavior of the solution $\Theta _{3,2}(x,t)$ given by Eq. (54) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 3c

(m $\rightarrow$ 1) By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the kink and anti-kink type soliton solutions (Fig. 22).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{3,3}(x,t)= & {} \frac{3(-A+\omega ) \tanh \bigg (\frac{p\xi \sqrt{-1+\frac{A}{\omega }}}{2\sqrt{2}kp}\bigg )^2}{4Ak\omega }. \end{aligned}$$

(59)

Fig. 22

The dynamical behavior of the solution $\Theta _{3,3}(x,t)$ given by Eq. (55) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 6a

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the WEF (Fig. 23).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{6,1}(x,t)= & {} -\frac{6kp^2T(\frac{A-\omega }{12k^2p^2\omega } +\frac{\wp \bigg (p\xi ,{\frac{1}{3}(-12AT+\frac{(A-\omega )^2}{4k^4p^4\omega ^2}),\frac{(A-\omega )(A^2-2A\omega +(1-72ATk^4p^4)\omega ^2)}{216k^6p^6\omega ^3}}\bigg )}{T})^\frac{1}{4}}{A}. \end{aligned}$$

(60)

Fig. 23

The dynamical behavior of the solution $\Theta _{6,1}(x,t)$ given by Eq. (56) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 6e

By substituting $\Upsilon =\Delta =\Pi =0$ in Eq. (5) and we get values of following parameters and we obtain the WEF (Fig. 24).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{6,2}(x,t)= & {} -\frac{12\sqrt{3kp^2T\sqrt{\frac{k^2p^2\sqrt{\frac{1}{T}}~\wp prime\bigg (P\xi ,{AT+\frac{(A-\omega )^2}{192k^4p^4\omega ^2},\frac{ATc^3}{6}}\bigg )}{-A+\omega +24k^2p^2\omega ~\wp \bigg (P\xi ,{AT+\frac{(A-\omega )^2}{192k^4p^4\omega ^2},\frac{ATc^3}{6}}\bigg ))}}}}{A}. \end{aligned}$$

(61)

Fig. 24

The dynamical behavior of the solution $\Theta _{6,2}(x,t)$ given by Eq. (57) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

Type 7

By substituting $\Delta =\Pi =0$, $\Upsilon =\frac{5\Lambda ^{2}}{36\Gamma }$ in Eq. (5) and we get values of following parameters and we obtained the WEF (Fig. 25).

$$\begin{aligned} \mu= & {} -\frac{6kp^2T}{A};~~~~\Lambda =\frac{-A+\omega }{4\omega k^2p^2\omega }, \nonumber \\ \Theta _{7}(x,t)= & {} -\frac{45(A-\omega )^3~\wp \bigg (p\xi ,{\frac{(A+\omega )^2}{72k^4p^4\omega ^2},\frac{(-A+\omega )^3}{3456k^6p^6\omega ^3}}\bigg )^2}{4Ak\omega ( -A+\omega +12k^2p^2\omega ~\wp \bigg (p\xi ,{\frac{(A+\omega )^2}{72k^4p^4\omega ^2}, \frac{(-A+\omega )^3}{3456k^6p^6\omega ^3}}\bigg )^2)}. \end{aligned}$$

(62)

Fig. 25

The dynamical behavior of the solution $\Theta _{7,1}(x,t)$ given by Eq. (58) is shown at $p=1$, $T=5$, $\gamma =20$, $K=0.7$, $\omega = 7$, $r =10$, $\alpha = -1$, $\beta = 3$, $\epsilon =1$

5 Results and discussion with graphical description

In this article, we have examined Atangana–Baleanu (AB) fractional system of equations for the ion sound and Langmuir waves (ISALWs) and HRE to gain different solitons. Under different conditions, we apply Sub-ODE procedure to both above models and perceived effective results. Tripathya and Sahoo (2020) derived exact solutions for ISLAWs equation. Baskonus and Bulut (2016) studied different modes of ISLAWs equations. Seadawy et al. (2019a discussed about structure of ISLAWs equation and also its applications. Ahmed et al. (2019a) generate Rogue waves and studied about relationshup of multipeak solitons for the system of equations of ISLAWs. Koonprasert and Punpocha (2016) applied F-Expansion method on Hirota–Ramani equation. Qi et al. (2004) acquired traveling solutions to Hirota equation. Zhao and Tam (2006) find soliton solutions for a coupled Ramani equation. We derived out bright, dark, singular and periodic wave solution for ISLAWs equation. We also retrieved bell type, kink type, periodic, rational, (JEF) and (WEF) solutions for Ramani equation. The bell type solution are shown by Eqs. (8), (21) and (58) while the kink type is represented by Eqs. (10) and (19). Some periodic solutions have also been derived and are given by Eqs. (8), (11), (23) and (24). A rational solution is also discussed in Eq. (9). Some JEF are found from Eqs. (12)–(14) along with the conditions mentioned therein. whereas the WEF are represented by Eqs. (15)–(17). In addition to these, some more solutions have also been given in Eq. (22) singular soliton. A graphical description of these results has also been given.

6 Conclusion

We describe exact solution of NLFEE above we study the graphical representation of various types of solutions. We obtained the different solutions of model name which consists of dark soliton, bright soliton, Jacobi elliptic solutions (JES), Weierstrass elliptic solitons (WES), hyperbolic solutions and parabolic solutions. For better understanding we express 3D, 2D and contour view. We claim that the acheive solutions are distinct and very helpful for the study of model name.