Efficient multiple-precision computation of the scaled complementary error function and the Dawson integral

Abstract

We present algorithms to approximate the scaled complementary error function, $\mathit{exp}\left({x}^{2}\right)erfc(x)$, and the Dawson integral, ${e}^{{-x}^{2}}\underset{0}{\overset{x}{\int }}{e}^{{t}^{2}}dt$, to the best accuracy in the standard single, double, and quadruple precision arithmetic. The algorithms are based on expansion in Chebyshev subinterval polynomial approximations together with expansion in terms of Taylor series and/or Laplace continued fraction. The present algorithms, implemented as Fortran elemental modules, have been benchmarked versus competitive algorithms available in the literature and versus functions built-in in modern Fortran compilers, in addition to comprehensive tables generated with variable precision computations using the Matlab™ symbolic toolbox. The present algorithm for calculating the scaled complementary error function showed an overall significant efficiency improvement (factors between 1.3 and 20 depending on the compiler and tested dataset) compared to the built-in function “Erfc_Scaled” in modern Fortran compilers, whereas the algorithm for calculating the Dawson integral is exceptional in calculating the function to 32 significant digits (compared to 19 significant digits reported in the literature) while being more efficient than competitive algorithms as well.

1 Introduction

The scaled complementary error function, commonly referred to as $erfcx(x)$, where x is a real variable, occurs frequently in physics and chemistry and is defined as [1,2,3],

$$erfcx\left(x\right)=\mathrm{exp}\left({x}^{2}\right)erfc\left(x\right)=\frac{2{e}^{{x}^{2}}}{\sqrt{\pi }}{\int }_{x}^{\infty }{e}^{-{t}^{2}}dt$$

(1)

In addition, the function is a central component in the computation of several other important functions of real and complex arguments of particular interest to scientists and researchers. For example, accurate and efficient calculations of the scaled complementary error function may be required for the evaluation of the Voigt line profile [4] and for the computations of the Faddeyeva or Faddeeva, $w(z),$ or plasma dispersion function, $Z=i\sqrt{\pi } w(z)$ [5, 6]. The latter, in turn, is called from tens to tens of thousands times in the calculation of a single point of the transcendental Gordeyev integral, ${G}_{\nu }\left(\omega ,\lambda \right)$ [7].

In many software packages and libraries, the function is computed to double precision using rational functions, as described in [1, 2]. Recently, evaluation of the function to higher precision is implemented in a number of modern Fortran compilers as a built-in function under the name “Erfc_Scaled” [8, 9].

Similarly, the transcendental Dawson integral [10] is of great importance to scientists and engineers. The integral is defined by,

$${Daw\left(x\right)=e}^{{-x}^{2}}\underset{0}{\overset{x}{\int }}{e}^{{t}^{2}}dt$$

(2)

One encounters this integration during the study of many physical phenomena such as heat conduction, electrical oscillations in certain special vacuum tubes, calculation of profile of absorption lines, and the propagation of electromagnetic radiation along the earth’s surface [11]. The integral is closely related to the imaginary error function, $erfi(x)$, where

$$erfi\left(x\right)= -i\;{erf}\left(ix\right)=\frac{2}{\sqrt{\pi }}\mathit{exp}\left({x}^{2}\right)Daw\left(x\right)=\frac{2}{\sqrt{\pi }}\underset{0}{\overset{x}{\int }}{e}^{{t}^{2}}dt$$

(3)

Dawson’s integral is an analytic odd function that vanishes at the origin. It can also be used in the calculation of the Faddeyeva/Faddeeva function, $w(z),$ or plasma dispersion function, $Z=i\sqrt{\pi } w(z)$, near the real axis [7, 12, 13].

Because of its importance to many scientific fields, several routines are developed in the literature to calculate the Dawson integral using single and double precision arithmetic [2, 14,15,16,17,18,19,20]. One of the most reliable of these routines is the one included in Algorithm 715 [2, 15]. The routine uses rational Chebyshev approximations, theoretically accurate to about 19 significant decimal digits. The present author is not aware of any published algorithm or computer code in a compiled computer language that calculates the function to accuracy better than the 19 significant digits introduced by Cody [2, 15].

Hardware capabilities of modern computing systems and the support of many new compilers to quadruple precision arithmetic helped to increase the interest in developing routines and computer codes using quadruple precision arithmetic. Although low precision arithmetic provides significant computational efficiency, their use in scientific computing raises the concern about preserving the accuracy and stability of the computation. High precision arithmetic seems to be indispensable in modern scientific computing. At present, high precision arithmetic dominates the supernova simulations [21], climate modeling [22], planetary orbit calculations [23], and Coulomb N-body atomic system simulations [24]. Mixed precision algorithms that combine low and high precisions have also emerged to address some of the accuracy and instability issues. Furthermore, the development of reference solutions that can be used for accuracy check is a continuing task.

In this paper, we introduce algorithms to compute these important functions using the standard single, double, and quadruple precisions based on truncated series expansions in Chebyshev subinterval polynomials in conjunction with asymptotic expressions in terms of Laplace continued fraction. The present algorithms are both accurate and efficient on top of being simple enough to be easily implemented into other software packages and added to computational libraries in different programing languages.

2 Algorithm

2.1 Scaled complementary error function

The present new algorithm for computing the scaled complementary error function exploits a combination of various numerical techniques for different regions of the real argument, x, as explained below.

2.1.1 Expansions for $|\mathrm{x}|<<1$

There exist series expansions for $erf(x)$ and $erfc(x)$ near $x=0$ [25,26,27], which can be used together with the Taylor expansion for $exp{(x}^{2})$ to calculate the scaled complementary error function for very small values of x where

$$\begin{array}{cc}{e}^{{x}^{2}}erfc\left({x}\right)=\left({\sum }_{\varvec{n}=0}^{\infty }\frac{{x}^{2{n}}}{\varvec{n}!}\right)\left(1-\frac{2}{\sqrt{{\varvec{\pi}}}}{\sum }_{{\varvec{k}}=0}^{\infty }\frac{{\left(-1\right)}^{{\varvec{k}}}{{\varvec{x}}}^{2{\varvec{k}}+1}}{\left(2{\varvec{k}}+1\right) {\varvec{k}}!}\right)& {for}\boldsymbol{ }\left|{x}\right|\end{array}\ll 1$$

(4)

Equation (4) can be rearranged into a form less sensitive to roundoff errors and written as [28],

$$\begin{array}{cc} {e}^{{x}^{2}}erfc \left({x}\right)=\left({\sum }_{{\varvec{n}}=0}^{\infty }\frac{{x}^{2{n}}}{{\varvec{n}}!}\right)-\frac{2{\varvec{x}}}{\sqrt{{\varvec{\pi}}}}{\sum }_{{\varvec{k}}=0}^{\infty }\frac{{\left({2{\varvec{x}}}^{2}\right)}^{{\varvec{k}}}}{\left(2{\varvec{k}}+1\right) }& {for}\boldsymbol{ }\left|{x}\right|\end{array}\ll 1$$

(5)

Taking 8 terms of the first series (expansion of $exp{({x}}^{2})$) and 8 terms of the second series in Eq. (5) produces a polynomial of the 17th degree in x, sufficient to calculate the ${erfcx}({x})$ function up to 32 significant digits for the region $|{x}|{\epsilon}[0,0.037]$. A fewer number of terms of the polynomial can be used to calculate the function either to lower accuracy or within narrower sub-regions closer to zero in this domain. For referencing, the polynomial is provided explicitly in the appendix section (Table 10), together with the number of terms required to satisfy the accuracy in each subinterval.

2.1.2 Chebyshev polynomials, ${\mathrm{T}}_{\mathrm{n}}(\mathrm{y})$

Chebyshev polynomials [29] have advantageous features that render them useful in developing numerical algorithms. There are four kinds of Chebyshev polynomials [29]. However, following the practice of some references in the literature, we use the expression “Chebyshev polynomial” to refer to the Chebyshev polynomial of the first kind, ${T}_{n}(y)$ where $y=\mathrm{cos\theta }$, with the real argument $y\;\epsilon\left[-1,1\right].$ Chebyshev polynomials of the first kind, ${T}_{n}(y)$, represent a set of orthogonal polynomials that are easy to obtain and apply. Hence, they are widely used in economizing the evaluation of transcendental functions. Expansion of functions in Chebyshev polynomials is favored over expansion in Fourier series for the latter being an infinite series rather than a polynomial. They are also favored over Taylor series expansion as the error resulting from the Taylor series is not uniform and the number of required terms, for a targeted accuracy, becomes incredibly larger the farther the point is from the origin of expansion. On the contrary, the error resulting from expansion in terms of Chebyshev polynomials is distributed uniformly over the given interval. The set of the functions ${T}_{n}\left(y\right)$ can be generated recursively [3, 30], and many software packages have routines to generate these functions. A recursive method to evaluate a linear combination of Chebyshev polynomials is also available [31]. The method is a generalization of Horner’s method for evaluating a linear combination of monomials [32].

For a variable $x\epsilon [a, b]$, a linear transformation is used to map it into the range [− 1, 1] where

$$y=\frac{2x-(b+a)}{b-a}$$

(6)

For approximating the scaled complementary error function, one can calculate the function in the region where $x\ge 0$, and use the relation

$$\mathit{exp}\left({x}^{2}\right)erfc\left(-|x|\right)=2\mathit{exp}\left({x}^{2}\right)-erfcx\left(|x|\right)$$

(7)

to find the function for negative values of x. Computationally, the expression in Eq. (7) accurately reduces to $2\mathit{exp}\left({x}^{2}\right)$ for $x\le -9.0$. However, the term $2\mathit{exp}\left({x}^{2}\right)$ undergoes inevitable overflow problem for values of $x\le -\sqrt{\mathrm{ln}\left(R{e}_{\mathrm{max}}\right)-\mathrm{ln}2}$ where $R{e}_{\mathrm{max}}$ is the largest finite floating-point number in the precision arithmetic under consideration. Needless to say that the polynomial resulting from Eq. (5) can be used for both positive and negative x-values in the region $|x|\epsilon [0, 0.037]$. Accordingly, for the rest of the domain, one only needs to calculate the function $\mathit{exp}\left({x}^{2}\right)erfc\left(|x|\right)$ and use Eq. (7) to find the function for negative values of x.

For unbound variables like our case, where $x\epsilon \left[0,\infty \right],$ various nonlinear mapping transformations can be used to map the infinite range to a finite one [33, 34]. In this algorithm, we nonlinearly map the independent variable $x\epsilon [0,\infty ]$ to the variable $t\epsilon [\mathrm{0,1}]$ where

$$t=\frac{c}{x+c}$$

(8)

where c is a constant.

The domain of t is divided into a fixed number of equal-sized sub-regions (20 for single and double precession and 100 for quad precision) where a truncated series in Chebyshev polynomials, leading to a polynomial P(t), is obtained to approximate the original function to the sought accuracy for the precision arithmetic under consideration in each region. The integrations involved in determining the coefficients of the polynomial, P(t), and the Chebyshev polynomials of the first kind have been calculated using variable precision arithmetic capabilities available in the Matlab symbolic toolbox.

A significant effort is devoted to iteratively choose a suitable value of the constant (for erfcx, $c=2.1$) to secure the targeted accuracy for the planned power of the polynomial for the fixed number of subintervals chosen. Evidently, the degree of the polynomial is precision-dependent as shown in Table 1. Although the range of the validity of the derived polynomials in the x-domain is from 0.0 to more than 500, for efficiency reasons, we switch to Laplace continued fraction at a smaller border as shown in Table 1 too.

Table 1 Degree of approximating polynomials, ${P}({t})$, resulting from truncated expansion in Chebyshev polynomials of the first kind and the range of applicability for approximating $erfcx(x)$, as a function of the used precision

It has to be noted that a transformation similar to that in Eq. (8) was introduced by S. Johnson in developing the MIT Faddeeva package [35] except that a constant of value 4.0 was used instead of 2.1. In Johnson’s code, the domain between 0 and 1 is divided into 100 equal divisions with a polynomial of degree 6 approximating the function in each division for double precision calculations.

2.1.3 Continued fraction and asymptotic expansion for large $\mathrm{x}$

Expansions in Chebyshev polynomials are used only for the ranges shown in Table 1, while for larger values of x, Laplace continued fraction is found to be more efficient. A computationally simple and efficient form of the continued fraction can be used where [36, 37]

$$\begin{array}{c}\exp\left(x^2\right)\;erfc\left(x\right)=\frac1{\sqrt\pi}\left(\frac{a_0}{x+}\frac{a_1}{x+}\frac{a_2}{x+}\frac{4_3}{x+}\dots\dots\frac{a_m}{x+}\dots\right)\\\mathrm{with}\;a_0=1,a_m=\frac m2\;\mathrm{for}\;m\geq1\end{array}$$

(9)

A number of 11 convergents of the continued fraction in Eq. (9) were found to be sufficient to secure accuracy in the order of 10⁻³² for calculating $erfcx(x)$ for $x\ge 48.0$. This number of convergents was found to be sufficient to secure an accuracy in the order of 10⁻¹⁶ for $x\ge 7.8$. A fewer number of convergents may be required to secure these accuracies for regions of greater values of x. The number of convergents, M, of the continued fraction required to secure the best accuracy for the precision arithmetic under consideration depends on the precision and can be economized by dividing the domain of computations into a set of subdomains.

It has to be noted that there also exists an asymptotic series expansion which can be written as follows [26]:

$$\mathrm{exp}\left({x}^{2}\right) erfc\left(x\right)=\frac{1}{x\sqrt{\pi }}\left[1+{\sum }_{k=1}^{\infty }{(-1)}^{k}\frac{1\cdot 3\cdot 5\cdot \cdot \cdot (2k-1)}{{(2{x}^{2})}^{k}}\right]$$

(10)

However, numerical experiments showed that the continued fraction is more efficient. Table 2 shows a summary of the subdomains, used in the present algorithm, as a function of the precision used.

Table 2 Number of convergents of the continued fraction and applied subdomain(s) as a function of the used precision

2.2 Dawson integral

Similar to the algorithm for erfcx(x), the present new algorithm for computing the Dawson integral uses a combination of various numerical techniques for different regions of the real argument, x, as explained below.

2.2.1 Expansions for small $|\mathrm{x}|$

Since $Daw(0)=0$, one can easily obtain a Maclaurin series, which is useful for evaluating the function near the origin, where [15]

$$Daw\left(x\right)= {\sum }_{n=0}^{\infty }\frac{{(-1)}^{n} {2}^{n}}{\left(2n+1\right)!!}{x}^{2n+1}$$

(11)

Although the series in (11) can be used to calculate $Daw\left(x\right)$ for the whole domain as it converges for any finite x (magnitude of the ratio of successive terms is $2{x}^{2}/(2n+3)$), it is impractical except for very small x because the convergence is delayed until n becomes greater than ${x}^{2}$−3/2.

Alternatively, a more efficient and convenient expansion of Daw(x) in the form of a continued fraction may be used where [11, 15],

$$Daw\left(x\right)=\frac{x}{1+} \frac{2{x}^{2}/3}{1-} \frac{4{x}^{2}/15}{1+} \frac{6{x}^{2}/35}{1-\dots }\dots .\frac{{\left(-1\right)}^{k+1}(2k{x}^{2})/(4{k}^{2}-1)}{1+\dots }$$

(12)

It has to be noted that the coefficients ${\left(-1\right)}^{{k}+1}(2k)/{(4k}^{2}-1)$ can be calculated in advance to improve the efficiency of calculating the continued fraction. In the present algorithm, we use the continued fraction in (12) to calculate $Daw(x)$ for small values of x. Table 3 shows the range in which Eq. (12) is used to satisfy the targeted accuracy as a function of the precision arithmetic used.

Table 3 Number of convergents from the continued fraction in Eq. (12) and the range of application in the present algorithm as a function of the precision arithmetic

2.2.2 Chebyshev polynomials ${\mathrm{T}}_{\mathrm{n}}(\mathrm{y})$

Similar to the case for $erfcx(x)$, a linear transformation is commonly used to map a variable $x\epsilon [a, b]$ defined over the range $[a, b]$ into the range [− 1, 1]. However, since Dawson’s integral is an odd function, one may approximate the integral for positive $x$ values and use the relation

$$Daw(-|x|)=-Daw(|x|)$$

(13)

to extend the calculation to the whole domain.

Accordingly, one only needs to expand the integral $Daw(x)$ in terms of truncated series in Chebyshev polynomials, for the range $\left[0,\infty \right]$ together with the use of the relation (13) to find the function for negative values of x. Yet, with such unbound domain, $b\to \infty$, a nonlinear mapping transformations (similar to what has been used with the algorithm for $erfcx$) can be used to map the infinite range to a finite one. The nonlinear mapping described in Eq. (8) above is used with a value of the constant $c$ equals 1.8 while the domain of t is divided, herein, into 100 equal subintervals. A Chebyshev polynomial P(t) is obtained to approximate the Dawson’s integral (in each subinterval) to the targeted accuracy for the precision arithmetic under consideration. Again, the degree of the polynomial is precision-dependent as shown in Table 4. It has to be noted that the value of the constant $c=1.8$ used herein is based on a number of numerical experiments; however, by no means one claims that this is an optimum value for the constant c although it is successful in generating the polynomials to the required accuracy.

Table 4 Degree of polynomials $P(t)$, used to approximate $Daw(x)$, and applied range as a function of the used precision

While the derived polynomials cover the main part of the x-domain, we switch to Laplace continued fraction at very small values of x (Eq. (12) above) and for large values of $x$ as explained in the next subsection, for efficiency reasons.

It is worth mentioning that, when using the Intel Fortran 64 Compiler “ifort” (Version 2021.6.0 running on Intel(R) 64) with double precision arithmetic, the accuracy of the present algorithm for $Daw(x)$ is found to be in the order of 10⁻¹⁵ although when using the GNU Fortran 8.1.0 compiler “gfortran”, one gets accuracy in the order of 10⁻¹⁶. Accordingly, we reworked this case to obtain the coefficients for the subinterval truncated series expansion in terms of Chebyshev polynomials for $\left(\frac{Daw(x)}{x}\right)$ instead of $Daw(x)$, which successfully produced the 10⁻¹⁶ accuracy for calculating $Daw(x)$ using any of the two compilers “gfortran” or “ifort.”

2.2.3 Continued fraction and asymptotic expansion for large $\mathrm{x}$

For values of x larger than those in Table 4, the use of Laplace continued fraction or asymptotic series expansion is more efficient. A simple continued fraction that can be used to approximate the Dawson’s integral for large values of x is written as follows [11]:

$$\begin{array}{c}Daw\left(x\right)\approx\frac{a_0}{2x-}\frac{a_1}{2x-}\frac{a_2}{2x-}\frac{a_3}{2x-\dots}\dots.\frac{a_m}{2x-\dots}\dots\\\mathrm{with}\;a_0=1,a_m=2m,m=1,2,3\dots\end{array}$$

(14)

Also, there exists an asymptotic series expansion for the integral, which can be written as follows:

$$Daw\left(x\right)\sim\sum\nolimits_{k=0}^\infty\;\frac{\left(2k-1\right)!!}{2^{k+1}x^{2k+1}}$$

(15)

where “!!” represents the double factorial.

However, the continued fraction is used in the present algorithm for efficiency reasons. Similar to the case of $erfcx(x)$, explained above, the number of convergents (M), from the continued fraction required to secure the targeted accuracy is a function of the precision used. Also, additional economization can be achieved by dividing the domain of computations using the continuing fraction into a set of subdomains. Table 5 shows the range in which Eq. (14) is used to satisfy the targeted accuracy as a function of the precision arithmetic under consideration.

Table 5 Number of convergents from the continued fraction in Eq. (14) and the range of application in the present algorithm as a function of the precision arithmetic

Further economization in evaluating the function in this large x region can be achieved through slicing the region in several sub-regions with the use of a smaller number of convergents.

3 Accuracy and efficiency comparisons

3.1 Erfcx(x)

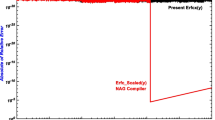
The present algorithm for calculating the erfcx(x) function has been implemented as a modern Fortran elemental module. An array of 40,001 points uniformly spaced on the logarithmic scale between 10⁻³⁰ and 10⁴ is used to perform the accuracy check of the present algorithm. Variable precision arithmetic from the Matlab™ [38] symbolic toolbox is used to generate the corresponding array of the product of $\mathrm{exp}\left({x}^{2}\right)$ and $erfc\left(x\right)$. The maximum absolute relative error obtained for any of the standard precisions used was in the same order as that obtained by Cody’s code [2], for single and double precision, and by the built-in “Erfc_Scaled” function for all three standard precisions, as shown in Fig. 1. Because of the logarithmic scale used with the y-axis, the majority of points for double and single precision do not appear in the figure as the absolute of the relative error for these points is zero.

Fig. 1

Absolute of relative error in calculating the scaled complementary error function $erfcx(x)$ using the present algorithm and the built-in function, $Erfc\_\mathrm{Scaled}(x)$. Calculations are performed using the GNU Fortran 8.1.0 (gfortran) with data generated using variable precision arithmetic offered in the Matlab symbolic toolbox as the reference

For efficiency comparison and because the time consumed per single-point evaluation is very short, we generate an array of 10⁶ points that are equally spaced on the logarithmic scale for two cases: a case of very wide range $x \epsilon [{10}^{-30}-{10}^{30}]$ and a case of practical range $x \epsilon [{10}^{-6}-{10}^{6}]$. The 10⁶ points of the $\mathrm{exp}\left({x}^{2}\right)erfc\left(x\right)$ function are calculated using the built-in function “Erfc_Scaled” and by the implementation of the present algorithm using quadruple, double, and single precision arithmetic. The average CPU time spent in the calculation using the present algorithm is compared to the CPU time consumed by the built-in “Erfc_Scaled” for all three standard precisions using two compilers: the GNU Fortran 8.1.0 (gfortran) and the Intel 2021.6.0 classic (ifort) compilers. For the cases of single and double precision arithmetic, the CPU times consumed in performing the same calculations using Cody’s algorithm (Algorithm 715) are considered in the comparison as well.

Table 6 shows the CPU time, in seconds, consumed in the evaluation of the 10⁶ points as described above using the GNU Fortran 8.1.0 (gfortran) compiler for all three standard precision arithmetic and for the two cases of very wide range of x and the practical range described above by the present algorithm and competitive algorithms including the built-in “Erfc_Scaled” function.

Table 6 Average CPU time consumed in calculating 10⁶ points uniformly distributed on the logarithmic scale for the two cases of wide range xϵ[10⁻³⁰ − 10³⁰] and the case of practical range xϵ[10⁻⁶ − 10⁶] using Cody’s code, the built-in Erfc_Scaled function and the present algorithm. Computations are performed using the GNU Fortran 8.1.0 (gfortran) compiler on an Intel® Core™ i7-7600U CPU @2.80 GHz processor in Windows 10 (64-bit operating system, × 64-based processor)

As it is clear from the results in the table, the present algorithm is considerably faster than both of Cody’s code and the built-in “Erfc_Scaled” function. Efficiency improvement for the wide range is greater than a factor of 2 (in general) and goes up to a factor of 5 for the case of quad precision.

Table 7 shows the same information as in Table 6 except that the calculations are performed using the Intel Fortran 64 Compiler Classic for applications running on Intel(R) 64, Version 2021.6.0. As it is clear from the results in the table, the present algorithm is more efficient than the built-in “Erfc_Scaled” function for the wide range by a factor greater than 2 for quad precision and, surprisingly, by a factor higher than an order of magnitude for double and single precision!. However, for the practical range [10⁻⁶–10⁶] the present algorithm is only slightly faster (between 25 and 30% improvement) for the quad precision, although, for the cases of double and single precision, the present algorithm is still faster by more than an order of magnitude.

Table 7 Average CPU time consumed in calculating 10⁶ points uniformly distributed on the logarithmic scale for the case of wide range xϵ[10⁻³⁰–10³⁰] and for the case of practical range xϵ[10⁻⁶–10⁶] using Cody’s code, the built-in Erfc_Scaled function and the present algorithm. Computations are performed using Intel Fortran 64 Compiler Classic for applications running on Intel(R) 64, Version 2021.6.0.compiler on an Intel® Core™ i7-7600U CPU @2.80 GHz processor in Windows 10 (64-bit operating system, × 64-based processor)

Figures 2, 3, and 4 show performance tests for each decade between 10⁻⁶ and 10⁶ (the region of interest or of useful and practical value) for all three standard precision arithmetic and using the “gfortran” compiler (part a) and “ifort” compiler (part b). The overall improvement of efficiency is clear in all of the three figures for the three standard precision and the two compilers.

Fig. 2

A stair-step plot per decade of CPU time, in seconds, consumed for 10.⁶ evaluations using quadruple precision arithmetic and the “gfortran” compiler (a) and the “ifort” compiler (b)

Fig. 3

A stair-step plot per decade of CPU time, in seconds, consumed for 10.⁶ evaluations using double precision arithmetic and the “gfortran” compiler (a) and the “ifort” compiler (b)

Fig. 4

A stair-step plot per decade of CPU time, in seconds, consumed for 10.⁶ evaluations using single precision arithmetic and the “gfortran” compiler (a) and the “ifort” compiler (b)

For timing comparison for negative x-values and for $0>x\ge -9.0$, the present code is faster than the built-in function “$Erfc\_Scaled$” by a factor greater than 3 for all precisions using the “gfortran” compiler. For negative x-values with $x<-9.0$ where the function is approximated by $2\;\mathit{exp}\left(x^2\right)$, the present code is also faster than the built-in function by a factor greater than 2 for double and single precision though it takes almost the same time as the built-in function for quad precision. With the “ifort” compiler, the present code is faster than the built-in “$Erfc\_Scaled$” function by a factor greater than 20 for single and double precision arithmetic for both of the above cases; i.e., $0>x\ge -9.0$ and $x<-9.0$ and factors greater than 4 and 2, when using quadruple precision for both cases, respectively.

3.2 Daw (x)

An array of 400001 points uniformly spaced on the logarithmic scale between 10⁻³⁰ and 10⁵ is used to perform the accuracy check of the present algorithm. A table of reference values corresponding to this array is generated using variable precision arithmetic from the Matlab [38] symbolic toolbox. The maximum absolute relative error obtained for the quadruple precision computations using the present algorithm is in the order of 10⁻³² as intended and as shown in Fig. 5. Figure 5 also shows the absolute of the relative error in calculating Daw(x) using the present algorithm together with the error resulting from using Algorithm715 with single and double precision arithmetic. For single and double precision calculations, the maximum of the absolute of relative error obtained using the present algorithm is in the order of 10⁻¹⁶ for double precision and 10⁻⁷ for single precision as expected. For the last two cases, calculations using Algorithm715 showed the same order for the maximum of the absolute of relative error which confirms the accuracy of the present algorithm for all standard precision arithmetic used.

Fig. 5

Absolute of relative error in calculating Dawson integral, $Daw(x)$ using the present algorithm and using Algorithm715 (for single and double precision arithmetic). Calculations are performed using the GNU Fortran 8.1.0 (gfortran) with data generated using variable precision arithmetic offered in the Matlab symbolic toolbox as the reference

A computer code that calculates the Dawson integral to quadruple precision arithmetic or to 32 significant digits in a compiled language is not available to the author for efficiency comparison. However, Algorithm715 [2] includes a function to calculate Dawson’s integral, which can be run using single and double precision arithmetic for efficiency comparison. Similar to the case of $erfcx(x)$, the time consumed to calculate a single point is very short. Accordingly, we report the time required for calculating the whole array of 400001 points. We repeat the calculations several hundreds of times and take the average time consumed per evaluation of the array for comparison.

Table 8 shows the total CPU time spent in calculating the 400001 points by Algorithm715 and by the present algorithm for both single and double precision arithmetic using the “gfortran” compiler. As can be seen from the table, the present algorithm is faster than Algorithm715 and takes only about 53–74% of the time spent by Algorithm715 for the computations.

Table 8 Average CPU time, in seconds, consumed in calculating 400,001 points of $Daw(x)$, uniformly distributed on the logarithmic scale, for a case of wide range $x\epsilon [{10}^{-30}-{10}^{30}]$ and a case of practical range $x\epsilon [{10}^{-6}-{10}^{6}]$. Calculations are performed using the GNU Fortran 8.1.0 (gfortran)

Similarly, Table 9 shows the same data as in Table 8 except that compilation is performed using the “ifort” compiler. The present algorithm is also faster than Algorithm715 and takes only about 49–61.1% of the time spent by Algorithm715 for the computations.

Table 9 Average CPU time, in seconds, consumed in calculating 400,001 points of $Daw(x)$, uniformly distributed on the logarithmic scale, for a case of wide range $x\epsilon [{10}^{-30}-{10}^{30}]$ and a case of practical range $x\epsilon [{10}^{-6}-{10}^{6}]$. Calculations are performed using the Intel Fortran 64 Compiler Classic for applications running on Intel(R) 64, Version 2021.6.0.compiler (ifort)

4 Conclusions

Efficient, multiple precision algorithms for the computation of the scaled complementary error function, $exp(x^2)\;erfc\left(x\right)$ and the Dawson integral, $Daw(x)$, are presented and implemented in the form of Fortran elemental modules. The accompanying Fortran codes can be run in single, double, and quadruple precision arithmetic at the convenience of the user by assigning the required precision to an integer “rk” in a subsidiary module “set_rk.” Results from the present code for $erfcx(x)$ are compared with the built-in “Erfc_Scaled” function, available in modern Fortran compilers showing that the present algorithm is considerably more efficient than the built-in function. With the “gfortran” compiler, the efficiency improvements for all tested data sets and all of the three precisions (single, double, and quadruple) are between a factor of 2 and a factor of 5. However, with the “ifort” compiler, efficiency improvements vary between a factor of 1.3 and a factor of 20 depending on the tested data set and the precision used.

The present code for $Daw(x)$ is distinctive in calculating the function to 32 significant digits. Results from the present code for $Daw(x)$ for double and single precision arithmetic are compared with calculation using the Dawson function from Algoritm715 showing that the present algorithm is also faster than Algorithm715. The efficiency improvements range between a factor of 1.35 and a factor of 2.0 depending on the tested dataset and the precision.

The present algorithms for $erfcx(x)$ and $Daw(x)$ can be easily implemented in any software package and to numerical libraries in any programming language with the possibility of extension to consider complex arguments in a future planned work.

Appendix. The polynomial of 17th degree resulting from Eq. (5), approximating the erfcx(x) function to 32 significant digits accuracy in the region |x|ϵ[0,0.037]

$$\begin{array}{c}erfcx\left(x\right)\sim\frac1{4410806400}\left\{\left(109395x^{16}+875160x^{14}+6126120x^{12}+3675672x^{10}+18378360x^8+\right.\right.\\\left.735134400x^6+2205403200x^4+4410806400x^2+4410806400x^{14}\right)-\frac1{\sqrt\pi}\left(65536x^{17}+557056x^{15}+\right.\\\begin{array}{c}4177920x^{13}+27156480x^{11}+149360640x^9+672122880x^7+2352430080x^5+5881075200x^3+\\\left.\left.8821612800x\right)\right\}\;\mathrm{for}\;x\leq0.037\end{array}\end{array}$$

Table 10 Minimum power of the above polynomial required to secure the accuracy in the range shown