1 Introduction

The solutions of many differential and integral equations, modeling physical phenomena and processes, are generally expressed in terms of special functions. These functions gather a great variety of challenging mathematical expressions including highly transcendental functions and integrals, and their notation has been consolidated over time. Numerical evaluation of special functions has been an active field of research since the introduction of computers into science in the 1950s with associated technical challenges underlining many foundational problems in scientific computing.

For their vast array of applications and their concrete standardized definitions, once a trustworthy algorithm and implementation are devised for any of the special functions, it typically lasts for decades. For example, single- and double-precision computer codes developed in the last few decades of the last century are still widely used [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Developing such algorithms can be a devious task of analyzing and combining a variety of different approximation schemes with a bewildering array of pitfalls and “corner cases” where approximations fail or numerical instabilities demand careful transformations. As a result, only a limited set of highly efficient implementations are available for many functions, and for some functions, there are no libraries at all. It is worth noting that there are libraries and software packages for arbitrary precision calculations of several special functions (i.e., to any number of digits), but these typically use extremely slow series methods and are impractically inefficient for large-scale calculations. Yet, there are numerous important applications that require massive evaluations of special functions while high precision (higher than the 16 significant digits characterizing the double precision arithmetic calculations) is indispensable. Some of these applications include electromagnetic scattering theory, theory of nonlinear oscillators, climate modeling, supernovae simulations, planetary orbit calculations, Schrodinger solutions for lithium and helium atoms, the Taylor algorithm for ordinary differential equations, and Coulomb N-body atomic system simulations in addition to many others [24,25,26,27,28]. Accordingly, both high accuracy (needing high precision) and high efficiency are requirements for practical physical problems.

An existing major gap in this regard is the unavailability of algorithms and computer codes for many special functions for mid-range quadruple or “quad” precision which (unlike truly arbitrary precision) are not too much slower than the double precision hardware and hence are practical for reasonably large calculations. Besides, current advancements in computer processing power and data storage capabilities in addition to the support of many modern compilers to high-precision arithmetic increase the interest in and facilitate the task of developing routines and computer codes using quadruple precision arithmetic for the above mentioned kind of problems. A code that can be run in “multiple” precision such as single, double, and quad precision arithmetic may require different algorithms or suitable tuning or adjustments for efficiency reasons.

This paper presents part of our efforts toward narrowing the abovementioned gap, where, herein, we develop accurate and efficient multiple precision algorithms to calculate the Fresnel’s sine and cosine integrals S(z) and C(z). These transcendental functions were primarily introduced in the calculation of the electromagnetic field intensity in a medium where light bends around opaque objects. Additional new applications include but not limited to the design of highways, railways, and rollercoasters.

2 Mathematical relations

Fresnel’s sine and cosine integrals S(z) and C(z) are widely used in physics, particularly in optics and electromagnetic theory where they arise in the description of near-field Fresnel diffraction phenomena. The functions are defined in a variety of equivalent forms in the mathematical literature [29,30,31]. For example, the functions S(z) and C(z) are defined by the oscillatory integrals:

$$S(z)={\int}_0^z\sin \left(\frac{\pi }{2}\ {t}^2\right) dt$$
(1)
$$C(z)={\int}_0^z\cos \left(\frac{\pi }{2}\ {t}^2\right) dt$$
(2)

The functions are also defined in the forms of the pairs S1(z), C1(z), and S2(z), C2(z) where:

$${S}_1(z)=\sqrt{\frac{2}{\pi }}{\int}_0^z\sin \left(\ {t}^2\right) dt$$
(3)
$${C}_1(z)=\sqrt{\frac{2}{\pi }}{\int}_0^z\cos \left(\ {t}^2\right) dt$$
(4)
$${S}_2(z)=\frac{1}{\sqrt{2\pi }}{\int}_0^z\frac{\sin \left(\ t\right)\ }{\sqrt{t}} dt=\frac{1}{2}{\int}_0^z{J}_{\frac{1}{2}}(t) dt$$
(5)
$${C}_2(z)=\frac{1}{\sqrt{2\pi }}{\int}_0^z\frac{\cos \left(\ t\right)\ }{\sqrt{t}} dt=\frac{1}{2}{\int}_0^z{J}_{-\frac{1}{2}}(t) dt$$
(6)

where J1/2(t) and J−1/2(t) refer to the ordinary Bessel functions of the first kind of orders ½ and −½, respectively. The three pairs of functions in (1), (2), (3), (4), and (5), (6) are related to each other by [29, 30]:

$$S(z)={S}_1\left(\sqrt{\frac{\pi }{2}}\ z\right)={S}_2\left(\frac{\pi }{2}{z}^2\right)$$
(7)
$$C(z)={C}_1\left(\sqrt{\frac{\pi }{2}}\ z\right)={C}_2\left(\frac{\pi }{2}{z}^2\right)$$
(8)

From the computational point of view, all forms of the Fresnel sine and cosine integrals can be computed using the same algorithm with a slight change in the argument as explained in Eqs. (7), (8).

Considering the form of the integrals given in (1), (2), it is easy to show that they can be also expressed in terms of the Faddeyeva or “Faddeeva” function, \({w}(z)\) [32,33,34,35,36] where:

$$S(z)=\frac{-1-i}4\left[\left(1-e^{\left(\frac{1-i}2\sqrt\pi\;z\right)^2}w\left(\frac{1-i}2\sqrt\pi\;z\right)\right)+i\left(1-e^{\left(\frac{1+i}2\sqrt{\pi\;}\;z\right)^2}w\left(\frac{1+i}2\sqrt\pi\;z\right)\right)\right]$$
(9)
$$C(z)=\frac{-1+i}4\left[\left(1-e^{\left(\frac{1-i}2\sqrt\pi\;z\right)^2}w\left(\frac{1-i}2\sqrt\pi\;z\right)\right)-i\left(1-e^{\left(\frac{1+i}2\sqrt{\pi z}\right)^2}w\left(\frac{1+i}2\sqrt\pi\;z\right)\right)\right]$$
(10)

Using the expressions (9) and (10) with some mathematical manipulation, one can show that:

$$S(x)=\frac{1}{2}-\frac{1}{2}\ \mathfrak{R}\left(w\left(\frac{i-1}{2}\sqrt{\pi }\ x\right)\right)\times \left(\cos \left(\frac{\pi }{2}{x}^2\right)+\sin \left(\frac{\pi }{2}{x}^2\right)\right)-\frac{1}{2}\mathfrak{T}\left(w\left(\frac{i-1}{2}\sqrt{\pi }\ x\right)\right)\times \left(\sin \left(\frac{\pi }{2}{x}^2\right)-\cos \left(\frac{\pi }{2}{x}^2\right)\right)$$
(11)

with S(iy) =  − iS(y)

Similarly:

$$C(x)=\frac{1}{2}-\frac{1}{2}\ \mathfrak{R}\left(w\left(\frac{i-1}{2}\sqrt{\pi }\ x\right)\right)\times \left(\cos \left(\frac{\pi }{2}{x}^2\right)-\sin \left(\frac{\pi }{2}{x}^2\right)\right)-\frac{1}{2}\mathfrak{T}\left(w\left(\frac{i-1}{2}\sqrt{\pi }\ x\right)\right)\times \left(\cos \left(\frac{\pi }{2}{x}^2\right)+\sin \left(\frac{\pi }{2}{x}^2\right)\right)$$
(12)

where C(iy) = iC(y)

The formulation of the functions as direct expressions in Faddeyeva function as in Eqs. (9), (10) and in Eqs. (11), (12) is not common in the literature although equivalent alternatives can be found.

Fresnel integrals are analytical functions defined for all complex values of z, over the whole complex plane. They are odd functions with the following symmetry relations

$$S\left(-z\right)=-S(z),\kern1.5em S\left(\overline{z}\right)=\overline{S(z)}$$
(13)
$$C\left(-z\right)=-C(z),\kern1.5em C\left(\overline{z}\right)=\overline{C(z)}$$
(14)

In addition, the integrals have simple limiting values at z = zero and z→∞ where:

$$S(0)=0,\kern2em \underset{z\to \pm \infty }{\lim }S(z)=\pm \frac{1}{2},$$
(15)
$$C(0)=0,\kern2em \underset{z\to \pm \infty }{\lim }C(z)=\pm \frac{1}{2}$$
(16)

It is also worth mentioning that the Fresnel integrals S(z) and C(z) have the following simple converging series representations for small |z|.

$$S(z)={z}^3\sum \nolimits_{k=0}^{\infty}\frac{2^{-2k-1}{\pi}^{2k+1}{\left(-{z}^4\right)}^k}{\left(4k+3\right)\left(2k+1\right)!}=\frac{\pi }{6}{z}^3\left(1+\sum \nolimits_{k=1}^{\infty}\prod \nolimits_{n=1}^k\left[-\frac{4n-1}{2n\left(2n+1\right)\left(4n+3\right)}{\left(\frac{\pi }{2}\ {z}^2\right)}^2\right]\right)$$
(17)
$$C(z)=z\sum \nolimits_{k=0}^{\infty}\frac{2^{-2k}{\pi}^{2k}{\left(-{z}^4\right)}^k}{\left(4k+1\right)(2k)!}=z\left(1+\sum \nolimits_{k=1}^{\infty}\prod \nolimits_{n=1}^k\left[-\frac{4n-3}{2n\left(2n-1\right)\left(4n+1\right)}{\left(\frac{\pi }{2}\ {z}^2\right)}^2\right]\right)$$
(18)

and the asymptotic expressions for z→∞ and |arg z|<π/2, in terms of the auxiliary functions or integrals f(z) and g(z) where:

$$S(z)=\frac{1}{2}-f(z)\cos \left(\frac{\pi }{2}\ {z}^2\right)-g(z)\sin \left(\frac{\pi }{2}\ {z}^2\right)$$
(19)
$$C(z)=\frac{1}{2}+f(z)\sin \left(\frac{\pi }{2}\ {z}^2\right)-g(z)\cos \left(\frac{\pi }{2}\ {z}^2\right)$$
(20)

The auxiliary functions f(z) and g(z) are defined by the integrals:

$$f(z)=\frac{1}{\pi \sqrt{2}}\ {\int}_0^{\infty}\frac{e^{-{z}^2t}}{\sqrt{t}\left({t}^2+1\right)}\ dt={\int}_0^{\infty }{e}^{-\pi zt}\cos \left(\frac{\pi }{2}{t}^2\right) dt$$
(21)
$$g(z)=\frac{1}{\pi \sqrt{2}}\ {\int}_0^{\infty}\frac{\sqrt{t}\ {e}^{-{z}^2t}}{\left({t}^2+1\right)}\ dt={\int}_0^{\infty }{e}^{-\pi zt}\sin \left(\frac{\pi }{2}{t}^2\right) dt$$
(22)

3 Foundation of the algorithms

The mathematical relations cited in the above section provide a solid foundation of the present algorithms for (x), C(x) and S(z), C(z) as explained below.

3.1 Series expansion for small |z|

For small |z| values, the series expansions in Eqs. (17) and (18) can be evaluated recursively in the forms:

$$S(z)=\frac{\pi }{6}{z}^3\left(1+\sum \nolimits_{k=1}^{\infty }{T}_{S,k}\right)$$
(23)
$$C(z)=z\left(1+\sum \nolimits_{k=1}^{\infty }{T}_{C,k}\right)$$
(24)

where:

$${T}_{S,0}=1,{T}_{S,k}={T}_{S,k-1}\cdot \frac{-\left(4k-1\right)}{2k\left(2k+1\right)\left(4k+3\right)}\ {\left(\frac{\pi }{2}\ {z}^2\right)}^2$$
(25)

and

$${T}_{C,0}=1,{T}_{C,k}={T}_{C,k-1}\cdot \frac{-\left(4k-3\right)}{2k\left(2k-1\right)\left(4k+1\right)}\ {\left(\frac{\pi }{2}\ {z}^2\right)}^2$$
(26)

For real input (z = x), the above recursive schemes work accurately up to x = 2.7 for quad precision, and up to x = 1.576 for single/double precision in calculating S(x) while the border for C(x) with quad precision changes to x = 3.0 though the border for single/double precision remains the same, i.e., x = 1.576. For the case of complex input where z = x + iy and y ≠ 0.0, the above recursive scheme of the series is used accurately for the region |z|2 ≤ 6.9 for S(z) and the region |z|2 ≤ 12.75 for C(z), securing accuracies of 7, 16, and 31 SD for single, double, and quadruple precision arithmetic, respectively. It has to be noted that the numerical factor depending on the index k in the above expressions can be evaluated in advance to improve the efficiency of the algorithm.

3.2 Asymptotic expressions for large |z|

For input values of large |z|, whether z is real or complex, the asymptotic expression in Eqs. (19) and (20) can be used together with the series expansions for the auxiliary functions f(z) and g(z) given by the following expressions to evaluate the Fresnel integrals where for \(\mid \arg z\mid \le \frac{\pi }{4}\)

$$f(z)\approx \frac{1}{\pi z}\ \left(1+\sum \nolimits_{k=1}^{\infty }{\left(-1\right)}^k\frac{1\cdot 3\cdot \cdot \cdot \left(4k-1\right)}{{\left(\pi {z}^2\right)}^{2k}}\right)\approx \frac{1}{\pi z}\ \left(1+\sum \nolimits_{k=1}^{\infty }{T}_{f,k}\right)$$
(27)
$$g(z)\approx \frac{1}{\pi z}\ \left(\sum \nolimits_{k=0}^{\infty }{\left(-1\right)}^k\frac{1\cdot 3\cdot \cdot \cdot \left(4k+1\right)}{{\left(\pi {z}^2\right)}^{2k+1}}\right)\approx \frac{1}{\pi^2{z}^3}\ \left(1+\sum \nolimits_{k=1}^{\infty }{T}_{g,k}\right)$$
(28)

with

$${T}_{f,0}=1,\kern0.5em {T}_{f,k}={T}_{f,k-1}\cdot -\frac{\left(4k-3\right)\left(4k-1\right)}{{\left(\pi {z}^2\right)}^2}$$
(29)

and

$${T}_{g,0}=1,\kern0.5em {T}_{g,k}={T}_{g,k-1}\cdot -\frac{\left(4k-1\right)\left(4k+1\right)}{{\left(\pi {z}^2\right)}^2}$$
(30)

While for \(\frac{\pi }{4}<\pm \mid \arg z\mid \le \frac{3\pi }{4}\), the following expressions are used for f(z) and g(z):

$$f(z)\approx \frac{1+i}{2}{e}^{\frac{\pi }{2}i{z}^2}+\frac{1}{\pi z}\ \left(1+\sum \nolimits_{k=1}^{\infty }{\left(-1\right)}^k\frac{1\cdot 3\cdot \cdot \cdot \left(4k-1\right)}{{\left(\pi {z}^2\right)}^{2k}}\right)$$
(31)
$$g(z)\approx \frac{1-i}{2}{e}^{\frac{\pi }{2}i{z}^2}+\frac{1}{\pi z}\ \left(\sum \nolimits_{m=0}^{\infty }{\left(-1\right)}^m\frac{1\cdot 3\cdot \cdot \cdot \left(4m+1\right)}{{\left(\pi {z}^2\right)}^{2m+1}}\right)$$
(32)

Similar to the implementation of the series for small |z|, the index-dependent numerical factors in the above expressions can be calculated in advance to improve the efficiency.

Accuracy degradation was found for input values of ∣ arg z ∣ near the real and the imaginary axes. For S(z) the present algorithm is applicable for \(3\times {10}^{-4}<\left|\frac{y}{x}\right|<2\times {10}^3\) where z = x + iy. While for C(z), the algorithm is applicable for \(4\times {10}^{-4}<\left|\frac{y}{x}\right|<2.2\times {10}^3\).

3.3 Intermediate range of |z|

3.3.1 Real input (z = x)

For the intermediate range of a real input variable, z = x, the present algorithm makes use of Chebyshev subinterval polynomial approximations with a combination of linear and nonlinear mapping. As Fresnel’s integrals are odd functions, we focus on the calculation of the functions for xϵ [0, ∞] and use the symmetry relations to extend the calculation to the x < 0.0 domain. Accordingly, for unbound variables like our case, where xϵ [0, ∞], various nonlinear mapping transformations can be used to map the infinite range to a finite one. Herein, we nonlinearly map the independent variable xϵ [0, ∞] to the variable tϵ [0, 1] where:

$$t=\frac{c}{x+c}$$
(33)

where c is a constant. To cover the whole domain of xϵ [0, ∞], the domain of tϵ [0, 1] is divided into a number of equal subintervals of borders bi and b(i+1) where bi + 1 − bi = bi − bi − 1. A linear transformation is then used to map it into the range [−1, 1] where:

$$y=\frac{2t-\left({b}_i+{b}_{i-1}\right)}{b_i-{b}_{i-1}}$$
(34)

The domain of t is divided into 200 equal-sized regions where a Chebyshev polynomial P(t) is obtained to approximate the original function to the sought accuracy for the precision arithmetic under consideration in each region. A significant effort is devoted to choose a suitable value of the constant c = 1.9 to secure the targeted accuracy for the planned power of the polynomial for the subintervals. Clearly, the degree of the polynomial is precision-dependent as shown in Table 1.

Table 1 Degree of Chebyshev polynomials and applied range for approximating S (x) and C(x) as functions of the used precision
Full size table

It has to be mentioned at this point that one can also calculate the functions to such high accuracy ~31 SD using the expression/expansion in terms of the half-integer order Bessel functions of the first kind as explained in the next subsection; however, it was found that the Chebyshev subintervals polynomial approximation is more efficient for real argument z = x.

3.3.2 Complex input (z = x + iy)

For complex input values z = x + iy, Fresnel integrals can be expressed in terms of half-integer order Bessel functions of the first kind, where:

$$S(z)=\sum \nolimits_{k=0}^{\infty }{J}_{2k+\frac{3}{2}}\left(\frac{\pi }{2}\ {z}^2\right)={J}_{3/2}\left(\frac{\pi }{2}\ {z}^2\right)+{J}_{\frac{7}{2}}\left(\frac{\pi }{2}\ {z}^2\right)+{J}_{\frac{11}{2}}\left(\frac{\pi }{2}\ {z}^2\right)+\dots$$
(35)
$$C(z)=\sum \nolimits_{k=0}^{\infty }{J}_{2k+\frac{1}{2}}\left(\frac{\pi }{2}\ {z}^2\right)={J}_{1/2}\left(\frac{\pi }{2}\ {z}^2\right)+{J}_{\frac{5}{2}}\left(\frac{\pi }{2}\ {z}^2\right)+{J}_{\frac{9}{2}}\left(\frac{\pi }{2}\ {z}^2\right)+\dots$$
(36)

The half-integer order Bessel functions in the above series follow the standard recurrence relation:

$${J}_{k+\frac{1}{2}-1}(z)=\frac{\left(2k+1\right)}{z}{J}_{k+\frac{1}{2}}(z)-{J}_{k+\frac{1}{2}+1}(z)$$
(37)

with \({J}_{k+\frac{1}{2}}(z)\to 0\) as k → ∞.

In practical computation, the above series are truncated at an appropriate order k = K, and the string of half-integer order Bessel functions, for a specific value of z, is computed efficiently by Miller’s algorithm [37]. Miller’s algorithm uses the standard recurrence relation in reverse order from k = K down to k = 0.

The use of conventional backward recurrence method requires a recurrence connecting successive elements of the sequence in addition to some normalizing relation such as a generating function or a single function value, if the recurrence is homogeneous.

Scaling the Bessel functions in Eqs. (35), (36) by a constant E (z) where \({J}_{k+\frac{1}{2}}(z)=E(z){F}_{k+\frac{1}{2}}(z)\), the recurrence relation (37) can be written for the sequence of functions \({F}_{k+\frac{1}{2}}(z)\) as:

$${F}_{\left(k-1\right)+\frac{1}{2}}(z)=\frac{\left(2k+1\right)}{z}{F}_{k+\frac{1}{2}}(z)-{F}_{\left(k+1\right)+\frac{1}{2}}(z)$$
(38)

Miller’s scheme assigns \({F}_{K+\frac{1}{2}}(z)=1\) and \({F}_{\left(K+1\right)+\frac{1}{2}}(z)\)=0 and uses the recurrence to compute \({F}_{\left(K-1\right)+\frac{1}{2}}\), \({F}_{\left(K-2\right)+\frac{1}{2}}\), …, \({F}_{(0)+\frac{1}{2}}\).

For complex argument, it is convenient to find the normalized Bessel function by the aid of the lowest order Bessel function where:

$$E(z)=\frac{J_\frac12(z)}{F_\frac12(z)}=\frac{\sqrt{\frac{2z}\pi}\;j_0(z)}{F_\frac12(z)}=\frac{\sqrt{\frac2{\pi z}}\;\sin(z)}{F_\frac12(z)}$$
(39)

or

$$E\left(\frac{\pi }{2}\ {z}^2\right)=\frac{\ \mathit{\sin}\left(\frac{\pi }{2}\ {z}^2\right)}{z\ {F}_{\frac{1}{2}}\left(\frac{\pi }{2}\ {z}^2\right)}$$
(40)

A central point is applying Miller’s algorithm is the choice of the “seed” order k = K needed to secure the targeted accuracy. When the required is the absolute value of the individual Bessel functions, one may reasonably take the seed order K such that \({J}_{K+\frac{1}{2}}(z)={10}^{-M}\)which implies that the error in each of the individual Bessel functions for k < K using Miller’s algorithm will be of the order of 10−M. However, for cases like our case where we are interested in the sum of the Bessel functions, one may satisfactorily take the seed order K such that \({J}_{K+\frac{1}{2}}(z)=\varepsilon\) where ε is the distance from 1.0 to the next larger floating point number in the precision under consideration. Since we are interested herein in calculating the sum of Bessel’s function, then to find the seed order k = K from which we start the backward recurrence according to Miller’s algorithm, one may set the term \({J}_{\nu}\approx \frac{{\left(z/2\right)}^{\nu }}{\Gamma \left(\nu +1\right)}=\varepsilon\), where Γ is the gamma function, and solve this transcendental equation, then K can be taken conservatively as the ceiling of the real value of ν. As can be seen in Fig. 1, the outmost border for using Miller’s algorithm for backtracking with single or double precision can be conservatively given by the equation:

$$K=\textrm{ceiling}\ \left(1.44\ \left|z\right|+23.1\right)\ \textrm{for}\ \left|z\right|\epsilon \left[2.8,7.5\right]$$
(41)
Fig. 1
figure 1

Linear fitting of the solution of the transcendental equation Jν ≈ (z/2)ν/Γ(ν + 1) = ε for single- or double- and quadruple-precision arithmetic

Full size image

and for quadruple precision by:

$$K=\textrm{ceiling}\ \left(1.59\ \left|z\right|+43.1\right)\ \textrm{for}\ \left|z\right|\epsilon \left[2.8,7.5\right]$$
(42)

4 Accuracy and efficiency comparison

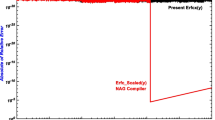
The present algorithms for Fresnel integrals S(x), C(x), S(z), and C(z) have been implemented into a modern Fortran elemental module. The module can be run using single-, double-, and quadruple-precision arithmetic. Accuracy check for S(x) and C(x) is performed for both functions using an array of 400,001 points uniformly spaced on the logarithmic scale between 10−30 and 106. The corresponding reference points were generated using the Maple mathematics symbolic software. The maximum absolute of relative error obtained for quadruple precision is in the order of 10−28 as shown in Fig. 2. When using double precision arithmetic, the maximum absolute of the relative error obtained rises to 10−10. This order of the absolute of the relative error when using double precision is the same as obtained from using Algorithm 723 [38] (based on Cody’s approximations (2)) as shown in Fig. 3. For better readability of Fig. 3, only 1600 points uniformly selected from the above mentioned 400,001 are used to show the accuracy comparison in Fig. 3. For several decades of small x, values, the relative error in calculating C(x) using the present algorithm is effectively zero.

Fig. 2
figure 2

Absolute of relative error obtained using the present algorithm with quadruple precision arithmetic for the Fresnel functions S(x) (a) and C(x) (b)

Full size image
Fig. 3
figure 3

Absolute of relative error obtained using Algorithm 723 and the present algorithm with double precision arithmetic for the Fresnel functions S(x) (a) and C(x) (b)

Full size image

The present authors are not aware of any competitive code in a compiled language that calculates S(x) and C(x) to accuracies in the range of 10−28, obtained by the present algorithms and computer code. Accordingly, the performance benchmark is achieved herein with comparison to results from Algorithm 723 using double precision arithmetic. Due to the relatively short time per evaluation, the abovementioned 400,001 points are evaluated tens of times, and the average CPU time per evaluation is reported in Table 2. Timing results in Table 2 are obtained using two compilers: the GNU Fortran 6.4.0 (gfortran) and the Intel 2021.6.0 classic (ifort) compilers. As the table shows, the present Fortran code is faster than Algorithm 723 by more than 70% when using “gfortran” where improvements by a factor of 2 are obtained when using the “ifort” compiler.

Table 2 Average CPU-time per evaluation in ns spent in calculating S(x) and C(x) for x in the range [10−30, 106] using Algorithm 723 as compared to the present algorithm
Full size table

Figures 4 and 5 show performance tests for each decade between 10−30 and 106 for both the Fresnel sine (part a) and Fresnel cosine (part b) using the “gfortran” and “ifort” Fortran compilers, respectively.

Fig. 4
figure 4

Stair-step plots per decade of CPU time, in seconds, consumed in 106 evaluations the “gfortran” compiler and double precision arithmetic for the Fresnel functions S(x) (a) and C(x) (b)

Full size image
Fig. 5
figure 5

Stair-step plots per decade of CPU time, in seconds, consumed in 106 evaluations using the “ifort” compiler and double precision arithmetic for the Fresnel functions S(x) (a) and C(x) (b)

Full size image

For complex arguments z = x + iy, y ≠ 0, accuracy check of the present functions S(z) and C(z) is performed using an array of 39,139 points for x and y ranging between 10−6 and 102 and uniformly spaced on the logarithmic scale, with the exclusion of points resulting in real and/or imaginary parts of the functions of magnitude larger than the largest finite floating point number using double precision arithmetic. Similar to the case of real input, the maximum absolute relative error obtained using quadruple precision is in the order of 10−28, and for double precision, it is in the order of 10−10 using the constraints \(3\times {10}^{-4}<\left|\frac{y}{x}\right|<2\times {10}^3\)for S(z) and \(4\times {10}^{-4}<\left|\frac{y}{x}\right|<2.2\times {10}^3\) for C(z).

Figures 6 and 7 show three-dimensional surface plots for the absolute of the relative error obtained in calculating the real and the imaginary parts of the functions S(z) and C(z) using double and quadruple precision, respectively. The range of the input values of x and y shown in Fig. 6 is xϵ[10−2, 15] and yϵ[10−2, 15]. Values of\(\mathfrak{R}\left(S(z)\right),\mathfrak{I}\left(S(z)\right),\mathfrak{R}\left(C(z)\right),\) and \(\mathfrak{I}\left(C(z)\right)\) corresponding to z = 15 + 15i is approximately equal to the largest finite floating point number in the double precision arithmetic. Evaluating these functions for input arguments of larger x and y would require the use of higher precision. The range of the input values of x and y shown in Fig. 7 is xϵ[10−2, 80] and yϵ[10−2, 80], and as a result, quadruple precision arithmetic has been used in calculating the data used in generating these figures.

Fig. 6
figure 6

Three-dimensional surface plots of the absolute of the relative error in calculating the real and imaginary parts of Fresnel integrals for x and y in the range [10−2, 15] using double precision: S(z) (a), C(z) (b)

Full size image
Fig. 7
figure 7

Three-dimensional surface plots of the absolute of the relative error in calculating the real and imaginary parts of Fresnel integrals for x and y in the range [10−2, 80] using quadruple precision: S(z) (a), C(z) (b)

Full size image

5 Conclusions

Numerical algorithms for efficient and highly accurate computations of Fresnel’s sine and cosine integrals S(z) and C(z) for real and complex arguments have been developed and implemented in an elemental Fortran module. The algorithms are more accurate, and the relevant Fortran implementation is more efficient than other competitive codes used for real arguments in the literature. The present algorithms, the Fortran implementation, are exceptional in calculating the functions, for most of the domain of interest, to accuracies in the order of 10−28 both for real and complex arguments. Efficiency improvements, between 70 and 100%, compared to competitive algorithms in the literature are obtained when using double-precision arithmetic, depending on the compiler used. The developed Fortran computer code can be run in single, double, or quad precision at the convenience of the user by the choice of an integer “rk” in a subsidiary module “set_rk.” Although, single precision arithmetic produces results with accuracies in the range of 10−4 for real arguments in the range of x < 106, it is not recommended for complex arguments due to deterioration in accuracy.