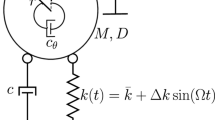Abstract
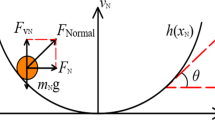
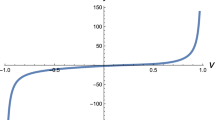
This paper proposes a theoretical framework and carries out numerical verification for suppressing homoclinic chaos of a class of vibro-impact oscillators by adding non-harmonic periodic excitations. Based on the Melnikov method of non-smooth systems, the theoretical sufficient conditions for suppressing homoclinic chaos are obtained by eliminating the simple zeros of the corresponding Melnikov function while retaining the infinite terms of the Fourier expansion of the non-harmonic periodic excitations. Furthermore, the effects of waveforms, amplitudes, initial phases, and impulse of the non-harmonic periodic excitations on chaos suppression are studied, and the optimal parameters for suppressing chaos are analytically obtained. Finally, the effectiveness of theories is verified by the vibro-impact Duffing oscillator. Numerical results show that chaos induced by the transversal intersection of homoclinic orbits can be weakened or even suppressed by adding the non-harmonic periodic excitations, and when the impulse transmitted by the non-harmonic periodic excitations is maximum, the effective amplitude for suppressing chaos is minimal. Moreover, there may be some phenomena that do not have too good a quantitative agreement between theoretical predictions and numerical results.














Similar content being viewed by others
Data availibility statement
The authors declare that all data generated or analysed during this study are included in this published article.
References
Goldman, P., Muszynska, A.: Dynamic effects in mechanical structures with gaps and impacting: order and chaos. J. Vib. Acoust. 116, 541–547 (1994)
Nordmark, A.B.: Non-periodic motion caused by grazing incidence in an impact oscillator. J. Sound Vib. 145, 279–297 (1991)
Brogliato, B.: Nonsmooth Mechanics. Springer, Berlin (1999)
Feeny, B.F., Moon, F.C.: Empirical dry-friction modelling in a forced oscillator using chaos. Nonlinear Dyn. 47, 129–141 (2007)
Kobori, T., Takahashi, M., Nasu, T., Niwa, N., Ogasawara, K.: Seismic response controlled structure with active variable stiffness system. Earthq. Eng. Struct. Dyn. 22, 925–941 (1993)
Nesterov, Y.: Excessive gap technique in nonsmooth convex minimization. SIAM J. Optim. 16, 235–249 (2005)
Banerjee, S., Verghese, G.: Nonlinear Phenomena in Power Electronics. IEEE Press, New York (2001)
Du, Z.D., Zhang, W.N.: Melnikov method for homoclinic bifurcation in nonlinear impact oscillators. Comput. Math. Appl. 50, 445–458 (2005)
Xu, W., Feng, J.Q., Rong, H.W.: Melnikov’s method for a general nonlinear vibro-impact oscillator. Nonlinear Anal. Theory Methods Appl. 71, 418–426 (2009)
Li, S.B., Wu, H.L., Zhou, X.X., Wang, T.T., Zhang, W.: Theoretical and experimental studies of global dynamics for a class of bistable nonlinear impact oscillators with bilateral rigid constraints. Int. J. Non-Linear Mech. 133, 103720 (2021)
Cao, Q.J., Wiercigroch, M., Pavlovskaia, E.E., Thompson, J.M.T., Grebogi, C.: Piecewise linear approach to an archetypal oscillator for smooth and discontinuous dynamics. Philos. Trans. R. Soc. 366, 635–652 (2008)
Li, S.B., Zhang, W., Hao, Y.X.: Melnikov-type method for a class of discontinuous planar systems and applications. Int. J. Bifurcat. Chaos 24, 1450022 (2014)
Li, S.B., Shen, C., Zhang, W., Hao, Y.X.: Homoclinic bifurcations and chaotic dynamics for a piecewise linear system under a periodic excitation and a viscous damping. Nonlinear Dyn. 79, 2395–2406 (2015)
Castro, J., Alvarez, J.: Melnikov-type chaos of planar systems with two discontinuities. Int. J. Bifurc. Chaos 25, 1550027 (2015)
Tian, R.L., Zhou, Y.F., Zhang, B.L., Yang, X.W.: Chaotic threshold for a class of impulsive differential system. Nonlinear Dyn. 83, 2229–2240 (2016)
Meucci, R., Gadomski, W., Ciofini, M., Arecchi, F.T.: Experimental control of chaos by means of weak parametric perturbations. Phys. Rev. E 49, R2528-2531 (1994)
Qu, Z.L., Hu, G., Yang, G.J., Qin, G.R.: Phase effect in taming nonautonomous chaos by weak harmonic perturbations. Phys. Rev. Lett. 74, 1736–1739 (1995)
Chacón, R.: Melnikov method approach to control of homoclinic/heteroclinic chaos by weak harmonic excitations. Phil. Trans. R. Soc. A 364, 2335–2351 (2006)
Ince, E.L.: Ordinary Differential Equations. Dover Publications, New York (1956)
Jackson, E.A.: Perspectives of Nonlinear Dynamics. Cambridge University Press, Cambridge (1991)
Martínez, P.J., Chacón, R.: Impulse-induced optimum signal amplification in scale-free networks. Phys. Rev. E 93, 042311 (2016)
Chacón, R.: Control of Homoclinic Chaos by Weak Periodic Perturbations. World Scientific, Singapore (2005)
Chacón, R.: Optimal control of wave-packet localization in driven two-level systems and curved photonic lattices: a unified view. Phys. Rev. A 85, 013813 (2012)
Chacón, R., Palmero, F., Cuevas-Maraver, J.: Impulse-induced localized control of chaos in starlike networks. Phys. Rev. E 93, 062210 (2016)
Martínez, P.J., Euzzor, S., Gallas, J.A.C., Meucci, R., Chacón, R.: Identification of minimal parameters for optimal suppression of chaos in dissipative driven systems. Sci. Rep. 7, 17988 (2017)
Palmero, F., Chacón, R.: Suppressing chaos in damped driven systems by non-harmonic excitations: experimental robustness against potential’s mismatches. Nonlinear Dyn. 108, 2643–2654 (2022)
Melnikov, V.K.: On the stability of the center for time periodic perturbations. Trans. Mosc. Math. Soc. 12, 1–57 (1963)
Guckenheimer, J., Holmes, P.: Nonlinear Oscillations. Dynamical Systems and Bifurcations of Vector Fields. Springer, New York (1983)
Wiggins, S.: Global Bifurcations and Chaos-Analytical Methods. Springer, New York (1988)
Lima, R., Pettini, M.: Suppression of chaos by resonant parametric perturbations. Phys. Rev. A 41, 726 (1990)
Braiman, Y., Goldhirsch, I.: Taming chaotic dynamics with weak periodic perturbations. Phys. Rev. Lett. 66, 2545–2548 (1991)
Chacón, R., Díaz Bejarano, J.: Routes to suppressing chaos by weak periodic perturbations. Phys. Rev. Lett. 71, 3103–3106 (1993)
Rajasekar, S.: Controlling of chaos by weak periodic perturbations in Duffing-van der Pol oscillator. Pramana 41, 295–309 (1993)
Lenci, S., Rega, G.: Optimal control of nonregular dynamics in a Duffing oscillator. Nonlinear Dyn. 33, 71–86 (2003)
Lenci, S., Rega, G.: Optimal control of homoclinic bifurcation: theoretical treatment and practical reduction of safe basin erosion in the Helmholtz oscillator. J. Vib. Control 9, 281–315 (2003)
Lenci, S., Rega, G.: Optimal numerical control of single-well to cross-well chaos transition in mechanical systems. Chaos, Solitons Fractals 15, 173–186 (2003)
Lenci, S., Rega, G.: Global optimal control and system-dependent solutions in the hardening Helmholtz-Duffing oscillator. Chaos, Solitons Fractals 21, 1031–1046 (2004)
Lenci, S., Rega, G.: A unified control framework of the non-regular dynamics of mechanical oscillators. J. Sound Vib. 278, 1051–1080 (2004)
Leung, A.Y.T., Liu, Z.R.: Suppressing chaos for some nonlinear oscillators. Int. J. Bifur. Chaos 14, 1455–1465 (2004)
Leung, A.Y.T., Liu, Z.R.: Some new methods to suppress chaos for a kind of nonlinear oscillator. Int. J. Bifur. Chaos 14, 2955–2961 (2004)
Yang, J., Jing, Z.: Controlling chaos in a pendulum equation with ultra-subharmonic resonances. Chaos, Solitons Fractals 42, 1214–1226 (2009)
Jimenez-Triana, A., Tang, W.K.S., Chen, G., Gauthier, A.: Chaos control in Duffing system using impulsive parametric perturbations. IEEE Trans. Circuits Syst. II Express Briefs 57, 305–309 (2010)
Chen, X.W., Jing, Z.J., Fu, X.L.: Chaos control in a pendulum system with excitations and phase shift. Nonlinear Dyn. 78, 317–327 (2014)
Du, L., Zhao, Y.P., Lei, Y.M., Hu, J., Yue, X.L.: Suppression of chaos in a generalized Duffing oscillator with fractional-order deflection. Nonlinear Dyn. 92, 1921–1933 (2018)
Chacón, R., Miralles, J.J., Martínez, J.A., Balibrea, F.: Taming chaos in damped driven systems by incommensurate excitations. Commun. Nonlinear Sci. Numer. Simulat. 73, 307–318 (2019)
Lenci, S., Rega, G.: A procedure for reducing the chaotic response region in an impact mechanical system. Nonlinear Dyn. 15, 391–409 (1998)
Lenci, S., Rega, G.: Controlling nonlinear dynamics in a two-well impact system. I: attractors and bifurcation scenario under symmetric excitations. Int. J. Bifur. Chaos 8, 2387–2407 (1998)
Lenci, S., Rega, G.: Controlling nonlinear dynamics in a two-well impact system . II: attractors and bifurcation scenario under unsymmetric optimal excitation. Int. J. Bifur. Chaos 8, 2409–2424 (1998)
Lenci, S., Rega, G.: Numerical control of impact dynamics of inverted pendulum through optimal feedback strategies. J. Sound Vib. 236, 505–527 (2000)
Lenci, S., Rega, G.: Periodic solutions and bifurcations in an impact inverted pendulum under impulsive excitation. Chaos, Solitons Fractals 11, 2453–2472 (2000)
Kunze, M.: Non-smooth Dynamical Systems. Springer, Berlin (2000)
Kukučka, P.: Melnikov method for discontinuous planar sytems. Nonlinear Anal. 66, 2698–2719 (2007)
Shi, L., Zou, Y., Küpper, T.: Melnikov method and detection of chaos for non-smooth systems. Acta Math. Appl. Sin. Engl. Ser. 29, 881–896 (2013)
Battelli, F., Fečkan, M.: Homoclinic trajectories in discontinuous systems. J. Dyn. Differ. Equ. 20, 337–376 (2008)
Battelli, F., Fečkan, M.: Bifurcation and chaos near sliding homoclinics. J. Differ. Equ. 248, 2227–2262 (2010)
Battelli, F., Fečkan, M.: Nonsmooth homoclinic orbits, Melnikov functions and chaos in discontinuous systems. Phys. D 241, 1962–1975 (2012)
Li, S.B., Ma, W.S., Zhang, W., Hao, Y.X.: Melnikov method for a class of planar hybrid piecewise-smooth systems. Int. J. Bifurc. Chaos 26, 1650030 (2016)
Li, S.B., Gong, X.J., Zhang, W., Hao, Y.X.: The Melnikov method for detecting chaotic dynamics in a planar hybrid piecewise-smooth system with a switching Manifold. Nonlinear Dyn. 89, 939–953 (2017)
Li, S.B., Zhang, W.: Melnikov Method and Its Applications of Global Dynamics for Plannar Non-Smooth Systems. Science Press, Beijing (2022)
Li, H.Q., Liao, X.F., Huang, J.J., Chen, G., Dong, Z.Y., Huang, T.W.: Diverting homoclinic chaos in a class of piecewise smooth oscillators to stable periodic orbits using small parametrical perturbations. Neurocomputing 149, 1587–1595 (2015)
Li, S.B., Ma, X.X., Bian, X.L., Lai, S.K., Zhang, W.: Suppressing homoclinic chaos for a weak periodically excited non-smooth oscillator. Nonlinear Dyn. 99, 1621–1642 (2020)
Li, S.B., Chen, J.Z., Kou, L.Y.: Suppressing homoclinic chaos for vibro-impact oscillators. Int. J. Bifurc. Chaos 32, 2250227 (2022)
Chacón, R., Uleysky, M.Y., Makarov, D.: Universal chaotic layer width in space-periodic Hamiltonian systems under adiabatic ac time-periodic forces. Europhys. Lett. 90, 40003 (2010)
Wei, M.-D., Hsu, C.-C.: Numerical study of nonlinear dynamics in a pump-modulation Nd:YVO\(_{4}\) laser with humped modulation profile. Opt. Commun. 285, 1366 (2012)
Cuevas-Maraver, J., Chacón, R., Palmero, F.: Impulse-induced generation of stationary and moving discrete breathers in nonlinear oscillator networks. Phys. Rev. E 94, 062206 (2016)
Chacón, R., Martínez, P.J., Binder, P.-M.: Bouncing states of a droplet on a liquid surface under generalized forcing. Phys. Rev. E 98, 042215 (2018)
Chacón, R., Martínez, J.A., Miralles, J.J.: Impulse-induced optimum control of escape from a metastable state by periodic secondary excitations. Phys. Rev. E 85, 066207 (2012)
Armitage, J.V., Eberlein, W.F.: Elliptic Functions. Cambridge University Press, Cambridge (2006)
Byrd, P.F., Friedman, M.D.: Handbook of Elliptic Integrals for Engineers and Scientists. Springer-Verlag, Berlin (1971)
Chacón, R.: Relative effectiveness of weak periodic excitations in suppressing homoclinic/heteroclinic chaos. Eur. Phys. J. B 30, 207–210 (2002)
Jin, L., Lu, Q.S., Twizell, E.H.: A method for calculating the spectrum of Lyapunov exponents by local maps in nonsmooth impact-vibrating systems. J. Sound Vib. 298, 1019–1033 (2006)
Acknowledgements
The authors gratefully acknowledge the support of the National Natural Science Foundation of China (NNSFC) through Grant Nos. 12172376, the Fundamental Research Funds for the Central Universities of Civil Aviation University of China through Grant No. 3122019144, the Postgraduate Scientific Research and Innovation Project of Civil Aviation University of China through Grant No. 2023YJSKC06008.
Funding
This study was founded by the National Natural Science Foundation of China through Grant Nos. 12172376, the Fundamental Research Funds for the Central Universities of Civil Aviation University of China through Grant No. 3122019144, the Postgraduate Scientific Research and Innovation Project of Civil Aviation University of China through Grant No. 2023YJSKC06008.
Author information
Authors and Affiliations
Contributions
SL: Conceptualization, methodology, reviewing, validation, supervision. RX: writing- original draft preparation, visualization, software, reviewing and editing. LK: validation, reviewing, supervision. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
The Hamiltonian equation of system (12) is
Let \(H\left( x,y\right) \)=\(H\left( 0,0\right) =0\), and get
which is equivalent to
The calculation process of the Melnikov function Eq. (14) is as follows:
where \(\Omega _{n}=\left( 2n+1\right) \Omega \).
Mark that
It is easy to obtain
Since
\(I_{21}\left( \Omega \right) \) can be reformed as
Note that
i.e.
which means
Substituting Eq. (A.6) into Eq. (A.5), yields
Similarly, get
Then the expression of \(I_{2}\left( \Omega \right) \) can be obtained as follows:
Let
so \(I_{2}\left( \Omega \right) =I_{3}\left( \Omega \right) \sin \left( \Omega \tau _{0}\right) \).
Since
\(I_{41}\left( \Omega _{n}\right) \) can be reformed as
Similarly, get
Then the expression of \(I_{4}\left( \Omega _{n}\right) \) can be obtained as follows:
Let
so \(I_{4}\left( \Omega _{n}\right) =I_{5}\left( \Omega _{n}\right) \cos \left( \Omega _{n}\tau _{0}+\left( 2n+1\right) \varphi \right) \).
Thus we obtain the Melnikov function Eq. (14) is as follows:
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Li, S., Xu, R. & Kou, L. Suppressing homoclinic chaos for a class of vibro-impact oscillators by non-harmonic periodic excitations. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-09649-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11071-024-09649-x