Suppressing chaos in damped driven systems by non-harmonic excitations: experimental robustness against potential’s mismatches

Abstract

The robustness of a chaos-suppressing scenario against potential mismatches is experimentally studied through the universal model of a damped, harmonically driven two-well Duffing oscillator subject to non-harmonic chaos-suppressing excitations. We consider a second order analogous electrical circuit having an extremely simple two-well potential that differs from that of the standard two-well Duffing model, and compare the main theoretical predictions regarding the chaos-suppressing scenario from the latter with experimental results from the former. Our experimental results prove the high robustness of the chaos-suppressing scenario against potential mismatches regardless of the (constant) values of the remaining parameters. Specifically, the predictions of an inverse dependence of the regularization area in the control parameter plane on the impulse of the chaos-suppressing excitation as well as of a minimal effective amplitude of the chaos-suppressing excitation when the impulse transmitted is maximum were experimentally confirmed.

1 Introduction

The problem of taming chaos of general (nonlinear) systems appears in many scientific and technological fields, including neuroscience [1], solid-state lasers [2], fluids [3], and discharge plasmas [4], among many other. This interest has resulted in a vast literature [5,6,7,8,9], including experimental investigations of chaos suppression [10,11,12,13,14,15]. One of the most effective suppressory methods in the context of dissipative non-autonomous systems is to apply judiciously chosen periodic excitations [16,17,18,19,20] while it is readily experimentally applicable [1, 2, 11,12,13, 15, 20,21,22,23,24,25]. Furthermore, the use of Melnikov analysis (MA) techniques has allowed the development of a theoretical approach to chaos suppression in damped driven systems, and which involves adding periodic chaos-suppressing (CS) excitations [26]. This MA-based approach has been shown to be reliable in suppressing chaos in a Duffing oscillator by a fine choice of the shape of the external periodic excitation [27], a generalized Duffing oscillator with fractional-order deflection [28], coupled arrays of damped, periodically forced, nonlinear oscillators [29, 30], as well as in starlike networks of dissipative nonlinear oscillators [31].

Traditionally, sinusoidal functions have been typically employed as representative of the periodic excitations involved (one chaos-inducing (CI) and the other CS) in the suppressory scenario (SS). While this choice is both mathematically and experimentally convenient, it imposes, however, a radical and unprofitable limitation in the SS, restricting thus its possible scope and applications. Thus, to properly probe and take advantage of the physics of the SS, one should consider CS excitations presenting generic characteristics of periodic excitations which are the output of nonlinear systems, i.e., those excitations generally represented by Fourier series—not just by a single harmonic term. Thus, the effect of the waveform of the CS excitations on the SS (once its amplitude and period are fixed) becomes a significant problem given the existence of an infinity of different waveforms.

In the present work, we provide experimental and analytical evidence that for a generic CS excitation f(t) having equidistant zeros, the impulse transmitted by the excitation over a half-period (hereafter referred to as simply the excitation’s impulse),

$$\begin{aligned} I\equiv \left| \int _{0}^{T/2}f(t){\mathrm {d}}t\right| , \end{aligned}$$

(1)

is a relevant quantity that characterizes the effectiveness of such CS excitation. Here, T is the period and I a quantity integrating the conjoint effects of the excitation’s amplitude, period, and waveform. Additionally, we explore the robustness of the SS against potential mismatches through the universal model of a damped, harmonically driven two-well Duffing oscillator by considering non-harmonic (elliptic) CS excitations. We compare the predictions from this theoretical model with experimental results from a second order analogue electrical circuit having an extremely simple two-well potential, which is similar but not identical to that of the two-well Duffing oscillator. The importance of the excitation’s impulse has been previously confirmed in different physical contexts, such as space-periodic Hamiltonian systems [32], laser systems [33], directed transport by symmetry breaking [34,35,36,37,38], oscillator networks [39], scale-free networks of signaling devices [40], control of wave-packet localization [41], suppression of chaos in dissipative driven systems [25], and bouncing droplets [42].

The rest of the paper is organized as follows. We study the effect of the CS excitation’s impulse by generalizing the standard sinusoidal CS excitation to a family of periodic functions which are related to the Jacobian elliptic functions [43] in Sect. 2, along with the aforementioned model that describes the SS. That section also describes the MA-based analytical predictions for the dissipative Duffing oscillator subject to a harmonic CI excitation and a non-harmonic (elliptic) CS excitation which satisfy a resonance condition with the primary CI excitation. Section 3 compares the theoretical predictions deduced in Sect. 2 with experimental results from a second order analogue electrical circuit describing the damped driven Duffing oscillator but having an extremely simple two-well potential, while some conclusions for the main findings of our work are presented in Sect. 4.

2 Theoretical approach

We shall investigate a simple and universal model for spatially bounded chaos in damped driven systems: a perturbed two-well Duffing oscillator described by the equation

$$\begin{aligned} \overset{..}{x}-x+\beta x^{3}=-\delta \overset{.}{x}+\gamma \sin (\omega t)+\gamma \eta f(t), \end{aligned}$$

(2)

where $T\equiv 2\pi /\omega$ and $\gamma$ are the period and amplitude, respectively, of the CI excitation, $\beta >0$, $\eta >0$ is an amplitude factor, while f(t) is a T-periodic CS excitation which is described below [cf. Eq. (3)], i.e., we shall concentrate on the case of the main resonance between the two excitations involved for the sake of effectiveness [7]. It is also assumed that the Duffing oscillator presents a chaotic attractor in the absence of any CS excitation $\left( \eta =0\right)$ and satisfies the MA requirements, i.e., the excitation and dissipation terms are small-amplitude perturbations $\left( 0<\delta ,\gamma ,\gamma \eta \ll 1\right)$ of the underlying conservative system $\overset{..}{x}=x-\beta x^{3}$ (see [44, 45] for the general background).

2.1 Chaos-suppressing excitation

Here, we consider the elliptic CS excitation

$$\begin{aligned} f(t)=N{\text {*}}{sn}\left( 4Kt/T+\Phi \right) {\text {*}}{dn}\left( 4Kt/T+\Phi \right) , \end{aligned}$$

(3)

where ${\text {*}}{sn}\left( \cdot \right) \equiv {\text {*}}{sn}\left( \cdot ;m\right)$ and ${\text {*}}{dn}\left( \cdot \right) \equiv {\text {*}}{dn}\left( \cdot ;m\right)$ are Jacobian elliptic functions of parameter m, $K\equiv K(m)$ is the complete elliptic integral of the first kind [43], $\Phi =\Phi \left( m,\varphi \right) \equiv 2K(m)\varphi /\pi$, $\varphi \in \left[ 0,2\pi \right]$, $T\equiv 2\pi /\omega$, and

$$\begin{aligned} N=N(m)\equiv \left[ a+b\left( 1+\exp \left\{ \frac{m-c}{d}\right\} \right) ^{-1}\right] ^{-1}, \end{aligned}$$

(4)

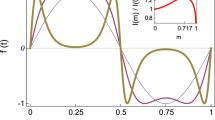
is a normalization function ($a\equiv 0.43932,b\equiv 0.69796,c\equiv 0.3727,d\equiv 0.26883$) which is introduced so that the elliptic CS excitation has the same period, T, and amplitude, 1, for any waveform (i.e., $\forall m\in \left[ 0,1\right]$; see Fig. 1, top panel). If $m=0$, then $f\left( t\right) _{m=0}=\sin \left( 2\pi t/T+\varphi \right)$, i.e., one recovers the standard case of a sinusoidal CS excitation, while for the limiting value $m=1$ the excitation vanishes. The effect of renormalization of the elliptic arguments is apparent: with T constant, solely the excitation’s impulse is varied by increasing the shape parameter m from 0 to 1. Observe that, as a function of the shape parameter m, the impulse transmitted by the CS excitation per unit of amplitude and unit of period

$$\begin{aligned} I=I(m)\equiv \frac{N\left( m\right) }{2K\left( m\right) } \end{aligned}$$

(5)

presents a single maximum at $m=m_{\max }^\mathrm{impulse}\simeq 0.717$ (see Fig. 1, bottom panel).

Fig. 1

Top: Chaos-suppressing T-periodic excitation f(t) vs t/T [Eqs. (3) and (4)] for three values of the shape parameter: $m=0$ (sinusoidal pulse, thin line), $m=0.717\simeq m_{\max }^\mathrm{impulse}$ (nearly square-wave pulse, regular line), and $m=0.9995$ (double-humped pulse, thick line). Bottom: Normalized first Fourier coefficient $a_{0}(m)/a_{0}(m=0)$ [Eq. (7), solid line] and CS excitation’s impulse $I(m)/I(m=0)\equiv \pi N(m)/(2K(m))$ [Eq. (5), dashed line] vs shape parameter m. We can see that the respective single maxima occur at very close values of the shape parameter: $m_{\max }\left( n=0\right) \simeq 0.642$ and $m_{\max }^\mathrm{impulse}\simeq 0.717$, respectively. (For interpretation of the colors in the figure(s), the reader is referred to the web version of this article)

The Fourier expansion of the elliptic CS excitation [Eq. (3)] reads

$$\begin{aligned} f(t)=\sum _{n=0}^{\infty }a_{n}(m)\sin \left[ \left( 2n+1\right) \left( \omega t+\varphi \right) \right] , \end{aligned}$$

(6)

where

$$\begin{aligned}&a_{n}(m)\equiv \frac{\pi ^{2}N(m)(n+\frac{1}{2})}{\sqrt{m}K^{2}(m)}\nonumber \\&\quad \qquad {\text {sech}}\left[ \frac{(n+\frac{1}{2})\pi K(1-m)}{K(m)}\right] . \end{aligned}$$

(7)

The Fourier coefficients $a_{n}(m)$ satisfy the following properties: (i) $a_{n}(m)$ exhibits a single maximum at $m=m_{\max }\left( n\right)$ such that $m_{\max }\left( n+1\right) >m_{\max }\left( n\right)$, $n=0,1,...$, (ii) $\lim _{m\rightarrow 1}a_{n}(m)=0$, (iii) the normalized functions $I(m,T)/I(m=0,T)\equiv \pi N(m)/(2K(m))$ and $a_{0}(m)/a_{0}(m=0)$ present, as functions of m, similar behaviors while their maxima verify that $m_{\max }^\mathrm{impulse}\simeq 0.717$ is very close to $m_{\max }\left( n=0\right) \simeq 0.65$ (see Fig. 1), and (iv) the Fourier expansion [Eq. (6)] is rapidly convergent over a wide range of values of the shape parameter. The following remarks may now be in order. First, regarding experiments, we considered the entire Fourier expansion of the elliptic CS excitation in order to obtain useful information concerning the effectiveness of the approximations used in the theoretical analysis as well as of the robustness of the SS. Second, regarding analytical estimates, property (iii) is relevant in the sense that it allows us to obtain a useful effective estimate of the chaotic threshold in the $\varphi -\eta$ control plane from MA by solely retaining the first harmonic of the Fourier expansion [Eq. (6)]:

$$\begin{aligned} f(t)\approx a_{0}(m)\sin \left( \omega t+\varphi \right) . \end{aligned}$$

(8)

2.2 Chaotic threshold from Melnikov analysis

The essential point of MA is the introduction of a function, the so-called Melnikov function (MF), $M\left( t_{0}\right)$, which provides a measure of the distance between the perturbed stable and unstable manifolds in the Poincaré section at $t_{0}$. If the Melnikov function presents a simple zero $\left( {\mathrm {d}}M/{\mathrm {d}}t_{0}\ne 0\right)$, the manifolds intersect transversally and chaotic instabilities result. From the Smale–Birkhoff theorem [44], the presence of such intersecting orbits implies that the Poincaré map has an invariant hyperbolic set: a Smale horseshoe, which is a hallmark of chaos. Regarding Eq. (2), note that keeping with the assumption of the MA, it is assumed that one can write $\delta =\varepsilon \delta ^{*} ,\gamma =\varepsilon \gamma ^{*},\gamma \eta =\varepsilon \gamma ^{*}\eta ^{*}$ where $\delta ^{*},\gamma ^{*},\eta ^{*}$ are of order one while $0<\varepsilon \ll 1$. After applying MA to Eq. (2), one straightforwardly obtains the MF:

$$\begin{aligned} M^{\pm }\left( t_{0}\right)&=-D\mp A\cos \left( \omega t_{0}\right) \mp \pi \gamma \eta \sqrt{\frac{2}{\beta }}\nonumber \\&\quad \times \sum _{n=0}^{\infty }a_{n}\left( m\right) b_{n}(\omega )\cos \left[ \Omega _{n}t_{0}+\left( 2n+1\right) \varphi \right] \end{aligned}$$

(9)

with $D\equiv 4\delta /3\beta$, $\Omega _{n}\equiv (2n+1)\omega$, $A\equiv \pi \gamma \omega \sqrt{2/\beta }{\text {sech}}(\pi \omega /2),$ $b_{n} (\omega )\equiv \Omega _{n}{\text {sech}}\left( \pi \Omega _{n}/2\right)$, and where the coefficients $a_{n}\left( m\right)$ are given by Eq. (7), while the negative (positive) sign refers to the left (right) homoclinic orbit of the underlying conservative Duffing oscillator $\left( \delta =\gamma =0\right)$:

$$\begin{aligned} x_{0,\pm }\left( t\right)&=\pm \sqrt{\frac{2}{\beta }}{\text {sech}} \left( t\right) , \end{aligned}$$

(10)

$$\begin{aligned} \overset{.}{x}_{0,\pm }\left( t\right)&=\mp \sqrt{\frac{2}{\beta } }{\text {sech}}\left( t\right) \tanh \left( t\right) . \end{aligned}$$

(11)

Let us assume that, in the absence of any CS excitation $\left( \eta =0\right)$, the damped driven two-well Duffing oscillator [Eq. (2)] presents chaotic behavior for which the respective MF,

$$\begin{aligned} M_{0}^{\pm }\left( t_{0}\right) \equiv -D\mp A\cos \left( \omega t_{0}\right) , \end{aligned}$$

(12)

has simple zeros, i.e., $D\leqslant A$ or

$$\begin{aligned} \gamma \geqslant \gamma _{th}\equiv \frac{2\sqrt{2}\delta \cosh \left( \pi \omega /2\right) }{3\pi \sqrt{\beta }\omega }, \end{aligned}$$

(13)

where the equal sign corresponds to the case of tangency between the stable and unstable manifolds [45]. If we now let the CS excitation act on the Duffing oscillator such that $B^{*}\leqslant A-D$, with

$$\begin{aligned} B^{*}&\equiv \pi \gamma \eta \sqrt{\frac{2}{\beta }}\times \\&\max _{t_{0}}\left\{ \sum _{n=0}^{\infty }a_{n}\left( m\right) b_{n} (\omega )\cos \left[ \Omega _{n}t_{0}+\left( 2n+1\right) \varphi \right] \right\} ,\nonumber \end{aligned}$$

(14)

then this relationship represents a sufficient condition for $M^{\pm }\left( t_{0}\right)$ to change sign at some $t_{0}$. Thus, a necessary condition for $M^{\pm }\left( t_{0}\right)$ to always have the same sign is

$$\begin{aligned} B^{*}>A-D\equiv B_{\min }. \end{aligned}$$

(15)

Since $a_{n}\left( m\right)>0,b_{n}(\omega )>0,n=0,1,2,...$, one straightforwardly obtains

$$\begin{aligned} B^{*}\leqslant \pi \gamma \eta \sqrt{\frac{2}{\beta }}\sum _{n=0}^{\infty } a_{n}\left( m\right) b_{n}(\omega ), \end{aligned}$$

(16)

and hence,

$$\begin{aligned} \eta&>\eta _{\min }\equiv \left( 1-\frac{D}{A}\right) R, \end{aligned}$$

(17)

$$\begin{aligned} R&\equiv \frac{\omega {\text {sech}}\left( \pi \omega /2\right) }{\sum _{n=0}^{\infty }a_{n}\left( m\right) b_{n}\left( \omega \right) }. \end{aligned}$$

(18)

Note that Eq. (17) provides a lower threshold for the amplitude of the CS excitation. Similarly, an upper threshold is obtained by imposing the condition that the CS excitation may not enhance the initial chaotic state (i.e., it does not increase the (initial) gap from the homoclinic tangency condition),

$$\begin{aligned} B^{*}\leqslant \pi \gamma \eta \sqrt{\frac{2}{\beta }}\sum _{n=0}^{\infty } a_{n}\left( m\right) b_{n}\left( \omega \right) <A+D\equiv B_{\max }, \end{aligned}$$

(19)

and hence,

$$\begin{aligned} \eta <\eta _{\max }\equiv \left( 1+\frac{D}{A}\right) R, \end{aligned}$$

(20)

which is a necessary condition for $M^{\pm }\left( t_{0}\right)$ to always have the same sign. Thus, the suitable (suppressory) amplitudes of the CS excitation must satisfy

$$\begin{aligned} \eta _{\min }<\eta <\eta _{\max }, \end{aligned}$$

(21)

while the width of the range of suitable amplitudes reads

$$\begin{aligned} \Delta \eta \equiv \eta _{\max }-\eta _{\min }=\frac{8\delta }{3\pi \gamma \sqrt{2\beta }\sum _{n=0}^{\infty }a_{n}\left( m\right) b_{n}\left( \omega \right) }. \end{aligned}$$

(22)

One finds that both the threshold amplitudes $\eta _{\min },\eta _{\max }$ and the width of the range of suitable amplitudes $\Delta \eta$ [Eq. (22)] present a single minimum at $m=m_{\min }$ as the shape parameter m is increased from 0 to 1 due to the dependence of the function R on the shape parameter (see Figs. 2 and 3). Note that this minimum $m_{\min }\equiv m_{\min }(T)$ is very near $m_{\max }^\mathrm{impulse}\simeq 0.717$ over a wide range of periods. However, one should not expect an exact agreement between $m_{\min }$ and $m_{\max }^\mathrm{impulse}$ for all periods owing to the dependence of the chaotic threshold on the common excitation period (main resonance). Thus, the proximity of the values $m_{\min }\equiv m_{\min }(T)$ and $m_{\max }^\mathrm{impulse}\simeq 0.717$ means that ever lower amplitudes $\eta _{\min }$ can suppress chaos as the impulse transmitted by the CS excitation approaches its maximum value, whereas the corresponding suppressory ranges $\Delta \eta$ also decrease in the same way as $\eta _{\min }$ owing to the impulse-induced enhancement of the chaos-inducing effectiveness of the CS excitation. It should be emphasized that this dependence of $\eta _{\max } ,\eta _{\min },\Delta \eta$ on the impulse transmitted by the CS excitation constitutes a bona fide characteristic of the impulse-induced chaos-control scenario.

Fig. 2

Contour plot of the function $\Delta \eta \equiv \eta _{\max }-\eta _{\min }$ [Eq. (22)] vs shape parameter m and period T. System parameters: $\gamma =0.29,\delta =0.25,\beta =1$

Fig. 3

Upper threshold amplitude $\eta _{\max }$ [Eq. (20), dotted line], lower threshold amplitude $\eta _{\min }$ [Eq. (17), solid line], and difference $\Delta \eta \equiv \eta _{\max }-\eta _{\min }$ [Eq. (22), dashed line] vs shape parameter m. $T=2\pi$ and the remaining parameters as in Fig. 2

Regarding suitable values of the initial phase difference $\varphi$, note that $\varphi$ determines the relative phase between $M_{0}^{\pm }\left( t_{0}\right)$ and

$$\begin{aligned} \mp \pi \gamma \eta \sqrt{\frac{2}{\beta }}\sum _{n=0}^{\infty }a_{p}\left( m\right) b_{n}\left( \omega \right) \cos \left[ \Omega _{n}t_{0}+\left( 2n+1\right) \varphi \right] \end{aligned}$$

irrespective of the shape parameter value. We therefore conclude from previous theory [7] that a sufficient condition for $\eta _{\min }<\eta <\eta _{\max }$ to also be a sufficient condition for suppressing chaos is that $M_{0}^{\pm }\left( t_{0}\right)$ and

$$\begin{aligned}&\mp \pi \gamma \eta _{\min ,\max }\sqrt{\frac{2}{\beta }}\sum _{n=0}^{\infty } a_{n}\left( m\right) b_{n}\left( \omega \right) \\&\quad \cos \left[ \Omega _{n}t_{0}+\left( 2n+1\right) \varphi \right] \end{aligned}$$

are in opposition. This yields the optimum suppressory value

$$\begin{aligned} \varphi _{opt}\equiv \pi \end{aligned}$$

(23)

for all $m\in \left[ 0,1\right]$ in the sense that it allows the widest amplitude range for the elliptic CS excitation.

To obtain a useful analytical estimate of the boundaries of the regions in the $\varphi -\eta$ control plane where chaos is suppressed, we assume the first-harmonic approximation is given by Eq. (8) instead of the entire Fourier expansion [cf. Eqs. (6) and (7)] in the remainder of this subsection. Indeed, recall that the value $m_{\max }^\mathrm{impulse}\simeq 0.717$ at which the CS excitation’s impulse presents a single maximum is very close to the value $m=m_{\max }\left( n=0\right) \simeq 0.642$ where the amplitude $a_{0}\left( m\right)$ [cf. Eq. (7)] presents a single maximum (see Fig. 1, bottom panel). Thus, we apply MA to the effective MF

$$\begin{aligned}&M_\mathrm{eff}^{\pm }\left( t_{0}\right) \nonumber \\&\quad =-D\mp A\cos \left( \omega t_{0}\right) \mp B_{0}\cos \left( \omega t_{0}+\varphi \right) , \end{aligned}$$

(24)

$$\begin{aligned}&B_{0} \equiv \pi \gamma \eta \sqrt{\frac{2}{\beta }}a_{0}\left( m\right) b_{0}\left( \omega \right) , \end{aligned}$$

(25)

while the effectiveness of the first-harmonic approximation $\left( \eta >0\right)$ at suppressing chaos will be examined by considering for example the effective MF $M_\mathrm{eff}^{+}\left( t_{0}\right)$ (the analysis of $M_\mathrm{eff}^{-}\left( t_{0}\right)$ is similar and leads to the same conclusions). To this end, it is convenient to use the normalized MF $M_{n}^{+}\left( t_{0}\right) \equiv M_\mathrm{eff}^{+}\left( t_{0}\right) /D$ to write

$$\begin{aligned} M_{n}^{+}\left( t_{0}\right)&=-1-\left( R^{\prime }+R^{\prime \prime } \cos \varphi \right) \cos \left( \omega t_{0}\right) \nonumber \\&\qquad +R^{\prime \prime }\sin \varphi \sin \left( \omega t_{0}\right) \nonumber \\&\leqslant -1+\sqrt{\left( R^{\prime }+R^{\prime \prime }\cos \varphi \right) ^{2}+R^{\prime \prime 2}\sin ^{2}\varphi }, \end{aligned}$$

(26)

where $R^{\prime }\equiv A/D,R^{\prime \prime }\equiv B_{0}/D$. If one now lets the first-harmonic approximation act on the system so that

$$\begin{aligned} \left( R^{\prime }+R^{\prime \prime }\cos \varphi \right) ^{2}+R^{\prime \prime 2}\sin ^{2}\varphi \leqslant 1, \end{aligned}$$

(27)

this relation represents a sufficient condition for $M_{n}^{+}\left( t_{0}\right)$ to be negative (or null) for all $t_{0}$. The equal sign in Eq. (27) yields the boundary of the region in the $\varphi -\eta$ plane where chaos is suppressed:

$$\begin{aligned} \eta =\frac{1}{a_{0}\left( m\right) }\left[ -\cos \varphi \pm \sqrt{\frac{\gamma _{th}^{2}}{\gamma ^{2}}-\sin ^{2}\varphi }\right] , \end{aligned}$$

(28)

with $\gamma >\gamma _{th}$ [cf. Eq. (13)], and where the two signs before the square root correspond to the two branches of the boundary (see Fig. 4). The following remarks may now be in order.

Fig. 4

Boundary function [Eq. (28)] encircling the region where chaos is suppressed in the $\varphi -\eta$ control plane for four values of the shape parameter: $m=0$ (dashed line), $m=0.717\simeq m_{\max }^\mathrm{impulse}$ (solid line), $m=0.93$ (dotted line), and $m=0.95$ (thin solid line). System parameters as in Fig. 3

First, the boundary function [Eq. (28)] represents a loop encircling the single regularization region in the $\varphi -\eta$ plane which is symmetric with respect to the optimal suppressory value

$$\begin{aligned} \varphi _{opt}\equiv \pi , \end{aligned}$$

(29)

i.e., the value of the initial phase difference for which the range of suitable suppressory values of $\eta$ is maximum. As expected, it is the same suppressory value than that found in the exact case of representing the elliptic CS excitation by its entire Fourier expansion [cf. Eq. (23)]. Remarkably, one finds that the effective amplitude of the CS excitation is minimal when the impulse transmitted is maximum (cf. Fig. 4).

Second, the area, $A_{R}$, enclosed by the boundary function [Eq. (28)] is straightforwardly obtained from previous theory [7]:

$$\begin{aligned} A_{R}=\frac{16\delta }{3\sqrt{2\beta }\pi \omega \gamma a_{0}(m)}. \end{aligned}$$

(30)

Observe that one finds $A_{R}\rightarrow 0$ as $\delta \rightarrow 0$, which corresponds to the limiting Hamiltonian case, as expected. More importantly, the normalized regularization area

$$\begin{aligned} \frac{A_{R}(m)}{A_{R}(m=0)}=\frac{a_{0}(m=0)}{a_{0}(m)} \end{aligned}$$

(31)

presents, as a function of the shape parameter, a single minimum at the m value where $a_{0}(m)$ presents a single maximum (see Fig. 1, bottom panel): $m_{\max }\left( n=0\right) \simeq 0.642$, which is very close to $m_{\max }^\mathrm{impulse}\simeq 0.717$. This inverse dependence of the regularization area on the impulse transmitted by the CS excitation represents a genuine feature of the present impulse-induced chaos-control scenario. By lowering the impulse transmitted one obtains larger regularization areas in the $\varphi -\eta$ control plane, the price to be paid being the requirement of larger amplitudes (cf. Fig. 4).

Third, the regularization area shrinks as the ratio $\gamma _{th}/\gamma$ diminishes, which means that the impulse-induced chaos-control scenario is sensitive to the strength of the initial chaotic state in the sense of its degree of proximity to the threshold condition [cf. Eq. (13)].

3 Experimental results

To explore the robustness of the above SS against potential mismatches, we compared the theoretical predictions deduced in Sect. 2 and the experimental results arising from a second-order analogue electrical circuit having an extremely simple two-well potential which retains the main characteristics of a Duffing-like electric oscillator. We followed Ref. [46] to implement the electrical circuit shown in Fig. 5a, where $R_{1} =R_{2}=R_{3}=10$ k$\Omega$, $R=20$ $\Omega$, $L=19$ mH, and $C=500$ nF. We considered an operational amplifier of the LM741 type, while the diodes $D_{1}$ and $D_{2}$ are general-purpose silicon devices.

Fig. 5

a Experimental setup of the analogue implementation of the damped driven Duffing oscillator. b Potential corresponding to a standard Duffing oscillator described by Eq. (2) ($\beta =1$, solid line) and that corresponding to the oscillator simulated by the circuit shown in version (a) (dashed line). The quantities plotted are dimensionless

Fig. 6

Time series of the chaotic signal $V_{c}(t)$ for $\gamma =$ 0.5 V, $f=1.5$ kHz, and $\eta =0$

The dynamics of this electrical circuit is described by a nonlinear differential equation that is quite similar to Eq. (2), and where the tension at the capacitor, $V_{c}$, plays the role of variable x in Eq. (2) (see Fig. 5b).

To make our analogue experimental implementation consistent with Eq. (2), we applied a periodic external voltage V(t) as

$$\begin{aligned} V(t)=\gamma \sin (\omega t)+\gamma \eta f(t), \end{aligned}$$

(32)

where the CS excitation f(t) is given by Eq. (3), and monitored the tension $V_{c}$ with an oscilloscope to characterize the resulting dynamics. For each set of control parameter values, we have implemented the function V(t) by generating it numerically in a computer and sending it to a programmable arbitrary waveform generator.

Firstly, we studied the case of a pure sinusoidal excitation $\left( \eta =0\right)$ and observed both periodic and chaotic oscillations depending on the values of the parameters $\gamma$ and $\omega$. For example, by selecting the values of the parameters $\gamma =0.5$ V and $f=1.5$ kHz, the system displayed a steady chaotic behavior, as is shown in Fig. 6.

Fig. 7

Experimental steady states (capacitor voltage) of the electrical circuit shown in Fig. 5a in the $\varphi -\eta$ parameter plane for two values of the shape parameter: a $m=0$ and b $m=0.95$. Green (blank) regions correspond to chaotic (periodic) states. Labels (I) and (II) denote regions of periodic behavior mentioned in the text, while dashed lines indicate the boundaries of the main central regularized regions centered around the optimal initial phase $\varphi =\varphi _{opt}=\pi$. Fixed parameters: $\gamma =$ 0.5 V, $f=1.5$ kHz

Secondly, we explored the suppressory effectiveness of the CS excitation f(t) [cf. Eq. (3)] when the circuit exhibits steady chaos in the absence of any CS excitation $\left( \eta =0\right)$. We systematically measured $V_{c}(t)$ for different values of the control parameters $\eta$, m, and $\varphi$, while keeping the remaining parameters fixed. To determine whether an experimental time series $V_{c}(t)$ corresponds to a periodic or chaotic state, we calculated its largest Lyapunov exponent following the method described in Ref. [47]. We found both periodic and chaotic states in the control parameter space $\left\{ \eta ,m,\varphi \right\}$. Figures 7 and 8 show representative examples of the experimental results.

Fig. 8

Bifurcation diagrams of the capacitor voltage $V_{c}$ as a function of a the shape parameter m for $\eta =1.7$ V a, and b the factor amplitude $\eta$ for $m=0$. Fixed parameters: $\gamma =$ 0.5 V, $f=1.5$ kHz, $\varphi =\varphi _{opt}=\pi$

The following remarks may now be in order.

First, our experimental results confirmed that the single optimal value of the initial phase difference $\varphi$ which regularizes the initial chaotic dynamics $\left( \eta =0\right)$ corresponds to $\varphi =\varphi _{opt}=\pi$ [cf. Eq. (29); see Fig. 7].

Second, starting from a periodic state for a sinusoidal CS excitation $\left( m=0\right)$, Fig. 8a shows how the capacitor voltage $V_{c}$ reaches a chaotic attractor over a wide range of m values that is centered at $m\approx m_{\max }\left( n=0\right) \simeq 0.642$, which is very close to $m_{\max }^\mathrm{impulse}\simeq 0.717$. Note that this is coherent with the second remark in Sect. 2, i.e., with the inverse dependence of the regularization area in the $\varphi -\eta$ control plane on the CS excitation’s impulse. Figure 8b shows successive windows of regularization as the factor amplitude $\eta$ is increased from 0 and $\varphi =\varphi _{opt}\equiv \pi$. Clearly, these regularization windows correspond to the regularization regions between chaotic bands shown in Fig. 7a. One finds that period-1 attractors only appear inside the central region of the main regularization region predicted from MA (cf. Sect. 2), while period-3 attractors typically appear in the remaining regularization windows.

Third, although there exists a (residual) chaotic annular band within the main regularization region predicted from MA for each value of the shape parameter m (cf. Figs. 7a, b), the features of the boundaries of such experimental regularization regions are quite similar to those of the predicted boundary functions [cf. Eq. (28)] for any value of the shape parameter (compare Figs. 4 and 9).

Fig. 9

Experimental boundaries encircling the main regularization regions in the $\varphi -\eta$ control plane for the same four values of the shape parameter as in Fig. 4: $m=0,0.717,0.93,0.95$. Fixed parameters: $\gamma =$ 0.5 V, $f=1.5$ kHz

Fig. 10

a Experimental values of the factor amplitude $\eta _{\exp }^{c}$ (see the text) and b normalized area $S(m)/S(m=0)$ in the $\varphi -\eta$ control plane corresponding to chaotic states versus shape parameter m. Fixed parameters: $\gamma =$ 0.5 V and $f=1.5$ kHz

Fig. 11

Experimental values of the factor amplitude $\eta$ corresponding to $\eta _{\max }^{\prime }$ ($\Box$), $\eta _{\min }^{\prime }$ ($\circ$), and $\Delta \eta ^{\prime } =\eta _{\max }^{\prime }-\eta _{\min }^{\prime }$ (*) (see the text) vs shape parameter m corresponding to the bands denoted by a (I) and b (II) in Fig. 7. Fixed parameters: $\gamma =$ 0.5 V and $f=1.5$ kHz

Lastly, Fig. 10 shows the highest experimental value of the amplitude factor $\eta$ which allows chaotic behavior, $\eta _\mathrm{exp}^{c}$, inside the deepest chaotic band in the $\varphi -\eta$ control plane versus the shape parameter m. One sees that $\eta _\mathrm{exp}^{c}=\eta _\mathrm{exp}^{c}\left( m\right)$ presents the same behavior than the upper threshold amplitude $\eta _{\max }\left( m\right)$ [cf. Eq. (20)], the lower threshold amplitude $\eta _{\min }\left( m\right)$ [cf. Eq. (17)], and the difference $\Delta \eta \left( m\right) \equiv \eta _{\max }\left( m\right) -\eta _{\min }\left( m\right)$ [cf. Eq. (22)] as a function of the shape parameter (compare Figs. 3 and 10a). Figure 10b also shows the normalized area, $S(m)/S(m=0)$, of the region in the $\varphi -\eta$ control plane with $\eta \in [0,$ $\eta _{\exp }^{c}]$ and $\varphi \in [0,$ $2\pi ]$ corresponding to chaotic states as a function of m. Remarkably, one finds that $S(m)/S(m=0)$ presents the same behavior than the normalized regularization area $A_{R}(m)/A_{R}(m=0)$ [cf. Eq. (31)] as a function of m, i.e., an inverse dependence on the impulse transmitted by the CS excitation. Furthermore, Fig. 11 shows the experimental values of the highest values, $\eta _{\max }^{\prime }$, the lowest values, $\eta _{\min }^{\prime }$, and the differences $\Delta \eta ^{\prime }\equiv \eta _{\max }^{\prime }-\eta _{\min }^{\prime }$ which are associated with the regularization bands denoted by (I) and (II) in Fig. 7 as functions of m. Once again, one sees that such variables present the same behavior than the upper threshold amplitude $\eta _{\max }\left( m\right)$ [cf. Eq. (20)], the lower threshold amplitude $\eta _{\min }\left( m\right)$ [cf. Eq. (17)], and the difference $\Delta \eta \left( m\right) \equiv \eta _{\max }\left( m\right) -\eta _{\min }\left( m\right)$ [cf. Eq. (22)] as a function of the shape parameter (compare Figs. 3 and 11).

4 Conclusion

In summary, we have experimentally studied the robustness of a chaos-suppressing scenario against potential mismatches through the universal model of a damped, harmonically driven two-well Duffing oscillator subject to non-harmonic chaos-suppressing excitations. Analytical estimates were obtained from Melnikov analysis characterizing the dependence of the suppressory scenario on the amplitude, period, and waveform of the chaos-suppressing excitation as well as on the dissipation coefficient. Our experiments reasonably confirmed these theoretical predictions, thus revealing a remarkable robustness of the chaos-suppressing scenario against potential mismatches. Specifically, the predictions of an inverse dependence of the regularization area in the control parameter plane on the impulse transmitted by the chaos-suppressing excitation as well as of a minimal effective amplitude of the chaos-suppressing excitation when the impulse transmitted is maximum were experimentally confirmed. These two remarkable properties of the external chaos-suppressing excitation hold when it acts as a parametric excitation [25], thus suggesting their universal character.

Some interesting open problems remain. Among them, the authors are presently exploring the robustness of the present suppressory scenario in networks of damped driven Duffing-like oscillators where the effect of varying the impulse transmitted by the chaos-suppressing excitations acting on particular nodes is expected to depend strongly on their number and degree of connectivity.