Moving mass over a viscoelastic system: asymptotic behaviours and insights into nonlinear dynamics

Abstract

Moving masses are of interest in many applications of structural dynamics, soliciting in the last decades a vast debate in the scientific literature. However, despite the attention devoted to the subject, to the best of the authors’ knowledge, there is a lack of analysis about the fate of a movable mass when it rolls or slips with friction on a structure. With the aim of elucidating the dynamics of the simplest paradigm of this system and to investigate its asymptotic response, we make reference to a two-degree-of-freedom model made of an elastically vibrating carriage surmounted by a spherical mass, facing the problem both theoretically and experimentally. In case of linear systems, the analytical solutions and the laboratory tests performed on ad hoc constructed prototypes highlighted a counterintuitive asymptotic dynamics, here called binary: in the absence of friction at the interface of the bodies’ system, the mass holds its initial position or, if nonzero damping acts, at the end of the motion it is in a position that exactly recovers the initial relative distance carriage–sphere. While the first result might be somewhat obvious, the second appears rather surprising. Such a binary behaviour is also confirmed for a Duffing-like system, equipped with cubic springs, while it can be lost when non-smooth friction phenomena occur, as well as in the case of elastic springs restraining the motion of the sphere. The obtained analytical results and the numerical findings, also confirmed by experimental evidences, contribute to the basic understanding of the role played by the damping parameters governing the systems’ dynamics with respect to its asymptotic behaviour and could pave the way for designing active or passive vibration controllers of interest in engineering.

1 Introduction

Problems of dynamic actions that vary with position play a crucial role in several applications of structural dynamics and have been widely investigated in the literature for many decades [1,2,3,4,5,6,7,8,9,10]. The seminal book by Frýba [11] analyses the effects of moving loads on solids and structures, as strings, rigid-plastic beams, thin-walled beams and beams on elastic foundations, frames and arches, plates and elastic spaces. Such problems are typically studied in transportation engineering since structures, as bridges, railways and roadways, are subjected to moving loads often generated by vehicles, which move with constant or variable speeds along the structure and produce inertial effects due to their masses and trajectories. In addition, the speed of the vehicles and the flexibility of the main structure are of great importance due to dynamic interaction phenomena. Indeed, an accurate estimation of such loads is required and mandatory for a reliable design, since a structure subjected to moving loads exhibits deflection and stresses significantly higher than in the static case. However, the problem is not strictly confined to transportation engineering, being relevant to structures of interest to the everyday life, as parking garages and aircraft carriers, high-speed precision machining, magnetic disc drives and cables transporting materials, to name a few. The moving loads, where their inertial effects should be taken into account, are more precisely called moving masses [12]. In fact, as illustrated by Ting et al. [13], when the velocity of the sliding mass is not relatively small, a coupling between the two bodies occurs and the inertial effects cannot be referred to the two structural parts as standalone.

In facing planar moving load problems, both the directions of the load and its velocity are quite often assumed as relevant, thus leading to a bidirectional dynamics, where the interaction between the load and the deformability of the supporting body assumes a paramount importance. In this perspective, several papers [14,15,16,17,18,19] analyse the effect of a mass moving along a flexible Euler–Bernoulli supported beam, focusing on the influence of the mass ratio and the bending rigidity of the beam on the dynamic response of the overall system. Lee and Kim [20] provide an analytical and numerical method for getting a response of an elastically simply supported Timoshenko beam to a moving load. Considering the problem of the motion of a sphere on a flexible cable, Aristoff et al. [21], by combining experimental and theoretical investigations, demonstrate that the time taken by a sphere for descending along an elastic beam, the so-called elastochrone, exceeds that from the classical brachistochrone.

All the above-mentioned works assume that deformations and deflections remain small. To overcome this limitation, an upgrade of moving mass problems is provided by Zhao et al. [22], who develop a theory for large deformations based on Cosserat rod theory for studying the dynamics of mass-cable systems. The problems of taut strings carrying a movable mass [23] or travelled by a train of forces [24] are also addressed in the literature. Also, the noteworthy paradox of the discontinuity in the trajectory close to the end support exhibited by the solution of string vibration under a moving mass has attracted attention [25]. In [26] the problem is studied through a kinematically exact nonlinear model, in which the motion of the point mass in the direction of the string in the reference configuration, say horizontal direction, is firstly considered unknown, while a driving force is assigned in the same direction. By assuming that the dynamic tension and the mass of the string are negligible, the existence of a horizontal reactive force at the mass–string contact, preventing the mass to reach the right support, is highlighted. Further upgrades of the mentioned study are introduced in [27, 28].

In addition to the dynamic modelling and the response analysis of beams and strings subjected to a moving mass/load, the vibration control of these structures is another important issue that has received great attention [29,30,31,32,33]: several control algorithms have been proposed to suppress the vibration of the beam thanks to the inertial and dissipative effects induced by the moving mass sliding on the support. The inertial and dynamic effects derived by the motion of an added solid mass are also becoming of increasing interest in the field of fluid mechanics [34,35,36].

Several papers focus on moving loads problems characterised by unidirectional dynamics, where the load/mass does not interact with the deformability of the supporting structures, which can be assumed as rigid. In particular, there is growing interest in devices that can actively or passively control the dynamics of bodies: a carried mass moving on a rigid track may be used to reduce its dynamic amplification, as in the case of tuned mass dampers [37, 38], or the motion of a mass inside rigid boxes can excite the locomotion of the overall system, as in the case of capsule robots [39,40,41].

However, although so many moving masses/loads problems have been in-depth investigated, with different purposes and applications and by adopting increasingly refined models, to the best of the author’s knowledge, no research paper focuses on the asymptotic behaviour of the simplest “toy system” case of an elastically vibrating rigid support with a mass free to move on it. To fill this gap, this paper deals with the dynamics of such a paradigmatic two degree-of-freedom (2-DOF) system, which allows predicting two different asymptotic responses of the mass. In the absence of friction at the interface between the carriage and the mass, the latter holds its initial position. If nonzero damping acts, at the end of the motion the mass is in a position that exactly recovers the initial relative distance carriage–sphere. This behaviour, which we call binary, has been found analytically in Sect. 2.1, and also experimentally reproduced, through an ad hoc designed ad 3D printed set-up, for the first time in Sect. 2.2. Then, the effects of some nonlinearities on the binary asymptotic behaviour are discussed in Sect. 3 by considering either Duffing [42,43,44,45] or dry friction [46,47,48] terms. A further example is conceived by connecting the carriage to the moving mass through nonlinear elastic springs allowing tunable, pre-stretch induced stiffness in Sect. 4. Then some conclusions are reported in Sect. 5.

2 Binary dynamics of the simplest “toy system”: analytical and experimental results

2.1 Analytical solution for the linearly elastic system with moving mass

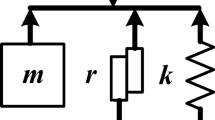
Let us consider a spherical mass moving on a sliding carriage, as shown in Fig. 1. In the hypothesis of small oscillations, the equations of the free vibration along the x direction are

$$\begin{aligned}&m_1\ddot{x}_1(t)+d\dot{x}_1(t)+k_1 x_1(t)\nonumber \\&\quad -c\left( \dot{x}_2(t)-\dot{x}_1(t)\right) =0, \end{aligned}$$

(1)

$$\begin{aligned}&m_2\ddot{x}_2(t)+c\left( \dot{x}_2(t)-\dot{x}_1(t)\right) =0, \end{aligned}$$

(2)

where $x_i,\,\dot{x}_i,\,\ddot{x}_i$ $i=\{1,2\}$ stand for displacement, velocity, acceleration, of carriage $(i=1)$ or sphere $(i=2)$ where the superimposed dot denotes the derivative with respect to time t. The masses of carriage and sphere are $m_1$ and $m_2,$ respectively; $k_1$ indicates the overall axial stiffness of the two springs anchored to the carriage; c and d are damping parameters.

Fig. 1

2-DOF model of a spherical mass moving on a sliding carriage

We emphasise that, in the first step, we assume that the dissipation-inducing terms, as dynamic friction at the interface between the spherical mass and the carriage or between the carriage wheels and the substrate, the air drag forces on the sphere and carriage and the damping induced by synergistic effects of air trapped into the helical springs and internal damping, and so on, are all represented as effective linear viscous damping. However, the orders of magnitude of the terms incorporated in the damping parameters can be significantly different. For instance, for a spherical steel mass moving with velocity v and having diameter $\phi ={0.03}\,{\hbox {m}},$ the air drag force, typically evaluated as $3\pi \mu _{a}v\phi$, with $\mu _a$ the air viscosity, is about 6 orders of magnitude lower than the rolling friction force, calculated as $2m_2g\mu _{s}/\phi$, being g acceleration of gravity and $\mu _{d}$ the dynamic friction coefficient, at the contact surface between the sphere and the vibrating carriage. These findings have been experimentally confirmed by ad hoc laboratory tests, which also allowed measuring the involved key parameters (see Sect. 2.2).

By setting $y_1(t)=\dot{x}_1(t)$ and $y_2(t)=\dot{x}_2(t),$ Eqs. (1)–(2) can be conveniently rearranged in matrix form as

$$\begin{aligned}{} & {} \begin{pmatrix} \dot{x}_1\\ \dot{x}_2\\ \dot{y}_1\\ \dot{y}_2 \end{pmatrix} = \begin{pmatrix} 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1\\ -k_1\,m_1^{-1}&{}0&{}-(c+d)\,m_1^{-1}&{}c\,m_1^{-1}\\ 0&{}0&{}c\,m_2^{-1}&{}-c\,m_2^{-1}\\ \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ y_1\\ y_2 \end{pmatrix},\nonumber \\ \end{aligned}$$

(3)

admitting the characteristic equation

$$\begin{aligned}{} & {} \eta \Bigg (m_1 m_2 \eta ^3 +\Bigg (d m_2 +c\left( m_1+m_2\right) \Bigg ) \eta ^2 \nonumber \\{} & {} \quad + (c d + k_1 m_2) \eta + k_1 c \Bigg )= 0, \end{aligned}$$

(4)

where, for ease of notation, the time dependence is implied.

Since Eq. (4) has a vanishing root, among the other three ones, at least one is real. Therefore, eigenvalues can be written in closed form by using Cardano’s solution [49]. For the range of parameters of interest, each eigenvalue has an algebraic multiplicity equal to 1,  and the problem is diagonalisable and characterised by a complete system of 4 eigenvectors. The general integral of the system, namely the vector $\textbf{y}(t)\equiv \left( x_1(t),x_2(t),y_1(t),y_2(t)\right) ^T,$ takes the form

$$\begin{aligned} \textbf{y}=c_1 \textbf{v}_1 +c_2 \textbf{v}_2 e^{\eta _2 t}+c_3 \textbf{v}_3 e^{\eta _3 t}+c_4 \textbf{v}_4 e^{\eta _4 t}, \end{aligned}$$

(5)

where $\textbf{v}_i,$ $i=\{1,\ldots ,4\},$ are the eigenvectors associated to the eigenvalues $\eta _i,$ and $c_i$ represent the constants of integration to be determined by imposing the initial conditions. Explicit expressions of eigenvalues and eigenvectors of Eq. (3) are reported in “Appendix A”.

To capture the key features of the response of the system as the parameters vary, we exploit the analytical solution and perform a sensitivity analysis through six representative examples (see Fig. 2), in which the parameters take nonnegative values and the initial conditions, with $\Delta x(0)$ the initial distance between the centres of gravity of carriage and sphere, are set as

$$\begin{aligned} \begin{aligned}&x_1(0)= {0.01}\,{\hbox {m}}, \\&x_2(0)=x_1(0) + \Delta x(0)={0.03}\,{\hbox {m}},\\&\dot{x}_1(0)=\dot{x}_2(0)= {0}\,{\hbox {m\, s}}^{-1}. \end{aligned} \end{aligned}$$

(6)

Fig. 2

Sensitivity analysis of the system made up of a spherical mass moving on a sliding carriage. In all graphics, but when null, the following parameters are assumed: $m_1={0.10}\,{\hbox {kg}}$, $m_2={0.04}\,{\hbox {kg}}$, $k_1={400}\,{\hbox {N\,m}}^{-1}$, $c={1}\,\hbox {N\,s\,m}^{-1}$, and $d=1$ or ${10}\,\hbox {N\,s\,m}^{-1}$

In Example A, $m_1<m_2$ and $c=d<d_{\text {crit}},$ being $d_{\text {crit}}=2\sqrt{m_1 k_1}$ the critical damping, thus leading to both the degrees of freedom showing harmonic damped responses (Fig. 2A).

In Example B, $m_1<m_2,$ $c<d$ and $d>d_{\text {crit}},$ and the response has overdamped behaviour on both the degrees of freedom (Fig. 2B).

More interestingly, Example C, where $m_1<m_2$ and $c>d=0,$ i.e. damping on the carriage is negligible, while mutual damping is present, both responses $x_1$ and $x_2$ are damped. By virtue of Eq. (2), we can substitute the term $-\,c(\dot{x}_2-\dot{x}_1)$ with $m_2\ddot{x}_2$ in Eq. (1), thus attaining $m_1\ddot{x}_1+k_1x_1=-\,m_2\ddot{x}_2,$ which, if compared with graphs shown in Fig. 2C, allows recognising that the force $-\,m_2\ddot{x}_2$ actually drives $x_1$ towards its rest position. This example shows that the moving mass exerts a damping action on the motion of the carriage. Despite an indirect damping is imparted on the carriage, the system in this case is different from classical tuned mass dampers, where typically the secondary mass is attached to the primary one through elastic constraints, modelled as springs [50]. Therefore, this system could represent the paradigm of a viscous tuned mass damper and it could pave the way for designing devices for the vibration control of interest in engineering.

Example D emphasises the damping role of a carried mass much larger than that of the carriage. Here, $m_1\approx 0$ and $c=d<d_{\text {crit}}$ lead to a response towards resting position without oscillation. Notice that to avoid division by zero, $m_1$ must be not null in Eq. (3), so that $m_1\approx 0$ in performed test stands for $m_1=10^{-80}\,{\hbox {kg}}.$

Furthermore, the most intriguing feature of responses, from A to D, as shown in Fig. 2, is that while the displacement $x_1$ (grey line) of the carriage invariably asymptotically approaches to 0,  the displacement $x_2$ of the sphere goes to $\Delta x(0).$ Indeed, chosen any reference point on the carriage, whatever is the initial displacement $x_1(0),$ the sphere, after the transient phase, reaches its rest position whose relative distance from the reference point will be equal to the initial relative distance $\Delta x(0),$ as if it remembered where it was at the beginning.

Fig. 3

Phase space plots for the carriage (top panels) and the sphere (bottom panels), by assuming $x_1(0)={0.01}\,{\hbox {m}}$ and $x_2(0)=x_1(0)+\Delta x(0)={0.03}\,{\hbox {m}}$, $m_1={0.10}\,{\hbox {kg}},\, m_2={0.04}\,{\hbox {kg}},\, k_1={400}\,{\hbox {N m}}^{-1},$ and $d={1}\,\hbox {N s m}^{-1}$. The damping parameter takes values $c={0}\,\hbox {N s m}^{-1}$ (left column panels) or $c={1}\,\hbox {N s m}^{-1}$ (right column panels)

We highlight that this interesting behaviour, computed in closed form by solving Eqs. (1)–(2) complemented with the initial conditions given by Eq. (6), is somehow unexpected and, to the best of authors’ knowledge, not reported in the scientific literature.

This behaviour changes abruptly for $c=0,$ c actually playing both the role of the coupling parameter between Eqs. (1)–(2) and that of a bifurcation parameter. Indeed, for $c=0,$ no interaction between the two bodies occurs and, for the initial conditions reported in Eq. (6), the sphere rests for any t,  which is an obvious consequence of the fact that, in such a case, $x_2(t)=x_2(0)+\dot{x}_2(0)t={0.03}\,{\hbox {m}}.$ In addition, we also emphasise that such a behaviour of the sphere is expected by physical intuition, that is even before observing that Eqs. (1)–(2) become mathematically uncoupled for $c=0.$

It is also interesting to observe that one expects two different behaviours also in case of two harmonic oscillators which are equal to each other but for the damping, being one damped and the other undamped. Indeed, the former system is structurally stable, while the latter not. In fact, in the case of the undamped harmonic oscillator, the action of any arbitrarily small damping force changes the qualitative behaviour of the solutions from that of a centre to a focus at the origin [51]. However, we emphasise that here the situation is different, or at least apparently less well documented. In fact, Eqs. (1)–(2) present two independent parameters of damping, namely c and d,  being only the former responsible for the behaviour we shall henceforth call binary. To recognise this, one can compare results from Examples A to D to those from two further ones (Fig. 2E and F), both characterised by $c=0$ and $d>0,$ chosen as representative of the second asymptotic behaviour of the sphere. In both cases, the sphere does not have any motion, resting in its initial position, while the carriage exhibits a damped motion, due to $d>0,$ with or without oscillations (respectively, underdamped for $m_1>0,$ or overdamped for $m_1\approx 0$).

Figure 3A and C shows the phase trajectories of carriage and Fig. 3B and D those of the sphere for the two cases shown in Fig. 2E $(c=0)$ and Fig. 2A $(c>0),$ emphasising the binary asymptotic behaviour and the counterintuitive response for $c>0$.

2.2 Experimental confirmation of the binary behaviour: 3D prototype and laboratory tests

With the aim of providing experimental validations of the analytical results, a prototype of the analysed model has been designed with the aid of the 3D CAD/CAM software Solid Edge [52] (see Fig. 4A and C) and then manufactured using Thermoplastic Polyurethane (TPU 92A) on the STRATASYS F170 3D printer.

In order to have the ability to adjust the inclination of the wheeled, main carriage (the blue-coloured element in Fig. 4B, C and D) and keep it horizontal, two supports have been 3D printed (black-coloured in Fig. 4B, C and D) and equipped with regulating bolts.

An aluminium rail surmounts the carriage to force the secondary mass into a perfectly unidirectional motion.

Fig. 4

3D CAD model of the laboratory set-up system (A and C); 3D printed prototype of the model (B and D); experimental set-up (E)

The carriage is connected to external clamps through pre-stretched elastic springs, as shown in Fig. 4B and D. The spring elasticity has been estimated through uni-axial tests performed on many specimens by means of the ElectroForce^® 200N 4 Motor Planar Biaxial TestBench machine (Fig. 4E). Because of pre-stretch, depending on the displacement of the carriage, a nonlinear response could be expected. However, in the small-on-large hypothesis, the linearity can still be retained, and the equivalent, effective stiffness is the mean value of those registered in the range of several pre-stretch values. From experimental evidence, the tangent modulus of the springs varies in the order of tens ${\hbox {N\,m}}^{-1}$.

Fig. 5

Experimental validation of the asymptotic binary behaviour for the free mass example, with parameters measured or derived from experimental calibration: $m_{1}={0.478}\,{\hbox {kg}}$, $m_{2}={0.152}\,{\hbox {kg}}$, $d={0.2}\,\hbox {N s m}^{-1},$ $k_{1}={10}\,{\hbox {N m}}^{-1},$ and c nullified by oiling (case A) or $c={0.06}\,\hbox {N s m}^{-1}$ (case B)

The primary mass to be considered is a compound of the masses of the carriage, wheels, rail, and elastic restraints and is measured as ${0.478}\,{\hbox {kg}}$, by using a precision scale. For the secondary mass, several steel spheres, from ${0.067}\,{\hbox {kg}}$ to ${0.288}\,{\hbox {kg}}$, have been utilised to have the possibility of reproducing either low mass ratio cases up to mass ratios greater than 0.5.

A high-speed Photron’s camera CMOS MINI FASTCAM AX100 (Fig. 4E) has been placed over the system to record displacements at a sampling rate of 4000 fps at image resolution of $1024\times 1024$ pixels.

By focusing on the free mass case, in order to grasp the binary behaviour provided by the analytical predictions of Sect. 2.1, two different experimental set-ups are organised: (i) the aluminium rail and the sphere have been oiled with the aim of nullifying the friction in the sphere–carriage interface and of reproducing the cases E and F of Fig. 2 (Fig. 5A); (ii) a TPU layer is mounted over the aluminium rail for increasing the friction between the sphere and the primary mass, thus replicating the non zero friction case (Fig. 5B). While the stiffness and mass parameters are experimentally measured, the damping coefficients c and d are calculated through curve-fitting aimed at converging the experimental results with the theoretical curves.

In case A, the initial distance between the centres of gravity of the carriage and the sphere is set as $\Delta x(0)={0.021}\,{\hbox {m}}$. For activating dynamics of the system, the carriage is initially displaced of ${0.025}\,{\hbox {m}}$ in the opposite direction to $\Delta x(0)$ (i.e. $x_1(0)=-\,{0.025}\,{\hbox {m}}$) and then released. From Fig. 5A, it can be seen that the theoretical curves, in terms of the time histories of displacement of the two masses, perfectly match the experimental points, confirming that no dynamic interaction occurs between the sphere and the carriage in the case of zero friction, with the sphere remaining at rest.

In case B, an initial step displacement $x_1(0)={0.03}\,{\hbox {m}}$ is imposed on the carriage, while the centres of gravity of sphere and carriage are vertically aligned, $\Delta x(0)={0.00}\,{\hbox {m}}$. From Fig. 5B, it can be observed that, with friction at the interface, the sphere actually returns to its initial relative position, i.e. $x_2$ approaches $\Delta x(0),$ in excellent agreement with the analytical time history.

Fig. 6

Displacements histories (A and D) and phase space plots for the carriage (B, E) and the sphere (C and F), by assuming $x_1(0)={0.01}\,{\hbox {m}}$ and $x_2(0)=x_1(0)+\Delta x(0)={0.03}\,{\hbox {m}}$. In all graphics, the following parameters are assumed: $m_1={0.10}\,{\hbox {kg}},\, m_2={0.04}\,{\hbox {kg}}, k_1={400}\,{\hbox {N\,m}}^{-1}$ and $d={1}\,\hbox {N\,s\,m}^{-1}.$ In graphics D, E and F, the damping parameter c is ${1}\,\hbox {N\,s\,m}^{-1}$

As already stated, several springs with different stiffness and spheres with different diameters, to represent cases with low, intermediate and high mass ratios, have been considered, while keeping invariant the primary mass. Invariably, tests showed the sphere achieving a rest position equal to the initial relative position between its centre of gravity and that of the carriage.

3 Effects of nonlinearities on the asymptotic behaviour of the system

In Sect. 2, the binary asymptotic behaviour of the system has been first analytically found and then confirmed through experimental validation. As above mentioned, by considering a linear system, this behaviour depends essentially on the parameter c.

In the following, to investigate the effects of nonlinearities on the dynamics of the system, especially with reference to the asymptotic behaviours, we consider two nonlinear models, the first equipped with nonlinear stiffness and the second with nonlinear damping.

The nonlinear differential equations will be integrated, for given initial conditions and over assigned time intervals from $t_{\min }$ to $t_{\max },$ using the general numerical differential equation solver NDSolve  available in Mathematica^®[53]. NDSolve has many different built-in methods for computing solutions and, by default, NDSolve automatically chooses the possibly most appropriate method for the differential equations under integration. Furthermore, during the integration process one method can call another, if needed.

The solution is found iteratively, starting at a particular value of the independent variable, and then taking a sequence of steps, trying eventually to cover the whole range $t_{\min }$ to $t_{\max }.$ NDSolve uses an adaptive procedure to determine the size of the steps, which is made smaller and smaller until the solution reached satisfies either the value of the chosen accuracy or precision, through error estimates. For a wide description of methods and available options for their settings, as well as of the control mechanisms set up for writing new user-defined numerical integration algorithms to be used as specifications for NDSolve, we refer to [54].

3.1 Duffing-like stiffness

We consider the elastic restraints as nonlinear and write the equations of motion of the system shown in Fig. 1 as

$$\begin{aligned}&m_1\ddot{x}_1(t)+d\dot{x}_1(t)+k_1 \left( \alpha +\beta \,{x_{1}(t)}^{2}\right) x_1(t)\nonumber \\&\quad -c\left( \dot{x}_2(t)-\dot{x}_1(t)\right) =0, \end{aligned}$$

(7)

$$\begin{aligned}&m_2\ddot{x}_2(t)+c\left( \dot{x}_2(t)-\dot{x}_1(t)\right) =0, \end{aligned}$$

(8)

$\alpha$ and $\beta$ being the coefficients specifying the nonlinear behaviour of the springs. It is immediate to recognise that Eqs. (7)–(8) correspond to a damped Duffing oscillator [42,43,44,45] coupled to a linear oscillator.

By setting $\alpha =1$, $\beta =2\times 10^{6}\,{{\hbox {m}}^{-2}}$, Fig. 6 shows the time histories and phase trajectories for both the two degrees of freedom. Notice that such a choice of parameters corresponds to the mono-stable Duffing model, which for $\beta ={0}\,{{\hbox {m}}^{-2}}$ reproduces the linear behaviour already discussed in Sect. 2.1. On the contrary, the large value adopted for $\beta$ in the numerical simulations presented below is aimed at emphasising the effect of the cubic term. The other parameters are the same adopted in the linear case, and the initial conditions are those set in Eq. (6).

Interestingly, the nonlinear stiffness does not change the asymptotic behaviours of the system, by still distinguishing the two limit cases: indeed, for $c=0,$ Eqs. (7)–(8) are uncoupled and the sphere rests in its initial position for any $t>0,$ while for $c>0$ the sphere restores its initial relative position with respect to the centre of gravity of the carriage. In fact, by comparing plots Figs. 2A and E to 6A and D, respectively, it can be seen that, despite the oscillations of the two bodies in the nonlinear case are quite different with respect to the linear counterpart, the asymptotic behaviours registered are perfectly recovered.

3.2 Non-smooth friction

The assumption of damping linear with velocity used in Sects. 2.1 and 3.1 is physically plausible when a sphere moves on a smooth surface, and nonlinear phenomena are negligible. While, for the problem under investigation, the predictions of such a simple model have been confirmed by the experimental tests reported in Sect. 2.2, in order to analyse more general systems, a nonlinear dissipation model is here considered, while the linear elasticity of the springs is retained.

In order to define a mutual nonlinear damping term that upgrades the linear one utilised in Eqs. (1)–(2), i.e. $f^{\mathcal {D}}_{\textrm{L}}(\dot{\xi })=c\,\dot{\xi },$ being $\dot{\xi }$ a dummy variable (for instance, in Eqs. (1)–(2), $\dot{\xi }=\dot{x}_2-\dot{x}_1$), the dry friction model [46,47,48] has been selected. Within this framework, let us consider a body resting on a rough surface under the action of an increasing external force. Before the body starts sliding, friction and external force are in equilibrium, the latter do not exceeding the static friction. Whenever the latter is overcome by a large enough applied force, then the friction decreases to the kinetic value [55]. Hence, by introducing the dimensionless stick (static) and slip (kinetic) friction coefficients $\mu _{1}$ and $\mu _{2},$ with $0<\mu _{2}\le \mu _{1},$ the mutual nonlinear damping force in Eqs. (1)–(2) is replaced with

$$\begin{aligned}{} & {} f^{\mathcal {D}}_{\text {NL}}\!\left( \dot{\xi }\right) =\frac{\mu _1 F_N }{v_{\text {r}}}\dot{\xi }+\left( 2\left( \mu _2 F_N-\chi v_{\text {r}}\right) \mathcal {H}\!\left( \dot{\xi }\right) \right. \nonumber \\{} & {} \quad \left. -\frac{F_N}{v_{\text {r}}}\left( \mu _1 \dot{\xi }+\mu _2 v_{\text {r}} \right) +\chi \left( \dot{\xi }+v_{\text {r}}\right) \right) \mathcal {H}\!\left( \big \vert \dot{\xi }\big \vert -v_{\text {r}}\right) .\nonumber \\ \end{aligned}$$

(9)

Terms in Eq. (9) comment as follows: $\mathcal {H}(\cdot )$ is the Heaviside unit step function equal to 0 for negative values of its argument and 1 otherwise, $F_{N}$ is the weight of the sphere (here acting normally to direction of the motion), $v_\text {r}>0,$ is the threshold reference velocity responsible for the transition from stick to slip behaviour of the dry friction [56,57,58], $\chi \ge 0$ is a damping parameter having dimensions of mass per time, as c in the linear case.

We emphasise that Eq. (9) approximates different friction models. In the limit $v_\text {r}\rightarrow 0^+$ and setting $\chi =0,$ Eq. (9) recovers the Amontons–Coulomb for $\mu _{1}=\mu _{2},$ and the stiction friction model for $\mu _{1}>\mu _{2}$ [59], both of which result in constant forces either for negative or positive velocities. However, for many different materials, friction has been experimentally shown to be velocity-strengthening [60], with a viscous-like damping becoming dominant [61], indeed simulated by Eq. (9) by setting $\chi >0.$

A qualitative graph of Eq. (9) is shown in Fig. 7.

Fig. 7

Qualitative graph of $f^{\mathcal {D}}_{\textrm{NL}}$ for $\mu _1>\mu _2$ and $\chi >0$

Fig. 8

Time histories, in terms of displacements (A) and velocities (B), and phase trajectories for the primary (C) and secondary mass (D). Initial conditions $x_1(0)={0.01}\,{\hbox {m}}$ and $x_2(0)=x_1(0)+\Delta x(0)={0.03}\,{\hbox {m}}$ are set. In all graphics, the following parameters are adopted: $m_1={0.10}\,{\hbox {kg}},\, m_2={0.04}\,{\hbox {kg}},\, k_1={400}\,{\hbox {N m}}^{-1}$ and $d={1}\,\hbox {N s m}^{-1}$. The parameters of the nonlinear dry friction model are set as follows: $\mu _{1}=0.509$, $\mu _{2}=\mu _{1}/2$, $F_{N}={0.3924}\,{\hbox {N}}$, $v_{r}={0.2}\,{\hbox {m s}}^{-1}$. The red dashed line in plot (A) marks the asymptotic behaviour of the linear counterpart of the system, and the dashed circle in plot (D) highlights the point of coordinates (0.02, 0.00) corresponding to the attractor in the damped linear case

Fig. 9

Time histories, in terms of displacements (A) and velocities (B). Initial conditions $x_1(0)={0.005}\,{\hbox {m}}$ and $x_2(0)=x_1(0)+\Delta x(0)={0.025}\,{\hbox {m}}$ are set. In all graphics, the following parameters are adopted: $m_1={0.10}\,{\hbox {kg}},\, m_2={0.04}\,{\hbox {kg}},\, k_1={400}\,{\hbox {N m}}^{-1}$ and $d={1.00}\,\hbox {N s m}^{-1}.$ The parameters of the nonlinear dry friction model are set as follows: $\mu _{1}=0.5097$, $\mu _{2}=\mu _{1}/2$, $F_{N}={0.3924}\,{\hbox {N}},$ $v_{r}={0.2}\,{\hbox {m s}}^{-1}$. Notice that, to compare results with those obtained in the linear case, the parameters are set to fulfil ${\mu _1 F_N }/{v_\text {r}}=c$

Fig. 10

Bifurcation diagrams showing as the asymptotic value of $\Delta x$ varies in function of $v_r,$ for the parameters set as: $m_1={0.10}\,{\hbox {kg}},$ $m_2={0.04}\,{\hbox {kg}},$ $k_1={400}\,{\hbox {N m}}^{-1},$ $d={1.00}\,\hbox {N s m}^{-1},$ $F_{N}={0.3924}\,{\hbox {N}}$, $\mu _1=0.51,$ $x_1(0)={0.01}\,{\hbox {m}}$, $x_2(0)=x_1(0)+\Delta x(0)$, $\Delta x(0)={0.02}\,{\hbox {m}}$, $\dot{x}_1(0)=\dot{x}_2(0)={0}\,{\hbox {m s}}^{-1}.$ The top panel A reports diagrams built by setting the dynamic friction coefficient $\mu _2=\mu _1/2$ and for seven different values of the dynamic viscosity $\chi .$ The bottom panel B shows diagrams for the damping coefficient $\chi ={0.10}\,\hbox {N s m}^{-1}$ and five different values of the ratio $\mu _2/\mu _1$

Fig. 11

2-DOF model of a spherical mass attached to a sliding carriage through pre-stretched nonlinear springs

Fig. 12

Displacement histories (A and D) and phase space plots (B, C, E and F) of the 2-DOF system made up of a spherical mass attached to the carriage through pre-stretched springs. In all graphics, the following parameters are assumed: $m_1={0.10}\,{\hbox {kg}},\,m_2={0.04}\,{\hbox {kg}}$, $k_{0}={50}\,{\hbox {N m}}^{-1}$, $k_1={400}\,{\hbox {N m}}^{-1}$, $\lambda _2=1.5,\,d={1}\,\hbox {N s m}^{-1}.$ In the graphics D, E and F the damping parameter $c={1} \,\hbox {N s m}^{-1}$ is set

The numerical integration of

$$\begin{aligned}&m_1\ddot{x}_1(t)+d\dot{x}_1(t)+k_1 x_1(t)+f^{\mathcal {D}}_{\textrm{NL}}\!\left( \dot{x}_1(t)-\dot{x}_2(t)\right) \nonumber \\&\quad =0, \end{aligned}$$

(10)

$$\begin{aligned}&m_2\ddot{x}_2(t)+f^{\mathcal {D}}_{\textrm{NL}}\!\left( \dot{x}_2(t)-\dot{x}_1(t)\right) =0, \end{aligned}$$

(11)

in the time range $t_{\min }={0}\,{\hbox {s}}$ to $t_{\max }=10^{3}\,{\hbox {s}}$ for a given set of mechanical parameters and the initial conditions reported in Eq. (6) allows plotting time histories, in terms of displacements and velocities, and phase trajectories elucidating that the stick–slip phenomenon arising between $m_1$ and $m_2$ strongly influences the oscillation of the overall system to a drastic change in its asymptotic behaviours.

In fact, unlike what happens in the previously analysed systems, the asymptotic binary behaviour is not confirmed in the general case. Let us consider the example shown in Fig. 8: despite $x_1$ asymptotically approaches 0 (Fig. 8A and C), the sphere does not invariably reach a rest position recovering the initial relative distance from the centre of gravity of the carriage (Fig. 8A and D), because of the strong nonlinear effect that arises in the first 0.2 s of the motion, during which the displacement and velocity histories of the sphere show stick phases alternating to slip motion (Fig. 8A and B). Notice that the change in the velocity slope and the kinks in the phase trajectories are related to the change in the friction coefficient at $\dot{\xi }=v_r$.

However, it must be emphasised that if the relative velocity $\dot{\xi }$ does not overcome the value of $v_r,$ the system essentially recovers the linear behaviour, as shown in Fig. 9. Reported results correspond to the numerical integration of Eqs. (10)–(10) by setting initial conditions tailored to ensure $\dot{\xi }<v_r,$ having the same $\Delta x(0)$ and initial velocities, but $x_1(0)$ halved with respect to Eq. (6),

$$\begin{aligned} \begin{aligned}&x_1(0)= 5\times 10^{-3}\,{\hbox {m}}, \\&x_2(0)=x_1(0) + \Delta x(0)={0.025}\,{\hbox {m}},\\&\dot{x}_1(0)=\dot{x}_2(0)= {0}\,{\hbox {m s}}^{-1}. \end{aligned} \end{aligned}$$

(12)

Furthermore, the same behaviour of the linear system can be obtained playing with the value of the parameter $v_r,$ as shown Fig. 10 through two bifurcation diagrams. Such diagrams are built by integrating the equation of motion for the initial conditions given in Eq. (6) and a fixed set of parameters, at threshold velocity in the range $10^{-6}\,{\hbox {m\,s}}^{-1}\le v_r\le {1}\,{\hbox {m\,s}}^{-1}$ (with a step of $10^{-3}\,{\hbox {m\,s}}^{-1}$). It can be recognised that a critical value $v_{r,\textrm{crit}}$ can be detected ($v_{r,\textrm{crit}}\approx {0.4635}\,{\hbox {m\,s}}^{-1}$ for the parameters chosen in the numerical computations) below which (i.e. $v_r<v_{r,\textrm{crit}}$) the asymptotic value of $\Delta x$ is different from $\Delta x(0),$ apart for a limited number of specific values of $v_r,$ while, for any $v_r\ge v_{r,\textrm{crit}},$ $\Delta x(t)$ asymptotically approaches $\Delta x(0),$ as in the linear case (see Fig. 10). Such a behaviour is confirmed for different values of the dynamic viscosity $\chi$ (Fig. 10A) and the friction ratio $\mu _2/\mu _1$ (Fig. 10B). The latter diagram also elucidates that whenever $\mu _2<\mu _1$ the bifurcation diagram contains jumps, for certain values of $v_r<v_{r,\textrm{crit}},$ becoming smaller and smaller as $\mu _2$ approaches $\mu _1.$

4 Tunable elastic constraints on moving mass: back to standard behaviours

As a final example, let us consider the system shown in Fig. 11, which is the same as that shown in Fig. 1, except that here the sphere is anchored to the carriage by means of two elastic springs of stiffness $k_{2L}$ and $k_{2R},$ which are assumed to be tunable through pre-stretching.

The equations of motion are written as

$$\begin{aligned}{} & {} m_1\ddot{x}_1(t)+d\dot{x}_1(t)+k_1 x_1(t)-c\left( \dot{x}_2(t)-\dot{x}_1(t)\right) \nonumber \\{} & {} \quad -\left( k_{2L}+k_{2R}\right) \left( {x_2}(t)-{x_1}(t)\right) =0, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} m_2\ddot{x}_2(t)+c\left( \dot{x}_2(t)-\dot{x}_1(t)\right) +\left( k_{2L}+k_{2R}\right) \nonumber \\{} & {} \quad \times \left( {x_2}(t)-{x_1}(t)\right) =0. \end{aligned}$$

(14)

In order ${k_{2\,L}}$ and ${k_{2R}}$ are tunable, we consider an incompressible Neo–Hookean constitutive law [62, 63], which allows writing

$$\begin{aligned} \begin{aligned}&k_{2L}=k_0\left( 1+2\lambda _{2L}^{-3}\right) ,\\&k_{2R}=k_0\left( 1+2\lambda _{2R}^{-3}\right) , \end{aligned} \end{aligned}$$

(15)

where $k_{0}$ represents a constant parameter related to the geometrical and mechanical characteristics of the springs and ${\lambda _{2\,L}}=l_{2\,L}/l_0$ and ${\lambda _{2R}}=l_{2R}/l_0$ indicate, respectively, the longitudinal stretches of springs set on the left and right side of the sphere, being $l_{0}$ the rest length and $l_{2\,L}$ and $l_{2R}$ the current lengths. Notice that, in the small-on-large hypothesis, the current length remains substantially equal to the mounting length, that is the distance between the sphere and the clamp (see Fig. 11). In addition to pre-stretch the spring, we assume $l_{2\,L}>l_0$ and $l_{2R}>l_0$. Here, since the rest length of both springs is the same, for the self-equilibrium condition, the stretches ${\lambda _{2L}}$ and ${\lambda _{2R}}$ are coincident $({\lambda _{2L}}={\lambda _{2R}}={\lambda _{2}})$ and the sphere is placed exactly in the middle of the carriage (Fig. 11), i.e. $\Delta x(0)={0}\,\textrm{m}$. Conversely, springs having different rest lengths imply not null relative position of the sphere with respect to the centre of gravity of the carriage.

By setting $y_1(t)=\dot{x}_1(t)$ and $y_2(t)=\dot{x}_2(t),$ Eqs. (13)–(14) can be conveniently rearranged in matrix form as

$$\begin{aligned} \begin{pmatrix} \dot{x}_1\\ \dot{x}_2\\ \dot{y}_1\\ \dot{y}_2 \end{pmatrix}= & {} \begin{pmatrix} 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1\\ -(k_1+k_2)\,m_1^{-1}&{}k_2\,m_1^{-1}&{}-\left( c+d\right) \,m_1^{-1}&{}c\,m_1^{-1}\\ k_2\,m_2^{-1}&{}-k_2\,m_2^{-1}&{}c\,m_2^{-1}&{}-c\,m_2^{-1}\\ \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ y_1\\ y_2 \end{pmatrix},\nonumber \\ \end{aligned}$$

(16)

where, for the sake of simplicity, $k_{2}={k_{2L}}+{k_{2R}}$ is set and the time dependence is implied. The characteristic equation associated to Eq. (3) is written as

$$\begin{aligned} \begin{aligned}&m_1 m_2 \gamma ^4 +\left( c\left( m_1+m_2\right) +d m_2\right) \gamma ^3 \\&\quad + \left( c d + k_1 m_2+\left( m_1+m_2\right) k_2\right) \gamma ^2\\&\quad + \left( c k_1+d k_2\right) \gamma +k_1 k_2 = 0, \end{aligned} \end{aligned}$$

(17)

solvable in closed form [49]. For the range of parameters of interest, the algebraic multiplicity of each eigenvalue is 1. Therefore, a complete system of 4 eigenvectors can be provided. The general integral of Eq. (16), i.e. $\textbf{z}(t)\equiv \left( x_1(t),x_2(t),y_1(t),y_2(t)\right) ^T,$ can be obtained as

$$\begin{aligned} \textbf{z}(t)= & {} d_1 \textbf{w}_1 e^{\gamma _1 t}+d_2 \textbf{w}_2 e^{\gamma _2 t}+d_3 \textbf{w}_3 e^{\gamma _3 t}\nonumber \\{} & {} +d_4 \textbf{w}_4e^{\gamma _4 t}, \end{aligned}$$

(18)

being $\textbf{w}_i,$ $i=\{1,\ldots ,4\},$ the eigenvectors associated to eigenvalues $\gamma _i,$ and $d_i$ represent the constants of integration depending on initial conditions. For the sake of brevity, the explicit expressions of eigenvalues and eigenvectors of Eq. (16) are given in Appendix A.

Based on the analytical solution given by Eq. (18), the displacement histories and the phase trajectories are provided in Fig. 12, for the initial conditions set as

$$\begin{aligned} \begin{aligned}&x_1(0)=x_2(0)= {0.01}\,{\hbox {m}}, \\&\dot{x}_1(0)=\dot{x}_2(0)= {0}\,{\hbox {m\,s}}^{-1}. \end{aligned} \end{aligned}$$

(19)

By examining all graphics reported in Fig. 12, one can observe that the binary asymptotic behaviour of the previous case is not confirmed.

In particular, for the system under investigation, a single asymptotic behaviour occurs: both the carriage and the sphere return to their initial position, related to the presence of the nonlinear pre-stretched springs, which maintain coupled the dynamics of the sphere and the carriage, also in the limit case of vanishing damping. However, despite the unique asymptotic behaviour in this last case may be somewhat expected, the possibility of modulating the pre-stress in the springs attached to the sphere can be interestingly exploited in order to emphasise some dynamic effects on the overall system; for instance, by properly tuning the nonlinear stiffness of the sphere, a reduction of the dynamic amplification of the carriage can be obtained, thus inducing a mass-damping effect on it.

5 Conclusions and perspectives

Although the problems of moving masses or loads have been addressed in the inherent literature over the years, somehow surprisingly no research paper focuses on the asymptotic behaviour of the simplest “toy system” case of an elastically constrained rigid system surmounted by a movable mass.

To face this issue, in the present paper, analytical solutions and numerical results were provided, by making reference to a 2-DOF model. The results were compared to experimental findings obtained by ad hoc designed and built-up prototype undergoing conditions that reproduced the mechanical response of the idealised structure. All the outcomes confirmed the non-trivial asymptotic behaviour predicted by theory and observed in the laboratory for different masses. In particular, when nonzero friction at the sphere–carriage interface is considered and other nonlinear phenomena can be neglected, the spherical mass counterintuitively returns to the arbitrarily prescribed relative sphere–carriage initial position. On the contrary, if the friction at the sphere–carriage interface vanishes, a second complementary behaviour occurs, that is the sphere holds its initial position over the entire observation time, regardless the vibration history of the support, this duality here called binary.

Furthermore, it was numerically shown that nonlinear elastic springs constraining the carriage do not change this binary asymptotic behaviour, while it can be either maintained or lost, depending on parameters or initial conditions if nonlinear friction phenomena are incorporated into the model for taking into account, for instance, stick–slip processes occurring at the interface. Also, it was found that additional elastic constraints applied to the spherical mass back the system to a standard behaviour. Apart from the value of the work per se, it is felt that the results could be helpfully employed for different engineering applications in order to design new optimal tuned mass dampers, also by exploiting the effects of nonlinearities.

Appendix

Here, for the sake of completeness, we report the eigenvalues and eigenvectors of Eqs. (3) and (16).

The eigenvalues of Eq. (3) are

$$\begin{aligned} \eta _1= & {} 0,\nonumber \\ \eta _2= & {} \frac{{{\left( \sqrt{G}+H \right) }^{1/3}}}{{3\,\,{2}^{1/3}}}-\frac{2^{1/3}L}{(\sqrt{G}+H)^{1 / 3}}-I,\nonumber \\ \eta _{3,4}= & {} \frac{(1 \pm j \sqrt{3}) L}{2^{2 / 3}(\sqrt{G}+H)^{1 / 3}}-\frac{(1 \mp j \sqrt{3})(\sqrt{G}+H)^{1 / 3}}{6\,\,2^{1 / 3}}\nonumber \\{} & {} \quad -I, \end{aligned}$$

(20)

where j is the imaginary unit and G, H, I and L are evaluated, respectively, as

$$\begin{aligned} G&=\frac{27}{m_1^4 m_2^4}\Biggl (4 c^4 k_1 m_1^3+ m_2^2(c+d)^2\nonumber \\&\quad \times \Big (k_1 m_2\big (2c(2c+d)-k_1 m_2\big )-c^2 d^2\Big )\nonumber \\&\quad +c^2 m_1^2\Big ( 4 k_1 m_2\big (c(3c-2d)\nonumber \\&\quad +2 k_1 m_2\big )-c^2 d^2\Big )+2 m_1 m_2 \nonumber \\&\quad \times \bigg (k_1 m_2\Big (c^2(6 c^2+c d+d^2)+2 k_1 m_2\nonumber \\&\quad \times \big (k_1 m_2-c\left( 5c+2d \right) \big )\Big )-c^3 d^2(c-d)\bigg )\Bigg ),\nonumber \\ H&= -\frac{2 (c+d)^3}{m_1^3} -\frac{3 (c+d)\Big (c(2c-d)-3 k_1 m_2\Big )}{m_1^2 m_2}\nonumber \\&\quad -\frac{3c \Big (c (2c-d)+6 k_1 m_2\Big )}{m_1 m_2^2}-\frac{2 c^3}{m_2^3},\nonumber \\ I&= \frac{c(m_1+m_2)+d m_2}{3 m_1 m_2},\nonumber \\ L&= \frac{3 m_1 m_2(c d+k_1 m_2)-\Big (c (m_1+m_2)+d m_2\Big )^2}{3 m_1^2 m_2^2}. \end{aligned}$$

(21)

The components of the ith eigenvector $\textbf{v}_i \equiv (v_{1i},v_{2i},v_{3i},v_{4i})^T$ of Eqs. (1) and (2), being the subscript $i\!=\!\{1,\ldots ,4\}$ referred to ith eigenvalue, are

$$\begin{aligned} v_{1i}= & {} \frac{c \eta _i}{M},\nonumber \\ v_{2i}= & {} \frac{k_1+\eta _i (c+d+m_1\eta _i)}{M},\nonumber \\ v_{3i}= & {} \frac{c \eta _i^2}{M},\nonumber \\ v_{4i}= & {} \frac{\eta _i \left( k_{1}+\eta _i (c+d+m_{1}\eta _{i})\right) }{M}, \end{aligned}$$

(22)

where M can be made explicit as

$$\begin{aligned} \begin{aligned} M=&\sqrt{\left( 1+\eta _i^2\right) \Biggl (k_1^2+2 k_1 \eta _i\left( c+d+m_1 \eta _i\right) +\eta _i^2\biggl (2 c^2+2 c\left( d+m_1 \eta _i\right) +\left( d+m_1 \eta _i\right) ^2\biggr )\Biggr )}.\\ \end{aligned} \end{aligned}$$

(23)

By substituting, in Eqs. (22) and (23), $\eta _i$ with the ith $(i=1,\ldots ,4)$ eigenvalue given by Eq. (20), taking into account Eq. (21), the closed-form expressions of the eigenvectors components given by can be made explicit.

The eigenvalues of the system (16) are

$$\begin{aligned} \gamma _{1,2}= & {} -\frac{g_{3}}{4 g_{4}}-\frac{1}{2} \sqrt{\frac{g_{3}^{2}}{4 g_{4}^{2}} +\frac{N^{1 / 3}}{32^{1 / 3} g_{4}}-\frac{2 g_{2}}{3 g_{4}}+\frac{P}{g_{4}}}\nonumber \\{} & {} \mp \frac{1}{2} \sqrt{\frac{g_{3}^{2}}{2 g_{4}^{2}}-\frac{N^{1 / 3}}{32^{1 / 3} g_{4}}-\frac{4 g_{2}}{3 g_{4}}-\frac{P}{g_{4}}-Q},\nonumber \\ \gamma _{3,4}= & {} \mp \frac{g_{3}}{4 g_{4}}+\frac{1}{2} \sqrt{\frac{g_{3}^{2}}{4 g_{4}^{2}} +\frac{N^{1 / 3}}{32^{1 / 3} g_{4}}-\frac{2 g_{2}}{3 g_{4}}+\frac{P}{g_{4}}} \nonumber \\{} & {} \mp \frac{1}{2} \sqrt{\frac{g_{3}^{2}}{2 g_{4}^{2}}-\frac{N^{1 / 3}}{32^{1 / 3} g_{4}}-\frac{4 g_{2}}{3 g_{4}}-\frac{P}{g_{4}}+Q}, \end{aligned}$$

(24)

being the coefficients N, P and Q given by

$$\begin{aligned}{} & {} N=2g_{2}^{3}-9{{g}_{1}}{{g}_{2}}{{g}_{3}}+27{{g}_{0}}g_{3}^{2} +27g_{1}^{2}{{g}_{4}}-72{{g}_{0}}{{g}_{2}}{{g}_{4}}\nonumber \\{} & {} \quad +\sqrt{{{\left( 2g_{2}^{3}\!-\!9{{g}_{1}}{{g}_{2}}{{g}_{3}}\!+\!27{{g}_{0}}g_{3}^{2}\!+\!27g_{1}^{2}{{g}_{4}}\!-\!72{{g}_{0}}{{g}_{2}}{{g}_{4}} \right) }^{2}} -4{{\left( g_{2}^{2}-3{{g}_{1}}{{g}_{3}}+12{{g}_{0}}{{g}_{4}} \right) }^{3}}},\nonumber \\{} & {} P=\frac{2^{1 / 3}\left( g_{2}^{2}-3 g_{1} g_{3}+12 g_{0} g_{4}\right) }{3 N^{1 / 3}},Q=\frac{4 g_{2} g_{3} g_{4}-8 g_{1} g_{4}^{2}-{g_{3}}^{3}}{4 g_{4}^{2} \sqrt{3\,\,2^{2 / 3} g_{3}^{2}+6 g_{4} N^{1 / 3}-2^{11 / 3} g_{2} g_{4}+3 \,\,2^{8 / 3} g_{4} P}}, \end{aligned}$$

(25)

and the parameters $g_i$

$$\begin{aligned}{} & {} {{g}_{0}}={{k}_{1}}{{k}_{2}},\nonumber \\{} & {} {{g}_{1}}=c{{k}_{1}}+d{{k}_{2}},\nonumber \\{} & {} {{g}_{2}}=cd+{{k}_{1}}{{m}_{2}}+{{k}_{2}}\left( {{m}_{1}+{m}_{2}}\right) ,\nonumber \\{} & {} {{g}_{3}}=c{{m}_{1}}+{{m}_{2}}\left( c+d\right) ,\nonumber \\{} & {} {{g}_{4}}={{m}_{1}}{{m}_{2}}. \end{aligned}$$

(26)

The components of the ith eigenvector $\textbf{w}_i \equiv (w_{1i},w_{2i},w_{3i},w_{4i})^T$ of Eqs. (13) and (14), with the subscript $i\!=\!\{1,\ldots ,4\}$ referred to ith eigenvalue, can be provided as

$$\begin{aligned} w_{1i}= & {} \frac{c{{\gamma }_{i}}+{{m}_{2}}\gamma _{i}^{2}+{{k}_{2}}}{R},\nonumber \\ w_{2i}= & {} \frac{c{{\gamma }_{i}}+{{k}_{2}}}{R},\nonumber \\ w_{3i}= & {} \frac{\gamma _{i}\left( c{{\gamma }_{i}}+{{m}_{2}}\gamma _{i}^{2}+{{k}_{2}}\right) }{R},\nonumber \\ w_{4i}= & {} \frac{\gamma _{i}\left( c{{\gamma }_{i}}+{{k}_{2}}\right) }{R}, \end{aligned}$$

(27)

with

$$\begin{aligned}{} & {} R=\nonumber \\{} & {} \sqrt{\left( 1+\gamma _{i}^{2} \right) \left( 2c{{m}_{2}}\gamma _{i}^{3}+m_{2}^{2}\gamma _{i}^{4}+4c{{\gamma }_{i}}{{k}_{2}}+2{{ {{k}_{2}} }^{2}}+2\gamma _{i}^{2}\left( {{c}^{2}}+{{m}_{2}}{{k}_{2}} \right) \right) }.\nonumber \\ \end{aligned}$$

(28)

By replacing, in Eqs. (27) and (28), $\gamma _i$ with the ith $(i=1,\ldots ,4)$ eigenvalue given by Eq. (24), taking into account Eqs. (25) and (26), the components of the eigenvectors can be written in explicit form.