Abstract
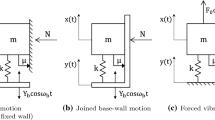
The stick-slip phenomenon is a jerking motion that may occur when two objects are forced to slide with friction over each other. There are many situations in which this motion can be observed in practice, for example, between the components of different kinds of seismic protection systems, such as the slabs of some friction dampers or the sliding elements of some base isolation systems. Such systems are generally designed to work in a smooth and flawless manner. However, it cannot be excluded that in particular situations undesired jerking motions may develop. These kinds of situations are widespread in all areas of engineering and may result in very complex nonlinear dynamic behavior even when only a small number of degrees of freedom are involved. Over the years, several investigations have been conducted to better understand the dynamic behavior of systems in which two components are forced to slide with friction over each other, the ultimate objective being to identify conditions that may disrupt their proper functioning and optimize their performance. The body of literature on this particular topic may be subdivided into two main categories. The first is represented by numerical studies performed by means of finite element models. The second approach, to which this work belongs, is conducted via simplified models which regard the considered system as a mechanical system endowed with a small number of degrees of freedom. A simple scheme for problems of this kind consists of a rigid block connected elastically to a rigid support, while its base is in contact with a moving rough surface. Both the support and surface can be assigned a prescribed motion. Despite its apparent simplicity, this model can provide some useful indications on the main features of many interesting physical systems. This contribution illustrates an analytical study conducted to better understand the nonlinear dynamic behavior of systems of this kind, with the objective of identifying the conditions that may disrupt their proper functioning. In particular, the equations of motion are solved analytically, the sticking and sliding phases are studied, the influence on the solution of some of the system main parameters is investigated, and some typical long-term responses of the system are discussed. Lastly, some results obtained by means of an expressly developed numerical procedure are illustrated.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Chopra, A.: Dynamics of Structures: Theory and Applications to Earthquake Engineering, 2nd edn. Prentice Hall Inc., Upper Saddle River (2003)
Grigorian, C., Popov, E.: Energy dissipation with slotted bolted connections, UCB/EERC-94/02, California University, Richmond, Earthquake Engineering Research Centre (1994)
Castaldo, P., Palazzo, B., Della Vecchia, P.: Seismic reliability of base-isolated structures with friction pendulum bearings. Eng. Struct. 95, 80–93 (2015)
Bhaskararao, A.V., Jangid, R.S.: Seismic analysis of structures connected with friction dampers. Eng. Struct. 28, 690–703 (2006)
Ozbulut, O., Bitaraf, M., Hurlebaus, S.: Adaptive control of base-isolated structures against near-field earthquakes using variable friction dampers. Eng. Struct. 33, 3143–3154 (2011)
Kavvadias, I., Vasiliadis, L.: Finite element modeling of single and multi-spherical friction pendulum bearings. In: 6th Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June (2017)
Den Hartog, J.: Forced vibrations with combined coulomb and viscous friction. Trans. ASME 53, 107–115 (1931)
Parnes, R.: Response of an oscillator to a ground motion with coulomb friction slippage. J. Sound Vib. 94, 469–482 (1984)
Hong, H.K., Liu, C.-S.: Non-sticking oscillation formulae for coulomb friction under harmonic loading. J. Sound Vib. 244, 883–898 (2001)
Shaw, S.W.: On the dynamic response of a system with dry friction. J. Sound Vib. 108, 305–325 (1986)
Butikov, E.I.: Spring pendulum with dry and viscous damping. Commun. Nonlinear Sci. Numer. Simul. 20, 298–315 (2015)
Andreaus, V., Casini, P.: Dynamics of friction oscillators excited by a moving base and/or driving force. J. Sound Vib. 245, 685–699 (2001)
Sampson, J., Morgan, F., Reed, D.W., Muskat, M.: Friction behavior during the slip portion of the stick-slip process. J. Appl. Phys. 14, 689–700 (1943)
Leine, R.I., Van Campen, D.H., De Kraker, A.: Stick-slip vibrations induced by alternate friction models. Nonlinear Dyn. 16, 41–54 (1998)
Stein, G.J., Zahoranský, R., Múčka, P.: On dry friction modelling and simulation in kinematically excited oscillatory systems. J. Sound Vib. 311, 74–96 (2008)
Licskó, G., Csernák, G.: On the chaotic behaviour of a simple dry-friction oscillator. Math. Comput. Simul. 95, 55–62 (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Bennati, S., Barsotti, R., Migliaccio, G. (2020). A Simple Model for Predicting the Nonlinear Dynamic Behavior of Elastic Systems Subjected to Friction. In: Carcaterra, A., Paolone, A., Graziani, G. (eds) Proceedings of XXIV AIMETA Conference 2019. AIMETA 2019. Lecture Notes in Mechanical Engineering. Springer, Cham. https://doi.org/10.1007/978-3-030-41057-5_115
Download citation
DOI: https://doi.org/10.1007/978-3-030-41057-5_115
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-41056-8
Online ISBN: 978-3-030-41057-5
eBook Packages: EngineeringEngineering (R0)