1 Introduction

A journal bearing (JB) is composed of a rotating journal (or shaft) held by a bearing housing. These two components are separated with a thin film of viscous lubricant, which is pressurised due to their relative motion. The JBs are widely used to support large and high-speed rotors due to their longevity, load capacity, and favourable damping capability [21]. A basic JB design called a circular or cylindrical journal bearing utilises the journal and housing with a circular cross section. More intricate designs with non-circular housings, self-equalising components [14], and active elements such as magnetorheological fluids [25] or variable geometry [10] are also used.

The distribution of the hydrodynamic (HD) pressure in lubricant is governed by the Navier–Stokes equations. However, the Reynolds equation (RE) [20, 34] is often used in engineering applications instead because it reduces a 3D problem into a 2D problem. A closed-form solution of the RE is somewhat complicated because it contains infinite summations [29]; thus, many approximate and numerical solutions covering the most frequent applications exist. Assuming infinitely short or infinitely long bearing [19] and considering specific cavitation conditions [20, 34], the RE can be simplified from a partial differential equation to an ordinary differential equation. The resulting analytical solutions have a reduced ability to respect boundary conditions such as oil grooves and holes. Therefore, numerical methods, including finite difference (FDM) [20, 34], finite element [18] and finite volume methods [24], are fairly popular among the engineering community. Unlike the analytical methods, which can directly express forces acting in the film [6, 19], the numerical methods evaluate the HD pressure, which needs to be integrated to obtain the HD forces. This approach is rather time-consuming; therefore, some remedies have been developed over the years. Traditionally, the HD forces can be estimated utilising a precomputed database or a fit function [6]. Some novel methods combine analytical and numerical approaches [23] or use deep learning techniques [27].

Because the HD forces are inherently nonlinear, they can induce several types of nonlinear phenomena [21]. The best-documented nonlinear phenomenon occurring in the JBs is oil whirl/whip [22]. Oil whirl can be predicted using so-called dynamic coefficients, which describe the linear relation between the HD forces with journal displacements and velocities around its equilibrium [15]. Oil whirl occurs after the journal surpasses the threshold speed and loses linear stability [22]. The unstable journal would oscillate with an exponentially growing magnitude. However, its motion is restricted by the bearing clearance in real-world bearings, and hence, dynamics beyond the threshold speed cannot be predicted by the linear model [33]. Muszynska [22] proved that flexible journals could be stabilised and further destabilised at speeds above the threshold speed. Wang and Khonsari [36, 37] later found that the threshold speed differs during run-ups and coast-downs due to subcritical bifurcation. Subcritical and supercritical bifurcations are strongly related to bearing parameters [4, 12], journal flexibility [36] and, in large machinery, also to the flexibility of bearing pedestals and foundations [9]. The studies above utilise the short bearing theory [19], which limits their generalisation [15, 33]. Since the numerical methods for the computation of the HD forces are cumbersome w.r.t. numerical continuation, several authors adopted higher terms of the Taylor series to approximate the nonlinear properties of finite JBs. Yang et al. [39] employed second-order terms, whereas El-Sayed and Sayed used second- [28] and third-order [16] terms to study bifurcations related to oil whirl.

Another type of nonlinear phenomenon stems from an interaction between the HD forces and forces due to rotating unbalance [21]. Barrett et al. [5] was one of the first to study this interaction in 1976. He discovered that the rotating unbalance could suppress vibration due to oil whirl. Some twenty years later, Brown et al. [8] found that the rotating unbalance could induce chaotic vibration. Adiletta et al. [1, 2] confirmed the possibility of the chaotic motion and predicted possible period-doubling, i.e. sub-synchronous vibration excited by the rotating unbalance. He also provided experimental data that confirmed the main observations but contained notable discrepancies. Sun et al. [35] expanded Adiletta’s work by assuming a flexible journal and temperature-dependent viscosity. He concluded that the flexible journal supported in the JBs can exhibit many families of asynchronous vibration. The works mentioned above have employed the short bearing theory [19] and analysed the system through simulations in the time domain. Akay et al. [3] applied the numerical continuation theory to examine nonlinear dynamics of the unbalanced overhung rotor. He found that interaction between cubic nonlinearities in the bearings and the rotating unbalance may cause bouncing moves of the journal, which were initially reported in systems with high unbalance [1] or rotor-stator contacts [11, 31].

Other nonlinear phenomena have connections with thermal effects [32] and friction or contact forces [11, 21]. Since these effects are out of the scope of this article, let us describe them only briefly. Non-uniform shear stress in the oil film can heat the journal surface due to HD friction. If only a small part of the surface is heated repeatedly, a shaft bends, changing the unbalance distribution. This thermal instability is called the Morton effect [17, 32]. Some bearings, especially those with tilting pads, are prone to sub-synchronous vibration associated with friction [11, 21]. Friction, however, is often not the root cause of the vibration but affects the bearing susceptibility to it. A typical example is pad fluttering, which occurs due to the excessive inertia of unloaded tilting bearing [26] and is greatly influenced by friction between movable components [21].

This research seeks the analysis of the subcritical behaviour of an unbalanced 2-DoF rotor supported in cylindrical JBs. The main goal is to study sub-synchronous periodic motion due to the interaction between the force due to rotating unbalance and the nonlinear HD forces. Although some researchers [1, 8, 35] have already studied the interaction, this work offers a novel insight into motion classification using the numerical continuation method. Similarly to  Ref. [3], the continuation method is applied directly to the equations of motion. Unlike Ref. [3], which utilises an isotropic cubic stiffness to establish nonlinear characteristics of the supports, this work incorporates the nonlinear HD forces based on the infinitely short JB model. This model has already been employed in many works, e.g. [7, 15, 30, 37]. However, these works apply the numerical continuation on the perfectly balanced rotor. The primary focus is placed on the subcritical behaviour of the system. More concretely, stability borderlines (the Neimark–Sacker bifurcation) and the period-doubling bifurcations are traced concerning rotor speed, static unbalance, and lightly- and heavily-loaded JBs. It is demonstrated that the period-doubling bifurcation occurs before reaching the Neimark–Sacker bifurcation. The results of the numerical continuation are also compared with transient simulations to verify their applicability.

2 Mathematical modelling

This section introduces a computational model of a rigid rotor supported on journal bearings. Equations of motions of the investigated system are described in Sect. 2.1. Nonlinear hydrodynamic force calculation is presented in Sect. 2.2. Section 2.3 is dedicated to the non-dimensional transformation of equations of motion for further analyses by continuation method.

2.1 Equations of motion

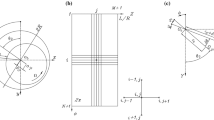
Let us assume rigid rotor with mass 2m which is symmetrically supported on two identical journal bearings. A scheme of the presented rotor system and applied forces is shown in Fig. 1.

Fig. 1
figure 1

A scheme of the considered rotor-bearing system with denoted forces

Full size image

The journal rotates with constant angular velocity \(\omega \), and the rotor is subjected to the gravity load, out-of-balance force and nonlinear hydrodynamic forces representing journal bearing support. Based on the orientation of applied forces depicted in Fig. 1, equations of motion can be written in the following form

$$\begin{aligned} \begin{bmatrix} m &{}\quad 0 \\ 0 &{}\quad m \end{bmatrix} \begin{bmatrix} \ddot{y}_J \\ \ddot{z}_J \end{bmatrix}= & {} \begin{bmatrix} -mg \\ 0 \end{bmatrix} + \begin{bmatrix} F_{hd,y} \\ F_{hd,z} \end{bmatrix}\nonumber \\{} & {} + \begin{bmatrix} \Delta mE \, \omega ^2 \sin (\omega t) \\ \Delta mE \, \omega ^2 \cos (\omega t) \end{bmatrix} \end{aligned}$$
(1)

where g is the gravitational acceleration, \(F_{hd,y},F_{hd,z}\) are the components of resultant hydrodynamic force and \(\Delta mE\) is the rotor static unbalance.

2.2 Hydrodynamic forces

Hydrodynamic pressure \(p=p \left( X,Z,t \right) \) is governed by the Reynolds equation considering several simplifying assumptions: a thin oil film, laminar flow of isoviscous and incompressible Newtonian fluid. General Reynolds equation has following form

$$\begin{aligned}{} & {} \frac{\partial }{\partial X} \left( \frac{h^3}{\mu } \frac{\partial p}{\partial X} \right) + \frac{\partial }{\partial Z} \left( \frac{h^3}{\mu } \frac{\partial p}{\partial Z} \right) \nonumber \\{} & {} \quad = 6 \, R \, \omega \, \frac{\partial h}{\partial X} + 12 \,\frac{\partial h}{\partial t}, \end{aligned}$$
(2)

where \(X,\,Z\) are the circumferential and axial coordinates, respectively, R is the bearing radius, \(\mu \) is the dynamic viscosity and h is the oil film height.

The Reynolds equation’s analytical solution in a closed form is well known for the case of plain cylindrical journal bearing with recommended aspect ratio \(L/D \le 0.5\) (infinitely short journal bearing (IS)). After using Gümbel cavitation boundary condition [20, 34] during the integration of hydrodynamic pressure, components of hydrodynamic force acting on the journal are determined by following expressions

$$\begin{aligned} F_{hd, r}^\textrm{IS}= & {} -\mu \textit{RL} \left( \frac{L}{c} \right) ^2 \left[ \frac{ \vert \omega -2\dot{\gamma }\vert \varepsilon ^2}{\left( 1-\varepsilon ^2\right) ^{2}} + \frac{\pi \left( 1+2\varepsilon ^2 \right) \dot{\varepsilon }}{2\left( 1-\varepsilon ^2\right) ^{5/2}}\right] , \end{aligned}$$
(3)
$$\begin{aligned} F_{hd,t}^\textrm{IS}= & {} \mu \textit{RL} \left( \frac{L}{c} \right) ^2 \left[ \frac{ \left( \omega -2\dot{\gamma } \right) \pi \varepsilon }{4\left( 1-\varepsilon ^2\right) ^{3/2}} + \frac{2\varepsilon \dot{\varepsilon }}{\left( 1-\varepsilon ^2\right) ^2} \right] , \nonumber \\ \end{aligned}$$
(4)

where \(R=D/2\) is the bearing radius, L is the bearing width, c is the radial (machined) clearance and \(\mu \) is the oil dynamic viscosity. Position of the journal in the bearing gap is defined by eccentricity e or relative eccentricity \(\varepsilon =e/c\) and attitude angle \(\gamma \)

$$\begin{aligned} e= & {} \sqrt{y_J^2(t) + z_J^2(t)}, \end{aligned}$$
(5)
$$\begin{aligned} \gamma (t)= & {} \left\{ \begin{array}{l l} \arccos \frac{z_J(t)}{e(t)}, &{} \quad y_J (t) > 0, \\ 2 \pi - \arccos \frac{z_J(t)}{e(t)}, &{} \quad y_J(t) < 0. \end{array} \right. \end{aligned}$$
(6)

In Eqs. (3) and (4), symbols \(\dot{\varepsilon }(t)\) and \(\dot{\gamma }(t)\) denote time derivation of relative eccentricity and attitude angle.

For numerical solution of the Reynolds equation, the finite difference method was employed. A uniform mesh of nodes \((i,j) \in \langle 1,M \rangle \times \langle 1, N \rangle \) with M nodes in circumferential and N nodes in the axial direction is considered to cover the bearing shell with spatial steps \(\Delta X, \Delta Z\) between the nodes. Partial derivatives in (2) are approximated by the central difference formulae which are based on the five-point computational stencil [20, 33]. Hydrodynamic pressure is calculated only in the nodes of inner mesh \((i,j) \in \langle 1,M-1 \rangle \times \langle 2, N-1 \rangle \) and considering following boundary conditions

$$\begin{aligned} p\left( 0, Z, t \right)= & {} p\left( 2\pi R, Z, t \right) , \end{aligned}$$
(7)
$$\begin{aligned} p\left( X, -\frac{L}{2}, t \right)= & {} p\left( X, \frac{L}{2}, t \right) = p_\textrm{amb}, \end{aligned}$$
(8)

where \(p_\textrm{amb}\) is the ambient pressure.

Formulation of the Reynolds equation for each node yields to the system of algebraic equations generally written in the matrix form

$$\begin{aligned} \textbf{A} \textbf{p} = \textbf{f}, \end{aligned}$$
(9)

where \(\textbf{A}\) is the sparse and diagonal coefficient matrix, \(\textbf{p}\) is the vector of unknown nodal hydrodynamic pressures \(p_{i,j}\) and \(\textbf{f}\) is the vector, which contains right-hand side of (2) and boundary conditions (7) and (8). Calculated nodal pressures need to fulfil Gümbel cavitation boundary condition

$$\begin{aligned} p_{i,j} = \left\{ \begin{array}{l l} p_{i,j}, &{} \quad \forall p_{i,j} \ge p_\textrm{amb}, \\ p_\textrm{amb}, &{} \quad \mathrm {else.} \end{array} \right. \end{aligned}$$
(10)

Finally, the Cartesian components of the hydrodynamic forces acting on the journal are evaluated from direct integration of pressure over the bearing surface based on simple trapezoidal rule which yields

$$\begin{aligned} F_{hd,y}^{\mathrm{{FDM}}} \approx - \sum \limits _{i=1}^{M-1} \sum \limits _{j=1}^{N} q(i,j) \, p_{i,j} \, \Delta X \Delta Z \sin \left( \frac{X_i}{R} \right) , \end{aligned}$$
(11)
$$\begin{aligned} F_{hd,z}^{\mathrm{{FDM}}} \approx - \sum \limits _{i=1}^{M-1} \sum \limits _{j=1}^{N} q(i,j) \, p_{i,j} \, \Delta X \Delta Z \cos \left( \frac{X_i}{R} \right) , \nonumber \\ \end{aligned}$$
(12)

where coefficient q(i, j) adjusts the size of the integration area and is given by a piecewise function

$$\begin{aligned} q(i,j) = \left\{ \begin{array}{lll} 0.5, &{} \forall \left( i = \left\{ 1,\,\dots ,\,M-1\right\} \wedge j = \left\{ 1,\,N\right\} \right) \\ 1, &{} \text{ else }. \end{array} \right. \nonumber \\ \end{aligned}$$
(13)

The following transformation from polar coordinates (t, r) to the fixed Cartesian system (y, z) is used

$$\begin{aligned} \begin{bmatrix} F_{hd,y}^{X} \\ F_{{hd},z}^{X} \end{bmatrix} = \begin{bmatrix} \cos \gamma &{} \sin \gamma \\ -\sin \gamma &{} \cos \gamma \end{bmatrix} \begin{bmatrix} F_{{hd},t}^{X} \\ F_{{hd},r}^{X} \end{bmatrix}, \end{aligned}$$
(14)

where superscript \(X = \text {IS}, {\mathrm{{FDM}}}\) designates the particular hydrodynamic bearing forces model.

2.3 Equations of motion in non-dimensional form

To compare the dynamic behaviour of proposed hydrodynamic bearing models, the mathematical model (1) will be transformed to non-dimensional form with respect to time and spatial coordinates using following expressions

$$\begin{aligned} \tau =\omega t, \quad \bar{y}_J = \frac{y_J}{c}, \quad \textrm{and} \quad \bar{z}_J = \frac{z_J}{c}, \end{aligned}$$
(15)

where \(\tau \) stands for non-dimensional time related to rotor angular speed \(\omega \) and \(\bar{z}_J\) and \(\bar{y}_J\) are non-dimensional coordinates of the journal centre related to bearing clearance c. The non-dimensional time \(\tau = \omega t\) has an impact to transformation of temporal derivatives, i.e. \(\dot{\Box } = \Box ' \omega \), where \(\dot{\Box } = \frac{\text {d}}{\text {d}t}\Box \) and \({\Box }' = \frac{\text {d}}{\text {d}\tau }\Box \).

Then, the mathematical model (1) can be rewritten using the relations introduced above in following general non-dimensional form

$$\begin{aligned} \begin{aligned}&{\bar{y}_J}'' = \frac{1}{mc\omega ^2}\left( F_{{hd},y}^{X} -mg + \Delta mE \, \omega ^2 \sin \tau \right) , \\&{\bar{z}_J}'' = \frac{1}{mc\omega ^2}\left( F_{{hd},z}^{X} + \Delta mE \, \omega ^2 \cos \tau \right) , \end{aligned} \end{aligned}$$
(16)

where superscript \(X = \textrm{IS}, {\mathrm{{FDM}}}\) will designate the bearing force model. Regarding model (16), following non-dimensional parameters can be obviously defined

$$\begin{aligned} \overline{\omega } = \omega \sqrt{\frac{c}{g}}, \quad A_{u} = \frac{\Delta m E}{mc}. \end{aligned}$$
(17)

The first one results from the term of gravity load and the second one results from the amplitude of the out-of-balance force.

In the case when analytical forms of hydrodynamic bearing forces for IS (3) and (4) are employed and considering the transformation of forces (14), the equation of motion can be further rewritten as

$$\begin{aligned} \begin{aligned}&{\bar{y}}_J'' = \frac{\lambda }{\bar{\omega }}\left( f_{hd,r}^{X}\sin \gamma + f_{{hd,t}}^{X}\cos \gamma \right) + A_{u} \sin \tau - \frac{1}{\bar{\omega }^2}, \\&{\bar{z}}_J'' = \frac{\lambda }{\bar{\omega }}\left( f_{hd,r}^{X}\cos \gamma - f_{hd,t}^{X}\sin \gamma \right) + A_{u} \cos \tau , \end{aligned}\nonumber \\ \end{aligned}$$
(18)

where we have defined non-dimensional bearing parameter

$$\begin{aligned} \lambda = \frac{\mu RL^3}{mc^{2.5}g^{0.5}}. \end{aligned}$$
(19)

The non-dimensional parts of hydrodynamic forces for the IS bearing have following form

$$\begin{aligned} f_{hd,r}^\textrm{IS}= & {} -\frac{\vert 1-2\gamma '\vert \varepsilon ^2}{(1-\varepsilon ^2)^{2}} + \frac{\pi (1+2\varepsilon ^2)\varepsilon '}{2(1-\varepsilon ^2)^{5/2}}, \end{aligned}$$
(20)
$$\begin{aligned} f_{hd,t}^\textrm{IS}= & {} \frac{(1-2\gamma ')\pi \varepsilon }{4(1-\varepsilon ^2)^{3/2}} + \frac{2\varepsilon \varepsilon '}{(1-\varepsilon ^2)^2}. \end{aligned}$$
(21)

Next, the non-dimensional parameters \(\bar{\omega }\) and \(\lambda \) will be advantageously used when comparing the dynamic behaviour of bearing models with analytical expressions of hydrodynamic forces and models with bearing forces gained integrally by solving the Reynolds equation using the finite difference method.

3 Solution strategy and stability analysis

This section will introduce and employ the dynamic analysis of the above-described system considering different approaches to modelling cylindrical journal bearing hydrodynamic forces. First, a detailed analysis of the IS cylindrical bearing, taking into account the analytical expressions of hydrodynamic forces (3) and (4) will be performed using the numerical continuation method [13]. In Sect. 4, the obtained results will be reconciled with results gained using the model, which adopts the direct solution of the Reynolds equation (2) by the FDM. These two approaches to the dynamical analysis of the system have the following consequences:

  • The model that uses the Reynolds equation’s direct solution gives more accurate results because it is not affected by simplifying assumptions compared to the IS model.

  • Numerical solution of the IS bearing model is significantly faster than the solution of the model based on the FDM in the time domain.

  • The numerical continuation can trace both stable and unstable branches of a given kind of solution (equilibria and limit cycle oscillation). Moreover, it can detect bifurcation points along the branches of the solution. This approach is primarily suitable for fully analytical models, i.e. the IS model.

Since the equations of motion of journal-bearing system reflect the out-of-balance force, which introduces a periodic excitation, the dynamic response of the system is primarily considered to form a limit cycle oscillation (LCO). The nonlinear bearing forces can exhibit different nonlinear phenomena in dependence on particular parameters of the system. As mentioned above, the parameters \(\lambda \), \(\overline{\omega }\) and \(A_{u}\) are suitable to be chosen as bifurcation parameters. For further analysis, it is convenient to transform the mathematical model (16) or (18) to corresponding state-space formulation, i.e. to a set of differential equations of the first order. In general, the mathematical model can be written in the state-space formulation as

$$\begin{aligned} {\varvec{x}}' = \varvec{f}^{X}(t,\varvec{x}, \varvec{\mu }), \end{aligned}$$
(22)

where the state-space vector is defined as

$$\begin{aligned} \varvec{x} = [x_1, x_2, x_3, x_4]^\textrm{T} = [\bar{y}_J, \bar{z}_J, \bar{y}'_J, \bar{z}'_J]^\textrm{T} \end{aligned}$$
(23)

and vector of bifurcation parameters is

$$\begin{aligned} {\varvec{\mu }} = [\overline{\omega }, \lambda , A_{u}]^\textrm{T}, \end{aligned}$$
(24)

where \(X = \textrm{IS}, \mathrm{{FDM}}\). These models can help better understand the journal bearings’ dynamic behaviour. They can also help to decide on the applicability of both models in specific applications based on their sufficient predictability of dynamical behaviour, especially in the subcritical operational area.

3.1 Stability of limit cycles

The dynamic behaviour of the systems is usually investigated for a given value of parameter \(\lambda \) in dependence on the angular speed \(\overline{\omega }\) which serves as a bifurcation parameter. One of the basic characteristics of journal-bearing systems lies in the fact that there exists a threshold (critical) angular speed \(\overline{\omega }_c\), when the dynamic response of the system becomes fully unstable. The system overcomes so-called total instability (TI). This property was analysed in detail for perfectly balanced rotors, e.g. in [7, 12, 15]. It has been shown that in the case of a perfectly balanced rotor, the dynamic response is formed in dependence on rotor angular velocity by a stable equilibrium curve. The stability of equilibrium is lost by means of Hopf bifurcation, and a LCO response is born. The Hopf bifurcation can be both sub- and supercritical in dependence on the parameter \(\lambda \).

The results obtained for the IS model presented in Figs. 2, 3, 4 and 5 show that this property is preserved in principle, but there is a different mechanism for how the stability of a particular LCO is lost. In the case of an unbalanced rotor, the response is primarily characterised by the LCO (black lines in the mentioned figures), which can lose its stability primarily in dependence on parameter \(\overline{\omega }\) by means of

  • the period-doubling (PD) bifurcation at \(\overline{\omega } = \overline{\omega }_\mathrm{{PD}}\), when the stability of 1-periodic LCO solution is lost and coexisting stable 2-periodic solution is born,

  • the Neimark–Sacker (NS) torus bifurcation appearing at \(\overline{\omega } = \overline{\omega }_c = \overline{\omega }_{\mathrm{{NS}}}\), when the stability of 1-periodic solution is lost and new long-period cycles of different stability types appears, so-called invariant torus cycle (ITC).

The Neimark–Sacker bifurcation points form a curve in 2-parameter bifurcation space, e.g. \((\overline{\omega },\lambda )\), which can be traced using continuation of codimension-2 bifurcation. This curve represents a borderline between stable LCOs and invariant torus cycles (ITCs). The stability of the ITCs can be captured from results gained by means of time-domain integration methods.

Moreover, the PD bifurcation points can be, similarly to NS bifurcation points, traced in a 2-parameter bifurcation space. The points then form curves which split the parameter space and introduce a borderline between areas with qualitatively different solutions. More details are presented in the next section using chosen examples.

Fig. 2
figure 2

Bifurcation diagram of the system response obtained for the IS model: synchronous LCO branches (stable ‘—’, unstable ‘\(\cdots \)’) for \(\lambda =0.2\) and \(\lambda = 1\) and excited by static unbalance \(A_{u} = 0.0481\); codim-2 branch of the NS bifurcation points in \((\overline{\omega },\lambda )\) space (stable ‘—’, unstable ‘\(\cdots \)’); NS bifurcation point ‘\(\Diamond \)’, PD bifurcation point ‘\(\square \)’

Full size image
Fig. 3
figure 3

Bifurcation diagram of the system response obtained for the IS model: synchronous LCO branches (stable ‘—’, unstable ‘\(\cdots \)’) for \(\lambda =0.2\) and \(\lambda = 1\) and excited by static unbalance \(A_{u} = 0.0481\); codim-2 branch of the PD bifurcation points in \((\overline{\omega },\lambda )\) space (stable ‘—’, unstable ‘\(\cdots \)’); NS bifurcation point ‘\(\Diamond \)’, PD bifurcation point ‘\(\square \)’

Full size image
Fig. 4
figure 4

Bifurcation diagram of the system response obtained for the IS model: synchronous LCO branches (stable ‘—’, unstable ‘\(\cdots \)’) for \(\lambda =0.2\) and \(\lambda = 1\) and excited by static unbalance \(A_{u} = 0.0481\); codim-2 branch of the PD bifurcation points in \((\overline{\omega },A_{u})\) space (stable ‘—’, unstable ‘\(\cdots \)’); NS bifurcation point ‘\(\Diamond \)’, PD bifurcation point ‘\(\square \)’

Full size image
Fig. 5
figure 5

Bifurcation diagram of the system response obtained for the IS model: synchronous LCO branches (stable ‘—’, unstable ‘\(\cdots \)’) for \(\lambda =0.2\) and \(\lambda = 1\) and excited by static unbalance \(A_{u} = 0.0481\); codim-2 branch of the NS bifurcation points in \((\overline{\omega },A_{u})\) space (stable ‘—’, unstable ‘\(\cdots \)’); NS bifurcation point ‘\(\Diamond \)’, PD bifurcation point ‘\(\square \)’

Full size image

3.2 Dynamic phenomena in subcritical area

In this section, the dynamics of the system in the non-dimensional form described by (22) will be studied. The behaviour is presented based on results gained using the numerical continuation of limit cycles and codim-2 continuationFootnote 1 of some chosen bifurcation points [13]. The dynamic properties of the system are studied in the space of parameters defined by (24) and for the IS model.

First, the system response to out-of-balance force with a given magnitude \(A_{u}\) in dependence on angular speed \(\overline{\omega }\) is analysed. The response is formed by stable synchronous LCO, whose branch is plotted in the bifurcation diagram by means of local extremes of the limit cycle of relative rotor eccentricity over one period of the response. The stable parts of the branches are plotted by solid black lines and the unstable ones by dashed black lines. For illustration, there are two chosen synchronous LCO branches displayed in Figs. 2, 3, 4 and 5. The upper one for \(\lambda = 1\) corresponds to lightly loaded rotor (journal static load \(W_1 = 2.24\) kN), while the bottom one with \(\lambda = 0.2\) displays the response of highly loaded rotor (journal static load \(W_2 = 11.2\) kN), see Table 1. The stability of synchronous LCOs is globally lost at \(\overline{\omega } = \overline{\omega }_\mathrm{{NS}}\) by means of the Neimark–Sacker torus bifurcation points, which are marked by “\(\Diamond \)” in the above-mentioned figures. Moreover, locally, the stability of synchronous LCOs is lost by means of period-doubling bifurcations at \(\overline{\omega } = \overline{\omega }_{\mathrm{{PD}}}\) (marked by “\(\square \)”), when a stable 2-periodic synchronous LCO is born. For clarity, these 2-periodic branches are not plotted in the diagrams.

Both NS and PD bifurcation points form branches in a two-parameter space composed of two chosen bifurcation parameters. Such a branch can be traced using numerical continuation. In Fig. 2, the blue lines correspond to a codim-2 branch of the NS points in parametric space \((\overline{\omega }, \lambda )\), while parameter \(A_{u}\) remains constant. Since the branch is plotted in (\(\overline{\omega }\), extremes of \(\varepsilon \)) space, the direction of increase in parameter \(\lambda \) is designated by the blue arrows in the figure. Similarly, in Fig. 3, branch of the PD bifurcation points is traced in parametric space \((\overline{\omega }, \lambda )\) and coloured by blue. The two couples of PD branches introduce borders of an area with 2-periodic synchronous LCO. The direction of parameter \(\lambda \) increase is designated by the blue arrow as well.

Table 1 Parameters of investigated rotor-bearing system
Full size table

Figure 4 shows codim-2 branches of PD bifurcation points in parametric space \((\overline{\omega }, A_{u})\). These branches differ for different values of parameter \(\lambda \). It can be seen that there is a critical value of parameter \(A_{u}^c=0.0294\) when for \(A_{u} < A_{u}^c\), the PD bifurcation points on the synchronous LCO branches disappear. Similarly, the branches of NS bifurcation points can be traced in parametric space \((\overline{\omega }, A_{u})\). So, it can be seen how the critical rotor speed \(\overline{\omega }_\mathrm{{NS}}\) increases with respect to the increasing amplitude of out-of-balance excitation. It is evident that as the unbalance grows, the system is then stable for smaller ranges of operational speeds.

4 Time domain simulation of cylindrical journal bearings

This section presents the transient simulation results and compares them with the numerical continuation results discussed in Sect. 3. The model of a 2-DoF rotor-bearing system discussed in Sect. 2.1 is utilised to simulate motion. The HD forces are evaluated using both the IS model and the FDM. The results are presented in the non-dimensional form for parameters \(\lambda = 0.2\) and \(A_{u} = \lbrace 0, 0.0241, 0.0481, 0.0602 \rbrace \), which corresponds, e.g. to dimensional parameters listed in Table 1.

The transient response was simulated for 10 s for each speed from the investigated speed range with speed-step \(\Delta \overline{\omega } = 0.01869\), which corresponds to 50 rpm considering the parameters from Table 1. The initial position was set to the static equilibrium point resulting from the static analysis, and the initial velocity was zero. The static analysis was performed using the Levenberg–Marquardt algorithm implemented in the fsolve Matlab function. The set of the ordinary differential equations (1) was solved by a variable-step, variable-order solver based on the numerical differentiation formulae implemented in the ode15s Matlab function. Solver tolerances were set to relative errors \(10^{-6}\) and absolute errors \(10^{-8}\). These values are based on some preliminary testing of the convergence.

4.1 Post-processing methods

The results of each investigated case are presented using a bifurcation diagram which depicts local extremes of the relative eccentricity \(\varepsilon \) against rotor speed \(\overline{\omega }\). The local extremes of \(\varepsilon \) are pictured in red (local maxima) and black (local minima). Each bifurcation diagram further shows the static equilibrium points (golden colour).

Selected sections of the bifurcation diagrams are displayed in the form of a journal trajectory. The trajectories contain Poincaré sections constructed from the journal positions at the start of each revolution. The trajectories are further examined using a numerical method proposed by Wolf et al. [38], which estimates the largest Lyapunov exponent \(L_{\textrm{max}}\) from the temporal evolution of the phase trajectory. The largest Lyapunov exponent \(L_{\textrm{max}}\) indicates how quickly the phase trajectory converges or diverges. This (exponential) rate of change is closely related to the predictability of the underlying time series [38]:

  1. 1.

    \(L_{\textrm{max}} < 0\) bit/s implies the phase trajectory converges to an asymptotically stable solution such as a fixed point trajectory.

  2. 2.

    \(L_{\textrm{max}} = 0\) bit/s implies that the phase trajectory does not converge to a single point, which is typical for closed trajectories, including a limit cycle or a limit torus.

  3. 3.

    \(L_{\textrm{max}} > 0\) bit/s indicates nontrivial time evolution of the phase trajectory. The exact classification of the corresponding attractor can be decided if the whole spectrum of Lyapunov exponents is known. A high value of \(L_{\textrm{max}}\) suggests a high level of entropy in the dynamic system, which is often associated with the chaotic nature of the system. However, \(L_{\textrm{max}} > 0\) does not guarantee global instability of the system because some strange attractors, which are locally unstable but globally stable, have positive \(L_{\textrm{max}}\).

\(L_{\textrm{max}}\) estimates obtained by Wolf’s method [38] are mildly sensitive to estimator parameters. Therefore, this work utilises 290 combinations of the parameters to compute running estimates of \(L_{\textrm{max}}\) for each analysed phase trajectory. The last 100 samples from each running estimate are further analysed, yielding 29,000 estimates of \(L_{\textrm{max}}\) for each analysed phase trajectory. Statistical characteristics such as median and quartiles hint at the expected value of \(L_{\textrm{max}}\) and its uncertainty bounds.

Fig. 6
figure 6

Bifurcation diagrams of the relative eccentricity of the journal response to static load, harmonic excitation by various static unbalances and hydrodynamic force obtained by the IS model and the finite difference method for bearing with parameter \(\lambda =0.2\)

Full size image
Fig. 7
figure 7

Journal orbits and Poincaré sections (black points) for bearing with parameter \(\lambda =0.2\) and static unbalance \(A_{u} = 0.0602\). Hydrodynamic force is calculated by the finite difference method

Full size image
Fig. 8
figure 8

Box chart of Lyapunov exponents \(\lambda _{\max }\) estimated from trajectories depicted in Fig. 7. Each blue box spans from the first quartile \(Q_{0.25}\) to the third quartile \(Q_{0.75}\) containing 50 % of estimates. Golden outliers are more than \(1.5 \left( Q_{0.75} - Q_{0.25}\right) \) away from the edges of the box. Black whiskers connect the edges of the box with the nonoutlier minimum or maximum. In general, the span delimited by the whiskers contains at least 99 % of estimates. Numbers indicate the median from the estimates and tolerances from the median to \(Q_{0.25}\) and \(Q_{0.75}\)

Full size image

4.2 Results and discussion

The left column in Fig. 6 shows the bifurcation diagrams obtained utilising the IS model of the HD forces. All unbalanced rotors experience the period-doubling between \(\overline{\omega } \approx 2.3\) and \(\overline{\omega } \approx 2.7\). The period-doubling bifurcation is barely visible in the case of the lowest static unbalance \(A_{u} = 0.0241\), but it still occurs. The width of the period-doubling region increases with the increasing magnitude of the static unbalance, which corresponds with the numerical continuation results presented in Fig. 4. If the HD forces are evaluated by the FDM instead of the IS model, the period-doubling bifurcation does not appear for \(A_{u} = \lbrace 0.0241,\,0.0481 \rbrace \), see the right column in Fig. 6. In these cases, the oil film damping presumably attenuates the sub-synchronous vibration accompanying the period-doubling bifurcation.

The authors’ previous work [15] supports this hypothesis, demonstrating that the employed HD force models differ in cross-coupling damping coefficients. The HD force calculated using the FDM has a more significant damping effect than the HD force evaluated by the IS model. Adiletta et al. [1] found the range of the angular speed at which the sub-synchronous vibration can be observed experimentally is smaller than expected based on the theoretical analysis. Since he used the IS model, it is reasonable to propose a hypothesis claiming that the IS model underestimates the dissipative force in the oil film. Figure 7 suggests that the trajectories emerging from the period-doubling bifurcation are at least marginally stable. The analysis of \(L_\textrm{max}\) supports this assumption. Figure 8 shows that \(L_\textrm{max}\) for \(\lambda = 0.2,\,A_{u} = 0.0602\) and \(\overline{\omega } = \left\{ 2.2989,\,2.3363\right\} \) is likely a non-positive number close to zero.

Oil whirl starts developing after surpassing the threshold speed, which is ca. \(\overline{\omega } = 2.9\) in the case of the IS model and \(\overline{\omega } = 2.9 - 3.1\) in the case of the FDM. According to the bifurcation analysis presented in the previous section, the threshold speed is associated with the Hopf bifurcation (a fixed point trajectory changes to a limit cycle) if the rotor is perfectly balanced or with the Neimark–Sacker bifurcation (a limit cycle changes to a torus trajectory) if the rotor is unbalanced. Here, several sub-synchronous vibrations dominate the response, with the most prominent component located at ca. \(0.4\,\overline{\omega }\). The majority of the components are incommensurable with the rotor speed, resulting in quasiperiodic motion. The corresponding trajectories are rather complicated and somewhat difficult to analyse. The trajectories at \(\overline{\omega } = \left\{ 3.0652,\,3.0839,\,3.1026,\,3.1587 \right\} \) fill a limited area after several hundred cycles as can be seen in Fig. 7. At \(\overline{\omega } = \left\{ 3.1213,\,3.147 \right\} \), the main sub-synchronous component becomes locked to \(0.4\,\overline{\omega }\). Hence, the quasiperiodic motion transforms into N-periodic motion.

Interestingly, Wolf’s method suggests that \(L_\textrm{max}\) of these trajectories is a non-negative number. These estimates are caused by subtle changes in vibration magnitudes through cycles, which are apparent in Fig. 7. There, the trajectory at \(\overline{\omega } = 3.1213\) appears to be pulsating, and the Poincaré points are scattered slightly. However, the Poincaré sections do not evidence strange attractors or chaos. Therefore, \(L_{\textrm{max}}\) estimates are probably non-negative because the analysed trajectories have very long transient parts and are not fully stabilised.

Finally, the trajectories become circular once the oil whirl develops fully, and the motion is 2-periodic.

5 Conclusions

This work provided a comprehensive analysis of the nonlinear dynamics of an unbalanced 2-DoF rotor supported on a cylindrical journal bearing (JB). The equations of motion utilised the infinitely short bearing theory to calculate hydrodynamic forces in the JB. The non-dimensional form of the equations of motion was subjected to numerical continuation concerning varying bearing parameter, static unbalance and rotor speeds. In addition, the results were validated with the time simulations. The time simulations employed the infinitely short (IS) bearing theory and the finite difference method (FDM). Based on the presented results, several keynotes can be summarised:

  • The period-doubling region (2-periodic stable solution) is born due to the static unbalance. The size of the region where the period-doubling occurs increases with the increasing magnitude of static unbalance.

  • Conditions at which the period-doubling occurs significantly depend on the employed hydrodynamic force model. The IS bearing theory predicts the period-doubling at lower rotor speeds than the estimate based on the FDM. Moreover, the size of the region where the period-doubling occurs is larger in the case of the IS bearing theory. Adiletta et al. [1] observed similar discrepancies between experimental data and the IS bearing model, suggesting that the FDM bearing model can be more suitable for predicting the behaviour of the actual rotor-bearing system.

  • The Neimark–Sacker bifurcation (torus bifurcation) appears at lower rotor speeds with the increasing static unbalance.

  • Non-dimensional rotor speed at which the Neimark–Sacker bifurcation occurs changes with the static unbalance if the FDM is employed. On the other hand, the rotor speed remains almost constant in the case of the IS bearing model.

  • The rotor trajectory changes from quasiperiodic to N-periodic en route from the Neimark–Sacker bifurcation to a fully developed oil whirl. The N-periodic motion occurs due to partial synchronisation of the sub-synchronous motion with the rotor speed.

In future work, the authors will focus on the nonlinear dynamics of the unbalanced rotor supported in other fixed-geometry JBs, particularly lemon-bore, offset and multi-lobe JBs. The existing literature suggests that such systems exhibit richer nonlinear behaviour than those analysed in this work. However, a comprehensive study of their subcritical behaviour under the unbalance excitation is still lacking.