Skip to main content
SpringerLink
Log in

Nonlinear modeling and analysis of rotors supported by magnetorheological squeeze film journal bearings

  • Modelling and analysis of mechanical systems dynamics
  • Published:
Meccanica Aims and scope Submit manuscript

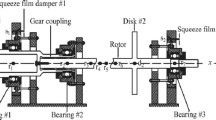
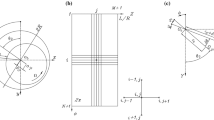
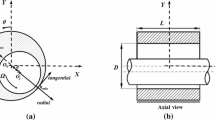
Abstract

The driver coupled to a driven system through mechanical couplings is very common in rotating machinery. These couplings can present angular and parallel misalignments with more or less degree due to manufacturing tolerances or maintenance proceedings. Theoretical and experimental analyses have been published demonstrating the effects of rotor misalignment and the vibration stability of rotor systems. In this work the nonlinear formulation of a magnetorheological fluid journal bearing is included in the finite element model that evaluates the nonlinear responses of a complete rotor system subject to rigid coupling misalignment. The modified Reynolds equations for Bingham viscoplastic materials are implemented in the finite element procedures to evaluate the nonlinear hydrodynamic reaction forces acting on the bearing positions. The finite element formulation for the shaft-line and mechanical couplings is based on the Timoshenko beam theory. Misalignment forces are calculated and included in the equations of motion. The nonlinear dynamic responses are calculated by the modified Newmark method incorporating the Newton–Raphson iteration method to find the equilibrium position at each time step. Bifurcation analysis demonstrates the influence of misalignment to obtain periodic and period-doubling orbit for the center position of the rotor. Results are demonstrated through displacements versus time and frequency responses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Muszynska A (1986) Whirl and whip-rotor/bearing stability problems. J Sound Vib 110(3):443–462

    Article  Google Scholar 

  2. Muszynska A (1988) Stability of whirl and whip in rotor bearing system. J Sound Vib 127(1):49–64

    Article  MathSciNet  Google Scholar 

  3. de Castro HF, Cavalca KL, Nordmann R (2008) Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model. J Sound Vib 317:273–293

    Article  Google Scholar 

  4. Jing J, Meng G, Sun Y, Xia S (2004) On the non-linear dynamic of a rotor-bearing system. J Sound Vib 274:1031–1044

    Article  Google Scholar 

  5. Wang JK, Khonsari MM (2006) Bifurcation analysis of a flexible rotor supported by two fluid-film journal bearing. J Tribol 128:594–603

    Article  Google Scholar 

  6. Irannejad M, Ohadi A (2017) Vibration analysis of a rotor supported on magnetorheological squeeze film damper with short bearing approximation: A contrast between short and long bearing approximations. J Vib Control 23(11):1808–1972

    Article  MathSciNet  Google Scholar 

  7. Adiletta G, Guido AR, Rossi C (1996) Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dyn 10:251–269

    Article  Google Scholar 

  8. Xu M, Marangoni RD (1994) Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, Part I: Theoretical model and analysis. J Sound Vib 176(5):663–679

    Article  Google Scholar 

  9. Xu M, Marangoni RD (1994) Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, part II: experimental validation. J Sound Vib 176(5):681–691

    Article  Google Scholar 

  10. Al-Hussain KM (2003) Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment. J Sound Vib 266:217–234

    Article  Google Scholar 

  11. Sekhar AS, Prabhu BS (1995) Effects of coupling misalignment on vibrations of rotating machinery. J Sound Vib 185(4):655–671

    Article  Google Scholar 

  12. Pennacchi P, Vania A, Chatterton S (2012) Nonlinear effects caused by coupling misalignment in rotors equipped with journal bearings. Mech Syst Signal Process 30:306–322

    Article  Google Scholar 

  13. Nabarrete A, Melo VY, Balthazar JM, Tusset AM. (2017) Nonlinear analysis of rotors with rigid coupling misalignment. In: Awrejcewicz J, Kamierczak M, Mrozowski J, Olejnik P. (Organizers). Vibration, Control and Stability of Dynamical Systems. DAB & M of TUL Press, Lodz, pp 323–334 ISBN 978-83-935312-5-7

  14. Fonseca GF, Nabarrete A (2019) Finite element analysis of magneto-rheological fluid embedded on journal bearings. In: Awrejcewicz J, Kamierczak M, Olejnik P (eds) Applicable solutions in non-linear dynamical systems. Lodz University of Technology, Lodz, pp 151–162 ISBN 978-83-66287-30-3

    Google Scholar 

  15. Wang J, Feng N, Meng G, Hahn EJ (2006) Vibration control of rotor by squeeze film damper with magnetorheological fluid. J Intell Mater Syst Struct 17:353–357

    Article  Google Scholar 

  16. Tichy JA (1993) Behavior of a squeeze film damper with an electrorheological fluid. Tribol Trans 36(1):127–133

    Article  Google Scholar 

  17. Nelson HD, McVaugh JM (1976) The dynamics of rotor-bearing systems using finite elements. J Eng Ind 98:593–599

    Article  Google Scholar 

  18. Nelson HD (1980) A finite rotating shaft element using Timoshenko beam theory. J Mech Des 102:793–803

    Google Scholar 

  19. Wada S, Hayashi H, Haga K (1973) Behavior of a bingham solid in hydrodynamic lubrication—part 1. Gen Theory Bull JSME 16(92):432–440

    Article  Google Scholar 

  20. Ginder JM, Davis LC (1994) Shear stresses in magnetorheological fluids: role of magnetic saturation. Appl Phys Lett 65(26):3410–3412

    Article  Google Scholar 

  21. Zapomel J, Ferfecki P, Forte PA (2012) A computational investigation of the transient response of an unbalanced rigid rotor flexibly supported and damped by short magnetorheological squeeze film dampers. Smart Mater Struct 21:1–12

    Article  Google Scholar 

  22. Wang J, Meng G, Hahn E (2003) Experimental study on vibration properties and control of squeeze mode mr fluid damper-flexible rotor system. In: ASME 2003 design engineering technical conferences and computers and information in engineering conference, Chicago, 2–6 September (2003) pp 1–5

  23. Bompos DA, Nikolakopoulos PG (2011) CFD simulation of magnetorheological uid journal bearings. Simul Model Pract Theory 19:1035–1060

    Article  Google Scholar 

  24. Bathe K-J (1996) Finite element procedures in engineering analysis. Prentice-Hall, New York

    Google Scholar 

  25. Zhang J (2020) A stable two-step time integration methods with controllable numerical dissipation for structural dynamics. Int J Numer Methods Eng 121:54–92

    Article  MathSciNet  Google Scholar 

  26. Chopra AK (1995) Dynamics of structures: theory and applications to earthquake engineering. Prentice-Hall, New York

    MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the Fundao de Amparo Pesquisa do Estado de So Paulo (FAPESP) for funding this reasearch with Grant No. 2015/20363-6.

Author information

Authors and Affiliations

  1. Aerospace Engineering, Aeronautics Institute of Technology (ITA), Praça Marechal Eduardo Gomes, 50 - Vila das Acácias, São José dos Campos, SP, 12228-900, Brazil

    Airton Nabarrete & Gustavo de Freitas Fonseca

Authors
  1. Airton Nabarrete
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gustavo de Freitas Fonseca
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Airton Nabarrete.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Funding

This study was funded by Fundao de Amparo Pesquisa do Estado de So Paulo (FAPESP) (Grant No. 2015/20363-6).

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nabarrete, A., de Freitas Fonseca, G. Nonlinear modeling and analysis of rotors supported by magnetorheological squeeze film journal bearings. Meccanica 56, 873–886 (2021). https://doi.org/10.1007/s11012-020-01245-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-020-01245-8

Keywords

Search

Navigation