1 Introduction

Journal bearing is one of the crucial elements used in industry. It has many applications in heavy-duty machinery whether moderate or high speed such as reciprocating engines [1, 2], turbomachines [3, 4], centrifugal pumps [5, 6] and turbocharger [7,8,9]. Many of these machines are required to spin at very high speeds to improve their efficiency. Therefore, it is important to investigate and evaluate the threshold whirling speed, because above this speed oil whirl may be occurred [10, 11]. However, some applications are reported to operate at speeds higher than this threshold value in the stable condition [12]. In addition, the experimental work of Muszynska [13], Deepak and Noah [14] showed that a stable whirling is occurred after threshold speed. Therefore, it is important to investigate the nonlinear dynamics behavior of journal bearings to improve the future design of rotating machinery.

The dynamic modelling of journal bearings requires the evaluation of the bearing forces. Since the fluid film pressure distribution inside the journal bearing can be described by Reynolds equation, the bearing forces can be obtained from the integration of the bearing fluid film pressure distribution. In case of short and long bearings, Reynolds equation can be approximated and simplified so that the bearing forces can be obtained analytically, see for example [6, 15, 16]. Nishimura et al. [6] investigated the nonlinear dynamics and stability of a vertical flexible rotor supported by short journal bearing. Castro et al. [15] investigated the nonlinear dynamics of rotors supported by journal bearings based on short bearing approximation. They investigated two types of instability, which are ‘oil whirl’ and ‘oil whip’ during run-up and run-down. In case of finite length bearings, where the analytical solution for Reynolds equation is not available, the bearing forces can be obtained by direct integration of Reynolds equation. In dynamic analysis, this integration is required to be done each time step, which is computationally expensive especially if very fine mesh is considered [17,18,19].

Alternatively, and more commonly is to represent the bearing forces using stiffness and damping coefficients. These coefficients are used to evaluate the bearing forces and to investigate the system dynamics. These coefficients are simply based on the Taylor expansion of the bearing forces. Much research considers only the linear first-order approximations, while others consider higher-order approximation [20,21,22]. There are different methods to obtain the bearing coefficients, such as experimental [23, 24] analytical [25,26,27], finite difference method(FDM) [28,29,30], finite element method (FEM) [31,32,33], meshless method with radial basis (MMRB) [34] and computational fluid dynamics (CFD) [35, 36].

Investigating the Hopf bifurcation stability is important because it represents the transformation from spin motion to periodic whirl motion. Although the bearing forces based on linear first-order approximation coefficients are sufficient to obtain the threshold speed, they are not sufficient to judge the stability of periodic solution and whether it is subcritical or supercritical bifurcation. In the case of subcritical bifurcation, if the amplitude of perturbation is located outside the limit cycle, the stability of the rotor bearing system is lost and the perturbation will trigger oil whip; subsequently, the system becomes unstable. If the perturbation is located inside the limit cycle, the rotor will stabilize at a point and the system will remain stable. In the case of supercritical bifurcation and above the threshold speed, the limit cycles are stable and they attract the rotor centre if the perturbation was inside or outside the limit cycle, which physically means that the rotor will whirl in this limit cycle [14, 37]. This motivates the researchers to use analytical solution for bearing forces where possible or to use higher-order bearing coefficients.

Dake et al. [38] investigated the nonlinear dynamics and stability of a rotor supported by hydrodynamic journal bearings. They investigated the stability based on both linear bearing coefficients and on bearing forces from the analytical solution. Smolik et al. [39] investigated the stability of rotor bearing system based on the threshold stability curves. They used different approaches to calculate the bearing forces, infinitely short, infinitely short approximation with correction factor for finite length bearing, finite difference, and finite element. They also investigated the run-up time and acceleration.

Miraskari et al. [40] investigated the nonlinear dynamics of flexible rotor supported by journal bearings. The second-order nonlinear bearing coefficients are obtained using the perturbation method. Then, they used a shooting method to evaluate the stability of the periodic solution. Chasalevris [41] investigated the Hopf bifurcation of flexible rotor supported by journal bearings. Chasalevris investigated the lemon bore and partial arc types of bearings. Chasalevris used Hopf bifurcation theory introduced by Hassard et al. [42] to investigate the stability of periodic solution.

The previous literature shows that many studies for the nonlinear dynamics of journal bearing are based on the analytical solution which is only available in case of short or long bearings. Little studies are done based on the second-order linear coefficient. Moreover, very little studies have been done on higher-order bearing coefficients. The main purpose of this study is to evaluate the third-order bearing coefficients using infinitesimal perturbation method. The obtained coefficients are used to investigate the stability of a flexible rotor/disc supported on two symmetric hydrodynamic journal bearings.

After this introduction, the numerical steps to obtain the journal bearing third-order bearing coefficients are presented on the mathematical model section. Then, the dynamic model of flexible rotor supported on two symmetric journal bearings is presented. The results of journal bearing coefficients and their verification and mesh sensitivity are presented on the results and discussion section. Moreover, the stability and continuation analysis of the dynamical model are discussed at the dynamical results subsection. Finally, the most important outcomes and conclusions are presented in the conclusion section.

2 Analytical model

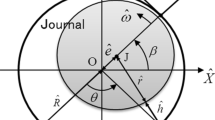
In this section, the pressure distribution of the journal bearing is evaluated and then used in the calculations of the stiffness and damping coefficients of the oil film journal bearing. Then, these coefficients are used in the dynamic modeling of the elastic rotor-bearing system. The model is for full circular journal bearing \(o_b\) is the center of the bearing, \(o_{js}\) is the center of the journal or shaft at the equilibrium position and \(o_j\) is the perturbed journal center. R is the radius of the bearing and \(R_j\) is the radius of the journal. The radial clearance is \(c=R-R_j\). The height of the oil film between the journal and the bearing at any angle is h. \({e_0, \theta }_0\) are the eccentricity and the attitude angle at the steady-state equilibrium. \(O_{js}\) is the center of the journal or shaft at the equilibrium position in terms of dimensionless coordinates and \(O_j\) is the perturbed journal center in terms of dimensionless coordinates , see Fig. 1c.

Fig. 1
figure 1

Full circular journal bearing: a schematic of the journal bearing coordinates, b journal bearing mesh, c perturbed journal bearing in dimensionless coordinates X and Y

Full size image

The pressure distribution inside the fluid film can be described by Reynolds equation as follows:

$$\begin{aligned}&\frac{1}{R^2}\frac{\partial }{\partial \phi }\left( \frac{\rho h^3}{12\mu }\frac{\partial p}{\partial \phi }\right) +\frac{\partial }{\partial z}\left( \frac{\rho h^3}{12\mu }\frac{\partial p}{\partial z}\right) \nonumber \\&\quad =\frac{{\Omega }}{2}\frac{\partial \left( \rho h\right) }{\partial \phi }+\rho \frac{\partial h}{\partial t}, \end{aligned}$$
(1)

where h and p are the oil film thickness and pressure, respectively. \(\phi \) is the angular coordinate with respect to vertical axis, t is the time in sec., \(\Omega \) is the rotational speed of the shaft in rad/sec.. x and y are the sectional bearing coordinates as shown in Fig. 1a. z is the axial coordinate as shown in Fig. 1b. The fluid film viscosity and density are \( \mu \) in \(\text {N\,s/m}^2 \) and \(\rho \) in \(\text {kg/m}^3\), respectively.

Reformulating the Reynolds equation Eq. (1) for the dimensionless representation, it can be written as:

$$\begin{aligned} \frac{\partial }{\partial \phi }\left( H^3\frac{\partial P}{\partial \phi }\right) +\frac{\partial }{\partial Z}\left( H^3\frac{\partial P}{\partial Z}\right) =\frac{\partial H}{\partial \phi }+2\frac{\partial H}{\partial \tau }, \end{aligned}$$
(2)

where H is the oil film dimensionless thickness, \(P=\frac{p}{6\mu \Omega }\left( \frac{c}{R}\right) ^2\) is the dimensionless pressure, \(Z=\frac{z}{R}\) is dimensionless location in the axial direction. The dimensionless time is \(\tau ={\Omega t}\). To evaluate the bearing coefficients, a small perturbation is introduced from the steady-state point as shown in Fig. 1c. The height in dimensionless can be presented as in Eq. (3). After perturbation, the eccentricity ratio, attitude angle and dimensionless height can be obtained from Eqs. (4), (5) and (6), respectively. Since the analysis in the present article is based on the third-order approximation, all the differences with order higher than three are omitted.

$$\begin{aligned} H=1+\varepsilon \cos {\left( \phi -\theta \right) }=\ 1+\varepsilon \cos {\left( \varphi \right) }, \end{aligned}$$
(3)

for which \(\varepsilon \) is the eccentricity ratio and \(\theta \) is the attitude angle, for a small perturbation

$$\begin{aligned} \varepsilon&= \varepsilon _0+\delta \varepsilon \ , \end{aligned}$$
(4)
$$\begin{aligned} \theta&= \theta _0+\delta \theta , \end{aligned}$$
(5)
$$\begin{aligned} H&= 1+\left( \varepsilon _0+\delta \varepsilon \ \right) \cos {\left( \varphi _0-\delta \theta \right) }\nonumber \\&=1+\left( \varepsilon _0+\delta \varepsilon \ \right) \left[ \cos {\left( \varphi _0\right) }\cos {\left( \delta \theta \right) }\nonumber \right. \nonumber \\&\quad \left. +\sin {\left( \varphi _0\right) }\sin {\left( \delta \theta \ \right) }\right] , \end{aligned}$$
(6)

For small \(\delta \theta \), substitute \( \cos {\left( \delta \theta \ \right) =1-}\frac{{\delta \theta }^2}{2}\) and \(\sin {\left( \delta \theta \ \right) =}\delta \theta -\frac{{\delta \theta }^3}{6}\), then Eq (6) can be written as

$$\begin{aligned} H= & {} 1+\left( \varepsilon _0+\delta \varepsilon \ \right) \left[ \cos {\left( \varphi _0\right) }\left( 1-\frac{\delta \theta ^2}{2}\right) \right. \nonumber \\&\left. +\,{\sin {\left( \varphi _0\right) }\left( \delta \theta -\frac{{\delta \theta }^3}{6}\right) }\ \right] . \end{aligned}$$
(7)

Equation (7) can be expanded as follows:

$$\begin{aligned} \begin{aligned} H&= 1+\varepsilon _0\cos {\left( \varphi _0\right) }+\varepsilon _0\delta \theta \sin {\left( \varphi _0\right) }{+\delta \varepsilon }\cos {\left( \varphi _0\right) }\\&\quad +\delta \varepsilon \ \delta \theta \sin {\left( \varphi _0\right) } \\&\quad -\frac{1}{2}\varepsilon _0{\delta \theta }^2\cos {\left( \varphi _0\right) }-\frac{{\delta \theta }^2}{2}\delta \varepsilon \cos {\left( \varphi _0\right) }\\&\quad - \varepsilon _0\frac{{\delta \theta }^3}{6}\sin {\left( \varphi _0\right) }-\frac{\delta \varepsilon \ {\delta \theta }^3}{6}\sin {\left( \varphi _0\right) } \\&= H_0+H_1+H_2+H_3+O\left( {\delta \theta }^4\right) , \end{aligned} \end{aligned}$$
(8)

for which

$$\begin{aligned} H_0&=1+\varepsilon _0\cos {\left( \varphi _0\right) }, \end{aligned}$$
(9)
$$\begin{aligned} H_1&=\varepsilon _0\delta \theta \sin {\left( \varphi _0\right) }{+\delta \varepsilon }\cos {\left( \varphi _0\right) }, \end{aligned}$$
(10)
$$\begin{aligned} H_2&= \delta \varepsilon \ \delta \theta \sin {\left( \varphi _0\right) }-\frac{1}{2}\varepsilon _0{\delta \theta }^2\cos {\left( \varphi _0\right) } , \end{aligned}$$
(11)
$$\begin{aligned} H_3&= -\frac{{\delta \theta }^2}{2}\delta \varepsilon \cos {\left( \varphi _0\right) }-\varepsilon _0\frac{{\delta \theta }^3}{6}\sin {\left( \varphi _0\right) }. \end{aligned}$$
(12)

Now it is important to transform the oil film height Eq. (8) from polar coordinates to Cartesian coordinates. From the geometry, Fig. 1c, the components \(\delta X\) and \(\delta Y\) can be written as:

$$\begin{aligned} \delta X&= \left( \varepsilon _0+\delta \varepsilon \right) \ \sin \left( \theta _0+\delta \theta \right) -\varepsilon _0\ \sin {\theta }_0 ,\end{aligned}$$
(13)
$$\begin{aligned} \delta Y&= \left( \varepsilon _0+\delta \varepsilon \right) \ \cos \left( \theta _0+\delta \theta \right) -\varepsilon _0\ \cos {\theta }_0. \end{aligned}$$
(14)

Expanding Eqs. (13–14) and reducing higher-order terms, we get the following relation:

$$\begin{aligned} \left\{ \begin{matrix}\delta X\\ \delta Y\\ \end{matrix}\right\} =\left[ \begin{matrix}\sin {\theta }_0\ &{} \cos {\theta }_0\\ \cos { \theta }_0&{}-\sin { \theta }_0\\ \end{matrix}\right] \left\{ \begin{matrix}\delta \varepsilon \\ \varepsilon _0\delta \theta \\ \end{matrix}\right\} .\ \end{aligned}$$
(15)

Reordering Eq. (15), we can obtain the following :

$$\begin{aligned} \left\{ \begin{matrix}\delta \varepsilon \\ \varepsilon _0\delta \theta \\ \end{matrix}\right\}= & {} \left[ \begin{matrix} \sin {\theta }_0\ &{} \cos {\theta }_0\\ \cos {\theta }_0&{}-\sin {\theta }_0\\ \end{matrix}\right] ^{-1}\left\{ \begin{matrix}\delta X\\ \delta Y\\ \end{matrix}\right\} \nonumber \\= & {} \left[ \begin{matrix} \sin {\theta }_0\ &{} \cos {\theta }_0\\ \cos {\theta }_0&{}-\sin {\theta }_0\\ \end{matrix}\right] \left\{ \begin{matrix} \delta X\\ \delta Y\\ \end{matrix}\right\} . \end{aligned}$$
(16)

Substituting the transformation relations in Eq. (16) into Eqs. (9–12) results in

$$\begin{aligned} H_0&= 1+\varepsilon _0\cos {\left( \varphi _0\right) }, \end{aligned}$$
(17)
$$\begin{aligned} H_1&= \delta X\sin {\phi +\delta Y\cos {\phi }}, \end{aligned}$$
(18)
$$\begin{aligned} H_2&=\frac{{\delta X}^2}{{2\ \varepsilon }_0}\left( 2\sin {\theta _0\cos {\theta _0\sin {\varphi _0}}}-\cos ^2\theta _0\cos {\varphi _0}\right) \nonumber \\&\quad +\frac{\delta X\ \delta Y}{{\ \varepsilon }_0}\left( \sin {\theta _0\cos {\theta _0\cos {\varphi _0}}}\nonumber \right. \\&\left. +\cos ^2\theta _0\sin {\varphi _0-\sin ^2\theta _0\sin {\varphi _0}}\right) \nonumber \\&+\frac{{\delta Y}^2}{{2\ \varepsilon }_0}\left( -2\sin {\theta _0\cos {\theta _0\sin {\varphi _0}}}-\sin ^2\theta _0\cos {\varphi _0}\right) . \end{aligned}$$
(19)

The dimensionless pressure distribution P(X, Y, \(X^\prime ,Y^\prime )\) in the fluid film can be expanded using Taylor expansion as follows:

$$\begin{aligned} P= & {} P_0+P_X\delta X+P_Y\delta Y+P_{X^\prime } \delta X^\prime +P_{Y^\prime }\delta Y^\prime \nonumber \\&+0.5P_{XX}\delta X^2+0.5P_{YY}\delta Y^2 \nonumber \\&+P_{XY}\delta X\delta Y+P_{XX^\prime }\delta X\delta X^\prime +P_{XY^\prime }\delta X\delta Y^\prime \nonumber \\&+P_{YX^\prime }\delta Y\delta X^\prime +P_{YY^\prime }\delta Y\delta Y^\prime \nonumber \\&+\frac{1}{6}P_{XXX}\delta X^3+\frac{1}{6}P_{YYY}\delta Y^3 \nonumber \\&+\frac{1}{2}P_{XXY}\delta X^2\delta Y+\frac{1}{2}P_{XYY}\delta X\delta Y^2 \nonumber \\&+\frac{1}{2}P_{XXX^\prime }\delta X^2\delta X^\prime \nonumber \\&+\frac{1}{2}P_{XXY^\prime }\delta X^2\delta Y^\prime +\frac{1}{2}P_{YYX^\prime }\delta Y^2\delta X^\prime \nonumber \\&+\frac{1}{2}P_{YYY^\prime }\delta Y^2\delta Y^\prime +P_{XYX^\prime } \delta X\delta Y\delta X^\prime \nonumber \\&+P_{XYY^\prime }\delta X\delta Y\delta Y^\prime , \end{aligned}$$
(20)

where \(X=\frac{x}{c},\ Y=\frac{y}{c},\ ^{\prime }=\frac{\mathrm {d}}{\mathrm {d}\tau } ,\tau =\Omega t, X^{\prime }=\frac{{\dot{x}}}{\Omega c},Y^{\prime }=\frac{{\dot{y}}}{\Omega c} \), \(\delta X=X-X_0,\delta Y=Y-Y_0\), for which \((X_0,Y_0) \) is the steady-state equilibrium position, and \(P_X=\frac{\partial P}{\partial X} , P_{XX}=\frac{\partial ^2P}{\partial X^2} , P_{XXX}=\frac{\partial ^3P}{\partial X^3}\ ,\ P_{XYY^\prime }=\frac{\partial ^3P}{\partial X\partial Y\partial Y^\prime }\) and so on.

To obtain the steady-state pressure \(P_0\) the Reynolds equation in Eq. (2) is solved using finite difference relations. The derivation of the first-, second- and third-order pressure gradients of Eq. (20) is discussed in “Appendix A”.

2.1 Nonlinear bearing forces

As the induced fluid film pressure, the dimensionless bearing forces \({{\bar{F}}}_X \) and \({{\bar{F}}}_Y\) are approximated to the third order using Taylor series, for which \({{\bar{F}}}_X=\frac{F_x}{W}\) and \({{\bar{F}}}_Y=\frac{F_y}{W}\) , where \(F_x\) is the bearing force in the x direction, \(F_y\) is the bearing force in y direction and W is the bearing load.

$$\begin{aligned} \begin{aligned} {{\bar{F}}}_\zeta&={{\bar{F}}}_{\zeta _0}+\frac{\partial {{\bar{F}}}_\zeta }{\partial X}\delta X+\frac{\partial {{\bar{F}}}_\zeta }{\partial Y}\delta Y+\frac{\partial {{\bar{F}}}_\zeta }{\partial X^{\prime }}\delta X^{\prime }+\frac{\partial {{\bar{F}}}_\zeta }{\partial Y^{\prime }}\delta Y^{\prime }\\&\quad +0.5\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial X^2}\delta X^2 \\&\quad +0.5\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial Y^2}\delta Y^2+\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial X\partial Y}\delta X\delta Y+\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial X\partial X^{\prime }}\delta X\delta X^{\prime }\\&\quad +\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial X\partial Y^{\prime }}\delta X\delta Y^{\prime }+\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial Y\partial X^{\prime }}\delta Y\delta X^{\prime }\\&\quad +\frac{\partial ^2{{\bar{F}}}_\zeta }{\partial Y\partial Y^{\prime }}\delta Y\delta Y^{\prime }+\frac{1}{6}\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X^3}\delta X^3+\frac{1}{6}\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial Y^3}\delta Y^3\\&\quad +0.5\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X^2\partial Y}\delta X^2\delta Y\\&\quad + 0.5\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X\partial Y^2}\delta X\delta Y^2+0.5\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X^2\partial X^{\prime }}\delta X^2\delta X^{\prime }\\&\quad +0.5\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X^2\partial Y^{\prime }}\delta X^2\delta Y^{\prime } \\&\quad + 0.5\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial Y^2\partial X^{\prime }}\delta Y^2\delta X^{\prime }+0.5\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial Y^2\partial Y^{\prime }}\delta Y^2\delta Y^{\prime }\\&\quad +\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X\partial Y\partial X^{\prime }}\delta X\delta Y\delta X^{\prime }+\frac{\partial ^3{{\bar{F}}}_\zeta }{\partial X\partial Y\partial Y^{\prime }}\delta X\delta Y\delta Y^{\prime } \end{aligned} \end{aligned}$$
(21)

where \(\zeta =X \) or Y.

The bearing forces in \(X,\ Y \) directions in Eq. (21) can be written using the bearing first-, second- and third-order coefficients as shown below:

$$\begin{aligned} \begin{aligned} {{\bar{F}}}_\zeta&= {{\bar{F}}}_{\zeta _0}+K_{\zeta X}\delta X+K_{\zeta Y}\delta Y\\&\quad +C_{\zeta X}\delta X^{\prime }+C_{\zeta Y}\delta Y^{\prime }\\&\quad +0.5K_{\zeta XX}\delta X^2 \\&\quad + 0.5K_{\zeta YY}\delta Y^2+K_{\zeta XY}\delta X\delta Y\\&\quad +C_{\zeta XX}\delta X\delta X^{\prime }+C_{\zeta XY}\delta X\delta Y^{\prime }\\&\quad +C_{\zeta YX}\delta Y\delta X^{\prime }+ C_{\zeta YY}\delta Y\delta Y^{\prime } \\&\quad +\frac{1}{6}K_{\zeta XXX}\delta X^3+\frac{1}{6}K_{\zeta YYY}\delta Y^3\\&\quad +0.5K_{\zeta XXY}\delta X^2\delta Y \\&\quad + 0.5K_{\zeta XYY}\delta X\delta Y^2+0.5C_{\zeta XXX}\delta X^2\delta X^{\prime }\\&\quad +0.5C_{\zeta XXY}\delta X^2\delta Y^{\prime } \\&\quad + 0.5C_{\zeta YYX}\delta Y^2\delta X^{\prime }+0.5C_{\zeta YYY}\delta Y^2\delta Y^{\prime }\\&\quad +C_{\zeta XYX}\delta X\delta Y\delta X^{\prime }+C_{\zeta XYY}\delta X\delta Y\delta Y^{\prime } \end{aligned} \end{aligned}$$
(22)
Fig. 2
figure 2

a Elastic rotor supported on two symmetric journal bearings. b Bearing coordinates

Full size image

for which \(X=\frac{x}{c}\) and \(Y=\frac{Y}{c}\) are the dimensionless coordinates, c is the radial clearance.

\(K_{ij}=\frac{k_{ij}\ c}{W}\) and \(C_{ij}=\frac{c_{ij}\ c\ \Omega }{W} \) are the dimensionless linear stiffness and damping coefficients, respectively, where \((i,j=X,Y)\). \(k_{ij}\) and \(c_{ij}\) are stiffness and damping dimensional coefficients, respectively.

\( K_{ijk}=\frac{k_{ijk}\ c^2}{W}\) and \(C_{ijk}=\frac{C_{ijk}\ c^2\Omega }{W}\) are the second-order dimensionless stiffness and damping coefficients, respectively, where \(i,j,k=X,Y\). \( k_{ijk} \) and \(c_{ijk}\) are the second-order stiffness and damping dimensional coefficients, respectively.

\(K_{ijkl}=\frac{k_{ijkl}\ c^3}{W}\) and \(C_{ijkl}=\frac{C_{ijkl}\ c^3\Omega }{W} \) are the third-order dimensionless stiffness and damping coefficients where \( i, j, k, l=X,Y\). \(k_{ijkl}\) and \(c_{ijkl}\) are the third-order stiffness and damping dimensional coefficients.

The bearing forces can be calculated by integrating the pressure over the area as shown below:

$$\begin{aligned} {{\bar{F}}}_X&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(23)
$$\begin{aligned} {{\bar{F}}}_Y&=\int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z. \end{aligned}$$
(24)

Comparing Eqs. (20), (22) to (24), the steady-state force can be obtained as:

$$\begin{aligned} {{\bar{F}}}_{X_0}&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_0\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z,\end{aligned}$$
(25)
$$\begin{aligned} {{\bar{F}}}_{Y_0}&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_0\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z. \end{aligned}$$
(26)

It is worth noting that through the present analysis the only steady-state load in y direction is the weight and no static load in x direction. Therefore, \(F_{x0}=0\) and \(F_{y0}=W \) which also means that

$$\begin{aligned} {{\bar{F}}}_{X_0}=0,{{\bar{F}}}_{Y_0}=1. \end{aligned}$$
(27)

Using this condition and by an iterative method, the steady-state attitude angle can be obtained. Also, the eight first-order coefficients can be obtained from the following equations.

$$\begin{aligned} K_{X\zeta }&=\int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_\zeta \sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z,\end{aligned}$$
(28)
$$\begin{aligned} K_{Y\zeta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta }\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(29)
$$\begin{aligned} C_{X\zeta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta ^\prime }\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(30)
$$\begin{aligned} C_{Y\zeta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta ^\prime }\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(31)

where \(\zeta =X\) or Y which means that by replacing \(\zeta \) by either X or Y the eight equations for the eight coefficients can be obtained from Eqs. (28–31). In addition, the fourteen second-order coefficients can be calculated from

$$\begin{aligned} K_{X\zeta \eta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta }\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(32)
$$\begin{aligned} K_{Y\zeta \eta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta }\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(33)
$$\begin{aligned} C_{X\zeta \eta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta ^\prime }\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z,\end{aligned}$$
(34)
$$\begin{aligned} C_{Y\zeta \eta }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta ^\prime }\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(35)

where each of \(\zeta \) and \( \eta \) can be either X or Y. This means that Eqs. (32–35) represent sixteen equations. These equations are reduced to fourteen equations because \(K_{XYX}=K_{XXY}\) and \(K_{YXY}=K_{YYX}\).

Similarly, the twenty third-order coefficients can be evaluated from the following equations:

$$\begin{aligned} K_{X\zeta \eta \gamma }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta \gamma }\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(36)
$$\begin{aligned} K_{Y\zeta \eta \gamma }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta \gamma }\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z,\end{aligned}$$
(37)
$$\begin{aligned} C_{X\zeta \eta \gamma }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta \gamma ^\prime }\sin {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(38)
$$\begin{aligned} C_{Y\zeta \eta \gamma }&= \int _{0}^{\frac{L}{R}}{\int _{0}^{2\pi }{-P_{\zeta \eta \gamma ^\prime }\cos {\phi }}}\ \mathrm {d}\phi \ \mathrm {d}Z, \end{aligned}$$
(39)

where each of \(\zeta ,\ \eta \ \) and \( \gamma \) can be either X or Y. This means that thirty-two equations can be obtained from Eqs. (36–39), but these equations are reduced to only twenty because of similarity of several coefficients such as \(K_{XYXX}=K_{XXYX}=K_{XXXY}\).

2.2 Rotor-bearing model

In this section, the analytical model for elastic rotor supported on two symmetric journal bearings is investigated. The model is four degree of freedom in x and y directions. In this model, both the mass of rotor inside the journal \(m_j\) and disk mass \(m_d\) are considered, as shown in Fig. 2. A static load 2W is applied on the disc.

The equations of motion for the presented system can be presented as:

$$\begin{aligned} \begin{aligned} 2m_j{\ddot{x}}_j+k_s\left( x_j-x_d\right)&=-2F_x \\ 2m_j{\ddot{y}}_j+k_s\left( y_j-y_d\right)&=-2F_y \\ m_d{\ddot{x}}_d+k_s\left( x_d-x_j\right)&=0 \\ m_d{\ddot{y}}_d+k_s\left( y_d-y_j\right)&=2W \end{aligned} \end{aligned}$$
(40)

For which \(m_j\) is the mass of shaft inside and around the journal and \(m_d\) is the sum of the disc and remaining part of the shaft mass, \(k_s\) is the shaft stiffness, \(F_x\) and \(F_y\) are the bearing forces in x and y directions, respectively, W is the bearing load and \(x_j, y_j, x_d, y_d\) are journal mass geometrical center and disc geometrical center current positions with respect to the journal steady-state position. \(m=m_d+2m_j\) is the total mass of the rotor.

Transforming the equations of motion Eq. (40) into dimensionless form, we get the following equations:

$$\begin{aligned} \begin{aligned} 2M_JX_J^{\prime \prime }+K_S\left( X_J-X_D\right)&=-2{{\bar{F}}}_X, \\ 2M_JY_J^{\prime \prime }+K_S\left( Y_J-Y_D\right)&= -2{{\bar{F}}}_Y, \\ M_DX_D^{\prime \prime }+K_S\left( X_D-X_J\right)&=0, \\ M_DY_D^{\prime \prime }+K_S\left( Y_D-Y_J\right)&=2, \end{aligned} \end{aligned}$$
(41)

where \( X_J=\frac{x_j}{c}, Y_J=\frac{y_j}{c},\ X_D=\frac{x_D}{c},\ Y_D=\frac{y_D}{c},\ ^{\prime }=\frac{\mathrm {d}}{\mathrm {d}\tau } ,\ ^{\prime \prime }=\frac{\mathrm {d}^2}{\mathrm {d}\tau ^2} ,\tau =\Omega t\)

\(X_J^{\prime \prime }=\frac{{\ddot{x}}_j}{{\Omega }^2c},\ Y_J^{\prime \prime }=\frac{{\ddot{y}}_j}{{\Omega }^2c},\ X_D^{\prime \prime }=\frac{{\ddot{x}}_d}{{\Omega }^2c},Y_D^{\prime \prime }=\frac{{\ddot{y}}_d}{{\Omega }^2c} , K_S=\frac{k_s\ c}{W}, M_J=\frac{m_j\Omega ^2c}{W}\) and \( M_D=\frac{m_d\Omega ^2c}{W}\).

\(M_J \) and \(M_D\) are the dimensionless masses of the journal and disc, respectively. Through the current paper, the following mass ratios are considered \({2M}_J=0.1{\bar{M}} \) and \(M_D=0.9 {\bar{M}}\), where \({\bar{M}}\) is the dimensionless total mass of the rotor. The dimensionless shaft stiffness is \(K_S\). The rotational speed is \( \Omega \), and the dimensionless time is \(\tau \). The dimensionless static equilibrium forces are \({{\bar{F}}}_{X_0}=0 \) and \({{\bar{F}}}_{Y_0}=1\).

Substituting Eqs. (22) and (27) in Eq. (41), and converting the resulting equations into the state space form, the final resulting equations can be written as:

$$\begin{aligned} \begin{array}{*{20}{c}} {x_1^\prime = \,}&{}{{x_2}} ,\\ {x_2^\prime = }&{}{\frac{{{K_s}\left( {{x_5} - {x_1}} \right) }}{{2{M_J}}} - \frac{1}{{{M_J}}}\left( \begin{aligned} {K_{XX}}{x_1} + {C_{XX}}{x_2} + {K_{XY}}{x_3} + {C_{XY}}{x_4} + 0.5\,{K_{XXX}}x_1^2 \\ + 0.5\,{K_{XYY}}x_3^2 + {K_{XXY}}{x_1}{x_3} + {C_{XXX}}{x_1}{x_2} + {C_{XXY}}{x_1}{x_4} \\ + {C_{XYX}}{x_3}{x_2} + {C_{XYY}}{x_3}{x_4} + \frac{1}{6}{K_{XXXX}}x_1^3 + \frac{1}{6}{K_{XYYY}}x_3^3 \\ + 0.5{K_{XXXY}}x_1^2{x_3} + 0.5{K_{XXYY}}{x_1}x_3^2 + 0.5{C_{XXXX}}x_1^2{x_2} + \\ 0.5{C_{XXXY}}x_1^2{x_4} + 0.5{C_{XYYX}}x_3^2{x_2} + 0.5{C_{XYYY}}x_3^2{x_4} + \\ {C_{XXYX}}{x_1}{x_3}{x_2} + {C_{XXYY}}{x_1}{x_3}{x_4} \\ \end{aligned} \right) }, \\ {x_3^\prime = }&{}{{x_4}} ,\\ {x_4^\prime = }&{}{\frac{{{K_s}\left( {{x_7} - {x_3}} \right) }}{{2{M_J}}} - \frac{1}{{{M_J}}}\left( \begin{aligned} 1 + {K_{YX}}{x_1} + {C_{YX}}{x_2} + {K_{YY}}{x_3} + {C_{YY}}{x_4} + 0.5\,{K_{YXX}}x_1^2 \\ + 0.5\,{K_{YYY}}x_3^2 + {K_{YXY}}{x_1}{x_3} + {C_{YXX}}{x_1}{x_2} + {C_{YXY}}{x_1}{x_4} \\ + {C_{YYX}}{x_3}{x_2} + {C_{YYY}}{x_3}{x_4} + \frac{1}{6}{K_{YXXX}}x_1^3 + \frac{1}{6}{K_{YYYY}}x_3^3 \\ + 0.5{K_{YXXY}}x_1^2{x_3} + 0.5{K_{YXYY}}{x_1}x_3^2 + 0.5{C_{YXXX}}x_1^2{x_2} \\ + 0.5{C_{YXXY}}x_1^2{x_4} + 0.5{C_{YYYX}}x_3^2{x_2} + 0.5{C_{YYYY}}x_3^2{x_4} + \\ {C_{YXYX}}{x_1}{x_3}{x_2} + {C_{YXYY}}{x_1}{x_3}{x_4} \\ \end{aligned} \right) }, \\ {x_5^\prime = }&{}{{x_6}} ,\\ {x_6^\prime = }&{}{\frac{{{K_s}\left( {{x_1} - {x_5}} \right) }}{{{M_D}}}}, \\ {x_7^\prime = }&{}{{x_8}} ,\\ {x_8^\prime = }&{}{\frac{{2 + {K_s}\left( {{x_3} - {x_7}} \right) }}{{{M_D}}}}, \end{array} \end{aligned}$$
(42)

where \(x_1=X_J,\ x_2=X_J^\prime , x_3=Y_J, x_4=Y_J^\prime , x_5=X_D ,\ x_6=X_D^\prime , x_7=\ Y_D, x_8=\ Y_D^\prime .\)

Finally, Eq. (42) can be written as:

$$\begin{aligned} {\mathbf {x}}^\prime ={\mathbf {f}}\left( {\mathbf {x}},\ {\bar{M}}\right) \end{aligned}$$
(43)

where \({\mathbf {x}}=[x_1\ x_2\ x_3\ x_4 \ x_5\ x_6\ x_7\ x_8] , {\bar{M}}=M_D+{2M}_J \) and \( \frac{\ M_J}{M_D}=\frac{1}{18}\).

The system of equations in Eq. (43) can have a periodic solution \(x(\tau )=x\left( \tau +T\right) \). This is occurred above what is called the threshold speed \(\left( {\bar{M}}\ge {{\bar{M}}}_{\mathrm{th}}\right) \), where T is the dimensionless periodic time of solution and \({{\bar{M}}}_{\mathrm{th}}\) is the dimensionless threshold mass of the system. This will be discussed in detail in the results section.

3 Results and discussion

In this section, the first-, second- and third-order bearing coefficients are calculated using infinitesimal perturbation analysis. The bearing coefficients are presented and listed for full circular journal bearing. Perturbation analysis is used to investigate the validity range of these coefficients. Afterwards, the bearing coefficients are used to investigate the dynamics of flexible rotor supported by two symmetric journal bearings.

3.1 Perturbation analysis

In this section, a perturbation analysis is used to validate the obtained bearing coefficients. This analysis is executed using un-grooved full circular journal bearing with L/D ratio of 1. This is done by applying displacement and velocity perturbations to the equilibrium point and then evaluated the obtained forces using four different methods. These methods are based on direct integration of Reynolds equation \(({{\bar{F}}}_{Re.})\), first-order coefficients \((\bar{F_1})\), second-order coefficients \(({{\bar{F}}}_2)\) and third-order coefficients \(({{\bar{F}}}_3)\). The component of these forces in X and Y directions is evaluated and plotted in Fig. 3. To investigate the validity range of the bearing linear and nonlinear coefficients in evaluating the nonlinear bearing forces around the equilibrium point, four different values of perturbations are used. The first one is \((\delta X=0.0001,\delta X^{\prime }=0.0001,\delta Y=0.0001 \ \) and \( \delta Y^{\prime }=0.0001)\), and its results are plotted in Fig. 3a. In Fig. 3, the left column represents the X component of the perturbation force and the right column represents the Y component of the perturbation force. All the subfigures of Fig. 3 are drawn versus the Sommerfeld number. Figures 3b, c and d are for perturbations \((\delta X=0.001,\delta X^{\prime }=0.001,\delta Y=0.001 \) and \( \delta Y^{\prime }=0.001)\), \((\delta X=0.01,\delta X^{\prime }=0.01,\delta Y=0.01 \) and \( \delta Y^{\prime }=0.01) \) and \( (\delta X=0.1,\delta X^{\prime }=0.1,\delta Y=0.1 \) and \( \delta Y^{\prime }=0.1)\ \), respectively. The figure results show that at low perturbations the forces evaluated using all the four methods are approximately the same as shown in Fig. 3a, b. However, by increasing the values of perturbation as in Fig. 3c, a significant deviation between the forces evaluated based on the nonlinear coefficients and that based on the direct Reynolds integration forces \(({{\bar{F}}}_{Re.})\) is recognized. The last case in Fig. 3d shows that at very low and high Sommerfeld number the deviation between the forces is larger than when \(S\in \left[ 0.1-0.6\right] \). Also, the x component of force approximation based on the third-order coefficients was closer to the forces based on direct integration of Reynolds equation at \(S<0.55 \) and y component of force approximation was closer to the forces based on direct integration of Reynolds equation when \(S<0.3\).

Fig. 3
figure 3

Semi-log plot for the dimensionless force components \({\bar{F}}_X\) and \({\bar{F}}_Y\) resulted from journal perturbation in X and Y directions for ungrooved journal bearing with \(L/D=1\) a \((\delta X=0.0001,\delta X^{\prime }=0.0001,\delta Y=0.0001 \ \) and \( \ \delta Y^{\prime }=0.0001)\), b \((\delta X=0.001,\delta X^{\prime }=0.001,\delta Y=0.001 \) and \( \delta Y^{\prime }=0.001) \), c \( (\delta X=0.01,\delta X^{\prime }=0.01,\delta Y=0.01 \ \) and \( \delta Y^{\prime }=0.01)\) and d \( (\delta X=0.1,\delta X^{\prime }=0.1,\delta Y=0.1 \) and \( \delta Y^{\prime }=0.1)\)

Full size image

3.2 Journal bearing coefficients and mesh sensitivity

In this section, the bearing linear and nonlinear coefficients based on first-, second- and third-order coefficients are evaluated. This is done using infinitesimal perturbation as discussed in the analysis section. The presented results are for un-grooved full circular journal bearing with L/D ratio of 1. The linear bearing coefficients are eight and plotted in Fig. 4 a. The nonlinear second-order bearing coefficients are fourteen and are plotted in Fig. 4b . The third-order coefficients are twenty and are plotted in Fig. 5. The effect of mesh size on the bearing coefficients is also investigated graphically for all the coefficients. Several mesh sizes are investigated, but only four cases are presented to avoid over density of the figures. The presented mesh sizes are selected to vary from coarse to fine mesh. These mesh sizes are \(50 \times 100, 100 \times 200, 150 \times 600 \) and \(200 \times 800\). In both Figs. 4 and 5, the color is used to differentiate the bearing coefficients and the line type is used to differentiate the mesh size as shown in the subfigures legend and the figure general legend. The results of Fig. 4 show that for the plotted coefficients the results of mesh \(100 \times 400, 150 \times 600\) and \(200 \times 800\) are identical over the full range of Sommerfeld number. The results of Fig. 5 show that the bearing coefficients obtained using mesh \(100 \times 400 \) converge with that \(200 \times 800\) in most coefficients. However, for \(K_{XXXX},C_{XXXX},K_{YXXX}\) and \( C_{YXXX}\) mesh \(100 \times 400\) is not sufficient. In addition, the figure shows that mesh \(150\times 600\) and \(200 \times 800\) results are converged for all coefficients. Therefore, mesh \(150\times 600\) was considered as minimum mesh used in coefficients evaluation during the present paper. Numerical values of the obtained parameters using mesh size of \(150\times 600\) are presented in Tables 2 and 3.

Fig. 4
figure 4

(Color online) Loglog plot for un-grooved journal bearing stiffness and damping coefficients(absolute) versus the Sommerfeld number. \(L/D=1\), a First-order bearing coefficients, b second-order bearing coefficients. In this figure the dotted line for mesh \(50\times 200\), dashed line for mesh \(100\times 400\), centerline for mesh \(150\times 600\) and solid line for mesh \(200\times 800\)

Full size image
Fig. 5
figure 5

(Color online) Loglog plot for un-grooved full circular journal bearing third-order stiffness and damping coefficients (absolute) versus the Sommerfeld number. L/D ratio is unity. In this figure, the dotted line for mesh \(50\times 200\), dashed line for mesh \(100\times 400\), centerline for mesh \(150\times 600\) and solid line for mesh \(200\times 800\)

Full size image

3.3 Verification with previous results

Here, the first-, second- and third-order bearing coefficients are compared with the results of Miraskari et al. [27]. However, the reference coefficients are calculated based on Reynolds short bearing equation. Eighteen selected bearing coefficients are used for the comparison. These are divided as follows: six first-order bearing coefficients which are plotted in the first row of Fig. 6 and six second-order bearing coefficients located in the second row of Fig. 6 and six third-order bearing coefficients plotted at the last row of Fig. 6. The finite bearing coefficients are obtained at \(L/D=0.5\) to approach the short bearing results, and these results are plotted using solid lines. The results of Miraskari et al. [27] are plotted using dashed lines. It is worth noting that the reference results are processed before plotting because the dimensionless parameters used in the reference paper are not the same with that considered in that paper. Figure 6 shows that the results of both methods are close to each other with a small deviation. This deviation can be explained by the fact that the short bearing Reynolds equation is a simplification to the general Reynolds equation.

Fig. 6
figure 6

First-, second- and third-order bearing coefficients using present finite bearing analysis at \(L/D=0.5\)(solid lines) versus coefficients obtained based on short bearing approximation(dashed lines) [27]

Full size image

3.4 Dynamic results

3.4.1 Stability analysis

In this section, the calculated bearing coefficients are used to investigate the dynamic analysis of the elastic rotor system presented in Fig. 2. Initially, the stability of the autonomous dynamical system in Eq. (42) is investigated. This is done by evaluating the dimensionless threshold mass \({{\bar{M}}}_{\mathrm{th}}=mc\Omega _{\mathrm{th}}^2/W\), which implicitly includes the threshold speed of the system. The dimensionless threshold mass \({{\bar{M}}}_{\mathrm{th}}\) can be evaluated using the eigenvalues of the Jacobian matrix \({\mathbf {J}}\left( {\mathbf {x}},\ {\bar{M}}\right) \) in Eq. (44) at the fixed points. The fixed points can be obtained by equating Eqs. (43) to zero. This results in \({\mathbf {x}}^*=\left[ \begin{matrix}0&{}0&{}\begin{matrix}0&{}0&{}\begin{matrix}0&{}0&{}\begin{matrix}2/K_s&{}0\\ \end{matrix}\\ \end{matrix}\\ \end{matrix}\\ \end{matrix}\right] ^T\).

$$\begin{aligned}&{\mathbf {J}}\left( {\mathbf {x}},\ {\bar{M}}\right) \nonumber \\&=\frac{\partial {\mathbf {x}}^{\prime }}{\partial {\mathbf {x}}}=\left[ \begin{matrix}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ J_{21}&{}J_{22}&{}J_{23}&{}J_{24}&{}\frac{K_s}{2M_J}&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0\\ J_{41}&{}J_{42}&{}J_{43}&{}J_{44}&{}0&{}0&{}\frac{K_s}{2M_J}&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ \frac{K_s}{M_D}&{}0&{}0&{}0&{}-\frac{K_s}{M_D}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}\frac{K_s}{M_D}&{}0&{}0&{}0&{}-\frac{K_s}{M_D}&{}0\\ \end{matrix}\right] , \end{aligned}$$
(44)

where

$$\begin{aligned} J_{21}&=-\frac{K_s}{2M_J } -\frac{1}{ M_J}\Bigg (K_{XX}+K_{XXX}x_1+K_{XXY}x_3\\&\quad +C_{XXX}x_2+C_{XXY}x_4+\frac{1}{2}K_{XXXX}x_1^2 \\&\quad +K_{XXXY}x_1x_3+\frac{1}{2}K_{XXYY}x_3^2\\&\quad +C_{XXXX}x_1x_2+C_{XXXY}x_1x_4\\&\quad +C_{XXYX}x_3x_2+C_{XXYY}x_3x_4\Bigg ), \\ J_{22}&= -\frac{1}{M_J}\Bigg (C_{XX}+C_{XXX}x_1+C_{XYX}x_3\\&\quad +\frac{1}{2}C_{XXXX}x_1^2 +\frac{1}{2}C_{XYYX}x_3^2+C_{XXYX}x_1x_3\Bigg ), \\ J_{23}&=-\frac{1}{M_J}\Bigg (K_{XY}+K_{XXY}x_1+K_{XYY}x_3+C_{XYX}x_2\\&\quad +C_{XYY}x_4+\frac{1}{2}K_{XYYY}x_3^2 \\&\quad +\frac{1}{2}K_{XXXY}x_1^2+K_{XXYY}x_1x_3+C_{XYYX}x_3x_2\\&\quad +C_{XYYY}x_3x_4+C_{XXYX}x_1x_2+C_{XXYY}x_1x_4\Bigg ),\\ J_{24}&=-\frac{1}{M_J}\Bigg (C_{XY}+C_{XXY}x_1+C_{XYY}x_3\\&\quad +\frac{1}{2}C_{XXXY}x_1^2 +\frac{1}{2}C_{XYYY}x_3^2+C_{XXYY}x_1x_3\Bigg ),\\ J_{41}&=-\frac{1}{M_J}\Bigg (K_{YX}+K_{YXX}x_1+K_{YXY}x_3+C_{YXX}x_2\\&\quad +C_{YXY}x_4+\frac{1}{2}K_{YXXX}x_1^2 \\&\quad +K_{YXXY}x_1x_3+\frac{1}{2}K_{YXYY}x_3^2+C_{YXXX}x_1x_2\\&\quad +C_{YXXY}x_1x_4+C_{YXYX}x_3x_2+C_{YXYY}x_3x_4\Bigg ),\\ J_{42}&= -\frac{1}{M_J}\Bigg (C_{YX}+C_{YXX}x_1+C_{YYX}x_3\\&\quad +\frac{1}{2}C_{YXXX}x_1^2 +\frac{1}{2}C_{YYYX}x_3^2+C_{YXYX}x_1x_3\Bigg ),\\ J_{43}&=-\frac{K_s}{2M_J}-\frac{1}{M_J}\Bigg (K_{YY}+K_{YXY}x_1\\&\quad +K_{YYY}x_3+C_{YYX}x_2+C_{YYY}x_4+\frac{1}{2}K_{YYYY}x_3^2\\&\quad +\frac{1}{2}K_{YXXY}x_1^2+K_{YXYY}x_1x_3\\&\quad +C_{YYYX}x_3x_2+C_{YYYY}x_3x_4\\&\quad + C_{YXYX}x_1x_2+C_{YXYY}x_1x_4\Bigg ),\\ J_{44}&=-\frac{1}{M_J}\Bigg (C_{YY}+C_{YXY}x_1+C_{YYY}x_3\\&\quad +\frac{1}{2}C_{YXXY}x_1^2+\frac{1}{2}C_{YYYY}x_3^2+C_{YXYY}x_1x_3\Bigg ). \end{aligned}$$

Evaluating the Jacobian matrix at fixed points \({\mathbf {x}}={\mathbf {x}}^*\) results in

$$\begin{aligned}&{{\mathbf {J}}\left( \bar{{\mathbf {M}}}\right) }_{\left( {\mathbf {x}}={\mathbf {x}}^*\right) }= \nonumber \\&\left[ \begin{matrix}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ frac{K_s}{2M_J}-\frac{K_{XX}}{M_J}&{}-\frac{C_{XX}}{M_J}&{}-\frac{K_{XY}}{M_J}&{}-\frac{C_{XY}}{M_J}&{}\frac{K_s}{2M_J}&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0\\ frac{K_{YX}}{M_J}&{}-\frac{C_{YX}}{M_J}&{}-\frac{K_s}{2M_J}-\frac{K_{YY}}{M_J}&{}-\frac{C_{YY}}{M_J}&{}0&{}0&{}\frac{K_s}{2M_J}&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ \frac{K_s}{M_D}&{}0&{}0&{}0&{}-\frac{K_s}{M_D}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}\frac{K_s}{M_D}&{}0&{}0&{}0&{}- \frac{K_s}{M_D}&{}0\\ \end{matrix}\right] .\nonumber \\ \end{aligned}$$
(45)

Evaluating the Jacobian matrix eigenvalues \(\left( \lambda _1,\ \lambda _2,\ \cdots ,\lambda _8\ \right) \) then reorder them in descending order such as \(Re\left( \lambda _1\right) \ge Re\left( \lambda _2\right) \ge \cdots \ge Re\left( \lambda _n\right) \). The value of the \( {\bar{M}}\) where \(Re\left( \lambda _1\right) =0\) is the threshold value \( {{\bar{M}}}_{\mathrm{th}}\). This analysis is repeated for the available range of Sommerfeld number.

Fig. 7
figure 7

(Color online) Rotor stability curves: a Three-dimensional stability plot. The z axis represents the threshold mass, the x axis represents the Sommerfeld number and the y axis represents the dimensionless shaft stiffness. b a section plot of Fig. 7a at \(K_s=1, 5, 10 \) and 20

Full size image

These results are presented in Fig. 7a, b. In Fig. 7 a, the threshold mass is plotted versus the Sommerfeld number and the dimensionless shaft stiffness in the range \(K_s \in [1-200]\). Figure 7b is considered as assembly of two-dimensional cross sections in Fig. 7a at four values of \( K_s\).

To investigate the stability of the periodic solution when the rotor speed exceeds the threshold speed the Monodromy matrix is evaluated from the Floquet multipliers [40, 43, 44]. For the details of the Monodromy analysis, see Appendix D. If the eigenvalues of Monodromy matrix is less than one, the periodic solution is stable limit cycle, i.e., supercritical Hopf bifurcation, and if the eigenvalue of the Monodromy matrix is greater than one, the periodic solution is unstable, i.e., subcritical Hopf bifurcation. This is plotted in Fig. 7 using solid and dashed lines where the solid lines indicate supercritical Hopf bifurcation, and the dashed lines represent subcritical bifurcation solution. The results of the figure show that for the present dynamical model decreasing the stiffness of the rotor shaft increases the possibility of subcritical Hopf bifurcation at large value of Sommerfeld number(small load).

Table 1 Selected points for dynamical analysis init\(=[0\ 0\ 0\ 0.1\ 0\ 0\ 2/K_s\ 0.1]\)
Full size table
Fig. 8
figure 8

Orbit plot for the journal geometrical center at different operating points I, II, III and IV as shown in Table 1. For all cases a first order (LA), b second order (NLA2), c third order (NLA3) d nonlinear (RNL). \(K_s=1,Init=[0\ 0\ 0\ 0.1\ 0\ 0\ 2/K_s\ 0.1]\)

Full size image
Fig. 9
figure 9

Orbit plot for the journal geometrical center at two operating conditions V and VI as shown in Table 1. For all cases a first order (LA), b second order (NLA2), c third order(NLA3) d nonlinear (RNL). \(K_s=20, Init=[0\ 0\ 0\ 0.1\ 0\ 0\ 2/K_s\ 0.1]\)

Full size image

3.4.2 Time response comparative study

In this section, selected points from the stability diagrams I, II, III, IV, V and VI are investigated using orbit plots of the shaft geometrical center. The input data for these cases are shown in Table 1 and presented in Fig. 7b. The comparative analysis is done using four different analyses. The first analysis is based on the linear first-order approximation of the bearing forces (LA). This analysis can be done using Eq. (42) while eliminating the second- and the third-order bearing coefficients. The second analysis is based on the nonlinear second-order approximation of the bearing forces, and this is done while reducing the third-order coefficients to zero (NLA2). The third analysis is based on the nonlinear third-order force approximation (NLA3) as stated in Eq. (42). The last analysis is based on the nonlinear force evaluated directly from Reynolds equation (RNL). In this analysis, the Reynolds equation is solved every time step to evaluate the bearing forces.

The six selected operating points are listed in Table 1. All the cases are for \(L/D\ =1\). The first two cases I, II are at \(S=0.148\) and for \(K_s=1\), the second two cases III, IV are at \(S=0.507, K_s=1\) and the last two cases V, VI are at \(S=0.507\) and \(K_s=20\). The cases I, III and V are below the threshold speed, and the cases II, IV and VI are above the threshold speed.

For case I and case III, where both of them are below the threshold speed the four analyses give the same response as shown in the first and third rows of Fig. 8. Case II and case IV are above the threshold speed for supercritical and subcritical cases according to the Monodromy bifurcation analysis. For case II, the response based on the linear analysis shows instability as the rotor hits the journal bearing. Both analyses based on the second-order coefficients (NLA2) and third-order coefficients (NLA3) show a stable limit cycles. However, the analysis based on direct solution of Reynolds (RNL) shows bifurcation leads to unstable limit cycle, then jumps to a larger stable limit cycle. This behavior for journal bearings is previously reported in [45, 46].

For case IV which is subcritical according to the Monodromy analysis. The first-order analysis shows unstable behavior above threshold speed, which is basically expected because analysis based on first-order (LA) is insensitive to bifurcation type [40]. In this case, the analyses based on NLA2 and NLA3 do not show the same response. The analysis based on second-order coefficients shows a stable limit cycle, while the analysis based on third-order coefficients shows unstable limit cycle. In this case, the nonlinear analysis RNL agrees with (NLA3) in showing unstable limit cycles. However, the RNL response shows a jump from unstable limit cycle to bigger stable limit cycle as shown in Fig. 8IV-d. The explanation for the difference between the third-order coefficient and RNL can be explained by the fact that the coefficients based on NLA3 are only valid in the neighborhood of the steady-state point and as the rotor receding from this point, these coefficients become not accurate as shown in the perturbation analysis.

Another two cases, V and VI, having higher rotor dimensionless stiffness are investigated, see Fig. 9. The dimensionless stiffness in this condition is \(K_s=20\). The stability diagram shows that all bifurcations for this case are supercritical. The orbit plot for the journal geometrical center is plotted at \(S=0.507\). The first case V is below the threshold speed, and the second case VI is above the threshold speed. The results show that for case V below the threshold speed all the four analyses show the same response. For case VI which is higher than the threshold speed the analysis based on first-order coefficients shows growing of the response until the journal hits the bearing. The analyses NLA2, NLA3 and RNL show stable limit cycles. The size of the limit cycles is not the same for the three cases. This can be explained by the fact that the bearing coefficients are evaluated to be correct in the vicinity of the steady-state point.

Fig. 10
figure 10

(Color online) Continuation analysis of flexible rotor supported on two symmetric journal bearings \(K_s=1\), for different eccentricity ratios a \(\varepsilon =0.24\) (column one), b \(\varepsilon =0.45\) (column two), c \(\varepsilon =0.55\) (column three), d \(\varepsilon =0.65\) (column four). The first row represents the limit cycle continuation, the second row represents a section in limit cycle continuation plot and the last row represents a top view of the limit cycle continuation plot

Full size image
Fig. 11
figure 11

(Color online) Continuation analysis of flexible rotor supported on two symmetric journal bearings \(\varepsilon =0.5\), for different rotor stiffness ratios a \(K_s=1\) (column one), b \(K_s=5\) (column two), c \(K_s=10\) (column three), d \(K_s=20\) (column four). The first row represents the limit cycle continuation, the second row represents a section in limit cycle continuation plot and the last row represents a top view of the limit cycle continuation plot

Full size image

3.4.3 Continuation analysis

In this section, numerical continuation is used to investigate the dynamics of the present model. The continuation analysis is based on the equations of motion based on the third-order nonlinear bearing coefficients. MatCont module is used for the present study which is a toolbox written in MATLAB language and it used for continuation analysis [47]. The continuation analysis is used to investigate the effect of changing the applied static load (Sommerfeld number) and the effect of changing the rotor stiffness as shown in Figs. 10 and 11, respectively.

To apply the continuation analysis, numerical integration is used to identify an equilibrium point below the threshold curve. From this point, continuation analysis is applied at variable \({\bar{M}}\) until reaching a Hopf bifurcation point which represent the threshold speed. From evaluating the Lyapunov exponent at this point, the type of Hopf bifurcation can be identified whether supercritical or subcritical. Then, limit cycle continuation is applied to investigate the rotor dynamics behind the threshold speed. MATCONT is used to identify the stability of limit cycles based on the modulus of Floquet multiplier [47]. If at least one multiplier has modulus greater than one, then the limit cycle is unstable. In Figs. 10 and 11, the stable limit cycles are presented by solid lines and the unstable limit cycles are presented by dotted lines.

In Fig. 10, the continuation analysis is applied at four values of eccentricity ratios (a) \(\varepsilon =0.24\) (column one), (b) \(\varepsilon =0.45\) (column two), (c) \(\varepsilon =0.55\) (column three), (d) \(\varepsilon =0.65\) (column four). These values are corresponding to four different static loads with Sommerfeld numbers 0.507, 0.216, 0.148 and 0.0983, respectively, see the four blue vertical dotted lines 7 b. The stiffness ratio of the rotor is \(K_s=1\). Increasing the eccentricity ratio at the equilibrium is associated with the increase in the applied load. From the four selected cases, case a represents subcritical bifurcation at \({\bar{M}}_{\mathrm{th}}=3.35\). The limit cycle continuation in that case shows an unstable limit cycles with the decrease in \({\bar{M}}\). At \({\bar{M}}\)=3.331, a limit point cycle is occurred (purple circle in Fig. 10) and the limit cycle becomes stable limit cycles. Further increase of \({\bar{M}}=3.333\) , another limit point cycle is occurred, and unstable limit cycle continues with the decrease of \({\bar{M}}\). At cases b and c where \(\varepsilon =0.45\) and \(\varepsilon =0.55\), supercritical bifurcation is occurred followed by stable limit cycle continuation. Further increase of \({\bar{M}}\) results in limit point cycle (purple circle in Fig. 10) at \({\bar{M}}=3.664\) and \({\bar{M}}=4.934\) in cases b and c, respectively. After this limit point cycle unstable limit cycles continuation is started. For case d which is supercritical bifurcation, a stable limit cycles are occurred. No limit point cycle is monitored within the investigated range.

In Fig. 11, a continuation analysis is done for four cases having \(\varepsilon =0.5\) and four different values of relative rotor stiffness (a) \(K_s=1\), (b) \(K_s=5\), (c) \(K_s=10\) and (d) \(K_s=20\), see the red dotted vertical dotted line in Fig. 7b. Results in Fig. 11 show the point of Hopf bifurcation for the four cases is at \({\bar{M}}_{\mathrm{th}}\)= 3.576, 8.673, 10.47 and 11.66, respectively. This indicates that the threshold speed increases with the increase of rotor stiffness ratio. In Fig. 11, although the type of Hopf bifurcation at the four different rotor stiffness ratio values is supercritical and the continuation analysis shows that at \(K_s\)=1, 5 and 20, limit point cycles are monitored with the increase of the dimensionless mass \({\bar{M}}\). These limit point cycles are colored in purple. After these limit point cycles, the continuation analysis shows that the limit cycles change from stable to unstable limit cycles. However, at \(K_s=10\), no limit point cycle is found within the investigated range. The continuation results presented in Fig. 11 show that increasing the rotor flexibility affects greatly the dynamics and stability of the rotor-bearing system.

4 Conclusion

In the present paper, the linear first and nonlinear second- and third-order bearing coefficients are obtained using infinitesimal perturbation method and finite difference method. The main conclusions from the present work are as follows:

  • A mesh of \(150\times 600\) is sufficient to obtain an accurate third-order bearing coefficients.

  • The perturbation analysis shows that the perturbation force based on the third-order coefficients are more accurate than that based on first- and second-order coefficients.

  • The rotor stiffness ratio and applied load are a crucial parameters affecting the type of rotor-bearing stability whether subcritical or supercritical. Additionally, they affect the continuation of limit cycles behind the threshold speed.

  • The orbit plot results show that the analysis based on the third-order bearing coefficients is closer to the analysis based on the complete solution of Reynolds equation than the analyses based on the first- and second-order bearing coefficients.

At the end of our conclusions, it is recommended to experimentally validate the present analysis with experimental work and to investigate the integration of controller to avoid the rotor-bearing instability.