A multi-sensing scheme based on nonlinear coupled micromachined resonators

Abstract

A new multi-sensing scheme via nonlinear weakly coupled resonators is introduced in this paper, which can simultaneously detect two different physical stimuli by monitoring the dynamic response around the first two lowest modes. The system consists of a mechanically coupled bridge resonator and cantilever resonator. The eigenvalue problem is solved to identify the right geometry for the resonators to optimize their resonance frequencies based on mode localization in order to provide outstanding sensitivity. A nonlinear equivalent model is developed using the Euler–Bernoulli beam theory while accounting for the geometric and electrostatic nonlinearities. The sensor's dynamics are explored using a reduced-order model based on two-mode Galerkin discretization, which reveals the richness of the response. To demonstrate the proposed sensing scheme, the dynamic response of the weakly coupled resonator is investigated by tuning the stiffness and mass of the bridge and cantilever resonators, respectively. With its simple and scalable design, the proposed system shows great potential for intelligent multi-sensing detection in many applications.

1 Introduction

Over the past decades, micro-electromechanical systems (MEMS)-based sensors have proven high reliability, low power consumption, and ease of integration, possibly becoming the most suitable candidate for ultrasensitive sensors [1]. The small size and high sensitivity of MEMS sensors allow their integration in a wide range of potential applications, including gyroscopes [2,3,4], accelerometers [5,6,7], mass sensors [8,9,10], and gas sensors [11,12,13].

The resonant MEMS sensors have gained massive success thanks to their ultra-small physical scale and ultra-high sensitivity. Resonant MEMS sensors rely on the ambient environment's influence on the resonators' resonance frequencies in different ways. The parameters related to the resonance frequencies include the resonator's mass, geometric shape, axial stress level, and stiffness. Besides, the corresponding equipment aiming at measuring resonant frequency shift has proven to reach a high resolution, which further enhances the MEMS sensors' sensitivity [14, 15]. In addition, the structure's nonlinearity features appear in the frequency response [16, 17], especially jump or bifurcation, further enhancing the detection process [18].

Research aiming to improve the MEMS sensors sensitivity has been conducted extensively in the past few years. Most works assessed the approach to miniaturize further the structure size from the micro-scale to the nanoscale [19,20,21]. A grand scheme of these sensors is the MEMS-based sensor that employs the phenomenon of mode localization. The latter introduces linear modal interaction behaviours, especially mode crossing and mode veering [22], which show great potential for sensitivity improvement. These modal interactions typically happen as the two modal frequencies of the system approach each other. Some research focuses on utilizing the mode coupling phenomenon to design high-performance sensors through mechanically and/or electrostatically coupled resonators [23, 24]. Zhang et al. [25] reported an acceleration sensing scheme based on electrostatically weakly coupled resonators and reached high amplitude ratio, which is 302 times higher than ratio used in resonance frequency theory. Other types of displacement sensors [26], pressure sensors [27], and ultra-small mass sensors [28] are also credible examples.

Compared to sensors based on linear behaviours, other designs closely related to nonlinear phenomena received significant attention, such as utilizing bistability [29] and detecting bifurcation points [30]. Although a sizeable nonlinear behaviour usually accompanies instability, the benefit of sensitivity and quality overwhelms the disadvantage. Electrostatically actuated MEMS resonators have been designed to detect forces [31], masses [32], and accelerations [30, 33]. The issue of stabilizing the response in the nonlinear regime has been widely studied. Kacem et al. [34] researched a dynamic stabilization technique for electrostatically actuated nanoresonators theoretically and experimentally. Their theory focused on actuating both primary and superharmonic resonances simultaneously. Besides, using the internal resonance induced between two bending modes is proven to be a possible solution for stabilizing mechanical oscillators [35]. Also, bifurcation phenomena have been utilized to enhance the sensitivity of MEMS sensors. Kumar et al. [36] operated a piezoelectric cantilever beam near the saddle-node bifurcation at its first natural frequency and detected the sudden jump in amplitude with the mass perturbation on resonator. In addition, the nonlinear designed MEMS resonator shows its potential in multi-sensing applications.

In the past few years, the topic of multiple sensing has received attention due to the increasing need for multiple parameters monitoring applications, especially in medical treatment, aerospace, and industry 4.0 [12, 13, 17]. The conventional solutions focus on the combination of different kinds of sensors [16]. For instance, Clifton et al. [37] developed multifunctional integrated sensors (MFISES) chip, combining numerous MEMS sensors into an integrated chip and benefits from the ultra-small size and high sensitivity of MEMS devices. Their MFISES device integrates 8 MEMS sensors on a single 2 mm × 2 mm die which obtains high sensing performance and low power consumption. However, the direct employment of multiple devices inevitably increases the system complexity and production cost. Some research studies investigated the realization the multiple sensing on a single device, e.g., Jaber et al. [13] demonstrated a resonant gas sensor actuated simultaneously near the first and second vibration modes, where monitoring the frequency shifts of these two modes due to physical stimuli, the detection of both environmental temperature and gas concentration is achieved.

This paper proposes a new sensing structure using the nonlinear response of electrostatically actuated coupled resonators. The sensor mainly consists of a mechanically coupled cantilever and bridge resonator. Different sensing targets are set for two resonators for multi-sensing purposes: the micro-gravimetric sensing for the cantilever and the stiffness sensing for the bridge. To investigate the rich nonlinear dynamic behaviour of the structure, a nonlinear theoretical model is developed using the Euler–Bernoulli beam theory while accounting for the geometric (i.e., dominated by cubic nonlinearity originated from the midplane stretching effect) and electric (i.e., dominated by quadratic nonlinearity) nonlinearities, respectively. The reduced-order model based on the two-mode Galerkin discretization and shooting technique are used to analyse the system. The influence of the resonators' geometric size, damping, actuation voltage, and actuation scheme is detailed and discussed theoretically. The sensor's multi-sensing ability is demonstrated by tracking the bifurcation frequency shift and peak frequency shift in the modes' shapes induced by mass and stiffness perturbations. The numerical results prove that this new kind of sensing structure could monitor concurrently two different kinds of perturbations with high efficiency through the nonlinear behaviour of the structure.

The present paper's structure is organized as follows. The geometric size of the multi-sensing scheme and the related problem formulation are introduced in Sect. 2. The theoretical results of the system's nonlinear behaviour, the sensing performance, and the parameter analysis are included in Sect. 3. In the end, the main conclusions of the research are summarized in Sect. 4.

2 Structure description and model

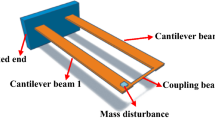
As displayed in Fig. 1, the multi-sensing scheme comprises a weakly coupled resonator, including cantilever and bridge resonators, mechanically coupled by a thin beam. The coupling strength could be controlled by changing the coupling position, the moment of inertia, and the coupling beam's length [38]. The detailed geometric parameters and physical properties of the coupled resonator system, considered to be fabricated from silicon, are listed in Table 1. Both cantilever and bridge resonators are driven electrostatically by a DC polarization voltage V_DC, and the AC harmonic actuation V_AC is given on one (or both) of them depending on the actuation theory. The system geometry is optimized to ensure that the first and second modes are similar.

Fig. 1

a 3D schematic of the multi-sensing scheme. b Top view of the coupled resonators

Table 1 Geometric parameters of the sensor structure

The two resonators would be used to operate different functions. The cantilever resonator would detect the mass perturbation while the bridge experiences the stiffness perturbation. The red component on the tip of the cantilever, as shown in Fig. 1, represents the mass perturbation set on the cantilever, which could be generated from the special coating in the practical design. The stiffness of the bridge resonator is another sensing target, which links to many factors like the thickness, stress and stretch, and the environmental temperature.

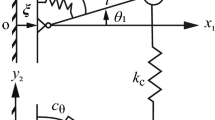
The sensor structure (Fig. 1) is composed of two microbeams (a bridge resonator and a cantilever resonator) with lengths ${L}_{1}$ and ${L}_{2}$ (${L}_{1}$>${L}_{2}$), respectively, width $b$ and thickness $h$. The coupling beam is functionalized to provide weak coupling, and its coupling strength significantly affects the sensor's sensitivity. Hence, quantifying and controlling the coupling beam's dimensions is crucial. Most of the sensors use an overhang to connect microbeams [30]. However, this coupling approach is challenging to model and practically control its coupling length [39]. Hence, the coupling beam with length ${L}_{c}$, width ${b}_{c}$, and same thickness with resonators is chosen and located at distance ${X}_{c}$. Under this condition, the structure of sensors could be modelled as two Euler–Bernoulli beams coupled with a rotational spring ${k}_{r}$ [40]. The torsional stiffness could be represented as:

$$ k_{r} = \frac{{G\beta b_{c} h^{3} }}{{L_{C} }} $$

(1)

where $G$ denotes the material's shear modulus (69.3 Gpa for silicon), and $\beta$ is a coefficient depending on the coupling beam's width $b_{c}$ and thickness h. By using Hamilton's principle and the equation of Euler–Bernoulli beams with distributed elements [41], the equations of motion governing the transverse deflections $\tilde{w}_{1}$ (for the bridge resonator) and $\tilde{w}_{2}$ (for the cantilever resonator) are:

$$ \begin{aligned} & EI\tilde{w}_{1}^{\prime \prime \prime \prime } + \rho A\ddot{\tilde{w}}_{1} + \tilde{c}_{1} \dot{\tilde{w}}_{1} + \left[ {\tilde{N} - \frac{EA}{{2L_{2} }}\mathop \int \limits_{0}^{{L_{1} }} \left( {\tilde{w}_{1}^{\prime } } \right)^{2} {\text{d}}x} \right]\tilde{w}_{1}^{\prime \prime } \\ & \quad - \tilde{k}_{r} \left( {\tilde{w}_{1}^{\prime } \left( {X_{c} } \right) - \tilde{w}_{2}^{\prime } \left( {X_{c} } \right)} \right)\delta^{\prime } \left( {\tilde{x} - \tilde{X}_{c} } \right) = \frac{1}{2}\varepsilon_{0} \frac{{b\left[ {V_{DC1} + V_{AC1} *\cos \left( {\tilde{\Omega }_{1} \tilde{t}} \right)} \right]^{2} }}{{\left( {d_{1} - \tilde{w}_{1} } \right)^{2} }} \\ \end{aligned} $$

(2)

$$ \begin{aligned} & EI\tilde{w}_{2}^{\prime \prime \prime \prime } + \left( {\rho A + \tilde{m}\delta \left( {\tilde{x} - \tilde{X}_{m} } \right)} \right)\ddot{\tilde{w}}_{2} + \tilde{c}_{2} \dot{\tilde{w}}_{2} - k_{r} \left( {\tilde{w}_{2}^{\prime } \left( {X_{c} } \right) - \tilde{w}_{1}^{\prime } \left( {X_{c} } \right)} \right)\delta^{\prime } \left( {\tilde{x} - \tilde{X}_{c} } \right) \\ & \quad = \frac{1}{2}\varepsilon_{0} \frac{{b\left[ {V_{DC2} + V_{AC2} *\cos \left( {\tilde{\Omega }_{2} \tilde{t}} \right)} \right]^{2} }}{{\left( {d_{2} - \tilde{w}_{2} } \right)^{2} }} \\ \end{aligned} $$

(3)

In Eqs. (2) and (3), the primes and dots denote the partial differentiation of transverse deflections ${\widetilde{w}}_{\mathrm{i}}(i=\mathrm{1,2})$ with respect to the beam position $\widetilde{x}$ and the time $\widetilde{t}$, respectively; $A$ and $I$ are the area and the moment of inertia of the rectangular cross section; $\delta$ is the Dirac delta function; and ${\widetilde{c}}_{1}$ and ${\widetilde{c}}_{2}$ denote the viscous damping. The parameters and corresponding values are defined in Table 2. Note that the AC voltage is imposed on only one resonator excitation at a time (i.e., if V_AC1 ≠ 0 means that V_Ac2 = 0 V and vice versa) to investigate the corresponding dynamic response of the proposed structure, while the DC polarization actuation is imposed to both resonators to enhance the associated quadratic nonlinearity.

Table 2 Physical parameters used in the governing equations of motion

After non-dimensionalizing and discretizing Eqs. (2) and (3) using the Galerkin procedure, the governing non-dimensional equations are written as follows:

$$ \begin{aligned} & \left( {\mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } {\text{d}}xu_{1} \left( {1 + \delta k} \right) + \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + c_{1n} \frac{{\partial u_{1} }}{\partial t} + k_{r} \left[ {u_{1} \left( {\varphi_{1}^{\prime } \left( {X_{c} } \right)} \right)^{2} - u_{2} \varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right]} \right)*\left( {1 - 2u_{1} \mathop \int \limits_{0}^{1} \varphi_{1}^{3} {\text{d}}x + u_{1}^{2} \mathop \int \limits_{0}^{1} \varphi_{1}^{4} {\text{d}}x} \right) \\ & \quad - \alpha_{1} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime 2} {\text{d}}x\left( {u_{1}^{3} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1} {\text{d}}x - 2u_{1}^{4} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1}^{2} {\text{d}}x + u_{1}^{5} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1}^{3} {\text{d}}x} \right) = \alpha_{2} \left[ {V_{DC1} + V_{AC1} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \mathop \int \limits_{0}^{1} \varphi_{1} {\text{d}}x \\ \end{aligned} $$

(4)

$$ \begin{aligned} & \left( {\mathop \int \limits_{0}^{{R_{L} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } {\text{d}}xu_{2} + \left( {1 + \delta m\left( {x - X_{m} } \right)} \right)\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + c_{{2{\text{n}}}} \frac{{\partial u_{2} }}{\partial t} + k_{r} \left[ {u_{2} \left( {\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right)^{2} - u_{1} \varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right]} \right) \\ & \quad {*}\left( {{\text{R}}_{d}^{2} - 2R_{d} u_{2} \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2}^{3} {\text{d}}x + u_{2}^{2} \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2}^{4} {\text{d}}x} \right) = \alpha_{2} \left[ {V_{DC2} + V_{AC2} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2} {\text{d}}x \\ \end{aligned} $$

(5)

where the $\delta k$ and $\delta m$ represent the linear stiffness variation on bridge resonator due to the external stimulus and the mass perturbation on cantilever resonator, respectively. The detailed derivation process and definition of parameters appearing in Eqs. (4) and (5) are given in Appendix.

Through Eqs. (4) and (5), the Jacobian matrix of the system is: $J = \left[ {\begin{array}{*{20}c} {\lambda_{1}^{2} } & \kappa \\ {\frac{\kappa }{1 + \eta }} & {\frac{{\lambda_{2}^{2} }}{1 + \eta }} \\ \end{array} } \right]$, where $\lambda_{1}^{2} = \mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } {\text{d}}x - 2\alpha_{2} V_{dc1}^{2} + k_{r} \left( {\varphi_{1}^{\prime } \left( {X_{c} } \right)} \right)^{2}$, $\lambda_{2}^{2} = \mathop \int \limits_{0}^{{R_{L1} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } {\text{d}}x - \frac{{2\alpha_{2} V_{dc2}^{2} }}{{R_{d}^{2} }} + k_{r} \left( {\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right)^{2}$, $\kappa = - k_{r} *\varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)$ and $\eta = \delta m\left( {x - X_{m} } \right)$.

Solving the eigenvalue problem through the Jacobian matrix gives the two lowest global resonant frequencies of the coupled system [42]:

$$ \left( {\lambda_{1}^{2} - \omega^{2} } \right)\left( {\frac{{\lambda_{2}^{2} }}{1 + \eta } - \omega^{2} } \right) - \frac{{\kappa^{2} }}{1 + \eta } = 0 $$

(6)

To verify the theoretical model and obtain the vibration mode shapes of the coupled resonators, a 3D multi-physics finite-element model in the commercial software COMSOL is used [43]. Figure 2 depicts the variation of the first two global natural frequencies with respect to the length of the cantilever by solving Eq. (6), while applying 0 V DC load to the system, as well as FEM simulations from COMSOL. The results show good matching between both methods validating the adopted analytical modal. Figure 2b, c shows the associated first two lowest mode shapes of the structure. Figure 2a demonstrates that when the length of the cantilever is ${ L}_{2}=277 \mu\mathrm{m}$, the two curves are close to each other, and the two lowest natural frequencies are around 54 kHz. For the rest of the analysis, the cantilever length will be fixed at ${ L}_{2}=278 \mu\mathrm{m}$.

Fig. 2

a Variation of the two lowest natural frequencies of the coupled system with respect to the length of the cantilever resonator. The DC load is kept equal to 0 V. The lines denote the theoretical results while the dots denote the FEM result from COMSOL. b and c show the top view and side view, respectively, show the first two vibration mode shapes of the mechanically coupled structure from COMSOL

We also analyse the effect of DC load on the lowest two natural frequencies by applying the same DC load, V_DC, to both resonators. Figure 3 depicts the variation of the first two global natural frequencies with respect to the DC load by solving Eq. (6). It shows that both the two lowest modes' resonance frequency would decrease with increasing DC polarization actuation due to the dominance of the quadratic nonlinearity (i.e., originated from the electrostatic force).

Fig. 3

Variation of the two lowest natural frequencies of the coupled system with respect to the DC load. The two resonators are subjected to the same V_DC

Figure 4 reports a parametric study of the preceding eigenvalue problem. The different colours of the figure represent the effect of stiffness on the bridge resonator, while the x-axis represents the effect of mass variation on the cantilever resonator. The light and dark colours denote the 1^st and the 2^nd lowest global natural frequencies, respectively. The results prove that both parameters could influence the resonance frequencies.

Fig. 4

The two lowest natural frequencies versus mass perturbation on the cantilever and stiffness perturbation on the bridge. Light-coloured lines and dark-coloured lines represent 1st and the 2nd natural frequencies, respectively

3 Results and discussion

This section discusses the nonlinear behaviour of the weakly coupled system. Continuous analyses using the shooting technique [38] are conducted to verify the effect of the different physical parameters. The referred parameters are given in Table 1.

3.1 Response dynamics of AC actuation on bridge

3.1.1 Continuous analysis for the characteristic points

Figure 5 shows the bifurcation points of the frequency response of global mode shapes as actuating the bridge resonator with ${V}_{DC1}=40V$ and ${V}_{AC1}=7.3V$, and the cantilever resonator with ${V}_{DC2}=10V$. The solid blue and green dotted lines represent stable and unstable branches, respectively. Three characteristic points (notes as red in Fig. 5) should be highlighted, the peak point in the W2 appears at 53.835 kHz, and two corresponding bifurcation points appear at 69.966 kHz and 57.327 kHz. The hardening behaviour in W1 generates a saddle-node bifurcation point at 69.966 kHz, and the peak in the W2 at 53.835 kHz is suitable for sensing. Near these two points, the tiny variation of perturbations could lead to an obvious change of transverse deflections, which show great potential to provide high sensitivity. The following parts will provide detailed discussions of the effects of different parameters on these two phenomena.

Fig. 5

Characteristic points of the frequency response under bridge actuating of ${V}_{DC1}=40V$ and ${V}_{AC1}=7.3V$, and cantilever actuating of ${V}_{DC2}=10V$: transverse deflection of a bridge W1 and b cantilever W2 (dotted lines represent unstable branches). The inset of b shows the nonlinear branch

The phase portraits and Poincaré sections for all three characteristic points are shown in Fig. 6. The red curves represent the peak point of W2 at 53.835 kHz, the blue curves represent the higher amplitude bifurcation point at 69.966 kHz, and the green curves represent the lower amplitude bifurcation point at 57.327 kHz, respectively. The phase portraits, which are generated from 200 cycles of steady-state time response, demonstrate elliptical orbits, and all Poincaré sections converge to a single point, proving that the response is periodic motion of period-1. It could be concluded that before the peak point of W2 at 53.835 kHz, both W1 and W2 phase portraits enlarge with increased frequency. Between 53.835 kHz (W2 peak) and 69.966 kHz (higher amplitude bifurcation point), W1 keeps enlarging while W2 starts to shrink. In the last stable branch larger than 57.327 kHz, the W1 and W2 phase portraits shrink with increased frequency. It should be pointed that the nonlinear behaviour determines the maximum transverse deflection of W1 while the maximum transverse deflection of W2 is further related to its natural frequency.

Fig. 6

Phase portrait (solid line) and Poincaré section (dots) for the three characteristic points revealed in Fig. 4; peak point at 53.835 kHz (red), bifurcation point at 69.966 kHz (blue) and bifurcation point at 57.327 kHz (green): a W1; b W2

3.1.2 AC actuation level on bridge

In Fig. 7, the DC polarization actuation is set as ${V}_{DC1}=40V$ and ${V}_{DC2}=10V$ on bridge and cantilever, respectively, and only AC actuation of different amplitudes ${V}_{AC1}$ is provided on the bridge resonator. Figure 7 indicates the complete response around the two lowest modes under different levels of AC actuation. (The amplitudes W1 and W2 are non-dimensional.) In Fig. 7a, b, the five curves are given the actuation ${V}_{AC1}$ of 1.0 V, 1.5 V, 2.0 V, 2.5 V, and 3.0 V. It can be noted that under low AC actuation levels, specifically from $1.0V$ (purple) to $2.0V$ (green), the frequency response is linear. When ${V}_{AC1}$ increases to $2.5V$ (yellow), hardening behaviour first appears, where the dotted line denotes the unstable branch. Additionally, the bifurcation jump frequency in W1 and the peak frequency in W2 obtain a similar value and lead to a potential 1:1 interaction (yellow curve). Three specific peaks are observed in the response: (i) the main peak appears near 52.8 kHz. It shifts to the right when the actuation ${V}_{AC1}$ increases and finally turns to the bifurcation jump. (ii) The small peak at 53.3 kHz, linked to the linear mode localization, remains at the same frequency. (iii) The small peak at 26.4 kHz is due to the order two superharmonic behaviour.

Fig. 7

Frequency response curves at different AC bridge actuation ${V}_{AC1}$ while ${V}_{DC1}=40V$, ${V}_{DC2}=10V$ and ${V}_{AC2}=0V$: a W1 and b W2 under low AC actuation of 1.0 V, 1.5 V, 2.0 V, 2.5 V, and 3.0 V; c W1 and d W2 under medium AC actuation of 4 V, 5 V, 6 V, and 7 V; e W1 and f W2 under high AC actuation of 8 V, 9 V, and 10 V. Dotted lines denote unstable branches. Amplitudes W1 and W2 are non-dimensional

When the actuation is increased from $4$ to $7V$, as shown in Fig. 7c, d, the bifurcation jump frequency in W1 continues to increase, and the peak frequency in W2 remains constant. When ${V}_{AC1}$ increases further from $8$ to $10V$, as Fig. 7e, f show, the 1:1 interaction disappears, and the response leads to a new unstable softening branch with maximum value of 0.56. To obtain the best performance in sensing through bifurcation jump and eliminate the risk of the unwanted unstable branch, the AC actuation of ${V}_{AC1}=7.3V$ is a convenient choice.

3.2 AC actuation level on cantilever

In this section, the system dynamics are simulated for different actuating schemes. More specifically, the DC actuation remains the same while the AC actuation is switched on the cantilever resonator. Compared to the response in Sect. 3.1.2, the linear behaviours of Figs. 7a, b and 8a, b in the two parts are quite similar: both actuating modes return two peaks, including the central peak at 53.3 kHz and the superharmonic peak at 26.4 kHz. Under high AC actuation, the frequency response curve around the second mode (Fig. 8c, d) shows a nonlinear softening behaviour as being dominated by quadratic nonlinearity. Besides, the level of nonlinearity is also lower than the bridge actuating result, which is insufficient to generate a noticeable bifurcation jump. By comparing the maximum amplitude of two frequency responses under high AC actuation (Figs. 7c, d and 8c, d), it could be found that the peak amplitude of W1 under bridge actuation (shown as red in Fig. 7c) is near 0.37, which is more than two times of the W1 (0.15) under cantilever actuation (shown as red in Fig. 8c). Hence, the AC bridge actuation is a better AC excitation method than the AC cantilever actuation because of the higher amplitude of the nonlinear bifurcation jump.

Fig. 8

Frequency response curves at different AC cantilever actuation ${V}_{AC2}$ while ${V}_{DC1}=40V$, ${V}_{DC2}=10V$ and ${V}_{AC1}=0V$: a W1 and b W2 under low AC actuation of 5 V, 10 V, 15 V and 20 V; c W1 and d W2 under high AC actuation of 24 V, 26 V, 28 V, and 30 V. Dotted lines denote unstable branches. Amplitudes W1 and W2 are non-dimensional

3.3 Effects of damping coefficient

Investigating the effect of damping on the sensor’s performance is vital for safe sensor operation and calibration. As particularly for gas sensors which represent the main direct application of the proposed system, the damping could be influenced by the gas type, gas concentration, temperature, and other parameters (especially since we are aiming for multi-gas detection); hence, it is crucial to study the effect of damping on the system dynamics.

The effects of damping coefficients (${\upzeta }_{1}$ and ${\upzeta }_{2}$) on the resonator response are depicted in Fig. 9. The value of damping influences the AC actuation needed to lead to nonlinear behaviour and the amplitude of the two resonators. Note that the values of damping ratios were chosen arbitrarily, but having the same order of magnitude as previous research studies [38, 44], to show the damping effect on the numerical simulations. Under ultra-low damping conditions (${\zeta }_{1}={\zeta }_{2}=2.222\times {10}^{-3}$) in Fig. 9a, b, the nonlinear jump appears in low actuation ${V}_{AC1}=1V$, while the softening behaviour first appears when ${V}_{AC1}=3V$. When ${\zeta }_{1}={\zeta }_{2}=1.111\times {10}^{-2}$, the AC actuation value of the first bifurcation jump and softening branch reaches 3 V and 9 V (Fig. 9c, d). Under high damping (${\zeta }_{1}={\zeta }_{2}=2.222\times {10}^{-2}$), 9 V AC actuation is not sufficient for the system to exhibit all the nonlinear features, the nonlinear jump first appears at 5 V, and the softening behaviour does not exist at such conditions (Fig. 9e, f).

Fig. 9

Frequency response curves at AC bridge actuation ${V}_{AC1}$ of 1 V, 3 V, 5 V, 7 V, and 9 V while ${V}_{DC1}=40V$, ${V}_{DC2}=10V$ and ${V}_{AC2}=0V$: a W1 and b W2 under low damping coefficient ${\zeta }_{1}={\zeta }_{2}=2.222\times {10}^{-3}$ (${\zeta }_{1}$ and ${\zeta }_{2}$ are chosen to keep damping ${c}_{1}={c}_{2}=0.1$, where $c=2\zeta {w}_{n}$ and ${\omega }_{n}=22.5$); c W1 and d W2 under medium damping coefficient ${\zeta }_{1}={\zeta }_{2}=1.111\times {10}^{-2}$ (${\zeta }_{1}$ and ${\zeta }_{2}$ are chosen to keep damping ${c}_{1}={c}_{2}=0.5$); e W1 and f W2 under high damping coefficient ${\zeta }_{1}={\zeta }_{2}=2.222\times {10}^{-3}$ (${\upzeta }_{1}$ and ${\upzeta }_{2}$ are chosen to keep damping ${c}_{1}={c}_{2}=1.0$). Dotted lines denote unstable branches. Amplitude of W1 and W2 is non-dimensional.

3.4 Effects of resonators' length

We investigate the effect of the resonators' lengths ${L}_{1}$ and ${L}_{2}$ on the system response. The AC actuation of ${V}_{AC1}$ equals to $7V$ in both cases, as shown in Fig. 10. It can be noted that the bridge length influences only the bifurcation jump frequency of the first natural frequency response W1 and does not influence the peak frequency of the second natural frequency response W2. In contrast, the cantilever length only affects the peak frequency of the second natural frequency response W2 and does not change the bifurcation jump frequency of the first natural frequency response W1.

Fig. 10

Frequency response curves at different resonator lengths under actuation of ${V}_{AC1}=7V$, ${V}_{DC1}=40V$, ${V}_{AC2}=0V$ and ${V}_{DC2}=10V$: a W1 and b W2 under different bridge lengths, ${L}_{1}$ of $690 \mu\mathrm{m}$, $700 \mu\mathrm{m}$, and $710 \mu\mathrm{m}$; c W1 and d W2 under different cantilever lengths, ${L}_{2}$ of $267\mu\mathrm{ m}$, $277 \mu\mathrm{m}$, and $287\mu\mathrm{ m}$. Dotted lines denote unstable branches. Amplitude W1 and W2 are non-dimensional. The inset of a shows the nonlinear branch

3.5 Effect of the resonator thickness

The thickness directly changes the stiffness of the two resonators: the thicker the resonator, the stiffer it gets and requires further AC actuation. The results are depicted in Fig. 11 with AC actuation of 7 V. Figure 11a shows that under the same AC actuation of 7 V, the response may exhibit all possibilities: the unstable softening branch ($2.5 \mu\mathrm{m}$), the bifurcation jump ($3 \mu\mathrm{m}$), and linear response ($3.5 \mu\mathrm{m})$.

Fig. 11

Frequency response curves at different thicknesses, $h$ of $2.5 \mu\mathrm{m}$, $3 \mu\mathrm{m}$, and $3.5 \mu\mathrm{m}$ under actuation of ${V}_{AC1}=7V$, ${V}_{DC1}=40V$, ${V}_{AC2}=0V$ and ${V}_{DC2}=10V$: a W1 and b W2. Dotted lines denote unstable branches. Amplitude of W1 and W2 are non-dimensional

3.6 Sensing scheme

The purpose of this research is simultaneously detecting two different physical stimuli by monitoring the dynamic response around the first two lowest modes of the single coupled structure. Hence, we desire to find that stiffness variation and mass variation change the response of the whole system in different ways, as Fig. 12 shows exactly. In Fig. 12a, b, the non-dimensional stiffness perturbation from −0.1 to 0.1 is given to the bridge resonator. The results show that bifurcation jumps in the first natural frequency response W1 in Fig. 12a changes due to stiffness variations on bridge resonator, while the peak value of the second natural frequency response W2 in Fig. 12b keeps constant. When it comes to mass perturbation on the cantilever resonator, the nonlinear jump remains in same largely in Fig. 12c. In contrast, the cantilever resonator's peak frequency and peak values in Fig. 12d are varying. Hence, it is possible to detect both the stiffness and mass perturbation applied on the bridge and cantilever resonators, respectively, by monitoring the nonlinear jump and peak frequency of the first two natural frequency responses. Thus, multi-sensing can be robustly performed.

Fig. 12

Parametric study of the frequency response curves under actuation of ${V}_{AC1}=7.3V$, ${V}_{DC1}=40V$, ${V}_{AC2}=0V$ and ${V}_{DC2}=10V$: a W1 and b W2 for different stiffness perturbation $\delta k$ of −0.1, −0.05, 0, 0.05, and 0.1; c W1 and d W2 for different mass perturbation $\delta m$ of 0, 0.01, 0.02, 0.03, 0.04, and 0.05. Dotted lines denote unstable branches. Amplitude of W1 and W2 is non-dimensional. The inset of a shows the nonlinear branch

Besides, the coupling between different modes of the structure would be an exciting topic to investigate. In previous research, the two lowest out-of-plane modes of vibration of the proposed structure (occurring at 178.22 kHz and 189.54 kHz) have a frequency ratio of 3.4 with the first two lowest in-plane modes, which suggests no internal resonance activation for the present case study among these modes. However, the activation of the internal resonance between in-plane and out-of-plane modes could happen for optimized structures as proven in the literature [45, 46]. This aspect would be addressed in future research investigating the sensing sensitivity as activating such nonlinear modal coupling.

4 Conclusions

In this paper, the nonlinear dynamics of two mechanically coupled micromachined resonators (cantilever and bridge resonators) were numerically investigated for potential multi-sensing applications. The concept is based on the simultaneous tracking of the resonance frequencies of the first and second lowest vibration modes. Stiffness and mass perturbations of the bridge and cantilever resonators, respectively, were found to have independent influence on the two vibration modes, demonstrating the promising potential of multi-sensing on a single device. Nonlinear behaviour, including bifurcation jumps and peaks as sensing targets, improves the accuracy and sensitivity of the sensor. The numerical model of the coupled system with geometric and electrostatic nonlinear terms is developed, demonstrating the multi-sensing feasibility. The continuous simulation of the structure is obtained, revealing the full nonlinear dynamics of the coupled system and the effect of different parameters, which is vital for the sensor's design. It is worth mentioning that the value of AC actuation directly relates to the system's nonlinearity. Medium levels of AC actuation linked to the nonlinear bifurcation jumps are suitable to gain the sensor's best performance and weaken the risk of unstable softening branches due to excessive driving input. The perturbation simulations demonstrate the response variation under two perturbations. The results indicate that stiffness and mass perturbations of the bridge and cantilever resonators independently influence the first two vibration modes, proving the promising performance of the multi-gas sensing concept.

The research introduces the methodology of the nonlinear coupled resonator in performing multi-parameters detection, which shows its potential for mixture gas analysis, vehicle propulsion system monitoring, and any industrial setting that requires multiple sensing. Future work will focus on the practical sensor system design and fabrication, specifically, the multi-gas sensor for binary gas mixture analysis with the matched testing circuit and platform. Additionally, this research chooses the first and second global modes to perform the sensing strategy. Instead of the low-order modes, the scheme actuating in higher-order modes may increase the response amplitude and improve the sensitivity, which is also a potential research direction. The above would include the investigation of potential activation of internal resonance among in-plane modes and out-of-plane modes of vibrations.

Appendix

The following variables and parameters are introduced:

$$ \begin{aligned} w_{1} & = \frac{{\tilde{w}_{1} }}{{d_{1} }};\;w_{2} = \frac{{\tilde{w}_{2} }}{{d_{1} }};\;x = \frac{{\tilde{x}}}{{L_{1} }};\;X_{c} = \frac{{\tilde{X}_{c} }}{{L_{1} }};\;X_{m} = \frac{{\tilde{X}_{m} }}{{L_{1} }};\;R_{L} = \frac{{L_{2} }}{{L_{1} }};\;R_{d} = \frac{{d_{2} }}{{d_{1} }};\;\tilde{m} = \frac{m}{{\rho AL_{1} }};\;t = \frac{{\tilde{t}}}{\tau }; \\ \Omega_{1} & = \tilde{\Omega }_{1} \tau ;\;\Omega_{2} = \tilde{\Omega }_{2} \tau ;\;\tau = \sqrt {\frac{{\rho AL_{1}^{4} }}{EI}} ;\;I = \frac{{bh^{3} }}{12};\;N = \frac{{\tilde{N}L_{1}^{2} }}{EI};\;k_{r} = \frac{{\tilde{k}_{r} L_{1} }}{EI};{ }\;\tilde{c}_{i} = \frac{{L_{1}^{4} c_{i} }}{EI\tau }; \;\alpha_{1} = 6{*}\left( {\frac{{d_{1} }}{h}} \right)^{2} ; \\ \alpha_{2} & = \frac{{\varepsilon_{0} bL_{1}^{4} }}{{2EId_{1}^{3} }};\;k_{r} = \frac{{G\beta b_{c} h^{3} }}{{L_{C} }} \\ \end{aligned} $$

(7)

By substituting the new introduced parameters in (7) into Eqs. (2) and (3), the non-dimensional equations of motion are presented as:

$$ \begin{aligned} & w_{1}^{\prime \prime \prime \prime } + \ddot{w}_{1} + c_{1} \dot{w}_{1} + \left[ {N - \alpha_{1} \mathop \int \limits_{0}^{1} \left( {w_{1}^{^{\prime}} } \right)^{2} {\text{d}}x} \right]*w_{1}^{\prime \prime } + k_{r} \left( {w_{1}^{\prime } \left( {X_{c} } \right) - w_{2}^{\prime } \left( {X_{c} } \right)} \right)\delta^{\prime } \left( {x - X_{c} } \right) \\ & \quad = \alpha_{2} \frac{{\left[ {V_{DC1} + V_{AC1} \cos \left( {\Omega_{1} t} \right)} \right]^{2} }}{{\left( {1 - w_{1} } \right)^{2} }} \\ \end{aligned} $$

(8)

$$ \begin{aligned} & w_{2}^{\prime \prime \prime \prime } + \left( {1 + \delta m\left( {x - X_{m} } \right)} \right)\ddot{w}_{2} + c_{2} \dot{w}_{2} + k_{r} \left( {w_{2}^{\prime } \left( {X_{c} } \right) - w_{1}^{\prime } \left( {X_{c} } \right)} \right)\delta^{\prime } \left( {x - X_{c} } \right) \\ & \quad = \alpha_{2} \frac{{\left[ {V_{DC2} + V_{AC2} \cos \left( {\Omega_{2} t} \right)} \right]^{2} }}{{\left( {R_{d} - w_{2} } \right)^{2} }} \\ \end{aligned} $$

(9)

with the following corresponding boundary conditions:

$$ w_{1} \left( {0,t} \right) = w_{1}^{\prime } \left( {0,t} \right) = w_{1} \left( {1,t} \right) = w_{1}^{\prime } \left( {1,t} \right) = 0 $$

(10)

$$ w_{2} \left( {0,t} \right) = w_{2}^{\prime } \left( {0,t} \right) = w_{2} \left( {R_{L} ,t} \right) = w_{1}^{\prime } \left( {R_{L} ,t} \right) = 0 $$

(11)

After multiplying both sides of Eqs. (8) and (9) by the $\left( {1 - w} \right)^{2}$, and applying the Galerkin method [41], it yields:

$$ \begin{aligned} & \left( {1 - w_{1} } \right)^{2} w_{1}^{\prime \prime \prime \prime } + \left( {1 - w_{1} } \right)^{2} \frac{{\partial^{2} w_{1} }}{{\partial t^{2} }} + \left( {1 - w_{1} } \right)^{2} c_{1} \frac{{\partial w_{1} }}{\partial t} - \left( {1 - w_{1} } \right)^{2} \alpha_{1} \mathop \int \limits_{0}^{1} \left( {w_{1}^{\prime } } \right)^{2} {\text{d}}x*w_{1}^{^{\prime\prime}} \\ & \quad + \left( {1 - w_{1} } \right)^{2} k_{r} \left( {w_{1}^{\prime } \left( {X_{c} } \right) - w_{2}^{\prime } \left( {X_{c} } \right)} \right)\delta^{\prime } \left( {x - X_{c} } \right) = \alpha_{2} \left[ {V_{DC1} + V_{AC1} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \\ \end{aligned} $$

(12)

$$ \begin{aligned} & \left( {R_{d} - w_{2} } \right)^{2} w_{2}^{\prime \prime \prime \prime } + \left( {R_{d} - w_{2} } \right)^{2} \left( {1 + \delta m\left( {x - X_{m} } \right)} \right)\frac{{\partial^{2} w_{2} }}{{\partial t^{2} }} + \left( {R_{d} - w_{2} } \right)^{2} c_{2} \frac{{\partial w_{2} }}{\partial t} \\ & \quad + \left( {R_{d} - w_{2} } \right)^{2} k_{r} \left( {w_{2}^{\prime } \left( {X_{c} } \right) - w_{1}^{\prime } \left( {X_{c} } \right)} \right)\delta^{\prime } \left( {x - X_{c} } \right) = \alpha_{2} \left[ {V_{DC2} + V_{AC2} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \\ \end{aligned} $$

(13)

The solutions of Eqs. (12) and (13) can be expressed as $w_{1} \left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{\infty } u_{1,i} \left( t \right)\varphi_{1,i} \left( x \right)$ and $w_{2} \left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{\infty } u_{2,i} \left( t \right)\varphi_{2,i} \left( x \right)$, where $\varphi_{1,i}$ and $\varphi_{2,i}$ are the ith linear undamped mode shape of microbeams 1 and 2. Then, the linear undamped eigenvalue equations are obtained:

$$ \varphi_{{1,{\text{i}}}}^{\prime \prime \prime \prime } = \beta_{1,i}^{2} \varphi_{1,i} ; \;\varphi_{{2,{\text{i}}}}^{\prime \prime \prime \prime } = \beta_{2,i}^{2} \varphi_{2,i} $$

(14)

$$ \beta_{1}^{2} = \mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } {\text{d}}x;\; \beta_{2}^{2} = \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } {\text{d}}x $$

(15)

By substituting Eqs. (14) and (15) into Eqs. (12) and (13), multiplying by ${\varphi }_{1,i}$, ${\varphi }_{2,i}$, and integrating from $x=0$ to $1$, $x=0$ to ${R}_{L}$, it yields:

$$ \begin{aligned} & \left( {\mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } {\text{d}}xu_{1} \left( {1 + \delta k} \right) + \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + c_{{1{\text{n}}}} \frac{{\partial u_{1} }}{\partial t} + k_{r} \left[ {u_{1} \left( {\varphi_{1}^{\prime } \left( {X_{c} } \right)} \right)^{2} - u_{2} \varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right]} \right){*}\left( {1 - 2u_{1} \mathop \int \limits_{0}^{1} \varphi_{1}^{3} {\text{d}}x + u_{1}^{2} \mathop \int \limits_{0}^{1} \varphi_{1}^{4} {\text{d}}x} \right) \\ & \quad - \alpha_{1} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime 2} {\text{d}}x\left( {u_{1}^{3} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1} {\text{d}}x - 2u_{1}^{4} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1}^{2} {\text{d}}x + u_{1}^{5} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1}^{3} {\text{d}}x} \right) = \alpha_{2} \left[ {V_{DC1} + V_{AC1} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \mathop \int \limits_{0}^{1} \varphi_{1} {\text{d}}x \\ \end{aligned} $$

(16)

$$ \begin{aligned} & \left( {\mathop \int \limits_{0}^{{R_{L} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } {\text{d}}xu_{2} + \left( {1 + \delta m\left( {x - X_{m} } \right)} \right)\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + c_{2n} \frac{{\partial u_{2} }}{\partial t} + k_{r} \left[ {u_{2} \left( {\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right)^{2} - u_{1} \varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right]} \right) \\ & \quad *\left( {R_{d}^{2} - 2R_{d} u_{2} \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2}^{3} {\text{d}}x + u_{2}^{2} \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2}^{4} {\text{d}}x} \right) = \alpha_{2} \left[ {V_{DC2} + V_{AC2} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2} {\text{d}}x \\ \end{aligned} $$

(17)

where the $\delta k$ and $\delta m$ represents the linear stiffness variation on bridge resonator due to the external stimulus and the mass perturbation on cantilever resonator, respectively.

The first and second local mode shapes for the bridge and cantilever are:

$$ \varphi_{1} \left( x \right) = - \cos \left( {4.73004x} \right) + \cosh \left( {4.73004x} \right) + \frac{{\sinh \left( {4.73004} \right) + \sin \left( {4.73004} \right)}}{{{\text{cosh}}\left( {4.73004} \right) - {\text{cos}}\left( {4.73004} \right)}}\left[ {{\text{sin}}\left( {4.73004x} \right) - {\text{sinh}}\left( {4.73004x} \right)} \right] $$

(18)

$$ \varphi_{2} \left( x \right) = K\left( { - \cos \left( {\frac{1.8751x}{{R_{L} }}} \right) + \cosh \left( {\frac{1.8751x}{{R_{L} }}} \right) + \frac{{\sin \left( {\frac{1.8751}{{R_{L} }}} \right) - \sinh \left( {\frac{1.8751}{{R_{L} }}} \right)}}{{{\text{cos}}\left( {\frac{1.8751}{{R_{L} }}} \right) - {\text{cosh}}\left( {\frac{1.8751}{{R_{L} }}} \right)}}\left[ {{\text{sin}}\left( {\frac{1.8751x}{{R_{L} }}} \right) - {\text{sinh}}\left( {\frac{1.8751x}{{R_{L} }}} \right)} \right]} \right) $$

(19)

where the coefficient K takes a value ensuring ${\int }_{0}^{{R}_{L}}{\varphi }_{2}^{2}{\mathrm{d}}x=1$.