Introduction

Mode localization is often observed in the near-symmetrical weakly coupled resonator (WCR) systems, where small disturbances of the parameters may lead to energy confinement in one or more vibration modes. This phenomenon was firstly investigated by Anderson, the Nobel Prize winner in 1977, who described the electron wave localization in a disordered lattice [1]. The mode localization is intrinsically linked to an abrupt divergence of the loci in the eigenvalue curve against parametric variations, termed “mode veering” or “loci veering” [2, 3]. Consequently, the natural frequencies and mode shapes of the coupled resonators may exhibit startling sensitivity when a parameter is varied. Taking advantage of this feature, the disorder of the weakly coupled resonator systems can be easily measured.

In recent years, the coupled micro-resonators were widely explored in micro-electromechanical systems (MEMSs) to detect an external stimulus, such as mass disturbance [4], or stiffness disturbance (caused by the displacement [5] and acceleration [6]). One of the common transduction mechanisms of sensors is the detection of the resonance frequency shift in response to the tiny change in mass and stiffness [7, 8]. Sensing based on the shift of resonance frequency possesses the advantages of ease of digitization, high precision, and large dynamic range. For the resonant accelerometers using this mechanism, the sensitivity varied from less than 10 Hz/g to more than 1000 Hz/g [9]. To improve the sensitivity, a variant resonant sensor system with strong mechanical coupling was proposed, where an improvement of more than 20% in sensitivity with moderate coupling ratios was observed [10]. However, the relative shift in resonance frequency for small variations of system parameters is still limited.

To further promote the efficiency of sensing, the eigenstate, or the amplitude ratio of the WCR is used as the output metric of the sensors. The mode localization and mode veering phenomenon resulting from the small symmetry-breaking disturbance would significantly change the mode shapes of the system. By measuring the eigenstate (amplitude ratio) shift, it was reported that orders of magnitude improvements in parametric sensitivity could be obtained as compared to that using the typical frequency-shift output metric [11, 12]. Based on this approach, ultra-high sensitivity were implemented for various applications, such as force sensing [13], mass sensing [14, 15], stiffness sensing [16], charge sensing [17], acceleration sensing [9] and tilt sensing [18]. Moreover, this type of sensor could be robust to environment drift in temperature and pressure, outperforming the frequency-shift based sensors [19]. The influence of the driving scheme on the sensitivity was also discussed. It was found that the sensitivity based on a single-sided driving scheme is approximately an order higher than that under double-sided driving, while sacrificing a certain degree of linear measurement range [20]. Some researchers also discussed the noise and resolution [21, 22] and coupling factor [23] in detail to further optimize the mode-localized resonant sensors. In general, lowering the coupling factor would increase the sensitivity, but would also decrease the frequency separation between two resonant peaks, thus reducing the resolution of the amplitude ratio variations [24]. Thus, there should be a lower limit for the coupling factor. To lower the coupling factor, a stiff anchor support was introduced as a mechanical coupler to improve the parametric amplitude ratio sensitivity [25].

It is noted that most of the sensitivities of the WCRs based on the eigenstate were calculated by the small perturbation theory or utilizing the Rayleigh–Ritz approach [11, 14,15,16,17, 23, 24]. The proper selection of basic functions is critical in representing the original mass-spring system. However, the eigenstate of the perturbed system would be much different from that of the undisturbed case for the WCR even though the disturbance is small. Thus, the Rayleigh–Ritz approach may lead to a large error in predicting the sensitivity in the mode localization region. Other than the relative change in the eigenstate, the output metric based on the relative change in the amplitude ratio exhibits a wide linear range in the mode localization region, however, may conversely yield a large nonlinear error in the mode veering zone [11, 14,15,16,17, 23, 24]. In other words, no matter whether the sensitivities are based on the change in eigenstate or the amplitude ratio, they both have a limited scope of application. To address this problem, several continually linear sensing methods by selecting the amplitude difference [26] and the subtraction of reciprocal amplitude ratios [27] were proposed.

In this paper, a mass sensor based on the micro-cantilever array is investigated. Rather than using the sensitivities based on conventional output metrics such as the eigenstate, the exact value of amplitude ratio, and the relative changes in eigenvalues and eigenstates, for the first time, a new metric of the sensitivity is derived based on the difference between the absolute values of amplitude ratios, which is valid in the full scope covering both mode veering region and mode localization region with high accuracy. The linearity of the proposed sensitivity is proven to be significantly better than that of the traditional amplitude ratio readout by theoretical and numerical study. The trade-off between resolution and sensitivity and the influence of damping and coupling factor is also discussed to provide a theoretical guide to designing mode-localized sensors. Lastly, the superior linearity of the proposed metric is experimentally verified based on a prototyped weakly coupled cantilever system.

Mathematical Modelling

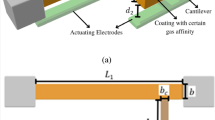
A weakly coupled resonator (WCR) system consisting of two identical micro-cantilevers weakly coupled by a coupling beam is shown in Fig. 1. The coupling factor can be adjusted by altering the geometry of the coupling beam.

Fig. 1
figure 1

Schematic of the weakly coupled micro-cantilevers with a mass disturbance

Full size image

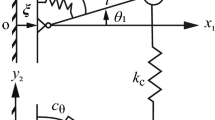
Each cantilever can be modelled as a resonator, while the coupling beam can be modelled as a spring connecting the resonators. Thus, the coupled micro-cantilever array is modelled as a simplified two-degree-of-freedom (2DOF) spring-mass-damper system, as shown in Fig. 2. k1, k2 and m1, m2 are the effective bending stiffnesses and effective masses of the two micro-cantilevers, respectively, while kc is the effective stiffness of the coupling beam. c1, c2 are the corresponding damping coefficients. A mass disturbance d may be applied at the end of Cantilever 1, which breaks the symmetry of the system. The governing equations of an undamped 2DOF weakly coupled resonator system are given as

$$\left[ {\begin{array}{*{20}l} {m_{1} } \hfill & 0 \hfill \\ 0 \hfill & {m_{2} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{x}_{1} } \hfill \\ {\ddot{x}_{2} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {k_{1} + k_{{\text{c}}} } \hfill & { - k_{{\text{c}}} } \hfill \\ { - k_{{\text{c}}} } \hfill & {k_{2} + k_{{\text{c}}} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ \end{array} } \right\},$$
(1)

where x1 and x2 are the displacements of the two resonators relative to the base, which are actually the transverse tip displacements of the beams. The solution of the system can be assumed as

$$\left\{ \begin{gathered} x_{1} = A_{1} \sin \left( {\omega t + \varphi } \right) \hfill \\ x_{2} = A_{2} \sin \left( {\omega t + \varphi } \right) \hfill \\ \end{gathered} \right.,$$
(2)

where A1 and A2 are the amplitudes of x1 and x2, respectively, while ω and φ are the frequency and the phase of the response.

Fig. 2
figure 2

Simplified two-degree-of-freedom (2DOF) dynamic model

Full size image

Submitting the assumed solutions and derivatives to the governing equations leads to

$$\left[ {\begin{array}{*{20}l} {k_{1} + k_{{\text{c}}} - m_{1} \omega^{2} } & { - k_{{\text{c}}} } \\ { - k_{{\text{c}}} } & {k_{2} + k_{{\text{c}}} - m_{2} \omega^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ \end{array} } \right\}.$$
(3)

The two eigenvalues thus can be obtained as

$$\omega_{1,2}^{2} = \left( {\frac{{k_{1} + k_{{\text{c}}} }}{{2m_{1} }} + \frac{{k_{2} + k_{{\text{c}}} }}{{2m_{2} }}} \right) \mp \sqrt {\left[ {\frac{{\left( {\frac{{k_{1} + k_{{\text{c}}} }}{{m_{1} }} + \frac{{k_{2} + k_{{\text{c}}} }}{{m_{2} }}} \right)}}{2}} \right]^{2} - \frac{{\left( {k_{1} + k_{{\text{c}}} } \right)\left( {k_{2} + k_{{\text{c}}} } \right) - k_{{\text{c}}}^{2} }}{{m_{1} m_{2} }}} .$$
(4)

Submitting the eigenvalues into the governing equations, one can get the amplitude ratio of the first mode (β1) and the second mode (β2) as follows

$$\beta_{1} = \frac{{A_{2}^{(1)} }}{{A_{1}^{(1)} }} = \frac{{\left( {k_{1} + k_{{\text{c}}} - m_{1} \omega_{1}^{2} } \right)}}{{k_{{\text{c}}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta_{2} = \frac{{A_{2}^{(2)} }}{{A_{1}^{(2)} }} = \frac{{\left( {k_{1} + k_{{\text{c}}} - m_{1} \omega_{2}^{2} } \right)}}{{k_{{\text{c}}} }}$$
(5)

where the superscripts (1) and (2) denote the first and second modes, respectively. Then, the normalized eigenstate (or eigenvector) can be expressed by

$${\mathbf{u}}_{1} = \frac{1}{{\sqrt {1 + \beta_{1}^{2} } }}\left[ {\begin{array}{*{20}l} 1 \hfill \\ {\beta_{1} } \hfill \\ \end{array} } \right],\quad {\mathbf{u}}_{2} = \frac{1}{{\sqrt {1 + \beta_{2}^{2} } }}\left[ {\begin{array}{*{20}c} 1 \\ {\beta_{2} } \\ \end{array} } \right].$$
(6)

Besides, the time-domain responses of the undamped system can be expanded as follows

$$\left\{ \begin{gathered} x_{1} = A_{1}^{(1)} \sin \left( {\omega_{1} t + \varphi_{1} } \right) + A_{1}^{(2)} \sin \left( {\omega_{2} t + \varphi_{2} } \right) \hfill \\ x_{2} = \beta_{1} A_{1}^{(1)} \sin \left( {\omega_{1} t + \varphi_{1} } \right) + \beta_{2} A_{1}^{(2)} \sin \left( {\omega_{2} t + \varphi_{2} } \right) \hfill \\ \end{gathered} \right.,$$
(7)

where \(A_{1}^{(1)} ,A_{1}^{(2)} ,\varphi_{1} ,\varphi_{2}\) are determined by initial conditions. If \(x_{1} = x_{10} ,x_{2} = x_{20} ,\dot{x}_{1} = 0,\dot{x}_{2} = 0\), one can obtain

$$A_{1}^{(1)} = \frac{1}{{\beta_{2} - \beta_{1} }}\left( {\beta_{2} x_{10} - x_{20} } \right), \, A_{1}^{(2)} = \frac{1}{{\beta_{1} - \beta_{2} }}\left( {\beta_{1} x_{10} - x_{20} } \right).$$
(8)

For the symmetric WCR system with no mass disturbance, the effective stiffnesses and masses of the two micro-cantilevers with no tip mass, and the coupling stiffness of the coupling beam can be obtained by [28, 29]

$$\left\{ \begin{gathered} k_{1} = k_{2} = k \approx \frac{3EI}{{L^{3} }} \hfill \\ k_{{\text{c}}} \approx \frac{{12E_{{\text{c}}} I_{{\text{c}}} }}{{L_{{\text{c}}}^{3} }} \hfill \\ m_{1} = m_{2} = m \approx 0.24267M_{{\text{b}}} \hfill \\ \end{gathered} \right.,$$
(9)

where E, I, L and Ec, Ic, Lc are the Young’s moduli, the area moments of inertial of the cross-sectional areas, and the lengths of the cantilever beam and the coupling beam, respectively. Mb is the distributed cantilever beam mass. The distributed mass of the coupling beam can be neglected. Then, the eigenvalues and normalized eigenstates (or eigenvectors) of the system without mass disturbance can be calculated as

$$\omega_{10,20}^{2} = \frac{{\left( {k + k_{{\text{c}}} } \right)}}{m} \mp \frac{{k_{{\text{c}}} }}{m},$$
(10)
$${\mathbf{u}}_{1}^{0} = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}l} 1 \hfill \\ 1 \hfill \\ \end{array} } \right],\quad {\mathbf{u}}_{2}^{0} = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}c} 1 \\ { - 1} \\ \end{array} } \right],$$
(11)

where the subscripts “10” and “20” denote the first and second eigenvalues (natural frequencies) and the superscripts “0” denote the eigenstates of the weakly coupled system without mass disturbance. These results are in accordance with the previous study on WCRs [23]. For the asymmetric WCR system with a mass disturbance d, the masses of the system become

$$m_{1} = m + d, \, m_{2} = m.$$
(12)

One can obtain the natural frequencies and amplitude ratios as

$$\omega_{1,2}^{{}} = \sqrt {\frac{{\left( {2m + d} \right)\left( {k + k_{{\text{c}}} } \right) \mp \sqrt {d^{2} \left( {k + k_{{\text{c}}} } \right)^{2} + 4m\left( {m + d} \right)\,k_{{\text{c}}}^{2} } }}{{2m\left( {m + d} \right)}}}$$
(13)
$$\left\{ \begin{gathered} \beta_{1} = \frac{{ - d\left( {k + k_{{\text{c}}} } \right) + \sqrt {d^{2} \left( {k + k_{{\text{c}}} } \right)^{2} + 4m\left( {m + d} \right)\,k_{{\text{c}}}^{2} } }}{{2mk_{{\text{c}}} }} \hfill \\ \beta_{2} = \frac{{ - d\left( {k + k_{{\text{c}}} } \right) - \sqrt {d^{2} \left( {k + k_{{\text{c}}} } \right)^{2} + 4m\left( {m + d} \right)\,k_{{\text{c}}}^{2} } }}{{2mk_{{\text{c}}} }} \hfill \\ \end{gathered} \right..$$
(14)

Finite Element Modelling

To validate the analytical natural frequencies and amplitude ratios of the weakly coupled resonator system, the governing equation can be numerically simulated using the ODE45 function in MATLAB. In addition, the finite element method (FEM) can be utilized to verify the theoretical results using the commercial package COMSOL Multiphysics.

The finite element model of the system is shown in Fig. 3. The length, width, and thickness of the constructed micro-cantilevers are 100 μm, 5 μm, and 1 μm, respectively. The gap distance between the two cantilevers is 10 μm. A coupling beam is positioned at the end to mechanically couple the neighboring cantilevers, the size of which is 10 × 1 × 0.1 μm3. The cantilevers are made of Polycrystalline silicon with the Young’s modulus, density and Poisson’s ratio being 80 GPa, 2330 kg/m3, and 0.28, respectively. The Young’s modulus, density and Poisson’s ratio of the coupling beam are 2 GPa, 1150 kg/m3 and 0.4, respectively. In addition, there is a lumped mass d at the end of one cantilever, which acts as a mass disturbance and will be varied in the following analysis. Based on Eq. (9), other parameters of the system used in the following theoretical analysis, including the approximate equivalent mass and stiffness, are as follows unless otherwise stated:

$$m = 282.7{\text{ pg,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \, k = 0.1{\text{ N/m, }}k_{{\text{c}}} = 0.002{\text{ N/m}}{.}$$
(15)
Fig. 3
figure 3

Finite element model of weakly coupled micro-cantilevers

Full size image

Undamped Free Vibration

Model Validation

Theoretical values of the natural frequencies and amplitude ratios of the lumped model can be obtained by Eqs. (13) and (14). To validate the accuracy of the analytical formula of natural frequencies and mode shapes, the free vibration responses of the undamped WCR system are simulated by the ODE45 function. The initial displacement of the WCR system is set to be x1 = 2 µm and x2 = 2 µm, while the initial velocities are set to be zeroes. System parameters are shown in Eq. (15).

For the undisturbed system (d = 0), the in-phase first mode would be triggered with a frequency of 94.658 kHz and an amplitude ratio of 1, as predicted by Eqs. (4), (5), and (8). Based on the FFT analysis, Fig. 4a and b shows the frequency spectra of the numerical free vibration responses obtained by ODE45. It is noted that the responses of the resonators are nearly the same as the system is symmetric. The frequency (f1 = 94.649 kHz) and amplitude ratio (|β1|= 1) shown in the ODE45 numerical results are in accordance with the theoretical values. The small error in the amplitude may be due to the leakage in the FFT analysis.

Fig. 4
figure 4

Frequency spectra of the numerical free vibration responses by ODE45: a x1 and b x2 without mass disturbance, and c x1 and d x2 with mass disturbance d = 10 pg

Full size image

For the system with a mass disturbance d = 10 pg, both the in-phase and out-phase modes are involved in the responses of the resonators. The natural frequencies and amplitude ratios of the two modes can be theoretically derived as f1 = 93.530 kHz, f2 = 96.013 kHz and β1 = 0.4578, β2 = -2.2618. Figure 4c and d shows the corresponding frequency spectra for the numerical free vibration responses, where the amplitude ratios can be calculated by dividing the modal amplitudes of two resonators in each mode. It is found that the natural frequencies (f1 = 93.549 kHz, f2 = 96.001 kHz) and amplitude ratios (|β1|= 0.4564, |β2|= 2.2045) of the two modes are also consistent with the theoretical values. In each mode, it is noted that the system energy begins to localise to one of the two resonators instead of distributing equally in each resonator.

Finite element modal analysis is also conducted using COMSOL Multiphysics to validate the lumped model. Figure 5 illustrates the results of the modal analysis of the cantilever array system with and without mass disturbance. The colour contours represent the vertical displacement of the cantilevers. Based on the displacements at the tip ends of the two cantilevers, the amplitude ratios are calculated as 0.4715 and -2.1914, respectively, which in general agree with the theoretical predictions (β1 = 0.4578, β2 = -2.2618). Furthermore, Fig. 6 compares the natural frequencies and amplitude ratios obtained by different methods with different mass disturbances. The consistency of the results illustrates that the lumped model and the formulas to calculate the natural frequency and mode shape (Eqs. (13) and (14)) are effective. In addition, the mass disturbance breaks the symmetry of the system such that one cantilever oscillates more than the other in the in-phase and out-phase modes, which is called “mode localization”.

Fig. 5
figure 5

Modal analysis using FEM: a in-phase and b out-phase modes without mass disturbance, and c in-phase and d out-phase modes with mass disturbance d = 10 pg

Full size image
Fig. 6
figure 6

Comparison of the a natural frequencies and b amplitude ratios obtained by different methods

Full size image

Conventional Output Metrics for Sensing

As can be seen in Fig. 6, the natural frequencies and the amplitude ratios of the WCR system vary with the mass disturbance. This characteristic can be used to sense the mass disturbance by measuring the change in the natural frequency [7, 8] or the amplitude ratio [20].

Figure 7 shows the analytical natural frequencies and amplitude ratios of two modes with varying mass disturbance. It is worth mentioning that the applied tip mass disturbance is positive in the concerned system and the negative mass disturbance is only plotted for illustration. It can be seen that the mode localization is associated with a mode veering zone, where the natural frequencies and amplitude ratios of the two modes do not cross but swop swiftly. Away from this mode veering zone, the amplitude ratios get further away from 1 with the increase of the mass disturbance, implying that the energy is confined in one of the resonators. It is noted that for the natural frequency and amplitude ratio, the mode localization region is mainly characterized by linearity, while the mode veering zone shows a nonlinearity. Thus, the natural frequency or amplitude ratio can be used for dynamic measurement only in the mode localization region with a relatively large disturbance.

Fig. 7
figure 7

Mode veering and localization of a theoretical natural frequencies and b theoretical dimensionless amplitude ratios of two modes with varying mass disturbance

Full size image

In addition, by referring to Eqs. (10–14), the relative changes in eigenvalues are obtained by

$$\left\{ \begin{gathered} \frac{{\omega_{{_{1} }}^{2} - \omega_{{_{10} }}^{2} }}{{\omega_{{_{10} }}^{2} }} = \frac{{\left( {2m + d} \right)\left( {k + k_{{\text{c}}} } \right) - \sqrt {d^{2} \left( {k + k_{{\text{c}}} } \right)^{2} + 4m\left( {m + d} \right)k_{{\text{c}}}^{2} } }}{{2k\left( {m + d} \right)}} - 1 \hfill \\ \frac{{\omega_{{_{2} }}^{2} - \omega_{{_{20} }}^{2} }}{{\omega_{{_{20} }}^{2} }} = \frac{{\left( {2m + d} \right)\left( {k + k_{{\text{c}}} } \right) + \sqrt {d^{2} \left( {k + k_{{\text{c}}} } \right)^{2} + 4m\left( {m + d} \right)k_{{\text{c}}}^{2} } }}{{2k\left( {m + d} \right)}} - 1 \hfill \\ \end{gathered} \right.$$
(16)

while the relative changes in the normalized eigenstates are given by

$$\left\{ \begin{gathered} \frac{{\left| {{\mathbf{u}}_{1} - {\mathbf{u}}_{1}^{0} } \right|}}{{\left| {{\mathbf{u}}_{1}^{0} } \right|}} = \left[ {2 - \sqrt 2 \frac{{1 + \beta_{1} }}{{\sqrt {1 + \beta_{1}^{2} } }}} \right]^{\frac{1}{2}} \hfill \\ \frac{{\left| {{\mathbf{u}}_{2} - {\mathbf{u}}_{2}^{0} } \right|}}{{\left| {{\mathbf{u}}_{2}^{0} } \right|}} = = \left[ {2 - \sqrt 2 \frac{{1 - \beta_{2} }}{{\sqrt {1 + \beta_{2}^{2} } }}} \right]^{\frac{1}{2}} \hfill \\ \end{gathered} \right..$$
(17)

The relative changes of the verified eigenvalues and eigenstates are somewhat different from the commonly used formulas in the previous study based on the perturbation theory or Rayleigh method as follows [11, 14,15,16,17, 23,24,25]

$$\frac{{\omega_{1,2}^{2} - \omega_{10,20}^{2} }}{{\omega_{10,20}^{2} }} = - \frac{d}{2m},\quad \frac{{\left| {{\mathbf{u}}_{1,2} - {\mathbf{u}}_{1,2}^{0} } \right|}}{{\left| {{\mathbf{u}}_{1,2}^{0} } \right|}} = \left( {\frac{1}{4} + \frac{k}{{4k_{{\text{c}}} }}} \right)\frac{d}{m}.$$
(18)

Figure 8 shows the eigenvalue and eigenstate obtained by Eqs. (16) and (17), compared with those calculated based on the perturbation theory (Eq. (18)). It can be seen that the relative change in the eigenstate is a few orders of magnitude larger than that in the eigenvalue, which was revealed in many previous studies [11, 12]. However, the perturbation theory results can only be consistent with the theoretical values when the mass disturbance is small enough (around the mode veering zone). This is understandable, because the mode shape would vary dramatically when mode localization occurs while the perturbation theory results are based on the use of the mode shape of the undisturbed system as an approximation. Thus, in the region of mode localization, the perturbation theory may lead to a large error in estimating the relative change. In other words, the commonly used sensitivity based on Eq. (18) derived from the perturbation theory can only be regarded as the first-order approximation around the unperturbed point and therefore they only have a limited range of accuracy.

Fig. 8
figure 8

The relative change in a the eigenvalue and b the normalized eigenstate changes as a function of the mass disturbance by analytical expression and perturbation theory

Full size image

By and large, the conventional output metrics both have a limited linear sensing range. The output metrics based on the natural frequency and amplitude ratio are applicable for large disturbances. The output metrics based on the relative changes in the eigenvalue and eigenstate are only applicable for very small disturbances, which can be approximated by the perturbation theory. For the large disturbance, the relative changes in the eigenvalue and eigenstate vary with the disturbance in a nonlinear fashion, and perturbation theory would fail to predict it.

Sensitivity Based on Difference between Amplitude Ratios

It can be seen that the linear sensing ranges of the amplitude ratio and relative change in the normalized eigenstate seems complementary to each other. However, it is necessary to determine the critical point for transferring the output metric, which is not convenient in practical use. Herein, we propose a sensitivity based on the difference between the absolute values of amplitude ratios that can cover the full range of sensing. Different from the exact value of the amplitude ratios, the new output metric is defined by

$$\chi = \left| {\beta_{2} } \right| - \left| {\beta_{1} } \right|.$$
(19)

Referring to Eq. (14), it can be derived that

$$\chi = \frac{{\left( {k + k_{{\text{c}}} } \right)d}}{{k_{{\text{c}}} m}}.$$
(20)

Figure 9a and b shows the linear fitting curves and the relative errors based on χ and amplitude ratios, respectively. It can be seen that the defined output metric χ is linearly proportional to the mass disturbance in the full scope (Fig. 9a), while the sensitivity based on amplitude ratios shows a large nonlinearity when the disturbance is small (Fig. 9b). Figure 9c and d shows the corresponding slopes of χ and amplitude ratios. The slope of χ can be obtained as 1.804 × 105 ppm/pg by Eq. (20), which can be regarded as the sensitivity of the system. It also corresponds to the slope of the linear fitting curve. However, the slope of the amplitude ratios varies near the mode veering zone. Thus, the two sensitivities based on the amplitude ratios of the two modes can only be evaluated away from the veering zone, which are the same and can be obtained as − 1.752 × 105 ppm/pg. The sensitivities based on two types of output metrics are in the same order of magnitude and the one based on χ (1.804 × 105 ppm/pg) is even more sensitive than the single amplitude ratio. More importantly, it covers the full range with a higher accuracy due to the complete linearity.

Fig. 9
figure 9

Linear fitting curves (left axis) and relative errors (right axis) of a χ and b amplitude ratios, and slopes of c χ and d amplitude ratios with varying mass disturbance

Full size image

Figure 10 shows the variation of χ with the mass disturbance in the presence of different coupling stiffnesses. Other parameters are still taken from Eq. (15). It can be seen that the slope with weak coupling is larger, which is beneficial for enhancing the sensitivity. However, according to Eq. (13), the weak coupling may also decrease the gap between the two resonance frequencies, which can reduce the resolution of the two resonant peaks. This influence is discussed in the next section for the damped forced vibration.

Fig. 10
figure 10

Comparison of the differences of the amplitude ratios (left axis) and sensitivities (right axis) with different coupling stiffnesses

Full size image

Damped Forced Vibration

With damping and harmonic base excitation, the governing equations of the system become

$$\left[ {\begin{array}{*{20}l} {m_{1} } \hfill & 0 \hfill \\ 0 \hfill & {m_{2} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{x}_{1} } \hfill \\ {\ddot{x}_{2} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {c_{1} } \hfill & 0 \hfill \\ 0 \hfill & {c_{2} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\dot{x}_{1} } \hfill \\ {\dot{x}_{2} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {k_{1} + k_{{\text{c}}} } \hfill & { - k_{{\text{c}}} } \hfill \\ { - k_{{\text{c}}} } \hfill & {k_{2} + k_{{\text{c}}} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {x_{1} } \hfill \\ {x_{2} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {m_{1} B{\text{e}}^{i\omega t} } \hfill \\ {m_{2} B{\text{e}}^{i\omega t} } \hfill \\ \end{array} } \right\},$$
(21)

where B is the amplitude of base acceleration. Assume the steady-state solution to be

$$x_{i} (t) = X_{i} {\text{e}}^{j\omega t} ,\quad i,j = 1,2.$$
(22)

Inserting Eq. (22) into Eq. (21), it follows that

$$\left[ {\begin{array}{*{20}l} { - \omega^{2} m_{1} + j\omega c_{1} + k_{1} + k_{{\text{c}}} } & { - k_{{\text{c}}} } \\ { - k_{{\text{c}}} } & { - \omega^{2} m_{2} + j\omega c_{2} + k_{2} + k_{{\text{c}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{1} } \\ {X_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {m_{1} B} \hfill \\ {m_{2} B} \hfill \\ \end{array} } \right\}.$$
(23)

Assuming that the damping and the stiffness of two resonators are identical, namely c1 = c2 = c and k1 = k2 = k, the amplitudes of the steady-state responses thus can be obtained by

$$\left\{ \begin{gathered} \left| {X_{1} } \right| = \mu_{1} B\sqrt {\frac{{\left[ { - \omega^{2} m_{1} m_{2} + \left( {k + k_{{\text{c}}} } \right)m_{1} + k_{{\text{c}}} m_{2} } \right]^{2} + \omega^{2} c^{2} m_{1}^{2} }}{{\left\{ {\omega^{4} m_{1} m_{2} - \omega^{2} \left[ {\left( {m_{1} + m_{2} } \right)\left( {k + k_{{\text{c}}} } \right) + c^{2} } \right] + k^{2} + 2kk_{{\text{c}}} } \right\}^{2} + \omega^{2} c^{2} \left[ {\omega^{2} \left( {m_{1} + m_{2} } \right) - 2\left( {k + k_{{\text{c}}} } \right)} \right]^{2} }}} \hfill \\ \left| {X_{2} } \right| = \mu_{2} B\sqrt {\frac{{\left[ { - \omega^{2} m_{1} m_{2} + \left( {k + k_{{\text{c}}} } \right)m_{2} + k_{{\text{c}}} m_{1} } \right]^{2} + \omega^{2} c^{2} m_{2}^{2} }}{{\left\{ {\omega^{4} m_{1} m_{2} - \omega^{2} \left[ {\left( {m_{1} + m_{2} } \right)\left( {k + k_{{\text{c}}} } \right) + c^{2} } \right] + k^{2} + 2kk_{{\text{c}}} } \right\}^{2} + \omega^{2} c^{2} \left[ {\omega^{2} \left( {m_{1} + m_{2} } \right) - 2\left( {k + k_{{\text{c}}} } \right)} \right]^{2} }}} \hfill \\ \end{gathered} \right.,$$
(24)

where μ is the correction factor for the lumped parameter model of the cantilever beam without or with a small tip mass, which can be approximately expressed by [30]

$$\mu_{i} = \frac{{\left( {M_{ti} /M_{{\text{b}}} } \right)^{2} + 0.603\left( {M_{ti} /M_{{\text{b}}} } \right) + 0.08955}}{{\left( {M_{ti} /M_{{\text{b}}} } \right)^{2} + 0.4637\left( {M_{ti} /M_{{\text{b}}} } \right) + 0.05718}},{\kern 1pt} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} i = 1,2,$$
(25)

where Mti is the tip mass of the ith cantilever beam. The correction factor is related to the ratio of tip mass to the beam distributed mass. If the mass of the coupling beam is neglected, Mt is actually the mass disturbance d for Cantilever 1, while Mt = 0 for Cantilever 2.

Model Validation and Sensitivity Analysis

To validate the analytical response, frequency domain analysis is conducted using COMSOL Multiphysics. The WCR structure is subjected to a base acceleration of 2 m/s2. The influence of the small mass disturbance on the damping ratio can be considered limited, thus the damping ratio of both beams is obtained by \(\zeta = c/(2\sqrt {km} )\). In the following FEM analysis, Rayleigh damping is adopted and ζ = 0.001 is used as the damping ratio of the first two modes.

Figure 11 shows the amplitude–frequency responses of the WCR system predicted by Eq. (24) compared with those obtained by FEM with different mass disturbances. The analytical results are in general consistent with the FEM results, though there is a slight shift in the resonance frequencies. The frequency shift may be due to the error in simplifying the distributed system to the lumped system by the use of equivalent mass and stiffness. Despite the shift in the resonance frequencies, the amplitudes and amplitude ratios at the resonance frequencies obtained by FEM are almost the same as the analytical results.

Fig. 11
figure 11

Amplitude-frequency responses of the tip of cantilever beams with mass disturbances: a 0 pg; b 10 pg; c 20 pg; d 30 pg and e 40 pg

Full size image

The variation of the analytical amplitude ratios at two resonance frequencies and the difference between them with the mass disturbance are summarized in Figs. 12a and b, respectively. These results are also compared with those from the modal analysis (free undamped vibration). It is shown that the amplitude ratios at the first two resonances are generally in accordance. In other words, the small damping has limited effect on the amplitude ratios. Thus, the sensitivity based on the difference between absolute values of amplitude ratios is applicable in the damped harmonic forced vibration and can still be estimated by Eq. (20).

Fig. 12
figure 12

Comparison of a analytical amplitude ratios and b difference between amplitude ratios χ obtained from modal analysis and damped forced vibration analysis

Full size image

Resolution Analysis

To identify the resonance frequencies, measure the amplitude ratios at both resonance frequencies and calculate their difference, the two resonant peaks should not overlap or interfere with each other. According to Eq. (10), the difference between the undisturbed resonance frequencies of the two modes can be calculated by

$$\omega_{20} - \omega_{10} = \frac{{2k_{{\text{c}}} }}{{m\left( {\omega_{20} + \omega_{10} } \right)}} \approx \frac{{k_{{\text{c}}} }}{k}\omega_{10} .$$
(26)

The difference between the resonance frequencies of the disturbed system would be larger due to the mass disturbance, which is also shown in Fig. 11. To recognize the resonance frequencies, the bandwidth of the resonance Δω should be smaller than the difference between the resonance frequencies, namely

$$\Delta \omega = 2\zeta \omega_{10} < \omega_{20} - \omega_{10} = \frac{{k_{{\text{c}}} }}{k}\omega_{10} .$$
(27)

Thus, the coupling stiffness and damping ratio should satisfy

$$k_{{\text{c}}} > 2k\zeta .$$
(28)

According to Eqs. (20) and (28), decreasing the coupling stiffness is beneficial for improving the proposed sensitivity, however, may reduce the resolution of the output metric. Herein, k = 0.1 N/m2, such that the value of kc should be kept above 0.02ζ.

Figure 13(a) shows the amplitude-frequency response of Cantilever 1 resonator with different coupling stiffnesses kc in the presence of ζ = 0.001 and d = 2 pg. It is noted that the second resonant peak moves closer to the first resonant peak with the decrease of kc. When kc equals 0.0002 (kc = 2kζ), the two modes cannot be completely separated, which is called “mode interaction”. Figure 13b shows the amplitude–frequency response with different damping ratios ζ in the presence of kc = 0.002 and d = 2 pg. Increasing the damping ratio will broaden the resonant bandwidth, which is not desirable for high resolution. When ζ equals 0.01 (kc = 2kζ), the two vibration modes cannot be distinguished. By and large, there is a trade-off between sensitivity and resolution when selecting the proper coupling stiffness. To ensure a certain resolution, there is a lower limit of the sensitivity, which is related to the damping ratio of the system.

Fig. 13
figure 13

Amplitude–frequency responses of Cantilever 1 under a different coupling stiffnesses (ζ = 0.001) and b different damping ratios (kc = 0.002) with a mass disturbance d = 2 pg

Full size image

Experimental Study

An experiment is conducted for qualitative validation of the mode localization and the effectiveness of the proposed sensitivity metric. The experimental setup is shown in Fig. 14. Two cantilevers made of copper are fixed to a clamp. A rubber band connects the two cantilevers, bringing the weak coupling. The prototype is tested under external harmonic base excitation using an electrodynamic shaker (Model: GW-V100, SignalForce). A frequency sweep between 35 and 45 Hz at a rate of 0.02 Hz/second is conducted with a base acceleration amplitude of 2 m/s2. The motions of the two cantilevers are measured by two laser displacement sensors (Model: CP08MHT80, Brand: Wenglor, Sensitivity: 5 mm/V). The output voltage signals are acquired by a voltage data acquisition (DAQ) module (Model: NI9229, Brand: National Instruments) and then converted to displacement responses.

Fig. 14
figure 14

Experimental setup of the weakly coupled resonators

Full size image

The approximate equivalent masses and stiffnesses of the prototype can be obtained following Eq. (9). The effective coupling stiffness kc can be obtained using Castigliano’s second theorem to calculate the deflection at points on which applied a force. All identified system parameters are summarized in Table 1.

Table 1 System parameters identified and used in analysis and simulation
Full size table

The small mass disturbance was implemented by attaching small Neodymium magnets at the tip of the lower cantilever and each magnet weights 0.1 g. The tip displacements of the two cantilevers with different mass disturbances have been measured as shown in Fig. 15. When there are no magnets attached (d = 0), there are still two peaks observed in Fig. 15a and b rather than a single peak as the theoretical prediction. It can be inferred that the small mass disturbance may be contributed by manufacturing tolerance. When two magnets are introduced (d = 0.2 g), it can be seen in Figs. 15c and d that there exists an obvious mode localization phenomenon (energy is concentrated in one certain resonator). When the mass disturbance is further increased (four magnets (d = 0.4 g) or six magnets (d = 0.6 g)), it is found that the amplitude of one cantilever is far greater than the other around the two resonance frequencies, and the difference in amplitude ratios increases, as shown in Fig. 15e–h.

Fig. 15
figure 15

Frequency responses of Cantilevers 1 and 2 from experiment: a and b without mass disturbance (d = 0); c and d with mass disturbance of two magnets (d = 0.2 g); e and f with mass disturbance of four magnets (d = 0.4 g) and; g and h with mass disturbance of six magnets (d = 0.6 g) on the lower cantilever

Full size image

The difference between the amplitude ratios at two resonance frequencies with the mass disturbance is summarized in Fig. 16 (dots), accompanied by a linear fitting curve (dashed line) and the theoretical prediction calculated by Eq. (20) (solid line). It is shown that the sensitivity based on the difference between absolute values of amplitude ratios is basically proportional to the mass disturbance, which agrees well with the theoretical prediction. The relative error (8%) may be due to the fact that the two fabricated cantilever beams were not perfectly identical. By and large, the experimental results show the same trend observed in the theoretical and finite element results. The range characterized by linearity can be applicable for mass sensing and the effectiveness of the proposed sensitivity is qualitatively validated.

Fig. 16
figure 16

Difference between amplitude ratios χ obtained from experiment

Full size image

Conclusions

In this work, a weakly coupled resonator system composed of two micro-cantilevers is analytically investigated for mass sensing. For the undamped free vibration, the analytical lumped model is verified through numerical study as well as finite element analysis. Conventional sensitivities based on the natural frequency, amplitude ratio, and relative change in the eigenvalue or eigenstate have a limited linear sensing range. Perturbation theory could only obtain accurate results for a very small disturbance. Thus, a new sensitivity based on the difference between the absolute values of amplitude ratios is proposed to enhance the degree of linearity, which is applicable for the full disturbance range with high precision. In addition to the modal analysis, the analytical difference between the amplitude ratios is also verified by the FEM result for the damped harmonic response, which is more useful for real applications. It is proved that the proposed sensitivity is also applicable for the damped harmonic vibration. The influence of the damping ratio and coupling factor on the resolution of mass sensing is also studied. The trade-off between the sensitivity and resolution when selecting the coupling factor is discussed. Finally, the effectiveness of the proposed sensitivity metric is also qualitatively validated by an experiment.