Triple sensing scheme based on nonlinear coupled micromachined resonators

Abstract

In the past few decades, advances in micro-electromechanical systems (MEMS) have produced robust, accurate, and high-performance devices. Extensive research has been conducted to improve the selectivity and sensitivity of MEMS sensors by adjusting the device dimensions and adopting nonlinear features. However, sensing multiple parameters is still a challenging topic. Except for the limited research focus on multi-gas and multimode sensing, detecting multiple parameters typically relies on combining several separate MEMS sensors. In this work, a new triple sensing scheme via nonlinear weakly coupled resonators is introduced, which could simultaneously detect three different physical stimuli (including longitudinal acceleration) by monitoring the dynamic response around the first three lowest vibration modes. The Euler–Bernoulli beam model with three-mode Galerkin discretization is used to derive a reduced-order model considering the geometric and electrostatic nonlinearities to characterize the resonator's nonlinear dynamics under the influence of different stimuli. The simulation results show the potential of the nonlinear coupled resonator to simultaneously perform triple detection.

1 Introduction

The last two decades have witnessed extensive research on micro-electromechanical systems (MEMS)-based sensors. By taking advantage of their proven high sensitivity, low power consumption, miniaturization design, and long-term stability, MEMS sensors are among the most suitable candidates for next-generation ultrasensitive sensors [1]. Recently, MEMS sensors have been utilized in a wide range of applications, including biosensors [2,3,4], medical treatment [5,6,7], gyroscopes [8,9,10], accelerometers [11,12,13], mass sensors [14,15,16], and gas sensors [17,18,19].

Nowadays, resonant MEMS sensors are one of the most widely used MEMS devices thanks to their ultra-high sensitivity and ultra-small physical scale toward a wide range of applications [20,21,22]. The main concept of resonant sensing technique, representing the basic concept of several recent sensor designs, is based on the resonator's resonance frequency shift led by external stimulus that is associated mainly with the alteration of either mass, stiffness, or axial stress level [23]. Various dynamical phenomena (i.e., linear and nonlinear) were adopted to enhance the sensitivity and the operation of resonant sensors, including mainly mode localization [24,25,26], structure's nonlinearity features (i.e., particularly bifurcations) [27,28,29], and multimode excitation [30,31,32].

On the other hand, MEMS inertial sensors have become excellent candidates for developing high-performance acceleration sensing systems. The latest MEMS accelerometers, including the capacitive [33, 34] and optical [35, 36] accelerometers, have advanced the resolution of sensing to sub-μg level, which reaches four orders of magnitude higher accuracy than the conventional accelerometer [37]. Differential designs, based on combining symmetric structures and adopting the results' difference as output, are also usually implemented to decrease the influence of ambient factors in MEMS accelerometer research [13, 37, 38]. The sensitive MEMS inertia sensors are gradually replacing the conventional inertia sensors in numerous applications, such as geological exploration, inertial navigation, aerospace, and commercial manufacture [20, 39].

In the past few years, the topic of multiple sensing has received more attention due to the increasing demand for multiple physical, chemical, and environmental sensing applications [40,41,42]. The multifunctional integrated sensors (MFISES) chip presented an optional solution for multiple sensing. The core concept of MFISES is integrating different MEMS sensors into a single chip and designing a proper circuit board to manage and transmit the sensor data [40, 42]. Benefiting from the high performance and ultra-small size of MEMS devices, the millimetre-sized chip could simultaneously monitor several parameters and showed great potential in different applications including geologic prospecting, indoor climate control, road activity monitoring, and chemical sensing [43, 44]. However, the integration of multiple sensors will inevitably lead to higher power consumption, larger size, and a more complicated system.

Therefore, the multiple parameters sensing in a single device is an interesting topic, which could simplify the sensing structure and decrease energy consumption. Limited research has been presented in the literature where, in this context, multi-gas sensing is the main targeted application. For instance, multi-gas MEMS sensor generally employs surface functionalization of a silicon chip as its sensing film and exposes the film to different concentrations of different gases. By analysing the frequency responses, the type and the concentration of gases could be distinguished [21]. Recently, adopting machine learning to handle the frequency responses is proven as a promising and accurate method. The machine learning algorithm is based on extracting several features (e.g., the difference between baseline and saturation, coefficient of determination, recovery time) and corresponding importance scores from response curves. After comprehensive training of the model, the algorithm could distinguish different types of gases and concentrations fast and precisely [32, 45, 46]. To increase the algorithm's accuracy, different kinds of coating and temperatures could be added to provide multidimensional raw data [46, 47]. Other research also reported monitoring reflectance colours from interactions between diverse gases and photonic 3D nanostructure as the algorithm's raw data [48]. Machine learning owes the potential of analysing the gas mixture application, however, still shows the limitation of being applied for other applications (i.e., sensing other stimuli rather than gas). On the other hand, the multimodal analysis showed great potential in multi-sensing applications [31], by allowing the exploitation of multiple modes of vibration of a resonant structure. Hajjaj et al. [30] presented an electrothermally heated bridge resonator operated near the buckling point as the main structure to build a thermal conductivity-based gas sensor. The bridge experiences convective heating or cooling depending on the thermal conductivity of gases, which in turn causes the stiffness variation of the bridge and finally shifts the bridge's resonance frequency in opposite directions. Due to the different behaviour of the frequency variation of the first (i.e., first symmetric mode) and second (i.e., first anti-symmetric mode) modes before and after buckling, the concentration of gas was proved to be accurately quantified by tracking the first natural frequency variation while the nature of the detected gas can be identified by tracking the variation of the second natural frequency. Based on the same concept, a simultaneous detection mechanism was reported for gas and magnetic [46], pressure and temperature [49], and multi-gas detection with the help of machine learning [32].

Thus far, a single device that can simultaneously detect three kinds of stimuli has not been reported. This paper proposes a new triple sensing scheme via nonlinear weakly coupled resonators for mass, stiffness, and acceleration sensing based on simultaneously tracking the first three vibration mode resonance frequencies of weakly coupled resonators. The sensing targets of mass, stiffness and acceleration could be used to design different MEMS sensor designs for motion (displacement, velocity, and acceleration) [17, 39, 50], force (and other forms of loading such as moment and torque) [15, 51], deformation [38, 39], stress, and strain [30] based on different mechanisms. Hence, this triple sensing scheme has the potential to fit complex application requirements by changing sensing targets and mechanisms, especially those applications requiring simultaneous detection of multiple physical parameters. At the same time, the triple sensing ability could directly decrease the number of sensors needed, hence decreasing the systematic complexity, energy consumption, and maintenance cost. For instance, lithium battery failure detection requires simultaneous monitoring of temperature and H₂ concentration [52, 53]; air-quality monitoring aims at different types of air pollutant concentration [54]; water quality monitoring application needs multiple analyzers of pH, flow rate, and temperature [55]. From another perspective, the proposed sensor with triple sensing capability, with low power consumption and a highly effective sensing scheme, is deemed an ideal candidate to be implemented in smart self-powered sensing systems [56]. In this article, the methodology of a triple sensing scheme will be explored. A nonlinear theoretical model is developed using the Euler–Bernoulli beam theory while accounting for the geometric and electrostatic nonlinearities. The reduced-order model based on the three-mode Galerkin discretization and shooting technique is used to analyze the system. The influence of the resonators' geometric size, damping, actuation voltage, and actuation scheme is presented and discussed. The sensor's multi-sensing ability is demonstrated by tracking the bifurcation frequency shift, the peak frequency shift, and the nonlinear behaviour change in the mode shapes induced by mass, stiffness, and acceleration perturbations.

The present paper's structure is organized as follows. The geometric properties of the triple sensing scheme and the related problem formulation are introduced in Sect. 2. The theoretical results of the system's nonlinear behaviour and the sensing performance are included in Sect. 3. Then, the parameter analysis including influence of resonators' length, thickness and damping are discussed in Sect. 4. In the end, the main conclusions of the research are summarized in Sect. 5.

2 Structure description and model

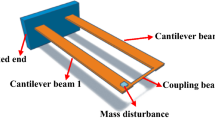
The proposed multi-sensing structure, shown in Fig. 1, comprises a weakly coupled resonator including a cantilever (${W}_{2}$) and two bridge resonators (${W}_{1}$ and ${W}_{3}$), mechanically coupled by two thin beams. The bridge resonator ${W}_{3}$ is connected with an inertial mass to sense the longitudinal acceleration. The coupling strength could be controlled by changing the coupling position, the moment of inertia, and the coupling beam's length [57]. The detailed geometric parameters and physical properties of the coupled resonator system, considered to be made of silicon, are listed in Table 1. Note that the AC voltage is imposed on only one resonator excitation at a time (i.e., if ${V}_{AC1} \ne 0$ means that ${V}_{AC2}={V}_{AC3}=0$ and vice versa) to investigate the corresponding dynamic response of the proposed structure, while the DC polarization actuation is imposed on all three resonators to enhance the associated quadratic nonlinearity (i.e., originated from the applied electrostatic force). The system geometry is optimized to ensure that the three resonators have almost equal resonance frequencies.

Fig. 1

3D schematic of the multi-sensing scheme

Table 1 Geometric parameters of the sensor structure

The triple sensing methodology can be explained by three aspects: (i) the stiffness variation on bridge resonator ${W}_{1}$ due to an external stimulus (e.g., temperature, gas/air flow or convective gas variation). (ii) the mass perturbation on cantilever resonator ${W}_{2}$ on account of the mass absorption on surface functionalization (e.g., gas or bio-cells absorption). (iii) the inertial mass will exert a longitudinally compressive force or tensile force on the bridge resonator ${W}_{3}$ due to the external acceleration at the horizontal direction. In the rest of the paper, we will investigate the influence of each of these parameters (i.e., stiffness of W₁, mass of W₂ and acceleration of W₃) on the dynamics of the proposed structure.

The three microbeams (two bridge resonators and one cantilever resonator) of the sensor structure (Fig. 1) with lengths ${L}_{1}$, ${L}_{2}$ and ${L}_{3}$ (${L}_{1}$= ${L}_{3}$> ${L}_{2}$), respectively, have the same width $b$ and thickness $h$. The coupling beam is optimised to provide weak coupling, since the coupling strength significantly affects the sensor's sensitivity and the nearness of the three lowest natural frequencies. Most mechanically coupled resonators use an overhang to connect microbeams [26]. However, this coupling approach is challenging to model and impractical to control its coupling length [25]. Hence, a coupling beam with length ${L}_{c}$, width ${b}_{c}$ and the same thickness as the resonators $h$ is chosen at distance ${X}_{c}$ from the anchors. Under these conditions, the proposed sensor structure can be modelled as three Euler–Bernoulli beams coupled with two rotational spring ${k}_{r}$ [58]. The torsional stiffness could be represented as:

$$ k_{r} = \frac{{G\beta b_{c} h^{3} }}{{L_{C} }} $$

(1)

where $G$ denotes the material's shear modulus (69.3 GPa for silicon), and $\beta$ is a coefficient depending on the coupling beam's width ${b}_{c}$ and thickness $h$ [58]. Note that the two coupling beams have the same parameters.

Since the coupling beam is modelled as a rotational spring in the structure, the coupling strength could be quantified as the spring's elasticity. This coupling strength could be controlled by changing the coupling position, the moment of inertia, and the coupling beam's length [57]. For instance, increasing the cross-sectional area of the coupling beam, which links to the moment of inertia, would increase the coupling strength; while increasing the coupling beam's length would decrease it. Additionally, the coupling beam is set near the fixed end of the resonators, where the torsion would be the dominant stress. Hence, the mass and the bending stiffness of the coupling beam are neglected in our model. Also, the first three vibration global mode shapes of the mechanically coupled structure are in the transverse direction, hence the transverse inertial effects of the coupling beam could be also ignored [59].

The sided bridge resonator ${W}_{3}$ is used to detect longitudinal acceleration. When the external longitudinal acceleration is applied to the sensor, the inertial mass generates a longitudinal compressive or tensile force depending on the acceleration direction. This induced force influences significantly the resonator ${W}_{3}$'s axial force, hence its resonance frequency [60]. The dynamics of the bridge resonator ${W}_{3}$ involve the motion of the inertia mass, which has the dimensional equation:

$$-M{\ddot{y}}_{3}-k{y}_{3}-k\left({y}_{3}-{u}_{3}\left({L}_{3}\right)\right)-M{W}_{a}=0$$

(2)

As shown in Fig. 2, ${y}_{3}$ represents the longitudinal movement of the inertial mass, $M$ represents the mass of inertial mass, $k$ represents the spring stiffness, ${W}_{a}$ represents the hull acceleration and ${u}_{3}\left({L}_{3}\right)$ represents the displacement of the ends of the microbeam [60]. For the system analysis, the acceleration ${W}_{a}$ is assumed to be constant to ensure that the whole device is in quasi-static state. Since the natural frequency of the moving mass's oscillations is much lower than the midrange of the beam resonator, the moving mass's acceleration ${\ddot{y}}_{3}$ is considered as sufficiently small compared to ${W}_{a}$; hence the relative acceleration of the inertial mass can be neglected [59], which leads:

Fig. 2

Schematic of the bridge resonator ${W}_{3}$ with inertial mass

$$-k{y}_{3}-k\left({y}_{3}-{u}_{3}\left({L}_{3}\right)\right)-M{W}_{a}=0$$

(3)

Hence it yields the expressions for the displacement of the inertial mass:

$${y}_{3}=\frac{1}{2k}\left(k{u}_{3}\left({L}_{3}\right)-M{W}_{a}\right)$$

(4)

We apply the geometrically nonlinear model of longitudinal vibrations of a rod on the beam dynamic motion analysis, based on the Bernoulli–Euler hypothesis [61]:

$$ \rho A\ddot{u}_{3} - EAu_{3}^{^{\prime\prime}} = EA\left( {\frac{1}{2}w_{3}^{^{\prime}2} } \right)^{^{\prime}} $$

(5)

where ${u}_{3}$ and ${w}_{3}$ denote the longitudinal displacement of the beam and the transverse displacement of the beam; $A$ and $I$ represent the cross-sectional area and moment of inertia, respectively.

A simplification can be made for Eq. (5): considering that the bridge resonator in this article is a slender beam of small radius of gyration, which has much higher axial natural frequency compared to transversal natural frequency. Hence, the inertia force of the rod in the longitudinal direction ($\rho A\ddot{u}$) could be neglected indicating that the axial deformation is mainly induced due to transversal deformation, which yields:

$$ - EAu^{\prime \prime } = EA\left( {\frac{1}{2}w^{\prime 2} } \right)^{^{\prime}} $$

(6)

with corresponding boundary conditions:

$$u\left(0\right)=0; N\left({L}_{3}\right)=k\left[{u}_{3}\left({L}_{3}\right)-{y}_{3}\right]$$

(7)

where $N\left({L}_{3}\right)$ is the longitudinal force at the end section. Combining Eqs. (4) and (7), the expression for the longitudinal force $N$ is:

$$N=k\left[{u}_{3}\left({L}_{3}\right)-\frac{1}{2k}\left(k{u}_{3}\left({L}_{3}\right)-M{W}_{a}\right)\right]$$

(8)

as ${u}_{3}\left({L}_{3}\right)={\int }_{0}^{{L}_{3}}{{{w}_{3}}^{^{\prime}}}^{2}dx$, it yields:$N=\frac{1}{2}\left[M{W}_{a}-\frac{1}{2}k{\int }_{0}^{{L}_{3}}{{{w}_{3}}^{^{\prime}}}^{2}dx\right]$

Next, by using Hamilton's principle and the Euler–Bernoulli beams with distributed elements [61], the equations of motion governing the transverse deflections ${\widetilde{w}}_{1}$ (for the bridge resonator ${W}_{1}$), ${\widetilde{w}}_{2}$ (for the cantilever resonator ${W}_{2}$), and ${\widetilde{w}}_{3}$ (for the bridge resonator ${W}_{3}$) are:

$$ \begin{gathered} EI\tilde{w}_{1}^{\prime \prime \prime \prime } + \rho A\ddot{\tilde{w}}_{1} + \tilde{c}_{1} \dot{\tilde{w}}_{1} + \left[ {\tilde{N} - \frac{EA}{{2L_{1} }}\mathop \int \limits_{0}^{{L_{1} }} \left( {\tilde{w}_{1}^{\prime } } \right)^{2} dx} \right]\tilde{w}_{1}^{\prime \prime } + \tilde{k}_{r} \left( {\tilde{w}_{1}^{^{\prime}} \left( {\tilde{X}_{c} } \right) - \tilde{w}_{2}^{^{\prime}} \left( {\tilde{X}_{c} } \right)} \right)\delta^{\prime } \left( {\tilde{x} - \tilde{X}_{c} } \right) \hfill \\ - \tilde{k}_{r} \left( {\tilde{w}_{1}^{\prime } \left( {\tilde{X}_{c} } \right) - \tilde{w}_{3}^{\prime } \left( {\tilde{X}_{c} } \right)} \right)\delta^{\prime } \left( {\tilde{x} - \tilde{X}_{c} } \right) = \frac{1}{2}\varepsilon_{0} \frac{{b\left[ {V_{DC1} + V_{AC1} *\cos \left( {\tilde{\Omega }_{1} \tilde{t}} \right)} \right]^{2} }}{{\left( {d_{1} - \tilde{w}_{1} } \right)^{2} }} \hfill \\ \end{gathered} $$

(9)

$$ \begin{gathered} EI\tilde{w}_{2}^{\prime \prime \prime \prime } + \left( {\rho A + \tilde{m}\delta \left( {\tilde{x} - \tilde{X}_{m} } \right)} \right)\ddot{\tilde{w}}_{2} + \tilde{c}_{2} \dot{\tilde{w}}_{2} + k_{r} \left( {\tilde{w}_{2}^{\prime } \left( {\tilde{X}_{c} } \right) - \tilde{w}_{1}^{\prime } \left( {\tilde{X}_{c} } \right)} \right)\delta^{\prime } \left( {\tilde{x} - \tilde{X}_{c} } \right) \hfill \\ = \frac{1}{2}\varepsilon_{0} \frac{{b\left[ {V_{DC2} + V_{AC2} *\cos \left( {\tilde{\Omega }_{2} \tilde{t}} \right)} \right]^{2} }}{{\left( {d_{2} - \tilde{w}_{2} } \right)^{2} }} \hfill \\ \end{gathered} $$

(10)

$$ \begin{gathered} EI\tilde{w}_{3}^{\prime \prime \prime \prime } + \rho A\ddot{\tilde{w}}_{3} + \tilde{c}_{3} \dot{\tilde{w}}_{3} + \frac{1}{2}\left[ {MW_{a} - \frac{1}{2}k\mathop \int \limits_{0}^{{L_{3} }} \left( {\tilde{w}_{3}^{\prime } } \right)^{2} dx} \right]\tilde{w}_{3}^{\prime \prime } \hfill \\ + \tilde{k}_{r} \left( {\tilde{w}_{3}^{\prime } \left( {\tilde{X}_{c} } \right) - \tilde{w}_{1}^{\prime } \left( {\tilde{X}_{c} } \right)} \right)\delta^{\prime } \left( {\tilde{x} - \tilde{X}_{c} } \right) = \frac{1}{2}\varepsilon_{0} \frac{{b\left[ {V_{DC3} + V_{AC3} *\cos \left( {\tilde{\Omega }_{3} \tilde{t}} \right)} \right]^{2} }}{{\left( {d_{3} - \tilde{w}_{3} } \right)^{2} }} \hfill \\ \end{gathered} $$

(11)

In Eqs. (9)–(11), the primes and dots denote the partial differentiation of the transverse deflections ${\widetilde{w}}_{\mathrm{i}}\left(i=\mathrm{1,2},3\right)$ with respect to the position of the beam $\widetilde{x}$ and time $\widetilde{t}$, respectively; $A$ and $I$ are the area and the moment of inertia of the rectangular cross-section; $\delta$ denotes the Dirac delta function.

The parameters and corresponding values are defined in Table 2.

Table 2 Physical parameters shown in the governing equations of motion, Eqs. (4)-(11)

After non-dimensionalizing and discretizing Eqs. (9)–(11) using the Galerkin procedure, the governing non-dimensional equations are written as follows:

$$ \begin{gathered} \left( {\frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + c_{1n} \frac{{\partial u_{1} }}{\partial t} + \mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } dxu_{1} \left( {1 + \delta k} \right) + k_{r} \left[ {u_{1} \left( {\varphi_{1}^{\prime } \left( {X_{c} } \right)} \right)^{2} - u_{2} \varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right]} \right. \hfill \\ \left. { + k_{r} \left[ {u_{1} \left( {\varphi_{1}^{\prime } \left( {X_{d} } \right)} \right)^{2} - u_{3} \varphi_{1}^{\prime } \left( {X_{d} } \right)\varphi_{3}^{\prime } \left( {X_{d} } \right)} \right]} \right)*\left( {1 - 2u_{1} \mathop \int \limits_{0}^{1} \varphi_{1}^{3} dx + u_{1}^{2} \mathop \int \limits_{0}^{1} \varphi_{1}^{4} dx} \right) \hfill \\ - \alpha_{1} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime 2} dx\left( {u_{1}^{3} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1} dx - 2u_{1}^{4} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1}^{2} dx + u_{1}^{5} \mathop \int \limits_{0}^{1} \varphi_{1}^{\prime \prime } \varphi_{1}^{3} dx} \right) = \alpha_{2} \left[ {V_{dc2} + V_{ac2} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \mathop \int \limits_{0}^{1} \varphi_{1} dx \hfill \\ \end{gathered} $$

(12)

$$ \begin{gathered} \left( {\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }}\left( {1 + \delta m\left( {x - X_{m} } \right)} \right) + c_{2n} \frac{{\partial u_{2} }}{\partial t} + \mathop \int \limits_{0}^{{R_{L1} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } dxu_{2} + k_{r} \left[ {u_{2} \left( {\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right)^{2} - u_{1} \varphi_{1}^{\prime } \left( {X_{c} } \right)\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right]} \right) \hfill \\ *\left( {R_{d1}^{2} - 2R_{d1} u_{2} \mathop \int \limits_{0}^{{R_{L1} }} \varphi_{2}^{3} dx + u_{2}^{2} \mathop \int \limits_{0}^{{R_{L1} }} \varphi_{2}^{4} dx} \right) = \alpha_{2} \left[ {V_{dc2} + V_{ac2} \cos \left( {\Omega_{2} t} \right)} \right]^{2} \mathop \int \limits_{0}^{{R_{L1} }} \varphi_{2} dx \hfill \\ \end{gathered} $$

(13)

$$ \begin{gathered} \left( {\frac{{\partial^{2} u_{3} }}{{\partial t^{2} }} + c_{3n} \frac{{\partial u_{3} }}{\partial t} + \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3} \varphi_{3}^{\prime \prime \prime \prime } dxu_{3} - k_{r} \left[ {u_{3} \left( {\varphi_{3}^{\prime } \left( {X_{c} } \right)} \right)^{2} + u_{1} \varphi_{3}^{\prime } \left( {X_{c} } \right)\varphi_{1}^{\prime } \left( {X_{c} } \right)} \right]} \right) \hfill \\ *\left( {R_{d2}^{2} - 2R_{d2} u_{3} \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3}^{3} dx + u_{3}^{2} \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3}^{4} dx} \right) + \left[ {N_{non} - K_{non} \mathop \int \limits_{0}^{{R_{L2} }} \left( {w_{3}^{\prime } } \right)^{2} dx} \right] \hfill \\ *\left( {R_{d2}^{2} u_{3}^{3} \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3}^{\prime \prime } \varphi_{3} dx - 2R_{d2} u_{3}^{4} \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3}^{\prime \prime } \varphi_{3}^{2} dx + u_{1}^{5} \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3}^{\prime \prime } \varphi_{3}^{3} dx} \right) \hfill \\ = \alpha_{3} \left[ {V_{dc3} + V_{ac3} \cos \left( {\Omega_{3} t} \right)} \right]^{2} \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3} dx \hfill \\ \end{gathered} $$

(14)

where ${N}_{\mathrm{non}}=\frac{\mathrm{M}\delta {W}_{a}{L}_{1}^{2}}{2EI}$, ${K}_{\mathrm{non}}=\frac{k{L}_{1}^{2}}{4EI}$. In Eqs. (12)–(14), $\delta k$, $\delta m$ and $\delta {W}_{a}$ represent correspondingly the linear stiffness variation on the bridge resonator ${W}_{1}$, the mass perturbation on the cantilever resonator ${W}_{2}$, and the hull acceleration which influences the bridge resonator ${W}_{3}$. The detailed derivation process and definition of parameters appearing in Eqs. (12)–(14) are given in the Appendix.

The first three local mode shapes for clamped–clamped and cantilever beams are:

$$ \begin{aligned} \varphi _{1} \left( x \right) = & - \cos \left( {4.73004x} \right) + \cosh \left( {4.73004x} \right) \\ & + \frac{{\sinh \left[ {4.73004} \right] + \sin \left[ {4.73004} \right]}}{{\cosh \left[ {4.73004} \right] - \cos \left[ {4.73004} \right]}}\left[ {\sin \left( {4.73004x} \right) - \sinh \left( {4.73004x} \right)} \right]; \\ \end{aligned} $$

$$ \begin{aligned} \varphi _{2} \left( x \right) = & K_{1} \left( { - \cos \left( {\frac{{1.8751x}}{{R_{{L1}} }}} \right) + \cosh \left( {\frac{{1.8751x}}{{R_{{L1}} }}} \right)} \right. \\ & + \left. {\frac{{\sinh \left( {\frac{{1.8751}}{{R_{{L1}} }}} \right) - \sin \left( {\frac{{1.8751}}{{R_{{L1}} }}} \right)}}{{\cosh \left( {\frac{{1.8751}}{{R_{{L1}} }}} \right) - \cos \left( {\frac{{1.8751}}{{R_{{L1}} }}} \right)}}\left[ {\sin \left( {\frac{{1.8751x}}{{R_{{L1}} }}} \right) - \sinh \left( {\frac{{1.8751x}}{{R_{{L1}} }}} \right)} \right]} \right) \\ \end{aligned} $$

$$ \begin{aligned} \varphi _{3} \left( x \right) = & K_{2} \left( { - \cos \left( {\frac{{4.73004x}}{{R_{{L2}} }}} \right) + \cosh \left( {\frac{{4.73004x}}{{R_{{L2}} }}} \right)} \right. \\ & + \left. {\frac{{\sinh \left[ {\frac{{4.73004}}{{R_{{L2}} }}} \right] + \sin \left[ {\frac{{4.73004}}{{R_{{L2}} }}} \right]}}{{\cosh \left[ {\frac{{4.73004}}{{R_{{L2}} }}} \right] - \cos \left[ {\frac{{4.73004}}{{R_{{L2}} }}} \right]}}\left[ {\sin \left( {\frac{{4.73004x}}{{R_{{L2}} }}} \right) - \sinh \left( {\frac{{4.73004x}}{{R_{{L2}} }}} \right)} \right]} \right). \\ \end{aligned} $$

The coefficients ${K}_{1}$ and ${K}_{2}$ take values ensuring ${\int }_{0}^{{R}_{L1}}{\varphi }_{2}^{2}dx=1$ and ${\int }_{0}^{{R}_{L2}}{\varphi }_{3}^{2}dx=1$. Through Eqs. (12)–(14), the Jacobian matrix of the system is: $J=\left[\begin{array}{ccc}{\lambda }_{1}^{2}& {\kappa }_{1}& {\kappa }_{2}\\ \frac{{\kappa }_{1}}{1+\eta }& \frac{{\lambda }_{2}^{2}}{1+\eta }& 0\\ {\kappa }_{2}& 0& {\lambda }_{3}^{2}\end{array}\right]$:where $\lambda_{1}^{2} = \mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } dx - 2\alpha_{2} V_{dc1}^{2} + 2k_{r} \left( {\varphi_{1}^{\prime } \left( {X_{c} } \right)} \right)^{2}$, $\lambda_{2}^{2} = \mathop \int \limits_{0}^{{R_{L1} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } dx - 2\alpha_{2} V_{dc2}^{2} + k_{r} \left( {\varphi_{2}^{\prime } \left( {X_{c} } \right)} \right)^{2}$, $\lambda_{3}^{2} = \mathop \int \limits_{0}^{{R_{L2} }} \varphi_{3} \varphi_{3}^{\prime \prime \prime \prime } dx - 2\alpha_{2} V_{dc3}^{2} + k_{r} \left( {\varphi_{3}^{\prime } \left( {X_{c} } \right)} \right)^{2}$, $\kappa_{1} = - k_{r} \varphi_{1}^{^{\prime}} \left( {X_{c} } \right)\varphi_{2}^{^{\prime}} \left( {X_{c} } \right)$, $\kappa_{2} = - k_{r} \varphi_{1}^{^{\prime}} \left( {X_{c} } \right)\varphi_{3}^{^{\prime}} \left( {X_{c} } \right)$, and $\eta = \delta m\left( {x - X_{m} } \right)$.

Solving the eigenvalue problem through the Jacobian matrix gives the three lowest global resonance frequencies of the coupled system [59].

To verify the theoretical model and simulate the vibration global mode shapes of the coupled resonators, a 3D multi-physics finite-element model is developed using commercial software COMSOL [62]. Figure 3a depicts the variation of the first three global natural frequencies with respect to the length of the cantilever by solving the eigenvalue problem, while applying 0 V DC load to the system, as well as the corresponding FEM simulations from COMSOL. The results show good matching between both methods validating that the adopted analytical modal and assumptions are correct and reliable. As varying the system control parameters (i.e., mass, stiffness and acceleration in this paper), the three natural frequencies come close to each other before they veer away, which would potentially lead to high sensor sensitivity [63]. Note that by choosing the frequency around the veering zone, modes are strongly coupled in this region leading to more rich dynamics compared to decoupled systems. The results suggest that the three natural frequencies veer to the nearest value, around 54 kHz when the length of the cantilever is ${L}_{2}=277$ μm. Hence for the rest of the analysis, the cantilever length will be fixed at ${L}_{2}=277$ μm. Figure 3b shows the associated first three lowest global mode shapes of the coupled structure.

Fig. 3

a Variation of the three lowest natural frequencies of the coupled system with respect to the length of the cantilever resonator, ${L}_{2}$. The DC load is kept equal to 0 V. The lines denote the numerical results while the dots denote the FEM result from COMSOL. b The first three vibration global mode shapes of the mechanically coupled structure from COMSOL for ${L}_{2}$=277 μm

The effect of DC load on the lowest three natural frequencies is analyzed. The full range of frequency curves until the pull-in of the three resonators ${W}_{1}$, ${W}_{2}$, and ${W}_{3}$ are shown in Fig. 4a–c, respectively. It depicts that the 2nd and 3rd natural frequencies almost remain the same after veering point while the 1st natural frequency decreases with the DC actuation until it finally pulls in at ${V}_{DC1}=177$ V, ${V}_{DC2}=175.5$ V, and ${V}_{DC3}=175$ V,respectively. Figure 4d, f depict that veering point of the 1st and 2nd natural frequencies at ${V}_{DC1}=46.4$ V and ${V}_{DC3}=36$ V, respectively.

Fig. 4

Variation of the three lowest natural frequencies of the coupled system with respect to the DC load: Frequency curves versus DC actuation ${V}_{DC1}$ while ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V (a), ${V}_{DC2}$ while ${V}_{DC1}=40$ V and ${V}_{DC3}=40$ V (b), ${V}_{DC3}$ while ${V}_{DC1}=40$ V and ${V}_{DC2}=10$ V (c); Zoomed view of the veering zone of frequency curves versus DC actuation ${V}_{DC1}$ while ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V (d), ${V}_{DC2}$ while ${V}_{DC1}=40$ V and ${V}_{DC3}=40$ V (e), ${V}_{DC3}$ while ${V}_{DC1}=40$ V and ${V}_{DC2}=10$ V (f). Dashed (red), dotted (green), and solid (blue) lines denote the 1st natural frequency, 2^nd natural frequency, and 3rd natural frequency, respectively

To perform the triple sensing scheme, the first three global modes should be coupled to each other near the veering zone to obtain the high sensitivity, however, shouldn't have nearly similar natural frequencies. Hence, we choose ${V}_{DC1}={V}_{DC3}=40$ V for the rest of the paper. Figure 4e shows that the three lowest natural frequencies experience a slight decrease when ${V}_{DC2}<15$ V. For convenience, we keep the DC actuation for ${W}_{2}$ as a safety value of ${V}_{DC2}=10$ V. Noted that all the values chosen for ${V}_{DC1}$, ${V}_{DC2}$, and ${V}_{DC3}$ are far from pull-in voltage to ensure safe operation of the system.

3 Results and discussion

This section discusses the nonlinear behaviour of the weakly-coupled system. Continuous analyses using the shooting technique [64] are conducted to verify the effect of the different physical parameters. The damping and acceleration values of ${\zeta }_{1}={\zeta }_{2}={\zeta }_{3}=1.111\times {10}^{-2}$ (${c}_{1}={c}_{2}={c}_{3}=0.5$ as $c=2\zeta {w}_{n}$ and ${w}_{n}=22.5$) and ${W}_{a}=0$ m/s² are chosen for the simulation.

3.1 Characteristic response dynamics

Figure 5 shows the characteristic points of the frequency response of global mode shapes as actuating the bridge resonator ${W}_{1}$ with ${V}_{DC1}=40$ V and ${V}_{AC1}=7.5$ V, the cantilever resonator ${W}_{2}$ with ${V}_{DC2}=10$ V and ${V}_{AC2}=0$ V, and the bridge resonator ${W}_{3}$ with ${V}_{DC3}=40$ V and ${V}_{AC3}=0$ V. The DC voltages are chosen to provide sufficient geometric nonlinearities. The solid blue and green dotted lines represent stable and unstable branches, respectively. Four characteristic points (noted as red in Fig. 5) should be highlighted, the peak point in the ${U}_{2}$ and ${U}_{3}$ appears at 54.141 kHz and 52.551 kHz, respectively. And the two corresponding bifurcation points appear at 71.269 kHz and 57.583 kHz. The hardening behaviour in ${U}_{1}$, indicating a saddle-node bifurcation point at 71.269 kHz, and the peaks in ${U}_{2}$ and ${U}_{3}$ at 54.141 kHz and 52.551 kHz are suitable for sensing [57]. Near these three points, small perturbations could lead to a notable change of transverse deflections, which shows great potential to provide high sensitivity. Hence, these three frequencies are chosen as characteristic frequencies for the sensing scheme. A detailed discussion follows regarding the effects of different parameters on these three observations.

Fig. 5

Characteristic points of the frequency response under bridge actuating, ${W}_{1}$, of ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V, ${V}_{AC1}=7.5$ V, ${V}_{AC2}=0$ V, and ${V}_{AC3}=0$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: transverse deflection of a bridge U1, b cantilever U2, and c bridge U3 (dotted lines represent unstable branches). Amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

3.2 Sensing scheme

3.2.1 Single perturbation simulation

3.2.1.1 Stiffness perturbation

The purpose of this research is the simultaneous detection of three different physical stimuli (including acceleration) by monitoring the dynamic response around the first three lowest modes of the single coupled structure. Hence, we aim to build a sensor methodology that can provide the simultaneous variation of stiffness, mass, and acceleration. In Fig. 6a–f, the non-dimensional stiffness perturbation from − 0.1 to 0.1 is given to the middle bridge resonator ${W}_{1}$. The results show that fold bifurcation jumps in the natural frequency response ${U}_{1}$ in Fig. 6d change due to stiffness variations on the bridge resonator, while the peak value of the natural frequency response ${U}_{2}$ in Fig. 6e and the natural frequency response ${U}_{3}$ in Fig. 6f remains constant.

Fig. 6

Parametric study of the frequency response curves under actuation of ${V}_{AC1}=7$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$ and c ${U}_{3}$ for different stiffness perturbation $\delta k$ of − 0.1, − 0.05, 0, 0.05, and 0.1; (d–f) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (a–c). Black lines (a–c) and dotted lines (d–f) denote unstable branches. Amplitude of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

3.2.1.2 Mass perturbation

When it comes to mass perturbation on the cantilever resonator ${W}_{2}$, the fold bifurcation jump and the peak frequency remain the same largely in Fig. 7d, f. In contrast, the cantilever resonator's peak frequency and peak values in Fig. 7e are decreasing with the increase of mass perturbation on cantilever.

Fig. 7

Parametric study of the frequency response curves under actuation of ${V}_{AC1}=7$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$ and c ${U}_{3}$ for different mass perturbation $\delta m$ of 0, 0.01, 0.02, 0.03, 0.04, and 0.05; (d–f) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (a–c). Black lines (a–c) and dotted lines (d–f) denote unstable branches. Amplitude of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

3.2.1.3 Acceleration perturbation

The situation of acceleration perturbation on the sided bridge resonator ${W}_{3}$ is different, specifically the longitudinal acceleration ${W}_{a}$ would compress or tense the resonator ${W}_{3}$ which would change resonator ${W}_{3}$'s geometric nonlinearity. As Fig. 8f shows, the variation of acceleration perturbation from − 0.2 m/s² to 0.2 m/s² would change the nonlinear behaviour of ${U}_{3}$ from hardening to softening, which also influences its peak frequency. However, the fold bifurcation jumps in the natural frequency response ${U}_{1}$ in Fig. 8d and the peak frequency in the frequency response ${U}_{2}$ in Fig. 8e won't change.

Fig. 8

Parametric study of the frequency response curves under actuation of ${V}_{AC1}=7$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$ and c ${U}_{3}$ for different mass perturbation $\delta {W}_{a}$ of − 0.2 m/s², − 0.1 m/s², 0 m/s², 0.1 m/s², and 0.2 m/s²; (d–f) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (a–c). Black lines (a–c) and dotted lines (d–f) denote unstable branches. Amplitude of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

Summarizing the three separate perturbation simulations, it is possible to detect the effect of stiffness, mass and acceleration perturbations applied on the three resonators, respectively, by monitoring the fold bifurcation jumps and peak frequencies of the first three natural frequency responses. Thus, triple-sensing can be robustly performed.

3.2.2 Independence study between different sensing mechanisms

3.2.2.1 Stiffness perturbation simulation under different acceleration

In Sect. 3.2.1, the triple sensing concept is proved on three kinds of perturbations. However, independence between the different sensing mechanisms is also needed in the sensing performance. In this section, the same stiffness and mass perturbation test is simulated with different constant acceleration values. For the stiffness perturbation tests Fig. 6d–f ($\delta {W}_{a}=0$ m/s²), Fig. 9d–f ($\delta {W}_{a}=-0.2$ m/s²), and Fig. 9j–l ($\delta {W}_{a}=0.2$ m/s²), it shows that the variation of acceleration only influences the nonlinearity of ${U}_{3}$ and its peak frequency (Figs. 6f, 9f and l), the stiffness variations only influence fold bifurcations in the natural frequency response ${U}_{1}$, but not change the peak value of the natural frequency response ${U}_{2}$.

Fig. 9

Parametric study of the frequency response curves under actuation of ${V}_{AC1}=7.5$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$: a ${U}_{1}$, b ${U}_{2}$ and c ${U}_{3}$ for different stiffness perturbation $\delta k$ of − 0.1, − 0.05, 0, 0.05, and 0.1 under $\delta {W}_{a}=-0.2$ m/s²; (d–f) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (a–c); g ${U}_{1}$, h ${U}_{2}$ and i ${U}_{3}$ for different stiffness perturbation $\delta k$ of − 0.1, − 0.05, 0, 0.05, and 0.1 under $\delta {W}_{a}=0.2$ m/s² (j–l) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (g-i). Black lines (a–c, g–i) and dotted lines (d–f, j–l) denote unstable branches. Amplitude of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

3.2.2.2 Mass perturbation simulation under different acceleration

Similar results appear in the mass perturbation tests Fig. 7d–f ($\delta {W}_{a}=0$ m/s²), Fig. 10d–f ($\delta {W}_{a}=-0.2$ m/s²), and Fig. 10j–l ($\delta {W}_{a}=0.2$ m/s²) as the mass variations only influence the peak value of the natural frequency response ${U}_{2}$, but not change the fold bifurcations in the natural frequency response ${U}_{1}$. Therefore, the sensing mechanism of acceleration is independent of the other sensing mechanisms.

Fig. 10

Parametric study of the frequency response curves under actuation of ${V}_{AC1}=7.5$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$: a ${U}_{1}$, b ${U}_{2}$ and c ${U}_{3}$ for different mass perturbation $\delta m$ of 0, 0.01, 0.02, 0.03, 0.04, and 0.05 under $\delta {W}_{a}=-0.2$ m/s²_; (d–f) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (a–c); g ${U}_{1}$, h ${U}_{2}$ and i ${U}_{3}$ for different mass perturbation $\delta m$ of 0, 0.01, 0.02, 0.03, 0.04, and 0.05 under $\delta {W}_{a}=0.2$ m/s²; (j–l) 2D sketches of the response focus on three characteristic frequencies of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ of (g–i). Black lines (a–c, g–i) and dotted lines (d–f, j–l) denote unstable branches. Amplitude of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

3.2.3 Analysis of sensing performance

In this section, the sensing performance of the proposed triple scheme has been evaluated. Based on the outcome of Fig. 4, three characteristic frequencies are chosen to perform this analysis, including the fold bifurcation jump frequency for ${W}_{1}$ (i.e., associated with the third global mode, ${Mode}_{3}$, at ${\omega }_{3}^{0}=$ 69.3 kHz), linear peak frequency (i.e., associated with the second global mode, ${Mode}_{2}$, at ${\omega }_{2}^{0}$=54.2 kHz) for ${W}_{2}$, and linear peak frequency (i.e., associated with the first global mode, ${Mode}_{1}$, at ${\omega }_{1}^{0}=$ 52.6 kHz) for ${W}_{3}$.

3.2.3.1 Qualitative identification of the triple sensing scheme

The steady-state time-histories (i.e. 400 cycles each) at the three characteristic frequencies are plotted as introducing various types of perturbations (mass, stiffness and acceleration) in Fig. 11, where arrows denote the inclusion of the corresponding perturbations (i.e., red denoting the original state and blue denoting the perturbed state).

Fig. 11

400 cycles of steady-state displacement–time response for three characteristic frequencies before (red) and after (blue) introducing different perturbations at 200 cycles under actuation of ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V, ${V}_{AC1}=7$ V, ${V}_{AC2}=0$ V, and ${V}_{AC3}=0$ V: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$ for stiffness perturbation $\delta k=0$ (red) and $\delta k=-0.1$ (blue); d ${U}_{1}$, e ${U}_{2}$, and f ${U}_{3}$ for mass perturbation $\delta m=0$ (red) and $\delta m=0.05$ (blue); g ${U}_{1}$, h ${U}_{2}$, and i ${U}_{3}$ for acceleration perturbation $\delta {W}_{a}=0$ m/s² (red) and $\delta {W}_{a}=0.2$ m/s² (blue); j ${U}_{1}$, (k) ${U}_{2}$, and (l) ${U}_{3}$ for triple perturbations $\delta k=\delta m=\delta {W}_{a}=0$ (red) and $\delta k=-0.1$, $\delta m=0.05$, $\delta {W}_{a}=0.2$ m/s² (blue). The amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and perturbations $\delta k$ and $\delta m$ are non-dimensional values. The red and blue curves in same graph have same frequencies

The stiffness perturbation of $\delta k=-0.1$ on the bridge resonator ${W}_{1}$, depicted in Fig. 11a–c, influences all three frequency responses due to the AC actuation applied on the bridge resonator. Particularly, it dramatically decreases the peak-to-peak value of ${U}_{1}$ from 0.672 to 0.021 and slightly increases the peak-to-peak value of ${U}_{2}$ and ${U}_{3}$, from 0.163 and 0.189 to 0.231 and 0.277, respectively. As shown in Fig. 11d–i, the mass perturbation of $\delta m=0.05$ on the cantilever, resonator ${W}_{2}$, and the acceleration perturbation of $\delta {W}_{a}=0.2$ m/s², resonator ${W}_{3}$, show similar effects on the response. Figure 11d–i indicate that $\delta m$ and $\delta {W}_{a}$ separately influence the amplitudes of ${U}_{2}$ and ${U}_{3}$, respectively, while no effect was observed on the other two characteristic frequencies.

To demonstrate the triple sensing scheme proposed in this paper, the response was evaluated as simultaneously introducing the three types of perturbations, as shown in Fig. 11j–l. As predicted, the three amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ experience observable variations. These results prove the feasibility of sensing three types of perturbations simultaneously by monitoring three characteristic frequency responses due to the rich dynamics of the proposed coupled system. The triple sensing scheme can be more automated and improved by implementing, for instance, machine learning techniques [32, 45, 46].

3.2.3.2 Quantitative analysis of sensing ability

The quantitative sensing ability of the proposed scheme at three characteristic frequencies has been studied in this section. The frequency shift curves of ${Mode}_{3}$(blue solid curve), ${Mode}_{2}$ (green dotted curve), and ${Mode}_{1}$(red dashed curve) under the perturbations of $\delta k$, $\delta m$, and $\delta {W}_{a}$ are plotted in Fig. 12a–c, respectively, where the slop represents the sensitivity of the corresponding modes, which are defined as follows:

$$ S_{k} = \left| {\frac{{\omega_{3} - \omega_{3}^{0} }}{\delta k}} \right|;\;S_{m} = \left| {\frac{{\omega_{2} - \omega_{2}^{0} }}{\delta m}} \right|;\,S_{{W_{a} }} = \left| {\frac{{\omega_{1} - \omega_{1}^{0} }}{{\delta W_{a} }}} \right| $$

(15)

where ${\omega }_{1}$, ${\omega }_{2}$, and ${\omega }_{3}$ are the shifted frequencies of ${Mode}_{1}$, ${Mode}_{2}$, and ${Mode}_{3}$ after introducing the corresponding perturbations, respectively.

Fig. 12

Characteristic frequencies curves versus different types of perturbations under actuation of ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V, ${V}_{AC1}=7.5$ V, ${V}_{AC2}=0$ V, and ${V}_{AC3}=0$ V: a stiffness perturbation $\delta k$; b mass perturbation $\delta m$; c acceleration perturbation $\delta {W}_{a}$. Perturbation $\delta k$ is non-dimensional value

From Fig. 12a, the frequency shift of ${Mode}_{3}$ observes a linear increase with the stiffness perturbation, $\delta k$, with sensitivity ${S}_{k}=7.81\mathrm{\%}$/kHz. The peak frequency of ${Mode}_{2}$ and ${Mode}_{3}$ show an almost zero slope with the stiffness perturbation $\delta k$ (i.e., $\delta k$ influences the fold bifurcation jump frequency of ${Mode}_{3}$ and has a negligible effect on the other two characteristic frequencies). A similar phenomenon occurs on mass perturbation $\delta m$, where the peak frequency of ${Mode}_{2}$ denotes high sensitivity (${S}_{m}=0.267\mathrm{ng}/\mathrm{kHz}$) with mass perturbation $\delta m$ while the other two curves keep zero slopes (i.e., $\delta m$ influences the peak frequency of ${Mode}_{2}$ and has a negligible effect on the other two characteristic frequencies).

The variation of the frequency shifts with acceleration perturbation, $\delta {W}_{a}$, differs from the other two kinds of perturbations. While the fold jump frequency of ${Mode}_{3}$ and peak frequency of ${Mode}_{2}$ maintain constant value with $\delta {W}_{a}$, the variation of the peak frequency of ${Mode}_{1}$ demonstrates clearly segmented behavior. Considering the output of Figs. 7f and 12c, one can note that the segmentation of the curve is related to the switch of the nonlinearity of resonator, ${W}_{3}$. When $\delta {W}_{a}<-0.3$ m/s² (noted as I), the ${Mode}_{3}$ shows hardening behavior and the sensitivity is ${S}_{{W}_{a}1}=90.62$ (μm m/s²)/Hz. In the acceleration range from − 0.3 m/s² to − 0.1 m/s² (noted as III), the resonator ${W}_{3}$ experiences a transition from hardening nonlinearity to softening nonlinearity while the sensitivity decreases to ${S}_{{W}_{a}2}=30.39$(μm m/s²)/Hz. In the softening nonlinearity zone, for $\delta {W}_{a}>-0.1$ m/s² (noted as III), the sensitivity reaches ${S}_{{W}_{a}3}=124.96$(μm m/s²)/Hz.

As previously noted, the triple sensing scheme is a novel design hence we couldn't compare the multi-sensing ability with the literature. However, it's possible to compare the single mass sensing ability with the existing mode-localized mass sensor. The sensitivity of the mode localization sensor from the literature is defined as the shift of the resonant frequency ratio: ${S}_{{\omega }_{2}}=\left|\frac{{\omega }_{2}-{\omega }_{2}^{0}}{{\omega }_{2}}\right|/\delta m$[65], where the definition of parameters is listed in Eqs. (15). Compare with the frequency shift sensitivity reported of 0.031%/pg [65] and 0.02%/pg [66], the mass sensitivity of the multi-sensing scheme is 0.00691%/pg. Although the sensitivity is relatively lower than the reported design, the multi-sensing ability is an irreplaceable advantage compared with existing structures. One should also note that the sensitivity can be improved by optimising the structure while keeping the same proposed scheme.

Hence, we can conclude that the triple sensing of the proposed scheme is theoretically realized by monitoring the characteristic frequencies’ variation of ${Mode}_{1}$, ${Mode}_{2}$, and ${Mode}_{3}$. Both stiffness and mass sensing mechanisms demonstrate high linearity and high sensitivity. The acceleration sensing mechanism does not show linearity due to the resonator nonlinearity switch while proving the potential of the proposed sensor.

3.3 Response dynamics of AC actuation

3.3.1 AC actuation level on bridge resonator ${{\varvec{W}}}_{1}$

In Fig. 13, the DC polarization actuation is set as ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, and ${V}_{DC3}=10$ V on three resonators ${W}_{1}$, ${W}_{2}$, and ${W}_{3}$, respectively, and only AC actuation of different amplitudes ${V}_{AC1}$ is provided on the bridge resonator. Figure 13 indicates the complete response around the three lowest modes under different levels of AC actuation (the amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ are non-dimensional). It can be noted from Fig. 13a–c that under low AC actuation levels, specifically from 1 V (purple curve) to 1.5 V (blue curve), the frequency response curves show a negligible effect of the nonlinearity (i.e., nearly linear response). When ${V}_{AC1}$ increases to $2$ V (green), hardening behaviour first appears, where the dotted line denotes the unstable branch. Three specific peaks are observed in the response: (i) the main peak on the bridge resonator ${U}_{1}$ appears near 54.7 kHz. It shifts to the right when the actuation ${V}_{AC1}$ increases and finally turns to the fold bifurcation, the jump phenomena induced by bifurcation would be proper sensing target [57]. (ii) Two small peaks at 52.7 kHz and 54.1 kHz, linked to the linear mode-localization, remain at the same frequency with the increase of actuation ${V}_{AC1}$. (iii) The small peak at 27.3 kHz is due to the order two superharmonic behaviour.

Fig. 13

Frequency response curves at different AC bridge actuation ${V}_{AC1}$ while ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V, ${V}_{AC2}=0$ V, and ${V}_{AC3}=0$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$ under low AC actuation of 1 V, 1.5 V, 2 V, 2.5 V, and 3 V; d ${U}_{1}$, e ${U}_{2}$, and f ${U}_{3}$ under medium AC actuation of 4 V, 5 V, 6 V, and 7 V; g ${U}_{1}$, h ${U}_{2}$, and i ${U}_{3}$ under high AC actuation of 8 V, 9 V, and 10 V. Black lines denote unstable branches. Amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

When the actuation is increased from $4$ V to $7$ V, as shown in Fig. 13d–f, the fold bifurcation jump frequency in ${U}_{1}$ continues to increase, and the peak frequency in ${U}_{2}$ and ${U}_{3}$ remains constant. When ${V}_{AC1}$ increases further from $8$ V to $10$ V, as shown in Fig. 13g–i, the response leads to a new unstable softening branch with a maximum value of 0.56 due to the dominance of the quadratic nonlinearity originating from the electrostatic force. To obtain the best performance in sensing through fold bifurcation jump and eliminate the risk of the unwanted unstable branch, the actuation of ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V, ${V}_{AC1}=7$ V or $7.5$ V, ${V}_{AC2}=0$ V, and ${V}_{AC3}=0$ V is a convenient choice. Under such actuation, the frequency response displays strong nonlinearity to generate a fold bifurcation for the sensing process (as shown by red curves in Fig. 13d–f), while doesn't reach excessive nonlinearity to lead to the emergence of multiple co-existing unstable branches (as blue curves in Fig. 13g–i show).

3.3.2 AC actuation level on cantilever resonator ${{\varvec{W}}}_{2}$

In this section, the system dynamics are simulated for different actuating schemes. More specifically, the DC actuation remains the same while the AC actuation is switched on the cantilever resonator ${W}_{2}$. Compared to the response in Sect. 3.3.1, the linear behaviours of Figs. 13a–c and 14a–c in the two parts are quite similar: both actuating modes return two peaks, including the central peak at 54.7 kHz and the superharmonic peak at 27.3 kHz. Under high AC actuation, the frequency response curve around the second mode (Fig. 14d–f) shows a combination of nonlinear softening and hardening behaviour as the existence of both the quadratic nonlinearity and the geometric nonlinearity. Besides, the level of nonlinearity is also lower than the bridge actuating result, which is insufficient to generate a noticeable fold bifurcation. By comparing the maximum amplitude of two frequency responses under high AC actuation (Figs. 13d–f and 14d–f), it could be found that the peak amplitude of ${U}_{1}$ under bridge actuation (red in Fig. 13d, represents ${V}_{AC1}=7$ V) is near 0.36, which is almost three times of the ${U}_{1}$ under cantilever actuation (red in Fig. 14d, represents ${V}_{AC2}=28$ V). Evidently, the AC bridge ${W}_{1}$ actuation has an overwhelming advantage compared to AC cantilever ${W}_{2}$ actuation on both lower actuation voltage and higher resonant amplitude.

Fig. 14

Frequency response curves at different AC bridge actuation ${V}_{AC1}$ while ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V, ${V}_{AC2}=0$ V, and ${V}_{AC3}=0$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$ under medium AC actuation of 5 V, 10 V, 15 V, and 20 V; d ${U}_{1}$, e ${U}_{2}$, and f ${U}_{3}$ under medium AC actuation of 22 V, 24 V, 26 V, and 28 V. Black lines denote unstable branches. Amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

3.3.3 AC actuation level on bridge resonator ${{\varvec{W}}}_{3}$

In Sect. 3.3.3, the AC actuation is switched on the bridge resonator ${W}_{3}$ while other actuations remain the same. Similar to Sect. 3.3.2, both subharmonic peak at 27.3 kHz and the central peak at 54.7 kHz could be observed (Fig. 15a–c), while Fig. 15d–f show a nonlinear softening behaviour as being dominated by quadratic nonlinearity. The appearances of the central peak at 54.7 kHz and the superharmonic peak at 27.3 kHz keep the same. However, the AC bridge ${W}_{3}$ actuation has similar limitations with AC cantilever ${W}_{2}$ actuation of lower actuation amplitude and not exhibiting fold bifurcations. Comparing the three different AC actuations, the AC bridge ${W}_{1}$ actuation is the best choice based on low actuation voltage, high resonant amplitude, and high sensitivity provided by the hardening fold bifurcation phenomenon.

Fig. 15

Frequency response curves at different AC bridge actuation ${V}_{AC1}$ while ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V, ${V}_{DC3}=40$ V and ${V}_{AC1}={V}_{AC2}=0$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$ under low AC actuation of 1 V, 2 V, 3 V, and 4 V. d ${U}_{1}$, e ${U}_{2}$, and f ${U}_{3}$ under medium AC actuation of 5 V, 5.2 V, 5.4 V, and 5.6 V. Black lines denote unstable branches. Amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

In this section, the influence of actuation voltages has been discussed. As increasing the AC actuation voltage, all three actuation scenarios show the variation in response from approximately linear behaviour to highly nonlinear. While actuating bridge resonator ${W}_{1}$ requires near 7 V to generate proper fold bifurcation, the cantilever resonator ${W}_{2}$ actuation requires a higher actuation level, i.e., 24 V, to reach nonlinear response. In addition, it shows a combination of nonlinear softening and hardening behaviour which is not suitable for the proposed sensing target. The bridge resonator ${W}_{3}$ actuation shows a nonlinear softening behaviour at 5.4 V which is also not suitable, for the proposed sensing target. Comparing the influence of the three different AC actuation, it could be concluded that the dynamic actuation of ${W}_{1}$ is the most convenient thanks to low actuation voltage, high resonant amplitude, and high sensitivity provided by the hardening fold bifurcation phenomenon.

3.4 Response dynamics of DC actuation

The influence of DC actuation is discussed in this section with the AC actuation of ${V}_{AC1}$ keeping as $7$ V, as shown in Fig. 16. It can be noted the DC actuation of ${V}_{DC1}$ influences all three frequency responses, the magnitude of ${V}_{DC1}$ directly links to the nonlinearity level. To obtain better sensing performance on fold bifurcation jump and get rid of unstable branches, ${V}_{DC1}=40$ V is chosen in the research. From Fig. 16d–i, it can be noted that the DC actuation level of ${V}_{DC2}$ and ${V}_{DC3}$ has nearly no influence on frequency responses. In consideration of the symmetry of the system, DC actuation of ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V are chosen.

Fig. 16

Frequency response curves at different resonator lengths under actuation of ${V}_{AC1}=7$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$ under DC actuation of ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V and different ${V}_{DC1}$ of 10 V, 20 V, 30 V, 40 V and 50 V; d ${U}_{1}$, e ${U}_{2}$, and f ${U}_{3}$ under DC actuation of ${V}_{DC1}=40$ V and ${V}_{DC3}=40$ V and different ${V}_{DC2}$ of 2.5 V, 5 V, 7.5 V, 10 V and 12.5 V; g ${U}_{1}$, h ${U}_{2}$, and i ${U}_{3}$ under DC actuation of ${V}_{DC1}=40$ V and ${V}_{DC2}=10$ V and different ${V}_{DC3}$ of 10 V, 20 V, 30 V, 40 V and 50 V. Black lines denote unstable branches. Amplitude ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

4 Effects of physical parameter

4.1 Effects of resonators' length

We investigate the effect of the resonators' lengths ${L}_{1}$, ${L}_{2}$, and ${L}_{3}$ on the system response. The AC actuation of ${V}_{AC1}$ equals to $6$ V in three cases, as shown in Fig. 17. It can be noted that each resonator's length only influences the corresponding resonator's natural frequency, however, has no influence on the other two resonators' natural frequencies. The change of single resonator's length would result in that three natural frequencies are not close to each other. Under such situation, the sensitivity would decrease.

Fig. 17

Frequency response curves at different resonator lengths under actuation of ${V}_{AC1}=6$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$ under different bridge ${W}_{1}$ lengths, ${L}_{1}$ of $680$ μm, $700$ μm, and $720$ μm; d ${U}_{1}$, e ${U}_{2}$, and f ${U}_{3}$ under different cantilever ${W}_{2}$ lengths, ${L}_{2}$ of $267$ μm m, $277$ μm m, and $287$ μm; g ${U}_{1}$, h ${U}_{2}$, and i ${U}_{3}$ under different bridge ${W}_{3}$ lengths, ${L}_{2}$ of $680$ μm m, $700$ μm m, and $720$ μm m. Dotted lines denote unstable branches. Amplitude ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

4.2 Effects of resonators' thickness

The thickness change is simulated to occur on all three resonators. As increasing the thickness, the whole system is stiffer and harder to actuate, hence increasing all three natural frequencies simultaneously and decreasing the response amplitude. The results are depicted in Fig. 18 with an AC actuation of 7.5 V. Figure 18a shows that under the same AC actuation of 7.5 V, the response may exhibit the nonlinear fold bifurcation jump at a different level: high-level nonlinearity (2.5 μm), medium-level nonlinearity (3 μm), and low-level nonlinearity (3.5 μm). The thickness variations also lead to the shift of the resonance frequencies. To obtain certain nonlinearity level and amplitude, the thickness of $3$ μm m would be a convenient choice.

Fig. 18

Frequency response curves at different thicknesses, $h$ of $2.5$ μm m, $3$ μm m, and $5$ μm m under actuation of ${V}_{AC1}=7.5$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${c}_{1}={c}_{2}={c}_{3}=0.5$ and ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$ and c ${U}_{3}$. Dotted lines denote unstable branches. Amplitude of ${U}_{1}$, ${U}_{2}$ and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional

4.3 Effects of damping

The effects of damping coefficients (${\zeta }_{1}$, ${\zeta }_{2}$, and ${\zeta }_{3}$) on the resonator response are depicted in Fig. 19. The value of damping influences the AC actuation needed to lead to nonlinear behaviour and the motion amplitude of the resonators. Note that the values of damping ratios were chosen arbitrarily but having the same order of magnitude as previous research studies [57, 67], to show the damping effect on the numerical simulations. As shown in Fig. 19, the damping value influences the energy loss of the system, larger damping value leads to more energy loss. Figure 19a shows that under the same AC actuation of 7.5 V, the system with high damping of ${\zeta }_{1}={\zeta }_{2}={\zeta }_{3}=2.222\times {10}^{-2}$ only gives low transverse deflection and low-level nonlinearity fold bifurcation jump, however, the system with low damping of ${\zeta }_{1}={\zeta }_{2}={\zeta }_{3}=4.444\times {10}^{-3}$ would exhibit the unstable softening branch.

Fig. 19

Frequency response curves at different damping, $c$ of $0.2$, $0.5$, and $1.0$ under actuation of ${V}_{AC1}=7.5$ V, ${V}_{AC2}=0$ V, ${V}_{AC3}=0$ V, ${V}_{DC1}=40$ V, ${V}_{DC2}=10$ V and ${V}_{DC3}=40$ V under ${W}_{a}=0$ m/s²: a ${U}_{1}$, b ${U}_{2}$, and c ${U}_{3}$. Amplitudes ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ and damping ${c}_{1}$, ${c}_{2}$, and ${c}_{3}$ are non-dimensional. Where $c=2\zeta {w}_{n}$ and ${w}_{n}=22.5$, the damping coefficient ${\zeta }_{1}={\zeta }_{2}={\zeta }_{3}=4.444\times {10}^{-3}$ when damping ${c}_{1}={c}_{2}={c}_{3}=0.2$; ${\zeta }_{1}={\zeta }_{2}={\zeta }_{3}=1.111\times {10}^{-2}$ when damping ${c}_{1}={c}_{2}={c}_{3}=0.5$; ${\zeta }_{1}={\zeta }_{2}={\zeta }_{3}=2.222\times {10}^{-2}$ when damping ${c}_{1}={c}_{2}={c}_{3}=1.0$

5 Conclusions

In this paper, the nonlinear dynamics of three mechanically coupled micromachined resonators (cantilever and bridge resonators) were numerically investigated for potential triple-sensing applications. The concept is based on the simultaneous tracking of the resonance frequencies of the first three lowest vibration modes. Stiffness, mass, and acceleration perturbations of the bridge and cantilever resonators, respectively, were found to have an independent influence on the three vibration modes, demonstrating the promising potential of triple-sensing on a single device. Nonlinear behaviour, including fold bifurcations and peaks as sensing targets, improves the accuracy and sensitivity of the sensor. The numerical model of the coupled system with geometric and electrostatic nonlinear terms is developed, demonstrating the triple-sensing's feasibility. The continuous simulation of the structure is obtained, revealing the full nonlinear dynamics of the coupled system and the effect of different parameters, which is vital for the sensor's design. It is worth mentioning that the value of AC actuation directly relates to the system's nonlinearity. Medium levels of AC actuation linked to the nonlinear fold bifurcations are suitable to gain the sensor's best performance and weaken the risk of unstable softening branches due to excessive driving input. The perturbation simulations demonstrate the response variation under three perturbations. The results indicate that stiffness, mass, and acceleration perturbations of the bridge and cantilever resonators independently influence the first three vibration modes, proving the promising performance of the triple-sensing concept. Compared to the state-of-the-art multi-sensing techniques, the methodology introduced in this research could be used to detect different types of stimuli and get customized for applications, which shows its potential for mixture gas analysis, industrial manufacture, aerospace, and other applications requiring multiple sensing.

The future work will focus on the practical sensor system design and fabrication and the corresponding multiple parameters sensing test. The increase in the types of stimuli and the combination of other sensing methodologies is also a potential research direction. Besides, the influence of the interaction of the system's parameters, (for instance, stiffness, damping, and temperature) on the system's sensing performance will be interesting to be further investigated as part of future work. Additionally, including more higher-order modes can enhance the results and lead to better understanding of the dynamics of the coupled systems around higher-order modes. One should note that operating the system at higher-order modes could be a potential approach to improve the accuracy of the model and the sensor's sensitivity instead of using the first three global modes.

Appendices

Appendix A: Structure modelling

The following variables and parameters are introduced:

$$ \begin{gathered} w_{1} = \frac{{\tilde{w}_{1} }}{{d_{1} }};w_{2} = \frac{{\tilde{w}_{2} }}{{d_{1} }};w_{3} = \frac{{\tilde{w}_{3} }}{{d_{1} }};x = \frac{{\tilde{x}}}{{L_{1} }};X_{c} = \frac{{\tilde{X}_{c} }}{{L_{1} }};X_{m} = \frac{{\tilde{X}_{m} }}{{L_{1} }};R_{L1} = \frac{{L_{2} }}{{L_{1} }};R_{L2} = \frac{{L_{3} }}{{L_{1} }};R_{d1} = \frac{{d_{2} }}{{d_{1} }};R_{d2} \hfill \\ = \frac{{d_{3} }}{{d_{1} }};m = \frac{{\tilde{m}}}{{\rho AL_{1} }};t = \frac{{\tilde{t}}}{\tau }; \Omega_{1} = \tilde{\Omega }_{1} \tau ;\Omega_{2} = \tilde{\Omega }_{2} \tau ;\Omega_{3} = \tilde{\Omega }_{3} \tau ;\tau = \sqrt {\frac{{\rho AL_{1}^{4} }}{EI}} ;I = \frac{{bh^{3} }}{12};N \hfill \\ = \frac{{\tilde{N}L_{1}^{2} }}{EI};N_{non} = \frac{{MW_{a} L_{1}^{2} }}{2EI};k_{r} = \frac{{\tilde{k}_{r} L_{1} }}{EI};c_{i} = \frac{{L_{1}^{4} \tilde{c}_{i} }}{EI\tau };K_{non} = \frac{{kL_{1}^{2} }}{4EI};\alpha_{1} = 6*\left( {\frac{{d_{1} }}{h}} \right)^{2} ;\alpha_{2} = \frac{{\varepsilon_{0} bL_{1}^{4} }}{{2EId_{1}^{3} }};k_{r} = \frac{{G\beta b_{c} h^{3} }}{{L_{C} }} \hfill \\ \end{gathered} $$

(A1)

By substituting the new introduced parameters in (A1) into Eqs. (9), (10), and (11), the non-dimensional equations of motion are presented as:

$${w}_{1}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\ddot{w}}_{1}+{c}_{1}{\dot{w}}_{1}+\left[N-{\alpha }_{1}{\int }_{0}^{1}{\left({w}_{1}^{\mathrm{^{\prime}}}\right)}^{2}dx\right]*{w}_{1}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{k}_{r}\left({w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{2}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)+{k}_{r}\left({w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{3}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)={\alpha }_{2}\frac{{\left[{V}_{DC1}+{V}_{AC1}\mathit{cos}\left({\Omega }_{1}t\right)\right]}^{2}}{{\left(1-{w}_{1}\right)}^{2}}$$

(A2)

$${w}_{2}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+\left(1+\delta m\left(x-{X}_{m}\right)\right){\ddot{w}}_{2}+{c}_{2}{\dot{w}}_{2}+{k}_{r}\left({w}_{2}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)={\alpha }_{2}\frac{{\left[{V}_{DC2}+{V}_{AC2}\mathit{cos}\left({\Omega }_{2}t\right)\right]}^{2}}{{\left({R}_{d1}-{w}_{2}\right)}^{2}}$$

(A3)

$${w}_{3}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\ddot{w}}_{3}+{c}_{3}{\dot{w}}_{3}+\left[{N}_{non}-{K}_{non}{\int }_{0}^{1}{\left({w}_{3}^{^{\prime}}\right)}^{2}dx\right]*{w}_{3}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{k}_{r}\left({w}_{3}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)={\alpha }_{2}\frac{{\left[{V}_{DC3}+{V}_{AC3}\mathit{cos}\left({\Omega }_{3}t\right)\right]}^{2}}{{\left({R}_{d2}-{w}_{3}\right)}^{2}}$$

(A4)

with the following corresponding boundary conditions:

$${w}_{1}\left(0,t\right)={w}_{1}^{^{\prime}}\left(0,t\right)={w}_{1}\left(1,t\right)={w}_{1}^{^{\prime}}\left(1,t\right)=0$$

(A5)

$${w}_{2}\left(0,t\right)={w}_{2}^{^{\prime}}\left(0,t\right)={w}_{2}\left({R}_{L1},t\right)={w}_{2}^{^{\prime}}\left({R}_{L1},t\right)=0$$

(A6)

$${w}_{3}\left(0,t\right)={w}_{3}^{^{\prime}}\left(0,t\right)={w}_{3}\left({R}_{L2},t\right)={w}_{3}^{^{\prime}}\left({R}_{L2},t\right)=0$$

(A7)

After multiplying both sides of Eqs. (A2), (A3), and (A3) by the ${\left(1-w\right)}^{2}$, ${\left({R}_{d1}-{w}_{2}\right)}^{2}$, and ${\left({R}_{d2}-{w}_{3}\right)}^{2}$, respectively, and applying the Galerkin method [61], it yields:

$${{\left(1-{w}_{1}\right)}^{2}w}_{1}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\left(1-{w}_{1}\right)}^{2}\frac{{\partial }^{2}{w}_{1}}{\partial {t}^{2}}+{{\left(1-{w}_{1}\right)}^{2}c}_{1}\frac{\partial {w}_{1}}{\partial t}-{\left(1-{w}_{1}\right)}^{2}{\alpha }_{1}{\int }_{0}^{1}{\left({w}_{1}^{\mathrm{^{\prime}}}\right)}^{2}dx*{w}_{1}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{{\left(1-{w}_{1}\right)}^{2}k}_{p}\left({w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{2}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)+{\left(1-{w}_{1}\right)}^{2}{k}_{p}\left({w}_{1}^{\mathrm{^{\prime}}}\left({X}_{d}\right)-{w}_{3}^{\mathrm{^{\prime}}}\left({X}_{d}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{d}\right)={\alpha }_{2}{\left[{V}_{dc2}+{V}_{ac2}\mathrm{cos}\left({\Omega }_{2}t\right)\right]}^{2}$$

(A8)

$${\left({R}_{d1}-{w}_{2}\right)}^{2}{w}_{2}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\left({R}_{d1}-{w}_{2}\right)}^{2}\left(1+m\left(x-{X}_{m}\right)\right)\frac{{\partial }^{2}{w}_{2}}{\partial {t}^{2}}+{\left({R}_{d1}-{w}_{2}\right)}^{2}{c}_{2}\frac{\partial {w}_{2}}{\partial t}+{k}_{r}\left({w}_{2}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)={\alpha }_{2}{\left[{V}_{dc2}+{V}_{ac2}\mathrm{cos}\left({\Omega }_{2}t\right)\right]}^{2}$$

(A9)

$${{\left({R}_{d2}-{w}_{1}\right)}^{2}w}_{1}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\left({R}_{d2}-{w}_{1}\right)}^{2}\frac{{\partial }^{2}{w}_{1}}{\partial {t}^{2}}+{{\left({R}_{d2}-{w}_{1}\right)}^{2}c}_{1}\frac{\partial {w}_{1}}{\partial t}+{\left({R}_{d2}-{w}_{1}\right)}^{2}*\left[{N}_{non}-{K}_{non}{\int }_{0}^{1}{\left({w}_{1}^{^{\prime}}\right)}^{2}dx\right]*{w}_{1}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{{\left({R}_{d2}-{w}_{1}\right)}^{2}k}_{r}\left({w}_{3}^{\mathrm{^{\prime}}}\left({X}_{c}\right)-{w}_{1}^{\mathrm{^{\prime}}}\left({X}_{c}\right)\right){\delta }^{\mathrm{^{\prime}}}\left(x-{X}_{c}\right)={\alpha }_{2}{\left[{V}_{dc3}+{V}_{ac3}\mathrm{cos}\left({\Omega }_{2}t\right)\right]}^{2}$$

(A10)

The solutions of Eqs. (A8), (A9), and (A10) can be expressed as ${w}_{1}\left(x,t\right)=\sum_{i=1}^{\infty }{u}_{1,i}\left(t\right){\varphi }_{1,i}\left(x\right)$, ${w}_{2}\left(x,t\right)=\sum_{i=1}^{\infty }{u}_{2,i}\left(t\right){\varphi }_{2,i}\left(x\right)$, and ${w}_{3}\left(x,t\right)=\sum_{i=1}^{\infty }{u}_{3,i}\left(t\right){\varphi }_{3,i}\left(x\right)$, where ${\varphi }_{1,i}$, ${\varphi }_{2,i}$, and ${\varphi }_{3,i}$ are the i-th linear undamped mode shape of microbeams ${W}_{1}$, ${W}_{2}$, and ${W}_{3}$. Then, the linear undamped eigenvalue equations are obtained:

$$ \varphi_{1,i}^{\prime \prime \prime \prime } = \beta_{1,i}^{2} \varphi_{1,i} $$

$$ \varphi_{2,i}^{\prime \prime \prime \prime } = \beta_{2,i}^{2} \varphi_{2,i} $$

$${\varphi }_{3,\mathrm{i}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}={\beta }_{3,i}^{2}{\varphi }_{3,i}$$

(A11)

$$ \beta_{1}^{2} = \mathop \int \limits_{0}^{1} \varphi_{1} \varphi_{1}^{\prime \prime \prime \prime } dx $$

$$ \beta_{2}^{2} = \mathop \int \limits_{0}^{{R_{L} }} \varphi_{2} \varphi_{2}^{\prime \prime \prime \prime } dx $$

$$ \beta_{3}^{2} = \mathop \int \limits_{0}^{{R_{L} }} \varphi_{3} \varphi_{3}^{\prime \prime \prime \prime } dx $$

(A12)

By substituting Eqs. (A11) and (A12) into Eqs. (A8), (A9), and (A10), multiplying by ${\varphi }_{1,i}$, ${\varphi }_{2,i}$, ${\varphi }_{3,i}$, and integrating from $x=0$ to $1$, $x=0$ to ${R}_{L1}$, and $x=0$ to ${R}_{L2}$, respectively. It yields the non-dimensional Eqs. (12), (13), and (14) in Sect. 2.

Appendix B: Continuous analysis of the characteristic points

The phase portraits and Poincaré sections for all three characteristic points are shown in Fig. 

Fig. 20

Phase portrait (solid line) and Poincaré section (dots) for the four characteristic points revealed in Fig. 3; peak points at 52.551 kHz (red) and 54.141 kHz (yellow), bifurcation points at 71.269 kHz (green) and 57.583 kHz (blue): a ${W}_{1}$; b ${W}_{2}$; c ${W}_{3}$

20. The red curves represent the peak point of ${U}_{3}$ at 52.551 kHz, the yellow curves represent the peak point of ${U}_{2}$ at 54.141 kHz, the green curves represent the higher amplitude bifurcation point at 71.269 kHz, and the blue curves represent the lower amplitude bifurcation point at 57.583 kHz, respectively. The phase portraits, which are generated from 200 cycles of steady-state time response, demonstrate elliptical orbits, and all Poincaré sections converge to a single point, proving that the response is periodic motion of period-1. It could be concluded that before the peak point of ${U}_{3}$ at 52.551 kHz, all ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ phase portraits enlarge with increased frequency. Between 52.551 kHz (${U}_{3}$ peak) and 54.141 kHz (${U}_{2}$ peak), ${U}_{1}$ and ${U}_{2}$ keep enlarging while ${U}_{3}$ starts to shrink. Between 54.141 kHz (${U}_{2}$ peak) and 71.269 kHz (higher amplitude bifurcation point), ${U}_{1}$ keeps enlarging while ${U}_{2}$ starts to shrink. In the last stable branch larger than 57.583 kHz, the ${U}_{1}$, ${U}_{2}$, and ${U}_{3}$ phase portraits shrink with increased frequency. It should be pointed out that the nonlinear behaviour determines the maximum transverse deflection of ${U}_{1}$ while the maximum transverse deflections of ${U}_{2}$ and ${U}_{3}$ are further related to their natural frequencies.