1 Introduction

Beginning at the end of 2019, a pneumonia epidemic caused by a new type of coronavirus has spread globally. This new type of coronavirus is named “Severe Acute Respiratory Syndrome-related Coronavirus type 2” (SARS-CoV-2) [1], and the pneumonia caused by it is called “Coronavirus disease 2019” (COVID-19) pandemic [2]. In order to curb the spread of the virus, the Chinese government implemented a series of effective and strict prevention and control measures in time. With the joint efforts of the government and the people, China’s prevention and control measures have achieved good results and the epidemic situation has been completely controlled. In the rest of the world, however, the spread of COVID-19 is still not under effective control, with increasing number of confirmed cases and deaths. According to the report by WHO, as of April 25, 2021, people infected by COVID-19 in the world reaches 145,216,414 with 3,079,390 deaths [3]. To make matters worse, three major variants of SARS-CoV-2 have been identified in the past few months in the UK, South Africa and Brazil, respectively [4]. They have commonly demonstrated an increase in transmissibility compared to wild-type (non-VOC) variants and rapidly replaced the wild-type variant in the relevant country [5]. They bring about a new wave of the current COVID-19 epidemic. Recently, the COVID-19 epidemic situation in India continues to worsen, with new confirmed cases in a single day repeatedly reaching new highs. The number of new confirmed cases exceeds 300,000 for several days, and the number of deaths also increases sharply [3]. For COVID-19, there is no specific drug [6]. Although some vaccines are already in use, their production cannot meet the demand at present. Therefore, strict prevention and control measures are the most effective way to slow down the spread of the epidemic. Governments and people around the world are working together to strengthen prevention and control, hoping to contain the further spread of COVID-19 at an early date and return the world to its past prosperity.

Mathematical models play important roles in epidemiology. They can help us to simulate, analyze and predict the epidemic spread system and seek optimal performance and intervention strategies [7, 8]. Based on the characteristics of COVID-19 epidemic, many related mathematical models have been proposed, such as fractional-order models [9,10,11,12] and stochastic models [13,14,15]. Applying “nonlinear autoregressive network with exogenous inputs” approach, a time series model is developed to forecast the impact of environmental stresses on the frequent waves of COVID-19 [16]. There are also many deterministic models for the spread of COVID-19 based on the different prevention measures in different countries. A time-delay SEIRS model is presented to study the spread of COVID-19 in [17]. The authors apply a deep learning technique “Self Organizing Map” to obtain the parametric values. A compartmental model considering the role of environmental contamination by COVID-infected individuals is presented in [18]. The authors use relevant data from South Africa to fit model parameters and study the impact of various control and mitigation strategies on the spread of COVID-19 in South Africa. In [19], a new SEIR model comprehensively considering the characteristics of COVID-19 and government intervention measures is proposed. The authors use Italian epidemic data from February 15 to June 30 to simulate the spread of COVID-19 in Italy. An SEIR model is used to forecast the effect of nationwide lockdown on the spread of COVID-19 in India [20]. Also about studying the spread of COVID-19 in India, a compartmental model considering quarantine and hospitalized isolation is formulated in [21], and the model parameters are fitted by the real data of India. In [22], the authors use an SEIR model to research the impact of vaccination and isolation on the spread of COVID-19 in Indonesia. The stability of the model is analyzed and the relevant data of Indonesia is applied for simulation. By considering the interactive effect of imported cases, isolating rate, diagnostic rate, recovery rate and mortality rate, a spread model of COVID-19 is established in [23]. In [24], an SIR model is employed to study the spread of COVID-19 in Italy, India, South Korea and Iran. By considering the different age structures, an age-structured SIQR model is proposed to track the spread of COVID-19 in India, Italy and USA [25]. Some improved SEIR models considering different factors are proposed to study the spread of COVID-19. For example, a nonlinear incidence rate is used [26]; government policy is considered [27]; some general control strategies, such as hospital, quarantine and external input, are considered [21, 28, 29], etc.

However, most of the existing models ignore several problems: 1) asymptomatic individuals can develop into symptomatic ones; 2) asymptomatic individuals can be diagnosed, and once diagnosed, asymptomatic individuals should be isolated; 3) individuals quarantined or hospitalized (isolated) cannot be considered as contagious as long as protective measures are appropriate. This paper studies the impact of strict prevention and control measures on the spread of COVID-19, improves the models in [21, 28, 29], and establishes a more reasonable spread model considering the above three neglected aspects to simulate the transmission dynamics of COVID-19. As validations, the model is used to simulate the spread of COVID-19 in Hubei and Hunan Provinces of China for a period of time. The actual data are divided into two categories: one is for fitting the model parameters and the other is for verifying the simulations of model. In particular, combined with the actual situation, the cure rate and died rate are fitted as time-varying functions. Sensitivity analysis of the parameters is also done to provide the basis for formulating prevention and control measures, and they are verified by simulation.

Table 1 Population classification
Full size table

An outline of this paper is as follows. In Sect. 2, we present a spread model of COVID-19 based on strict epidemic prevention measures and analyze some properties of solutions of the model. Equilibria and basic reproductive number of the model are derived in Sect. 3. Stability of equilibria, including the disease-free equilibrium and endemic equilibrium, are analyzed in Sect. 4. In Sect. 5, with the real data of Hubei Province in China, the model parameters are estimated, and simulations are conducted to analyze the spread dynamics of COVID-19 in Hubei and Hunan Provinces. Sensitivity analyses for the previously estimated values of parameters are made in Sect. 6. Some concluding remarks are given in Sect. 7.

Fig. 1
figure 1

The state transformation process of individuals

Full size image
Table 2 Description of symbols
Full size table

2 Spread model

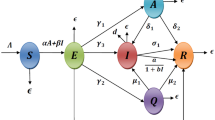
According to the spread characteristics of COVID-19 and the epidemic prevention measures, we divide the entire population into eight groups, as shown in Table 1. Individuals in group A or I are both infected and infectious. Their transforming relationship is shown in Fig. 1, and descriptions of the parameters are shown in Table 2. All the parameters are nonnegative. S(t) represents the number of susceptible individuals at time t, abbreviated as S, and the rest of the state variables are similar. \(N(t)=S(t)+E(t)+Q(t)+A(t)+I(t)+J(t)+R(t)\) is the number of the entire population at time t. M is the average number of new arrivals per day in the region, including births and migrants.

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\text {d}S}{\text {d}t}=M-\frac{uS\left( \alpha A+\beta I \right) }{N-Q-J}-\upsilon S \\&\frac{\text {d}E}{\text {d}t}=\frac{uS\left( \alpha A+\beta I \right) }{N-Q-J}-({{\delta }_{1}}+{{\delta }_{2}}+{{\delta }_{3}}+\upsilon )E \\&\frac{\text {d}Q}{\text {d}t}={{\delta }_{1}}E-({{\eta }_{1}}+{{\eta }_{2}}+\upsilon )Q \\&\frac{\text {d}A}{\text {d}t}={{\delta }_{2}}E-({{\sigma }_{1}}+{{\sigma }_{2}}+{{\sigma }_{3}}+\upsilon )A \\&\frac{\text {d}I}{\text {d}t}={{\delta }_{3}}E+{{\sigma }_{2}}A-({{\gamma }_{1}}+{{\gamma }_{2}}+\upsilon )I \\&\frac{\text {d}J}{\text {d}t}={{\gamma }_{1}}I+{{\eta }_{1}}Q +{{\sigma }_{1}}A -(\theta +\mu +\upsilon )J \\&\frac{\text {d}R}{\text {d}t}={{\sigma }_{3}}A+{{\eta }_{2}}Q+{{\gamma }_{2}}I+\theta J-\upsilon R \\ \end{aligned} \right. \end{aligned}$$
(1)

with the initial conditions

$$\begin{aligned} (S(0),E(0),Q(0),A(0),I(0),J(0),R(0))\ge 0. \end{aligned}$$

and the state space

$$\begin{aligned} \begin{aligned} {{\mathbb {R}}^{7}_{+}}&=\left\{ (S(t),E(t),Q(t),A(t),I(t),J(t),R(t)):\right. \\&\quad \left. (S(t),E(t),Q(t),A(t),I(t),J(t),R(t))\ge 0 \right\} . \end{aligned} \end{aligned}$$

Remark 1

D(t) satisfies the differential equation

$$\begin{aligned} \frac{\text {d}D}{\text {d}t}=\mu J(t). \end{aligned}$$
(2)

Since Eq. (2) is independent of the equations in model (1), it is omitted in model (1) to make the mathematical analysis more concise.

For COVID-19, we consider preventive measures for three classes of people in model (1).

  1. (a)

    Quarantined (Q) and confirmed (J) individuals. The epidemic prevention measures for these persons are the most stringent. They are completely isolated so that they have no chance to infect susceptible persons;

  2. (b)

    Exposed (E), asymptomatic (A) and symptomatic (I) individuals. The prevention and control measures for these persons are mainly tracking quarantine and isolated treatment. The parameters \({{\delta }_{1}}, {{\sigma }_{1}}, {{\gamma }_{1}}\) represent the quarantined/isolated efficiency of these three types of infected individuals, respectively.

  3. (c)

    Susceptible (S) individuals. The prevention and control measures for these persons mainly include traffic control, maintaining social distance, implementing curfew, etc., in order to protect them from getting infected. \(1-u\) represents the strength of these measures. The smaller the u, the greater the prevention and control efforts.

There are two basic properties of system (1) as follows.

Proposition 1

For the given initial condition

$$\begin{aligned} (S(0),E(0),Q(0),A(0),I(0),J(0),R(0))>{\mathbf {0}}, \end{aligned}$$

the solution of system (1) satisfies \((S(t),E(t),Q(t),A(t),I(t),J(t),R(t))>{\mathbf {0}}\) for all \(t>0\).

Proof

The proof is by contradiction. Assume that there exists \({{t}_{1}}>0\) such that at least one of \(S(t_1),E(t_1),Q(t_1),A(t_1),I(t_1),J(t_1)\) and \(R(t_1)\) is not positive. By continuity of solution, this implies that there exists \({{t}_{0}}\) such that at least one of \(S(t_0),E(t_0),Q(t_0),A(t_0),I(t_0),J(t_0)\) and \(R(t_0)\) is equal to 0. Without loss of generality, we assume that \(t_0\) is the minimal time with such property.

  1. (a)

    If \(S({{t}_{0}})=0\), then \({{\left. \frac{\text {d}S}{\text {d}t} \right| }_{t={{t}_{0}}}}=M>0\), which implies that there exists \(\varepsilon >0\) such that S(t) is strictly monotone increasing in interval \(({{t}_{0}}-\varepsilon ,{{t}_{0}}+\varepsilon )\). Let \({{t}_{2}}\in ({{t}_{0}}-\varepsilon ,{{t}_{0}})\). Then, \(S({{t}_{2}})<S({{t}_{0}})=0\), and since \(S(0)>0\), there exists \(t_3\in (0,t_2)\) such that \(S(t_3)=0\) by Bolzano’s theorem, which contradicts the assumption of \(t_0\).

  2. (b)

    If \(S({{t}_{0}})>0\) and \(E({{t}_{0}})=0\), then

    $$\begin{aligned} {{\left. \frac{\text {d}E}{\text {d}t} \right| }_{t={{t}_{0}}}}=\frac{uS({{t}_{0}})\left( \alpha A({{t}_{0}})+\beta I({{t}_{0}}) \right) }{N({{t}_{0}})-Q({{t}_{0}})-J({{t}_{0}})}\ge 0. \end{aligned}$$

    There are two cases:

    1. (1)

      \({{\left. \frac{\text {d}E}{\text {d}t} \right| }_{t={{t}_{0}}}}>0\). In this case, a contradiction can be obtained similar to a).

    2. (2)

      \({{\left. \frac{\text {d}E}{\text {d}t} \right| }_{t={{t}_{0}}}}=0\). It is easy to know that \(E(t)=0\) for all \(t\ge 0\) is the solution with \(E(0)=0\). This is a contradiction to the uniqueness of the solution since \(E(0)>0\) and \(E(t_0)=0\).

    3. (c)

      If \(S({{t}_{0}})>0, E({{t}_{0}})>0\) and \(Q({{t}_{0}})=0\), then

      $$\begin{aligned} {{\left. \frac{\text {d}Q}{\text {d}t} \right| }_{t={{t}_{0}}}}={{\delta }_{1}}E({{t}_{0}})>0. \end{aligned}$$

      As in the case of (a), a contradiction is arrived. By the same token, \(A(t_0)=0,I(t_0)=0,J(t_0)=0\) or \(R(t_0)=0\) all lead to contradictions. Thus, the proof is completed. \(\square \)

Proposition 2

The system (1) is bounded in \({{\mathbb {R}}^{7}_{+}}\).

Proof

Adding all the equations in (1) yields

$$\begin{aligned} \frac{\text {d}N}{\text {d}t}=M-\upsilon N-\mu J\le M-\upsilon N. \end{aligned}$$

By differential inequality in [30], it follows

$$\begin{aligned} 0<N(t)\le \frac{M}{\upsilon }+ \left[ N(0)-\frac{M}{\upsilon }\right] e^{-\upsilon t}. \end{aligned}$$

Let \({\hat{M}}=max \left\{ N(0),\frac{M}{\upsilon }\right\} \). Taking \(t\rightarrow + \infty \), one obtains \(0<N(t)\le {\hat{M}}\). Hence, the system (1) is bounded in \({{\mathbb {R}}^{7}_{+}}\). \(\square \)

Remark 2

By Propositions 1 and 2, it follows that the set

$$\begin{aligned} \varOmega =\left\{ \begin{aligned}(S,E,Q,A,I,J,R):&(S,E,Q,A,I,J,R)\ge 0, \\&S+E+Q+A+I+J+R\le {\hat{M}} \end{aligned}\right\} \end{aligned}$$

is a positively invariant set of the system (1).

3 Equilibria and basic reproductive number

In this section, the equilibria and the basic regenerative number of the system (1) are discussed. Let

$$\begin{aligned} \left\{ \begin{aligned}&{{f}_{1}}=M-\frac{uS\left( \alpha A+\beta I \right) }{N-Q-J}-\upsilon S=0 \\&{{f}_{2}}=\frac{uS\left( \alpha A+\beta I \right) }{N-Q-J}-{\delta }E=0 \\&{{f}_{3}}={{\delta }_{1}}E-{\eta }Q=0 \\&{{f}_{4}}={{\delta }_{2}}E-{\sigma }A=0 \\&{{f}_{5}}={{\delta }_{3}}E+{{\sigma }_{2}}A-{\gamma }I=0 \\&{{f}_{6}}={{\gamma }_{1}}I+{{\eta }_{1}}Q+{{\sigma }_{1}}A -mJ=0 \\&{{f}_{7}}={{\sigma }_{3}}A+{{\eta }_{2}}Q+{{\gamma }_{2}}I+\theta J-\upsilon R=0 \\ \end{aligned} \right. \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{aligned}&\delta ={{\delta }_{1}}+{{\delta }_{2}}+{{\delta }_{3}}+\upsilon , \eta ={{\eta }_{1}}+{{\eta }_{2}}+\upsilon , \\&\quad \sigma ={{\sigma }_{1}}+{{\sigma }_{2}}+{{\sigma }_{3}}+\upsilon ;\\&\gamma ={{\gamma }_{1}}+{{\gamma }_{2}}+\upsilon ,\quad m=\theta +\mu +\upsilon . \end{aligned} \end{aligned}$$

First, from \(A= I= 0 \), it follows that \(E= Q = J = 0 \). Thus, an unique disease-free equilibrium can be obtained:

$$\begin{aligned} {{P}_{0}}=\left( \frac{M}{\upsilon },0,0,0,0,0,0 \right) . \end{aligned}$$

Next, we use the next-generation approach [7, 31] to calculate the basic reproductive number. Let

The Jacobian matrices of \({\mathbf {F}}\) and \({\mathbf {V}}\) at \({{P}_{0}}\) are as follows:

$$\begin{aligned} \tilde{\mathbf {F}}= & {} \left( \begin{matrix} 0 &{} 0 &{} u\alpha &{} u\beta &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{matrix} \right) ,\\ \tilde{\mathbf {V}}= & {} \left( \begin{matrix} \delta &{} 0 &{} 0 &{} 0 &{} 0 \\ -{{\delta }_{1}} &{} \eta &{} 0 &{} 0 &{} 0 \\ -{{\delta }_{2}} &{} 0 &{} \sigma &{} 0 &{} 0 \\ -{{\delta }_{3}} &{} 0 &{} -{{\sigma }_{2}} &{} \gamma &{} 0 \\ 0 &{} -{{\eta }_{1}} &{} -{{\sigma }_{1}} &{} -{{\gamma }_{1}} &{} m \\ \end{matrix} \right) . \end{aligned}$$

Then, the basic reproductive number is

$$\begin{aligned} {{\Re }_{0}}\text {=}\rho (\tilde{\mathbf {F}}{{\tilde{\mathbf {V}}}^{-1}})=u\left( \frac{\alpha {{\delta }_{2}}}{\delta \sigma }+\frac{\beta {{\delta }_{3}}\sigma +\beta {{\sigma }_{2}}{{\delta }_{2}}}{\delta \sigma \gamma } \right) . \end{aligned}$$
(4)

At the end of this section, the endemic equilibrium is given. Assume that the number of infected individuals be nonzero, i.e., \(I > 0\) or \(A> 0\). Then, we have \(E\ne 0\) by the second equation of (3). From the last five equations of (3), we obtain

$$\begin{aligned} \begin{aligned}&A=\frac{{{\delta }_{2}}}{\sigma }E,\quad Q= \frac{{{\delta }_{1}}}{\eta }E ,\quad I=\frac{{{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}}}{\sigma \gamma }E, \\&J=\left[ \frac{{{\gamma }_{1}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{m\sigma \gamma }+\frac{{{\eta }_{1}}{{\delta }_{1}}\sigma +\eta {{\delta }_{2}}{{\sigma }_{1}}}{m\sigma \eta } \right] E, \\&R=\frac{1}{\upsilon }\left[ \frac{{{\sigma }_{3}}{{\delta }_{2}}}{\sigma }+ \frac{{{\eta }_{2}}{{\delta }_{1}}}{\eta }+\frac{{{\gamma }_{2}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{\sigma \gamma }\right. \\&\qquad \qquad \quad +\frac{\theta {{\gamma }_{1}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{m\sigma \gamma }\\&\left. \qquad \qquad \quad + \frac{\theta ({{\eta }_{1}}{{\delta }_{1}}\sigma +\eta {{\delta }_{2}}{{\sigma }_{1}})}{m\sigma \eta } \right] E.\\ \end{aligned} \end{aligned}$$

Notice that \(N-Q-J=S+E+A+I+R\). Substituting the above results into the second equation of (3) yields

$$\begin{aligned} E=\frac{S}{q}({{\Re }_{0}}-1), \end{aligned}$$
(5)

where

$$\begin{aligned} q&=1+\frac{{{\delta }_{2}}}{\sigma }+\frac{{{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}}}{\sigma \gamma }\\&\quad + \frac{1}{\upsilon }\left[ \frac{{{\sigma }_{3}}{{\delta }_{2}}}{\sigma }+\frac{{{\eta }_{2}}{{\delta }_{1}}}{\eta } +\frac{{{\gamma }_{2}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{\sigma \gamma } \right. \\&\quad \left. + \frac{\theta {{\gamma }_{1}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{m\sigma \gamma }+ \frac{\theta ({{\eta }_{1}}{{\delta }_{1}}\sigma +\eta {{\delta }_{2}}{{\sigma }_{1}})}{m\sigma \eta } \right] . \end{aligned}$$

Adding the first two equations of (3), and combining with Eq. (5), one obtains the unique S:

$$\begin{aligned} {{S}_{e}}=\frac{qM}{\delta ({{\Re }_{0}}-1)+q\upsilon }. \end{aligned}$$

Thus, a unique possible endemic equilibrium \({{P}_{e}}=({{S}_{e}},{{E}_{e}},{{Q}_{e}},{{A}_{e}},{{I}_{e}},{{J}_{e}},{{R}_{e}})\) of system (1) is obtained, where

$$\begin{aligned} \begin{aligned} {{S}_{e}}&=\frac{qM}{\delta ({{\Re }_{0}}-1)+q\upsilon },\quad \\ {{E}_{e}}&=\frac{{{S}_{e}}}{q}({{\Re }_{0}}-1),\quad {{A}_{e}}=\frac{{{\delta }_{2}}}{\sigma }{{E}_{e}},\\ {{Q}_{e}}&=\frac{{{\delta }_{1}}}{\eta }{{E}_{e}}, \quad {{I}_{e}}=\frac{{{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}}}{\sigma \gamma }{{E}_{e}},\\ {{J}_{e}}&=\left[ \frac{{{\gamma }_{1}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{m\sigma \gamma }+\frac{{{\eta }_{1}}{{\delta }_{1}}\sigma +{\eta }{{\delta }_{2}}{{\sigma }_{1}}}{m\sigma \eta } \right] {{E}_{e}}, \\ R_e&=\frac{1}{\upsilon }\left[ \frac{{{\sigma }_{3}}{{\delta }_{2}}}{\sigma }+ \frac{{{\eta }_{2}}{{\delta }_{1}}}{\eta }\right. \\&\quad +\frac{{{\gamma }_{2}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{\sigma \gamma } \\&\quad \left. + \frac{\theta {{\gamma }_{1}}({{\delta }_{3}}\sigma + {{\delta }_{2}}{{\sigma }_{2}})}{m\sigma \gamma }+ \frac{\theta ({{\eta }_{1}}{{\delta }_{1}}\sigma +\eta {{\delta }_{2}}{{\sigma }_{1}})}{m\sigma \eta } \right] E_e. \end{aligned} \end{aligned}$$
(6)

By the foregoing analysis, we have the following conclusion:

Theorem 1

If \({{\Re }_{0}}\le 1\), system (1) has a unique disease-free equilibrium \({{P}_{0}}\), and no endemic equilibrium. If \({{\Re }_{0}}> 1\), system (1) has not only a unique disease-free equilibrium \({{P}_{0}}\), but also a unique endemic equilibrium \({{P}_{e}}\).

4 Stability analysis of equilibria

In this section, the stabilities of the disease-free equilibrium and endemic equilibrium are analyzed, which are closely related to the value of \({\Re }_{0}\). The main results are as follows.

Theorem 2

The disease-free equilibrium \({{P}_{0}}\) of system (1) is locally asymptotically stable if \({{\Re }_{0}}< 1\), but unstable if \({{\Re }_{0}}> 1\).

Proof

The Jacobian matric of system (1) at \({{P}_{0}}\) is

$$\begin{aligned} {{{\mathbf {J}}}_{{{P}_{0}}}}=\left( \begin{matrix} -\upsilon &{} 0 &{} 0 &{} -u\alpha &{} -u\beta &{} 0 &{} 0 \\ 0 &{} -\delta &{} 0 &{} u\alpha &{} u\beta &{} 0 &{} 0 \\ 0 &{} {{\delta }_{1}} &{} -\eta &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} {{\delta }_{2}} &{} 0 &{} -\sigma &{} 0 &{} 0 &{} 0 \\ 0 &{} {{\delta }_{3}} &{} 0 &{} {{\sigma }_{2}} &{} -\gamma &{} 0 &{} 0 \\ 0 &{} 0 &{} {{\eta }_{1}} &{} {\sigma }_{1} &{} {{\gamma }_{1}} &{} -m &{} 0 \\ 0 &{} 0 &{} {{\eta }_{2}} &{} {{\sigma }_{3}} &{} {{\gamma }_{2}} &{} \theta &{} -\upsilon \\ \end{matrix} \right) . \end{aligned}$$
(7)

Its characteristic polynomial is

$$\begin{aligned} 0= & {} \det (\lambda {{{\mathbf {E}}}_{7}}-{{{\mathbf {J}}}_{{{P}_{0}}}})=(\lambda +m){{(\lambda +\upsilon )}^{2}}(\lambda +\eta )\\&\left| \begin{matrix} \lambda +\delta &{} -u\alpha &{} -u\beta \\ -{{\delta }_{2}} &{} \lambda +\sigma &{} 0 \\ -{{\delta }_{3}} &{} -{{\sigma }_{2}} &{} \lambda +\gamma \\ \end{matrix} \right| . \end{aligned}$$

It can be seen that \({{\mathbf {J}}}_{{{P}_{0}}}\) has at least four negative real eigenvalues \({{\lambda }_{1}}=-m,{{\lambda }_{2}}={{\lambda }_{3}}=-\upsilon \) and \({{\lambda }_{4}}=-\eta \). Thus, we only need to discuss the roots of the following equation:

$$\begin{aligned} \begin{aligned} 0&=\left| \begin{matrix} \lambda +\delta &{} -u\alpha &{} -u\beta \\ -{{\delta }_{2}} &{} \lambda +\sigma &{} 0 \\ -{{\delta }_{3}} &{} -{{\sigma }_{2}} &{} \lambda +\gamma \\ \end{matrix} \right| \\&=(\lambda +\delta )(\lambda +\sigma )(\lambda +\gamma )-u\beta {{\delta }_{2}}{{\sigma }_{2}}\\&\quad -u\beta {{\delta }_{3}}(\lambda +\sigma )-u\alpha {{\delta }_{2}}(\lambda +\gamma ). \end{aligned} \end{aligned}$$
(8)

Consider the case of \({{\Re }_{0}}<1\) first. Equation (8) is rewritten as

$$\begin{aligned} 1= & {} \frac{u\beta {{\delta }_{2}}{{\sigma }_{2}}}{(\lambda +\delta )(\lambda +\sigma )(\lambda +\gamma )}+\frac{u\beta {{\delta }_{3}}}{(\lambda +\delta )(\lambda +\gamma )}\\&+\frac{u\alpha {{\delta }_{2}}}{(\lambda +\delta )(\lambda +\sigma )}\triangleq H(\lambda ). \end{aligned}$$

It is not difficult to know that \(H(\lambda )\) is a decreasing function on \([0,+\infty )\). Suppose that Eq. (8) has a nonnegative real part solution \({{\lambda }^{\text {*}}}=a+bi\), that is, \(a\ge 0\). Then,

$$\begin{aligned} \begin{aligned} 1&=\left| H({{\lambda }^{*}}) \right| \\&\le \left| \frac{u\beta {{\delta }_{2}}{{\sigma }_{2}}}{({{\lambda }^{*}}+\delta )({{\lambda }^{\text {*}}}+\sigma )({{\lambda }^{\text {*}}}+\gamma )} \right| \\&\quad +\left| \frac{u\beta {{\delta }_{3}}}{({{\lambda }^{\text {*}}}+\delta )({{\lambda }^{\text {*}}}+\gamma )} \right| \\&\quad +\left| \frac{u\alpha {{\delta }_{2}}}{({{\lambda }^{\text {*}}}+\delta )({{\lambda }^{\text {*}}}+\sigma )} \right| \\&=\frac{u\beta {{\delta }_{2}}{{\sigma }_{2}}}{\left| {{\lambda }^{*}}+\delta \right| \left| {{\lambda }^{\text {*}}}+\sigma \right| \left| {{\lambda }^{\text {*}}}+\gamma \right| }+\frac{u\beta {{\delta }_{3}}}{\left| {{\lambda }^{*}}+\delta \right| \left| {{\lambda }^{\text {*}}}+\gamma \right| }\\&\quad +\frac{u\alpha {{\delta }_{2}}}{\left| {{\lambda }^{*}}+\delta \right| \left| {{\lambda }^{\text {*}}}+\sigma \right| } \\&\le H(a)\le H(0)={{\Re }_{0}}<1, \end{aligned} \end{aligned}$$

which is a contradiction. Therefore, when \({{\Re }_{0}}<1\), all solutions of Eq. (8) have negative real parts. Thus, all eigenvalues of \({{{\mathbf {J}}}_{{{P}_{0}}}}\) have negative real parts, which implies that \(P_0\) is locally asymptotically stable.

Now consider the case of \({{\Re }_{0}}>1\). Equation (8) can be rewritten as

$$\begin{aligned}&{{\lambda }^{3}}+(\delta +\sigma +\gamma ){{\lambda }^{2}}+(\delta \sigma +\sigma \gamma +\gamma \delta \nonumber \\&\quad -u\beta {{\delta }_{3}}-u\alpha {{\delta }_{2}})\lambda +\delta \sigma \gamma (1-{{\Re }_{0}})=0. \end{aligned}$$
(9)

Let \({{\lambda }_{5}},{{\lambda }_{6}},{{\lambda }_{7}}\) be three solutions to Eq. (8). Then, according to the relationship between roots and coefficients, we have

$$\begin{aligned} \left\{ \begin{aligned}&{{\lambda }_{5}}+{{\lambda }_{6}}+{{\lambda }_{7}}=-(\delta +\sigma +\gamma )<0 ,\\&{{\lambda }_{5}}{{\lambda }_{6}}{{\lambda }_{7}}=u\beta ({{\delta }_{2}}{{\sigma }_{2}}+{{\delta }_{3}}\sigma )+u\alpha {{\delta }_{2}}\gamma -\delta \sigma \gamma \\&=\delta \sigma \gamma ({{\Re }_{0}}-1)>0. \end{aligned}\right. \end{aligned}$$
(10)

There are two cases about \({{\lambda }_{5}},{{\lambda }_{6}}\) and \({{\lambda }_{7}}\) implied by Eq. (10):

  1. (a)

    They are all reals. In this case, there must be one positive and two negative;

  2. (b)

    One is real and the other two are conjugate complex. In this case, the real one must be positive.

In a word, Eq. (8) has a positive root if \({{\Re }_{0}}>1\), which implies that \({{{\mathbf {J}}}_{{{P}_{0}}}}\) has a positive eigenvalue. Thus, system (1) is unstable at \({{P}_{0}}\). \(\square \)

Theorem 3

The disease-free equilibrium \({{P}_{0}}\) of system (1) is globally asymptotically stable if \({{\Re }_{0}}< 1\).

Proof

Adopt the method in [32]. Let \({{\mathbf {y}}}=(S,R)\in {{\mathbb {R}}^{2}}\) (uninfected groups), \({{\mathbf {z}}}=(E,Q,A,I,J)\in {{\mathbb {R}}^{5}}\) (infected groups) and \({{\mathbf {y}}_{0}}=\left( \frac{M}{\upsilon },0 \right) \in {{\mathbb {R}}^{2}}\). Then, system (1) can be written as

$$\begin{aligned}&\frac{\text {d}{\mathbf {y}}}{\text {d}t}=G({\mathbf {y}},{\mathbf {z}}), \\&\frac{\text {d}{\mathbf {z}}}{\text {d}t}=H({\mathbf {y}},{\mathbf {z}}),\quad H({\mathbf {y}},{\mathbf {0}})={\mathbf {0}}. \end{aligned}$$
  1. (a)

    The solution to the differential equation \(\frac{\text {d}{\mathbf {y}}}{\text {d}t}=G({\mathbf {y}},{\mathbf {0}})=\left( \begin{matrix} M-\upsilon S \\ -\upsilon R \\ \end{matrix} \right) \) is

    $$\begin{aligned} \left\{ \begin{aligned}&S={{k}_{1}}{{e}^{-\upsilon t}}+\frac{M}{\upsilon } \\&R={{k}_{2}}{{e}^{-\upsilon t}} \\ \end{aligned} \right. , \quad {{k}_{1}},{{k}_{2}}\in \mathbb {R}. \end{aligned}$$

    Taking \(t\rightarrow +\infty \), we have \({\mathbf {y}}=(S,R)\rightarrow (\frac{M}{\upsilon },0)={{\mathbf {y}}_{0}}\), which shows that \({{\mathbf {y}}_{0}}\) is globally asymptotically stable for \(\frac{\text {d}{\mathbf {y}}}{\text {d}t}=G({\mathbf {y}},{\mathbf {0}})\).

  2. (b)

    \(H({\mathbf {y}},{\mathbf {z}})\) can be written as \(H({\mathbf {y}},{\mathbf {z}})={\mathbf {C}}{\mathbf {z}}^T-\tilde{H}({\mathbf {y}},{\mathbf {z}})\), where

    $$\begin{aligned} \left. {\mathbf {C}}=\frac{\partial H }{\partial {\mathbf {z}}}\right| _{({\mathbf {y}}_0,{\mathbf {0}})}=\left( \begin{matrix} -\delta &{} 0 &{} u\alpha &{} u\beta &{} 0 \\ {{\delta }_{1}} &{} -\eta &{} 0 &{} 0 &{} 0 \\ {{\delta }_{2}} &{} 0 &{} -\sigma &{} 0 &{} 0 \\ {{\delta }_{3}} &{} 0 &{} {{\sigma }_{2}} &{} -\gamma &{} 0 \\ 0 &{} {{\eta }_{1}} &{} {{\sigma }_{1}} &{} {{\gamma }_{1}} &{} -m \\ \end{matrix} \right) , \end{aligned}$$

    which is an M-matrix (non-diagonal element nonnegative), and

    $$\begin{aligned} \tilde{H}({\mathbf {y}},{\mathbf {z}})=\left( \begin{matrix} u\alpha A\left( 1-\frac{S}{N-Q-J} \right) +u\beta I\left( 1-\frac{S}{N-Q-J} \right) \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{matrix} \right) \ge 0, \quad \forall ({\mathbf {y}},{\mathbf {z}})\in \varOmega . \end{aligned}$$

    By Remark 2, \(\varOmega \) is an invariant set of system (1). By the theorem in [32], the disease-free equilibrium \({{P}_{0}}\) of system (1) is globally asymptotically stable if \({{\Re }_{0}}< 1\). \(\square \)

Theorem 4

The endemic equilibrium \({{P}_{e}}\) of system (1) is locally asymptotically stable if \({{\Re }_{0}}>1\).

Proof

The Jacobian matric of system (1) at \({{P}_{0}}\) is (7). Choose u as a bifurcation parameter. According to \({{\Re }_{0}}=1\), it is easy to obtain

$$\begin{aligned} {{u}^{*}}=\frac{\delta \sigma \gamma }{\gamma \alpha {{\delta }_{2}}+\beta \sigma {{\delta }_{3}}+\beta {{\sigma }_{2}}{{\delta }_{2}}}. \end{aligned}$$

Then, 0 is a simple eigenvalue of \({{{\mathbf {J}}}_{{{P}_{0}}}}\) at \(u={{u}^{*}}\), and other eigenvalues have negative real parts. In fact, by \({{\Re }_{0}}=1\) when \(u={{u}^{*}}\), Eq. (9) becomes

Therefore, the Jacobian matric \({{{\mathbf {J}}}_{{{P}_{0}}}}\) at \(u={{u}^{*}}\) has a zero eigenvalue, without loss of generality, let \(\lambda _7=0\). Moreover, we have

$$\begin{aligned}&{{\lambda }_{5}}+{{\lambda }_{6}}=-(\delta +\sigma +\gamma )<0, \\&\quad \begin{aligned} {{\lambda }_{5}}{{\lambda }_{6}}&\quad =\delta \sigma +\sigma \gamma +\gamma \delta -{{u}^{*}}(\beta {{\delta }_{3}}+\alpha {{\delta }_{2}}) \\&\quad =\delta \sigma +\sigma \gamma +\gamma \delta \\&\qquad -\frac{\delta \sigma \gamma }{\gamma \alpha {{\delta }_{2}}+\beta \sigma {{\delta }_{3}}+\beta {{\sigma }_{2}}{{\delta }_{2}}}(\beta {{\delta }_{3}}+\alpha {{\delta }_{2}}) \\&\quad =\frac{\beta {{\sigma }_{2}}{{\delta }_{2}}(\delta \sigma +\sigma \gamma +\gamma \delta )+\gamma \alpha {{\delta }_{2}}(\sigma \gamma +\gamma \delta )+\beta \sigma {{\delta }_{3}}(\delta \sigma +\sigma \gamma )}{\gamma \alpha {{\delta }_{2}}+\beta \sigma {{\delta }_{3}}+\beta {{\sigma }_{2}}{{\delta }_{2}}}>0, \end{aligned} \end{aligned}$$

which implies that the real parts of \(\lambda _5\) and \(\lambda _6\) are both negative. Thus, 0 is a simple eigenvalue of \({{{\mathbf {J}}}_{{{P}_{0}}}}\) at \(u={{u}^{*}}\), and other eigenvalues have negative real parts.

A right eigenvector corresponding to the eigenvalue 0 of \({{{\mathbf {J}}}_{{{P}_{0}}}}\) at \(u={{u}^{*}}\) is not hard to obtain, denoted by \({\mathbf {p}}={{\left( {{p}_{1}},{{p}_{2}},{{p}_{3}},{{p}_{4}},{{p}_{5}},{{p}_{6}},{{p}_{7}} \right) }^{T}}\), where

$$\begin{aligned}&{{p}_{1}}=-\frac{\delta }{\upsilon }{{p}_{2}},\quad {{p}_{2}}>0,\quad {{p}_{3}}=\frac{{{\delta }_{1}}}{\eta }{{p}_{2}},\quad {{p}_{4}}=\frac{{{\delta }_{2}}}{\sigma }{{p}_{2}}, \\&{{p}_{5}}=\frac{\sigma {{\delta }_{3}}+{{\sigma }_{2}}{{\delta }_{2}}}{\sigma \gamma }{{p}_{2}},\quad \\&{{p}_{6}}=\left[ \frac{{{\eta }_{1}}\sigma {{\delta }_{1}}+{\eta }{{\sigma }_{1}}{{\delta }_{2}}}{\sigma \eta m}+\frac{{{\gamma }_{1}}(\sigma {{\delta }_{3}}+{{\sigma }_{2}}{{\delta }_{2}})}{\sigma \gamma m} \right] {{p}_{2}}, \\&{{p}_{7}}=\left[ \frac{{{\sigma }_{3}}{{\delta }_{2}}}{\sigma }+\frac{{{\eta }_{2}}{{\delta }_{1}}}{\eta }\right. \\&\qquad \quad +\frac{{{\gamma }_{2}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{\sigma \gamma } \\&\qquad \quad \left. + \frac{\theta {{\gamma }_{1}}({{\delta }_{3}}\sigma +{{\delta }_{2}}{{\sigma }_{2}})}{m\sigma \gamma }+\frac{\theta ({{\eta }_{1}}{{\delta }_{1}}\sigma +\eta {{\delta }_{2}}{{\sigma }_{1}})}{m\sigma \eta } \right] \frac{{{p}_{2}}}{\upsilon }. \end{aligned}$$

Similarly, a left eigenvector corresponding to the eigenvalue 0 of \({{{\mathbf {J}}}_{{{P}_{0}}}}\) at \(u={{u}^{*}}\) is denoted by \({{{\mathbf {q}}}^{T}}=\left( {{q}_{1}},{{q}_{2}},{{q}_{3}},{{q}_{4}},{{q}_{5}},{{q}_{6}},{{q}_{7}} \right) \), where

$$\begin{aligned}&{{q}_{1}}=0,\quad {{q}_{2}}>0,\quad {{q}_{3}}=0,\quad {{q}_{4}}=\frac{{{u}^{*}}(\alpha \gamma +\beta {{\sigma }_{2}})}{\gamma \sigma }{{q}_{2}}, \\&{{q}_{5}}=\frac{{{u}^{*}}\beta }{\gamma }{{q}_{2}},\quad {{q}_{6}}=0,\quad {{q}_{7}}=0. \end{aligned}$$

Let \(S={{y}_{1}},E={{y}_{2}},Q={{y}_{3}},A={{y}_{4}},I={{y}_{5}},J={{y}_{6}},R={{y}_{7}}\), we have

$$\begin{aligned} \begin{aligned} a&={\left. {\sum \limits _{i,j,k=1}^{7}{{{q}_{k}}{{p}_{i}}{{p}_{j}}\frac{{{\partial }^{2}}{{f}_{k}}}{\partial {{y}_{i}}\partial {{y}_{j}}} }}\right| _{{\mathbf {y}}={{P}_{0}},u={{u}^{*}}}}\\&=-\frac{2{{u}^{*}}\upsilon {{q}_{2}}}{M}(\alpha {{p}_{4}}+\beta {{p}_{5}})({{p}_{2}}+{{p}_{4}}+{{p}_{5}}+{{p}_{7}})<0,\\ b&={\left. {\sum \limits _{i,k=1}^{7}{{{q}_{k}}{{p}_{i}}\frac{{{\partial }^{2}}{{f}_{k}}}{\partial {{y}_{i}}\partial u} }}\right| _{{\mathbf {y}}={{P}_{0}},u={{u}^{*}}}}\text {=}{{q}_{2}}(\alpha {{p}_{4}}+\beta {{p}_{5}})>0. \end{aligned} \end{aligned}$$

According to Theorem 4.1 in [33], the endemic equilibrium \({{P}_{e}}\) of system (1) is locally asymptotically stable if \({{\Re }_{0}}>1\). \(\square \)

According to Theorems 2 and 4, a forward bifurcation (transcritical bifurcation) occurs at \(\Re _0=1\) in system (1). Let \(E^*\) be the value of E(t) when system (1) is in equilibrium. Then,

$$\begin{aligned} {{E}^{*}}=\left\{ \begin{aligned} 0, \quad&{{\Re }_{0}}\le 1 \\ {{E}_{e}}, \quad&{{\Re }_{0}}>1 \\ \end{aligned} \right. . \end{aligned}$$

Taking \(E^*\) as an example, the bifurcation diagram is shown in Fig. 2. The disease-free equilibrium of system (1) is stable if \({{\Re }_{0}}< 1\), but unstable if \({{\Re }_{0}}>1\). However, the endemic equilibrium is locally asymptotically stable if \({{\Re }_{0}}>1\).

Fig. 2
figure 2

Forward bifurcation (\(M=1500, \theta = 0.1, \mu =0.01\) and the values of remaining parameters are shown as in Table 3)

Full size image

Theorems 2 and 3 show that the number of people infected by COVID-19 I(t) will eventually become zero when \({{\Re }_{0}}<1\), i.e., the epidemic will be brought under control and COVID-19 will disappear. Theorem 4 shows that I(t) will stabilize around a positive constant when \({{\Re }_{0}}>1\), forming an endemic disease, i.e., COVID-19 will not disappear, but coexist with humans, and may break out again at any time. People certainly hope that COVID-19 disappear as soon as possible, which means that the basic regenerative number \({{\Re }_{0}}\) should be controlled below 1. In the absence of specific drugs and vaccines, its spread can only be slowed by non-pharmacological interventions.

From expression (4) of \({{\Re }_{0}}\), the following measures can be taken to reduce the spread of COVID-19:

  1. (a)

    Strengthen the quarantine for close contacts (exposed persons), so that the number of infected persons (groups A and I) mixed in the susceptible population will be reduced, i.e., increase \({{\delta }_{1}}\), and then \({{\delta }_{2}}\) and \({{\delta }_{3}}\) will decrease.

  2. (b)

    Increase the isolation rate of infected individuals (groups A and I), i.e., increase \({{\sigma }_{1}}\) and \({{\gamma }_{1}}\).

  3. (c)

    Implement the control measures mentioned previously for susceptible individuals: that means reducing u.

Among the above measures, (a) and (c) are very effective and can significantly reduce \({{\Re }_{0}}\), which is consistent with the actual situation, especially (c).

Fig. 3
figure 3

The spread dynamics of COVID-19 when \(\Re _0=0.2271<1\). (\(S(0) = 50000, E(0) = 700, Q(0) = 800, A(0) = 200, I(0) = 80, J(0) = 500, R(0) = 200, M=800, \theta = 0.1, \mu =0.01, u=0.3, \beta = 3.8, \alpha =0.45\beta , \delta _1=0.8, \delta _2=0.04, \delta _3 = 0.01, \sigma _1 = 0.2, \sigma _2 = 0.1, \sigma _3 = 0.15, \gamma _1 = 0.1, \gamma _2 = 0.046, \eta _1 = 0.5, \eta _2 = 0.15\).)

Full size image

5 Model calibration and simulation

In this section, the stability of the equilibria (including the disease-free equilibrium and endemic equilibrium) are verified by simulations. The parameters of model (1) are estimated by using the real data of Hubei Province in China and then simulate the spread of COVID-19 in Hubei and Hunan Provinces.

Fig. 4
figure 4

The spread dynamics of COVID-19 when \(\Re _0=3.01145>1\). (\(u=1, \delta _1=0.2, \sigma _1 = 0.1\), values of the initial states and other parameters are the same as Fig. 3.)

Full size image
Fig. 5
figure 5

Fitting of \(\theta (t)\) and \(\mu (t)\)

Full size image

5.1 Stability of equilibria

Taking one day as the simulation step length, and choosing different parameter values, we simulate the spread dynamics of COVID-19 in two cases of \(\Re _0<1\) and \(\Re _0>1\). The spread dynamics of COVID-19 in 100 days when \(\Re _0=0.2271<1\) is shown in Fig. 3. It can be seen from Fig. 3a that the undiagnosed infected individuals (the infectious source of COVID-19, including asymptomatic and symptomatic) are completely cleared on about the 50th day, which means that after about 50 days later, the spread of COVID-19 is completely controlled. Figure 3b shows that the number of confirmed cases J(t) is reduced to 0 on about the 70th day. At this time, COVID-19 is completely eliminated. Figure 3 verifies that the disease-free equilibrium is asymptotically stable when \(\Re _0<1\).

The spread dynamics of COVID-19 in 10000 days when \(\Re _0=3.01145>1\) is shown in Fig. 4. As shown in Fig. 4a, there are still active undiagnosed infected individuals (\(A(t)>0\) and \(I(t)>0\)) even after 10,000 days when \(\Re _0=3.01145\), which means COVID-19 is not completely controlled and continues to spread among the population. The number of confirmed cases J(t) is also maintained at around 4000 (Fig. 4b). From Fig. 4, it can be seen that the number of people in each group tends to be stable over time, which verifies Theorem 4. When \(\Re _0>1\), the endemic equilibrium is locally asymptotically stable, and COVID-19 will coexist with humans. According to (6), we obtain \(A_e = 250, I_e = 321, E_e = 2185, Q_e = 672, J_e = 3573\). By Theorem 4, A(t), I(t), E(t), Q(t) and J(t) will converge to 250, 321, 2185, 672 and 3573, respectively.

5.2 Estimation of model parameters and spread dynamics of COVID-19 in Hubei

In this subsection, model (1) is used to simulate the spread of COVID-19 in Hubei Province, China. Firstly, the parameters of the model are estimated applying the relevantly real data of Hubei. In the early stage, a large number of people were infected, leading to a severe shortage of medical resources, including hospital beds, medical staff and medical protective supplies. As a result, many patients could not be hospitalized in time. Patients with mild symptoms are required to be self-isolated at home, which leads to increased infections among family members and cannot block the spread of COVID-19. Since early February 2020, with the strong intervention of the Chinese government, a large number of existing medical institutions were rapidly converted to isolation wards and two large temporary hospitals were built to treat severe cases; a large number of medical workers and supplies were mobilized from other provinces in China to aid Hubei province; large public places, such as exhibition centers, were transformed into simple temporary hospitals, known as “shelter hospitals,” to collectively isolate and treat patients with mild symptoms; some hotels and schools were set as places for quarantined observation of close contacts, etc. The purpose of these measures is to gather infected people as many as possible for isolation, treatment or medical observation to completely cut off the source of infection of COVID-19. Model (1) is based on these strong epidemic prevention measures. Given that there were many suspected patients in the early stage and the daily nucleic acid testing ability was limited, many cases could not be diagnosed in time; so the early data could not accurately reflect the spread of COVID-19. Therefore, we choose 21 days of data from February 14 to March 5, 2020, to calibrate the model; that is, to estimate the parameters in the model. The real data come from the official Web site of the Chinese Health Commission [34] and Hubei Health Commission [35]. With the increased number of medical staff and medical supplies and the accumulation of diagnostic and treatment experience, the case fatality rate gradually decreases and the cure rate continuously increases. Therefore, assume that \(\theta =\theta (t)\) and \(\mu =\mu (t)\) are both functions of time, which is more consistent with the reality. The real-time data about COVID-19 reported by the health department mainly include: the number of confirmed cases (hospitalizations), the number of deaths due to COVID-19, the number of cured and discharged patients, etc. \(\theta =\theta (t)\) and \(\mu =\mu (t)\) are fit with a first-order function and an exponential function, respectively, to the actual report data, as shown in Fig. 5 and the fitting results as follows:

$$\begin{aligned} \theta (t)= & {} 0.00388t + 0.01157,\quad \\ \mu (t)= & {} \mu (t)=0.00279{{e}^{-0.04828t}}. \end{aligned}$$
Fig. 6
figure 6

Currently confirmed cases

Full size image
Table 3 Values of parameters
Full size table
Table 4 Initial values of states
Full size table

Almost all confirmed cases are symptomatic patients, and once diagnosed, they will be hospitalized for isolation and treatment. As a result, the number of confirmed cases is the number of inpatients, including all patients in hospitals and shelter hospitals. We used the reported data of currently confirmed cases (the number of cases currently being isolated and treated in hospitals) and the solution J(t) of model (1) to do the least square fitting [7] to estimate values of the parameters. Because of the strong anti-epidemic measures implemented by the government and the active cooperation of the public, we assume that \(u=0.3\). At this time, since population mobility is almost nonexistent and the number of births within 21 days is limited, it can be considered that \(M=0\). The population of Hubei Province is about 58 million. Due to the epidemic prevention and control measures, the vast majority of people could not go out or make contact with the outside world. Therefore, assume that the initial value of actually susceptible people is \(S(0)=500,000\). Take February 14 as the time of \(t = 0\); the fitting simulation is shown in Fig. 6, where the points represent the actually reported data, and the curve represents the model solution J(t). The estimated values of model parameters are shown in Table 3, and the initial values of states are shown in Table 4. The mean relative error can be used to evaluate the fitting effect, and it is defined as follows:

where X(i) is the true value, \({\hat{X}}(i)\) is the fitted value and n is the number of data. It can be calculated that the mean relative error of the currently confirmed cases fitting is \({{E}_{MRE}}=0.8942\%\).

Fig. 7
figure 7

Simulation and verification in Hubei. The points are the real reported data, and the curves are the solutions of differential Eq. (11) associated with system (1)

Full size image
Fig. 8
figure 8

Fitting of \(\theta (t)\) and J(t) in Hunan

Full size image
Table 5 Mean relative error
Full size table
Table 6 Initial values of states
Full size table

We validate the model using the actually reported data on cumulative number of confirmed cases, cured cases and deaths. According to model (1), the cumulative number of confirmed cases (hospitalized cases) \(J_c(t)\), cured cases Z(t) and dead cases D(t) on day t is as follows:

$$\begin{aligned} J_c(t)= & {} \int _{0}^{t}{\left[ {{\gamma }_{1}}I(t) +{{\sigma }_{1}}A(t) +{{\eta }_{1}}Q(t) \right] \text {d}t}\\&+J_c(0),\quad Z(t)=\int _{0}^{t}{\theta (t)J(t)\text {d}t}+Z(0) \end{aligned}$$

and

$$\begin{aligned} D(t)=\int _{0}^{t}{\mu (t)J(t)\text {d}t}+D(0), \end{aligned}$$

respectively. Initial values J(0), Z(0) and D(0) are the cumulative number of confirmed cases, cured cases and dead cases actually reported on February 14, respectively, as shown in Table 2. Then, the differential equations associated with system (1) are obtained as follows:

$$\begin{aligned} \begin{aligned}&\frac{\text {d}J_c}{\text {d}t}={{\gamma }_{1}}I(t) +{{\sigma }_{1}}A(t) +{{\eta }_{1}}Q(t),\\&\frac{\text {d}Z}{\text {d}t}=\theta (t)J(t),\\&\frac{\text {d}D}{\text {d}t}=\mu (t)J(t). \end{aligned} \end{aligned}$$
(11)

The simulation results and the mean relative errors are shown in Fig. 7 and Table 5, respectively. It can be seen that model (1) is basically consistent with the actual data and can reflect the spread dynamics of COVID-19 under the strong intervention of the government. According to the values of parameters in Table 3, \({{\Re }_{0}}=0.24512\) is given, which is already much less than 1 and indicates that the spread of COVID-19 has been almost controlled.

Fig. 9
figure 9

Simulation and verification in Hunan

Full size image

5.3 Spread dynamics of COVID-19 in Hunan

The prevention and control measures are the same in all parts of China, so the spread dynamics of COVID-19 in China almost have no difference. Therefore, model (1) is suitable for Hubei Province and other parts of China. In this subsection, the model is used to simulate the spread of COVID-19 in Hunan Province of China and compare it with the real data [34, 36]. The early cases in Hunan Province all had travel history in Hubei. Under strict prevention and control measures, it was easy to control the spread of COVID-19 in Hunan, so finally the confirmed cases were only more than one thousand. We choose 21 days from January 29 to February 18, 2020, to simulate. Adopting the estimated values in Table 3, there are only initial values of several states of model (1) in Hunan which need to be estimated. Let \(S(0) = 500000\) since the population of Hunan and Hubei provinces are similar, and \(M = 0\). In these 21 days, the cumulative deaths due to infection by COVID-19 were only 4, which was a small proportion and can be ignored, that is, \(\mu =0\). Firstly, the cure rate per day \(\theta (t)\) within the 20 days was fitted by a line, see Fig. 8a. The fitting result is

$$\begin{aligned} \theta (t)=0.0042t+0.00065. \end{aligned}$$

Similarly, the initial values of the states are estimated by using the actual data of confirmed cases. The results are shown in Table 6 and Fig. 8b. According to the estimated values of the initial states, the simulation of cumulative confirmed case \(J_c(t)\) and cumulative cured case Z(t) is shown in Fig. 9a and b, respectively. The mean relative errors of fitting and simulations are shown in Table 7. It can be seen that the simulation results of the model are basically consistent with the actual data, which indicate that model (1) can truly reflect the spread dynamics of COVID-19 under the strict prevention and control measures.

Fig. 10
figure 10

The curves of \(\Re _0\) with respect to various isolation rates. (The values of related parameters are shown in Table 3.)

Full size image
Fig. 11
figure 11

The spread dynamic of COVID-19 about different u

Full size image
Fig. 12
figure 12

The spread dynamic of COVID-19 about different \(\delta _1\)

Full size image

5.4 Comparison with related work

The real data with respect to COVID-19 in a certain area generally includes the number of daily new confirmed cases, daily cured cases and daily died cases, the number of cumulatively confirmed cases, cumulatively cured cases and cumulatively deaths, and the number of currently confirmed cases, etc. However, most of the studies use only one or two of them in parameter fitting and model verification. For example, the real data in [19, 21, 22] and [20] is only the number of cumulatively confirmed cases and currently confirmed cases, respectively. In [10], the number of cumulatively confirmed cases and that of cumulative deaths are used, while the number of daily new confirmed cases and that of cumulatively confirmed cases are adopted in [29]. It is not difficult to see that almost all the real data about COVID-19 in Hubei and Hunan are used in subsections 5.2 and 5.3. The number of daily newly cured cases, daily died cases and currently confirmed cases are employed to fit the parameters. The remaining real data are used to verify model (1). Using multiple sets of actual data to fit the parameters can improve the accuracy of the fitting. The comparison between the model simulation results and multiple sets of actual data can better reflect the rationality of the model.

6 Sensitivity analysis of \({{\Re }_{0}}\)

Taking the model in [29] as an example, the real data of COVID-19 in Hubei are used to perform parameter fitting and simulation verification. Similarly, the parameters are fitted by the number of currently confirmed cases. Then, the model is employed to simulate the number of cumulatively confirmed cases, cumulatively cured cases and cumulatively died cases. Compared with the real data, the mean relative errors of fitting and simulations are shown in the third row of Table 5. Obviously, model (1) is more consistent with real data and can better reflect the actual spread dynamics of COVID-19.

According to Sect. 5.1, the basic reproductive number \(\Re _0\) plays an important role for analyzing the dynamics of system (1) and COVID-19. COVID-19 remains in the population, and the number of infected individuals stabilizes around a positive constant if \(\Re _0>1\). In this case, the disease will become endemic in the population. The number of infected individuals gradually declines to zero, and COVID-19 disappears from the population if \(\Re _0<1\). In order to reduce the spread of COVID-19, which measures are most effective needs to be considered, in other words, which parameters have the greatest impact on the basic regenerative number \({{\Re }_{0}}\) should be analyzed. This is the sensitivity of parameter, which refers to the relative change of relevant variables caused by the change of some parameters. Suppose that function f is differentiable to parameter x, then the sensitivity index of f for x is defined as [37]

$$\begin{aligned} \varUpsilon _{f}^{x}=\frac{\partial f}{\partial x}\frac{x}{f}. \end{aligned}$$

Sensitivity index \(\varUpsilon _{f}^{x}\) reflects the robustness of function f to variable x. Specifically, with values of other variables (or parameters) remaining unchanged, if \(\varUpsilon _{f}^{x}>0\), f increases (or decreases) by \(\varUpsilon _{f}^{x}\%\) when x increases (or decreases) by \(1\%\) ; if \(\varUpsilon _{f}^{x}<0\), f decreases (or increases) by \(-\varUpsilon _{f}^{x}\%\) when x increases (or decreases) by \(1\%\). Sensitivity indices of basic regenerative number \({{\Re }_{0}}\) to each parameter are shown in Table 3. For example, the sensitivity index of \({{\Re }_{0}}\) to \(\beta \) is 0.77220 (\(\varUpsilon _{{\Re }_{0}}^{\beta }=0.77220\)), which means that if \(\beta \) increases by \(10\%\) and other parameters remain unchanged, then \({{\Re }_{0}}\) will increase by \(7.7220\%\). Similarly, since \(\varUpsilon _{{\Re }_{0}}^{\delta _1}= -0.93088\), increasing \(\delta _1\) by \(10\%\) decreases \({{\Re }_{0}}\) by \(9.3088\%\). It can be seen from Table 3 that the parameters with large sensitivity index are \(u,\delta _1,\beta ,\delta _2,\gamma _1\) and \(\delta _3\) in turn, which tells us that the effective measures to reduce \({{\Re }_{0}}\) include strengthening interventions to reduce population exposure (decreasing u), strengthening trace and quarantine of close contacts (increasing quarantine rate \(\delta _1\)), strengthening safeguard measures to hospitalize as many symptomatic patients as possible (increasing \(\gamma _1\)), and so on. These results are consistent with the analysis at the end of Section 4. Let \(\Re _0\) be a function of \(\delta _1, \sigma _1\) and \(\gamma _1\), respectively. For different values of u, the curves of \(\Re _0\) about \(\delta _1, \sigma _1\) and \(\gamma _1\) are shown in Fig. 10. As shown in Fig. 10a, \(\Re _0\) is a decreasing and concave-up function of \(\delta _1\) for different u. When u is smaller and \(\delta _1\) is larger, \(\Re _0\) is smaller. Figure 10b and c shows similar results.

Some parameters can be adjusted for simulation and comparison to intuitively reflect the impacts of corresponding prevention and control measures on the spread of COVID-19. Take Hunan Province, China, as an example. According to sensitivity analysis, u has the greatest impact on the basic reproductive number \({{\Re }_{0}}\), followed by \(\delta _1\). We focus on the impact of different u on the spread of COVID-19 firstly. Keeping other parameters unchanged, let \(u=0.2,0.3\) and 0.4, respectively. The simulations are shown in Fig. 11. The corresponding basic reproductive numbers are 0.16341, 0.24512 and 0.32682, respectively. It can be seen that the smaller the u, the smaller the basic reproductive number \(\Re _0\), and the fewer confirmed cases. It shows that taking prevention and control measures for susceptible people is indeed an effective way to control the spread of COVID-19. Similarly, keeping the other parameters unchanged (where \(u=0.3\)), let \(\delta _1 = 0.5, 0.71533\) and 0.9, respectively. The spread dynamic of COVID-19 is shown in Fig. 12, and the corresponding basic reproductive numbers are 0.34054, 0.24512 and 0.19763, respectively. The larger the quarantine rate (\(\delta _1\)), the correspondingly fewer the infected individuals (sources of infection) who have not been quarantined, and the smaller the basic reproductive number \(\Re _0\). As shown in Fig. 12, the larger the \(\delta _1\), the more the confirmed cases (the fewer the source of infection) in the early stage, which leads to fewer infected individuals in the later stage. Therefore, the quarantine rate of infected individuals (\(\delta _1\)) also plays an important role in controlling the spread of COVID-19.

7 Conclusion

One year has passed since COVID-19 firstly appeared. However, COVID-19 is still in the stage of global pandemic. In particular, several variants of COVID-19 were discovered in some countries recently, which have been confirmed more infectious, and pose even greater challenges to epidemic prevention and control. Although vaccination against COVID-19 has been carried out in some countries, its output cannot satisfy current needs and the conditions for mass vaccination are not yet in place. Strict epidemic prevention measures of non-pharmacotherapy intervention are still needed to prevent further spread of the epidemic. Based on this background, this paper establishes a mathematical model to simulate the spread of COVID-19 under some strict epidemic prevention measures. The existence and stability of equilibria are analyzed. The parameters of the proposed model are estimated using the real data in Hubei. As validations, this model is used to simulate the spread of COVID-19 in Hubei and Hunan provinces of China for a period of time. Experimental results show that the model can well simulate the spread dynamic of COVID-19 under certain strict prevention and control measures. Reducing the contact rate of the population and increasing the quarantine rate of infected individuals are the most effective non-pharmaceutical intervention measures for controlling COVID-19 by the sensitivity analysis of the parameters. Through the modeling and analyses of this paper, we hope to provide some useful insights for formulating epidemic prevention measures to contain the spread of COVID-19 [38, 39]. In order to establish more precise and accurate model to simulate and predict the spread dynamic of COVID-19, we will fully consider the influence of different types of co-infected people and collect relevant actual data in future research. The proposed method can be applied to rumor propagation in social networks [40].