1 Introduction

The pandemic coronavirus disease (COVID-19) is caused by a newly discovered coronavirus called SARS-CoV-2, which can spread from an infected person’s mouth or nose in small liquid particles when they cough, sneeze, speak, sing or breathe [1]. Such easy transmission routes coupled with frequent human mobility quickly result in explosive outbreak around the world. As of September 22, 2021, this disease has attacked about 214 countries, with a total of over 230 million confirmed cases and over 4.7 million deaths [1]. COVID-19 is disrupting global health, economic, political, and social systems and is posing comprehensive threats to people around the world.

The ongoing COVID-19 pandemic exhibits a clear time-space evolution. As the first case was reported in Wuhan, China, on December 29, 2019, the disease has spread to all the provinces in China within a month [2]. By February 21, 2020, it has occurred in 27 countries, and the number of infected countries quickly increases to over 170 in late March. The infection size rose sharply from 282 to over 5 million during the 5-month period. Such fast diffusion and hierarchical structures in time and place were possibly shaped by human behaviors (e.g., communication, work, and movement). For example, after initial emergence in China, travel-related cases started appearing in other parts of the world with strong travel links to Wuhan [3]. This pattern along with the special characteristics of COVID-19: (1) high pathogenicity and hidden transmission among humans [4], (2) large asymptomatic patients with infectivity [5], (3) short serial interval [6], and (4) massive susceptibility [7], makes it very difficult to assess the risk and control the infection. Surveillance data indicate that the erupting infection of COVID-19 in China was quickly restrained due to the strict all-around interventions. Simulating its further potential progress in different circumstances and recognizing the spatiotemporal transmission dynamics can help to clarify the roles of the involved factors (e.g., human behavior, virus evolution, and intervention), identify the high-risk region, and guide the designing of targeted interventions in resource-limited settings. Yet little work is found in this regard.

Technically speaking, pure statistical model and mapping analysis can quantitatively tell the transmission pattern of epidemics. Mathematical frameworks incorporated epidemiological survey data can further capture its intrinsic variability in time and space, which are used increasingly in interdisciplinary studies [8]. Focusing on the COVID-19 pandemic, many epidemiology-inspired models, including SIR, SIS, and SEIR models, had been built to study the spreading patterns [9,10,11,12,13,14]. By simulating the underlying infection process, these studies found that (1) real-time mobility data from Wuhan can well elucidate the incidence rates in the cities across China [15]; (2) various non-pharmaceutical interventions are effective in controlling the spread of the disease [13, 16,17,18,19]; and (3) mobility networks of air travel can predict the global diffusion pattern at the early stages of the outbreak, and an unconstrained mobility would have significantly accelerated COVID-19 spread [20]. Due to the complexity and heterogeneity of COVID-19 diffusion, more efforts are needed to reveal its spatiotemporal dynamics [14, 21].

This paper goes a further step to provide a new modeling framework with consideration of human mobility and surveillance data to clarify the hidden dynamics accounting for COVID-19 spatiotemporal transmission in China. Based on the deterministic compartment model, a multi-population transmission model of COVID-19 is established by ordinary differential equations (ODE). Qualitative theory is used to analyze the propagation dynamics of the model, including the expression of the basic reproduction number and the equilibria, the global stability of the disease-free and endemic equilibria. Finally, this model is applied to investigate the detailed transmission patterns of COVID-19 across the provinces in China.

2 Modeling framework

To simulate the spatiotemporal transmission of COVID-19 across different regions, a new meta-population dynamic model is proposed in this section. Based on the epidemiology features of COVID-19 and compartmental theory, the following basic assumptions are proposed.

  • During the outbreak of COVID-19 infection, humans are divided into susceptible (\(S_{i}\)), exposed (\(E_{i}\)), preclinical infectious (\(I_{i}^{p}\)), subclinical infectious (\(I_{i}^{s}\)), clinical infectious (\(I_{i}^{c}\)) and recovered (\(R_{i}\)) classes. Here \(I_{i}^{p}\) and \(I_{i}^{s}\) are inapparent infections, and \(I_{i}^{c}\) are apparent infections. The sum of these classes constitute the total population size, that is, \(N_{i}=S_{i}+E_{i}+I_{i}^{p}+I_{i}^{s}+I_{i}^{c}+R_{i}\). It is assumed that \(N_{i}\) is a constant, in which birth rate equals to death rate d. Here, the subscript i denotes the location of these parameters.

  • The infection routes follow susceptible-latent-infected-recovered process. Individuals can be infected through contact with infectious individuals and then experience an incubation period \(1/\eta \). Exposed individuals progress to preclinical infectious (with probability \(\phi \)) and subclinical infectious (with probability \(1-\phi \)). Subclinical infections with mild or no symptoms could not be easily found and treated, but they can self-recover after time \(1/\gamma \). Preclinical infections become clinical and develop symptoms after time \(1/\delta \). They receive treatment and are cured successfully through time \(1/\omega \).

  • When novel coronavirus carried by infected humans invades into a virgin area, people there (local residents and visitors from other regions) could be infected with certain probability. The model takes into account such spatial diffusion by incorporating a migration matrix P, in which element \(P_{ij}\) denotes the average duration per unit time that the residents in region i stay in region j. It satisfies \(P_{ij} \ge 0\) and \(\sum _{j}P_{ij} = 1\). Here residents can move around any other region, which may be infected outside and bring virus home. Specifically, due to human mobility, the real number of human population in region j is \({{\tilde{N}}}_j = \sum _{k}P_{kj}N_{k}\), and the average proportions of preclinical, subclinical, clinical infections stay in region j are \(\sum _{k}P_{kj}{I_{k}^{p}}/{{\tilde{N}}}_j\), \(\sum _{k}P_{kj}I_{k}^{s}/{{\tilde{N}}}_j\), and \(\sum _{k}P_{kj}{I_{k}^{c}}/{{\tilde{N}}}_j\), respectively. Parts of susceptible residents of region i (i.e., \(P_{ij}S_{i})\) could be infected in region j at rate \(\lambda _{j}\).

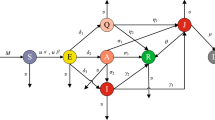
Based on the above assumption, the essential features of the model framework are depicted in Fig. 1. Accordingly, the governing equations for simulating the spatiotemporal transmission dynamics of COVID-19 are illustrated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}S_{i}}{\mathrm{d}t}= \mathrm{d}N_{i}-\sum _{j=1}^{n}\lambda _{j}P_{ij}S_{i}\\ \displaystyle \qquad \qquad \times \frac{\sum _{k=1}^{n}P_{kj}\left( I_{k}^{p}+\alpha I_{k}^{s}+\beta I_{k}^{c}\right) }{\sum _{k=1}^{n}P_{kj}N_{k}}-\mathrm{d}S_{i}, \\ \displaystyle \frac{\mathrm{d}E_{i}}{\mathrm{d}t}= \sum _{j=1}^{n}\lambda _{j}P_{ij}S_{i}\frac{\sum _{k=1}^{n}P_{kj}\left( I_{k}^{p}+\alpha I_{k}^{s}+\beta I_{k}^{c}\right) }{\sum _{k=1}^{n}P_{kj}N_{k}}\\ \displaystyle \qquad \qquad -(\eta +d)E_{i}, \\[12pt] \displaystyle \frac{\mathrm{d}I_{i}^{p} }{\mathrm{d}t}= \phi \eta E_{i}-(\delta +d)I_{i}^{p}, \\[12pt] \displaystyle \frac{\mathrm{d}I_{i}^{s} }{\mathrm{d}t}= (1-\phi ) \eta E_{i}-(\gamma +d)I_{i}^{s}, \\[12pt] \displaystyle \frac{\mathrm{d} I_{i}^{c}}{\mathrm{d}t}=\delta I_{i}^{p}-(\omega +d)I_{i}^{c}, \\[12pt] \displaystyle \frac{\mathrm{d}R_{i}}{\mathrm{d}t}= \gamma I_{i}^{s}+\omega I_{i}^{c}-\mathrm{d}R_{i}, \\[12pt] \end{array} \right. \end{aligned}$$
(1)

where \(\lambda _{j}\) is the specific transmission rate in region j. The interpretation of other model parameters is presented in Table 1.

Fig. 1
figure 1

Flow diagram on COVID-19 transmission with human mobility among different regions

Full size image
Table 1 Description of parameters in the proposed model
Full size table

Since model (1) is a high-dimensional nonlinear ODE system, it is impossible to obtain its analytical solution. To illustrate the long-term evolutions of model solutions and the robustness of these solutions to different initial conditions, the following two sections will explore the model behaviors mathematically, in which the basic reproduction number and the stability are discussed. By doing so, one can formulate the coupling pattern between disease transmission and human mobility and obtain the conditions under which the disease will die out or persist.

3 Basic reproduction number

The basic reproduction number \(R_{0}\), as one of the most important theoretical concepts in epidemiology, acts as the critical measure of the transmissibility [23]. \(R_{0}\) is interpreted as the average number of secondary cases that are produced by a single primary case in a fully susceptible population [23]. In what follows, it is written \({\mathbf{S}} = {\left( {{S_1},{S_2}, \ldots ,{S_n}} \right) ^T}\) and similarly for \({\mathbf{E}},{{\mathbf{I}}^{\mathbf{p}}},{{\mathbf{I}}^{\mathbf{s}}},{{\mathbf{I}}^{\mathbf{c}}},{\mathbf{R}}\) and \({\mathbf{N}}\). Let \(A_{p}\) be a \(n\times n\) matrix, defined as

$$\begin{aligned}{A_p} = \left( {\begin{array}{*{20}{c}} {{P_{11}}}&{} \cdots &{}{{P_{1n}}}\\ \vdots &{} \ddots &{} \vdots \\ {{P_{n1}}}&{} \cdots &{}{{P_{nn}}} \end{array}} \right) \left( \begin{array}{l} {\lambda _1}\frac{{P_1^T}}{{P_1^T{\mathbf{N}}}}\\ {\lambda _2}\frac{{P_2^T}}{{P_2^T{\mathbf{N}}}}\\ \quad \,\; \vdots \\ {\lambda _n}\frac{{P_n^T}}{{P_n^T{\mathbf{N}}}} \end{array} \right) , \end{aligned}$$

where the column vector \({P_i}\) is the i-th column of matrix \({\left( {{P_{ij}}} \right) _{n \times n}}\). Then, system (1) can then be rewritten as the following vectorial notation:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{{\mathrm{d}{\mathbf{S}}}}{{\mathrm{d}t}} = \mathrm{d}{\mathbf{N}} - {\mathrm{diag}}({\mathbf{S}})\left( {{A_p}{{\mathbf{I}}^{\mathbf{p}}} + \alpha {A_p}{{\mathbf{I}}^{\mathbf{s}}} + \beta {A_p}{{\mathbf{I}}^{\mathbf{c}}}} \right) \\ \displaystyle \qquad \qquad -\mathrm{d}{\mathbf{S}},\\[12pt] \displaystyle \frac{{\mathrm{d}{\mathbf{E}}}}{{\mathrm{d}t}} = {\mathrm{diag}}({\mathbf{S}})\left( {{A_p}{{\mathbf{I}}^{\mathbf{p}}} + \alpha {A_p}{{\mathbf{I}}^{\mathbf{s}}} + \beta {A_p}{{\mathbf{I}}^{\mathbf{c}}}} \right) \\ \displaystyle \qquad \qquad - \left( {\eta + d} \right) {\mathbf{E}},\\[12pt] \displaystyle \frac{{\mathrm{d}{{\mathbf{I}}^{\mathbf{p}}}}}{{\mathrm{d}t}} = \phi \eta {\mathbf{E}} - \left( {\delta + d} \right) {{\mathbf{I}}^{\mathbf{p}}},\\[12pt] \displaystyle \frac{{\mathrm{d}{{\mathbf{I}}^{\mathbf{s}}}}}{{\mathrm{d}t}} = \left( {1 - \phi } \right) \eta {\mathbf{E}} - \left( {\gamma + d} \right) {{\mathbf{I}}^{\mathbf{s}}},\\[12pt] \displaystyle \frac{{\mathrm{d}{{\mathbf{I}}^{\mathbf{c}}}}}{{\mathrm{d}t}} = \delta {{\mathbf{I}}^{\mathbf{p}}} - \left( {\omega + d} \right) {{\mathbf{I}}^{\mathbf{c}}}\\[12pt] \displaystyle \frac{{\mathrm{d}{\mathbf{R}}}}{{\mathrm{d}t}} = \gamma {{\mathbf{I}}^{\mathbf{s}}} + \omega {{\mathbf{I}}^{\mathbf{c}}} - \mathrm{d}{\mathbf{R}}.\\[12pt] \end{array} \right. \end{aligned}$$
(2)

Here for \(u \in {R^n}\), diag(u) denotes the \({n \times n}\) diagonal matrix whose main diagonal is u. According to the biological significance, the initial values of model variables are set to be nonnegative, and then, the expressions of (2) can ensure that the solutions will always stay in

$$\begin{aligned} \Omega {\mathrm{= }}\Bigg \{ \left( {{\mathbf{S}},{\mathbf{E}},{{\mathbf{I}}^{\mathbf{p}}},{{\mathbf{I}}^{\mathbf{s}}},{{\mathbf{I}}^{\mathbf{c}}},{\mathbf{R}}} \right) \in R_ + ^{6n}|0&\le {\mathbf{S}},{\mathbf{E}},{{\mathbf{I}}^{\mathbf{p}}},{{\mathbf{I}}^{\mathbf{s}}},{{\mathbf{I}}^{\mathbf{c}}},{\mathbf{R}}\\&\le {\mathbf{N}} \Bigg \}. \end{aligned}$$

Hence, \(\Omega \) is a compact absorbing and positively invariant set for (2). Direct calculation yields that system (2) has a disease-free equilibrium, denoted by \(Q_{0}= \left( {{{\mathbf{S}}^{\mathbf{0}}},{{\mathbf{E}}^{\mathbf{0}}},{{\mathbf{I}}^{{\mathbf{p0}}}},{{\mathbf{I}}^{{\mathbf{s0}}}},{{\mathbf{I}}^{{\mathbf{c0}}}},{{\mathbf{R}}^{\mathbf{0}}}} \right) = \left( {{\mathbf{N}},{\mathbf{0}},{\mathbf{0}},{\mathbf{0}},{\mathbf{0}},{\mathbf{0}}} \right) .\)

The basic reproduction number \(R_{0}\) is calculated by using the theory of next-generation matrix [23]. It is written as \(R_{0}=\rho (\mathrm{FV}^{-1})\), where F is the rate of occurring new infections, and V is the rate of transferring individuals outside the original group [23]. Here \(\rho \) represents the spectral radius of matrix. Based on model (1), direct calculation yields that:

$$\begin{aligned} F = \left( {\begin{array}{*{20}{c}} {\mathbf{O}}&{}{\mathrm{diag}({\mathbf{N}}){A_p}}&{}{\alpha \mathrm{diag}({\mathbf{N}}){A_p}}&{}{\beta \mathrm{diag}({\mathbf{N}}){A_p}}\\ {\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}}\\ {\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}}\\ {\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}} \end{array}} \right) , \end{aligned}$$

and

$$\begin{aligned} V = \left( {\begin{array}{*{20}{c}} {\left( {\eta + d} \right) {\mathbf{I}}}&{}{\mathbf{O}}&{}{\mathbf{O}}&{}{\mathbf{O}}\\ { - \phi \eta {\mathbf{I}}}&{}{\left( {\delta + d} \right) {\mathbf{I}}}&{}{\mathbf{O}}&{}{\mathbf{O}}\\ { - \left( {1 - \phi } \right) \eta {\mathbf{I}}}&{}{\mathbf{O}}&{}{\left( {\gamma + d} \right) {\mathbf{I}}}&{}{\mathbf{O}}\\ {\mathbf{O}}&{}{ - \delta {\mathbf{I}}}&{}{\mathbf{O}}&{}{\left( {\omega + d} \right) {\mathbf{I}}} \end{array}} \right) . \end{aligned}$$

where \({\mathbf{I}}\) denotes a identity matrix, and \({\mathbf{O}}\) is the zero matrix. It follows from the characteristic equation of \(FV^{-1}\) that the basic reproduction number is given by:

$$\begin{aligned} {R_0}= & {} \rho \left( \left( \frac{{\phi \eta }}{{\left( {\eta + d} \right) \left( {\delta + d} \right) }} + \frac{{\left( {1 - \phi } \right) \eta \alpha }}{{\left( {\eta + d} \right) \left( {\gamma + d} \right) }}\right. \right. \nonumber \\&\left. \left. + \frac{{\phi \eta \delta \beta }}{{\left( {\eta + d} \right) \left( {\delta + d} \right) \left( {\omega + d} \right) }} \right) \mathrm{diag}({\mathbf{N}}){A_p} \right) . \end{aligned}$$
(3)

The three components of the \(R_{0}\) are separately contributed by the infections in preclinical, subclinical, and clinical states. Since the characteristic equation in (3) is a polynomial of degree n for eigenvalue, it is impossible to calculate its analytic expression.

4 Global stability

The results concerning the global dynamics of system (2) are analyzed in this section.

Theorem 4.1

System (2) has a unique endemic equilibrium \({Q^*}\).

Proof

It is denoted as the expression of endemic equilibrium by \({{\mathbf{S}}^{\mathbf{*}}},{{\mathbf{E}}^{\mathbf{*}}},{{\mathbf{I}}^{{\mathbf{p*}}}},{{\mathbf{I}}^{{\mathbf{s*}}}}\) and \({{\mathbf{I}}^{{\mathbf{c*}}}}\). Based on the equilibrium definition, letting the right-hand side of system (2) to be zeros and substituting \({{\mathbf{S}}^{\mathbf{*}}}, {{\mathbf{E}}^{\mathbf{*}}}, {{\mathbf{I}}^{{\mathbf{s*}}}}\), and \({{\mathbf{I}}^{{\mathbf{c*}}}}\) by \({\mathbf{I}}^{{\mathbf{p*}}}\), an equation is obtained about \({{\mathbf{I}}^{{\mathbf{p*}}}}\) as

$$\begin{aligned} \begin{array}{ll} f\left( {{{\mathbf{I}}^{{\mathbf{p*}}}}} \right) = m_{1}{{\mathbf{I}}^{{\mathbf{p*}}}} (\mathrm{diag}{\left( {m_{2} {A_p}{{\mathbf{I}}^{{\mathbf{p*}}}}}) \right) ^{ - 1}}\left( {\mathrm{d}{\mathbf{I}} + m_{2} {A_p}{{\mathbf{I}}^{{\mathbf{p*}}}}} \right) \\ \qquad \qquad \quad - \mathrm{d}{\mathbf{N}}, \end{array} \end{aligned}$$

where

$$\begin{aligned} {m_1}= & {} \frac{{\left( {\eta + d} \right) \left( {\delta + d} \right) }}{{\phi \eta }},\\ {m_2}= & {} 1 + \frac{{\alpha \left( {1 - \phi } \right) \left( {\delta + d} \right) }}{{\phi \left( {\gamma + d} \right) }} + \frac{{\beta \delta }}{{\omega + d}}. \end{aligned}$$

Substituting \({{\mathbf{I}}^{{\mathbf{p*}}}}\) by \({\mathbf{0}}\) and \({\mathbf{N}}\) yields that \(f\left( {\mathbf{0}} \right) = - \mathrm{d}{\mathbf{N}} < {\mathbf{0}},\) and

$$\begin{aligned} f\left( {\mathbf{N}} \right)= & {} {m_1}{\mathbf{N}}(\mathrm{diag}{\left( {{m_2}{A_p}{\mathbf{N}}}) \right) ^{ - 1}}\left( {d{\mathbf{1}} + {m_2}{A_p}{\mathbf{N}}} \right) - \mathrm{d}{\mathbf{N}}\\\ge & {} \frac{{\left( {\delta + d} \right) }}{\phi }{\mathbf{N}}(\mathrm{diag}{\left( {{A_p}{\mathbf{N}}}) \right) ^{ - 1}}\left( {{A_p}{\mathbf{N}}} \right) \\&- \mathrm{d}{\mathbf{N}} = \frac{{\left( {\delta + d} \right) }}{\phi }{\mathbf{N}} - \mathrm{d}{\mathbf{N}} > {\mathbf{0}}. \end{aligned}$$

It follows from the zero-point theorem that system (2) has at least one positive equilibrium. Furthermore, due to \(f'\left( {{{\mathbf{I}}^{\mathbf{p}}}} \right) = {m_1}{\mathbf{I}} > {\mathbf{0}},\) f is an increasing function. Hence, there exists a unique positive endemic equilibrium in the compact set \(\Omega \). \(\square \)

Theorem 4.2

If \({R_0} < 1\), the disease-free equilibrium \(Q_{0}\) of system (2) is globally asymptotically stable.

Proof

Since the total number of human population is a constant, the first equation of system (2) can be ignored. Substituting \({{\mathbf{S}}} \) by \(({{\mathbf{N}}} - {\mathbf{E}} - {\mathbf{I}}^{\mathbf{p}} - {{\mathbf{I}}^{\mathbf{s}}} - {{\mathbf{I}}^{\mathbf{c}}} - {\mathbf{R}})\), it is obtained

$$\begin{aligned}&\displaystyle \frac{{\mathrm{d}{\mathbf{E}}}}{{\mathrm{d}t}} = {\mathrm{diag}}\left( {{\mathbf{N}} - {\mathbf{E}} - {{\mathbf{I}}^{\mathbf{p}}} - {{\mathbf{I}}^{\mathbf{s}}} - {{\mathbf{I}}^{\mathbf{c}}} - {\mathbf{R}}} \right) \\&\quad \left( {{A_p}{{\mathbf{I}}^{\mathbf{p}}} + \alpha {A_p}{{\mathbf{I}}^{\mathbf{s}}} + \beta {A_p}{{\mathbf{I}}^{\mathbf{c}}}} \right) - \left( {\eta + d} \right) {\mathbf{E}}\\&\quad \le {\mathrm{diag}}{(\mathbf{N})}\left( {{A_p}{{\mathbf{I}}^{\mathbf{p}}} + \alpha {A_p}{{\mathbf{I}}^{\mathbf{s}}} + \beta {A_p}{{\mathbf{I}}^{\mathbf{c}}}} \right) - \left( {\eta + d} \right) {\mathbf{E}}. \end{aligned}$$

The corresponding comparison system is:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{{\mathrm{d}{{{\bar{\mathbf{E}}}}}}}{{\mathrm{d}t}} = {\mathrm{diag}}{(\mathbf{N})}\left( {{A_p}{{{{\bar{\mathbf{I}}}}}^{\mathbf{p}}} + \alpha {A_p}{{{{\bar{\mathbf{I}}}}}^{\mathbf{s}}} + \beta {A_p}{{{{\bar{\mathbf{I}}}}}^{\mathbf{c}}}} \right) \\ \displaystyle \qquad \qquad - \left( {\eta + d} \right) {{{\bar{\mathbf{E}}}}},\\[12pt] \displaystyle \frac{{\mathrm{d}{{{{{\bar{\mathbf{I}}}}}}^{\mathbf{p}}}}}{{\mathrm{d}t}} = \phi \eta {{{\bar{\mathbf{E}}}}} - \left( {\delta + d} \right) {{{{\bar{\mathbf{I}}}}}^{\mathbf{p}}},\\[12pt] \displaystyle \frac{{\mathrm{d}{{{{{\bar{\mathbf{I}}}}}}^{\mathbf{s}}}}}{{\mathrm{d}t}} = \left( {1 - \phi } \right) \eta {{{\bar{\mathbf{E}}}}} - \left( {\gamma + d} \right) {{{{\bar{\mathbf{I}}}}}^{\mathbf{s}}},\\[12pt] \displaystyle \frac{{\mathrm{d}{{{{{\bar{\mathbf{I}}}}}}^{\mathbf{c}}}}}{{\mathrm{d}t}} = \delta {{{{\bar{\mathbf{I}}}}}^{\mathbf{p}}} - \left( {\omega + d} \right) {{{{\bar{\mathbf{I}}}}}^{\mathbf{c}}}. \end{array} \right. \end{aligned}$$
(4)

It is clear that model (4) is a linear system, and the coefficient matrix of its variables in the right-hand side is exactly the matrix \((F - V)\). Hence, when \({R_0} = \rho \left( {F{V^{ - 1}}} \right) < 1\), the unique equilibrium \(\left( {{\mathbf{E}},{{\mathbf{I}}^{\mathbf{p}}},{{\mathbf{I}}^{\mathbf{s}}},{{\mathbf{I}}^{\mathbf{c}}}} \right) = \left( {{\mathbf{0}},{\mathbf{0}},{\mathbf{0}},{\mathbf{0}}} \right) \) of this linear system (4) is globally asymptotically stable. Since

$$\begin{aligned} \frac{{\mathrm{d}{\mathbf{E}}}}{{\mathrm{d}t}} \le \frac{{d{{{\bar{\mathbf{E}}}}}}}{{\mathrm{d}t}},\frac{{\mathrm{d}{{\mathbf{I}}^{\mathbf{p}}}}}{{\mathrm{d}t}} \le \frac{{\mathrm{d}{{{{{\bar{\mathbf{I}}}}}}^{\mathbf{p}}}}}{{\mathrm{d}t}},\frac{{\mathrm{d}{{\mathbf{I}}^{\mathbf{s}}}}}{{\mathrm{d}t}} \le \frac{{\mathrm{d}{{{{{\bar{\mathbf{I}}}}}}^{\mathbf{s}}}}}{{\mathrm{d}t}},\frac{{\mathrm{d}{{\mathbf{I}}^{\mathbf{c}}}}}{{\mathrm{d}t}} \le \frac{{\mathrm{d}{{{{{\bar{\mathbf{I}}}}}}^{\mathbf{c}}}}}{{\mathrm{d}t}}. \end{aligned}$$

According to the comparison theorem, with the same initial conditions, it has \(\mathbf{E}(t)\le {{\bar{\mathbf{E}}}(t)}\), \(\mathbf{I}^{p}(t)\le {{\bar{\mathbf{I}}}^{p}(t)}\), \(\mathbf{I}^{s}(t)\le {{\bar{\mathbf{I}}}^{s}(t)}\), and \(\mathbf{I}^{c}(t)\le {{\bar{\mathbf{I}}}^{c}(t)}\) for any \(t>0\), yielding that \(Q_{0}\) is globally asymptotically stable when \({R_0} < 1\). \(\square \)

The graph-theoretic method presented in [24, 25] is used to analyze the global stability of the endemic equilibrium.

Theorem 4.3

If \({R_0} > 1\), then the unique endemic equilibrium \(Q^*\) of system (2) is globally asymptotically stable in \(\Omega \).

Proof

Denote

$$\begin{aligned} {D_i}= & {} {S_i} - S_i^* - S_i^*\ln \frac{{{S_i}}}{{S_i^*}} + {E_i} - E_i^* - E_i^*\ln \frac{{{E_i}}}{{E_i^*}}, \\ {D_{n + i}}= & {} I_i^p - I_i^{p*} - I_i^{p*}\ln \frac{{I_i^p}}{{I_i^{p*}}}, \\ {D_{2n + i}}= & {} I_i^s - I_i^{s*} - I_i^{s*}\ln \frac{{I_i^s}}{{I_i^{s*}}}, \\ {D_{3n + i}}= & {} I_i^c - I_i^{c*} - I_i^{c*}\ln \frac{{I_i^c}}{{I_i^{c*}}}, {{\tilde{N}}}_j = \sum \limits _{k = 1}^n {{P_{kj}}} {N_k}, \end{aligned}$$

where the variables with superscript as star are the expressions of endemic equilibrium in model. Using the inequality \(1 - x + \ln x \le 0\), for \(x > 0\), direct differentiation yields:

$$\begin{aligned}&{D_i}^\prime = \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*{\ell _j}}^* + \mathrm{d}S_i^* - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}{S_i}{\ell _j}} \\&\qquad - \mathrm{d}{S_i} - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\frac{{S_i^*}}{{{S_i}}}{\ell _j}}^* - d\frac{{S_i^*S_i^*}}{{{S_i}}} \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*{\ell _j}} + \mathrm{d}S_i^* + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}{S_i}{\ell _j}} \\&\qquad - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\frac{{{E_i}}}{{E_i^*}}{\ell _j}}^* - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}{S_i}\frac{{E_i^*}}{{{E_i}}}{\ell _j}} \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*{\ell _j}}^* \\&\quad \le \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*{\ell _j}}^* - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}{S_i}{\ell _j}} \\&\qquad - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\frac{{S_i^*}}{{{S_i}}}{\ell _j}^*} + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*{\ell _j}} \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}{S_i}} - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\frac{{{E_i}}}{{E_i^*}}{\ell _j}^*} \\&\qquad - \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}{S_i}\frac{{E_i^*}}{{{E_i}}}{\ell _j}} + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*{\ell _j}^*} \\&\quad = \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\varpi _j^p} \left( {1 - \frac{{{S_i}I_k^p}}{{S_i^*I_k^{p*}}} - \frac{{S_i^*}}{{{S_i}}} + \frac{{I_k^p}}{{I_k^{p*}}}} \right) \\&\qquad {\mathrm{+ }}\sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\alpha \varpi _j^s} \left( {1 - \frac{{{S_i}I_k^s}}{{S_i^*I_k^{s*}}} - \frac{{S_i^*}}{{{S_i}}} + \frac{{I_k^s}}{{I_k^{s*}}}} \right) \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\beta \varpi _j^c} \left( {1 - \frac{{{S_i}I_k^c}}{{S_i^*I_k^{c*}}} - \frac{{S_i^*}}{{{S_i}}} + \frac{{I_k^c}}{{I_k^{c*}}}} \right) \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\varpi _j^p} \left( {1 + \frac{{{S_i}I_k^p}}{{S_i^*I_k^{p*}}} - \frac{{{E_i}}}{{E_i^*}} - \frac{{E_i^*{S_i}I_k^p}}{{{E_i}S_i^*I_k^{p*}}}} \right) \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\alpha \varpi _j^s} \left( {1 + \frac{{{S_i}I_k^s}}{{S_i^*I_k^{s*}}} - \frac{{{E_i}}}{{E_i^*}} - \frac{{E_i^*{S_i}I_k^s}}{{{E_i}S_i^*I_k^{s*}}}} \right) \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\beta \varpi _j^c} \left( {1 + \frac{{{S_i}I_k^c}}{{S_i^*I_k^{c*}}} - \frac{{{E_i}}}{{E_i^*}} - \frac{{E_i^*{S_i}I_k^c}}{{{E_i}S_i^*I_k^{c*}}}} \right) \\&\quad \le \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\varpi _j^p} \left( {\frac{{I_k^p}}{{I_k^{p*}}} - \ln \frac{{I_k^p}}{{I_k^{p*}}} + \ln \frac{{{E_i}}}{{E_i^*}} - \frac{{{E_i}}}{{E_i^*}}} \right) \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\alpha \varpi _j^s} \left( {\frac{{I_k^s}}{{I_k^{s*}}} - \ln \frac{{I_k^s}}{{I_k^{s*}}} + \ln \frac{{{E_i}}}{{E_i^*}} - \frac{{{E_i}}}{{E_i^*}}} \right) \\&\qquad + \sum \limits _{j = 1}^n {{\lambda _j}{P_{ij}}S_i^*\beta \varpi _j^c} \left( {\frac{{I_k^c}}{{I_k^{c*}}} - \ln \frac{{I_k^c}}{{I_k^{c*}}} + \ln \frac{{{E_i}}}{{E_i^*}} - \frac{{{E_i}}}{{E_i^*}}} \right) \\&\quad = :{a_{i,n + i}}{G_{i,n + i}} + {a_{i,2n + i}}{G_{i,2n + i}} + {a_{i,3n + i}}{G_{i,3n + i}}. \end{aligned}$$

Here,

$$\begin{aligned} {\ell _j}^*= & {} \frac{1}{{{{\tilde{N}}}_j}} {\sum \limits _{k = 1}^n {{P_{kj}}\left( {I_k^{p*} + \alpha I_k^{s*} + \beta I_k^{c*}} \right) } } ,\\ {\ell _j}= & {} \frac{1}{{{{\tilde{N}}}_j}} {\sum \limits _{k = 1}^n {{P_{kj}}\left( {I_k^{p} + \alpha I_k^{s} + \beta I_k^{c}} \right) } } ,\\ \varpi _j^p= & {} \frac{1}{{{{\tilde{N}}}_j}} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{p*}} } , \;\\ \varpi _j^s= & {} \frac{1}{{{{\tilde{N}}}_j}} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{s*}} } ,\; \varpi _j^c = \frac{1}{{{{\tilde{N}}}_j}} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{c*}} } .\end{aligned}$$

Similarly,

$$\begin{aligned} {{D'}_{n + i}}= & {} \phi \eta {E_i} - \phi \eta E_i^*\frac{{I_i^p}}{{I_i^{p*}}} - \phi \eta {E_i}\frac{{I_i^{p*}}}{{I_i^p}} + \phi \eta E_i^* \\= & {} \phi \eta E_i^*\left( {1 - \frac{{{E_i}I_i^{p*}}}{{E_i^*I_i^p}} - \frac{{I_i^p}}{{I_i^{p*}}} + \frac{{{E_i}}}{{E_i^*}}} \right) \\\le & {} \phi \eta E_i^*\left( {\frac{{{E_i}}}{{E_i^*}} - \ln \frac{{{E_i}}}{{E_i^*}} + \ln \frac{{I_i^p}}{{I_i^{p*}}} - \frac{{I_i^p}}{{I_i^{p*}}}} \right) \\=: & {} {a_{n + i,i}}{G_{n + i,i}}.\\ {{D'}_{2n + i}}= & {} \left( {1 - \phi } \right) \eta {E_i} - \left( {1 - \phi } \right) \eta E_i^*\frac{{I_i^s}}{{I_i^{s*}}} \\&- \left( {1 - \phi } \right) \eta {E_i}\frac{{I_i^{s*}}}{{I_i^s}} + \left( {1 - \phi } \right) \eta E_i^*\\= & {} \left( {1 - \phi } \right) \eta E_i^*\left( 1 - \frac{{{E_i}I_i^{s*}}}{{E_i^*I_i^s}} - \frac{{I_i^s}}{{I_i^{s*}}} + \frac{{{E_i}}}{{E_i^*}} \right) \\\le & {} \left( {1 - \phi } \right) \eta E_i^*\left( {\frac{{{E_i}}}{{E_i^*}} - \ln \frac{{{E_i}}}{{E_i^*}} + \ln \frac{{I_i^s}}{{I_i^{s*}}} - \frac{{I_i^s}}{{I_i^{s*}}}} \right) \\= & {} :{a_{2n + i,i}}{G_{2n + i,i}}.\\ {{D'}_{3n + i}}= & {} \delta I_i^p - \delta I_i^{p*}\frac{{I_i^c}}{{I_i^{c*}}} - \delta I_i^p\frac{{I_i^{s*}}}{{I_i^s}} + \delta I_i^{p*} \\= & {} \delta I_i^{p*}\left( {1 - \frac{{I_i^pI_i^{c*}}}{{I_i^{p*}I_i^c}} - \frac{{I_i^c}}{{I_i^{c*}}} + \frac{{I_i^p}}{{I_i^{p*}}}} \right) \\\le & {} \delta I_i^{p*}\left( {\frac{{I_i^p}}{{I_i^{p*}}} - \ln \frac{{I_i^p}}{{I_i^{p*}}} + \ln \frac{{I_i^c}}{{I_i^{c*}}} - \frac{{I_i^c}}{{I_i^{c*}}}} \right) \\=: & {} {a_{3n + i,n + i}}{G_{3n + i,n + i}}. \end{aligned}$$

and

$$\begin{aligned} {a_{i,n + i}}= & {} \frac{{\lambda _j}{P_{ij}}S_i^*}{{{\tilde{N}}}_j} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{p*}}},\\ {a_{i,2n + i}}= & {} \frac{{\lambda _j}{P_{ij}}S_i^*\alpha }{{{\tilde{N}}}_j} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{s*}} },\\ {a_{i,3n + i}}= & {} \frac{{\lambda _j}{P_{ij}}S_i^*\beta }{{{\tilde{N}}}_j} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{c*}} }, \end{aligned}$$

as well as \({a_{n + i,i}} = \phi \eta E_i^*,{a_{2n + i,i}}{\mathrm{= }}\left( {1 - \phi } \right) \eta E_i^*,{a_{3n + i,i}}{\mathrm{= }}\delta I_i^{p*}.\) Let \(A = {\left( {{a_{ij}}} \right) _{n \times n}}\) with \({a_{ij}} > 0\) as defined above and otherwise zero. The corresponding weighted digraph is shown in Fig. 2. Along each of the cycles on the graph, it is verified that \(\sum {{G_{ij}}} = 0;\) for instance, \({G_{i,n + i}} + {G_{n + i,i}} = 0,{G_{j,n + i}} + {G_{n + j,j}} + {G_{i,n + j}} + {G_{n + i,i}} = 0,\) and so on. It follows from Theorem 3.5 in [24] that there exist constants \(c_{i}\) such that \(D=\sum _{i} c_{i}D_{i}\) is a Lyapunov function for system (2). Let \({c_1} = \cdots = {c_n} =1\), and

$$\begin{aligned} {c_{n + i}}= & {} \sum \limits _{j = 1}^n \frac{ \left( {{c_j}{a_{j,n + i}} + {c_j}{a_{j,3n + i}}} \right) }{a_{n + i,i}},\\ {c_{2n + i}}= & {} \sum \limits _{j = 1}^n \frac{ {c_j}{a_{j,2n + i}}}{a_{2n + i,i}} ,\; {c_{3n + i}} = \sum \limits _{j = 1}^n \frac{{c_j}{a_{j,3n + i}} }{a_{3n + i,n + i}}.\end{aligned}$$

Further computation leads to

$$\begin{aligned} {c_{n + i}}= & {} \sum \limits _{j = 1}^n \Bigg [ \frac{{\lambda _j}{P_{ij}}S_i^*}{{{\tilde{N}}}_j\phi \eta E_i^*} \Bigg ( {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{p*}}}\\&+ \beta \sum \limits _{k = 1}^n {{P_{kj}}I_k^{c*} } \Bigg ) \Bigg ],\\ {c_{2n + i}}= & {} \sum \limits _{j = 1}^n \left( \frac{{\lambda _j}{P_{ij}}S_i^*\alpha }{(1 - \phi )\eta E_i^*{{\tilde{N}}}_j} \sum \limits _{k = 1}^n {P_{kj}}I_k^{s*} \right) ,\\ {c_{3n + i}}= & {} \sum \limits _{j = 1}^n \left( \frac{{\lambda _j}{P_{ij}}S_i^*\beta }{\delta I_i^{p*}{{\tilde{N}}}_j} {\sum \limits _{k = 1}^n {{P_{kj}}I_k^{c*}} } \right) . \end{aligned}$$
Fig. 2
figure 2

Digraph representation of the matrix A of transmission used to determine the coefficients in the Lyapunov function D

Full size image
Table 2 Province and its abbreviation in China
Full size table

Hence, with the functions \({D_i}\) and constants \({c_i}\) given above, the expression

$$\begin{aligned} D= & {} \sum \limits _{i = 1}^n {{c_i}{D_i}} + \sum \limits _{i = 1}^n {{c_{n + i}}{D_{n + i}}} \\&+ \sum \limits _{i = 1}^n {{c_{2n + i}}{D_{2n + i}}} + \sum \limits _{i = 1}^n {{c_{3n + i}}{D_{3n + i}}} \end{aligned}$$

is a Lyapunov function for system (2). Its derivative is:

$$\begin{aligned} D'= & {} \sum \limits _{i = 1}^n {{c_i}\left( {\frac{{{S_i} - S_i^*}}{{{S_i}}}{S_i}^\prime + \frac{{{E_i} - E_i^*}}{{{E_i}}}{E_i}^\prime } \right) } \\&+ \sum \limits _{i = 1}^n {{c_{n + i}}\left( {\frac{{I_i^p - I_i^{p*}}}{{I_i^p}}I{{_i^p}^\prime }} \right) } \\&+ \sum \limits _{i = 1}^n {{c_{2n + i}}\left( {\frac{{I_i^s - I_i^{s*}}}{{I_i^s}}I{{_i^s}^\prime }} \right) } \\&+ \sum \limits _{i = 1}^n {{c_{3n + i}}\left( {\frac{{I_i^c - I_i^{c*}}}{{I_i^c}}I{{_i^c}^\prime }} \right) } . \end{aligned}$$

When \(D' = 0\) in the set \(\left\{ R _ + ^{5n} \right\} \), one can readily verify that \({S_i} = S_i^*,{E_i} = E_i^*,I_i^p = I_i^{p*},I_i^s = I_i^{s*},I_i^c = I_i^{c*}\). For the left system,

$$\begin{aligned} \frac{{d{R_i}}}{{\mathrm{d}t}} = \gamma I_i^{s*} + \omega I_i^{c*} - d{R_i}. \end{aligned}$$
(5)

it is clear that system (2) has a unique equilibrium \({R_i} = R_i^*\), which is global asymptotically stable. Using LaSalle’s invariance principle, it is concluded that the endemic equilibrium \(Q^*\) is global asymptotically stable in \(\Omega \). \(\square \)

5 Application to the outbreak in China

In this section, the proposed model is applied to analyze the spatiotemporal transmission dynamics of COVID-19 in Chinese provinces (see Table 2). Daily records of human infections were collected from authoritative data report. The permanent population size in each province was released by the 2019 National Bureau of Statistics. The daily migration data among provinces are collected from Baidu migration data (https://qianxi.baidu.com/). Specifically, the element in migration matrix P is defined as \(P_{ij}=\kappa Q_{i} c_{ij}\), where \(Q_{i}\) is the migration scale in region i and \(c_{ij}\) is the proportion of migration scale from region i to region j (both of which were extracted from Baidu migration data), and \(\kappa \) is a adjustive constant for modulating the data into the model.

The model is validated by using Markov chain Monte Carlo (MCMC) method to fit the daily reported cases in 26 provinces (with cases more than 101 from January 5, 2020, to March 15, 2020). Here 6 parameters (\(\beta \), \(\alpha \), \(\kappa \), and the initial values of E, \(I^{c}\) and \(I^{p}\) in HuB) were estimated by MCMC. Since HuB province is considered to be the infection source, it is assumed that there is no infections in other provinces at initial time. The transmission rate \(\lambda _{i}\) is derived from the effective reproduction number \(R_{t}\) in province i. \(R_{t}\) represents the number of new morbidity cases caused by an average morbidity case at time t. Here the \(R_{t}\) in each province is estimated from the time series of its indigenous cases. Based on the Bayesian framework, \(R_{t}\) is calculated by the EpiEstim package in R language software [26], in which the intergenerational time follows gamma distribution, with the mean value and standard deviation as 7.5 and 3.4, respectively [27].

The fitting results are shown in Figs. 3 and S1 (in Supplementary Information). It is found that the model performed well in fitting the daily reported incidences, except the data in some provinces such as HeB, ZJ, HeN, HuN, CQ, and GZ. The fitting deviations are possibly due to the spatiotemporal heterogeneity of transmission parameters and detection efficiency. PRCC coefficients are used as global sensitivity to quantify the response of model outputs to the variation of the estimated parameters. By averaging the daily PRCC coefficients in the operation of fitting daily incidences, it is found that the output is strongly sensitive to the effective transmission rate of clinical infection (\(\beta \)) and the relative coefficient of migration matrix (\(\kappa \)), followed by the effective transmission rate of subclinical infection (\(\alpha \)). Yet it seems that in the entire infection process the output is scarcely sensitive to the initial condition of the model. The reason for the negative correlation of \(\beta \) and \(\kappa \) with model output is that for given \(R_{t}\), small values of \(\beta \) and \(\kappa \) mean large transmission rate \(\lambda \).

In the following simulations of the model, it is set that (1) the initial conditions are \(E(0)=50, {I^p}(0)={I^s}(0)={I^c}(0)=35\) in Figs. 4, 5 and S6, and \(E(0)={I^p}(0)={I^s}(0)={I^c}(0)=20\) in Figs. 6, 7 and 8; (2) the impact of human mobility is reflected by the migration matrix P, and its values are selected from Baidu migration data during 2020 and 2021; and (3) multiple interventions (including social distancing, quarantine and wearing masks) are measured by different values of the effective reproduction number \(R_{t}\), in which the largest and minimum values are separately \(R_{t}=3.56\) and \(R_{t}=0.59\), corresponding to the situations of no intervention (in early infection stage [January 5 to January 22, 2020] in HuB) and rigorous intervention (in the mid and late stage of infection [January 23 to February 12, 2020] in HuB).

Fig. 3
figure 3

The fitting results of the COVID-19 cases in China. a Fitting daily new cases in HuB, where the light shaded area is the 95% confidence interval (CI) for all 1000 simulations, and the blue curve is the median of the model output; b relationship between predicted and observed cases in HuB. a sensitivity of daily cases to the model parameters as indicated by PRCC values

Full size image
Fig. 4
figure 4

The accumulative number of cases in each province before and after the intervention, in case of different locations (HuB, BJ, SH, GD, XZ) of initial infection. The human mobility information is adopted from the data during January 23 to March 20, 2021. The transmission rate \(\lambda \) in Figures (a), (b), (c) and (d), (e), (f) is separately determined by the mean values of effective reproduction number before and after the intervention

Full size image
Fig. 5
figure 5

The cumulative number of cases in China with the human mobility data: a from January 23 to March 20, 2021, and b from January 23 to May 20, 2021, in case of no intervention. The abscissa is the location that has unique infection source at the initial time. The yellow part is the contribution by the location with initial infections

Full size image

Figure 4 shows the impacts of intervention on the evolution of COVID-19 in China, with different initial infection sites (i.e., HuB, BJ, SH, GD and XZ). The migration data during January 23, and March 20, 2021, are integrated into the model for simulating the transmission process under two modes: few intervention and rigorous intervention. These two modes are reflected by the choices of the reproduction number, whose values in each province are taken as the means of the effective reproduction number at the beginning of the outbreak (January 1–22, 2020) and after the intervention (January 23–February 12, 2020), respectively. For simulating the transmission for 57 days, the following patterns are observed in Fig. 4. First, in case of substituting the early \(R_{t}\) into the model, the infection burden could increase hundreds of times, in which the numbers of total clinical infections in China could reach 111.08, 64.61, 66.71, 57.62 and 13.59 million with separate source of initial infection in HuB, BJ, SH, GD and XZ. Second, in case of substituting the latter \(R_{t}\) into the model, the above numbers reduce sharply to 228, 288, 215, 232 and 154. Moreover, the regions around the source of initial infection would likely suffer more serious attack, in which the highest attack rates are 0.28 in HuB and 0.14 in GZ with source in HuB, 0.20 in TJ and 0.12 in HuB with source in BJ, 0.10 in JS and 0.09 in AN with source in SH, 0.15 in GZ and 0.09 in HuB with source in GD, 0.19 in XZ and 0.1 in QH with source in XZ.

Figure 5 shows the ranking of total infections in China with a unique infection source at initial time and human mobility at the entire process. Here it is assumed that there is no implementation of intervention, which is realized by setting the reproduction number in each province to be the value in early infection stage in HuB (equal 3.56). By simulating the transmission process through 57 days, it is found that (1) the initial infection located in HeN, ZJ, SH, JS and AH would cause the top five numbers of human clinical cases (over 300 million); (2) when the initial infection is located in XZ, QH, JL, HLJ, XJ, it would lead to smallest clinical infection sizes (around 142–183 million). Moreover, by simulating the transmission process through 120 days, it is observed that the infection would reach a saturated state: more than 1.1 billion people could be infected clinically, no matter where the infection initially occurs. In this case, all provinces reach the highest levels of new infections after about two months (see Fig. S3), but the attack rate exhibits spatial heterogeneity, in which the area near the initial infection source usually suffers worse.

Figure 6 shows the impacts of different initial conditions and human mobility on the evolution of COVID-19 transmission across Chinese provinces, in case of no intervention. It is observed that more sites with initial infection and more frequency of human mobility would yield a little faster diffusion of the disease (that is more obvious in early infection period) and a little earlier arriving of the peak. When the disease starts to spread from January 23, 2021, the numbers of human cases would reach peak around early April or late March, in case of one initial infection site(XZ), or two initial infection sites (HeN and GD). However, in case of all sizes with the initial infection, the peak is arriving around the middle of March, regardless of population mobility. In these four settings, the serious infection would last for over three months and cause similar number of total infections (that is, 1.3 billion clinical/subclinical cases). After that the disease will still prevail in human population in very low incidence rate.

Fig. 6
figure 6

Time series of daily new cases in each province with different outbreak sites at initial time and human mobility data from January 23, 2021, to May 20, 2021, in case of no intervention

Full size image
Fig. 7
figure 7

Time series of daily new cases in China with different timing of travel ban and different basic reproduction number. Here human mobility data are from January 23 to July 4, 2021

Full size image
Fig. 8
figure 8

Dependence of COVID-19 infection on the basic reproduction number \(R_{0}\) in China (a and b), and the sensitivity of \(R_{0}\) to the model parameters as indicated by PRCC values. The accumulative number in a is the total infections during the first 400 days. Human mobility data in a and b starts on January 23, 2021, and future data are obtained by averaging those in previous time. PRCC coefficients in c with \(*\) indicate that the corresponding parameters are significantly different from zero (with p-values < 0.05)

Full size image

Figure 7 shows the evolution dynamics of COVID-19 in China with different patterns of intervention, in case of only GD as the initial infection site. Here the impacts of intervention and human mobility are quantified by the basic reproduction number \(R_{0}\) and travel ban, respectively. It is found that (1) slight increase of \(R_{0}\) would cause rapid transmission and high morbidity around China, (2) travel ban among the provinces in China as early as possible can postpone the propagation a little bit and possibly reduce total morbidity, and (3) the control effect of travel ban is not significant (especially for large \(R_{0}\)), only when the travel is restricted at first. Specifically, by simulating the spatiotemporal transmission process for 162 days, it is observed that (1) if \(R_{0} = 3.56\), 2.5,  2,  1.5, and 1.1, human infections would increase rapidly after 14, 29, 56, 72, and 81 days since the introduction of the infection, respectively; (2) when \(R_{0} = 3.56, 2.5\), and 2, the number of infections would reach the peak around March 27, May 2, and Jun 7, resulting in total clinical infections to be 1.1, 1.0, and 0.8 billion (regardless when to start travel ban after outbreak), but the numbers would reduce vastly to 92.8, 75.9 and 85.7 million if travel ban starts before outbreak; (3) when \(R_{0} =2\), if travel ban is implemented after 1 day, 10 days and 20 days of the break, the transmission could be postponed 2 day, 5 day, and 18 days (compared with the case without travel ban), resulting in 735.5, 865.6 and 876.21 million of human clinical infections; and (4) in case of rigorous intervention (\(R_{0}<1\)), it is impossible for travel to trigger disease outbreak.

Figure 8 shows the relationship between the basic reproduction number \(R_{0}\) and human infections in China as well as the transmission parameters. It is found that the increase of \(R_{0}\) easily stimulates disease prevalence and causes quick arrive and high level of the incidence peak, with a positive linear (sublinear) correlation between \(R_{0}\) and the incidence peak (total infections). If \(R_{0}\) increase from 2.4 to 3.2, the accumulative number of human infections (including subclinical and clinical cases) increases from 1.26 to 1.38 billion during 400 days. Sensitivity analysis indicates that the most sensitive parameter governing \(R_{0}\) is the transmission rate \(\lambda \), followed by the percentage of clinical infections (\(\phi \)), time span from preclinical to clinical infection (\(1/\delta \)) and the relative infectivity of clinical infection (\(\beta \)).

6 Discussion

The COVID-19 pandemic is posing increasing threats to public health around the world. Clear information about its epidemiologic features and transmission patterns can help to control and prevent COVID-19 transmission. The present study is an attempt to provide a modeling framework allowed for inferring its spatiotemporal transmission patterns by focusing on its outbreak in the provinces of China.

Since the outbreak of COVID-19, many epidemiological models have been proposed and applied to study its propagation. Focusing on the spatiotemporal transmission, modeling framework includes mathematical model (e.g., ordinary/partial differential equation [9,10,11,12, 16, 17, 20], difference equations [13]), computational model (e.g., agent-based model [18] and next-generation algorithm [19]), and statistical model (e.g., stochastic model [14] and ArcGIS [21]). Inspired by existing studies, this paper presented a new mathematical model via ODEs, which couples the intrinsic transmission dynamics, including the disease evolution in humans among different states (susceptible, exposed, infectious and recovered), infection action by human–human contact, and human mobility among different regions. Moreover, the effects of human behavior and control strategy were characterized by model parameters, which can regulate the spatiotemporal infectivity and transmissibility. Finally, MCMC algorithm was employed to estimate the uncertain parameters and then to evaluate the model. Here the compartmental deterministic principle used in this model is similar to those in literature [9,10,11,12,13,14, 20], and the spatial transmission route connecting by human mobility is consistent with epidemiological survey and related models [15, 20, 28, 29]. Moreover, the model covers more transmission details, including preclinical, subclinical, and clinical infection [17, 30], and can be validated by fitting multiple spatiotemporal data with fewer uncertain parameters. It captures the time-varying infectivity by incorporating the estimated values of the time series of the effective reproduction number, instead of formulating it by a time function. The approach technique has reference significance in the development of disease modeling.

By validating the proposed model with surveillance data in Chinese provinces, the spatiotemporal transmission dynamics and the effects of human mobility and interventions were clarified, which offers the following clues for guiding COVID-19 control.

First, there is a unique epidemic threshold, denoted by basic reproduction number \(R_{0}\), which can totally determine whether COVID-19 proceeds among multiple regions. If \(R_{0}<1\), no matter how many infection sources there are, COVID-19 will always die out. Otherwise, the disease will persist in each region. \(R_{0}\) can unite infectivity in each region by human mobility. Such mobility contributes to transmission in two ways: susceptible persons in other regions could be infected when traveling to outbreak area, and infected persons may bring COVID-19 virus from outbreak area to other regions. Particularly, when \(R_{0}>1\), no region can escape from infection if there exists human mobility among them. This \(R_{0}\) is most sensitive to transmission rate \(\lambda \), followed by the percentage of clinical infections. Hence reducing \(\lambda \) is most effective to lessen \(R_{0}\).

Second, the effects of the implemented intervention in China are further evaluated. By using the proposed model to simulate the long-term transmission process, it is found that if the interventions (e.g., social distancing and city lockdown) had not been implemented in China, COVID-19 would prevail all around China and the serious infection would last over three months, resulting in over 1.1 billion clinical patients and 0.2 billion subclinical patients. In this case, more than 92.3% population in China would be infected clinically/subclinically by COVID-19 virus. The estimated effects of interventions are much more significant than previous results, which claimed that (1) if without non-pharmaceutical interventions in China, the number of cases was predicted to be 7.6 million by February 29, 2020 [16], or 37 million by March 5, 2020 [31], or increase the total infections by 93.7% [32]. The reason for the severity of our estimation could be that this study highlights the intrinsic spatiotemporal transmission dynamics and the total infection process.

Third, the role of human mobility in COVID-19 transmission is further clarified. Similarly to previous studies [13, 21, 32], it is verified that human mobility (by travel) can spark new infections in virgin areas and high frequency of human mobility in reality has driven COVID-19 diffusion across the 31 provinces of China. The present paper further indicates that the effects of human mobility in the spatiotemporal transmission of COVID-19 are more prominent in two cases: early stage of infection and when \(R_{0}\) is a little bigger than one. If without intervention inside region, then human mobility would accelerate disease propagation across different regions, but it could not modify the number of total infections, unless travel is banned at the very beginning of infection. Hence, regional human migration plays as a trigger in the preliminary stage of infection, and then, locally contracted infection dominates the following transmission process. The results demonstrate that non-pharmaceutical intervention is the core strategy, and travel ban at the same time can slow down the process and suppress incidence rate.

Fourth, the transmission patterns of COVID-19 in the whole country are further inferred. The initial infection located in central and east of China (HeN, ZJ, SH, JS and AH) would easily stimulate quick outbreak and large infection, but adverse consequence is observed if initial infection is located in west and northeast of China (XJ, HLJ, QH, XZ, GS, NMG, and YN), in that there exists less population flow. Yet if without any intervention, the transmission would continue three months, and then, no matter where the outbreak occurs and how many sits do initial infection locate, the infections of COVID-19 would reach a saturation level, and more than 92.3% people in China would be infected. After that the incidence would keep at very low rate due to herd immunity. Yet as the increase of susceptible people, another modest wave of infection could occur after about 400 days.

In view of current situation of COVID-19 pandemic, China is facing high risk of sporadic outbreaks due to imported infections and is making great efforts for prevention. To control this disease, beside promoting vaccination (that is precisely what China is doing), the present study suggests that (1) identifying and isolating imported case is the primary mission, which can be accomplished by monitoring the travelers from foreign countries by tight and thorough surveillance system, and (2) in case of autochthonous infection, strict non-pharmaceutical interventions must be taken as soon as possible, including tracking close contacts and quarantine, travel restriction, lockdown of high risky community. Indeed, such intervention strategies are exactly as China is implementing. By doing so, more than 99.99% human infections would have been avoided according to this study.

Here several limitations need to be clarified. (1) The COVID-19 incidence data were based on public report information, which may yield data deviation from reality. (2) The biological parameters applied in the proposed model were extracted from the literature, which may show geographical disparities. (3) The model did not take into account the potential factors such as the difference of immunity and infectivity. Nevertheless, the model captured the dynamic evolution of disease in time and place and incorporated the biologically intuitive parameterizations. It matches well with spatiotemporal data by fitting several parameters, lending confidence to the analysis and justifying the model’s further generalization.

In summary, this paper develops an inference technique for identifying the transmission patterns of COVID-19, and it is applied to explore its diffusion process in the provinces of China. The proposed model takes into account the essential effects of human mobility and disease evolution, which allow to capture the hidden spatiotemporal dynamics and internal mechanism of COVID-19 transmission. The obtained results support the interventions that are being implemented in China.

Designated parameters The bold capital letters denote \(n\times 1\)-dimensional column vectors. The letters with superscript as star are the expressions of the unique endemic equilibrium in the model. Number 0 and letter O separately represent a \(n\times 1\) column vector and a \(n\times n\) matrix, each element of which is zero. The Chinese provinces and their abbreviations are shown in Table 2.