Age-group-targeted testing for COVID-19 as a new prevention strategy

Abstract

Robust testing and tracing are key to fighting the menace of coronavirus disease 2019 (COVID-19). This outbreak has progressed with tremendous impact on human life, society and economy. In this paper, we propose an age-structured SIQR model to track the progression of the pandemic in India, Italy and USA, taking into account the different age structures of these countries. We have made predictions about the disease dynamics, identified the most infected age groups and analysed the effectiveness of social distancing measures taken in the early stages of infection. The basic reproductive ratio ${\mathfrak {R}}_0$ has been numerically calculated for each country. We propose a strategy of age-targeted testing, with increased testing in the most proportionally infected age groups. We observe a marked flattening of the infection curve upon simulating increased testing in the 15–40 year age groups in India. Thus, we conclude that social distancing and widespread testing are effective methods of control, with emphasis on testing and identifying the hot spots of highly infected populations. It has also been suggested that a complete lockdown, followed by lockdowns in selected regions, is more effective than the reverse.

1 Introduction

COVID-19, a respiratory disease caused by a new strain of coronavirus (SARS-CoV-2), has spread to almost every part of the world, since first reported in 31 December 2019 [1]. WHO declared this outbreak a ‘Public Health Emergency of International Concern’ on 30 January 2020. As of 30 April 2020, it has caused 2,33,824 deaths with 33,03,544 confirmed cases of infection. Till date, USA has the largest number of fatalities, followed by Italy. USA reports 1,095,023 cases, with 3226 cases per million people, though the statistics have still been evolving due to the large variability in testing performed by different countries as of now [2].

In the absence of any vaccine to prevent and contain the spread of novel coronavirus disease, COVID-19, as well as the lack of an established treatment regimen to cure this disease (beyond mitigation of symptoms), effective non-pharmaceutical interventions are needed to contain the epidemic and minimize morbidity and mortality associated with this respiratory disease. As the COVID-19 pandemic has swept across the globe, now affecting almost all countries, measures for mitigation have been put in place that include strict lockdown to less restrictive people movement but all aiming to achieve social distancing of different degrees to balance the socio-economic impacts of the lockdown and the disease. Robust testing and tracing are key to containing the pandemic and effectively ‘flattening’ the infection curve, both by distributing cases over a longer period of time and by reducing the total number of cases, and thus lowering the epidemic peak. Governments and health agencies have banked on mathematical models to guide towards the goal of optimizing available resources to attain maximal benefits of mitigation measures. Mathematical models are often based on certain assumptions; however, these are continually improved upon through adjustments guided by emerging data, and eventually, these models become more reliable in helping navigate through such situations. Here, we leverage the emerging information from COVID-19 in different countries, mainly USA, Italy and India, to develop a COVID-19 specific model that can inform on effective interventions for coronavirus containment. As people of different age groups have responded differently to coronavirus, we utilized the age-stratified data of COVID-19 to develop a system that can inform on more effective prevention strategies. We particularly focused on India where COVID-19 seems to have not peaked yet despite the most restrictive lockdown imposed for over a month now. Our model recommends that testing and tracing be ramped up in the 15–40-year age-group population in India in order to flatten the infection curve in shortest time possible in the current situation. We further demonstrate this by computing the basic reproductive ratio ${\mathfrak {R}}_0$ at different times and following an age-group-targeted intervention.

The novel coronavirus is thought to have originated in bats and eventually infected humans, due to the similarity in the genome sequence of SARS-CoV-2 to that of a bat coronavirus [3]. Human-to-human transmission has also been established. So far, we observe different transmission and fatality rates in different countries. One of the main reasons for this is differing age groups and social contact structures. In order to study this effect, we use social contact matrices, which show contact patterns of an age group with others and are used to parametrize mathematical methods to understand the transmission patterns. Schenzle [4] used an age-structured SEIR model with 21 age groups to study the spread of measles, a disease which mostly affects children. This method has previously been applied to respiratory diseases like influenza [5], pertussis [6] and varicella [7]. Given that COVID-19 transmission patterns are very similar to those of respiratory diseases caused by other viruses, we can get valuable information by studying COVID-19 disease dynamics through an age-structured model.

It has been observed that social distancing, isolating infected populations and quarantine are effective ways of containing the epidemic. After receiving the best available medical intervention to date, a quarter of critically ill patients still die, signifying that the host response to the virus is an important factor [8]. Thus, the government and hospitals need to procure supportive care equipment in sufficient amounts. Initiating the process of flattening the curve by these above-mentioned methods provides the time to prepare for supportive care. With social distancing becoming a preventive strategy, many countries have announced partial or complete lockdowns. Numerous companies are also advising their employees to ‘work from home’. Due to this, patterns of mixing between people change, the effects of which are hard to represent with classical compartmental disease models. However, it is essential to understand these changing contact patterns in order to more accurately model the disease dynamics. Considering the differential impacts of an infectious disease on people in different age groups, perhaps due to a number of reasons including physiology, immunity, mobility, and social contact and behaviour, an infectious disease model must consider differential age-group disease dynamics. Recently, some new approaches about age structure population models have been proposed in [9, 10]. Age-structured models offer better approximations of reality and also give health organizations better tools to develop age-group-targeted control strategies.

Here, we have simulated the spread of novel coronavirus using such an age-structured SIQR model. We have fitted our model to the current situations in Italy and USA and have estimated age-wise mortality rates. Side by side, we compared this with the scenario in India. We have also analysed the success of lockdown measures adopted by these countries qualitatively and have projected the effects of further lockdowns. We examine whether starting off with a complete lockdown which is then gradually lifted in specific areas is more effective than the reverse, i.e. declaration of lockdown regionally followed by a nationwide lockdown. Finally, we have proposed a novel method of age-group-targeted testing to tackle the situation and have also showed how it can help in flattening the curve effectively.

This manuscript is organized as follows. In Sect. 2, we formulate the mathematical framework of an SIQR epidemic model. In Sect. 3, we analyse the predictions made by a numerical simulation of our model. In Sect. 4, we propose control strategies and their intended impacts. Finally, in Sect. 5, we discuss the conclusions. The basic reproductive ratio ${\mathfrak {R}}_0$ is calculated in “Appendix A”, and various parameters used in our numerical simulation are tabulated in “Appendix B”.

2 The proposed model system

The mathematical framework of an age-structured SIQR epidemiological model is formulated. In order to construct the model, our assumptions are stated as follows:

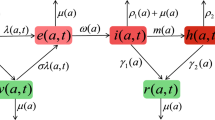
• 1. The entire population, N, is divided into four compartments: susceptible population, S (which are under risk of contracting the infection), infected population, I (which consists of infectious, both symptomatic and asymptomatic, or untested individuals), quarantined population, Q (which are removed from all contacts within the entire population and are hence not infectious) and recovered class, R (which are recovered from infection). Therefore, we have $N=S+I+Q+R$. In order to keep track of disease-induced death, we assign an additional compartment of fatalities, F.

• 2. Each population of SIQR and F is further subdivided into M age classes. Individuals within the same compartment interact with other individuals proportional to a coefficient of interaction $C_{ij}$, which specifies the average contact between age classes i and j, with $0 < i, j \le M$.

• 3. There is no recruitment of the susceptible population and no natural death in any compartment. There is also no aging of individuals.

• 4. The disease is transmitted from the infected to the susceptible population with age class i, i.e. compartment $S_i$, at a rate $\beta \lambda _i$. Here, $\beta$ is the transmission probability, and $\lambda _i$ is the weighted coefficient of contact of age class i with the entire infected population.

  $$\begin{aligned}&\lambda _{i} \;=\; \sum _{j=1}^M \left[ C_{ij} \frac{I_j}{S_j +I_j+R_j}\right] \end{aligned}$$

• 5. Individuals from compartment $S_i$ move into compartment $I_i$ and become infective immediately.

• 6. Individuals from compartment $I_i$ move into compartment $Q_i$ at a rate $\delta _i$ and are no longer infectious.

• 7. The infected and quarantined populations, $I_i$ and $Q_i$, recover and move into the recovered population, $R_i$, at rates $\epsilon$ and $\gamma$, respectively.

• 8. The populations $I_i$ and $Q_i$ suffer disease-induced death, at a common rate of $\mu _i$.

Fig. 1

Schematic diagram of the interacting population within a certain age class, for the model (1)

A schematic diagram of the interacting population is presented in Fig. 1. Thus, the transmission process is formulated by the following system of differential equations:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}S_i}{\mathrm{d}t} \;&=\;-\beta \lambda _i S_i,\\ \frac{\mathrm{d}I_i}{\mathrm{d}t} \;&=\; \beta \lambda _i S_i \,-\, (\delta _i\,+\,\epsilon \,+\,\mu _i)I_i,\\ \frac{\mathrm{d}Q_i}{\mathrm{d}t} \;&=\; \delta _i I_i \,-\, (\gamma \,+\,\mu _i)Q_i, \\ \frac{\mathrm{d}R_i}{\mathrm{d}t} \;&=\; \epsilon I_i \,+\, \gamma Q_i,\\ \frac{\mathrm{d}F_i}{\mathrm{d}t} \;&=\; \mu _i(I_i \,+\, Q_i). \end{aligned} \end{aligned}$$

(1)

The initial conditions are $S_i(0)>0, ~I_i(0)> 0, ~ Q_i(0)> 0, ~R_i(0)=0, ~F_i(0)=0$. All the parameters in the system are positive quantities.

We break down the age-structured social contact matrix, $C = [C_{ij}]_{M\times M}$, into the contributions from households, workplaces, schools (all educational institutions) and other areas (market places, restaurants, cinema halls, shopping malls, etc.), represented by $C_H$, $C_W$, $C_S$ and $C_O$, respectively. Each of these is weighted with coefficients $\alpha _H$, $\alpha _W$, $\alpha _S$ and $\alpha _O$, which we change over time to reflect the effect of lockdown on social contact.

$$\begin{aligned} C \;&=\; \alpha _{H} C_{H} \,+\, \alpha _{W} C_{W} \,+\, \alpha _{S} C_{S} \,+\, \alpha _{O} C_{O}. \end{aligned}$$

For example, during the time period when all educational institutes are closed, we set $\alpha _S = 0$. We note that when Italy and USA announced partial lockdowns, the coefficients $\alpha$ have been fitted to the existing data. It must also be noted that even during a complete lockdown, the contributions to the contact matrix from work and other areas are never zero, as people involved in essential services continue work and marketplaces must operate to some degree. Lockdowns also induce an increase in household contact, as people are staying at home more [11]. For numerical simulation, we have collected data on the times and nature of lockdown imposed, starting from the closure of schools and universities to complete lockdowns [12,13,14]. A complete lockdown in India was declared on 25 March 2020. USA declared a national emergency on 13 March 2020, followed by various statewise guidelines and orders to ‘stay at home’. Italy had also proceeded towards lockdown step by step, with a lockdown of the northern provinces on 8 March 2020 and a nationwide lockdown from 10 March 2020 onwards.

The parameters $\delta _i$, $\gamma$ and $\epsilon$ have been assumed, using known rates of infection, recovery and the first appearance of symptoms. We assume the onset of symptoms, detection and isolation in 5.2 days on average [15] for infected individuals. We also assume that an individual stays quarantined for 14 days, which is the average recovery period for a symptomatic individual [16]. In addition, we assume that unidentified infected individuals, either asymptomatic or untested, can proceed straight to recovery after 15 days of infection on average. The parameters $\beta$ and $\mu _i$ have been fitted to existing case and fatality data. The values of $\beta$ for India, USA and Italy are 0.024, 0.034 and 0.041, respectively. The values of the remaining parameters are listed in “Appendix B” (Tables 2, 4). It must be noted that we choose to interpret currently reported cases to belong in the quarantined compartment, Q, which is a subset of the total infected population. We have also chosen our initial conditions such that $I_i(0) = Q_i(0)$, on the assumption that cases are underreported where exactly half of all infected individuals are identified (quarantined).

For India and Italy, we use $M = 16$ age classes, equally dividing the range of ages 0–80 years. Due to unavailability of data, we use $M = 15$ age classes for the USA, over a range 0–75 years. For each country, we have set up 5M differential equations, which we have integrated using the python module ‘numpy’. We have collected COVID-19 case and mortality data up to 30 April 2020 for each country from Worldometers [2]. We have also collected age-structure data from PopulationPyramid [17] and social contact data from Prem et al. [18]. The age classes and initial susceptible population data are presented in Table 3.

3 Simulation analysis

The infection curves predicted by our model are shown in Fig. 2. We note that our model predicts a fairly symmetric infection curve, whose peak trails behind the peak of the quarantined population. USA and India continue an upward growth, while Italy’s infection curve has begun to drop. If current conditions continue without any new measures being taken, active cases are predicted to reach peak within 3 months for USA and around 5 months for India. We also predict that everything will be normal in 6 months for Italy, without considering the effect of herd immunity. On the other hand, it may take a year at worst for India and USA to fully recover. By ‘normal’, we mean that the number of infected individuals has dropped below one thousand, which represents a sufficiently small number of cases relative to the populations of the countries in consideration to be fully identified and isolated.

Fig. 2

Predicted variation in infected and quarantined populations in a India, b USA and c Italy. The vertical green line marks the date 1 May 2020. (Color figure online)

We observe a common trend in infected age groups across all three countries, in that the young- and middle-aged groups (between 10 and 40 years of age) have the largest numbers of infected people, relative to the initial susceptible population size of that age group. We estimate this by measuring the drop in $S_i$ from its initial value $S_{i, 0}$ and compare the values $(S_{i, 0} - S_i) / S_{i, 0}$ across all age groups i over time, as shown in Fig. 3. This may be explained by larger contact coefficients $\alpha$ among themselves and other age groups. The population within this age group is also highly mobile, in each country. On the other hand, data suggest that infection is less common in children [19]. Dr. Calum Semple, Professor at Liverpool University, stated that ‘We know that lung development doesn’t finish until teenage years. ACE2 is highly regulated in lung development. Because of that the “lock” might be expressed differently in kids’ lungs’ [20]. Hence, we have identified the 15–20-year-old age group to be the most infected age group across all three countries (Fig. 3). In our proposed control strategy, we thus place less emphasis on individuals younger than 15 years.

Fig. 3

Relative decrease in susceptible populations by age group in a India, b USA and c Italy

Fig. 4

Simulation data fitted to case data in a India, b USA and c Italy. Fatalities are shown in d India, e USA and f Italy. Note that the ‘infected’, ‘quarantined’, ‘total infected’ and ‘dead’ curves are simulated, while the ‘actual cases’ and ‘actual deaths’ datapoints have been obtained from Worldometers [2]

Considering different mortality rates across different age groups has very little effect on the total infection and mortality curves, both qualitatively and quantitatively. We note that Italy’s mortality curve in Fig. 4f has begun to flatten, far quicker than our model would suggest. We may explain this by noting that the reported mortality rates, which we used to fit our model, are likely inaccurate due to factors such as sampling bias and the changing capability of health care system. With time, as Italy continues to improve medical facilities and mobilize doctors and nurses, patients receive better care and facilities are no longer swamped as they were in the early stages of the pandemic. We also note that with time, the mechanisms by which COVID-19 causes death might be better understood by scientists and practitioners, so the observed lower mortality rate may also be explained by better, more effective treatment and the identification of drugs which improve survival chances. Presently, the overall mortality rate is the highest in Italy, followed by India and the USA (Fig. 4). Interpreting these mortality rates is complicated by the fact that pre-existing medical conditions play a major role and are somewhat correlated with age. Fatality rates may also be inflated by limited testing and the resulting selection bias in which asymptomatic individuals are not accounted for. In addition, the fact that our model omits 75–80-year age group in the USA, despite a high expected mortality rate in that group, may explain why our model predicts a lower mortality rate in USA, compared to India and Italy.

The basic reproductive ratio ${\mathfrak {R}}_0$ can be interpreted as the expected number of cases directly caused by a single infected individual in a completely susceptible population. When ${\mathfrak {R}}_0> 1$, the infection spreads in the population, and it does so more rapidly with higher ${\mathfrak {R}}_0$. When ${\mathfrak {R}}_0< 1$, the infection eventually dies out, and the system proceeds towards the disease-free equilibrium. We have calculated ${\mathfrak {R}}_0$ for the three countries, as presented in Table 1. A lower ${\mathfrak {R}}_0$ value for India initially indicates a comparatively slower spread of disease than in USA and Italy. Figure 6 illustrates the decrease in ${\mathfrak {R}}_0$ with the implementation of social distancing measures. The drop in ${\mathfrak {R}}_0$ is significant in all cases, although only Italy shows ${\mathfrak {R}}_0< 1$, which is enough for the disease to die out.

Concerningly, our model shows very little impact of the lockdown in India, compared to the projections without one. After fitting our model to case numbers before the implementation of social distancing measures, our model predicts that complete stop of contact between people outside their home, or even a 50% reduction in such contact, is not consistent with subsequent reported cases. The three different countries show different degrees of reduction in contact, in terms of different control coefficients $\alpha$. This effective reduction in contact in India seems to be far less than in USA, which in turn is less than in Italy. In the case of Italy, data look promising, suggesting that the implementation of lockdown was more successful.

4 New strategies and their impact

The effectiveness of control strategies can be measured by the basic reproductive ratio ${\mathfrak {R}}_0$. The parameters which can practically reduce ${\mathfrak {R}}_0$ are the contact coefficients, $\alpha$ and the rate of quarantine of infected individuals, $\delta _i$. Social distancing works well at reducing interpersonal contact, but we can see that implementation issues can severely damage its effectiveness. By sufficiently increasing the number of tests carried out, we can identify and quarantine infected individuals more quickly, thus indirectly increasing $\delta _i$. This means that infected individuals would have a lower probability of infecting a susceptible individual. On the other hand, testing rates are limited by the medical resources of each country. While South Korea has managed to test a large fraction of their population, in countries with very large populations such as India, randomized testing for the entire population is not feasible. Hence, we suggest an age-group-targeted testing initiative, where the age groups with the largest number of infected individuals are targeted. In addition, economic activities have come to a halt during lockdown in India. Barclays has estimated a loss of up to 234.4 billion USD in India [21]. Practically, it may not be possible to continue a complete lockdown indefinitely. Only a multipronged approach can successfully combat an outbreak of infectious disease. Though we have not provided any medical insights, they should go hand in hand with the strategies we propose here.

Fig. 5

The effect of targeted testing on the infected and quarantined populations in India, shown by the dashed curves. The vertical green line marks the date 1 May 2020. (Color figure online)

We discuss two strategies below.

• 1. Keeping in mind that individuals in the age group 15–40 years are most likely to catch infection, we emphasize testing more people from this age group rather than randomized testing. This will help in isolating infected people and restrict their disease transmission.

  The impact of such a strategy is evident from the curves in Fig. 5. The corresponding change in ${\mathfrak {R}}_0$ is illustrated in Fig. 6b. We see that although ${\mathfrak {R}}_0$ has not dropped below 1, our strategy offers a significant improvement.

  For this simulation, we have increased the value of $\delta _i$ for the targeted age group 15–40 years, which corresponds to $i \in \{4, 5, 6, 7, 8\}$ (Table 2). The initial population sizes of these age groups are shown in Table 3. We have assumed that infected members of these groups can proceed to quarantine in 4.8 days, on average. For the remaining groups, we increase the detection period to 5.4 days. Concentrating testing on groups most likely to have infected members helps bring them out of contact with the susceptible population and hence flatten the infection curves. This in turn lowers the peak number of critical cases, thus distributing the workload of medical facilities over a longer period of time. The peak is also observed far later than with normal rates of testing, although normalcy is restored not much later.

• 2. We suggest that a complete lockdown, followed by lockdowns in selected regions, is more effective than the reverse. As symptoms take time to manifest, infection can spread very rapidly to areas not under sufficient lockdown. However, if the majority of infected individuals can by identified and isolated by testing during the lockdown period, subsequent lockdowns can target those areas with larger infected populations. This would effectively reduce disease transmission across a country. We suggest that introducing a lockdown in slow phases, as was done in Italy and USA, may not have been as effective as a complete lockdown introduced in the early stages of the pandemic. However, we do acknowledge differences in the socio-economic structures and dynamics of different countries, which demand differential strategies tailored individually to their underlying structures. Our model is ill equipped to model lockdowns in selected regions, but we have approximated this effect with reduced contact coefficients $\alpha$.

5 Discussions and conclusions

Our model of COVID-19 dynamics allows us to make some useful predictions and modify pre-existing strategies to obtain better results. This model has been tuned with available data of social contact matrices and reported deaths and infected individuals available till 30 April 2020. Methods of testing and social distancing are known to tackle this kind of situation. In the context of this novel disease, we have re-examined these methods. It must be noted that in our model, we have interpreted the number of reported cases as the number of symptomatic or tested cases, and we assume that they are transferred to quarantine as soon as they are confirmed positive. The actual number of COVID-19 cases is much higher than reported, which is consistent with the nature of the reported infection curve.

We must note that as of 27 April 2020, India has conducted 5,00,000 tests. This is a major step up from the initial 15,000 tests before the declaration of lockdown. At this milestone of tests, India has recorded around 28,000 positive cases, as opposed to USA’s 1,20,000 and Italy’s 80,000 cases [22]. India has also observed a comparatively lower mortality rate. This can be explained by her disproportionately young population, together with the low rate of infection and transmission in the younger age groups. The mean age of India’s population is 26.8, compared to USA’s 38.2 and Italy’s 45.4 [23].

We acknowledge that there are uncertainties in determining the model parameters due to unavailability of proper data and that this may lead to incorrect predictions. We note that the use of mortality data is partially motivated by the fact that such figures are more likely to be reliable, as opposed to infection numbers which suffer from under-reporting. The choice of a single transmission coefficient $\beta$ across all age groups is because of the lack of age-group-specific estimates on transmission probabilities, as well as the complexity of fitting such coefficients for each of the 16 age groups even if available. Similarly, disease-induced mortality rates across the infected (both symptomatic and asymptomatic) and quarantined populations have been assumed to be the same, $\mu$. While these rates may indeed differ among these groups in reality since severe cases are frequently quarantined, we justify this assumption with our simulation which closely mimics the trends in available data without introducing additional parameters. Furthermore, we emphasize, again because of these reasons, that factors such as age-dependent immunity have not been incorporated into our model, and the coefficients $\lambda _i$ merely reflect normalized amounts of contact between age classes. Our initial conditions $I_i(0) = Q_i(0)$, which reflect the assumption that half of the cases are reported, may be adjusted with better estimates of the fraction of reported cases. The assumption that births, natural deaths and aging are absent is valid only over relatively short periods of time. We have also focused on the population below 80 years of age, as the rest of the population is significantly small. With these assumptions, we can clearly say that our model can make short-term predictions, but cannot reliably make long-term forecasts. In this instance, we have run our simulation for a maximum time period of 10 months. We also acknowledge that partial lockdowns of infection hot spots are not well modelled by our method, which considers a given region as a whole. With the availability of reliable data, we may be able to apply our model on smaller populations and make region-wise predictions. We also postpone the application of targeted testing to other countries, such as USA and Italy, for further study.

Through this study, we have offered a more efficient, country-specific COVID-19 model for informing on strategies to contain the SARS-CoV-2 pandemic. Our contribution of a new age-stratified model will aid government and health agencies and will spur further research in COVD-19 modelling. The implications of our proposed work are timely as this is still an emerging situation in many countries and perhaps broad as well, as viral pandemics are predicted to keep re-emerging in the near future, perhaps in different shades or shapes. Keeping in mind that all models are merely approximations of reality, we hope that this model can aid in developing policy, with economic and medical perspectives.

Appendices

Calculation of ${\mathfrak {R}}_0$

Here, we find the basic reproduction number using the next-generation method [24]. We first linearize the system of equations (1) at disease-free equilibrium, where $I_i = Q_i = R_i = F_i = 0$. Hence, when the infected and quarantined populations are small, their dynamics are described by the following system.

Fig. 6

The variation of the basic reproductive number ${\mathfrak {R}}_0$ with time in a India, b India, with the effect of targeted testing in blue, c USA and d Italy. (Color figure online)

$$\begin{aligned} \begin{aligned} \dot{I_i} \;&=\; \sum _{j = 1}^M \left[ \beta C_{ij} \frac{N_i}{N_j} I_j\right] \,-\, (\delta _i + \epsilon + \mu _i)I_i, \\ \dot{Q_i} \;&=\; \delta _i I_i \,-\, (\gamma + \mu _i) Q_i. \end{aligned} \end{aligned}$$

(2)

We collect the infected and quarantined compartments in the vector $\mathbf {v} \;=\; (I_1 \cdots I_M \; Q_1 \cdots Q_M)^T$. We can thus rewrite the system (2) in the form $\frac{d}{dt}\mathbf {v} \;=\; L\mathbf {v}$, where L is the $2M\times 2M$ matrix described as follows:

$$\begin{aligned} \begin{aligned} L \;&=\; \begin{pmatrix}L^{II} &{} L^{IQ} \\ L^{QI} &{} L^{QQ}\end{pmatrix}, \\ L^{II}_{ij} \;&=\; {\left\{ \begin{array}{ll} \beta C_{ij} \frac{N_i}{N_j} \,-\, (\delta _i + \epsilon + \mu _i), &{}\quad i = j \\ \beta C_{ij} \frac{N_i}{N_j}, &{}\quad i \ne j \end{array}\right. } \\ L^{IQ}_{ij} \;&=\; 0, \\ L^{QI}_{ij} \;&=\; {\left\{ \begin{array}{ll} \delta _i, &{}\quad \quad \quad \quad \;\; i = j\\ 0, &{}\quad \quad \quad \quad \;\; i \ne j\\ \end{array}\right. } \\ L^{QQ}_{ij} \;&=\; {\left\{ \begin{array}{ll} -(\gamma + \mu _i), &{}\quad i = j\\ 0. &{}\quad i \ne j\\ \end{array}\right. } \end{aligned}\nonumber \\ \end{aligned}$$

(3)

We further break $L \;=\; T - V$, where the transmission matrix, T, represents the influx of newly infected individuals, and the transition matrix, V, represents the movement between the infected compartments. They are calculated numerically as follows:

$$\begin{aligned} \begin{aligned} T&= \begin{pmatrix}T^{II} &{} T^{IQ} \\ T^{QI} &{} T^{QQ}\end{pmatrix}, \\ T^{II}_{ij}&= \beta C_{ij}\frac{N_i}{N_j}\\ T^{IQ}_{ij}&= T^{QI}_{ij} \;=\; T^{QQ}_{ij} \;=\; 0, \\ V&= T \,-\, L. \end{aligned} \end{aligned}$$

(4)

The basic reproductive number ${\mathfrak {R}}_0= \rho (TV^{-1})$ is simply calculated as the spectral radius of the matrix $TV^{-1}$ (Table 1, Fig. 6).

Table 1 The basic reproductive number ${\mathfrak {R}}_0$

List of parameters

Here, we list the parameters used in our numerical simulation (Tables 2, 3 and 4).

Table 2 Parameters and their values

Table 3 The initial susceptible population sizes by age class i

Table 4 The mortality rates $\mu _i$